Identifying Time Measurement Tampering in the Traversal Time and Hop Count Analysis (TTHCA) Wormhole Detection Algorithm
Abstract
: Traversal time and hop count analysis (TTHCA) is a recent wormhole detection algorithm for mobile ad hoc networks (MANET) which provides enhanced detection performance against all wormhole attack variants and network types. TTHCA involves each node measuring the processing time of routing packets during the route discovery process and then delivering the measurements to the source node. In a participation mode (PM) wormhole where malicious nodes appear in the routing tables as legitimate nodes, the time measurements can potentially be altered so preventing TTHCA from successfully detecting the wormhole. This paper analyses the prevailing conditions for time tampering attacks to succeed for PM wormholes, before introducing an extension to the TTHCA detection algorithm called ΔT Vector which is designed to identify time tampering, while preserving low false positive rates. Simulation results confirm that the ΔT Vector extension is able to effectively detect time tampering attacks, thereby providing an important security enhancement to the TTHCA algorithm.1. Introduction
A Mobile ad hoc Network (MANET) is a self-configuring arrangement of wireless nodes which can communicate with each other without requiring core infrastructure such as routers and base stations. They can be deployed in a range of application domains including military communications, vehicular and sensor networks, and as an access mechanism to the Internet in scenarios where nodes are out-of-radio range, such as in underground transport systems.
The open nature and absence of dedicated routers mean that MANETs are especially vulnerable to routing attacks [1,2] which can lead to severe disruption of network communications. The wormhole attack [3] is one of the most serious MANET routing threats since it is relatively easy to launch, difficult to detect and can yet cause significant communications disruption. A wormhole creates a fictive shortcut link in the network with the intention to attract data packets to traverse specific nodes. It involves two collaborating malicious nodes forwarding routing packets to each other. When a malicious node captures a routing packet, it is encapsulated within a new packet and tunnelled to the other wormhole node, which then extracts the routing packet before relaying it to its neighbours. As a consequence, malicious nodes can appear as neighbours despite being located several hops from each other.
Wormhole attacks can be launched in two ways: hidden mode (HM) and participation mode (PM) [4]. The former captures and forwards routing packets to each other without modifying the actual packets, so the wormhole nodes never appear in routing tables. In contrast, PM nodes process routing packets as any pair of legitimate nodes and thus appear in a wormhole infected route as two contiguous nodes.
Wormhole nodes can forward routing packets to each other using either an in-band (I-B) or out-of-band (O-B) communication link. I-B tunnels packets between the malicious nodes via genuine network nodes so it is easy to launch, while the O-B link is more complex because it requires an external communication channel, i.e., network cable or directional antenna, to establish a direct link between the wormhole nodes.
Designing effective and robust wormhole detection schemes means considering all four modes with each mandating different requirements upon the detection mechanism. Various detection strategies have been proposed and these can be broadly classified into: (i) neighbour validation and (ii) end-to-end techniques.
Neighbour validation schemes like packet leashes [3] and [5] are only effective for HM wormhole attacks because they rely on every node checking the validity of its neighbours and since PM wormhole nodes appear as legitimate neighbours in a route, they can avoid being detected by simply ignoring the validity check. Other schemes like statistical wormhole apprehension using neighbours (SWAN) [6] identify a wormhole by the number of neighbours, though this is only effective for HM wormholes since PM wormholes do not increase the number of neighbours for a legitimate node.
In contrast, end-to-end detection techniques measure and analyse node activity and route features such as the geographical positions of nodes [7–11], the frequency of node appearances in routes [9–11], hop count (HC) information [12] or round trip time (RTT) of routing packets [13–16]. Such techniques are typically used to detect PM wormholes, but have a number of recurring limitations including, the inability to detect all wormhole variants, the requirement of dedicated hardware, reliance on certain MANET environments, and high computational overheads and/or bandwidth loads upon the network.
The traversal time and hop count analysis (TTHCA) algorithm is a new wormhole detection technique [17] designed as a security extension to the ad hoc on demand distance vector (AODV) [18] routing protocol. It combines the benefits of RTT-based approaches with HC analysis, to provide improved detection for all wormhole types, under a variety of network scenarios. RTT-based wormhole detection schemes, such as wormhole attack prevention (WAP) [13], transmission time-based mechanism (TTM) [15] and delay per hop indication (DelPHI) [14], offer low overhead solutions in terms of hardware, computation and throughput, but have the limitation that variations in a node's packet processing time i.e., the sum of the queuing delay and service time must be small. In a real MANET, nodes can exhibit high packet processing time variations, a feature the neighbour probe acknowledge (NPA) method [16] addresses by employing the standard deviation of the RTT as an accurate metric. NPA has not however, been tested in large scale networks and is inherently computationally heavier than either TTHCA or other RTT-based techniques because it uses encryption and time-stamped digital signatures to guarantee the security of the routing packets. In TTHCA, packet traversal times (PTT) are measured instead of the RTT of a routing packet, as this more accurately reflects the distance between a source and destination node. The corollary is that TTHCA affords significantly superior wormhole detection and lower false positive (FP) performance than RTT-based solutions, while concomitantly affording low computational overheads.
A potential drawback of TTHCA is that under specific conditions, PM wormhole nodes can alter the time measurements and prevent the wormhole from being detected. In TTHCA, PTT is estimated by initially allowing each intermediate node to measure the packet processing time of the AODV route request (RREQ) and route reply (RREP) packets, before adding this measurement value ΔTi to a ΔTTOT parameter in the RREP packet. Upon receiving the RREP, the source node can calculate PTT by subtracting ΔTTOT from the RTT. A wormhole is suspected if the PTT is unrealistically high in relation to the HC. By falsely increasing ΔTTOT, a PM wormhole node can evade being detected because this results in a smaller PTT than is in fact, the case. Time tampering attacks are not relevant to HM wormholes because as mentioned above, they never process the routing packets.
This paper analyses the time tampering problem and investigates its impacts on TTHCA wormhole detection performance. A solution is presented to accurately identify time tampering in PM I-B wormholes by introducing a ΔT Vector extension into the TTHCA algorithm. The ΔT Vector replaces the ΔTTOT parameter in the RREP packet with a list of the individual ΔTi values from all intermediate nodes. A malicious node must thus produce a falsely inflated ΔTi in order to perform a successful time tampering attack. By using the ΔT Vector extension, a tampered ΔTi can be accurately identified by the source node as it typically is significantly higher than a healthy ΔTi.
The remainder of the paper is organized as follows: Section 2 presents a brief overview of the TTHCA algorithm before Section 3 investigates time tampering attacks and the specific conditions necessary for this security breach to ensue. The new ΔT Vector extension is then introduced in Section 4 and its performance analysed in Section 5 for diverse MANET scenarios. Finally, some concluding comments are provided in Section 6.
2. The Traversal Time and Hop Count Analysis (TTHCA) Algorithm
In TTHCA, a source node firstly measures the RTT of the AODV route discovery packets, which is the time between sending the RREQ packet and receiving the RREP packet. Each intermediate node measures the processing time of the RREQ and RREP packets (ΔTi) and this is added to the ΔTTOT parameter in the RREP packet. Hence, once a RREP packet is received by the source node:
A wormhole is then suspected if:
When a wormhole is suspected, all intermediate nodes on the route are added to a graylist [12] which is broadcasted throughout the MANET together with a new RREQ. All graylist nodes are then omitted during the next route discovery procedure resulting in a new unique route. Graylist broadcasting is repeated until a healthy route is found.
3. Time Tampering in TTHCA
The TTHCA wormhole detection algorithm is predicated on the assumption that a wormhole route will exhibit an unrealistically high PTT per HC. Wormhole nodes however, can potentially prevent TTHCA from detecting infected routes by adding a fictive packet processing time ΔTF to the ΔTTOT parameter of the RREP packet. It is important to stress that time tampering is not a modification attack per se as the PM wormhole node never alters any routing packet parameters, but instead produces false measurement information. This means schemes designed to prevent packet alteration by for example, encrypting all routing packet parameters, will be ineffectual against a TTHCA time tampering attack.
As a wormhole infected route has a high PTT/HC, the malicious nodes must artificially produce a lower PTT than in reality for that route to avoid detection and this can be accomplished by increasing ΔTTOT. Since ΔTTOT ≫ PTT and ΔTi may incur large fluctuations due to for example, variable network traffic loads, it is difficult for the wormhole nodes to be aware of exactly how to set ΔTF as it must be precisely defined within the narrow time window that exists to effectively achieve time measurement tampering. This window is bounded by:
So if the tampered ΔTF is too small, TTHCA is still able to detect the route as a wormhole because PTT/HC is higher than the threshold in Equation (3). Conversely, if ΔTF is made too high the resulting PTT at the source node will be negative.
Pragmatically it is not feasible for a malicious node to exactly know the time tampering window since it can only be aware of the values of R and S in Equation (4). Successful time tampering is still feasible however, if the malicious nodes (M1 and M2) can estimate the RTT of the wormhole link (RTTWH). In an I-B link, RTTWH can have high variations due to variable packet processing times at the nodes through which the wormhole is tunnelled, making the precise estimation of RTTWH challenging. One approach for estimating RTTWH for PM wormhole links is to use tightly synchronized clocks. During route discovery, wormhole node M1 adds exact time information as an adjunct parameter within the tunnelled packet as it forwards the RREQ to the other malicious node M2. Upon receiving this tunnelled RREQ, M2 estimates the precise propagation delay of the RREQ through the wormhole tRREQ by comparing the received time information with its own clock. A similar process occurs when M2 returns RREP to M1, with time information again being added as the RREP is tunnelled to M2. When M1 receives the tunnelled RREP, it calculates tRREP to give:
M1 then adds the fictive time value ΔTF defined as:
Alternatively, the wormhole nodes can split the time tampering attack into two steps. Firstly, M2 adds the fictive value:
So ΔTF= ΔTF1+ ΔTF2 is then added to ΔTTOT.
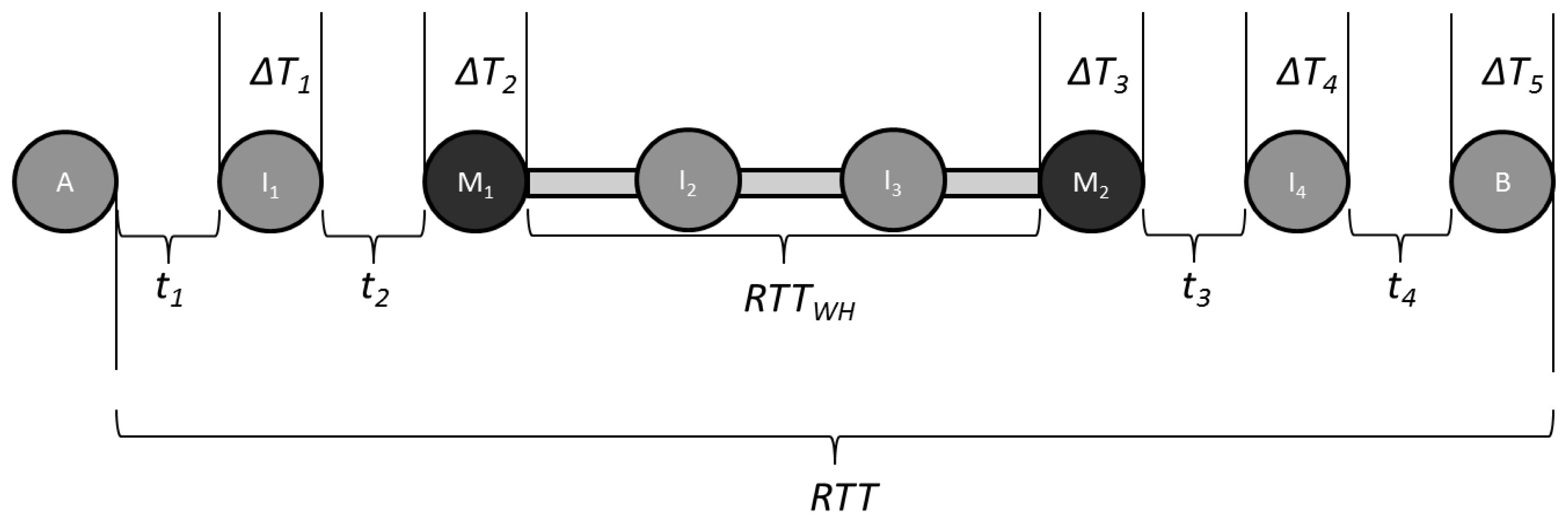
To illustrate the conditions that must exist for TTHCA time tampering to be achieved, consider the MANET example in Figure 1, where a PM I-B wormhole is formed by nodes M1 and M2 which tunnel routing packets between each other via I2 and I3.
It is assumed for simplicity that all nodes are in an idle state, have identical hardware and the inter-node distance is the same, so the ti and ΔTj values are constant. Let ti= 1,600 ns for all i and ΔTj= 8 ms for all j, where j = i + 1. If RTTWH= 16.0048 ms then RTT = 56.0112 ms. For this PM I-B scenario, the HC is 5 and ΔTTOT= 40 ms, so from Equation (2), source node A calculates PTT = 8.0056 ms giving PTT/HC = 1.60112 ms. If it is assumed R = 250 m, then from Equation (3) the upper bound for PTT/HC = 833 ns which means TTHCA will successfully detect the wormhole. Using Equation (4), it can be determined that both I2 and I5 are able to prevent detection by increasing ΔTTOT within the range:
This means the time tampering window is only 8.33 μs wide and while this is a stringent constraint, if synchronized clocks are being used by both M1 and M2, it is still realistically an achievable design tolerance.
Analysis for a wide range of network and wormhole attack conditions reveals that a sufficient and necessary condition for a wormhole to avoid being detected is to uphold either Equations (6) or (7) and (8). In this PM I-B example, both M1 and M2 will calculate ΔTF= 16.003133 ms which implies the tampered value falls within the window Equation (4) to avoid being discovered. In these circumstances, the false measurement ΔTTOT= 56.003133 ms so from Equation (2), the source node A measures PTT = 4,033 ns and PTT/HC = 806 ns meaning this wormhole route will go undetected by TTHCA.
4. ΔT Vector TTHCA Extension
Section 3 showed that the essential condition for the TTHCA algorithm to be unable to detect a wormhole route is for the malicious nodes to increase ΔTTOT within the strict bounds defined in Equation (4). Any successful tampered ΔTTOT will always be greater than the actual ΔTTOT though simply analysing ΔTTOT as a sum of individual ΔTi values will not necessarily identify the wormhole route because these usually exhibit high variance.
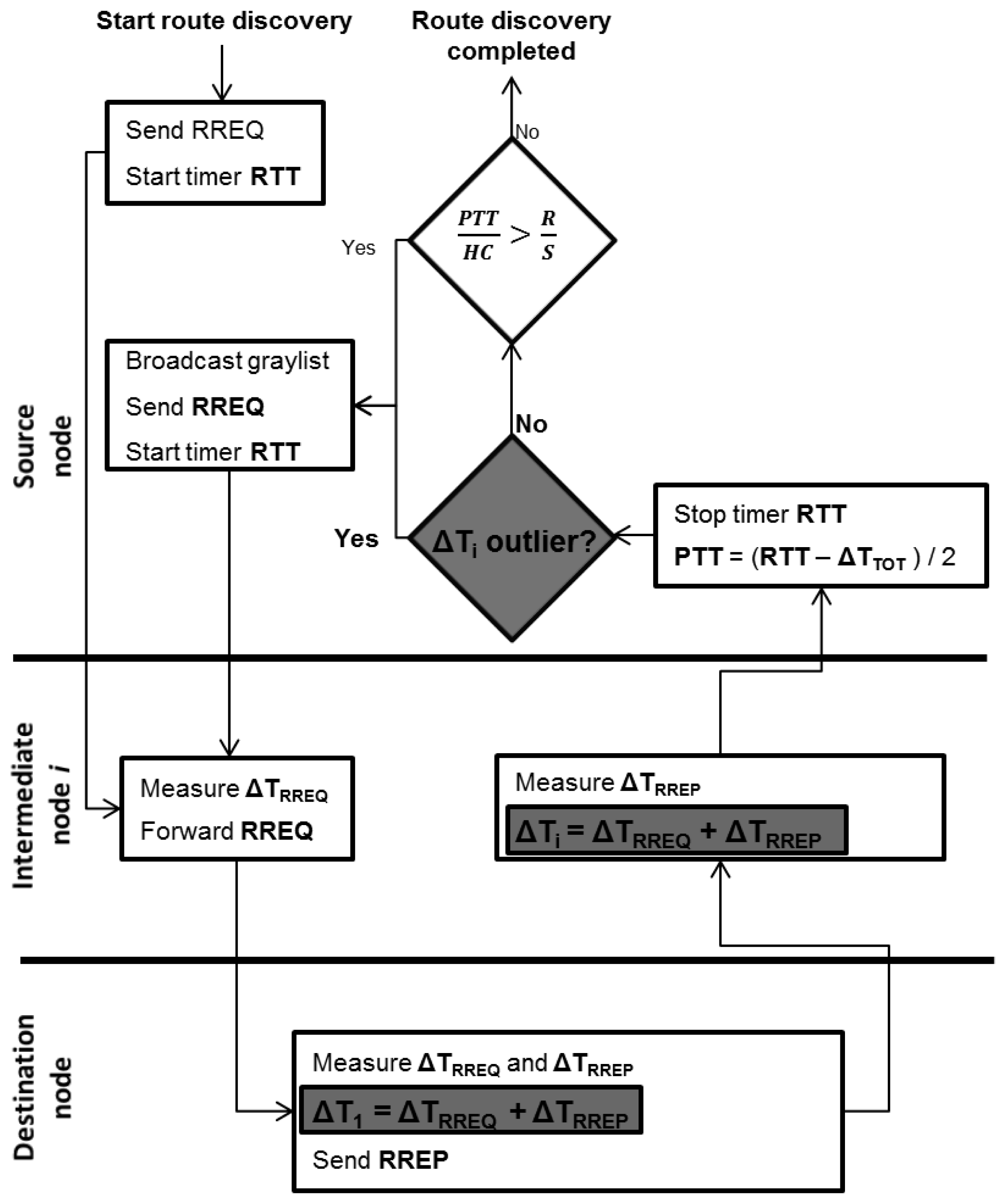
In this paper, to analyse ΔTi for each intermediate node, ΔTTOT is replaced by a new ΔT Vector comprising all the measured ΔTi values. This extension means that some new features for the TTHCA route discovery process are introduced to support the embedding of the ΔT Vector as shown in the Figure 2 flowchart, with the shaded blocks highlighting these new elements.
The RREQ and graylist broadcast procedures remain as in original TTHCA [17], but instead of using a ΔTTOT parameter, the ΔT Vector is included in the RREP packet by the destination node. The time taken from receiving the RREQ until sending the RREP at the destination node is added as the first element ΔT1. Each intermediate node receiving and forwarding the RREP then adds its ΔTi (ΔTRREQ + ΔTRREP) as a new element in the ΔT Vector.
When the RREP is received by the source node, each ΔTi element of the ΔT Vector consists of the processing times incurred by the RREQ and RREP packets. If a PM wormhole attack is launched alongside a time tampering attack, at least one of the ΔT Vector elements will be falsely increased in accordance with Equations (6), (7) and (8). A suitable outlier detection technique can then be applied to identify tampered ΔTi values (see Section 4.1) from the ΔT Vector dataset. If a suspicious ΔTi is identified, TTHCA then requests a new route by issuing a graylist broadcast. If no suspicious ΔTi is found, the normal PTT/HC analysis is performed for both HM and PM wormhole detection.
4.1. Identifying Tampered ΔTi Measurement
The ΔT Vector extension is founded on the premise a malicious node can only modify its own ΔTi which is a pragmatic assumption since in real MANET environments routing packets must be secured from modification attacks for the routing process to be trustworthy. A wormhole link typically consists of two malicious nodes, so a ΔT Vector received through any wormhole infected route will include either one or two tampered ΔTi values. It is possible to distinguish tampered ΔTi values from healthy ΔTi measurements by applying an appropriate outlier detection technique, such as the Grubb's test [19], Dixon's Q-test [20] or the Box plot method [21], though several conditions can affect the performance of the chosen outlier method. In this context, two distinct MANET scenarios are defined:
- CASE 1:
A node has been a part of the network for some time and generated a track record of ΔTi values gained from ΔT Vectors from earlier route discovery procedures. In this scenario, the availability of a large number of ΔTi samples can be reasonably assumed.
- CASE 2:
A node has joined the MANET for the first time and so the only available ΔTi values are those existing in the ΔT Vector.
Due to the inherently dynamic nature of a MANET, several different types of ΔTi distributions can arise which will impact on the performance of the outlier detection scheme. The ideal is when all MANET nodes have identical hardware and the network traffic loads are low. Such a condition would result in negligible ΔTi variations and time tampering is then straightforward to detect. This is not however, a realistic MANET situation because there are a myriad of factors which can cause ΔTi variations. For example, mixed node processing capacities and packet service times, allied with high network traffic loads in certain parts of the MANET can lead to queuing delays at specific nodes.
In a heterogeneous MANET consisting of uniformly distributed nodes where the network traffic load is low and there are no queuing delays, the ΔTi values can be assumed to follow a linear distribution. In MANETs with high network traffic load variations however, some of the ΔTi values will include queuing delays which will be much greater than the actual packet service times [22]. The ΔTi values will then tend to follow a nonlinear distribution where a small portion of the ΔTi values are significantly higher than the average. For such a distribution, it is very challenging to discriminate a tampered from a normal ΔTi value as a modified ΔTi can potentially be lower than a healthy ΔTi if the tampered measurement contains no queuing delay, while the healthy ΔTi does.
The outlier detection method selected for time tampering detection purposes must therefore be applicable to both large and small ΔTi datasets i.e., CASE 1 and CASE 2 respectively, as well as for both linearly and non-linearly distributed measurements.
5. Performance Analysis
The performance of the ΔT Vector extension has been rigorously analysed using the Dixon Q-test [20] as the outlier detection technique to identify tampered ΔTi values for a PM I-B wormhole infected route. The Q-test was chosen because of its simplicity and applicability to small and large datasets, making it appropriate for both the CASE 1 and CASE 2 scenarios. While the Q-test is only capable per se of detecting a single outlier, it can be applied to detect either one or two tampered ΔTi values provided the right-tailed variant is used to separately test the two largest ΔTi values. The outlier test is thus performed by first ranking the ΔT vector in order and then respectively calculating two Q values:
Time tampering is suspected if either Q1 or Q2 is greater than the corresponding critical Q-value for the chosen confidence level. For this analysis, a low confidence level (80%) has been chosen, since from a security perspective, a higher time tampering detection rate is preferable to a low FP detection.
Both the time tampering and FP detection performance for the ΔT Vector extension were analysed using a custom designed tool which simulated differently sized ΔT Vectors to reflect variable HC routes. ΔTi values were produced by randomly generating packet processing times for each node, with variable inter-node distances considered for each route.
The operating system (OS) for each MANET node was assumed to support multiprogramming with a scheduler assigning equal time slices to each process in rotation. Such an OS approximately implements processor-sharing so a logical processor executes each multiprogrammed task, with the processing capacity of a logical processor being the ratio of the physical processor capacity and the multiprogramming level. While nodes will typically have different physical processing capacities and multiprogramming levels, the equivalent multiprogramming level for each node will be relatively stable. A MANET having logical processors with diverse, yet stable processing capabilities is thus assumed to handle routing packets, so the corresponding packet service times for each node is assumed to be constant. Many concurrent route detection procedures can lead to routing packet queues in MANET nodes, since received routing packets must be sequentially processed to uphold route table updating requirements. For this reason, the packet processing times (ΔTRREQ/RREP) have been generated using the M/D/1 queuing model [23], which assumes Poisson-distributed packet arrivals, deterministic service times of routing packets, a single central processing unit and an infinite maximum queue length. Hence, at each node:
Time tampering detection performance for the CASE 1 and CASE 2 scenarios will now be respectively considered, where time tampering attacks on TTHCA are simulated in accordance with Equations (7) and (8). Note that the results presented relate solely to the ΔT Vector time tampering detection performance of the TTHCA algorithm, and not to the wormhole attack detection rates, which have already been rigorously presented in [17]. The simulation parameter settings used throughout the experiments are given in Table 1, with a detailed description of the customised simulation tool being provided in Appendix A.
5.1. CASE 1: MANET Nodes with ΔTi Track Records
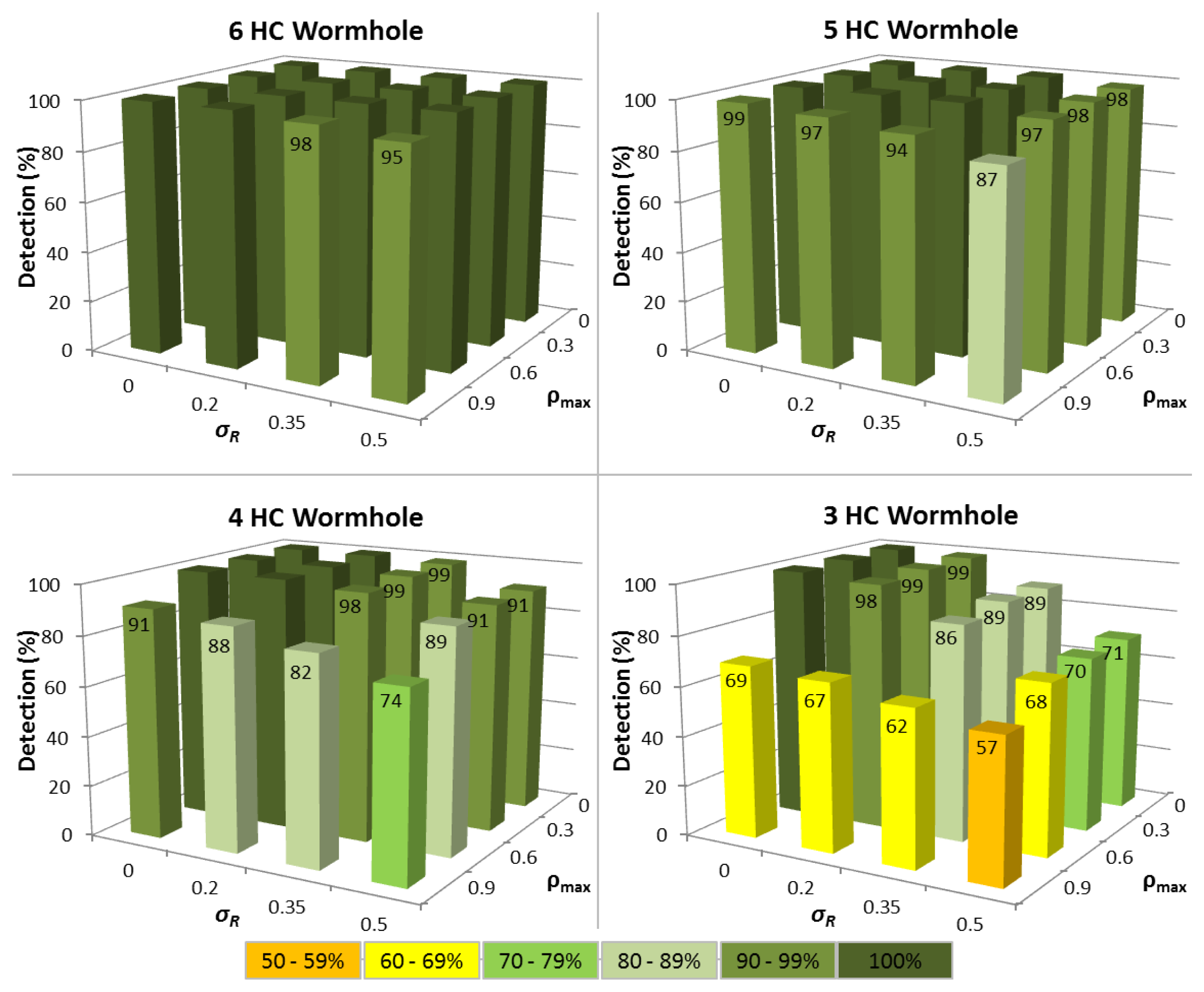
In the first series of experiments, the situation where a node has been in the MANET for a period of time is analysed and there are at least 15 ΔTi values available. Figure 3 shows the impact of variations in both routing packet service time (σR) and network traffic load (ρmax) upon the time tampering detection performance for different wormhole lengths.
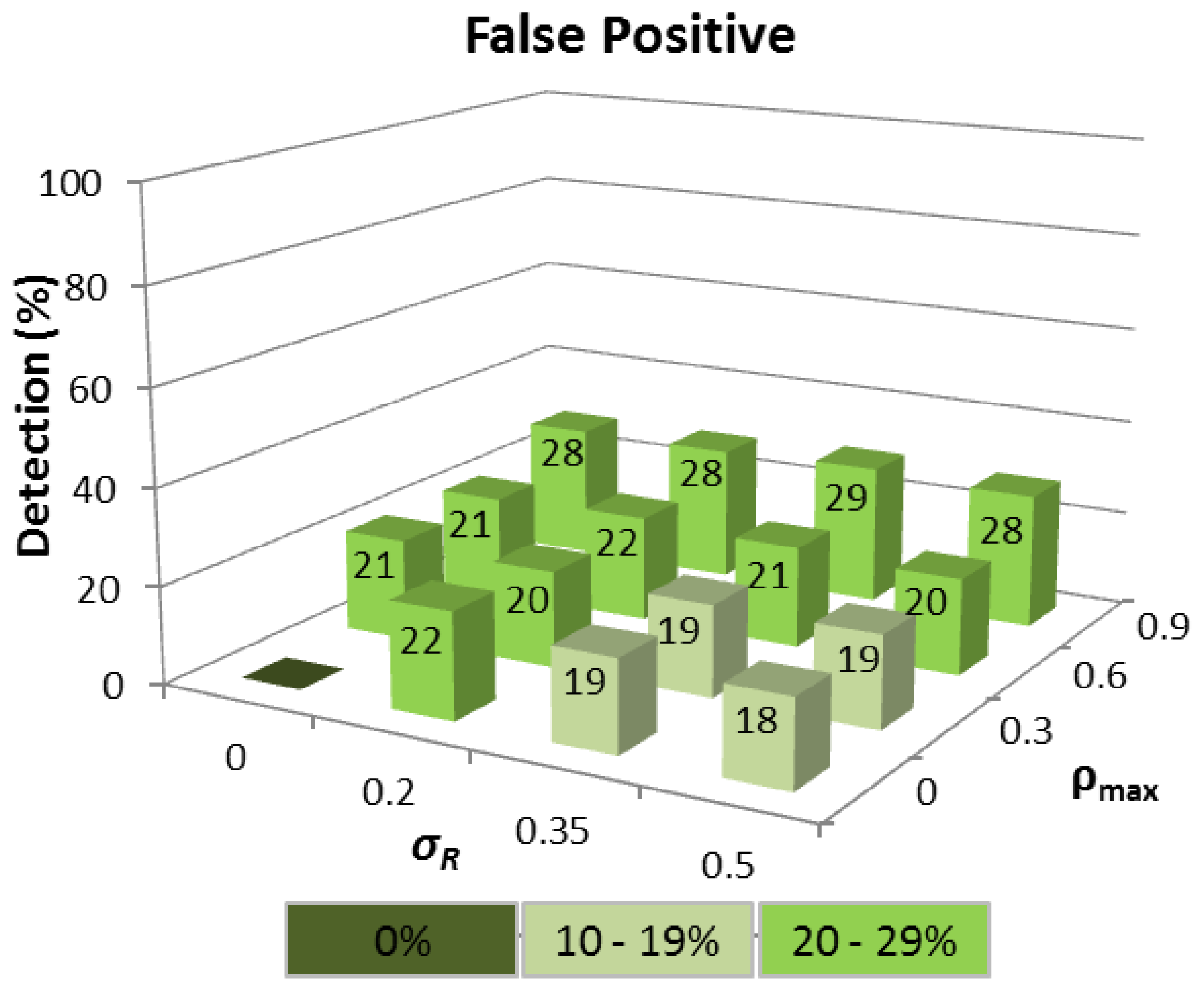
The results reveal that for the ideal case where ΔTi is constant, so all nodes have identical hardware and multiprogramming level (σR= 0), and each node carries negligible network traffic load (ρmax= 0), then 100% time tampering detection is achieved for all wormhole lengths with no corresponding FP being detected (see Figure 4). Predictably, as variations in ΔTi increase, the detection rate falls and FP increase, though the time tampering detection rate is still at least 86% for all wormhole lengths analysed even when σR= 0.35 and ρmax= 0.6.
For wormhole lengths ≥5 hops, at least 94% of tampered ΔTi values can be successfully detected under all conditions when σR = 0.5 and ρmax = 0.9, with the detection rate being 87% for a wormhole HC of 5. A notably aspect of the performance of the ΔT Vector extension, is that a minimum of 74% of tampered ΔTi values can still be detected even when the wormhole HC is 4. Pragmatically, this means that successful time tampering in wormholes ≥4 hops will be extremely difficult to achieve since the probability of avoiding detection is less than 30%.
For 3 HC wormholes, the time tampering detection performance drops markedly when there are variations in either network traffic load or routing packet service times, because a healthy node can then often produce a higher ΔTi than a tampered ΔTi. This reflects the situation of when heavy network traffic loads (ρ ≈ 1) unavoidably cause longer queuing delays and/or high multiprogramming levels lead to increased service times for routing packets. In contrast, the wormhole nodes and those nodes through which routing packets are tunneled may continue to have negligible loads (ρ ≈ 0) and correspondingly short packet service times.
Despite this decline in performance, tampered ΔTi values can still be detected with an accuracy of 57% for 3 HC wormholes, when σR= 0.5 and ρmax= 0.9. This still characterises a noteworthy enhancement to TTHCA, especially when cognisance is made of the stringent criteria necessary to launch a time tampering attack in the first instance.
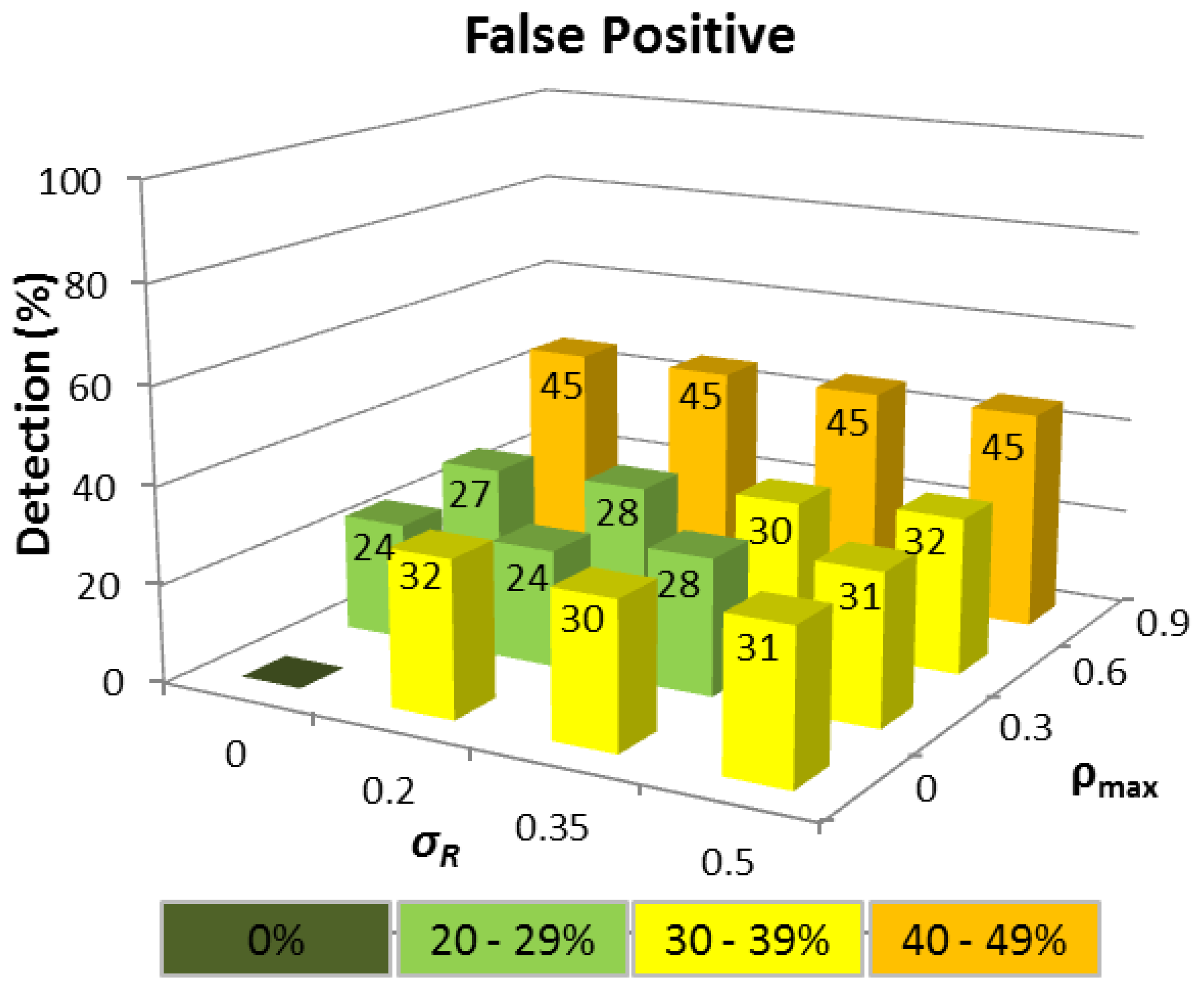
The corresponding FP detection rate remains ≈20% for the σR range considered, provided ρmax ≤ 0.6 because the Q-test compares the difference between the two largest ΔTi values in relation to the difference between ΔTMAX and ΔTMIN, which will be approximately constant, regardless of the interval, provided the ΔTi values are linearly distributed. When ρmax = 0.9, the FP rate rises because the queuing delay of a node increases rapidly as ρ tends to 1, and the ΔTi distributions are no longer linear. This means that a ΔTi value produced by a node with a high network traffic load can easily become confused with a tampered ΔTi. Realistically however, even a FP rate of ≈30% is still a satisfactory outcome since FP detection does not automatically mean that a route between a source and destination node cannot be established, but rather that an alternative route must be chosen other than the shortest path in terms of HC.
5.2. CASE 2: MANET Nodes without ΔTi Track Records
The second set of experiments analysed the situation when a new node joins the MANET and requests a route for the first time. The same conditions are employed as in Section 5.1, though now it is assumed that only between three and 15 ΔTi values are available for the node requesting the new route, since there is no a priori knowledge about previously measured ΔTi values. The corresponding time tampering detection results are displayed in Figure 5.
The absence of any track record meant that detection performance was not as consistent as CASE 1, though a time tampering detection rate of ≥80% has still been achieved for all wormhole HC when σR ≤ 0.2 and ρmax ≤ 0.6. For wormholes ≥5 hops, at least 68% of tampered ΔTi values were correctly detected even when σR= 0.5 and ρmax= 0.9. The equivalent FP detection rates displayed in Figure 6, were slightly higher than in CASE 1 for ρmax ≤ 0.6 for example, and performance was more sensitive to high network traffic load variations (ρmax = 0.9) due to the smaller number of ΔTi samples. Nevertheless, even a FP rate of 45% when ρmax= 0.9 can still be deemed acceptable as more than half of all possible routes are available.
The time tampering detection performance is thus less robust in CASE 2 when no ΔTi track record is available, though this does represent the worst possible MANET situation, when a new node performs its first route discovery procedure. As a node runs the route discovery procedure more often, the corresponding time tampering detection rate will quickly improve and converge towards the results presented for CASE 1. This infers that to strengthen the time tampering detection performance for new nodes, it is prudent to run a few route discovery procedures before starting to communicate within the network. This could for instance, be accomplished by specifying within the routing protocol that a node is not allowed to communicate within the network until it has collected a minimum of 15 ΔTi samples.
5.3. Network Overheads and Computational Complexity
One of the consequences of the ΔT Vector extension is a larger RREP packet as it must contain the individual ΔTi values of all intermediate nodes of a route, while the original TTHCA mechanism only requires the sum ΔTTOT. The size of the ΔT Vector is dependent on the route HC, so if for example each ΔTi value is represented by 32 bits, then on a route from a source node S to a destination node D with intermediate nodes I1 and I2, RREP will comprise a ΔT Vector length of 32 bits, 64 bits and 96 bits when respectively received by I2, I1 and S. This contrasts with the corresponding RREP packet in the TTHCA algorithm which will have a 32 bits ΔTTOT value for each node. While a ΔT Vector with more than one element theoretically increases the transmission and reception time requirements for the routing packet, when cognisance is taken of the high bandwidths available in modern wireless technologies, the extended RREP packets will have negligible impact upon performance.
A second ramification of the ΔT Vector extension is the increased FP detection rate. From the network performance perspective, this means that the shortest route in terms of HC is not always available, as highlighted in both Sections 5.1 and 5.2. This does not necessarily imply decreased performance in terms of route delay since FP detection can in many cases lead to a positive outcome as routes with intermediate nodes with very high traffic loads will be omitted.
A formal complexity analysis for the new ΔT Vector extension reveals the only supplementary cost incurred compared with the original TTHCA algorithm is the outlier detection scheme performed by the source node. If the Dixon Q-test is used as the outlier method, the only extra computations needing to be performed relate to the ranking of ΔT Vector values. Since the ΔT Vector length equals the route HC, the time complexity for ranking is O(HC2). This ranking however, can be implemented as a linear search of 4 ΔT values, since the Q-test only uses the three largest and the smallest ΔT value. This results in a time complexity for the new ΔT Vector extension of O(HC), which is the same as TTCHA [17]. The corresponding FP performance of ΔT Vector extension also needs to be analysed because these are identified even when there are no errors in the measured node processing times. If the probability of a FP is p, then the probability of i FP occurring before a healthy route is located will be (1−p)·pi. The average number of route discovered before a healthy route can therefore be expressed as p/(1−p). So for p < 0.5, on average up to one FP will be discovered before a healthy route is identified for the ΔT Vector extension. The worst case in a single wormhole MANET is thus, on average three algorithm executions when a wormhole infected route is found before a healthy route is located. In contrast, the impact of FP on the TTHCA algorithm is less problematic because a FP is only identified when there are time measuring errors [17].
In summary, this formal analysis has shown the new ΔT Vector extension has the same linear time complexity as the original TTHCA algorithm, with the rider that because of FP occurrences, one additional execution cycle of the ΔT Vector extension may be necessitated, though this still affords a very effective lightweight protection mechanism against time tampering for TTHCA.
6. Conclusions and Future Research
The traversal time and hop count analysis (TTHCA) algorithm is a MANET wormhole detection technique, introduced as an extension to the ad hoc distance vector (AODV) routing protocol. A latent security threat to TTHCA is that as each intermediate node and the destination node measures the packet traversal time, a participation mode (PM) wormhole node can potentially provide false measurement values and avoid detection. This paper has analysed the conditions for a time tampering attack and proposed a security mechanism for TTHCA called the ΔT Vector extension for detecting false time values in PM in-band (I-B) wormholes. This requires the destination node and each intermediate node to add their individual processing times of the route request (RREQ) and route reply (RREP) packages (ΔTi) to a vector parameter in the RREP instead of using a single total packet processing time parameter (ΔTTOT) as in the original TTHCA algorithm. This makes each individual ΔTi measurement available for a node requesting a route and suspicious ΔTi values caused by PM I-B wormhole nodes can thus be identified by an outlier detection method. The ΔT Vector extension offers a notable security enhancement to the original TTHCA wormhole detection algorithm by providing an effective time tampering detection mechanism for PM wormholes, while retaining many of the smart features of TTHCA, particularly being a low-cost algorithm in terms of both computational complexity and network overheads.
In terms of future research, minimisation of false positive (FP) detections incurred by the ΔT Vector extension is an important objective. The FP rate can potentially be decreased by not including nodes suspected of time tampering to the graylist, since a high ΔTi caused by time tampering is permanent compared with a temporarily high ΔTi due to queuing delays. An alternative strategy is to choose a higher confidence level for the outlier detection, though this will proportionally reduce the corresponding time tampering detection performance of the ΔT Vector mechanism.
Appendix A
Custom Tool for Simulating Different Sized ΔT Vectors
This section investigates the software tool used to generate the simulated ΔTi values, with all variables with their initialised values being displayed in Table A1. To enable the interested reader to faithfully reproduce this tool, the documented pseudo-code showing the creation of a ΔTiVector during both the RREQ broadcast and corresponding RREP response phases is provided in Tables A2 and A3 respectively.
| Variable | Description |
|---|---|
| HCWH = user defined | Wormhole length (number of hops) |
| HC = [3,15] | Randomly chosen for each route. Includes both the actual route HC and HCWH |
| tRREQ = 0 | Tunnelling delay of RREQ through wormhole link |
| tRREP= = 0 | Tunnelling delay of RREP through wormhole link |
| M1 = 1 | Malicious node #1 |
| M2 = M1+ HCWH | Malicious node #2 |
| i = 1 | ΔT Vector index |
| Code Section | Description/motivation |
|---|---|
| FOR I = 1 to HC: | I=1 is the first intermediate node and I = HC is the destination node |
| ρ = [ 0, ρmax] | Random traffic load assigned for each node |
| TS-I = randomly chosen from a linear distribution with user defined relative standard deviation (σR) | Every node (I) is assigned a random packet service time. |
| ΔTRREQ-I calculated according to Equation (11) | RREQ processing time at each node calculated according to the M/D/1 queuing model. |
| dI= random between 150m and 250m | Distance between node I and I-1 |
| IF I > M1 AND I < M2 THEN tRREQ = tRREQ + dI/S + ΔTRREQ-I | RREQ tunnelled propagation delay through the wormhole is the sum of ΔTRREQ-I at each intermediate node and PTT between M1 and M2. |
| IF I = M2 THEN tRREQ = tRREQ + dI/S ΔTF2 = tRREQ + R/S | PTT between I (M2) and I-1 is added to tRREQ and M2 calculates ΔTF1 to be added to its ΔTi when it receives the corresponding RREP. |
| END FOR |
| Code Section | Comments |
|---|---|
| FOR I = HC to 1: | As it is a RREP broadcast, the iteration starts at I = HC. |
| ρ = [ 0, ρmax] | Random traffic load is assigned for each node to reflect a potential change in network traffic conditions between processing RREQ and RREP. |
| ΔTRREP-I calculated according to Equation (11) | RREP processing time at each I follows the M/D/1 queuing model. Since the service time of both RREQ and RREP is assumed constant, TS-I from Table A2 is used. |
| ΔTi = ΔTRREQ-I + ΔTRREP-I | Processing delays of both RREQ and RREP added to the ΔT Vector (ΔTi) |
| IF I < M2 AND I > M1 THEN tRREP = tRREP + dI/S + ΔTRREP-I | RREP tunnelled propagation delay through the wormhole is the sum of all ΔTRREP at intermediate nodes and the PTT between M2 and M1. |
| ELSE Increment i | If I is a legitimate intermediate node then ΔT Vector index is incremented. |
| IF I = M2 THEN tRREP = tRREP + di/S ΔTi = ΔTi + ΔTF2 | The PTT between I (M2) and I-1 is added to tRREP and M2 increments its entry in ΔT Vector with ΔTF2 which was calculated during the RREQ broadcast process. |
| IF I = M1 THEN ΔTF1 = tRREP + R/S ΔTi = ΔTi + ΔTF1 | M1 calculates ΔTF1 with which ΔTi is incremented. |
| END FOR |
Conflict of Interest
The authors declare no conflict of interest.
References
- Agrawal, S.; Jain, S.; Sharma, S. A survey of routing attacks and security measures in mobile ad-hoc networks. J. Comput. 2011, 3, 41–48. [Google Scholar]
- Karlsson, J.; Dooley, S.L.; Pulkkis, G. Routing security in mobile ad-hoc networks. Issue Inform. Sci. Inform. Technol. 2012, 9, 369–383. [Google Scholar]
- Hu, Y.; Perrig, A.; Johnson, D.B. Packet Leashes: A Defence Against Wormhole Attacks in Wireless Networks. Proceedings of the 22nd Annual Joint Conference of the IEEE Computer and Communications, San Francisco, CA, USA, 1–3 April 2003; pp. 1976–1986.
- Khabbazian, M.; Mercier, H.; Bhargava, V.K. NIS02-1: Wormhole Attack in Wireless Ad hocNetworks: Analysis and Countermeasure. Proceedings of the Global Telecommunications Conference (GLOBECOM’06), San Francisco, CA, USA, 27 November–1 December 2006; pp. 1–6.
- Khabbazian, M.; Mercier, H.; Bhargava, V.K. Severity analysis and countermeasure for the wormhole attack in wireless ad hoc networks. IEEE Trans. Wirel. Commun. 2009, 8, 736–745. [Google Scholar]
- Song, S.; Wu, H.; Choi, B.-Y. Statistical Wormhole Detection for Mobile Sensor Networks. Proceedings of the 4th International Conference on Ubiquitous and Future Networks, Phuket, Thailand, 4–6 July; pp. 322–327.
- Khurana, S.; Gupta, N. FEEPVR: First End-to-End Protocol to Secure Ad hocNetworks with Variable Ranges Against Wormhole Attacks. Proceedings of the 2nd International Conference on Emerging Security Information, Cap Esterel, France, 25–31 August 2008; pp. 74–79.
- Gupta, N.; Khurana, S. SEEEP: Simple and Efficient End-to-End Protocol to Secure Ad hocNetworks Against Wormhole Attacks. Proceedings of the 4th International Conference on Wireless and Mobile Communications (ICWMC’08), Athens, Greece, 27 July–1 August 2008; pp. 13–18.
- Qian, L.; Song, N.; Li, X. Detecting and Locating Wormhole Attacks in Wireless Ad hocNetworks Through Statistical Analysis of Multi-Path. Proceedings of the IEEE Wireless Communications and Networking Conference, New Orleans, LA, USA, 13–17 March 2005; pp. 2106–2111.
- Su, M. WARP: A wormhole-avoidance routing protocol by anomaly detection in mobile ad hoc networks. Comput. Secur. 2010, 29, 208–224. [Google Scholar]
- Azer, M.A.; El-Kassas, S.M.; El-Soudani, M.S. Immuning Routing Protocols from the Wormhole Attack in Wireless Ad hocNetworks. Proceedings of the 4th International Conference on Systems and Networks Communications, Porto, Portugal, 20–25 September 2009; pp. 30–36.
- Jen, S.; Laih, C.; Kuo, W. A hop-count analysis scheme for avoiding wormhole attacks in MANET. Sensors 2009, 9, 5022–5039. [Google Scholar]
- Choi, S.; Kim, D.-Y.; Lee, D.-H.; Jung, J.-I. WAP: Wormhole Attack Prevention Algorithm in Mobile Ad hocNetworks. Proceedings of the IEEE International Conference on Sensor Networks, Ubiquitous and Trustworthy Computing, Taichung, Taiwan, 11–13 June 2008; pp. 343–348.
- Chiu, H.S.; Lui, K.-S. DelPHI: Wormhole Detection Mechanism for Ad hocWireless Networks. Proceedings of the 1st International Symposium on Wireless Pervasive Computing, Phuket, Thailand, 16–18 January 2006.
- Tran, P.V.; Hung, L.X.; Lee, Y.; Lee, S.; Lee, H. TTM: An Efficient Mechanism to Detect Wormhole Attacks in Wireless Ad-HocNetworks. Proceedings of the 4th IEEE Consumer Communications and Networking Conference, Las Vegas, NV, USA, 11–13 January 2007; pp. 593–598.
- Zhou, J.; Cao, J.; Zhang, J.; Zhang, C.; Yu, Y. Analysis and Countermeasure for Wormhole Attacks in Wireless Mesh Networks on a Real Testbed. Proceedings of the IEEE 26th International Conference on Advanced Information Networking and Applications, Fukuoka, Japan, 26–29 March 2012; pp. 59–66.
- Karlsson, J.; Dooley, L.S.; Pulkkis, G. A new MANET wormhole detection algorithm based on traversal time and hop count analysis. Sensors 2011, 11, 11122–11140. [Google Scholar]
- Perkins, C.E.; Royer, E.M. Ad-HocOn-Demand Distance Vector Routing. Proceedings of the Second IEEE Workshop on Mobile Computing Systems and Applications, New Orleans, LA, USA, 25–26 February 1999; pp. 90–100.
- Grubbs, F.E. Procedures for detecting outlying observations in samples. Technometrics 1969, 11, 1–21. [Google Scholar]
- Dean, R.B.; Dixon, W.J. Simplified statistics for small numbers of observations. Anal. Chem. 1951, 23, 636–638. [Google Scholar]
- Tukey, J.W. Exploratory Data Analysis; Addison-Wesley: Reading, MA, USA, 1977. [Google Scholar]
- Gao, C.; Jäntti, R. Least-Hop Routing Analysis of On-Demand Routing Protocols. Proceedings of the 1st International Symposium on Wireless Communication Systems (ISWCS’04), Mauritius, 20–22 September 2004; pp. 215–219.
- Gross, D.; Shortle, J.F.; Thompson, J.M.; Harris, C.M. Fundamentals of Queueing Theory, 4th ed.; Wiley-Interscience: New York, NY, USA, 2008; pp. 53–65. [Google Scholar]

| Parameter | Settings |
|---|---|
| Distance between two successive nodes (d) | Randomly set: 150 m–250 m |
| Packet propagation speed (S) | 3 × 108 m/s |
| Routing packet service time per node distribution (TS) | Randomly chosen from linear probability distributions for variable σR |
| Routing packet processing time per node distribution (ΔTRREQ/RREP) | Calculated from Equation (11) |
| Network traffic load per node distribution (ρ) | Randomly 0 ≤ ρ ≤ ρmax for variable ρmax |
| Route HC | Randomly set: 3–15 |
| Number of samples per test case | 100,000 |
| Wormhole attack type | PM I-B |
| Time tampering attack | Launched according to Equations (7) and (8) |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/
Share and Cite
Karlsson, J.; Dooley, L.S.; Pulkkis, G. Identifying Time Measurement Tampering in the Traversal Time and Hop Count Analysis (TTHCA) Wormhole Detection Algorithm. Sensors 2013, 13, 6651-6668. https://doi.org/10.3390/s130506651
Karlsson J, Dooley LS, Pulkkis G. Identifying Time Measurement Tampering in the Traversal Time and Hop Count Analysis (TTHCA) Wormhole Detection Algorithm. Sensors. 2013; 13(5):6651-6668. https://doi.org/10.3390/s130506651
Chicago/Turabian StyleKarlsson, Jonny, Laurence S. Dooley, and Göran Pulkkis. 2013. "Identifying Time Measurement Tampering in the Traversal Time and Hop Count Analysis (TTHCA) Wormhole Detection Algorithm" Sensors 13, no. 5: 6651-6668. https://doi.org/10.3390/s130506651




