Progress in the Development of CdZnTe Unipolar Detectors for Different Anode Geometries and Data Corrections
Abstract
: CdZnTe detectors have been under development for the past two decades, providing good stopping power for gamma rays, lightweight camera heads and improved energy resolution. However, the performance of this type of detector is limited primarily by incomplete charge collection problems resulting from charge carriers trapping. This paper is a review of the progress in the development of CdZnTe unipolar detectors with some data correction techniques for improving performance of the detectors. We will first briefly review the relevant theories. Thereafter, two aspects of the techniques for overcoming the hole trapping issue are summarized, including irradiation direction configuration and pulse shape correction methods. CdZnTe detectors of different geometries are discussed in detail, covering the principal of the electrode geometry design, the design and performance characteristics, some detector prototypes development and special correction techniques to improve the energy resolution. Finally, the state of art development of 3-D position sensing and Compton imaging technique are also discussed. Spectroscopic performance of CdZnTe semiconductor detector will be greatly improved even to approach the statistical limit on energy resolution with the combination of some of these techniques.1. Introduction
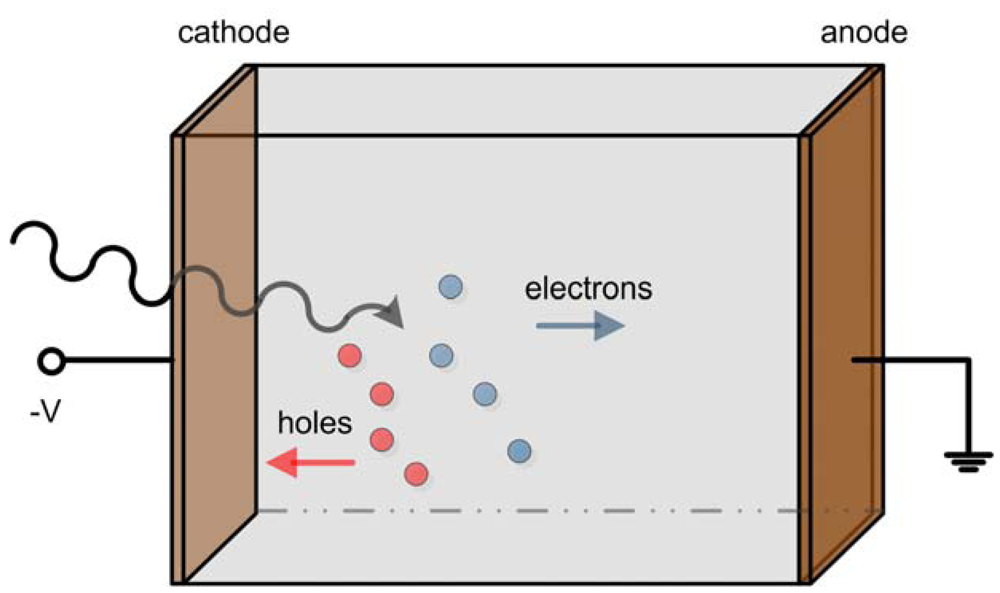
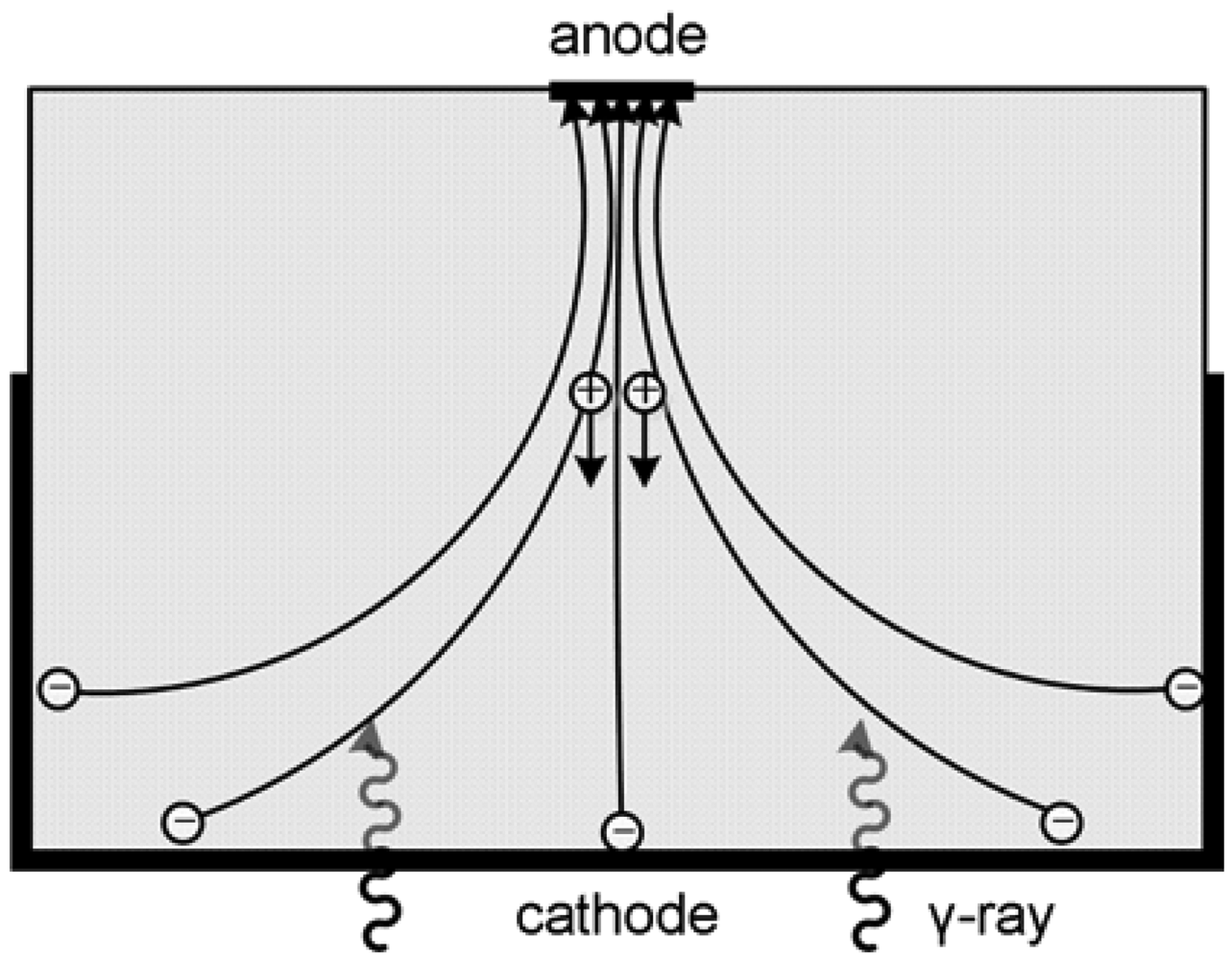
Semiconductor nuclear radiation detectors have experienced a rather rapid development in the last few decades. A major characteristic of this type of detector is the capability of converting γ-rays directly into electronic signals. In comparison to scintillators, semiconductor detectors avoid the random effects associated with scintillation light production, propagation and conversion to electrical signal in such a way that they represent the main alternative to scintillator-based single photon imaging systems. Compared to established use of Si and Ge, cadmium zinc telluride (CdZnTe) is the most promising material for radiation detectors with high atomic number (good stopping power), large band-gap (room-temperature operation), and the absence of significant polarization effects [1,2]. The incident gamma-ray interacts with the semiconductor and excites electron-hole pairs, that are proportional to the deposited energy and drifts apart under the applied electric field. Electrons drift towards the anode and holes drift towards the cathode (Figure 1). Charge signal is induced on the electrodes of the detector by the moving charge carriers. It is due to the direct conversion from the energy deposition by gamma-ray interaction to electric signal that semiconductor detector can easily achieve high energy resolution and spatial resolution [3]. In practice, CdZnTe materials exhibit varying degrees of charge carrier trapping, which in fact is the dominant problem that has limited their energy resolution. Our group at the Molecular Imaging Lab of Peking University is developing micro single-photon emission computed tomography (SPECT) for small animal imaging. This paper reviews the techniques of overcoming hole trapping problems for CdZnTe detector, including particular irradiation configuration of the same, electronic methods to distinguish events from a large contribution of the holes and the various electrode designs. We also review the state of art development of 3-D position sensing and Compton imaging techniques using CZT detectors.
2. Theoretical Principles
The collection efficiency of charge carriers is a crucial property that affects the energy resolution of semiconductor detectors. This efficiency is always reduced by charge carriers trapping that results from crystal defects and the poor charge transport properties of charge carriers. For example, grain boundaries that are generated during crystal growth can seriously trap charge carriers [4]. It has been shown that spatial non-uniformity of semiconductor materials will cause a loss of energy resolution [5,6]. In addition, the mean drift length of electrons is typically of the order 1 cm while this length of holes is much lower than that of electrons with values around 0.1 cm under typical electric fields of 1,000 V/cm. With poor charge collection, the charge signal induced on the electrode is reduced, which is more pronounced for events that occur further away from the collecting electrode. This is how the position-dependent signal variation is produced.
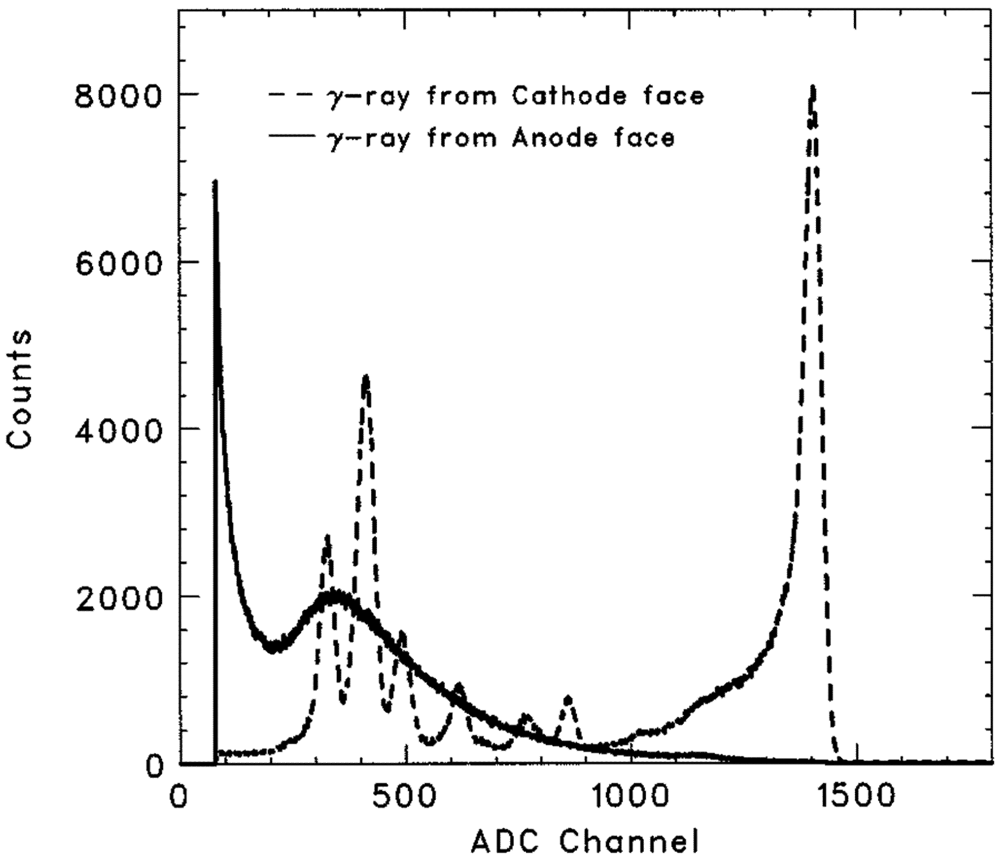
Figure 2 shows two typical spectra obtained with a CdZnTe planar detector when irradiated from anode and cathode side, respectively. The anode-irradiating spectrum has no peak because most of the holes are trapped due to a long drift distance to the cathode. However, the peak can be clearly resolved on the cathode-irradiating spectrum. Since the amplitude of the induced charge signal depends on the depth of interaction (DOI), the cathode-irradiating spectrum still shows a tailing.
2.1. Shockley-Ramo Theory
As already stated, the charge carriers that are generated by γ-photon energy deposit drift towards the corresponding electrodes. Shockley and Ramo proposed a method in 1940s to calculate the induced charge by introducing a concept of “weighting potential” [8–10]. The charge variance (ΔQL) that is achieved by a moving charge q from interaction position xi to xf and induced on the electrode (L), can be calculated according to Equation (1):
2.2. Static Charge Analysis and Capacitance Coupling Method
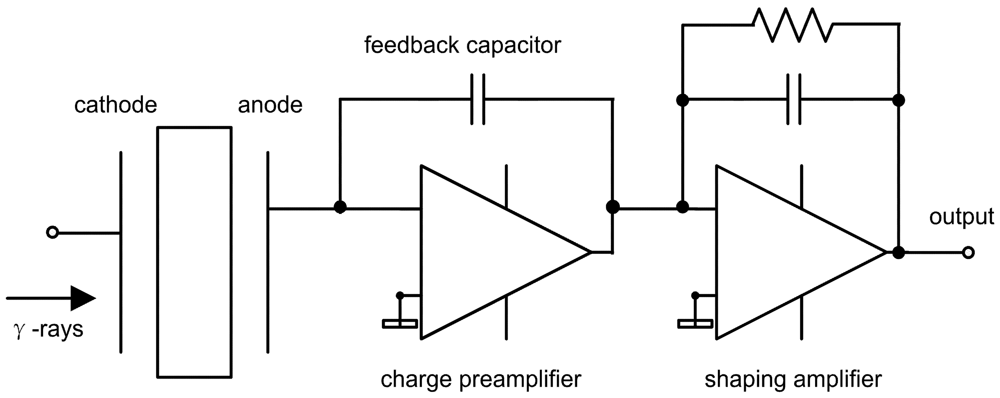
Another approach to calculate the output charge on the electrode, called “static charge analysis and capacitance coupling method”, was introduced by Lingren and Butler [11]. What is shown in Figure 3 is a typical amplification circuit model. The total amount of charge (Qtotal) that is generated on the feedback capacitor consists of two parts—free electrons that are collected directly by the electrodes and the charges induced by trapped carriers within the detector (Equation (2)):
The amount of charge, which is induced on an anode by infinitesimal charges dQef(x) and dQhf(x), is equal to the infinitesimal charge multiplied by a weighting factor. This weighting factor is a ratio of the capacitance from the interaction point to the collecting anode to the total capacitance from that point to all electrodes. Thus the infinitesimal induced charges (dQei(x) and dQhi(x)) on the anode can be given as:
3. Techniques to Reduce Hole Trapping
Energy resolution is one of the main performance parameters for gamma ray detectors. As seen from Figure 2, the low energy branch in a typical spectrum always presents as a tailing. This tailing primarily results from hole trapping and degrade energy resolution; it is a necessary requirement to overcome hole trapping in order to improve detector performance. Three ways to achieve this: configuring irradiation direction, distinguishing events with a large contribution of holes using electronic methods and minimizing the sensitivity to holes through detector geometry design.
3.1. Irradiation Direction Configuration
As mentioned previously, hole trapping limits detector performance. This is because a long tail is produced in the measured spectrum due to incomplete charge collection. It was observed that irradiation from cathode side can contribute to reducing this effect [7] because the counts of events that are excited near the cathode are increased, thus minimizing the probability of hole trapping. This irradiation configuration is more effective for low energy rays in thin detectors. Another advantage of using the cathode-irradiating configuration is the uniform trigger rate effect, since using a cathode electronic signal to trigger the acquisition of electrode pulse heights can lead to much more uniform event acquisition response than using anode pixel signal [13].
Another irradiation configuration, in which the irradiation direction is orthogonal to the applied electric field, was being considered as a way of overcoming the compromise between good spectroscopy and acceptable detection efficiency [14,15]. In configuration of this type, the interaction position information can be obtained experimentally due to the fact that the photopeak centroid value is correlated with interaction position. And different detector thicknesses can be chosen in order to get the required detection efficiency. Nevertheless, a tradeoff between the required energy resolution and irradiated area should be considered. This method is particularly useful for developing detectors when high detection efficiency is required.
3.2. Pulse Shape Correction
Electronic methods have also been used to improve the spectrometric performance of CdZnTe detectors, such as pulse shape discrimination (PSD) [16–19] and pulse rise-time compensation (PRC) [17,20]. Both of these techniques are implemented in combination with hardware and software. PSD method was developed to distinguish events with a large contribution from hole trapping since events with a large degree of hole trapping always present an output pulse with a long rise-time. These events can be eliminated in such a way that high spectral resolution can be achieved at the cost of rejecting a fraction of the pulses, thus resulting in a drastic loss in detection efficiency. Alternatively, PRC method was developed to allow for reducing the loss of efficiency while obtaining energy resolution improvement. The aim of PRC is to compensate pulse amplitude of those events with severe hole trapping according to pulse shape characteristic. Different approaches were reported to realize PRC through different bi-parametric spectrums (BPS), such as “pulse amplitude & pulse rise-time” spectrum [17] as well as “fast/slow ratio & slow signal” spectrum [20]. BPS is a useful analysis tool and has a real advantage in spectrum correction, e.g., scattering rejection [2,21].
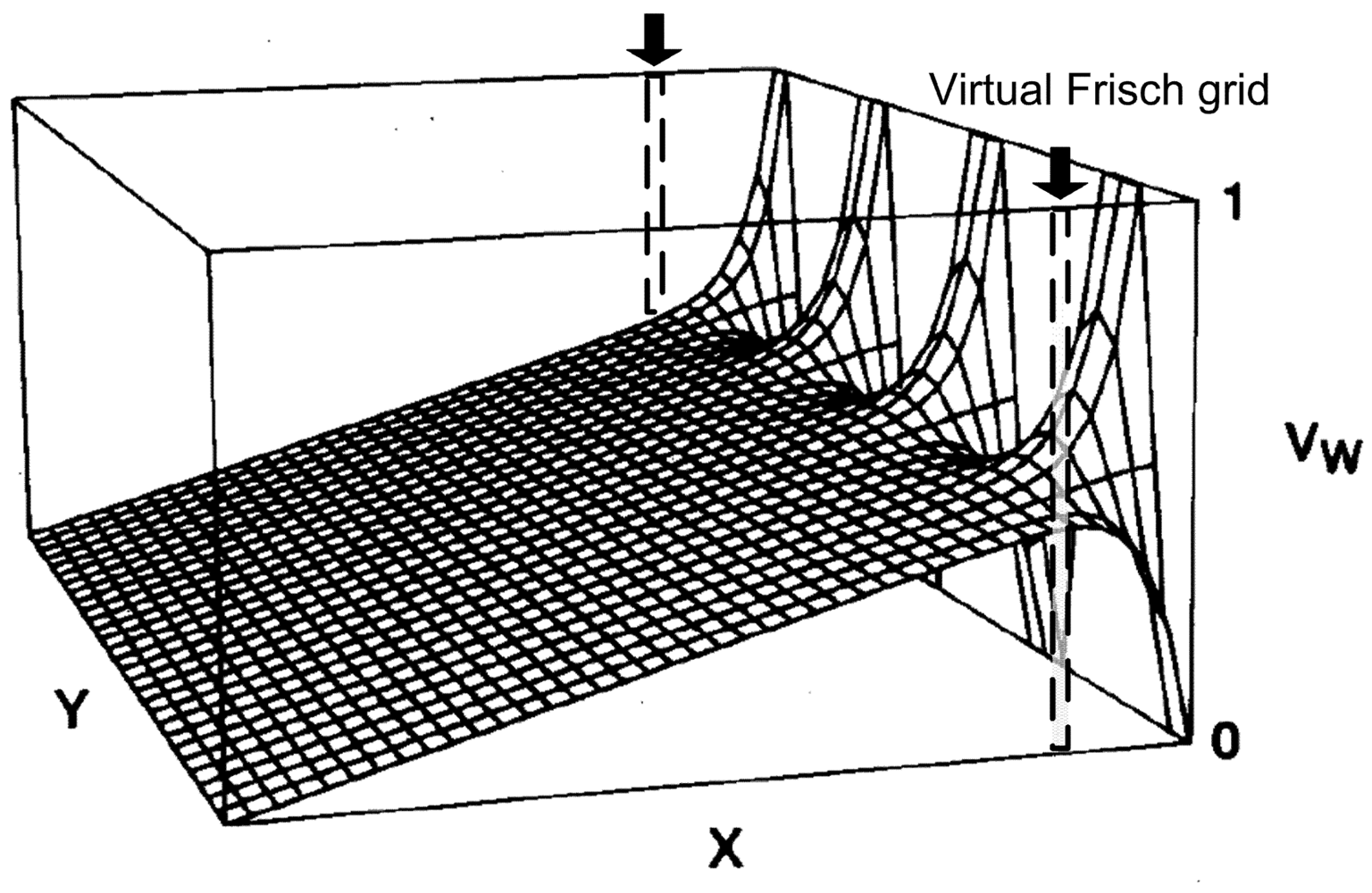
A novel algorithm, used for rejecting incomplete charge collection (ICC) events in CdZnTe detectors, was proposed by Bolotnikov et al. [22]. This method is based on a BPS that is reflected in R-T function and features for reducing the Compton continuum in the energy spectrum. The R-T function is a unique function of the detector correlating the ratio of cathode to anode signal and drift times measured for each detected event. Some events falling out of a curve that represents the correlation function were regarded as ICC events and thus rejected. In this way, the Compton continuum and the low-energy tail of the energy spectrum can be greatly reduced without affecting the photopeak efficiency significantly. This algorithm is much more effective in correcting virtual Frisch-grid CdZnTe detectors and can also be employed practically for any single charge sensing type detectors.
4. Unipolar Detectors of Different Anode Geometries
To some extent, both of the methods mentioned in Sections 3.1 and 3.2 can reduce hole trapping effect on the charges that are collected by electrodes; these methods still remaining insufficient to obtain a good quality energy resolution. In addition, drastic losses in detection efficiency are caused with a limited improvement in energy resolution, especially with thicker detectors. Therefore, the approaches mentioned above could be adjunct methods to obtain better energy resolution or furthermore could be used in certain occasions where efficiency is a less important parameter. Unipolar detector designs, however, have been developed to overcome the deleterious effects of hole trapping problem. The most effective and successful prototype models, listed and mentioned below, include the Frisch-grid device, pixelate detectors, coplanar grid detectors, hemispherical electrodes and strip detectors.
4.1. Frisch Grid Device
Frisch grid effect
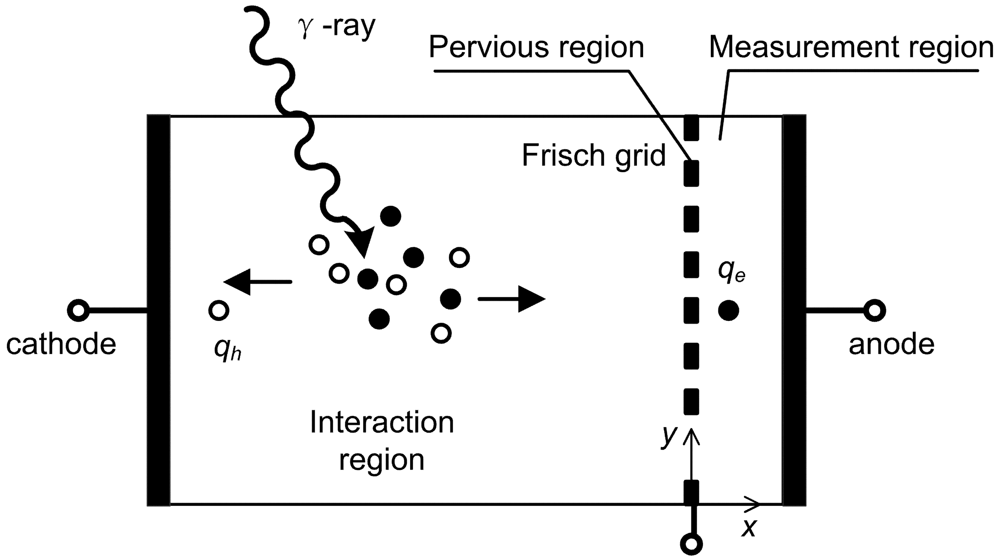
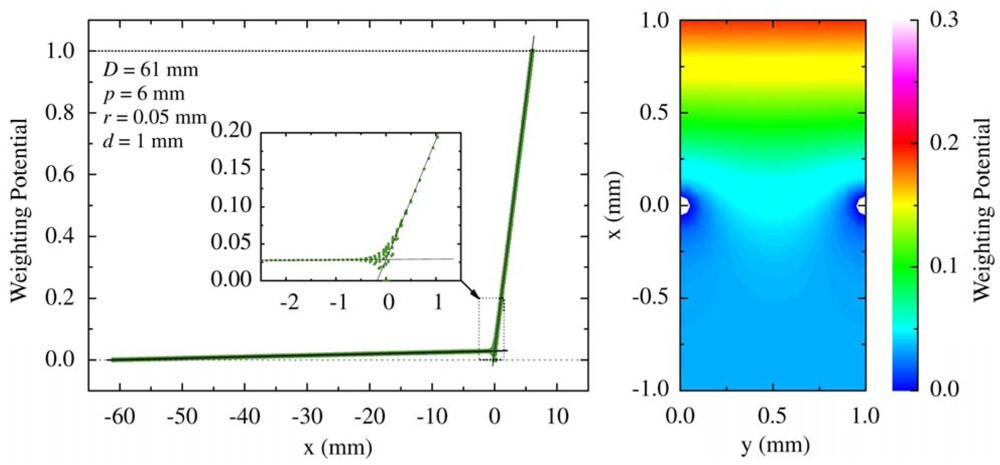
Frisch-grid-based design that was introduced by Frisch [23] was originally used for gas-filled ion chambers. The aim of this design was to make the induced charge on the collecting electrode insensitive to the carriers with lower mobility. Thus the induced charge can be measureed primarily from the carriers with higher mobility. A general configuration of a Frisch grid ion chamber is shown in Figure 4. A Frisch grid is placed in the vicinity of the anode so that three distinctive regions are formed. The region between cathode and Frisch grid is called interaction region where most gamma rays interact, and the region between anode and Frisch grid is the measurement region where the induced charges are measured. The pervious region, where charge carriers pass through, is underneath the Frisch grid. According to Shockley-Ramo theory, the weighting potential (Figure 5) can be obtained by setting the potential of the anode to 1 and the cathode and Frisch grid to 0 [24]. From this viewpoint, the weighting potential in the interaction region is invariable so that charge motion in this region has no contribution to the induced charge on the anode. As a result, the detector is primarily sensitive to the electron charge carriers passing through the measurement region.
Frisch grid detectors
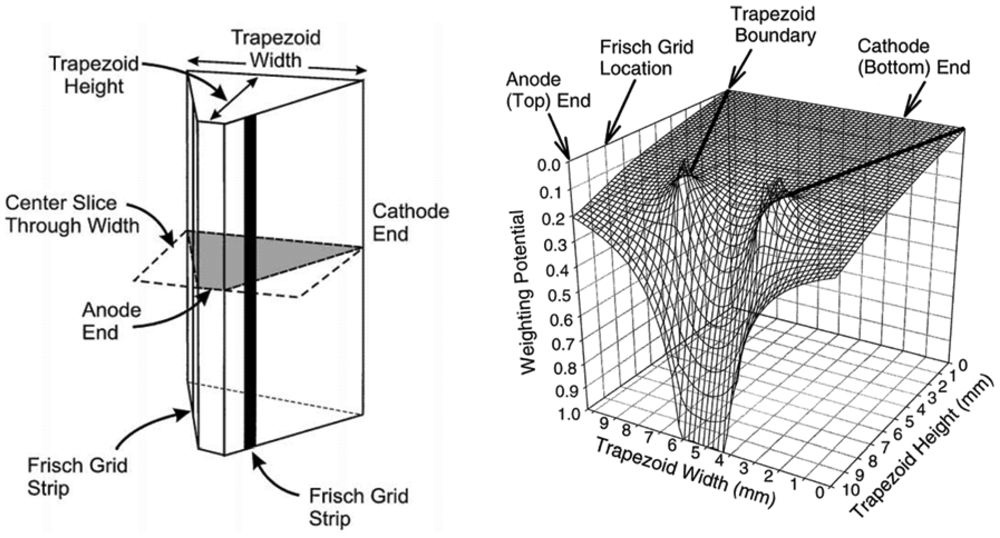
The most studied structures for such semiconductor detectors include the Frisch strip detector [24,26], trapezoid prism detector [27,28] and insulated Frisch ring detector [29–34]. The first single model was built by McGregor et al. [24,26] with two parallel metal strip electrodes on opposite faces of the device. The metal strips, similar to Frisch grid, have a small width and are placed near the anode so that the measurement region is considerably smaller than the interaction region. In addition, a negative voltage can be applied to both of the two side strips to assist electrons in drifting towards the anode. Energy resolution of 5.91% FWHM at 662 keV gamma rays was obtained with this configuration. This result is less-than-ideal; nevertheless, it was a great improvement in energy resolution in comparison with planar detectors. It was also observed that energy resolution results were correlated with width-to-length ratio of the strip. Another version of the Frisch grid device, called the trapezoid prism detector (Figure 6), was developed by combining geometric weighting effect, small pixel effect (mentioned in Section 3.3.2) and Frisch grid effect [27]. Main characteristic of this device is its geometric shape design, e.g., a larger volume of interaction region. This allows the fraction of events occurring in the interaction region to become dramatically increased. Accordingly, the gamma ray sensitivity in this region is enhanced. The energy resolution achieved with this device is 2.68% at FWHM for 662 keV gamma rays without any correction or processing, and that performance exceeds the Frisch strip detector by an enormous amount. The additional study have also demonstrated the soundness of this design [28].
Both of the two structures mentioned above suffer from severe surface leakage currents between the grid and anode, especially under conditions of higher applied voltage. This problem is definitely a limitation for detectors when trying to gain better performance. The capacitive Frisch grid detector (or “insulated Frisch ring detector”, Figure 7) designed by McGregor and colleagues [29,30,33] was based on the concept of screening effect [34].
This design consists of a bar-shape detector and a conductive ring with a thin layer of dielectric material between them, which greatly reduces the leakage current between the grid and anode due to the non-contacting effect. Excellent results of energy resolution were obtained of 1.7% FWHM at 662 keV. It should be noted that a problem of poor detector response in the pulse-height spectra often occurs due to the slow-rising events phenomenon, and that a chemical treatment for surface processing can be applied to solve this problem [30]. Several design parameters were investigated using finite-element analysis (FEA). These design parameters focus on the anode areas, the ratio of screen length to device height, the ratio of anode diameter to device height and the ratio of insulator thickness to relative permittivity [31,32]. The aim of the FEA simulation is to derive a compressed weighting potential toward the anode and thus improving energy resolution.
4.2. Pixelate Electrodes
Small pixel effect
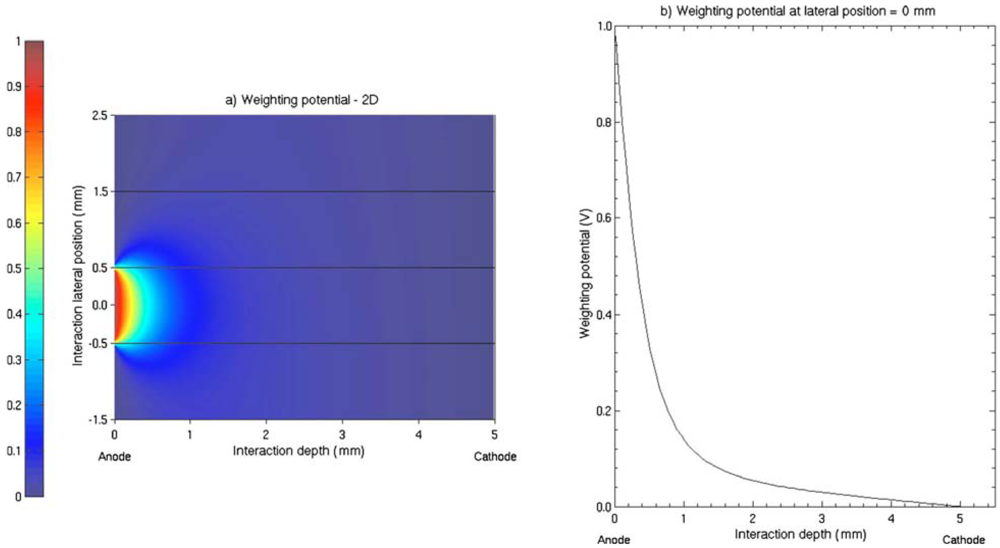
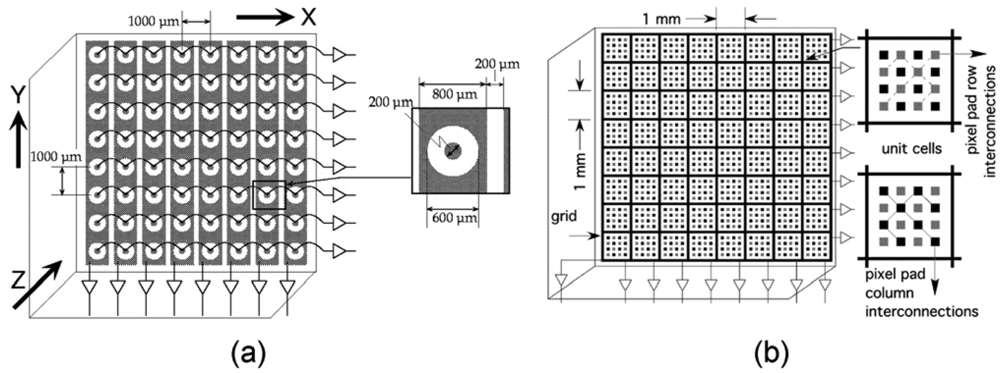
Pixelate detectors are the best choice for use in medical imaging since they allow directly for position determination, and semiconductor pixel arrays are more attractive than scintillators in that they can obtain better energy resolution easily [35]. The basic structure of pixel arrays is shown in Figure 8(a). The basis of this design is that charge extraction becomes more localized near the anode as the ratio of width to thickness of the pixel cell (aspect ratio) is decreased. This effect is called “small pixel effect” or “near-field effect”, which is explained in detail by Barrett et al. in [36]. The weighting potential distribution is shown in Figure 9.
Commonly, the small-pixel-effect device can deliver good energy resolution with the required corresponding pixel size, and has the advantage of rendering information on spatial interaction locations. Therefore, it allows for operation as an imaging array similar to some scintillation crystal imaging arrays. Experimental results confirm the single charge carrier sensing property of CdZnTe pixelate detectors based on this small pixel effect [38,39]. Among the design considerations are optimal detector thickness [38] and optimal contact geometries [40]. A suitable “aspect ratio” can obtain good energy resolution and detection efficiency; and optimal contact geometry, including pixel size and width of gap and grid, will enhance the charge efficiency on the pixel contacts and reduce charge collection differences resulting from interaction depth variations.
Recently, prototypes of pixelate detectors were developed by several groups, such as the detectors by Electronic, Technology, and Instrumentation Laboratory, French Atomic Energy Commission (CEA-LETI) [42,43] and University of Arizona (UA) [44,45]. A detector developed by CEA-LETI has a large active area (180 × 215 mm2, see Figure 10) and reaches an energy resolution of 4.7% FWHM at 140 keV with BP correction [42]. A semiSPECT detector reported by UA is characteristic of small pixel size (typically 0.38 mm) and high sensitivity. The spatial resolution along the axis is 1.45 mm and the energy resolution is 10% FWHM at 140 keV. There was also a kind of pixelate CdZnTe drift detector reported by Kuvveletli and Budtz-Jørgensen in 2005 [46]. Energy resolution of this drift detector is 3% FWHM at 122 keV with pixels of 0.2 mm dimensions. A commercial micro-SPECT system using a CdZnTe pixelate detector was reported in 2006 [47,48].
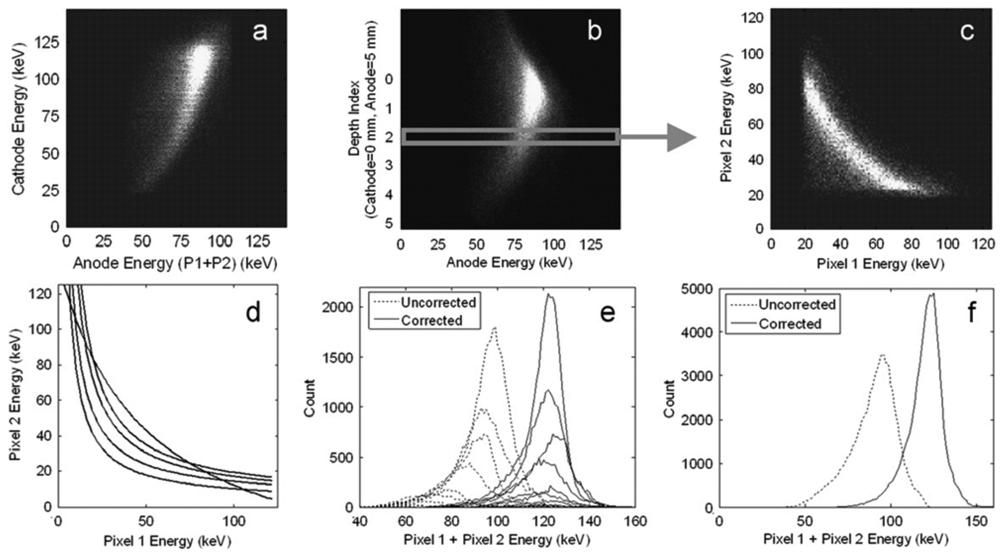
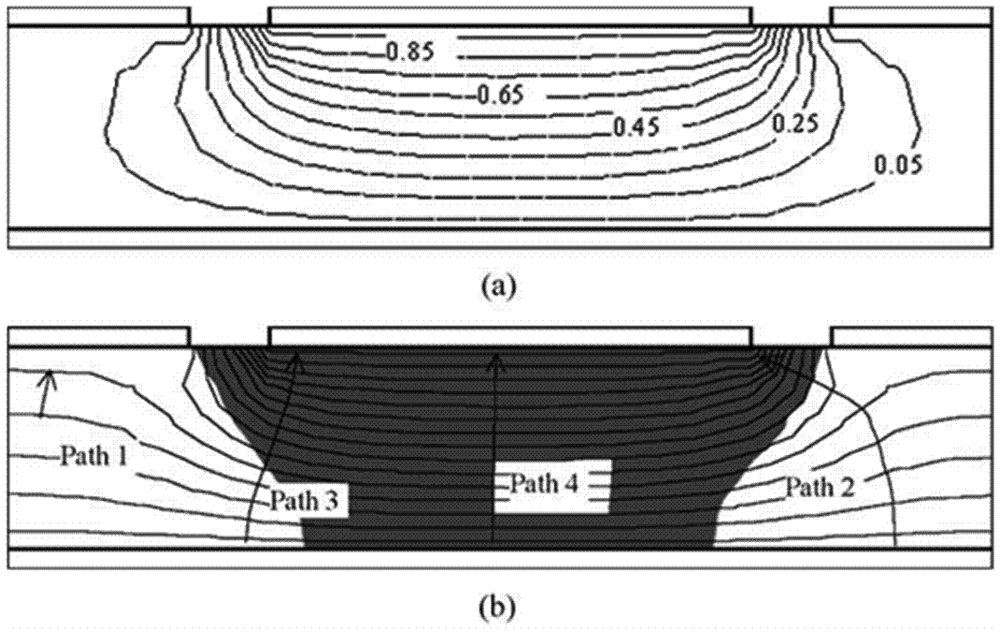
One drawback of pixelate detectors is that the pixelate devices suffer from charge sharing problem among pixels. The electronics to solve this problem can be challenging. A data correction method (Figure 11) was reported to correct two-pixel charge sharing events [49]. According to this method, the output signal reduction results from two aspects: induced charge dependence of DOI and the influence of lateral interaction location on charge collection efficiency. The induced charge is dependent on the DOI because of some electron trapping and non-zero weighting potential distribution in the region far away from the anode. The charge inefficiency phenomenon due to the lateral interaction location can be seen in Figure 11(c). The events distribution does not follow a diagonal line as it should have because charge sharing occurs between two adjacent pixels. The sum signal of the two charge sharing pixels between the anode pads has more electron loss. Therefore, both corrections, including a DOI correction and a lateral interaction correction, should be applied together to solve charge sharing problem (Figure 11).
4.3. Coplanar-Grid Detectors
The coplanar-grid electrode concept, first reported by Luke [50,51] and based on the principle of Frisch grids, was an innovative single charge sensing method using parallel strip electrodes on the anode. These strip electrodes are connected in an alternate manner to form two banks of grid electrodes (Figure 9(b), here we call them electrode 1 and 2). One set of the grids, electrode 1, are applied by a slightly higher positive voltage than that of electrode 2. Thus the selected charge carriers are always collected by electrode 1. The output signal can be obtained by reading the difference signal between these two sets of electrodes.
The weighting potential distribution that is obtained using finite element analysis is shown in Figure 12. It is obvious that there is an abrupt variance for weighting potential distribution in the vicinity of anode. Hence, only the carriers drifting to the area near the anode will contribute a lot to the induced charge on the electrode. The weighting potential distribution effect, which is formed in this structure, is equivalent to that formed by two parallel strips on side surfaces (dashed line in Figure 12) on a Frisch grid detector. Therefore, the charge collecting effect is much similar to that of Frisch grid detector. From the perspective of “capacitance coupling method” analysis, the weighting factor Ca(x)/Ct(x) is equal to x/(2L) since the area of collecting electrodes is just one-half of that of the similar planar detector. With this version of detector, an energy resolution of 3.1% FWHM at 662 keV was obtained initially [50,51] and the most promising result was as good as 1.3% FWHM in [52]. However, that result is still much worse than theoretical predicted value of ∼0.3% FWHM.
The key for coplanar grid design is that the weighting potential of the two anode grids are almost equal inside most of the detector volume except the vicinity of the anode. Therefore the subtraction of the two anode grids signal achieves a near-zero weighting potential inside most of the volume. As a result the subtraction signal is only sensitive to the motion of electrons in the vicinity of the anode. Several factors resulting in performance degradation have been studied [4,50,53,54], including electron trapping due to the spatial non-uniformity of the CdZnTe materials and coplanar grid electrode patterns. Luke solved the electron trapping problem that affects the detector performance by reducing the gain of non-collecting grid signals, however, such a compensation method only provides a correction in the circumstance that electron trapping is linear with interaction depth [50,51,53]. A further study by He's group proposed a correction method for electron trapping in the non-linear case using a position sensing technique [52,55]. This technique also shows that better energy resolution can be obtained for those events near cathode than that near anode, whereas electron trapping would be the most severe for events generated near cathode since they drift the longest distance to reach the anode. From this viewpoint, it can be inferred that the primary limiting factor that results in resolution degradation is not the electron trapping. He et al. verified this point and identified the problems of non-symmetric effect that causes detector performance degradation. By adding a boundary electrode and then adjusting the strip width of the outermost grids [56], the detector performance was more uniform at different interaction depths.
A drawback of coplanar-grid detector is that it requires two sets of output readout electronics, which inevitably will import more electronic noises. In addition, there is a trade-off between the excessive noise and collection efficiency of the coplanar anodes. The bias voltage should be sufficient to collect enough carriers but cannot reach a very high level before electric noises and leakage currents begin to overwhelm the effective signals.
4.4. Hemispherical Electrodes
The basic concept of hemispherical electrodes is to increase the electric field in the region of the detector where carrier trapping is more frequent, thus attaining a uniform charge collection across the whole area of the detector [57–59]. As shown in Figure 13, this version of electrode is designed with such a shape that there is a small plane anode and a nearly spherical surface as the cathode.
Such a design has two primary effects: one is that a higher electric field near the anode can sweep holes more effectively; the other effect is that more charge carriers are generated near the cathode and the holes concentration near the anode is very small. The combination of these two effects renders the hemispherical electrodes as a single-charge-sensing electrode. With this configuration, energy resolution of 6% FWHM at 662 keV was obtained using a detector with dimensions of 10 × 10 × 5 mm3[60]. This kind of detector, which was designed by Parnham et al. [61] with a full-area anode and an extended cathode, is commercially available. The dimension of this detector is 5 × 5 × 5 mm3 with energy resolution of less than 1.9% FWHM at 662 keV achieved with the optimal configuration.
4.5. Strip Electrodes
A research group at the University of New Hampshire Space Science Center developed the earliest prototype of CdZnTe strip detector [62–64]. This device was designed using a monolithic CdZnTe substrate with orthogonal strips on each surface, so that a “pixel” is generated in the overlapping area of two cross orthogonal strips. Position determination can be achieved with this design and good spatial resolution could be obtained with small width strips. Furthermore, a concept of signal analysis was proposed in which the pulse height of neighboring strips can be used to locate individual events more precisely and their sum is a more accurate measurement of gamma ray energy. The drawbacks of this two-sided electrode design are that the signal on cathode, which has a comparatively slow rise-time, still suffers from hole trapping and that it needs electronic readout on both of the two sides.
Three-electrode model
The new concept of “three-electrode model” or “coplanar pixel and control electrode model”, which was reported in 1997 by Lingren et al. [65] and Butler [66], aimed at suppressing the long spectrum tail at low energy. This model consists of three electrodes: the cathode, the anode (the collecting electrode) and a control electrode (Figure 14). Many of such models can be connected together to form a gamma ray detector (Figure 8(c)). The control electrode has two functions: one is to assist the anode in focusing most of the charge carriers from the entire volume of the detector; the other function is to reduce electron trapping by shaping the electric field in the detector in such a way that electrons will reach the anode much faster. The real electric field and weighting potential distribution of the three-electrode are shown in Figure 15. Both of the electric field and weighting potentials near the anode are intensive so that the induced charge is independent of interaction position. Therefore, both of the energy resolution and photopeak efficiency can be greatly improved by mitigating the contribution of hole trapping on the output signal. Based on this basic three-electrode idea, a multiple electrode detector model that was equipped with five electrodes was reported in 2007. (more details can be seen in [67].
Detector design
Two kinds of strip detector (Figure 16), an orthogonal coplanar strip detectors [69,70] and a charge-sharing strip detector [13], were developed by the University of New Hampshire and based on the concept of the three-electrode model metioned above. Both of these designs belong to single-sided detector that can contribute N2 pixels but only need 2N electronics, which greatly reduce the power requirement and complexity of the device electronics. As for the orthogonal strip detector, a bias voltage difference is required to be applied between the anode and control electrode. This difference value is dependent on its geometric design [68,71]. A higher difference value would result in more leakage current. Typical signals generated in this version detector are shown in Figure 17. X- and Y-coordinates of the event interaction location could be identified by the “strip signal” and “pixel row signal” respectively. Furthermore, the interaction depth (Z-coordinate value) can be inferred qualitatively from the characteristics of the cathode signal or quantitatively from the ratio of the cathode signal to the largest “pixel row signal”. With this design, energy resolution of 1% FWHM at 662 keV was obtained with a 5 mm thick detector [13].
Compared to an orthogonal strip detector, the advantages of the charge-sharing strip detector include: (1) the electronics are simplified due to fact that the row and column electrodes are identical and therefore their output signals are of the same shape; (2) the grid electrodes have a larger area and thus they can provide a more effective non-collecting signal than that provided by the individual strip electrodes in orthogonal strip detector. The disadvantage, however, is that electronic noises are generated from so many pads and also by adding the signal of these pads. Further design details for the two versions of detectors, including the analog processing circuits design [72], edge and corner effect problems [73], and how to balance the pad dimensions and the detector thickness (electron clouds effedt) [13,74–76], can be referred in corresponding references.
Another kind of strip detector concept, which is called drift strip detector, was first introduced in 1987 and developed using silicon material [77]. Then Patt et al. [78] applied this design to developing a high-Z compound semiconductor detector using HgI2 and fabricated a detector prototype that achieved an energy resolution of 0.9% at 662 keV.
The first CdZnTe drift detector was developed in the Danish Space Research Institute [79,80] and its schematic diagram is shown in Figure 18. This type of detector is single-sided with a planar electrode on one side and strip electrodes on the other side. An readout anode is in the center surrounded by several drift electrodes, which provide an electrostatic shield to the readout anode so that the sensitivity to hole trapping is reduced. The best energy resolution performance obtained with this detector is 0.8% at 356 keV with spectrum correction for hole trapping [81]. In such a detector, DOI can also be derived by analyzing a parameter R, which is the ratio of the signal on the cathode to that on the readout anode. Compared with a coplanar grid detector, this drift strip detector has simpler electronics since no summing and subtracting circuits are needed.
A summary of the features and performances of CdZnTe detectors with different geometries mentioned above is shown in Table 1. Some studies focus on the effect of different electrode geometries, aiming to compare the performance of them. For example, the performance of detectors with different anode contact geometries was investigated in [82] using the same crystal and same output electronics. The results show that it is the detector with single pixel geometry that presents the best performance for both low- and high-energy gamma ray sources.
5. 3-D Position Sensing Technique and Compton Imaging Detector
Electron trapping problems
Although hole trapping is the key factor in degrading spectrum performance, electron trapping does exist in practice. It was observed experimentally that around 5–10% of electrons that are generated by γ-ray interactions are trapped on a 1 cm thick CdZnTe detector [52]. The electron trapping effect on the signals on electrodes was found in Luke's coplanar grid detector because the subtraction signal is dependent of DOI [51]. Luke solved this problem by reducing the gain of non-collecting grid signal in order to compensate for the electron charge losses. However, this compensation method is based on an assumption that the electron trapping is a linear function of DOI. Therefore, it can only be used on occasions where electron trapping is not too severe and is spatially uniform. A more accurate method for correcting electron trapping in the non-linear case was first reported by He et al. [52] using the depth sensing method. The DOI can be inferred by the ratio of the cathode to anode signal and a position resolution of 0.9 mm FWHM at 122 keV was obtained. With electron trapping correction, detector performance would be further improved.
The first prototype of 3-D position sensing spectrometer was developed and introduced by He et al. [83,84] based on the 2-D position sensing method and depth sensing technique using a pixelate detector array. This 3-D position sensing technique can be effectively used for correcting material non-uniformity and electron trapping. It also has advantages in analyzing detector response so that the possible defects that significantly degrade the energy resolution can be identified clearly. For example, it was demonstrated experimentally that small lateral size electron-trapping defects do significantly degrade energy resolution of the corresponding pixels, but larger ones do not [85]. Another three generations of spectrometers were subsequently reported in 2004 [86], 2005 [87,88], 2007 [89] and 2012 [90] with different generations of ASIC readout systems respectively.
Depth sensing technique in CdZnTe enables Compton imaging [91–93], which can be used to localize the position of radiation source. Compton scatters generated in the CdZnTe detectors will give rise to two gamma-ray interaction events. When both of the energy and position of the two events are measured using 3-D position technique, the direction of the radiation source can be determined by a back projection cone. Compton imaging technique makes it possible to perform intelligent gamma-ray spectroscopy. A typical Intelligent Personal Radiation Locator (IPRL) system was developed and reported by GE researchers [94]. This IPRL detector consists of multiple CdZnTe modules and each module has a CdZnTe crystal with dimensions of 15 × 15 × 10 mm3. Having a tatal volume of approximately 700 cm3 and weighing under 900 g, the IPRL system (Figure 19) can achieve an energy resolution of 5% FWHM at 122 keV and a location accuracy of less than 4 m.
A corresponding networked system of IPRLs was also designed to improve the abilities of detection, localization, and identification for potential radiological threats [95]. For Compton imaging camera, the angular resolution is a key performance parameter. However, it is limited by the lateral position resolution that is always determined by the pixel pitch dimensions of the detector. A sub-pixel position sensing method was studied by Zhu et al. [96] based on non-charge-collecting transient signals [97,98]. The fundamental is that the peak amplitudes of the eight-adjacent neighboring transient signals are dependent of the lateral position of the electron clouds that enter the anode region. This method breaks though the limit of position resolution by pixel pitch of CdZnTe detectors and effectively improves the angular resolution of Compton imaging camera.
6. Conclusions
The CdZnTe semiconductor is now regarded as the most promising candidate for the next generation of gamma ray detectors, with the increasing demand for gamma ray imaging devices and significant progress in producing high quality crystals. For imaging devices, CdZnTe semiconductor can obtain good energy resolution easily in comparison with scintillation detectors. Furthermore, spectroscopic performance can be improved effectively by designing special electrode geometry and developing new electronic signal processing techniques. Some technique renders the energy resolution to be greatly improved to below 1% FWHM. However, there is still some room for improvement in real applications, including production of large and uniform crystals, design of very small electrodes (<100 microns), signal processing methods and Application Specific Integrated Circuit (ASIC) with low electronic noise and leakage current. The combination of these techniques will produce a gamma ray detector with good energy resolution and detection efficiency.
Acknowledgments
This work is supported by the National Key Instrumentation Development Project Foundation of China (2011YQ030114), the National Basic Research Program of China (973 Program, 2011CB707500); the National Natural Science Foundation of China (11104058) and the Natural Science Foundation of Hebei Province (A2011201155). We thank Thomas FitzGibbon, Asael Papour from UCLA and Ivan Vuletic for commenting on the draft of the manuscript.
References
- Bradford Barber, H. Applications of semiconductor detectors to nuclear medicine. Nucl. Instrum. Methods Phys. Res. A 1999, 436, 102–110. [Google Scholar]
- Verger, L.; Boitel, M.; Gentet, M.C.; Hamelin, R.; Mestais, C.; Mongellaz, F.; Rustique, J.; Sanchez, G. Characterization of CdTe and CdZnTe detectors for gamma-ray imaging applications. Nucl. Instrum. Methods Phys. Res. A 2001, 458, 297–309. [Google Scholar]
- Kaufman, L.; Ewins, J.; Rowan, W.; Hosier, K.; Okerlund, M.; Ortendahl, D. Semiconductor Gamma-Cameras in Nuclear Medicine. IEEE Trans. Nucl. Sci. 1980, 27, 1073–1079. [Google Scholar]
- Luke, P.N.; Eissler, E.E. Performance of CdZnTe coplanar-grid gamma-ray detectors. IEEE Trans. Nucl. Sci. 1996, 43, 1481–1486. [Google Scholar]
- Brunett, B.A.; Van Scyoc, J.M.; Schlesinger, T.E.; James, R.B. The spatial response of CdZnTe gamma-ray detectors as measured by gamma-ray mapping. Nucl. Instrum. Methods Phys. Res. A 2001, 458, 76–84. [Google Scholar]
- Luke, P.N.; Amman, M.; Lee, J.S. Factors affecting energy resolution of coplanar-grid CdZnTe detectors. IEEE Trans. Nucl. Sci. 2004, 51, 1199–1203. [Google Scholar]
- Takahashi, T.; Watanabe, S. Recent progress in CdTe and CdZnTe detectors. IEEE Trans. Nucl. Sci. 2001, 48, 950–959. [Google Scholar]
- Shockley, W. Currents to Conductors Induced by a Moving Point Charge. J. Applied Phys. 1938, 9, 635–636. [Google Scholar]
- Ramo, S. Currents Induced by Electron Motion. Proc. IRE 1939, 27, 584–585. [Google Scholar]
- He, Z. Review of the Shockley-Ramo theorem and its application in semiconductor gamma-ray detectors. Nucl. Instrum. Methods Phys. Res. A 2001, 463, 250–267. [Google Scholar]
- Lingren, C.L.; Butler, J.F. Evaluating the performance of semiconductor radiation detectors through static charge analysis. IEEE Trans. Nucl. Sci. 1998, 45, 1723–1725. [Google Scholar]
- Purcell, E.M. Electricity and Magnetism; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Macri, J.R.; Hamel, L.A.; Julien, M.; Miller, R.S.; Donmez, B.; McConnell, M.L.; Ryan, J.M.; Widholm, M. Single-sided CZT strip detectors. IEEE Trans. Nucl. Sci. 2004, 51, 2453–2460. [Google Scholar]
- Del Sordo, S.; Abbene, L.; Caroli, E.; Mancini, A.M.; Zappettini, A.; Ubertini, P. Progress in the development of CdTe and CdZnTe semiconductor radiation detectors for astrophysical and medical applications. Sensors 2009, 9, 3491–3526. [Google Scholar]
- Auricchio, N.; Caroli, E.; de Cesare, G.; Donati, A.; Dusi, W.; Hage-Ali, M.; Landini, G.; Perillo, E.; Siffert, P. Investigation of response behavior in CdTe detectors versus interelectrodic charge formation position. Proceedings of Nuclear Science Symposium, Toronto, ON, Canada, 8–14 November 1998.
- Ivanov, V.I.; Garbusin, V.A.; Dorogov, P.G.; Loutchanski, A.E.; Kondrashov, V.V. Spectrometric characteristic improvement of CdTe detectors. IEEE Trans. Nucl. Sci. 1995, 42, 258–262. [Google Scholar]
- Keele, B.D.; Addleman, R.S.; Troyer, G.L. A method to improve spectral resolution in planar semiconductor gamma-ray detectors. IEEE Trans. Nucl. Sci. 1996, 43, 1365–1368. [Google Scholar]
- Bargholtz, C.; Fumero, E.; Mårtensson, L. Model-based pulse shape correction for CdTe detectors. Nucl. Instrum. Methods Phys. Res. A 1999, 434, 399–411. [Google Scholar]
- Cardoso, J.M.; Simões, J.B.; Menezes, T.; Correia, C.M.B.A.; Simões, J.B.l.; Menezes, T.; Correia, C.M.B.A. CdZnTe spectra improvement through digital pulse amplitude correction using the linear sliding method. Nucl. Instrum. Methods Phys. Res. A 2003, 505, 334–337. [Google Scholar]
- Auricchio, N.; Amati, L.; Basili, A.; Caroli, E.; Donati, A.; Franceschini, T.; Frontera, F.; Landini, G.; Roggio, A.; Schiavone, F.; et al. Twin shaping filter techniques to compensate the signals from CZT/CdTe detectors. IEEE Trans. Nucl. Sci. 2005, 52, 1982–1988. [Google Scholar]
- Shor, A.; Eisen, Y.; Mardor, I. Optimum spectroscopic performance from CZT γ- and X-ray detectors with pad and strip segmentation. Nucl. Instrum. Methods Phys. Res. A 1999, 428, 182–192. [Google Scholar]
- Bolotnikov, A.E.; Camarda, G.S.; Cui, Y.; De Geronimo, G.; Fried, J.; Gul, R.; Hossain, A.; Kim, K.; Yang, G.; Vernon, E.; et al. Rejecting incomplete charge-collection events in CdZnTe and other semiconductor detectors. Nucl. Instrum. Methods Phys. Res. A 2012, 664, 317–323. [Google Scholar]
- Frisch, O. British Atomic Energy Report BR-49; Atomic Energy Research Establishment: Harwell, UK, 1944. [Google Scholar]
- McGregor, D.S.; He, Z.; Seifert, H.A.; Wehe, D.K.; Rojeski, R.A. Single charge carrier type sensing with a parallel strip pseudo-Frisch-grid CdZnTe semiconductor radiation detector. Appl. Phys. Lett. 1998, 72, 792–794. [Google Scholar]
- Göök, A.; Hambsch, F.J.; Oberstedt, A.; Oberstedt, S. Application of the Shockley-Ramo theorem on the grid inefficiency of Frisch grid ionization chambers. Nucl. Instrum. Methods Phys. Res. A 2012, 664, 289–293. [Google Scholar]
- McGregor, D.S.; He, Z.; Seifert, H.A.; Rojeski, R.A.; Wehe, D.K. CdZnTe semiconductor parallel strip Frisch grid radiation detectors. IEEE Trans. Nucl. Sci. 1998, 45, 443–449. [Google Scholar]
- McGregor, D.S.; Rojeski, R.A.; He, Z.; Wehe, D.K.; Driver, M.; Blakely, M. Geometrically weighted semiconductor Frisch grid radiation spectrometers. Nucl. Instrum. Methods Phys. Res. A 1999, 422, 164–168. [Google Scholar]
- McGregor, D.S.; Nishanth, Y.R.; Wehe, D.K. Low-energy gamma-ray characterization of a trapezoidal-shaped geometrically weighted Frisch grid CdZnTe gamma-ray spectrometer. Nucl. Instrum. Methods Phys. Res. A 2001, 457, 230–244. [Google Scholar]
- McNeil, W.J.; McGregor, D.S.; Bolotnikov, A.E.; Wright, G.W.; James, R.B. Single-charge-carrier-type sensing with an insulated Frisch ring CdZnTe semiconductor radiation detector. Appl. Phys. Lett. 2004, 84, 1988–1990. [Google Scholar]
- Bolotnikov, A.E.; Camarda, G.S.; Carini, G.A.; Wright, G.W.; McGregor, D.S.; McNeil, W.; James, R.B. New results from performance studies of Frisch-grid CdZnTe detectors. Proc. SPIE 2004, 5540, 33–45. [Google Scholar]
- Hu, D.; Wang, L.; Min, J.; Qin, K.; Zhang, J.; Huang, J.; Xia, Y. Study on capacitive Frisch grid CdZnTe detector parameter optimization and fabrication. Phys. Status Solidi 2010, 7, 1700–1702. [Google Scholar]
- Shi, Z.; Wang, L.; Min, J.; Qin, K.; Liang, X.; Zhang, J.; Huang, J.; Tang, K.; Xia, Y. Study on the spectrum improvement of a capacitive Frisch grid structure for CdZnTe Detector. Radiat. Measur. 2011, 46, 457–460. [Google Scholar]
- Bolotnikov, A.E.; Camarda, G.C.; Carini, G.A.; Fiederle, M.; Li, L.; McGregor, D.S.; McNeil, W.; Wright, G.W.; James, R.B. Performance characteristics of Frisch-ring CdZnTe detectors. IEEE Trans. Nucl. Sci 2006, 53, 607–614. [Google Scholar]
- Montemont, G.; Argues, M.; Verger, L.; Rustique, J. A capacitive Frisch grid structure for CdZnTe detectors. Proceedings of IEEE Nuclear Science Symposium, Lyon, France, 15–20 October 2000; pp. 9–12.
- Barber, H.B.; Apotovsky, B.A.; Augustine, F.L.; Barrett, H.H.; Dereniak, E.L.; Doty, F.P.; Eskin, J.D.; Hamilton, W.J.; Marks, D.G.; Matherson, K.J.; et al. Semiconductor pixel detectors for gamma-ray imaging in nuclear medicine. Nucl. Instrum. Methods Phys. Res. A 1997, 395, 421–428. [Google Scholar]
- Barrett, H.H.; Eskin, J.D.; Barber, H.B. Charge transport in arrays of semiconductor gamma-ray detectors. Phys. Rev. Lett. 1995, 75, 156–159. [Google Scholar]
- Montemont, G.; Gentet, M.C.; Monnet, O.; Rustique, J.; Verger, L. Simulation and design of orthogonal capacitive strip CdZnTe detectors. IEEE Trans. Nucl. Sci. 2007, 54, 854–859. [Google Scholar]
- Brunett, B.A.; Van Scyoc, J.M.; James, R.B.; Schlesinger, T.E. CdZnTe pixel array detectors and implications for producing large volume gamma-ray spectrometers. J. Appl. Phys. 1999, 86, 3926–3933. [Google Scholar]
- Abbene, L.; Del Sordo, S.; Agnetta, G.; Biondo, B.; Caroli, E.; Mangano, A.; Russo, F.; Stephen, J.B.; Ventura, G.; Carlino, A.; et al. Investigation on pixellated CZT detectors coupled with a low power readout ASIC. Proceedings of IEEE Nuclear Science Symposium, Dresden, Germany, 19– 25 October 2008; pp. 478–483.
- Bolotnikov, A.E.; Boggs, S.E.; Chen, C.M.H.; Cook, W.R.; Harrison, F.A.; Schindler, S.M. Optimal contact geometry for CdZnTe pixel detectors. Proc. SPIE 2000, 4141, 243–252. [Google Scholar]
- Myronakis, M.E.; Darambara, D.G. Monte Carlo investigation of charge-transport effects on energy resolution and detection efficiency of pixelated CZT detectors for SPECT/PET applications. Med. Phys. 2011, 38, 455–467. [Google Scholar]
- Verger, L.; Gentet, M.C.; Gerfault, L.; Guillemaud, R.; Mestais, C.; Monnet, O.; Montemont, G.; Petroz, G.; Rostaing, J.P.; Rustique, J. Performance and perspectives of a CdZnTe-based gamma camera for medical imaging. IEEE Trans. Nucl. Sci. 2004, 51, 3111–3117. [Google Scholar]
- Mestais, C.; Baffert, N.; Bonnefoy, J.P.; Chapuis, A.; Koenig, A.; Monnet, O.; Ouvrier Buffet, P.; Rostaing, J.P.; Sauvage, F.; Verger, L. A new design for a high resolution, high efficiency CZT gamma camera detector. Nucl. Instrum. Methods Phys. Res. A 2001, 458, 62–67. [Google Scholar]
- Kastis, G.A.; Wu, M.C.; Balzer, S.J.; Wilson, D.W.; Furenlid, L.R.; Stevenson, G.; Barber, H.B.; Barrett, H.H.; Woolfenden, J.M.; Kelly, P.; et al. Tomographic small-animal imaging using a high-resolution semiconductor camera. IEEE Trans. Nucl. Sci. 2002, 49, 172–175. [Google Scholar]
- Kim, H.; Furenlid, L.R.; Crawford, M.J.; Wilson, D.W.; Barber, H.B.; Peterson, T.E.; Hunter, W.C.; Liu, Z.; Woolfenden, J.M.; Barrett, H.H. SemiSPECT: A small-animal single-photon emission computed tomography (SPECT) imager based on eight cadmium zinc telluride (CZT) detector arrays. Med. Phys. 2006, 33, 465–474. [Google Scholar]
- Kuvvetli, I.; Budtz-Jorgensen, C. Pixelated CdZnTe drift detectors. IEEE Trans. Nucl. Sci. 2005, 52, 1975–1981. [Google Scholar]
- Wagenaar, D.J.; Zhang, J.; Kazules, T.; Vandehei, T.; Bolle, E.; Chowdhury, S.; Parnham, K.; Patt, B.E. In vivo dual-isotope SPECT imaging with improved energy resolution. Proceedings of IEEE Nuclear Science Symposium, San Diego, CA, USA, 29 October– 1 November 2006; pp. 3821–3826.
- Parnham, K.B.; Chowdhury, S.; Li, J.; Wagenaar, D.J.; Patt, B.E. Second-Generation, Tri-Modality Pre-Clinical Imaging System. Proceedings of IEEE Nuclear Science Symposium, San Diego, CA, USA, 29 October– 1 November 2000; pp. 1802–1805.
- Wangerin, K.; Du, Y.; Jansen, F. CZT performance for different anode pixel geometries and data corrections. Nucl. Instrum. Methods Phys. Res. A 2011, 648 (Suppl. 1), S37–41. [Google Scholar]
- Luke, P.N. Single polarity charge sensing in ionization detectors using coplanar electrodes. Appl. Phys. Lett. 1994, 65, 2884–2886. [Google Scholar]
- Luke, P.N. Unipolar charge sensing with coplanar electrodes-application to semiconductor detectors. IEEE Trans. Nucl. Sci. 1995, 42, 207–213. [Google Scholar]
- He, Z.; Knoll, G.F.; Wehe, D.K.; Miyamoto, J. Position-sensitive single carrier CdZnTe detectors. Nucl. Instrum. Methods Phys. Res. A 1997, 388, 180–185. [Google Scholar]
- Luke, P.N. Electrode configuration and energy resolution in gamma-ray detectors. Nucl. Instrum. Methods Phys. Res. A 1996, 380, 232–237. [Google Scholar]
- Luke, P.N.; Amman, M.; Prettyman, T.H.; Russo, P.A.; Close, D.A. Electrode design for coplanar-grid detectors. IEEE Trans. Nucl. Sci. 1997, 44, 713–720. [Google Scholar]
- He, Z.; Knoll, G.F.; Wehe, D.K.; Rojeski, R.; Mastrangelo, C.H.; Hammig, M.; Barrett, C.; Uritani, A. 1-D position sensitive single carrier semiconductor detectors. Nucl. Instrum. Methods Phys. Res. A 1996, 380, 228–231. [Google Scholar]
- He, Z.; Knoll, G.F.; Wehe, D.K.; Du, Y.F. Coplanar grid patterns and their effect on energy resolution of CdZnTe detectors. Nucl. Instrum. Methods Phys. Res. A 1998, 411, 107–113. [Google Scholar]
- Malm, H.L.; Canali, C.; Mayer, J.W.; Nicolet, M.A.; Zanio, K.R.; Akutagawa, W. Gamma-ray spectroscopy with single-carrier collection in high-resistivity semiconductors. Appl. Phys. Lett. 1975, 26, 344–346. [Google Scholar]
- Zanio, K. Use of various device geometries to improve the performance of CdTe detectors. Rev. Phys. Appl. 1977, 12, 343–347. [Google Scholar]
- Siffert, P. Cadmium telluride and related materials as x-ray and gamma-ray detectors: A review of recent progress. Proc. SPIE 1994, 2305, 98–109. [Google Scholar]
- Zanio, K.; Krajenbrink, F.; Montano, H. CdTe detectors from Indium-doped Tellurium-rich solutions. IEEE Trans. Nucl. Sci. 1974, 21, 315–321. [Google Scholar]
- Parnham, K.; Glick, J.B.; Szeles, C.; Lynn, K.G. Performance improvement of CdZnTe detectors using modified two-terminal electrode geometry. J. Cryst. Growth 2000, 214–215, 1152–1154. [Google Scholar]
- Doty, F.P.; Butler, J.F.; Hink, P.L.; Macri, J.R. Performance of submillimeter CdZnTe strip detectors. Proceedings of IEEE Nuclear Science Symposiumand Medical Imaging Conference, San Francisco, CA, USA, 21– 28 October 1995; pp. 80–84.
- Macri, J.R.; Apotovsky, B.A.; Butler, J.F.; Cherry, M.L.; Dann, B.K.; Drake, A.; Doty, F.P.; Guzik, T.G.; Larson, K.; Mayer, M.; et al. Development of an orthogonal-stripe CdZnTe gamma radiation imaging spectrometer. IEEE Trans. Nucl. Sci. 1996, 43, 1458–1462. [Google Scholar]
- Hamel, L.A.; Macri, J.R.; Stahle, C.M.; Odom, J.; Birsa, F.; Shu, P.; Doty, F.P. Signal generation in CdZnTe strip detectors. IEEE Trans. Nucl. Sci. 1996, 43, 1422–1426. [Google Scholar]
- Lingren, C.L.; Apotovsky, B.; Butler, J.F.; Conwell, R.L.; Doty, F.P.; Friesenhahn, S.J.; Oganesyan, A.; Pi, B.; Zhao, S. Cadmium-zinc-telluride, multiple-electrode detectors achieve good energy resolution with high sensitivity at room-temperature. Proceedings of IEEE Nuclear Science Symposium, Albuquerque, NM, USA, 9–15 November 1997; pp. 127–131.
- Butler, J.F. Novel electrode design for single-carrier charge collection in semiconductor nuclear radiation detectors. Nucl. Instrum. Methods Phys. Res. A 1997, 396, 427–430. [Google Scholar]
- Abbene, L.; Del Sordo, S.; Fauci, F.; Gerardi, G.; La Manna, A.; Raso, G.; Cola, A.; Perillo, E.; Raulo, A.; Gostilo, V.; et al. Spectroscopic response of a CdZnTe multiple electrode detector. Nucl. Instrum. Methods Phys. Res. A 2007, 583, 324–331. [Google Scholar]
- Hadong, K.; Cirignano, L.; Shah, K.; Squillante, M.; Wong, P. Investigation of the energy resolution and charge collection efficiency of Cd(Zn)Te detectors with three electrodes. IEEE Trans. Nucl. Sci. 2004, 51, 1229–1234. [Google Scholar]
- McConnell, M.L.; Macri, J.R.; Ryan, J.M.; Larson, K.; Hamel, L.A.; Bernard, G.; Pomerleau, C.; Tousignant, O.; Leroux, J.C.; Jordanov, V.T. Three-dimensional imaging and detection efficiency performance of orthogonal coplanar CZT strip detectors. Proc. SPIE 2000, 4141, 157–167. [Google Scholar]
- Jordanov, V.T.; Macri, J.R.; Clayton, J.E.; Larson, K.A. Multi-electrode CZT detector packaging using polymer flip chip bonding. Nucl. Instrum. Methods Phys. Res. A 2001, 458, 511–517. [Google Scholar]
- Mayer, M.; Hamel, L.A.; Tousignant, O.; Macri, J.R.; Ryan, J.M.; McConnell, M.L.; Jordanov, V.T.; Butler, J.F.; Lingren, C.L. Signal formation in a CdZnTe imaging detector with coplanar pixel and control electrodes. Nucl. Instrum. Methods Phys. Res. A 1999, 422, 190–194. [Google Scholar]
- Larson, K.; Jordanov, V.T.; McConnell, M.L.; Macri, J.R.; Ryan, J.M.; Drake, A.; Hamel, L.A.; Tousignant, O. Analog processing of signals from a CZT strip detector with orthogonal coplanar anodes. Proc. SPIE 2000, 4141, 336–341. [Google Scholar]
- Mardor, I.; Shor, A.; Eisen, Y. Edge and corner effects on spectra of segmented CdZnTe detectors. IEEE Trans. Nucl. Sci. 2001, 48, 1033–1040. [Google Scholar]
- Donmez, B.; Macri, J.R.; McConnell, M.L.; Ryan, J.M.; Widholm, M.; Narita, T.; Hamel, L.A. Further studies of single-sided charge-sharing CZT strip detectors. Proc. SPIE 2005, 5922, 62–70. [Google Scholar]
- Donmez, B.; Macri, J.R.; McConnell, M.L.; Ryan, J.M.; Widholm, M.; Hamel, L.A.; Narita, T. Continued studies of single-sided charge-sharing CZT strip detectors. Proceedings of IEEE Nuclear Science Symposium, San Juan, Puerto Rico, 23–29 October 2005; pp. 1408–1411.
- Hamel, L.A.; Benoit, M.; Donmez, B.; Macri, J.R.; McConnell, M.L.; Narita, T.; Ryan, J.M. Optimization of single-sided charge-sharing strip detectors. Proceedings of IEEE Nuclear Science Symposium, San Diego, CA, USA, 29 October–1 November 2006; pp. 3759–3761.
- Kemmer, J.; Lutz, G. New detector concepts. Nucl. Instrum. Methods Phys. Res. A 1987, 253, 365–377. [Google Scholar]
- Patt, B.E.; Iwanczyk, J.S.; Vilkelis, G.; Wang, Y.J. New gamma-ray detector structures for electron only charge carrier collection utilizing high-Z compound semiconductors. Nucl. Instrum. Methods Phys. Res. A 1996, 380, 276–281. [Google Scholar]
- van Pamelen, M.A.J.; Budtz-Jørgensen, C. Novel electrode geometry to improve performance of CdZnTe detectors. Nucl. Instrum. Methods Phys. Res. A 1998, 403, 390–398. [Google Scholar]
- van Pamelen, M.A.J.; Budtz-Jørgensen, C. CdZnTe drift detector with correction for hole trapping. Nucl. Instrum. Methods Phys. Res. A 1998, 411, 197–200. [Google Scholar]
- Kuvvetli, I.; Budtz-Jørgensen, C.; Gerward, L.; Stahle, C.M. Response of CZT drift-strip detector to X- and gamma rays. Radiat. Phys. Chem. 2001, 61, 457–460. [Google Scholar]
- Washington, A.; Teague, L.; Duff, M.; Burger, A.; Groza, M.; Buliga, V. The effect of various detector geometries on the performance of CZT using one crystal. J. Electr. Mater. 2011, 40, 1744–1748. [Google Scholar]
- He, Z.; Li, W.; Knoll, G.F.; Wehe, D.K.; Berry, J.; Stahle, C.M. 3-D position sensitive CdZnTe gamma-ray spectrometers. Nucl. Instrum. Methods Phys. Res. A 1999, 422, 173–178. [Google Scholar]
- Li, W.; He, Z.; Knoll, G.F.; Wehe, D.K.; Berry, J.E. A data acquisition and processing system for 3D position sensitive CZT gamma-ray spectrometers. IEEE Trans. Nucl. Sci. 1999, 46, 1989–1994. [Google Scholar]
- Feng, Z.; Zhong, H.; Xu, D. Analysis of detector response using 3-D position-sensitive CZT gamma-ray spectrometers. IEEE Trans. Nucl. Sci. 2004, 51, 3098–3104. [Google Scholar]
- Feng, Z.; Zhong, H.; Xu, D.; Knoll, G.F.; Wehe, D.K.; Berry, J.E. Improved resolution for 3-D position sensitive CdZnTe spectrometers. IEEE Trans. Nucl. Sci. 2004, 51, 2427–2431. [Google Scholar]
- Zhang, F.; He, Z. 3D position-sensitive CdZnTe gamma-ray spectrometers: Improved performance with new ASICs. Proc. SPIE 2004, 5540, 135–143. [Google Scholar]
- Feng, Z.; Zhong, H.; Knoll, G.F.; Wehe, D.K.; Berry, J.E. 3-D position sensitive CdZnTe spectrometer performance using third generation VAS/TAT readout electronics. IEEE Trans. Nucl. Sci. 2005, 52, 2009–2016. [Google Scholar]
- Feng, Z.; Zhong, H.; Seifert, C.E. A prototype three-dimensional position sensitive CdZnTe detector array. IEEE Trans. Nucl. Sci. 2007, 54, 843–848. [Google Scholar]
- Zhang, F.; Herman, C.; He, Z.; De Geronimo, G.; Vernon, E.; Fried, J. Characterization of the H3D ASIC readout system and 6.0 cm 3-D position sensitive CdZnTe detectors. IEEE Trans. Nucl. Sci. 2012, 59, 236–242. [Google Scholar]
- Du, Y.F.; He, Z.; Knoll, G.F.; Wehe, D.K.; Li, W. Evaluation of a Compton scattering camera using 3-D position sensitive CdZnTe detectors. Nucl. Instrum. Methods Phys. Res. A 2001, 457, 203–211. [Google Scholar]
- Xu, D.; He, Z.; Lehner, C.E.; Zhang, F. 4-pi Compton imaging with single 3D position-sensitive CdZnTe detector. Proc. SPIE 2004, 5540, 144–155. [Google Scholar]
- Du, Y.; Li, W.; Yanoff, B.; Gordon, J.; Castleberry, D. 4 pi direction sensitive gamma imager with RENA-3 readout ASIC. Proc. SPIE 2007, 67060V, 1–10. [Google Scholar]
- Yanoff, B.D.; Du, Y.; Dixon, W.V., Iii; Rao, N.K.; Li, W.; Claus, B.; Topka, T.; Moore, B.; Gordon, J.S. GE intelligent personal radiation locator system. Proc. SPIE 2009, 7306, 1–11. [Google Scholar]
- Cooper, D.A.; Ledoux, R.J.; Kamieniecki, K.; Korbly, S.E.; Thompson, J.; Ryan, M.; Roza, N.; Perry, L.; Hwang, D.; Costales, J.; Kuznetsova, M. Intelligent Radiation Sensor System (IRSS) Advanced Technology Demonstration (ATD). Proceedings of IEEE International Conference on Technologies for Homeland Security (HST), 8–10 November 2010, Waltham, MA, USA; pp. 414–420.
- Zhu, Y.; Anderson, S.E.; He, Z. Sub-pixel position sensing for pixelated, 3-d position sensitive, wide band-gap, semiconductor, gamma-ray detectors. IEEE Trans. Nucl. Sci. 2011, 58, 1400–1409. [Google Scholar]
- Burks, M.; Jordan, E.; Hull, E.; Mihailescu, L.; Vetter, K. Signal interpolation in germanium detectors for improved 3-D position resolution. Proceedings of IEEE Nuclear Science Symposium, Rome, Italy, 16–22 October 2004; pp. 1114–1118.
- Williams, C.S.; Baker, W.P.; Burggraf, L.W.; Adamson, P.E.; Petrosky, J.C. Toward simultaneous 2D ACAR and 2D DBAR: Sub-pixel spatial characterization of a segmented HPGe detector using transient charges. IEEE Trans. Nucl. Sci. 2010, 57, 860–869. [Google Scholar]







| Geometry Type | Advantages | Disadvantages | Best Performance in Energy Resolution (FWHM) |
|---|---|---|---|
| Planar electrode | Simple structure | Severe hole trapping problems | — |
| Frisch strip and trapezoid prism electrode | Simple structure | Existing leakage currents between the grid and anode | 2.68% at 662 keV |
| Insulated Frisch ring electrode | Eliminating leakage currents between the grid and anode | More complicated design and fabrication technique | 1.70% at 662 keV |
| Pixelate electrode | Higher charge collection efficiency; suitable for medical imaging | Charge sharing problems | <3% at 140 keV |
| Coplanar grid electrode | Overcoming hole trapping more effectively | Needing more output readout electronics; more electronic noises | 1.3% at 662 keV |
| Hemispherical electrode | Uniform charge collection | Complicated geometry design | <1.9% at 662 keV |
| Orthogonal coplanar strip electrode | Less complexity for the device electronics | Leakage current in anode | 1.0% at 662 keV |
| charge-sharing strip electrode | Simplified electronics and more effective non-collecting signal | More electronic noise | <6% at 122 keV |
| Drift strip electrode | The sensitivity to hole trapping is reduced due to the electrostatic shield to the readout anode | More electronic noises | 0.8% at 356 keV |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhang, Q.; Zhang, C.; Lu, Y.; Yang, K.; Ren, Q. Progress in the Development of CdZnTe Unipolar Detectors for Different Anode Geometries and Data Corrections. Sensors 2013, 13, 2447-2474. https://doi.org/10.3390/s130202447
Zhang Q, Zhang C, Lu Y, Yang K, Ren Q. Progress in the Development of CdZnTe Unipolar Detectors for Different Anode Geometries and Data Corrections. Sensors. 2013; 13(2):2447-2474. https://doi.org/10.3390/s130202447
Chicago/Turabian StyleZhang, Qiushi, Congzhe Zhang, Yanye Lu, Kun Yang, and Qiushi Ren. 2013. "Progress in the Development of CdZnTe Unipolar Detectors for Different Anode Geometries and Data Corrections" Sensors 13, no. 2: 2447-2474. https://doi.org/10.3390/s130202447




