Satellite- and Epoch Differenced Precise Point Positioning Based on a Regional Augmentation Network
Abstract
: Precise Point Positioning (PPP) has been demonstrated as a simple and effective approach for user positioning. The key issue in PPP is how to shorten convergence time and improve positioning efficiency. Recent researches mainly focus on the ambiguity resolution by correcting residual phase errors at a single station. The success of this approach (referred to hereafter as NORM-PPP) is subject to how rapidly one can fix wide-lane and narrow-lane ambiguities to achieve the first ambiguity-fixed solution. The convergence time of NORM-PPP is receiver type dependent, and normally takes 15–20 min. Different from the general algorithm and theory by which the float ambiguities are estimated and the integer ambiguities are fixed, we concentrate on a differential PPP approach: the satellite- and epoch differenced (SDED) approach. In general, the SDED approach eliminates receiver clocks and ambiguity parameters and thus avoids the complicated residual phase modeling procedure. As a further development of the SDED approach, we use a regional augmentation network to derive tropospheric delay and remaining un-modeled errors at user sites. By adding these corrections and applying the Robust estimation, the weak mathematic properties due to the ED operation is much improved. Implementing this new approach, we need only two epochs of data to achieve PPP positioning converging to centimeter-positioning accuracy. Using seven days of GPS data at six CORS stations in Shanghai, we demonstrate the success rate, defined as the case when three directions converging to desired positioning accuracy of 10 cm, reaches 100% when the interval between the two epochs is longer than 15 min. Comparing the results of 15 min' interval to that of 10 min', it is observed that the position RMS improves from 2.47, 3.95, 5.78 cm to 2.21, 3.93, 4.90 cm in the North, East and Up directions, respectively. Combining the SDED coordinates at the starting point and the ED relative coordinates thereafter, we demonstrate the performance of RTK PPP with standard deviation of 0.80, 1.34, 0.97 cm in the North, East and Up directions.1. Introduction
It has been more than ten years since precise point positioning (PPP) theory was proposed [1]. PPP has been demonstrated as a valuable technique for single stations positioning over continents, even on a global scale [2,3]. It has been considered an effective tool for precise orbit determination of low Earth orbiting [4], real-time water vapor estimation [5], early warning systems [6] and so on. Usually, the convergence time of traditional PPP requires tens of minutes to achieve the desired centimeter-positioning accuracy [7,8] as the ambiguities in PPP are non-integral and they are conventionally not fixed to integers [9]. The main factors influencing ambiguities fixing in PPP are the non-integral un-calibrated fractional offsets (UFOs) [10,11]. The UFOs are absorbed by the un-differenced ambiguity estimates and their integer properties are thus destroyed [7,12,13]. Integer ambiguity fixing can shorten the convergence time and improve the accuracy of PPP. However, it still takes approximately 15–20 min to achieve the first integer ambiguity solution. In order to further shorten the initialization time, the regional reference network augmented strategy was presented in [14–17], by which the precise atmospheric delay corrections of users are generated by making use of a regional reference network.
The above mentioned strategies focus on the PPP ambiguity resolution. Following the strategy of satellite- and epoch difference (SDED) [8], we differentiate between the observations of adjacent epochs and differences between satellites to remove ambiguities and receiver clocks. As a result, the number of parameters is reduced significantly. The remaining parameters are unknown coordinates and tropospheric delay, where tropospheric delay could be accurately modeled by implementing a interpolation model based on a reference network. On the other hand, the numeric stability of the normal equation is degraded when making epoch differences, because the geometry changes slowly between adjacent epochs. To overcome this problem, we apply the Robust Estimation strategy [18] in our differential PPP. The differential PPP approach thus avoids the ambiguity resolution and residual phase modeling procedure and may improve the robustness of PPP applications. In the following, Section 2 introduces the differential PPP theory and its augmentation method using a regional network; Section 3 introduces the prototype software system used in this study; Section 4 shows the validation results and the discussion; finally, Section 5 summarizes the main points and the conclusions.
2. Differential PPP Based on Regional Network
Network augmented PPP (Net-aPPP) [14–17] follows the idea from RTK, where atmospheric delay (troposphere and ionosphere) and other residual errors at user stations could be represented by a model based on the inputs from reference stations. By adding the corrections from the model, the tropospheric and ionospheric and other residual errors are corrected and thus do not appear in the estimation. Consequently, the correlation between parameters is reduced and the PPP solution convergence will be faster. The computation of Net-aPPP is accomplished at user stations and therefore is more flexible and efficient. However, in the above mentioned Net-aPPP approach, the correlation between ambiguities and coordinates still exists. Epoch-differenced (ED) strategy, which removes ambiguities, has been demonstrated to be efficient and accurate in the estimation of satellite clocks [8,19,20]. In GNSS positioning, the ED strategy is generally used to estimate the coordinate difference between adjacent epochs. Li et al. [8,21], demonstrated the application of the ED strategy in the absolute PPP positioning. In this Section we first describe the SDED theory, and afterwards the refinement of SDED approach by applying augmentation corrections is discussed.
2.1. SDED Based Ambiguity-Free Equation
Assuming that the residual errors of satellite orbit and clock could be neglected, the ionosphere-free (L3) combinations can be written as follows:
The superscript of “j” indicates tracked satellite. Lj is the ionosphere-free phase observation of j; ρj is geometric range between receiver and satellite; δ is the receiver clock error; bj is the ambiguity of L3 phase observation; Tj is the tropospheric delay; εj is the phase noise of L3 observation.
For one receiver tracking two satellites (j,i) simultaneously, the single-differenced measurements between satellite can be used to eliminate the receiver clocks. By taking differences of L3 observation of satellite i and j, we obtain:
Equation (2) is the defined as the satellite-differenced (SD) equation. Assuming there are no cycle slips between two adjacent epochs, the ambiguity term bj,i in Equation (2) can be further eliminated by differencing the SD observations at the adjacent epoch n and n−1 (n = 2…n1, n1 is total number of defined epochs):
Equation (4) is defined as the SDED based ambiguity-free equation.
2.2. Network Based Corrections of Tropospheric Delay and Un-Modeled Error
Although the main parts of the tropospheric delay are canceled by forming differences between adjacent epochs, there are still residual components in Equation (4). Due to the correlation between parameters, it is difficult to obtain a quick and reliable estimation of both coordinates and tropospheric parameters. A better solution is to model tropospheric delay rather than to estimate it. Following the RTK method, the modeling of atmospheric delay has been studied by a large number of researchers [22–24]. The general idea is the interpolation based on a reference network. The atmospheric delays at reference stations could be accurately estimated while they could be modeled at user stations. In practice, the wet part of tropospheric delay (Zwd) of user stations is interpolated, while the dry part (Zhd) is corrected using a standard Saastamoinen model. The interpolation model [23] is:
Mathematically, the SDED method is sensitive to the epoch-wise un-modeled errors (UMEs). These errors include satellite related errors (orbits and clocks) and appear to be similar at a regional scale. At reference stations, we could calculate the remaining un-modeled errors. With estimated tropospheric delay, fixed coordinates of the reference station, clocks and orbits, the SDED UMEs of reference stations can be retrieved from the SDED observations. Similar to Equation (5), the SDED UMEs at user station can be computed based on the inverse distance weighted model:
2.3. Coordinate Estimation
Substituting the interpolated tropospheric delay corrections and computed UMEs into Equation (4), and linearizing Equation (4), Equation (4) can be re-written in a matrix form:
The coordinate estimation using Equation (8) could be used as the starting point for kinematic positioning thereafter, i.e., after observing in static mode for a short period, a user station could run kinematically afterwards. The strategy for user kinematic PPP positioning is as following: SDED starting points + epoch-wise coordinates differences. In this strategy, the SDED coordinates from Equation (8) are used as known coordinates and epoch-wise coordinates differences (relative coordinates) are derived following the ED described in Bock et al. [4]. The final absolution coordinates are epoch-wisely accumulated using the initial and relative coordinates. The precision of relative coordinates is normally at mm level, therefore the precision of kinematic coordinates is similar to that of the starting points.
3. Realization of Network Based Differential PPP
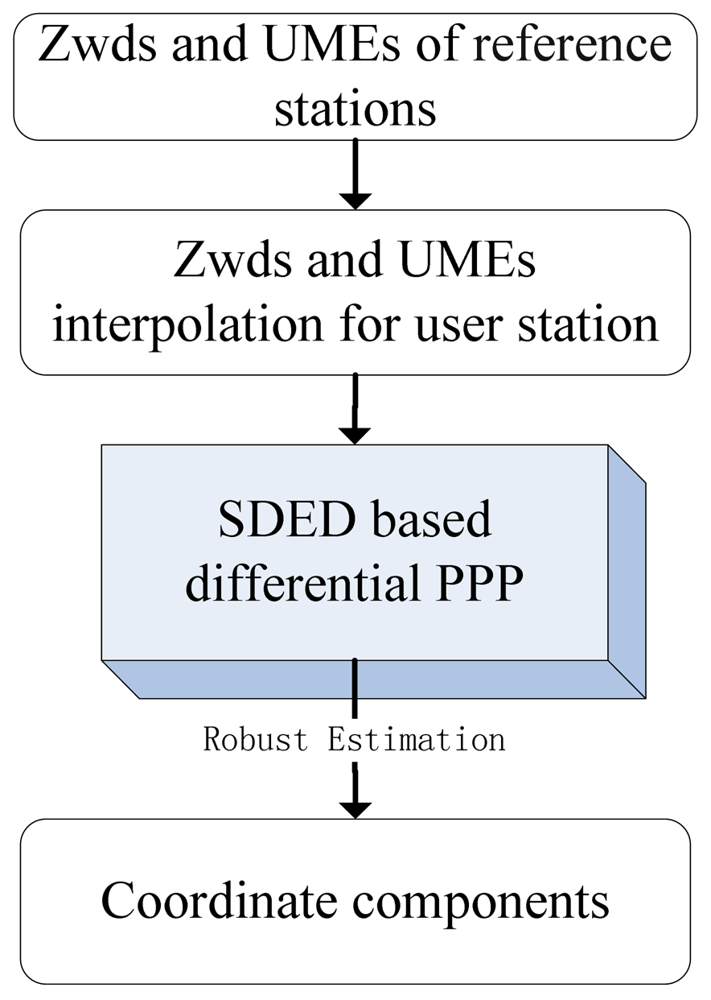
According to Equation (8), the precise coordinate estimations of user station could be obtained by applying the corrections of tropospheric delay and un-modeled error. A prototype software for the SDED based differential PPP was developed. The flow chart of the software is shown in Figure 1.
The preprocessing of phase data is based on the Melbourne-Wuebbena and Geometry-free combination to detect cycle slips and outliers. For real-time applications, the orbit and clock are from the predicted ultra-rapid orbits and real-time estimated clocks. The correction models including the phase wind-up, Earth tides, relativistic effects, antenna phase center offset and variation, etc. are implemented according to IERS convention 2003 [25] or IGS recommendation. At reference stations, the Saastamoinen model [26] is used to get the a priori correction and the wet part is estimated with an interval of 1 h. The Zwds at user stations are interpolated using the Zwds which are estimated by setting up a Pice-Wise-Constant (PWC) parameter at an interval of 1 h at reference stations.
The robust estimation [18] is used in parameter estimation procedure, where for each observation the weight function is as follows:
4. Experimental Validations
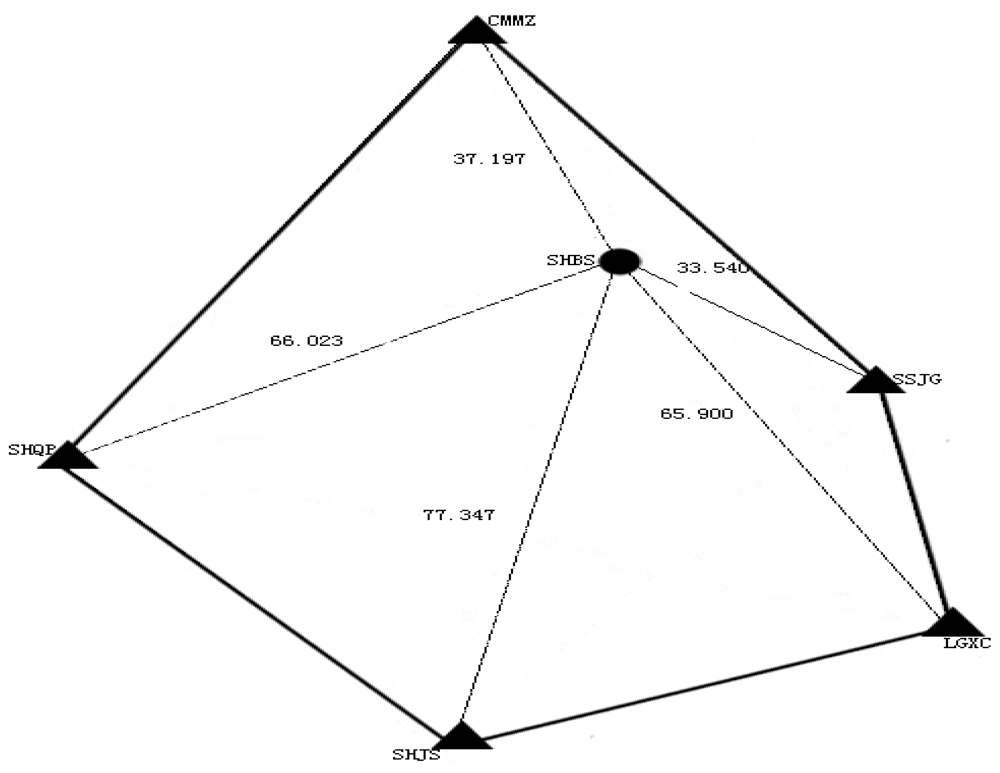
In order to test the proposed method, one week (DOY 011 to DOY 017, 2009) data from six stations (SHBS, CMMZ, SHQP, SHJS, LGXC and SSJG) of Shanghai Continuous Operation Reference Station (CORS) network are used. Each station has 12-h observations for each day. The station SHBS is taken as user station and the other five stations are used as reference stations to derive the correction information. Data sampling is 30 s and elevation cut-off angle is set to 9 degrees. The reference and user stations are shown in Figure 2. The averaged inter-station distance is about 56 km.
4.1. Interpolated Zwds
Taking the Zwds estimated at the five reference stations, the Zwds of the station SHBS are interpolated with the method described in Section 2.2. Comparison between estimated and interpolated Zwds is illustrated in Figure 3. In Figure 3, the Zwds of all stations (including SHBS) are first estimated by setting up a Pice-Wise-Constant (PWC) parameter at an interval of 1 h. Afterwards, Zwds of SHBS are interpolated based on the estimated Zwds of the other stations and are compared to the previous estimation. The RMS is 2.26 mm.
4.2. Retrieved Un-Modeled Errors
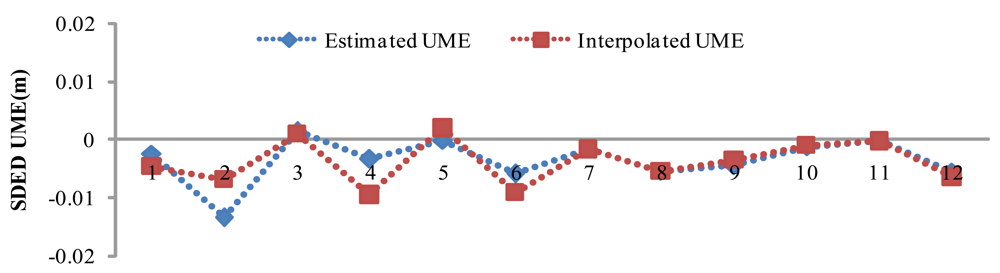
The SDED UMEs of the all the stations can be retrieved using Equation (4). Using the retrieved SDED UMEs at the five reference stations, SDED UMEs at SHBS are interpolated according to Equation (7). Figure 4 illustrates for satellite pair PRN20 and PRN28 the retrieved SDED UMEs in 2 h with an interval of 10 min. Comparing the interpolated and estimated UMEs, we found very good agreement with RMS of 3 mm, which validates the idea of UMEs interpolation of user station.
Figure 5 illustrates the SDED UMEs for all satellites with PRN20 being the reference satellite. It is observed that SDED UMEs are sometimes more than 2 cm, e.g., PRN02, PRN04, PRN10, PRN13, PRN17 and PRN32.
4.3. Success Rate
SDED-based differential PPP was performed for SHBS for the whole week. As two epochs of data are sufficient to derive station coordinates, we split the 12-h observations into 72 10-min and 48 15-min sessions for each day. Each session thus contains only two epochs of data with the interval at 10-min or 15-min. Differential PPP was carried out to verify the robustness and efficiency of the proposed SDED approach. The estimators of Least Square (LS) and Robust Estimation (RE) were tested by different strategies. The difference between strategy 1 and 6 is in the tropospheric delay handling: it is corrected using models in strategy 1, while it is being estimated in strategy 6. Table 1 presents for each tested strategy the success rate of differential PPP under the sampling of 10 min and 15 min. The success rate is defined as the case that the difference between the estimated and the known coordinate components are less than 10 cm. For comparison, the traditional PPP (NORM-PPP) method was tested using the observations (sampling at 30 s) within the same time window and the results were listed in Table 1 as well.
The success rate shown in Table 1 of different strategies indicates that the residual tropospheric delays affect the positioning results, although they can be partly eliminated by the epoch and satellite difference. The study strategy 1 is actually the normal SDED PPP [21], its success rate is only 36% due to the correlation between tropospheric parameters and coordinates. Applying the tropospheric delay corrections, the success rate of LS improves from 36% to 52%. Another improvement of 6% (in case of LS) and 32% (in case of RE) of success rate is achieved when we further apply the UME corrections. This improvement validates the contribution of UME estimation. Comparing the results of Robust Estimation to that of Least Square estimation, we see that success rate has notable improvement as bad SDED observations are down weighted in the robust estimation. Comparing the success rate of 10 min and 15 min, there is a general 10% improvement in success rate when the interval between the two epochs is increased to 15 min. By correcting tropospheric delay and UMEs, all sessions implementing differential PPP successfully meet the threshold and reach the desired accuracy.
4.4. SDED Positioning Accuracy
Position RMSs are calculated based on results from sessions with 10-min and 15-min intervals. Table 2 shows for each tested strategy the RMS (in cm) of coordinates with respect to the known coordinates in the North, East and Up directions at the interval of 10 min and 15 min, respectively.
Similar to the success rate discussed in previous section, the position results show also the improvement due to the corrections of tropospheric delays and UMEs. From the results, we see RE performs better than LS in all cases with the best result improved from 2.47, 3.95, 5.78 cm to 2.21, 3.93, 4.90 cm in the North, East and Up directions, respectively. Similarly, the cases where UME corrections are applied behave better than the others. All the cases of differential PPP have a better precision than NORM-PPP with the best strategy (strategy 6) has around 50% improvement in all three coordinate components.
4.5. Kinematic Positioning
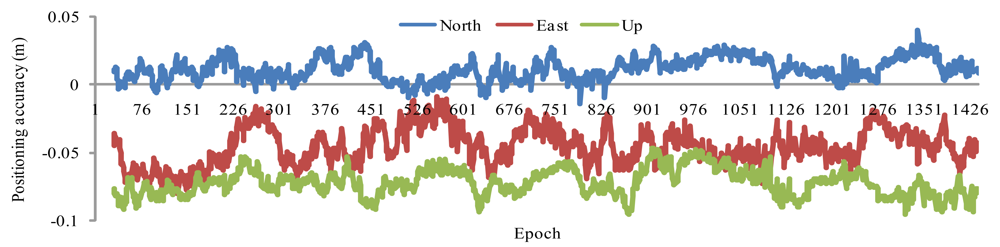
To demonstrate the RTK applications of our new SDED approach, SHBS is used as a kinematic station. We use the first RTK strategy described in Section 2.3 to derive kinematic PPP coordinates. The first two epochs of data sampling at 15 min is used to derive coordinates at the starting point, data sampling is then set to 30 s in RTK PPP thereafter. Figure 6 shows the RTK coordinates differences for DOY 011 with respect to the known coordinates. We notice that there are offsets of few centimeters for each component, which are introduced by the SDED initial coordinates. Removing the offsets, the coordinate standard deviation (STD) is of 0.80, 1.34, 0.97 cm in the North, East and Up directions.
5. Discussion and Conclusions
This study introduces a differential PPP approach based on a regional reference augmentation network, where ambiguity and receiver clock are removed by the SDED model. The corrections of tropospheric delay and UME at user station are interpolated from the estimated Zwds and retrieved UMEs of reference stations. In addition, the Robust Estimation is implemented to overcome the defect of the weakened geometry caused by the SDED model.
The approach presented in the paper has been validated using one-week data from a regional network in Shanghai. From the experiment, we see the interpolated Zwds and UMEs have an accuracy of 2.26 mm and 3 mm, respectively. Using the interpolated corrections, differential PPP is performed with estimators of Least Square and Robust Estimation. The position results and success rate indicate that the RE performs better than the LS. The PPP position accuracy of RE is at the cm level for an interval longer than 10 min. The success rate of RE with an interval longer than 15 min reaches 100% and position accuracy reaches 2.21, 3.93, 4.90 cm in the North, East and Up directions. Comparing the results from our new approach to that of NORM-PPP, we see remarkable improvements in both convergence and precision.
The differential PPP approach improves PPP positioning with shorter convergence-time and more reliable results. In real-time applications, the user station observes firstly in static mode for around 15 min and runs kinematically afterwards. Results show the kinematic PPP coordinates precision (STD) is of 0.80, 1.34, 0.97 cm in the North, East and Up directions, with offsets of a few centimeters in each component.
Acknowledgments
This research is supported by the National Natural Science Foundation of China (NSFC) (No. 40974018) and 100 Talents Programme of The Chinese Academy of Sciences. Anonymous reviewers are acknowledged for their valuable comments and suggestions.
References
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar]
- Kouba, J. A possible detection of the 26 December 2004 Great Sumatra Andaman Islands earthquake with solution products of the international GNSS service. Stud. Geophys. Geodaet. 2005, 49, 463–483. [Google Scholar]
- Rodrigo, F.; Marcelo, C.; Richard, B. Analyzing GNSS data in precise point positioning software. GPS Solut. 2011, 15, 1–13. [Google Scholar]
- Bock, H.; Hugentobler, U.; Springer, T.; Beutler, G. Efficient precise orbit determination of LEO satellites using GPS. Adv. Space Res. 2002, 30, 295–300. [Google Scholar]
- Chen, J.; Ge, M.; Dousa, J.; Gendt, G. Evaluation of EPOS-RT for Real-time Deformation Monitoring. J. Glob. Position. Syst. 2009, 8, 1–5. [Google Scholar]
- Chen, J.; Ge, M.; Vennebusch, M.; Deng, Z.; Gendt, G.; Rothacher, M. Progress of the real-time GNSS software development at GFZ. Oral Presentation at International GNSS Service Analysis Center Workshop, Miami Beach, FL, USA, 2–6 June 2008; pp. 2–6.
- Geng, J.; Meng, X.; Dodson, A.H.; Teferle, F.N. Integer ambiguity resolution in precise point positioning: Method comparison. J. Geod. 2010, 84, 569–581. [Google Scholar]
- Li, H.; Chen, J.; Wang, J.; Hu, C.; Liu, Z. Network based Real-time Precise Point Positioning. Adv. Space Res. 2010, 46, 1218–1224. [Google Scholar]
- Teunissen, P.J.G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar]
- Blewitt, G. Carrier phase ambiguity resolution for the global positioning system applied to geodetic baselines up to 2000 km. J. Geophys. Res. 1989, 94, 10187–10203. [Google Scholar]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar]
- Collins, P. Isolating and estimating undifferenced GPS integer ambiguities. Proceedings of ION National Technical Meeting, San Diego, CA, USA, 28–30 January 2008; pp. 720–732.
- Mercier, F.; Laurichesse, D. Zero-difference ambiguity blocking properties of satellite/receiver widelane biases. Proceedings of European Navigation Conference, Toulouse, France, 23–25 April 2008.
- Ge, M.; Zou, X.; Dick, G.; Jiang, W.; Wickert, J.; Liu, J. An alternative Network RTK approach based on undifferenced observation corrections. Proceedings of ION GNSS 2010, Portland, OR, USA, 21–24 September 2010.
- Li, X.; Zhang, X.; Ge, M. Regional reference network augmented precise point positioning for instantaneous ambiguity resolution. J. Geod. 2011, 85, 151–158. [Google Scholar]
- Teunissen, P.; Odijk, D.; Zhang, B. PPP-RTK: Results of CORS network-based PPP with integer ambiguity resolution. J. Aeronaut. Astronaut. Aviat. 2010, 42, 223–230. [Google Scholar]
- Zhang, B.; Teunissen, P.; Odijk, D. A novel un-differenced PPP-RTK concept. J. Navig. 2011, 64, S180–S191. [Google Scholar]
- Yang, Y. Robust estimation of Geodetic Datum Transformation. J. Geod. 1999, 73, 264–268. [Google Scholar]
- Han, S.C.; Kwon, J.H.; Jekeli, C. Accurate absolute GPS positioning through satellite clock error estimation. J. Geod. 2001, 75, 33–43. [Google Scholar]
- Ge, M.; Chen, J.; Dousa, J.; Gendt, G.; Wickert, J. A computationally efficient approach for estimating high-rate satellite clock corrections in realtime. GPS Solut. 2012, 16, 9–15. [Google Scholar]
- Li, H.; Wang, J.; Chen, J.; Hu, C. The research on the rapid static precise point positioning based on ridged estimation. Acta Astron. Sin. 2009, 50, 438–444. [Google Scholar]
- Wanninger, L. Improved AR by regional differential modeling of the ionosphere. Proceedings of 8th International Technical Meeting of the Satellite Division of the US Institute of Navigation, Palm Springs, CA, USA, 12–15 September 1995; pp. 55–62.
- Zhang, J.; Lachapelle, G. Precise estimation of residual tropospheric delays using a regional GPS network for real-time kinematic applications. J. Geod. 2001, 75, 255–266. [Google Scholar]
- Jensen, A.B.O.; Ovstedal, O. The effect of different tropospheric models on precise point positioning in kinematic model. Surv. Rev. 2008, 40, 173–187. [Google Scholar]
- McCarthy, D.D., Petit, G., Eds.; IERS 2003 Conventions; Verlag des Bundes für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2004; p. 127.
- Saastamoinen, J. Atmospheric correction for the troposphere andstratosphere in radio ranging of satellites; The Use of Artificial Satellites for Geodesy, Geophysics Monograph Series; Henriksen, S.W., Mancini, A., Chovitz, B.H., Eds.; American Geophysical Union: Washington, DC, USA, 1972; Volume 15, pp. 247–251. [Google Scholar]


| Estimator | Strategy | Correction | Success rate | |
|---|---|---|---|---|
| 10-min | 15-min | |||
| LS | 1 | No | 36 | 27 |
| 2 | Zwd | 52 | 63 | |
| 3 | UME and Zwd | 58 | 77 | |
| RE | 4 | Zwd | 70 | 81 |
| 5 | UME and Zwd | 85 | 100 | |
| NORM-PPP | 6 | 46 | 60 | |
| Estimator | Corrections | 10 min | 15 min | ||||
|---|---|---|---|---|---|---|---|
| North | East | Up | North | East | Up | ||
| LS | Zwd | 7.68 | 10.19 | 12.47 | 4.13 | 5.96 | 6.20 |
| UME and Zwd | 7.49 | 9.11 | 11.35 | 2.47 | 3.95 | 5.78 | |
| RE | Zwd | 6.11 | 8.43 | 10.02 | 2.44 | 3.82 | 5.62 |
| UME and Zwd | 5.35 | 6.50 | 8.12 | 2.21 | 3.93 | 4.90 | |
| NORM-PPP | 7.93 | 10.23 | 12.56 | 4.51 | 7.86 | 8.91 | |
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, H.; Chen, J.; Wang, J.; Wu, B. Satellite- and Epoch Differenced Precise Point Positioning Based on a Regional Augmentation Network. Sensors 2012, 12, 7518-7528. https://doi.org/10.3390/s120607518
Li H, Chen J, Wang J, Wu B. Satellite- and Epoch Differenced Precise Point Positioning Based on a Regional Augmentation Network. Sensors. 2012; 12(6):7518-7528. https://doi.org/10.3390/s120607518
Chicago/Turabian StyleLi, Haojun, Junping Chen, Jiexian Wang, and Bin Wu. 2012. "Satellite- and Epoch Differenced Precise Point Positioning Based on a Regional Augmentation Network" Sensors 12, no. 6: 7518-7528. https://doi.org/10.3390/s120607518




