Prediction of Gap Asymmetry in Differential Micro Accelerometers
Abstract
: Gap asymmetry in differential capacitors is the primary source of the zero bias output of force-balanced micro accelerometers. It is also used to evaluate the applicability of differential structures in MEMS manufacturing. Therefore, determining the asymmetry level has considerable significance for the design of MEMS devices. This paper proposes an experimental-theoretical method for predicting gap asymmetry in differential sensing capacitors of micro accelerometers. The method involves three processes: first, bi-directional measurement, which can sharply reduce the influence of the feedback circuit on bias output, is proposed. Experiments are then carried out on a centrifuge to obtain the input and output data of an accelerometer. Second, the analytical input-output relationship of the accelerometer with gap asymmetry and circuit error is theoretically derived. Finally, the prediction methodology combines the measurement results and analytical derivation to identify the asymmetric error of 30 accelerometers fabricated by DRIE. Results indicate that the level of asymmetry induced by fabrication uncertainty is about ±5 × 10−2, and that the absolute error is about ±0.2 μm under a 4 μm gap.1. Introduction
The development of micro-electro-mechanical-systems (MEMS) usually involves the fabrication of small structures with relative errors larger than that observed in traditional fabrication technology. Therefore, evaluating the level of structural error and its influence in micro-fabrication has significance in the design of new devices and improvement of processes. Given the immaturity and diversity of micro fabrication techniques, researchers and institutions adopt evaluation methods with focus and specificities particular to such approaches. For example, Cigada used the electrical method to measure the dynamic behaviors of a MEMS gyroscope with fabrication error [1]; Wittwer predicted the error effect on compliant mechanisms from the perspective of dimensions and materials [2]; and Pugno suggested a novel method for predicting the strength of microstructures with complex geometries that arise from micro processes [3]. Aside from direct measurements or prediction methods, design methodologies have been proposed to reduce the dependence of device performance on microfabrication errors; these methodologies include optimization [4–7] and robust design technologies [8–10]. Error prediction in the current work was indirectly carried out to evaluate gap asymmetry in differential capacitors of micro accelerometers fabricated by deep reactive-ion etching (DRIE). DRIE is a highly anisotropic etching process used to create microstructures with high aspect ratios; it is extensively used to fabricate micro accelerometers [11], micro gyroscopes [12,13], micro switches [14–16], micro actuators [17], micro gears [18] and so on. Gap asymmetry pertains to the disproportion between the capacitive gaps of two capacitors that form a differential sensor. Its occurrence causes the calibration line to deviate from its origin and forms zero bias output; that is, the output voltage of a force-balanced accelerometer is no longer zero under zero acceleration input [19,20]. Consequently, the measurement ranges in the positive and negative directions differ, and feedback circuit parameters cannot be established in a similar manner as those designed under ideal conditions. Thus, identifying the level of asymmetry in structures is urgently needed before differential sensors with new performance requirements can be designed.
The rest of the paper is structured as follows: Section 2 presents the centrifuge tests conducted in this study, and the observations of zero bias in accelerometers fabricated by DRIE. Section 3 discusses the prediction process, including the analytical derivation and reverse calibration method. Finally, Section 4 provides the results of the proposed experimental–theoretical method.
2. Asymmetric Phenomenon during Testing
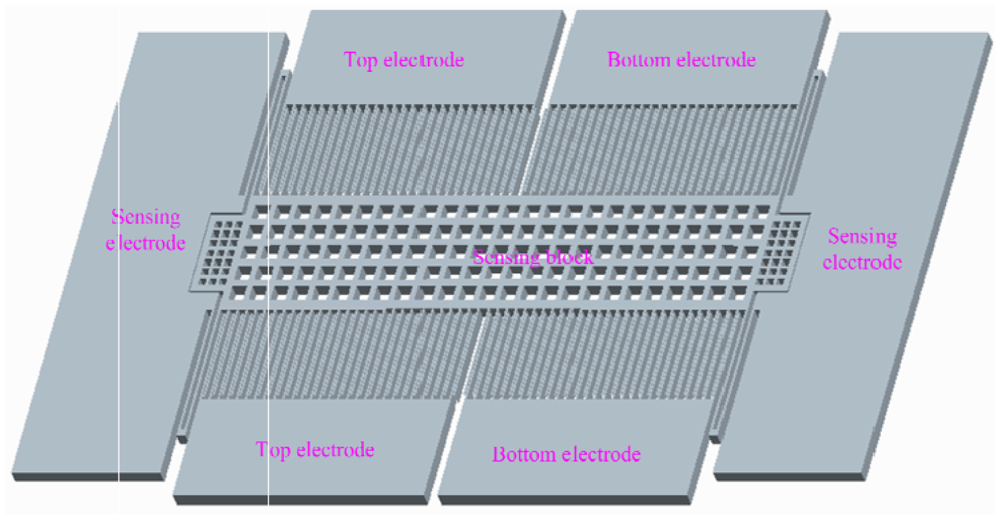
Micro accelerometers are fabricated using DRIE bulk silicon technology and silicon bonding technology to provide high sensitivity and large signal output. These components have been proven successful in MEMS devices. The structure of the micro accelerometer used in this study is shown in Figure 1, which presents only a quarter of the entire structure. It consists of a folded beam, comb capacitors, and a sensing mass block. Accelerometer tests and calibration are performed on a centrifuge, which can simulate the acceleration field using a designed rotation speed. In the testing process, the sensitive direction of the accelerometer is along the radius of the circumrotating platform, thus the acceleration input is due to the centripetal acceleration resulting from uniform circular motion of the centrifuge platform. The range of acceleration input in this paper is between−55 G (where G is the acceleration of gravity) and +55 G, and the increment of test points is 5 G. We call the proposed experiment the bi-directional measurement method, which involves two independent processes intended to separate the influence of the feedback circuit from the structure gap error on bias output.
“Bi-” refers to two opposite ways of loading bias input voltage on the electrodes of the capacitors. For the positive direction, the top electrode shown in Figure 2 is connected to the positive voltage +V and the bottom electrode is connected to a voltage −V. For the negative direction, the power polarity is reversed (i.e., the top electrode is connected to −V and the bottom electrode is connected to +V).
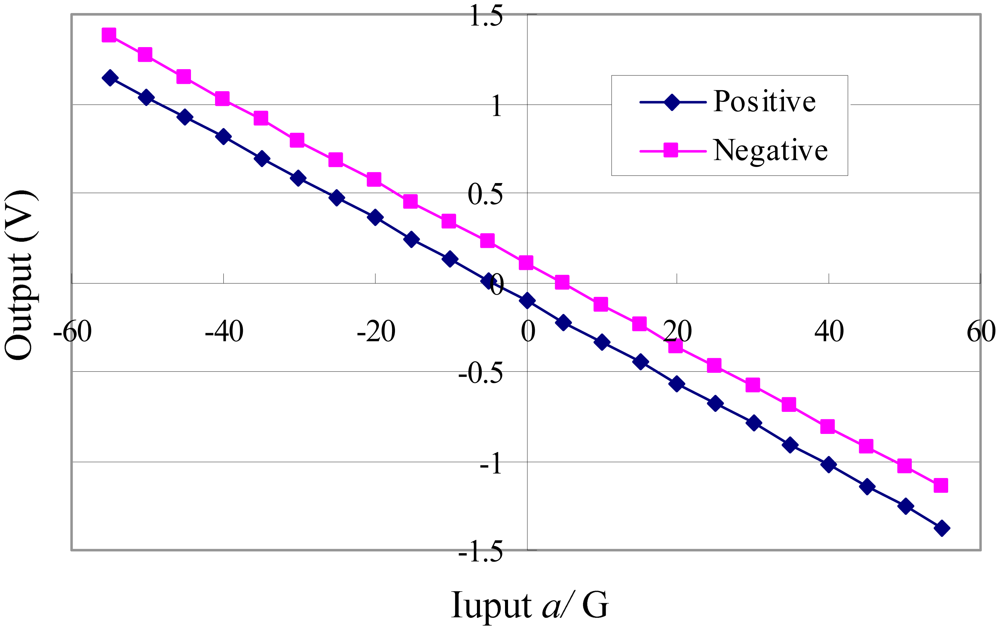
The data are depicted in Figure 3. The experimental data indicate that the output voltage of the accelerometer under zero input is nonzero in both directions. This output is generally called zero bias, which is originally influenced by the asymmetry in the accelerometers. The asymmetry is caused by fabrication error and the zero error arising from the differential feedback circuit.
3. Prediction Method
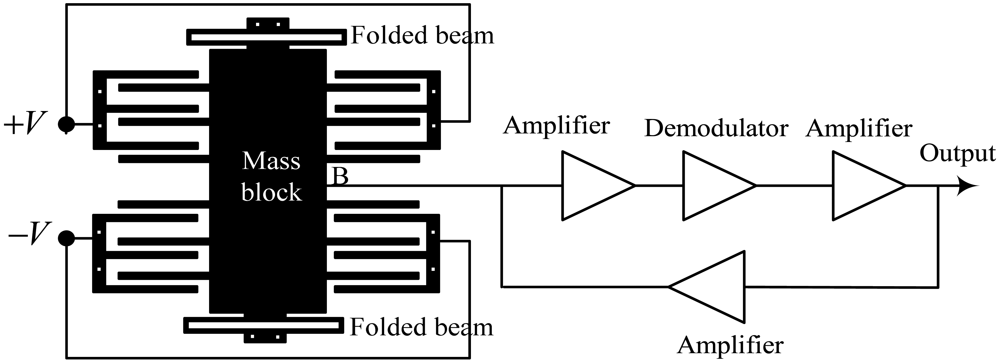
Identifying the effect of asymmetric error on the accelerometer requires deriving and analyzing the operation principle of the sensor. The diagram of a typical differential accelerometer structure is shown in Figure 4. The structure comprises three core components: a movable mass block that converts acceleration into an inertial force, a differential capacitor structure for driving and sensing, and an electric circuit for feedback and signal output. The movable mass is suspended by folded beams at each end and deflects in the plane of the substrate under applied acceleration. A voltage signal is induced on the movable beams as a result of the change in differential capacitance caused by the movement of mass. Instantaneously, this signal is demodulated and amplified to yield a feedback voltage, which is applied to the movable beams via a feedback circuit. Consequently, an electrostatic force is generated, which drags the movable mass back to the zero position, and the accelerometer output is constituted by the amplified version of the feedback voltage. Under ideal conditions, the two groups of comb fingers that form the differential capacitors have similar overlap plate areas and gap distances. The output is zero under an ideal sensing circuit and zero input. In the actual engineering test, however, a zero bias output is generated because of fabrication error and circuit bias, discussed in the succeeding sections.
3.1. Analytical Relationship
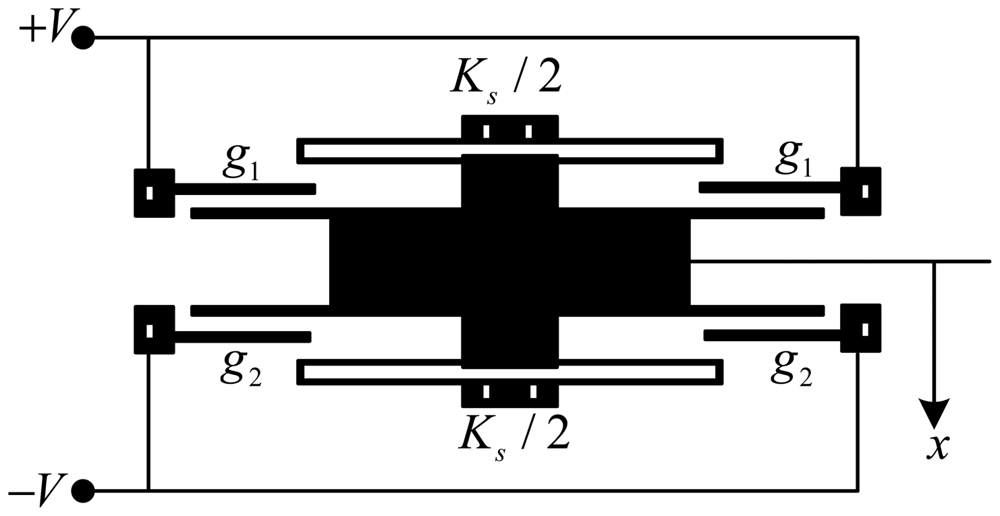
The gap asymmetry caused by the micro fabrication is considered first. Its equivalent value is represented by the average value, which equals the ratio of the sum of the capacitor gaps and gap number (Figure 5). g1 and g2 are the average values of the top and bottom electrode gaps, respectively. g1 ≠ g2 reflects the asymmetry from the fabrication. When the bias voltages are applied to the fixed plates of the capacitors, the mass block moves to a position where the mechanical force equals the electrostatic force under closed-loop control.
Assuming that the sensing circuit is of an ideal state, the instantaneous feedback voltage on the block subjected to bias voltage can be expressed as:
When a voltage is applied, the mass block moves because of the asymmetry induced by the electrostatic force produced by the top and bottom capacitors. The movement deforms the supporting beams. The resultant force of the mass block can therefore be expressed as:
The balance position of the mass block is where the resultant force is zero, Fr = 0, and the values of the average gaps under balance can be obtained by solving Equations (2)–(5).
To simplify, we set one average value g1 = g0, and the other average value g2 = g0 + e, where e is the asymmetric error from micro fabrication. Thus, the expressions of electrostatic force become:
When the frequency of the driving voltage is considerably larger than the natural frequency of the mass block, the electrostatic forces can be calculated using the effective value of the voltage. According to the law of action and reaction, when the external acceleration is applied to the accelerometer, inertial force Fa must equal the resultant force of the electrostatic force and mechanical force Fr, with the signs reversed. Thus, we obtain:
Therefore, the input acceleration can be expressed as a function of output voltage:
We conclude that the presence of E yields a nonzero constant term Ag in Equation (12). Hence, the bias output voltage is nonzero when the input acceleration is zero. Another cause of bias output is the presence of deviation Vb in the differential sensing circuit. Assuming that the mechanical structure of the sensor is ideally symmetric, the feedback voltage applied to the mass block is:
According to the preceding derivation, the input acceleration can be expressed as:
The output voltage is:
Therefore, the input can be expressed in terms of the output as follows:
We conclude that the existence of a circuit deviation also leads to bias output voltage because of the nonzero constant term Ac induced by nonzero Vb in Equation (21).
The influence of the structure and circuit error has been analyzed under deep feedback control. Gain value M is more than four orders of 10, resulting in two consequences: the mass block moves along a linear region under low acceleration input, and the influence of the gap asymmetry of the sensor structure is significantly larger than that of the circuit bias. Thus, the relationship can be expressed as:
The conclusion derived from Equation (24) is characterized by two aspects: First, the first term on the right indicates the effect of the asymmetric error on the bias acceleration at zero point. Its value is equal to the distance from the cross point of the relationship curve and axis Vout = 0 to the original point. It is also independent of the parameters of the closed-loop control circuit. Second, the second term on the right indicates how the asymmetric error influences the linear constant of the calibration function.
3.2. Reverse Calibration
Reverse calibration pertains to input acceleration calibrated as a function of output voltage. According to the analytical procedure, formulating the input function of the output is more direct and clear than formulating the output function of the input. Thus, reverse calibration is introduced to study the gap asymmetric error resulting from micro fabrication. The results of the reverse calibration based on the least-squares method are:
Figure 6 shows the reverse calibration curve lines of the experimental data. The plot directly indicates that the output voltage is nonzero when the acceleration is zero because of the asymmetric error. Figure 7 illustrates the relative errors of calibration, which indicate that the errors are less than 4.5%.
3.2. Prediction of Asymmetric Error
The theoretical–experimental prediction is established on the analytical and calibration functions. The ratio of constant term to linear term coefficient is selected in predicting the error, and can be expressed as:
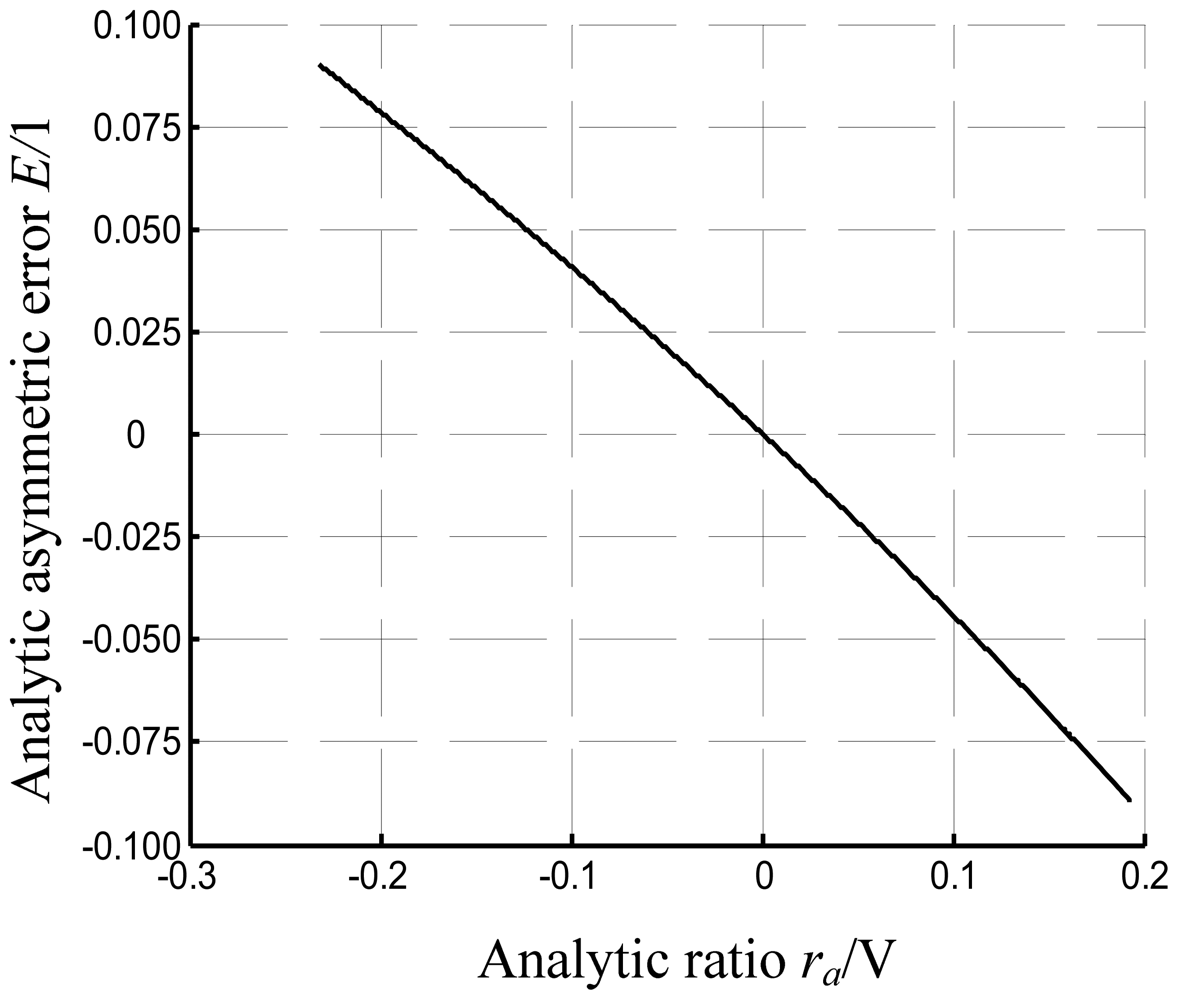
The conclusion derived from Equation (27) is that the ratio is now independent of the mass of the sensing block, AC bias, and gain value of the closed loop. The relationship between the error and ratio is depicted in Figure 8, and the parameters of the system are given in Table 1.
The reverse calibration result of a selected sensor leads to the coefficient ratio:
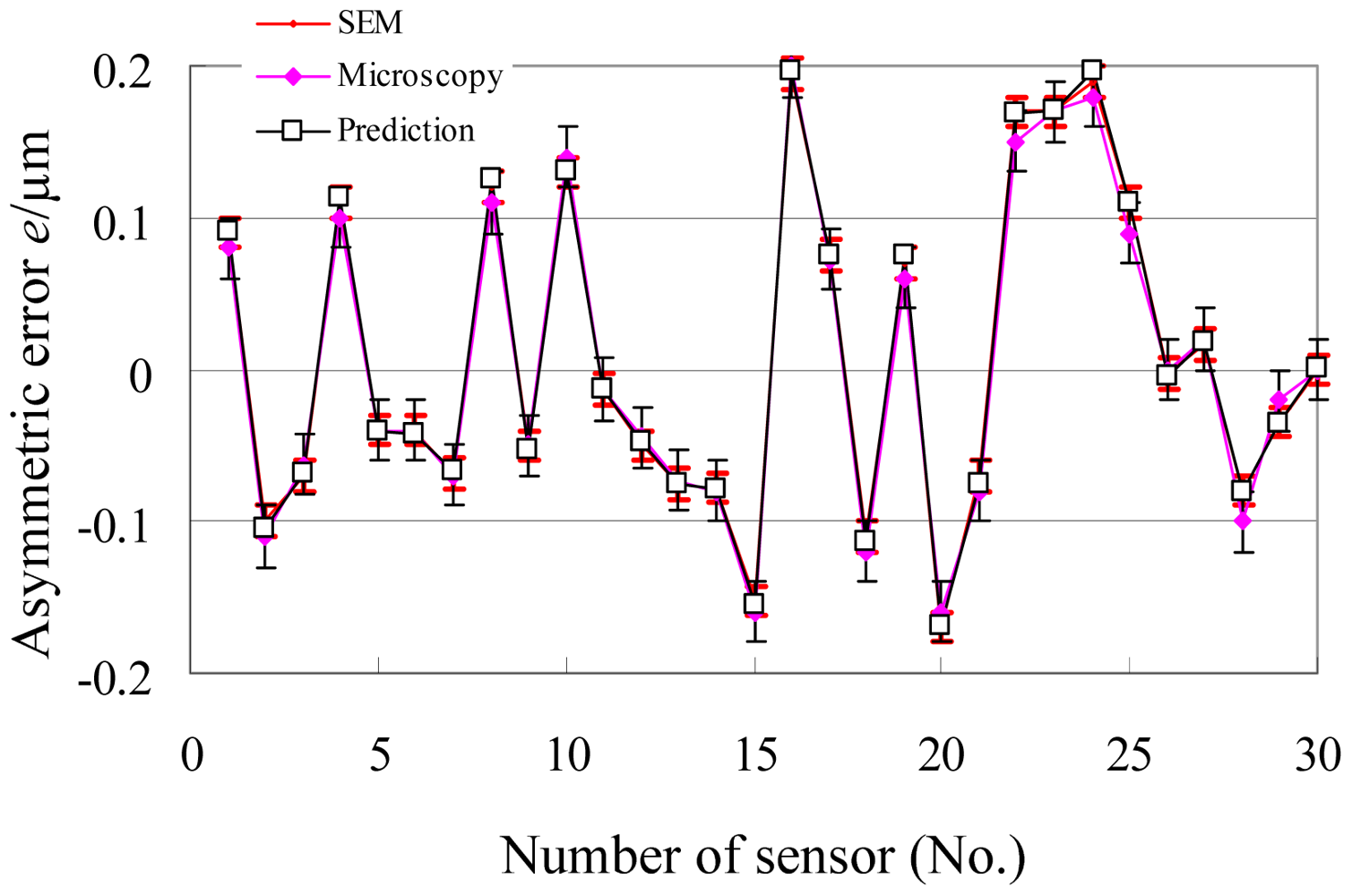
Therefore, the predicted relative error that arises from the tested accelerometer is about 4 × 10−2, and the absolute error is about 0.16 μm at an average gap of 4 μm. Under common conditions of engineering design, 30 sensors are tested and predicted. The results are shown in Figure 9. The range of the predicted errors is about ± 5 × 10−2, and that of the absolute error is about ±0.2 μm under a 4 μm gap. For verification, those sensors are investigated by optical microscopy and SEM, from which the finger images are shown in Figure 10. The measurement results of gap asymmetry are all in the range of ±0.2 μm, even considering the measuring error (Figure 11).
4. Conclusions
A fabrication error prediction technique based on a mature MEMS device is presented in this paper. The combined analytical and reverse calibration methods enable direct and clear gap error prediction. Reverse calibration is suitable for deriving the relationship, and the analytical relationship provides the guidelines for rational calibration. In addition, the absence of a quadric term improves prediction precision.
The ratio of the prediction coefficients eliminates the need to calculate the values of parameters, which are difficult to determine. The prediction indicates that the range of relative asymmetric error is about ±5 × 10−2, and that the absolute error is about ±0.2 μm under a 4 μm gap. These results coincide with the values measured by optical microscopy and SEM.
Acknowledgments
This research was partially supported by National Natural Science Foundation of China (Grant No. 51175437), Fundamental Research Funds for the Central Universities (Grant No. ZYGX2011J085). The authors would like to acknowledge Zhang Fengtian, Shi Zhigui and Du Lianming for their assistance in fabrication and experiments.
References
- Cigada, A.; Leo, E.; Vanali, M. Electrical method to measure the dynamic behaviour and the quadrature error of a MEMS gyroscope error. Sens. Actuators A Phys. 2007, 134, 88–97. [Google Scholar]
- Wittwer, J.W. Predicting the Effects of Dimensional and Material Property Variations in Micro Compliant Mechanisms. M.S. Thesis, Brigham Young University, Provo, UT, USA, 2001. [Google Scholar]
- Pugno, N.; Peng, B.; Espinosa, H.D. Predictions of strength in MEMS components with defects—A novel experimental-theoretical approach. Int. J. Solids Struct. 2005, 45, 647–661. [Google Scholar]
- Wittwer, J.W.; Gomm, T.; Howell, L.L. Surface micromachined force gauges: Uncertainty and reliability. J. Micromech. Microeng. 2002, 12, 13–20. [Google Scholar]
- Shavezipur, M.; Ponnambalam, K.; Hashemi, S.M.; Khajepour, A. A probabilistic design optimization for MEMS tunable capacitors. Microelectron. J. 2008, 39, 1528–1533. [Google Scholar]
- Bronson, J.R. Modeling and Control of MEMS Micromirror Arrays with Nonlinearities and Parametric Uncertainties. Ph.D. Thesis, University of Florida, Gainesville, FL, USA, 2007. [Google Scholar]
- Rajagopalan, S. Error Analysis and Optimal Pose Selection for IN-SITU Fabrication of Mechanisms. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2000. [Google Scholar]
- Wittwer, J.W.; Baker, M.S.; Howell, L.L. Robust design and model validation of nonlinear compliant micromechanisms. J. Microelectromech. Syst. 2006, 15, 33–41. [Google Scholar]
- Coultate, J.K.; Fox, C.H.J.; William, S.M.; Malvern, A.R. Application of optimal and robust design methods to a MEMS accelerometer. Sens. Actuators A Phys. 2008, 142, 88–96. [Google Scholar]
- Han, J.S.; Kwak, B.M. Robust optimal design of a vibratory microgyroscope considering fabrication errors. J. Micromech. Microeng. 2001, 11, 662–671. [Google Scholar]
- van Drieenhuizen, B.P.; Maluf, N.I.; Opris, I.E.; Kovacs, G.T.A. Force-balanced accelerometer with mG resolution, fabricated using silicon fusion bonding and deep reactive ion etching. Proceedings of 1997 International Conference on Solid State Sensors and Actuators, Chicago, IL, USA, 16–19 June 1997.
- Xie, H.; Fedder, G.K. A DRIE CMOS-MEMS gyroscope. Proc. IEEE 2002, 2, 1413–1418. [Google Scholar]
- Xie, H.; Fedder, G.K. Fabrication, characterization, and analysis of a DRIE CMOS-MEMS gyroscope. IEEE Sens. J. 2003, 3, 622–631. [Google Scholar]
- Tang, M.; Liu, A.Q.; Agarwal, A.; Zhang, Q.X.; Win, P. A new approach of lateral RF MEMS switch. Analog. Integr. Circuits Signal Proc. 2004, 40, 165–173. [Google Scholar]
- Li, J.; Zhang, Q.X.; Liu, A.Q. Advanced fiber optical switches using deep RIE (DRIE) fabrication. Sens. Actuators A Phys 2003, 102, 286–295. [Google Scholar]
- Huang, J.M.; Liew, K.M.; Wong, C.H.; Rajendran, S.M.; Tan, J.A.; Liu, Q. Mechanical design and optimization of capacitive micromachined switch. Sens. Actuators A Phys 2001, 93, 273–285. [Google Scholar]
- Li, J.; Liu, A.Q.; Zhang, Q.X. Tolerance analysis for comb-drive actuator using DRIE fabrication. Sens. Actuators A Phys 2006, 125, 494–503. [Google Scholar]
- Fu, K.; Knobloch, A.J.; Martinez, F.C.; Walther, D.C.; Fernandez-Pello, C.; Pisano, A.P.; Liepmann, D. Design and experimental results of small-scale rotary engines. Proceedings of 2001 ASME International Mechanical Engineering Congress and Exposition, New York, NY, USA, 11–16 November 2001.
- Chen, W.; Zhao, Z.; Liu, X.; Lin, Y. Damping analysis of asymmetrical Comb accelerometer. Key Eng. Mater 2007, 353-358, 2597–2600. [Google Scholar]
- Aaltonen, L.; Rahikkala, P.; Saukoski, M.; Halonen, K. High-resolution continuous-time interface for micromachined capacitive accelerometer. Int. J. Circuit Theory Appl 2009, 37, 333–349. [Google Scholar]
- Middellehoek, S. Micro Mechanical Transducers: Pressure Sensor, Accelerometers and Gyroscopes; Elsevier: New York, NY, USA, 2000; pp. 333–335. [Google Scholar]





| Parameters | Values |
|---|---|
| DC voltage (Vd) (V) | 4.5 |
| Coefficient (M0) | 0.4 |
| Ratio of Stiffness (R) | 0.1906 |
| Initial gap designed (μm) | 4 |
© 2012 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhou, W.; Li, B.; Peng, B.; Su, W.; He, X. Prediction of Gap Asymmetry in Differential Micro Accelerometers. Sensors 2012, 12, 6857-6868. https://doi.org/10.3390/s120606857
Zhou W, Li B, Peng B, Su W, He X. Prediction of Gap Asymmetry in Differential Micro Accelerometers. Sensors. 2012; 12(6):6857-6868. https://doi.org/10.3390/s120606857
Chicago/Turabian StyleZhou, Wu, Baili Li, Bei Peng, Wei Su, and Xiaoping He. 2012. "Prediction of Gap Asymmetry in Differential Micro Accelerometers" Sensors 12, no. 6: 6857-6868. https://doi.org/10.3390/s120606857





