DOA Estimation for Local Scattered CDMA Signals by Particle Swarm Optimization
Abstract
: This paper deals with the direction-of-arrival (DOA) estimation of local scattered code-division multiple access (CDMA) signals based on a particle swarm optimization (PSO) search. For conventional spectral searching estimators with local scattering, the searching complexity and estimating accuracy strictly depend on the number of search grids used during the search. In order to obtain high-resolution and accurate DOA estimation, a smaller grid size is needed. This is time consuming and it is unclear how to determine the required number of search grids. In this paper, a modified PSO is presented to reduce the required search grids for the conventional spectral searching estimator with the effects of local scattering. Finally, several computer simulations are provided for illustration and comparison.1. Introduction
Adaptive array techniques have been developed for enhancing the performance of code-division multiple access (CDMA) systems. In the CDMA system, each user employs a unique pseudo-noise (PN) codeword to identify their data stream. Each user’s transmission interferes with all the other users and causes multiple access interference (MAI). The use of antenna arrays as a tool for improving coverage, reducing interference, and increasing capacity in CDMA systems has attracted significant interest [1]. Multiple propagation is common in cellular systems, which may result from local scatters in the vicinity of the sources. In macrocellular environments, high base station antennas will receive these locally scattered signals from the mobile terminal, which are coherent and confined to a narrow angular region [2]. In addition, the observation period is assumed to be short in comparison to the coherence time of the channel so that the channel may be modeled as time-invariant. A mobile terminal with local scattering can be well approximated by a single point source, as seen from the base station. The model can express the mobile and coherent interference from the surrounding environment under non line-of-sight conditions as another arithmetical model. In cellular radio systems, antenna array processing is considered to be a useful method to solve problems such as multipath and co-channel interference and increase capacity [1]. There have been some studies appraising the impact of a local scattering channel model on CDMA system, which propose uniform linear array (ULA) geometry [3]. They use a first-order Taylor expansion to linearize the nonlinear conventional array manifold produced by scatters and develop the generalized array manifold (GAM) model which can obtain better nominal DOA estimation for mobiles. Here, the multiple signal classification (MUSIC) searching function derived by the steering vector of the GAM model is termed as GMUSIC. However, in all these studies, estimation of direction of arrival (DOA) of the desired signals is required. Array outputs aligned with code-matched filter can make the DOA estimation of multiple sources equivalent to that for single source localization problem in a noisy environment. With the advantage of code-matched filter inherent in the CDMA system, it has been proved that the multiple signal classification estimator [4] can obtain an unbiased DOA estimation with low mean-square-error (MSE) [5]. It also contributes to solving the limitation that the number of array elements must be more than the number of impinging sources, but for a conventional spectral searching DOA estimator such as MUSIC, its searching complexity and estimating accuracy strictly depend on the number of search grids used during the search. This is time consuming and it is unclear how to determine the required number of search grids. Thus, in this paper, we will focus on the GAM model of ULA to employ the DOA estimation in multipath reflection scenario from scatters.
Particle swarm optimization (PSO) is a population-based stochastic optimization paradigm, in which each agent, named particle, of the population, named swarm, is thought of as a collision-proof bird and used to represent a potential solution [6]. Like a genetic algorithm (GA), PSO starts by initializing a population of random solutions and searches for optima by updating generations. But, PSO does not use any evolution operators. In PSO, particles fly through the problem space by following their own experience and the best experience attained by the swarm as a whole. In contrast to analytical or general heuristic methods, PSO is computationally efficient and has great capability of escaping local optima [7,8]. In addition, a key characteristic of PSO is that the algorithm itself is highly robust yet remarkably simple to implement, while processing similar capabilities as other evolutionary algorithms such as GA [9]. A maximum likelihood (ML) criterion with hard-constraint PSO based solution applied to DOA estimation is proposed in [10], that explores the potentially superior performance at less computational costs. The same PSO algorithm based on the ML methodology is also derived in [11], where the cost function is an extension of the ML criteria that were originally developed for angle estimation with some of the sensors that are perfectly calibrated, while others are uncalibrated. Recently an adaptive PSO algorithm has been successfully applied in ML optimization solutions [12]. In another report a combined fuzzy adaptive PSO and differential evolution are also used to solve economic dispatch problems [13]. In this paper, a modified adaptive inertia weight PSO (APSO) is proposed to rationally balance the global exploration and local exploitation abilities of the particle to the GMUSIC criteria function [3] for CDMA signals. The resulting estimator is called APSO-GMUSIC, where a simple and effective measure, individual search ability, is defined to indicate whether each particle lacks global exploration ability in each dimension. By employing APSO to treat our optimization problem of the desired signal direction angle θ. The DOA, obtained by the APSO-GMUSIC estimator, converges to the optimal or near optimal solution. Simulation results show that the proposed APSO-GMUSIC estimator is very suitable to treat the DOA estimation for CDMA signals in a local scattered scenario.
2. System Model
2.1. Array Data Model
Consider a DOA estimation scenario in a CDMA system with P users. The data bit bp(t) ∈ {−1, 1} of the pth user is spread by a pseudo-noise (PN) signature waveform cp(t) for p = 1, 2, …, P. The signature waveform of the pth user is composed of a spreading sequence of L chips, i.e., , where is the lth spreading chip for the pth user and pTc(t) is the spreading pulse of duration Tc. Thus, the transmitted signal of the pth user during a bit interval Tb can be represented by:
Employing the code-matched filter and DOA estimation algorithm, we propose a receiving base station of CDMA communication system with a uniform linear array (ULA). The antenna array consists of M identical omidirectional elements and receives line-of-sight signals from P users that arrive at the array from different bearing angles θ1, θ2, …, θp with respect to the broadside of array in a cell/sector. Assume that the array element space is d. The direction vector associated with the pth user is given by:
2.2. MUSIC Algorithms for Local Scattering Channels
To show how the spatial signatures depend on the spatial distribution of the multipath propagation, we assume that the time dispersion produced by the multipath propagation is small compared to the reciprocal of the signal’s bandwidth, the time delay may be approximated as a phase shift , where fc is the carrier frequency, and τph is the time delay associated with the hth scattered signal from the pth source arriving at the array. Let sp(t) be the signal scattered by the pth user. Due to the multipath propagation near the pth user, its contribution to the array is modeled as a superposition of Np scattered rays. Then, the data received at the array is given by M × 1 vector form:
For high angular resolution subspace methods, the MUSIC algorithm is a kind of DOA estimation technique based on eigenvalue decomposition (EVD), which is also called the noise subspace-based method. The eigendecomposition of Equation (7) can be expressed as:
As the angular spread Δ̃ph of the hth scattered ray from the pth source arriving at the array is relatively small, a first-order Taylor expansion of in Equation (4) may be approximated as follows [14]:
Therefore, the pth user’s despread and sampled array vector signal ỹp can be represented as:
The correlation matrix of Equation (12) in the observation interval is given by:
The eigendecomposition of Equation (13) can be expressed as:
With the GAM model, the MUSIC searching function of Equation (9) can be expanded into a MUSIC with local scattering. The MUSIC searching function derived by the steering vector of the GAM model in Equation (10), which is termed as GMUSIC and can be expressed as:
2.3. Problem Formulation
Recently, a much more computationally efficient and more accurate parameter estimating approach via polynomial rooting method has been proposed to improve the spectral searching approaches for reducing the computational load. Due to the fact the scanning vector A̅(θ) of the GMUSIC is not Vandermonde structure, GSp(θ, ρ) cannot be implemented by using the polynomial rooting approach. The computational complexity of the classical subspace approach of MUSIC estimator is about 12M3 complex multiplications (CM) for computing EVD of a M × M dimension matrix. Let the search number be B. Therefore, the total required CM for computing Equation (15) of the GMUSIC estimator is about 12M3 + BM2. The performance of the abovementioned spectral searching approach is governed by the scanning grid size and the number of search grids while implementing the high-resolution DOA estimation. A major problem of GMUSIC type algorithms is the heavy computational load incurred with spatial spectral search when a smaller grid size is adapted. However, it is time consuming and the optimum search grid size is not clear. Smaller grid size can improve estimate accuracy, but the required computational load also becomes relatively larger (e.g., if grid sizes are set to 1°, 0.1° and 0.01°, then the required search numbers B = 181, 1,801, and 18,001, respectively.). With the number of particle population PN and the maximum number of iterations kmax, the computational complexity of our APSO approach is about PN × kmax. Hence, the computational complexity of APSO is smaller than the GMUSIC. Therefore, in order to reduce computational load, this paper investigates the feasibility of applying the PSO to replace the spectrum searching approach. As a result, the proposed PSO-based searching GMUSIC estimator does not increase the computational complexity, but significantly reduces the searching process requirement compared with the spectrum searching GMUSIC.
3. The Proposed PSO Based Searching Algorithms
Due to the fact that the performance of the abovementioned spectral searching GMUSIC estimator is governed by the scanning grid size and the number of search grids while implementing the high-resolution DOA estimation, it is time consuming and the search grid is not clear. In this section, we present PSO based searching approaches by maximizing the fitness function of GMUSIC at each iteration.
3.1. HPSO-GMUSIC Estimator
In order to reduce the scanning accurate angle problems of high computation cost, we use the PSO to replace scan in the ULA. For time-space signal processing, each particle can be treated as a point in the P-dimensional problem space and a swarm consisting of D random particles and then searches for best position (solution) by updating generations until exceeding the limit of iteration number. The position of the ith particle is represented as θi = [θi1, θi2, …, θiP], the rate of the position change (velocity) for ith particle is represented as vi = [vi1, vi2, …, viP]. The best previous position of the ith particle, which gives the best fitness value, is recorded as pi = [pi1, pi2, …, piP]. And, the index of the best particle among all the particles in the population is represented by pg = [pg1, pg2, …, pgp] and called global best location. In every iteration, the local bests and global bests are determined through evaluating the fitness values of the current population of particles. Two factors characterize a particle status on the search space: its position and velocity. The P-dimensional position for the ith particle in the kth iteration can be denoted as θi(k) = [θi1(k), θi2(k), …, θiP(k)]. Similarly, the velocity for the ith particle in the kth generation can be described as vi(k)= [vi1(k), vi2(k) …, viP(k)]. The velocity and the position of the ith particle at the (k + 1)th iteration for i = 1, 2, …, D and k = 1, 2, …, kmax are updated according to the following equations:
A particle position vector is converted to a candidate solution vector in the problem space through a suitable mapping. The score of the mapped vector evaluated by a GMUSIC function is regarded as the fitness of the corresponding particle. For time-space signal processing, the DOA GMUSIC estimation problem in this paper is to find the ith particle position or estimate angle θip(k) of the pth user to maximize the following fitness function:
At the end of iteration, global best location pgp (kmax) is the final estimated angle defined as θ̂p = pgp(kmax). The final global best position pg (kmax) is taken as the GMUSIC estimates of users. As a result, the PSO with linear decreasing inertia weight, particle velocity limitation, and particle position clipping is termed as hard-constraint PSO GMUSIC (HPSO-GMUSIC). Unfortunately, the HPSO-GMUSIC is not so facile to implement for its overhead on computing the search space mapping, particle velocity limitation and particle position clipping. In this paper, we present a more feasible and efficient modified PSO algorithm for the HPSO-GMUSIC estimator.
3.2. The Proposed Multiple Adaptive Inertia Weight
The inertia weight is critical for the performance of PSO, which balances global exploration and local exploitation abilities of the swarm. In other words, the inertia weight w(k) is employed to control the impact of the previous history of velocities on the current velocity, thereby influencing the trade-off between global and local exploration abilities of the “flying points”. A large inertia weight tends to facilitate searching new area and global exploration. Conversely, a small inertia weight facilitates local exploitation in the current search area. Suitable selection of the inertia weight provides a balance between global and local exploration abilities and thus requires less iteration on average to find the optimum. During the search every particle dynamically changes its position, so every particle locates in a complex environment and faces different situation. Therefore, each particle along every dimension may have different trade off between global and local search abilities. According to [15], it has been shown that the performance of the PSO algorithm with linearly decreasing inertia weight has the ability to quickly converge, but the PSO may lack global search ability at the end of a run and may fail to find the required optima in cases when the problem to be solved is too complicated and complex. But to some extent, this can be overcome by employing a self-adapting strategy for adjusting the inertia weight. In this subsection, inertia weight is dynamically adapted for every particle along every dimension. A measure, individual search ability, which characterizes the faced situation for every particle is defined. Basing on this measure, the particle could decide to whether to increase or decrease the values of inertia weight by means of the transfer function. The fine strategy of dynamically adjusting inertia weight could lead to improvement in performance of PSO.
For velocity updating, the last two parts of Equation (16) can be viewed as the accelerations parts and can be defined as aip(k) = c1·rand(•)·(pip(k) – θip(k)) and agp(k) = c2·rand(•)·(pip(k) – θip(k)), where rand(•) is independent random number with uniformly distributed between [0,1]. So we could consider that the particle is moving with velocity of vip(k) and acceleration of aip(k) and agp(k). But, agp(k) is the dominant term for improving convergence rate. Suppose that the mass of the ith particle in the pth dimension is normalized to 1 kg. According to the principle of mechanics, agp(k) = fip(k), where fip(k) is an outside force, which is put on the particle comes from the “pulling” of pip(k) and pgp(k). For ULA, the DOA is a one-dimensional searching problem. In order to make the particle fly towards optimal region quickly, vip(k) should turn to the direction of fip(k) as soon as possible. Define the error between pip(k) and θip(k) is zip(k) = pgp(k) – θip(k). Let mip(k) = |zip(k)|/θmax which is a number between 0 and 1. The velocity update problem of the ith particle on the pth dimension can be divided into two classes:
Firstly, vip(k) and zip(k) are in the same direction, zip(k)/vip(k) ≥ 0. If mip(k) is relatively large, it means the particle is in the right direction, but the velocity is too small. Therefore, the particle needs to speed up, and the inertia weight wip(k) needs to be set larger. If mip(k) is relatively small, it means the particle has come to the location, that is near the optimal region. So the velocity of this particle should slow down and the neighborhood of the state should be searched carefully, and wip(k) should be set smaller.
On the other hand, consider vip(k) and zip(k) on different direction, zip(k)/vip(k) < 0. If mip(k) is relatively large, it means that the particle’s state is far from the optimal region. So the particle needs to change its velocity as soon as possible, and the inertia weight wip(k) needs to be set smaller. If mip(k) is relatively small, it means that it’s not urgent for the particle to change its direction on this dimension, and wip(k) could be set a large value.
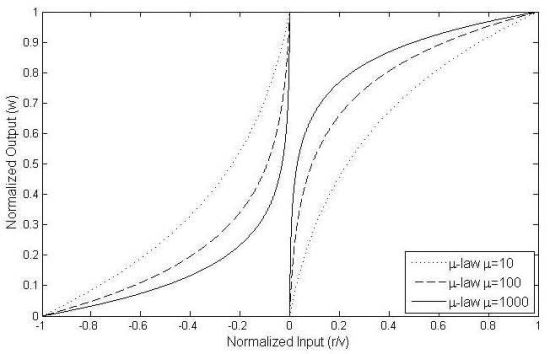
Based on the aforementioned analysis, an adaptive inertia weight strategy is proposed and is shown in Table 1. The individual normalized search ability of the ith particle along the pth dimension is defined as mip(k). It is noted that the value of wip(k) is a function of mip(k). To get a balance of global search and local search ability, wip(k) cannot be too large or too small, thus wip(k) is limited in the range of [wmin, wmax], which is like the process of normalization. Therefore, we used μ-law algorithm to achieve our strategy for every particle along every dimension, normalization of the mip(k) to w̅ip(k). The μ-law algorithm is a companding scheme used in telephone network [16]. Increasing the value of u, the dynamic range capability of μ-law can be improved and defined by:
In Equation (21), wmin be added to avoid particles from stopping moving. The curves of wip(k) with wmin = 0 using different μ can be plotted in Figure 1. Then, we also investigate the sensitivity for APSO-GMUSIC with different values of μ However, it accords with our strategy for different μ. Thus, μ-law algorithm with μ = 100 is chosen. Note that for every particle in population, wip(k) is unique and can be computed individually. Therefore, the single inertia weight wip(k) can be replaced by a multiple adaptive inertia weight wip(k). The proposed APSO-GMUSIC seems to be robust to control parameters due to the intrinsic advantages of the algorithm and the separation of the problem-independent PSO kernel from newly introduced problem-specific features in our design for adaptive multiple inertia weight. Finally, the steps for implementing the APSO-GMUSIC are shown in Figure 2 and described in the list that follows.
4. Computer Simulations
Several computer simulations for illustration and comparison are presented in this section. We use a 6-element ULA with half wavelength for simulation. Consider an asynchronous CDMA system with PN codes of length 31 and BPSK modulation. The spatial signature up is generated by Np = 30 independent identically distributed local scatters with uniform random angular spread of width 2Δ̃p. It is assumed that Δ̃p is uniformly distributed over the interval [−Δp, Δp]. Each scatter has equal power and is randomly, uniformly distributed over [0, 2π]. The value of parameter ρ is assumed to be known. Eight users are impinging on the array with random impinging angles of uniform distribution in the interval [−90°, 90°]. All signal powers are set to be 20 dBW. The additive background noise is assumed to be white Gaussian distribution with zero-mean and unit Watts of power. For GMUSIC, the search resolution (grid) is set to 1°, 0.1°, and 0.01° under the search range of [−90°, 90°]. The root-mean-squared error (RMSE) is calculated in an average manner as , where F indicates the number of independent simulation runs, P is the number of users, θ̂jp is the pth estimate DOA achieved in the jth run, and θp is the true DOA of the pth user. The PSO parameters chosen for all the experiments are summarized in Table 2. All PSO algorithms start with random initializations and are terminated if the maximum iteration kmax is reached or the global best particle position is not updated in 20 successive iterations. Every simulation result is presented after 200 data bits were processed and it is averaged by F = 103 independent Monte Carlo runs with independent noise samples for each run.
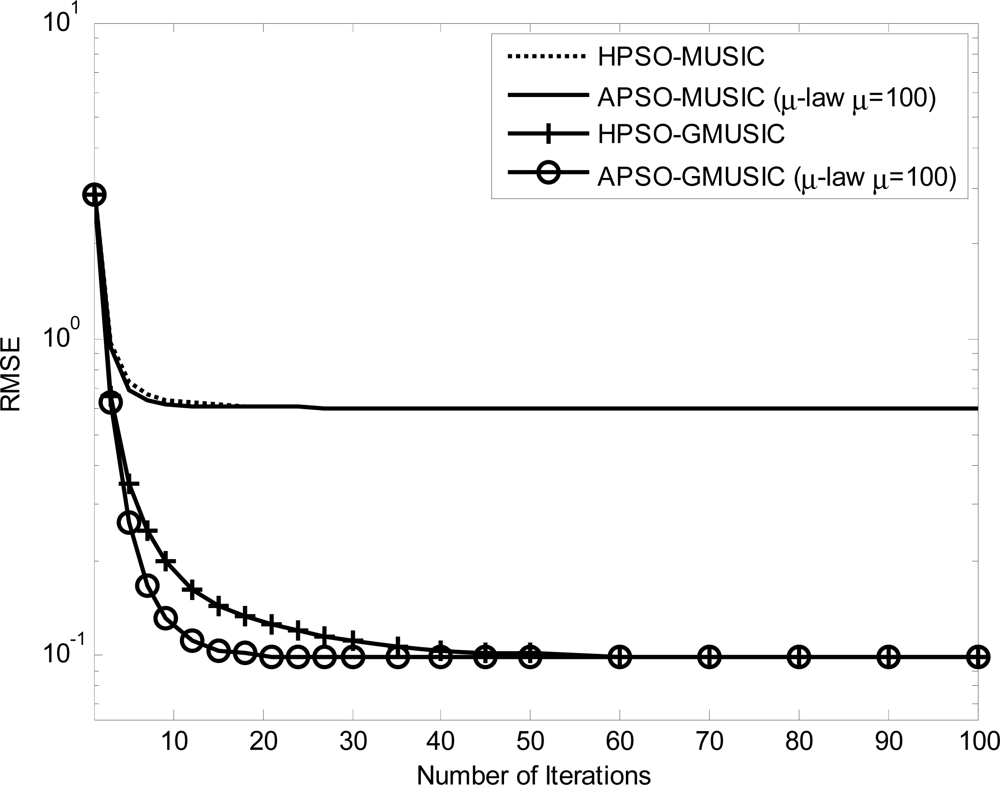
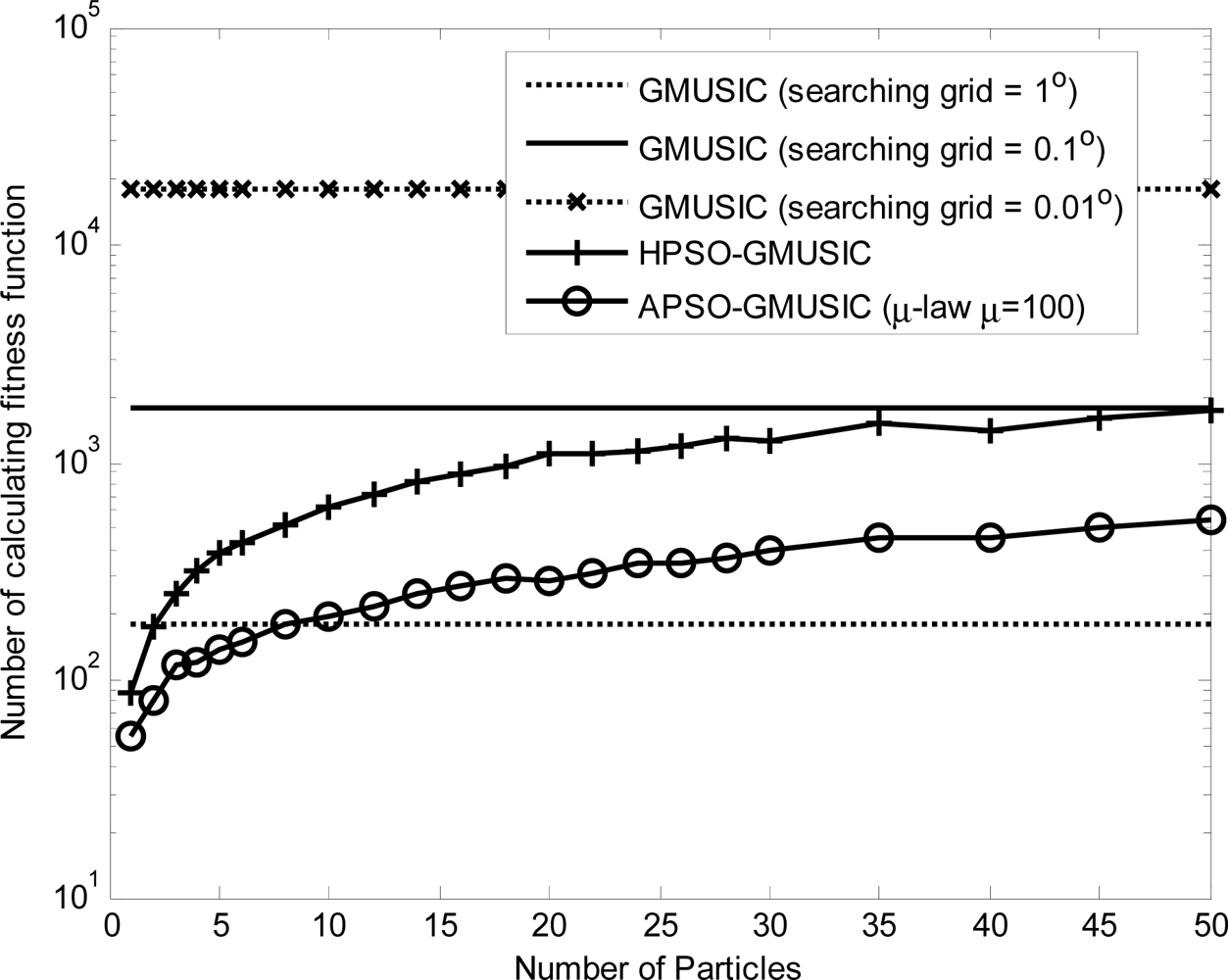
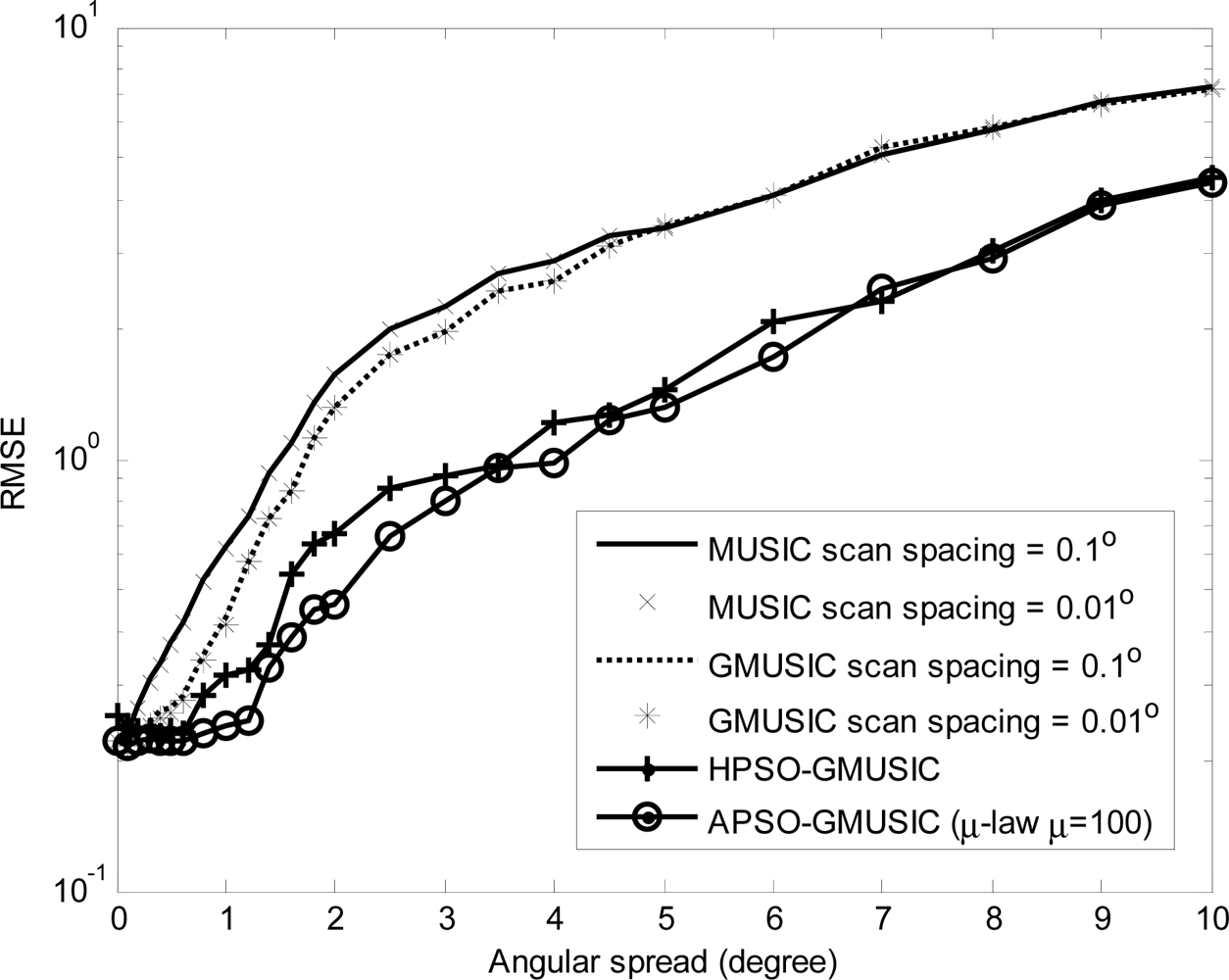
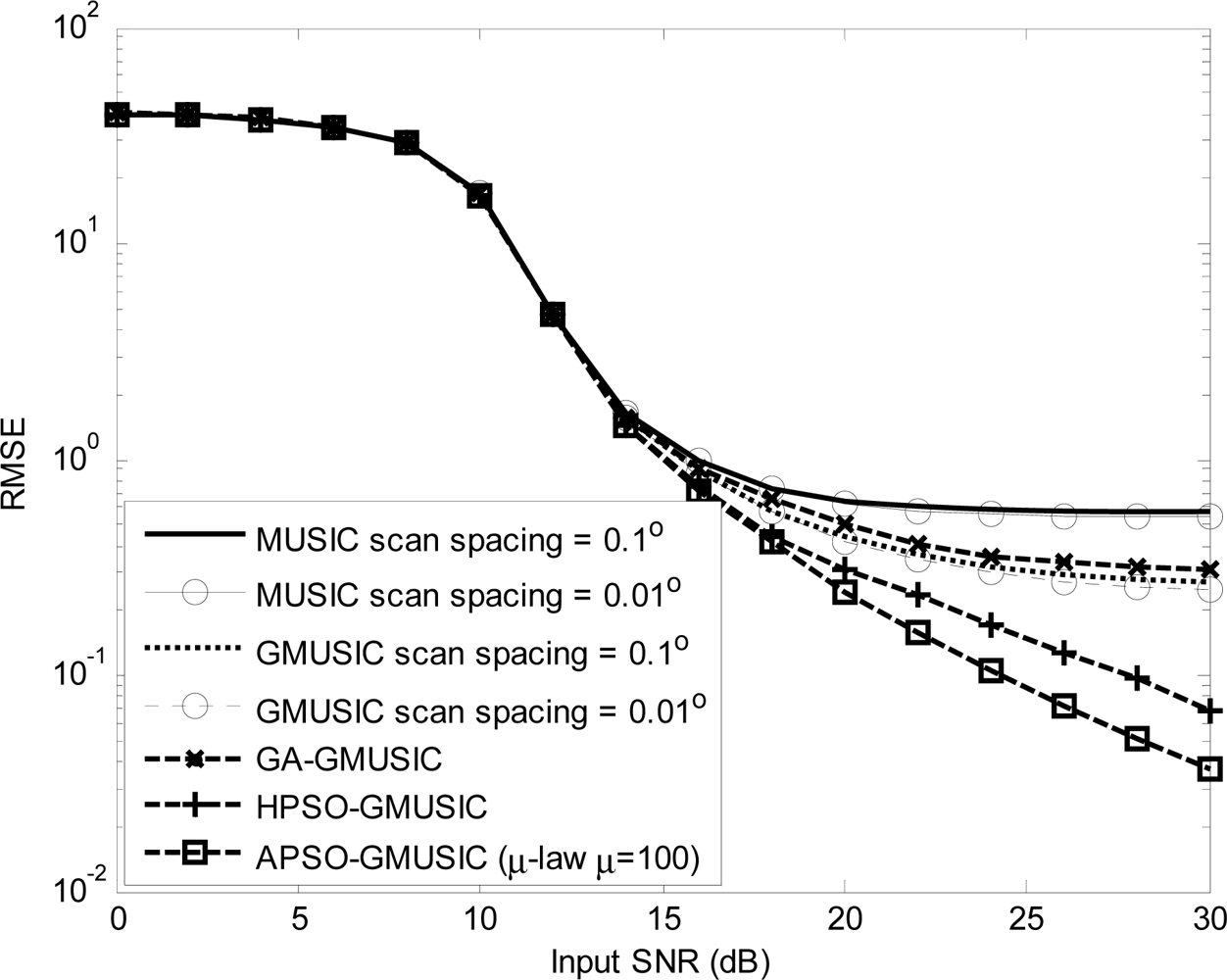
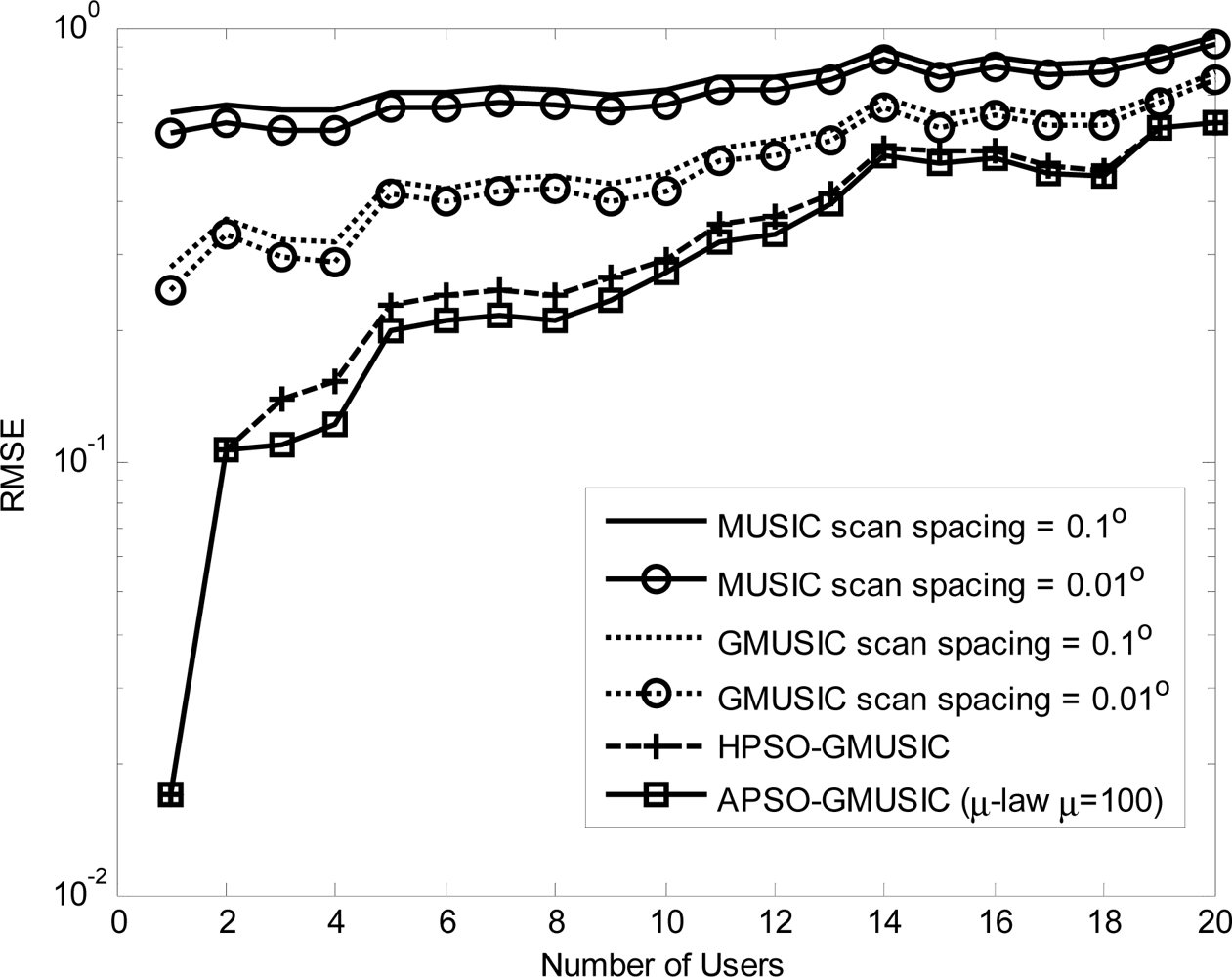
Comparison results with other estimators, including the GMUSIC, HPSO-GMUSIC and APSO-GMUSIC with μ = 100 to DOA estimation error are presented. Figure 3 depicts the convergence in terms of DOA RMSE versus the number of iterations. As a result, the HPSO-GMUSIC requires more iterations to achieve convergence. Note that the proposed APSO-GMUSIC achieves fast convergence with the selected parameters, which means that it needs less iterations to approach the desired global extreme. Figure 4 shows the required number of calculating fitness function (B) versus number of particles. For the number of particles in the population, more particles may increase success in searching for optima due to sampling state space more thoroughly. However, more particles require more evaluation cost. The HPSO-GMUSIC needs more particles to approach the desired global extreme. It is confirmed that the proposed PSO-based searching approaches can reduce the computational complexity of the GMUSIC due to the searching process. As expected, this figure also provides a great improvement over the convergence rate on optimization problems. In fact, additional adaptive multiple inertia weight operation can improve the searching speed and RMSE performance further. Figure 5 presents the RMSE of DOA estimation versus varying angular spreads. We note that the subspace-based techniques show serious degradation when faced with local scatters. Local scattering may be viewed as a form of model error and gives rise to the perturbation of the noise subspace. Again, these figures show that the proposed APSO-GMUSIC method yields significantly superior performance over the other methods in the presence of local scatters. For comparison, the result of GA-GMUSIC estimator is also provided. The same parameters of GA-GMUSIC estimator are used in [17]. Figure 6 shows the RMSE versus different SNR of the desired user for angular spreads 2Δp = 1°. For the low SNR case, all of methods may produce highly biased estimates. Clearly, with the compatible searching resolution, the APSO-GMUSIC can save the required number of searching grids and improve the RMSE performance, as compared with the other estimators. The GA-GMUSIC has a poor performance than HPSO-GMUSIC and APSO-GMUSIC. It is well known that premature convergence degrades the performance of GA and reduces the search ability [18]. In addition, it has been shown that the performance of the PSO algorithm with linearly decreasing inertia weight has the ability to quickly converge, the PSO may lack global search ability at the end of a run and may fail to find the required optima in cases when the problem to be solved is too complicated and complex [19]. But to some extent, this can be overcome by employing the proposed adaptive multiple strategy for adjusting the inertia weight. Finally, in Figure 7, we compare the RMSE performance against the number of active user P, given SNR = 20 dBW and angular spread 2Δp = 1°. Basically, the RMSE is increased quite steadily with the increase of P. It can be observed that the APSO-GMUSIC obtain more performance improvement when the number of users P is reasonably increasing. Among them, the proposed APSO method achieves the lowest RMSE.
5. Conclusions
In this paper, we have presented a PSO based searching DOA estimation method, named APSO, which uses the GMUSIC searching function for CDMA signals. With the code-matched filter, the MAIs after code-decorrelation appear as noises for CDMA signals. The rooting MUSIC method is suboptimal in the presence of the noise and MAI and the GMUSIC cannot be implemented by using the polynomial rooting approach. However, the proposed techniques reduce the required search grids for the conventional spectral searching estimators. In the previous work on DOA estimation using PSO algorithm [10], hard constraints have been taken, during each iteration of PSO algorithm. In this paper, multiple inertia weight has been incorporated in PSO. In conjunction with a modified PSO for angle searching, the proposed approach can reduce the required computational load for the conventional spectral searching MUSIC estimator with local scattering. Moreover, the convergence of the proposed approach is much faster. Computer simulations have demonstrated the effectiveness of the proposed approach. Furthermore, a common drawback with MUSIC-like technique is that it is a suboptimal estimator and tends to suffer from low performance due to low SNR, small sample size, and correlated sources. Thus, how to develop a cheaper way and work well with correlated or even coherent sources will be important in the future work.
Acknowledgments
The author would like to thank the anonymous reviewers for their valuable and constructive comments, which helped to improve the presentation of the paper.
References
- Ottersten, B. Array Processing for Wireless Communication. Proceedings of 8th IEEE Signal Processing Workshop on Statistical Signal and Array Processing, Corfu, Greece, 24–26 July 1996; pp. 466–473.
- Astely, D.; Ottersten, B. The effects of local scattering on direction of arrival estimation with MUSIC. IEEE Trans. Signal Proc 1999, 47, 3220–3234. [Google Scholar]
- Astely, D.; Ottersten, B.; Swindlehurst, A.L. Generalised array manifold model for wireless communication channels with local scattering. IEE Proc. Radar, Sonar Navig 1998, 145, 51–57. [Google Scholar]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag 1986, 34, 276–280. [Google Scholar]
- Chiang, C.T.; Chang, A.C. DOA estimation in the asynchronous DS-CDMA system. IEEE Trans. Antennas Propag 2003, 51, 40–47. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. Proceedings of IEEE International Conference on Neural Networks, Path, Australia, 27 November–1 December 1995; 4, pp. 1942–1948.
- Shi, Y.; Eberhart, R. A Modified Particle Swarm Optimizer. Proceedings of IEEE International Conference on Evolutionary Computation, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73.
- Shi, Y.; Eberhart, R. Comparing Inertia Weights and Constriction Factors in Particle Swarm Optimization. Proceedings of the Congress on Evolutionary Computation, La Jolla, CA, USA, 16–19 July 2000; 1, pp. 84–88.
- Shi, Y.; Eberhart, R. Comparison between genetic algorithms and particle swarm optimization. Lect. Notes Comput. Sci 1998, 1447, 611–616. [Google Scholar]
- Li, M.; Lu, Y. Maximum likelihood DOA estimation in unknown colored noise fields. IEEE Trans. Aerospace Electron. Syst 2008, 44, 1079–1090. [Google Scholar]
- Li, M.; Lu, Y. Source bearing and steering-vector estimation using partially calibrated arrays. IEEE Trans. Aerospace Electron. Syst 2009, 45, 1361–1372. [Google Scholar]
- Zeng, J.; He, Z.; Liu, B. Maximum Likelihood DOA Estimation Using Particle Swarm Optimization Algorithm. Proceedings of CIE ’06 International Conference on Radar, Shanghai, China, 16–19 October 2006; pp. 1–4.
- Niknam, T.; Mojarrad, H.D.; Nayeripour, M. A new hybrid fuzzy adaptive particle swarm optimization for non-convex economic dispatch. Int. J. Innov. Comput. Inf. Control (IJICIC) 2011, 7, 189–202. [Google Scholar]
- Chang, A.C.; Jen, C.W. Subspace-based techniques for 2-D DOA estimation with uniform circular array under local scattering. J. Chin. Inst. Eng 2006, 29, 663–673. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Empirical Study of Particle Swarm Optimization. Proceedings of the Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999; 3, pp. 1945–1950.
- Haykin, S. Communication Systems, 4th ed; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Chang, A.C.; Hung, J.C. Combining GA and INWES approach to DOA estimation of CDMA signals. Neural Comput. Appl 2010, 19, 1003–1011. [Google Scholar]
- Fogel, D.B. Evolutionary Computation: Toward a New Philosophy of Machine Intelligence; IEEE: New York, NY, USA, 1995. [Google Scholar]
- Panigrahi, B.K.; Pandi, V.R.; Das, S. Adaptive particle swarm optimization approach for static and dynamic economic load dispatch. Energy Convers. Manag 2008, 49, 1407–1415. [Google Scholar]

| Value of wip (k) | Value of mip (k) | |||
|---|---|---|---|---|
| Small | Middle | Large | ||
| Directions of vip (k) and zip (k) | Same | small | middle | large |
| Opposite | large | middle | small | |
| c1 | c2 | The number of particles | The number of iterations | Constraints | wmax | wmin | Inertia weight feature | |
|---|---|---|---|---|---|---|---|---|
| HPSO | 2 | 2 | 20 | 20 | Hard constraint | 0.9 | 0.4 | Single and linearly |
| APSO | 1.1 | 0.1 | Multiple and used μ–law |
© 2012 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chang, J.-C. DOA Estimation for Local Scattered CDMA Signals by Particle Swarm Optimization. Sensors 2012, 12, 3228-3242. https://doi.org/10.3390/s120303228
Chang J-C. DOA Estimation for Local Scattered CDMA Signals by Particle Swarm Optimization. Sensors. 2012; 12(3):3228-3242. https://doi.org/10.3390/s120303228
Chicago/Turabian StyleChang, Jhih-Chung. 2012. "DOA Estimation for Local Scattered CDMA Signals by Particle Swarm Optimization" Sensors 12, no. 3: 3228-3242. https://doi.org/10.3390/s120303228