An Efficient Lagrangean Relaxation-based Object Tracking Algorithm in Wireless Sensor Networks
Abstract
:1. Introduction
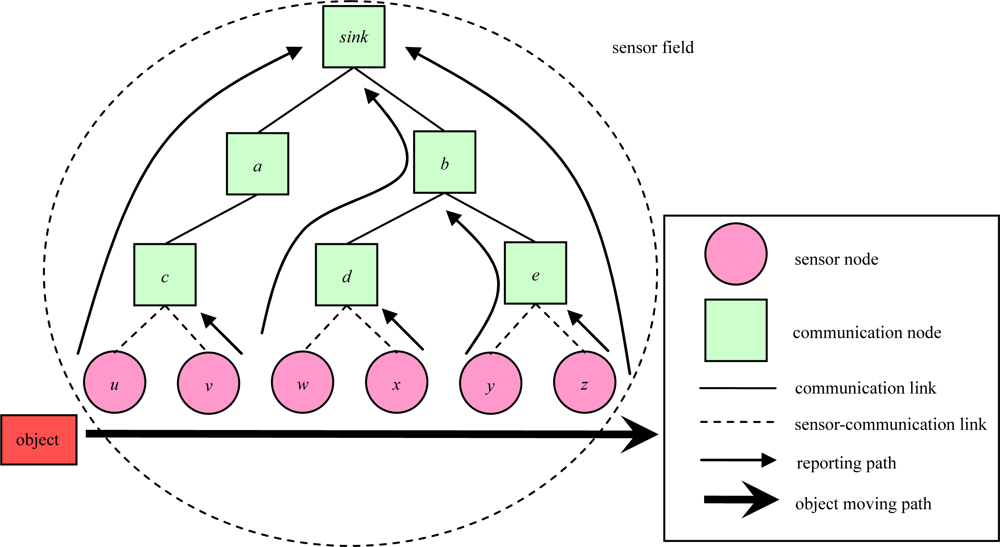
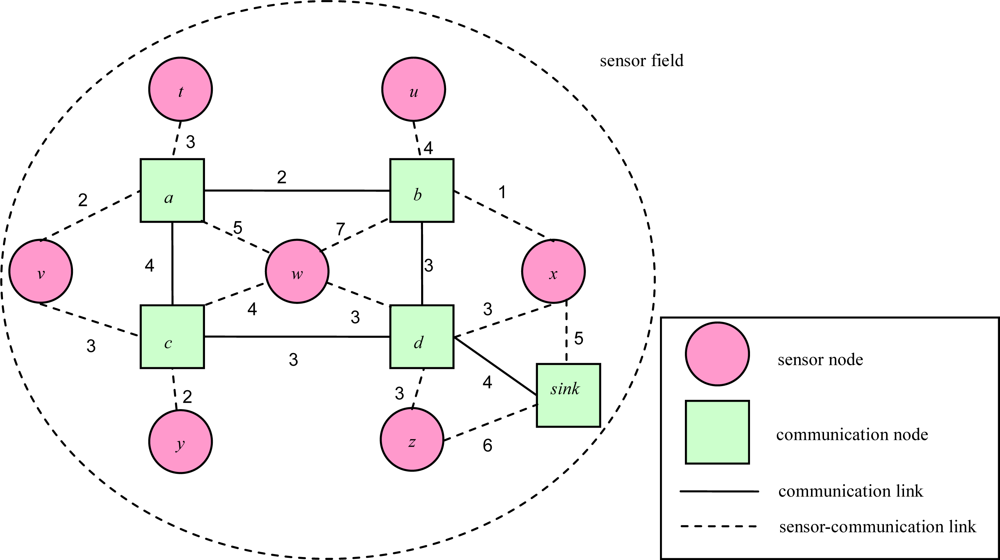
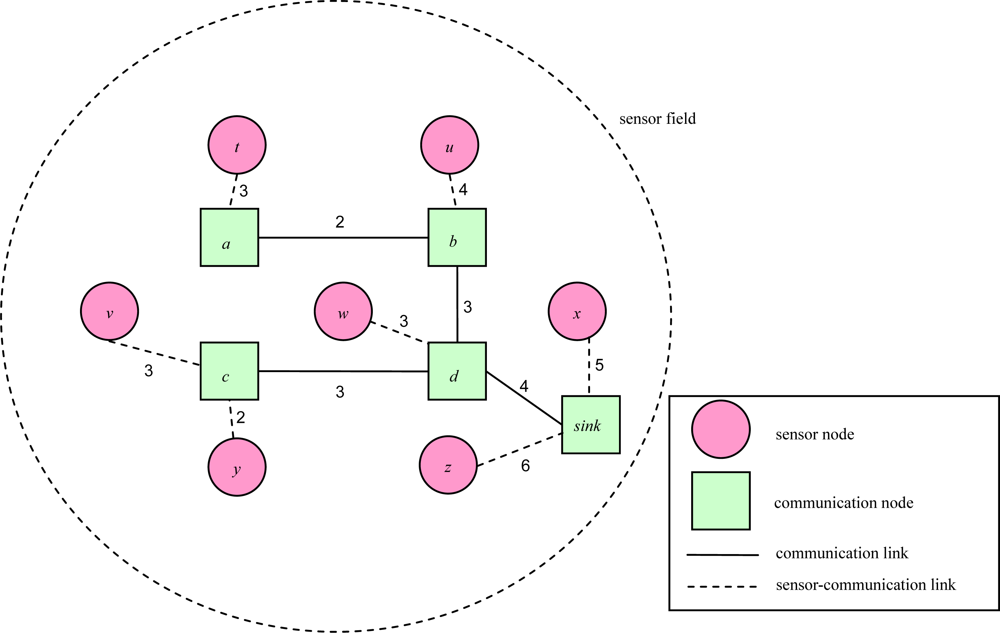
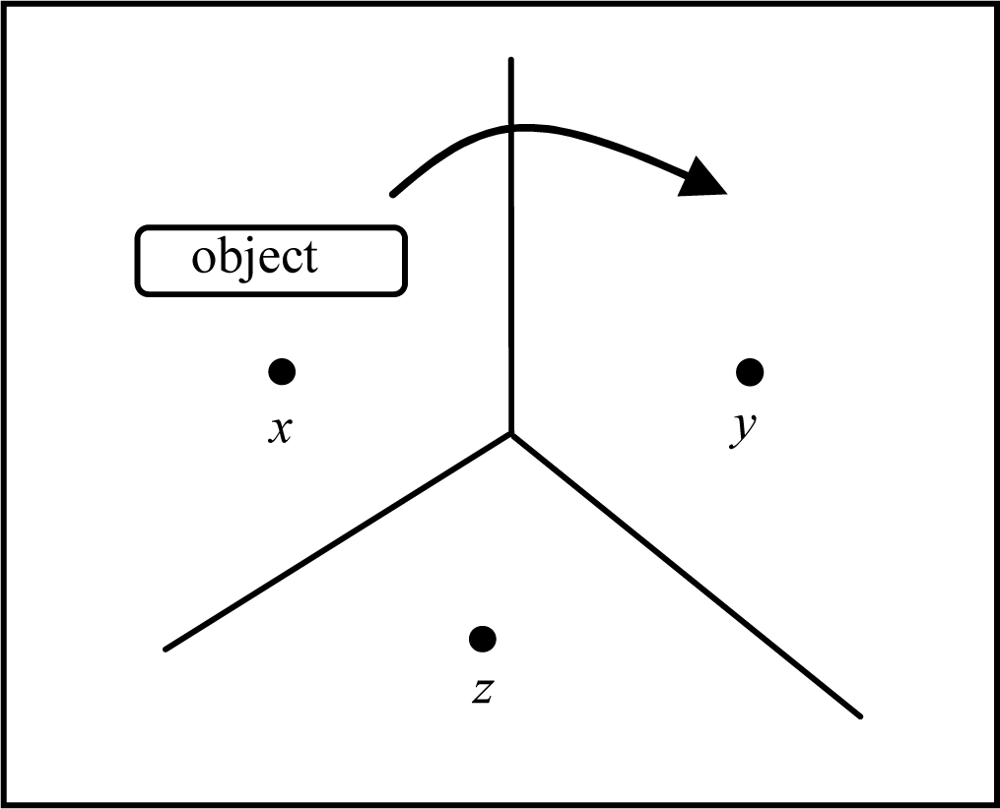
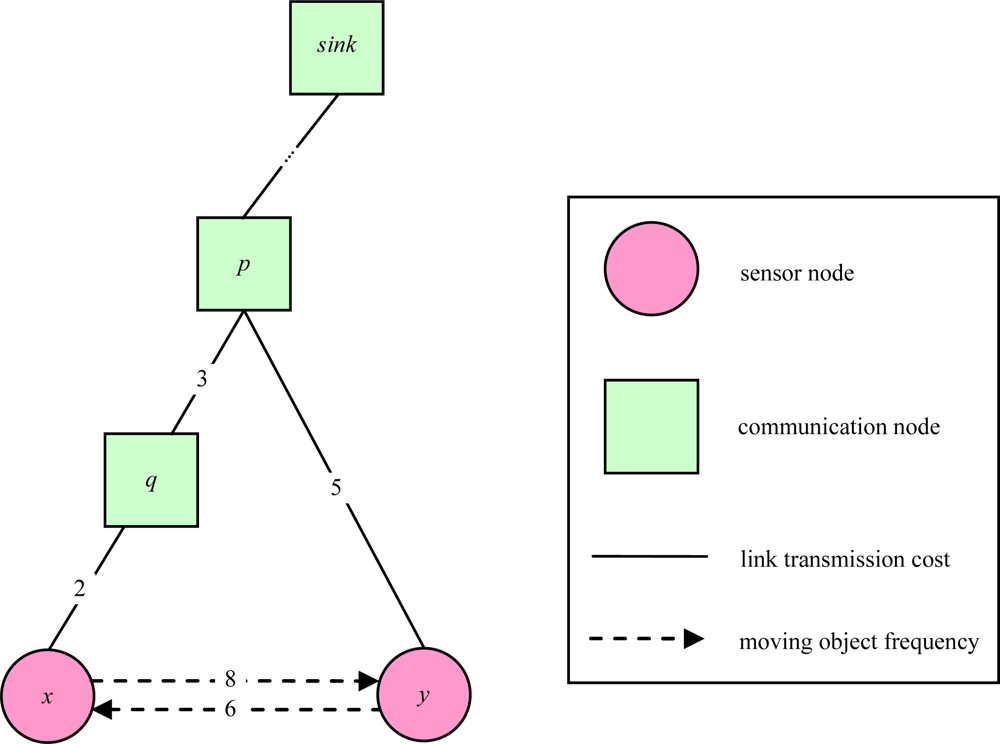
2. Problem Description
3. Problem Formulation
| Problem (IP1): |
|---|
| Objective function: |
| subject to: |
- Constraint (1.1): Routing constraint which uses one path from sensor node s to sink node only.
- Constraint (1.2): Tree constraint of avoiding cycles. Any outgoing link of a node to communication node is equal to 1 on the object tracking tree.
- Constraint (1.3): Routing constraint. Once the path, xsp, is selected and the tree link (i, j) is on the path, the decision variable, , must set to be 1.
- Constraint (1.4): Sensor y must use one or more tree links (i,j) to report location of object when object moves from sensor x to sensor y. Therefore, must be greater than or equal to 1.
- Constraints (1.5–1.6): Decision variables xsp and equal to 0 or 1.
| Problem (IP2): |
|---|
| Objective function: |
| subject to: |
- Constraint (2.1): Routing constraint which uses one path from sensor node s to sink node only.
- Constraint (2.2): Tree constraint of avoiding cycles. Any outgoing link of node to communication node is equal to 1 on the object tracking tree.
- Constraint (2.3): Routing constraint. Once the path, xsp, is selected and the tree link (i, j) is on the path, the decision variable, , must set to be 1.
- Constraints (2.4–2.5): There are variable-transformation constraints. If , reporting location of object will use the tracking link (i, j) when object moves from sensor x to sensor y, must set to be 1, and 0 otherwise.
- Constraint (2.6): Sensor y must use one or more tracking link (i,j) to report object’s location when object moves from sensor x to sensor y. Therefore, must be greater than or equal to 1.
- Constraints (2.7–2.9): Decision variables xsp, , and equal to 0 or 1.
4. Solution Approach
4.1. Lagrangean Relaxation
| Problem (LR): |
|---|
| Objective function: |
| subject to: (2.1), (2.2), (2.6), (2.7), (2.8), and (2.9). |
| Sub-problem 1: (related to the decision variables) |
|---|
| Objective function: |
| subject to: (2.6) and (2.9). |
| Sub-problem 2: (related to the decision variables xsp) |
|---|
| Objective function: |
| subject to: (2.1) and (2.7). |
| Sub-problem 3: (related to the decision variables) |
|---|
| Objective function: |
| subject to: (2.2) and (2.8). |
| Sub-problem 4: (Constant Part) |
|---|
| Objective function: |
| Dual Problem (D): |
|---|
| Objective function: |
| subject to: |
4.2. Getting Primal Feasible Solutions
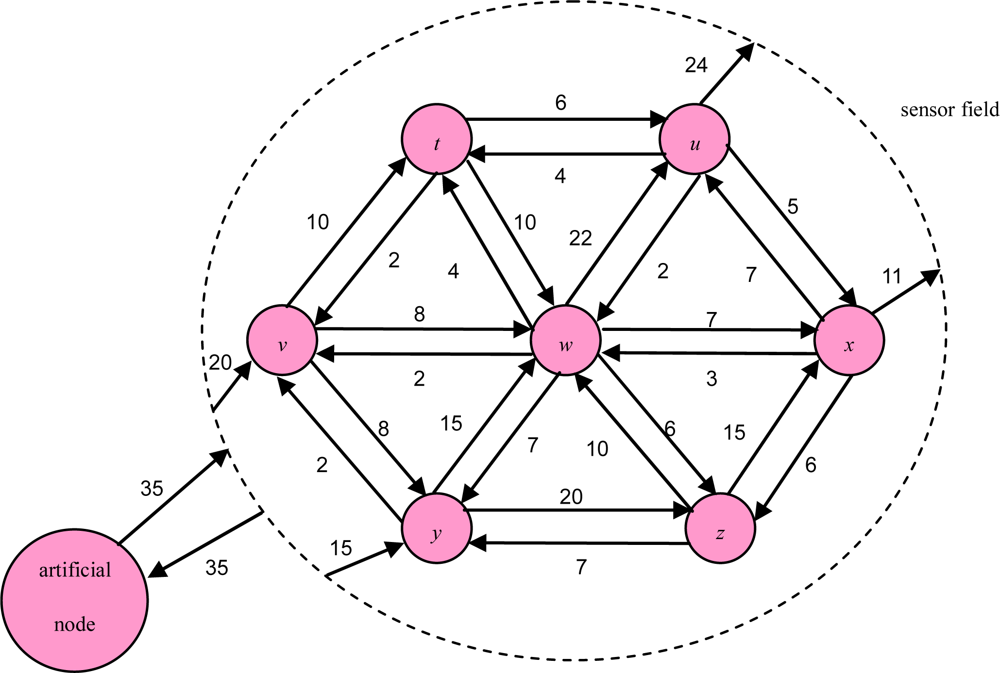
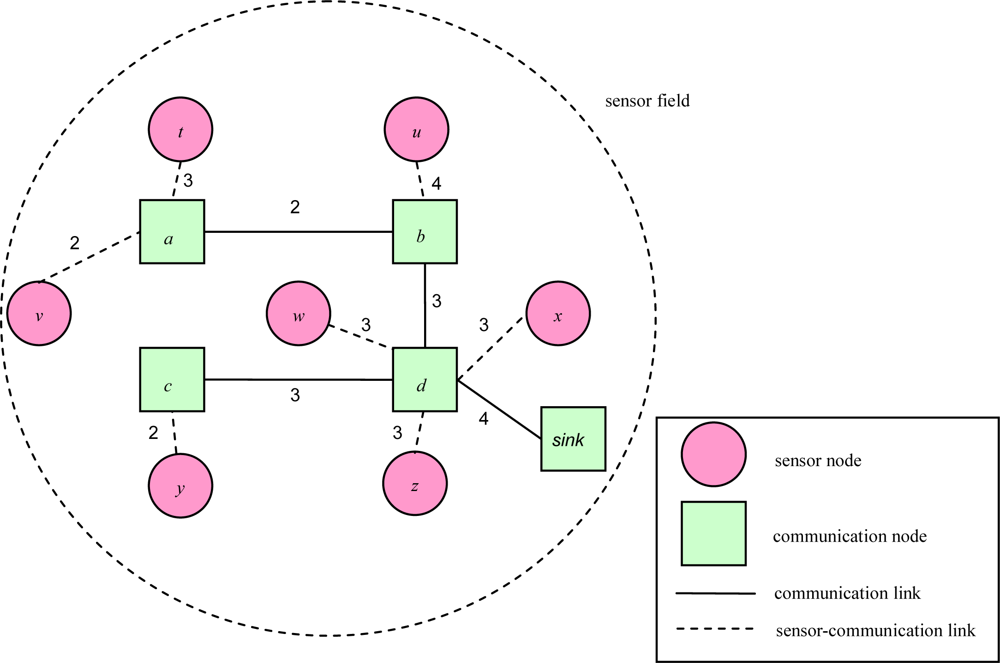
5. Computational Experiments
5.1. Experiments Environment
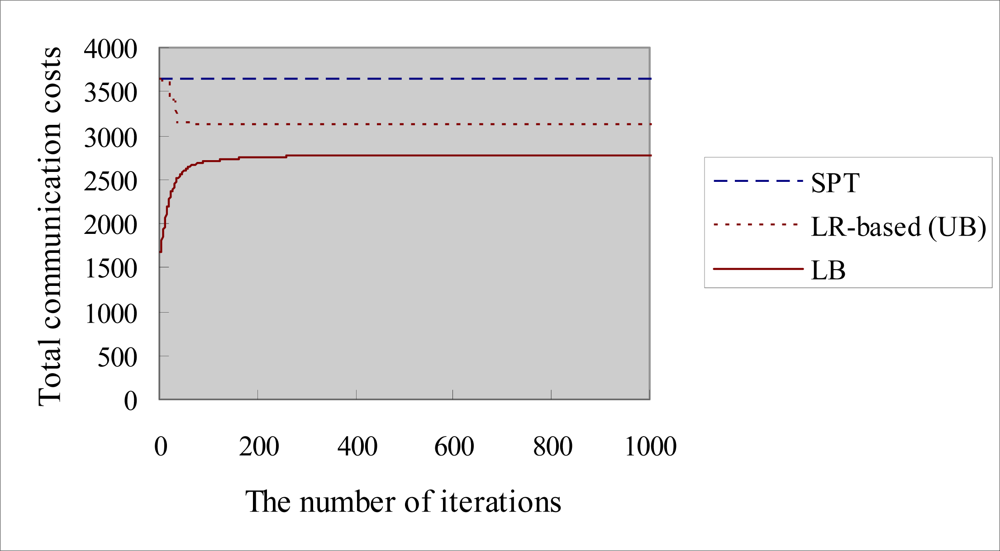
5.2. Experimental Results
6. Conclusions
References
- Akyildiz, IF; Sankarasubramaniam, WSY; Cayirci, E. Wireless Sensor Networks: A Survey. Elsevier J. Comput. Netw 2002, 38, 393–422. [Google Scholar]
- Akyildiz, IF; Sankarasubramaniam, WSY; Cayirci, E. A Survey on Sensor Networks. IEEE Commun. Mag 2002, 40, 102–114. [Google Scholar]
- Xu, Y; Lee, WC. On Localized Prediction for Power Efficient Object Tracking in Sensor Networks. Proceedings of the 23rd International Conference on Distributed Computing Systems Workshops, Providence, RI, USA, May 19–22, 2003; pp. 434–439.
- Xu, Y; Winter, J; Lee, WC. Prediction-based Strategies for Energy Saving in Object Tracking Sensor Networks. IEEE International Conference on Mobile Data Management, Berkeley, CA, USA, January 19–22, 2004; pp. 346–357.
- Xu, Y; Winter, J; Lee, WC. Dual Prediction-based Reporting for Object Tracking Sensor Networks. Proceedings of The First Annual International Conference on Mobile and Ubiquitous Systems: Networking and Services, Boston, MA, USA, August 22–26, 2004; pp. 154–163.
- Kung, HT; Vlah, D. Efficient Location Tracking Using Sensor Networks. Proceedings of IEEE Wireless Communications and Networking Conference, New Orleans, LA, USA, March 16–20, 2003; pp. 1954–1961.
- Lin, CY; Tseng, YC. Structures for In-network Moving Object Tracking in Wireless Sensor Networks. Proceedings of IEEE First International Conference on Broadband Networks, San Jose, CA, USA, October 25–29, 2004; pp. 718–727.
- Lin, CY; Peng, WC; Tseng, YC. Efficient In-Network Moving Object Tracking in Wireless Sensor Networks. IEEE Trans. Mob. Comput 2006, 5, 1044–1056. [Google Scholar]
- Bhatti, S; Jie, X. Survey of Target Tracking Protocols Using Wireless Sensor Network. Proceedings of Fifth International Conference on Wireless and Mobile Communications, Cannes, French Riviera, France, August 23–29, 2009; pp. 110–115.
- Lin, FYS; Yen, HH; Lin, SP. A Novel Energy-Efficient MAC Aware Data Aggregation Routing in Wireless Sensor Networks. Sensors 2009, 9, 1295–2147. [Google Scholar]
- Lin, FYS; Yen, HH; Lin, SP. Delay QoS and MAC Aware Energy-Efficient Data-Aggregation Routing in Wireless Sensor Networks. Sensors 2009, 9, 7711–7732. [Google Scholar]
- Wen, YF; Lin, FYS; Kuo, WC. A Tree-based Energy-efficient Algorithm for Data-Centric Wireless Sensor Networks. Proceedings of 21st International Conference on Advanced Networking and Applications, Niagara Falls, Ontario, Canada, May 21–23, 2007; pp. 202–209.
- Liu, BH; Ke, WC; Tsai, CH; Tsai, MJ. Constructing a Message-Pruning Tree with Minimum Cost for Tracking Moving Objects in Wireless Sensor Networks is NP-Complete and an Enhanced Data Aggregation Structure. IEEE Trans. Comput 2008, 57, 849–863. [Google Scholar]
- Fisher, ML. The Lagrangean Relaxation Method for Solving Integer Programming Problem. Manage. Sci 1981, 27, 1–18. [Google Scholar]
- Fisher, ML. An Applications Oriented Guide to Lagrangian Relaxation. Interfaces 1985, 15, 10–21. [Google Scholar]
- Cartigny, J; Simplot, D; Stojmenovic, I. Localized Minimum-energy Broadcasting in ad hoc Networks. Proceedings of IEEE INFOCOM, San Francisco, CA, USA, March 30–April 3, 2003; pp. 2210–2217.



| Mode | Current | |
|---|---|---|
| Radio | Rx | 19.7 mA |
| Tx(−10 dBm) | 11 mA | |
| Tx(−5 dBm) | 14 mA | |
| Tx(0 dBm) | 17.4 mA | |
| Given Parameters | |
|---|---|
| Notation | Description |
| S | The set of all sensor nodes. |
| C | The set of all communication nodes, including sink node. |
| o | Artificial node outside the sensor field. |
| R | The set of the object moving frequency from x to y, ∀x, y ∈ S ∪ {o}, x ≠ y. |
| L | The set of all links, (i, j)∈ L, i≠j. |
| A | The set of transmission costs a(i,j) associated with link (i, j). |
| Ps | The set of all candidate paths p between a pair of nodes, s and sink, ∀s ∈ S. |
| Indicate Parameter | |
|---|---|
| Notation | Description |
| δp(i,j) | The value of indicator function is 1 if link (i, j) is on path p, and 0 otherwise. |
| Decision Variables | |
|---|---|
| Notation | Description |
| xsp | 1 if the sensor node s uses the path p to reach the sink node, and 0 otherwise. |
| 1 if the sensor node s uses the link (i, j) to reach the sink node, and 0 otherwise. | |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
| Decision Variables | |
|---|---|
| Notation | Description |
| 1 if (reporting object’s location uses the link (i,j) when object moves from sensor x to sensor y), and 0 otherwise, x ≠ y. | |
| Parameter | Value |
|---|---|
| Number of nodes | 12–105 (depend on each case) |
| Number of iterations | 5,000 |
| Improvement counter threshold | 49 |
| Initial upper bound | 1010 |
| Initial lower bound | −1010 |
| Initial scalar of step size | 2 |
| Initial multiplier | 0 |
| Number of nodes | Zdu | ZIP2 | Gap | SPT | Improvement Ratio to SPT | |
|---|---|---|---|---|---|---|
| 12 | Problem 1 Problem 2 | 2,774 3,416 | 3,127 3,906 | 0.13 0.14 | 3,630 4,460 | 0.16 0.14 |
| 23 | Problem 1 Problem 2 | 17,850 17,385 | 20,725 20,282 | 0.16 0.17 | 22,491 21,839 | 0.09 0.08 |
| 36 | Problem 1 Problem 2 | 42,410 42,775 | 49,970 50,411 | 0.18 0.18 | 57,553 57,787 | 0.15 0.15 |
| 50 | Problem 1 Problem 2 | 89,824 77,905 | 78,807 88,195 | 0.14 0.13 | 99,639 102,796 | 0.11 0.17 |
| 105 | Problem 1 Problem 2 | 326,529 328,911 | 371,438 355,546 | 0.14 0.08 | 508,314 511,402 | 0.37 0.44 |
| Problem | Time Complexity |
|---|---|
| Sub-problem (SUB1) | O(|S|2|L|) |
| Sub-problem (SUB2) | O(|S|3) |
| Sub-problem (SUB3) | O(|S|2|L|) |
| Sub-problem (SUB4) | O(|S|2|L|) |
| Getting primal feasible solutions | O(|S|2) |
| Lagrangean dual problem | O(I|S|2|L|)* |
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lin, F.Y.-S.; Lee, C.-T. An Efficient Lagrangean Relaxation-based Object Tracking Algorithm in Wireless Sensor Networks. Sensors 2010, 10, 8101-8118. https://doi.org/10.3390/s100908101
Lin FY-S, Lee C-T. An Efficient Lagrangean Relaxation-based Object Tracking Algorithm in Wireless Sensor Networks. Sensors. 2010; 10(9):8101-8118. https://doi.org/10.3390/s100908101
Chicago/Turabian StyleLin, Frank Yeong-Sung, and Cheng-Ta Lee. 2010. "An Efficient Lagrangean Relaxation-based Object Tracking Algorithm in Wireless Sensor Networks" Sensors 10, no. 9: 8101-8118. https://doi.org/10.3390/s100908101





