Concurrent Initialization for Bearing-Only SLAM
Abstract
:1. Introduction
2. Related Work
3. Problem Statement
3.1. Sensor motion model
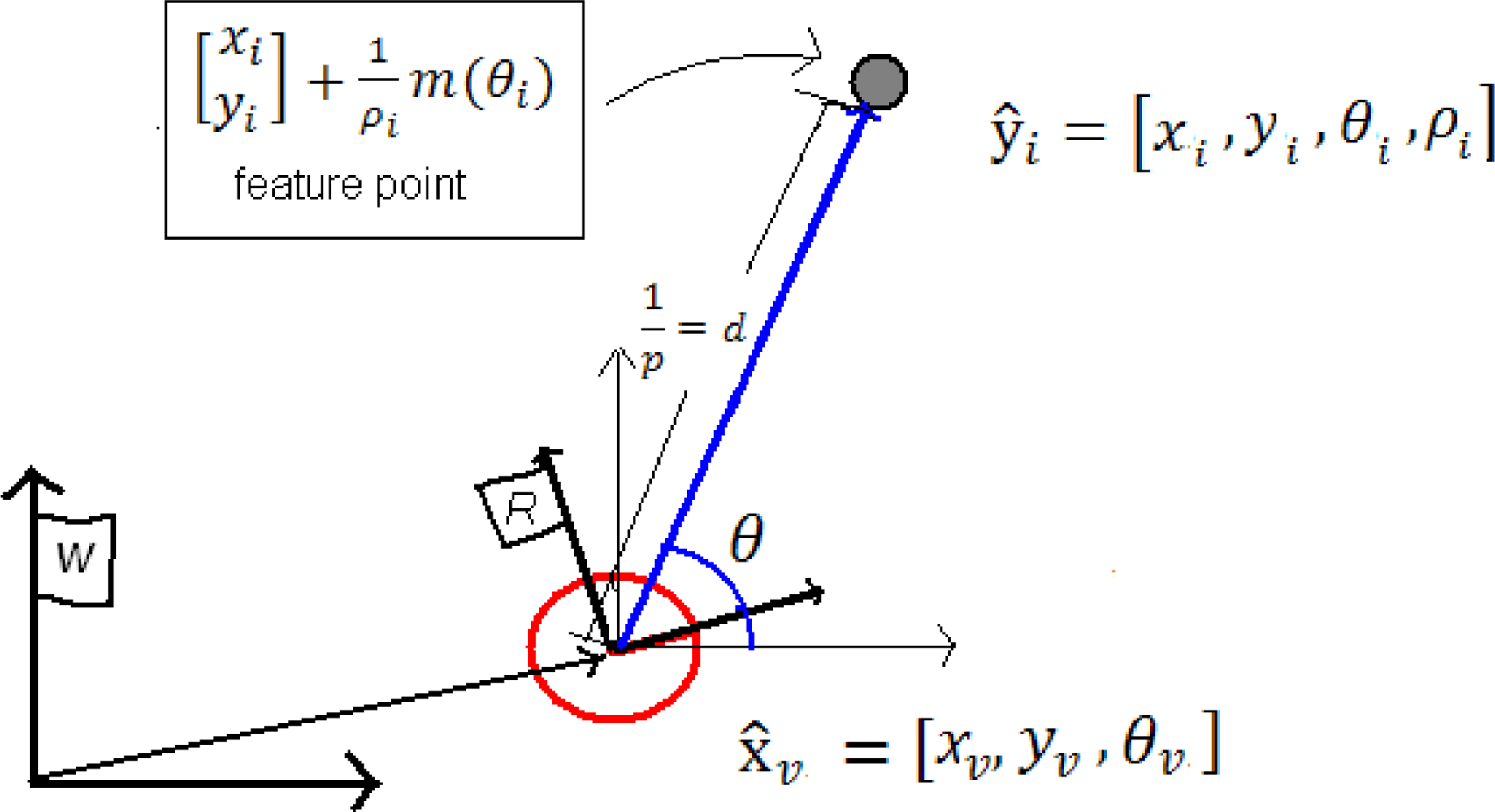
3.2. Features definition and measurement model
3.3. ID-Undelayed initialization
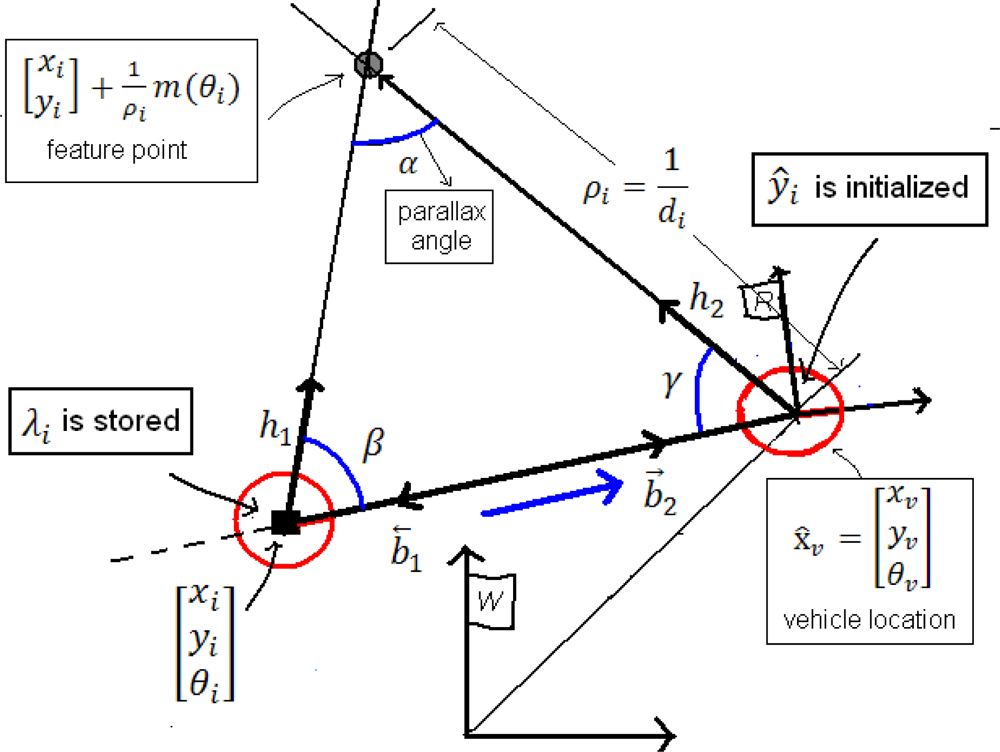
3.4. ID-Delayed initialization
- The base-line b.
- λi, using its associated data (x1, y1, θ1, z1, σ1x, σ1y, σ1θ).
- The current state (xv, yv, θv, z, σxv, σyv, σθv).
3.5. Undelayed vs. Delayed
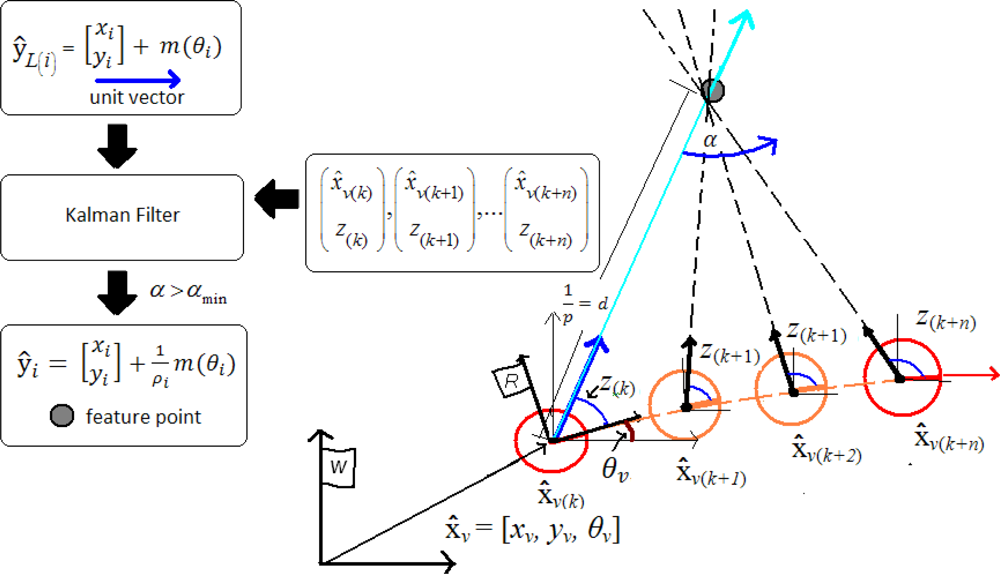
4. Concurrent Initialization
4.1. Undelayed stage
4.2. Delayed stage
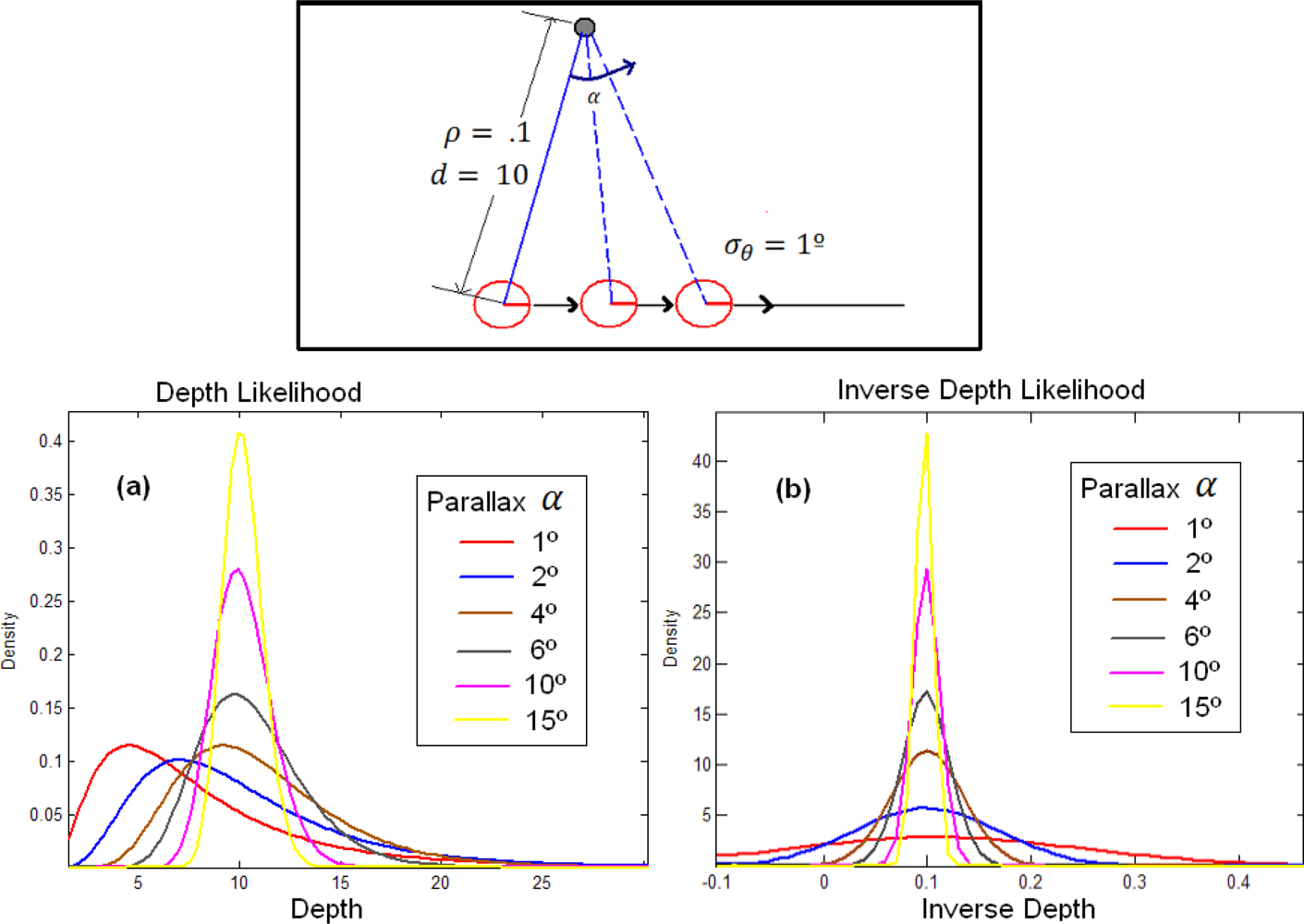
4.3. Updating depth
4.4. Measurement
- - For features ŷi measurement Equation 7 is used. A value of 2 to 6 times the real error of the bearing sensor is considered for the measurement process.
- - Features ŷL(i) are supposed to be very far from the sensor and therefore it is assumed that its corresponding bearing measurement zi will remain almost constant. The measurement prediction model is simply:
- - For near features ŷL(i), the bearing measurement zi will change rapidly. Due to this fact the standard deviation of the bearing sensor σz for features ŷL(i), (in update Kalman equations) is multiplied by a high value c, (c = 10e10 were used in experiments). An interesting issue, to be treated for further work, could be the dynamical estimation of parameter c.
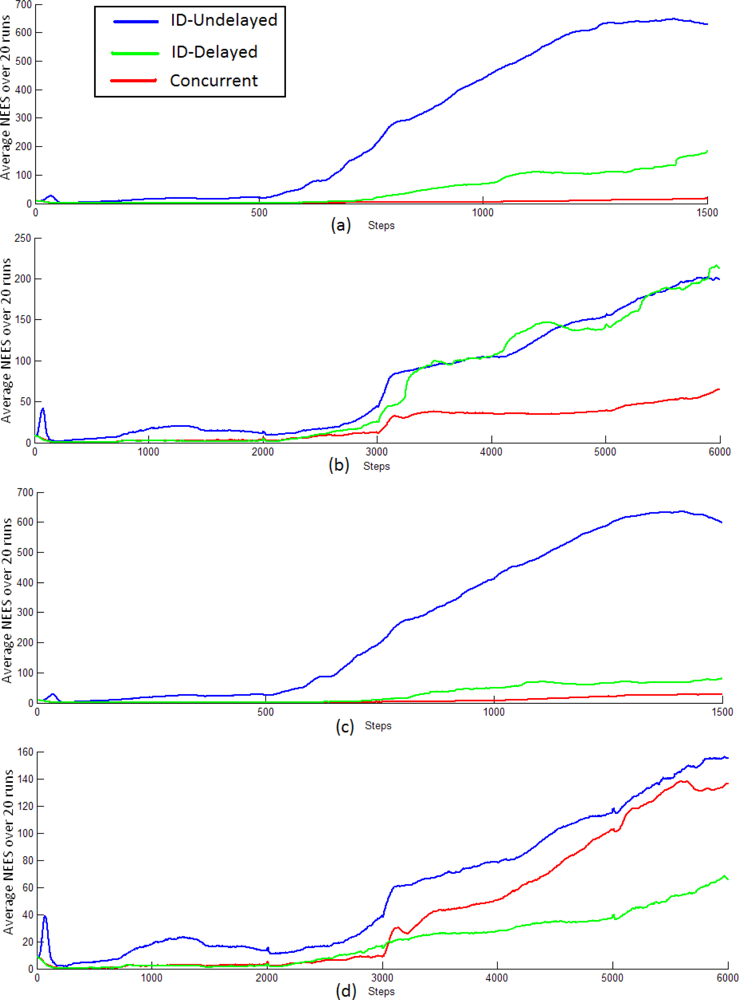
5. Experiments
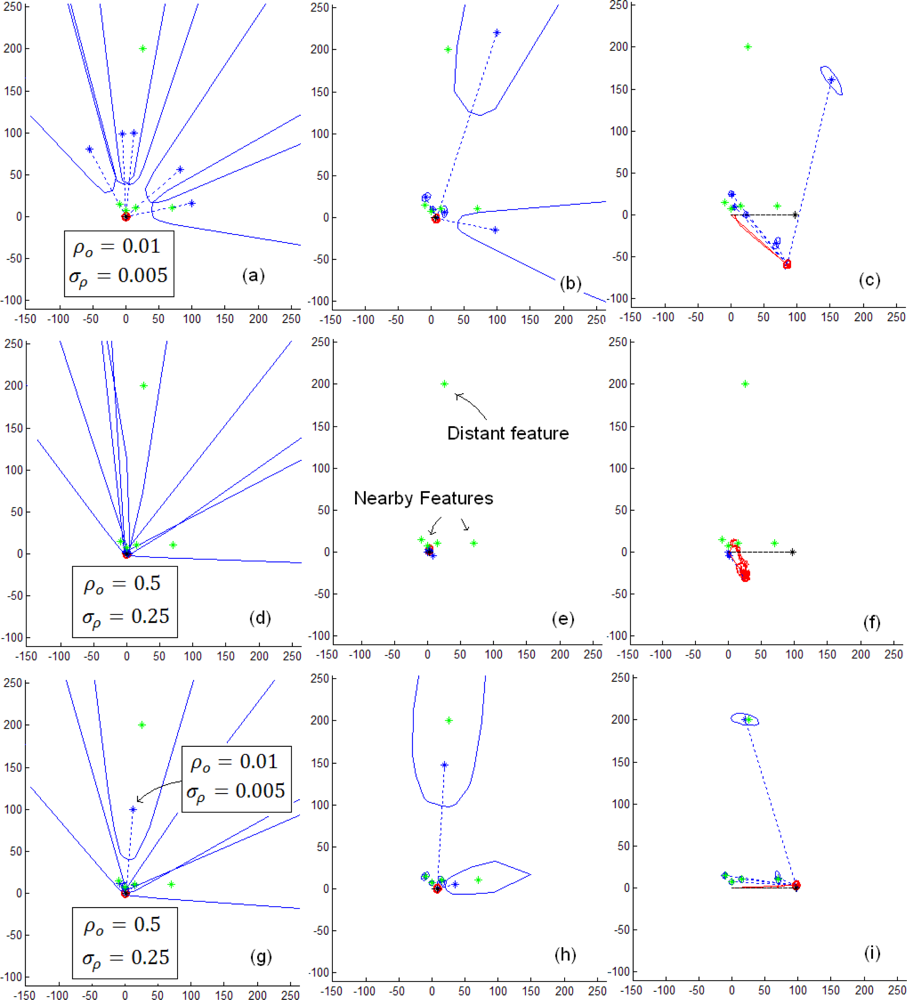
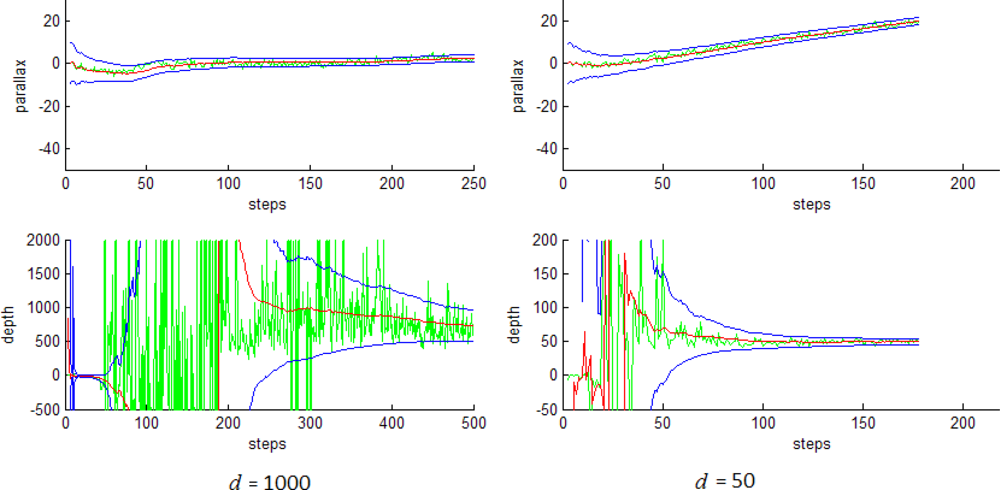
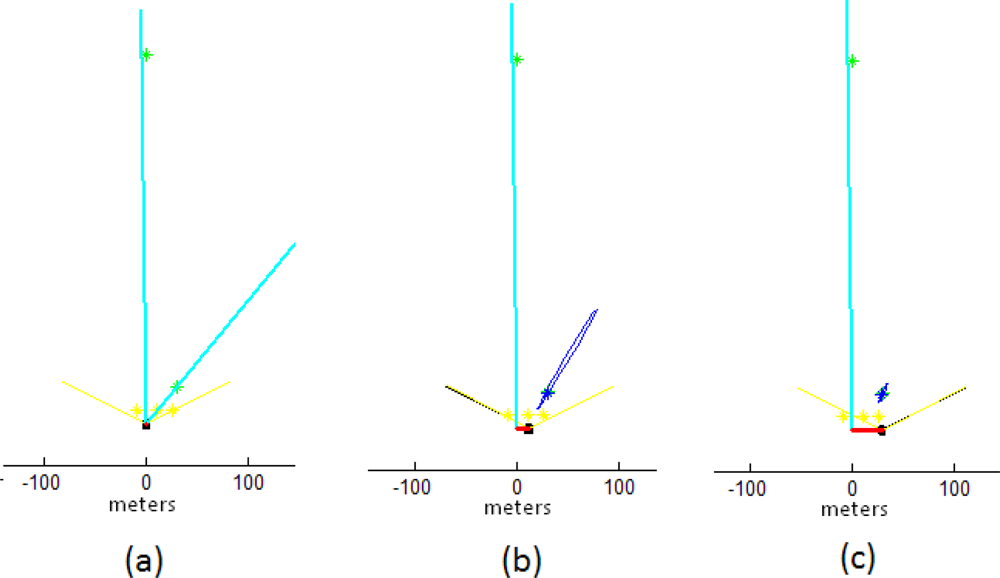
5.1. Initialization process of distant and near features
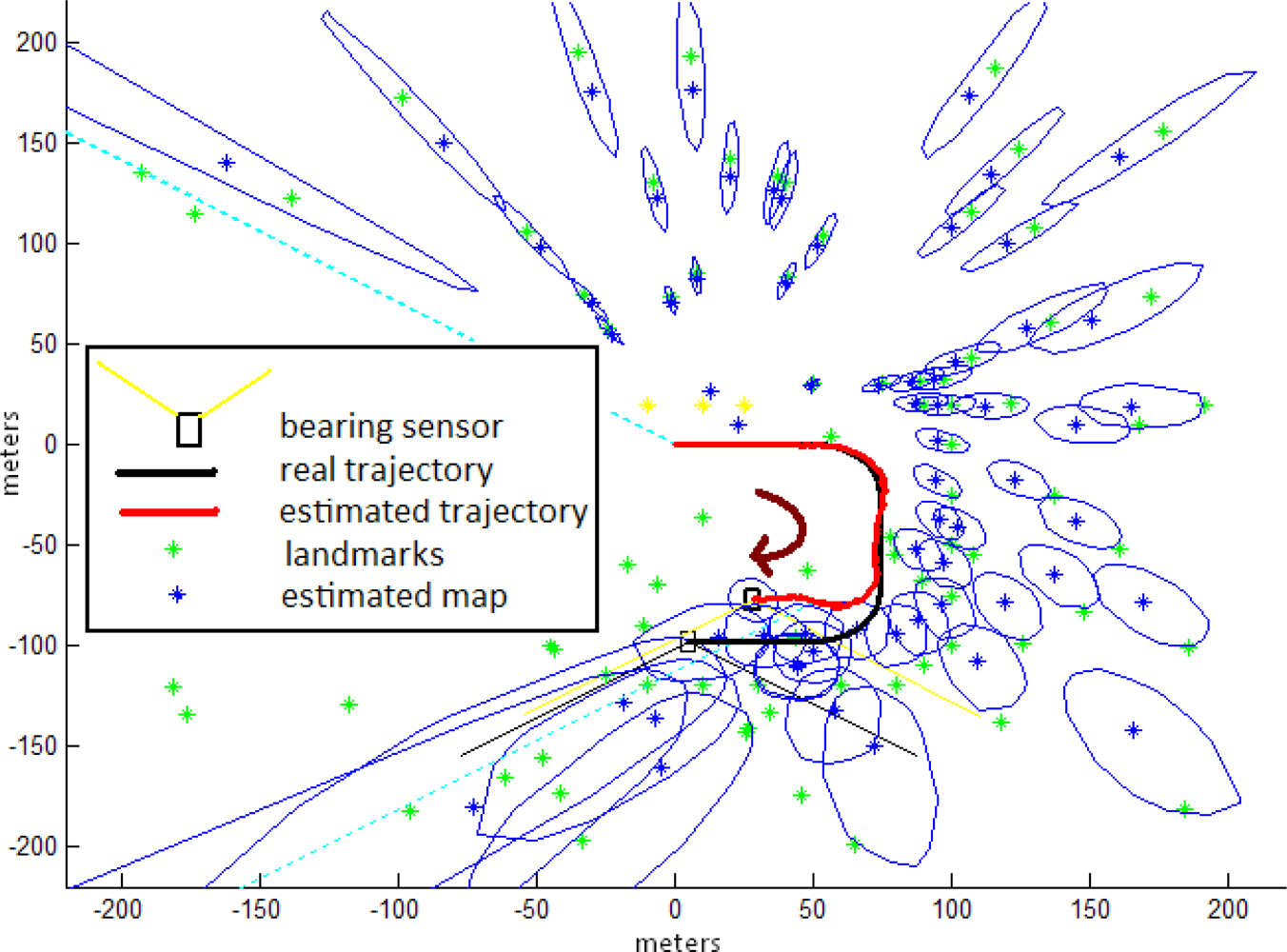
5.2. Comparative study
6. Conclusions
Acknowledgments
References
- Vázquez-Martín, R.; Núñez, P.; Bandera, A.; Sandoval, F. Curvature-based environment description for robot navigation using laser range sensors. Sensors 2009, 9, 5894–5918. [Google Scholar]
- Durrant-Whyte, H.; Bailey, T. Simultaneous localization and mapping: part I. IEEE Rob. Autom. Mag 2006, 13, 99–110. [Google Scholar]
- Bailey, T.; Durrant-Whyte, H. Simultaneous localization and mapping: part II. IEEE Rob. Autom. Mag 2006, 13, 108–117. [Google Scholar]
- Davison, A. Real-time simultaneous localization and mapping with a single camera. Proceedings of the ICCV’03, Nice, France, October 13–16, 2003.
- Munguía, R.; Grau, A. Single sound source SLAM. In Lecture Notes in Computer Science; Springer: Berlin, Germany, 2008; Volume 5197, pp. 70–77. [Google Scholar]
- Williams, G.; Klein, G.; Reid, D. Real-time SLAM relocalisation. Proceedings of the ICCV’07, Rio de Janeiro, Brazil, October 14–20, 2007.
- Chekhlov, D.; Pupilli, M.; Mayol-Cuevas, W.; Calway, A. Real-time and robust monocular SLAM using predictive multi-resolution descriptors. In Advances in Visual Computing; Springer Berlin/Heidelberg: Berlin, Germany, 2006; pp. 276–285. [Google Scholar]
- Munguía, R.; Grau, A. Closing loops with a virtual sensor based on monocular SLAM. IEEE Trans. Instrum. Measure 2009, 58, 2377–2385. [Google Scholar]
- Deans, H.; Martial, M. Experimental comparison of techniques for localization and mapping using a bearing-only sensor. Proceedings of International Symposium on Experimental Robotic, Waikiki, HI, USA, December 11–13, 2000.
- Strelow, S.; Sanjiv, D. Online motion estimation from image and inertial measurements. Proceedings of Workshop on Integration of Vision and Inertial Sensors (INERVIS’03), Coimbra, Portugal, June 2003.
- Bailey, T. Constrained initialisation for Bearing-Only SLAM. Proceedings of IEEE International Conference on Robotics and Automation (ICRA’03), Taipei, Taiwan, September 14–19, 2003.
- Kwok, N.M.; Dissanayake, G. Bearing-only SLAM in indoor environments. Proceedings of Australasian Conference on Robotics and Automation, Brisbane, Australia, December 1–3, 2003.
- Kwok, N.M.; Dissanayake, G. An efficient multiple hypotheses filter for bearing-only SLAM. Proceedings of International Conference on Intelligent Robots and Systems (IROS’04), Sendai, Japan, September 28–October 2, 2004.
- Kwok, N.M.; Dissanayake, G. Bearing-only SLAM using a SPRT based gaussian sum filter. Proceedings of IEEE International Conference on Robotics and Automation (ICRA’05), Barcelona, Spain, April 18–22, 2005.
- Peach, N. Bearing-only tracking using a set of range-parametrised extended Kalman filters. IEE Proc. Control Theory Appl 1995, 142, 21–80. [Google Scholar]
- Davison, A.; Gonzalez, Y.; Kita, N. Real-Time 3D SLAM with wide-angle vision. Proceedings of IFAC Symposium on Intelligent Autonomous Vehicles, Lisbon, Portugal, July 5–7, 2004.
- Jensfelt, P.; Folkesson, J.; Kragic, D.; Christensen, H. Exploiting distinguishable image features in robotics mapping and localization. Proceedings of European Robotics Symposium, Palermo, Italy, March 16–17, 2006.
- Sola, J.; Devy, M.; Monin, A.; Lemaire, T. Undelayed initialization in bearing only SLAM. Proceedings of IEEE International Conference on Intelligent Robots and Systems, Edmonton, Canada, August 2–6, 2005.
- Lemaire, T.; Lacroix, S.; Sola, J. A practical bearing-only SLAM algorithm. Proceedings of IEEE International Conference on Intelligent Robots and Systems, Edmonton, Canada, August 2–6, 2005.
- Eade, E.; Drummond, T. Scalable monocular SLAM. Proceedings of IEEE Computer Vision and Pattern Recognition, New York, NY, USA, June 17–22, 2006.
- Montemerlo, M.; Thrun, S.; Koller, D.; Wegbreit, B. FastSLAM: Factored solution to the simultaneous localization and mapping problem. Proceedings of National Conference on Artificial Intelligence, Edmonton, AB, Canada, July 28–29, 2002.
- Montiel, J.M.M.; Civera, J.; Davison, A. Unified inverse depth parametrization for monocular SLAM. Proceedings of Robotics: Science and Systems Conference, Philadelphia, PA, USA, August 16–19, 2006.
- Munguía, R.; Grau, A. Delayed inverse depth monocular SLAM. Proceedings of the 17th IFAC World Congress, Coex, Seoul, Korea, July 6–11, 2008.
- Andrade-Cetto, J.; Sanfeliu, A. Environment Learning for Indoor Mobile Robots. A Stochastic State Estimation Approach to Simultaneous Localization and Map Building (Springer Tracts in Advanced Robotics); Springer: Berlin, Germany, 2006; Volume 23. [Google Scholar]
- Montiel, J.M.M.; Davison, A. Visual compass based on SLAM. Proceedings of IEEE International Conference on Robotics and Automation, Orlando, FL, USA, May 15–19, 2006.
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Bailey, T.; Nieto, J.; Guivant, J.; Stevens, M.; Nebot, E. Consistency of the ekf-slam algorithm. Proceedings of IEEE International Conference on Intelligent Robots and Systems, Beijing, China, December 4–6, 2006.
| Approach | Delayed / Undelayed | Initial representation | Estimation |
|---|---|---|---|
| Deans [9] | Delayed | Bundle adjustment | EKF |
| Strelow [10] | Delayed | Triangulation | IEKF |
| Bailey [11] | Delayed | Triangulation | EKF |
| Davison [16] | Delayed | Multi-Hypotheses | EKF |
| Kwok (a) [13] | Delayed | Multi-Hypotheses | PF |
| Kwok (b) [14] | Undelayed | Multi-Hypotheses | PF |
| Sola [18] | Undelayed | Multi-Hypotheses | EKF |
| Lemaire [19] | Delayed | Multi-Hypotheses | EKF |
| Jensfelt [17] | Delayed | Triangulation | EKF |
| Eade [20] | Delayed | Single Hypotheses | FastSLAM |
| Montiel [22] | Undelayed | Single Hypotheses | EKF |
| Munguía[23] | Delayed | Triang.- S. Hypotheses | EKF |
| This work | Delayed-Undelayed | KF-Triang.- S. | EKF |
| Test | aWx | aWy | aWθ | Δt |
|---|---|---|---|---|
| a | 4 | 4 | 2 | 1/30 |
| b | 4 | 4 | 2 | 1/120 |
| c | 6 | 6 | 3 | 1/30 |
| d | 6 | 6 | 3 | 1/120 |
| Method | Δt = 1/30 | Δt = 1/120 | a | b | c | d |
|---|---|---|---|---|---|---|
| ID-Undelayed | 76s | 302s | 2 | 1 | 0 | 2 |
| ID-Delayed | 60s | 235s | 9 | 2 | 11 | 4 |
| Concurrent | 94s* | 376s* | 0 | 0 | 0 | 0 |
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Munguía, R.; Grau, A. Concurrent Initialization for Bearing-Only SLAM. Sensors 2010, 10, 1511-1534. https://doi.org/10.3390/s100301511
Munguía R, Grau A. Concurrent Initialization for Bearing-Only SLAM. Sensors. 2010; 10(3):1511-1534. https://doi.org/10.3390/s100301511
Chicago/Turabian StyleMunguía, Rodrigo, and Antoni Grau. 2010. "Concurrent Initialization for Bearing-Only SLAM" Sensors 10, no. 3: 1511-1534. https://doi.org/10.3390/s100301511







