A B-spline curve consists of segments, with each segment of degree k constructed by k+1 sequential control points. Let t = (u–u_i)/(u_i+1 –u_i), the segment has the following matrix form [16,17] in the nonempty interval [u_i,u_i+1]: (1) p i ( t ) = [ 1           t           t 2       ⋯       t k ] M i k + 1 [ V i − k           V i − k + 1       ⋯       V i ] Twhere t ∈ [0,1] and V is the vector of k+1 control points. The number of control points are denoted as i = k,k+1, ⋯,n+1 and the ith basis matrix, M i k + 1, is the matrix form of B-spline basis in order k.

The whole curve can thus be represented as: (2) P ( t ) = ∑ i = k n p i ( t ) = ∑ i = k n ∑ j = 0 k a i ( j ) t j                     = ∑ i = k n ∑ j = 0 k ( ∑ l = 0 k M i k + 1 ( j ,   l ) V i − k + l ) t jwhere (3) a i ( j ) = ∑ l = 0 k M i k + 1 ( j ,   l ) V i − k + l

Equally, a part of the B-spline surface in the nonempty area [u_i,u_i+1) × [v_i,v_i+1) can be represented as: (4) s i , j ( t ,   w ) = T k 1 M i , u k 1 + 1 V i , j h ( M j , v k 2 + 1 ) T W k 2 Twhere T_k1 = [1 t t² ⋯ t^k₁] and W k 2 T = [ 1           w           w 2       ⋯       w k 2 ] T with t = (u–u_i)/(u_i+1 –u_i) and w = (v–v_i)/(v_i+1 –v_i), where u,v ∈ [u_i,u_i+1) × [v_i,v_i+1). M i , u k 1 + 1 and M j , v k 2 + 1 are the ith and jth basis matrixes in [u_i,u_i+1) and [v_i,v_i+1), respectively.

The whole surface is then represented as follow:

The volume can be expressed as [18]: (6) V = ∫ z 1 z 2 A ( Z ) d zwhere A(z) is the area of the slice at depth z.

As the equations given by Equation 1 to Equation 4, let ∂ S ( t ,   w ) ∂ t and ∂ S ( t ,   w ) ∂ w denote the derivatives of S(u,v) with respect to t and w.

The computation of the area of a slice at depth z is: (7) A ( z ( w ) ) = ∑ j = k 2 n ∫ 0 1 Y ( t ,   w ) × ∂ X ( t ,   w ) ∂ t d twhere Y(t,w) is given by Equation 6, and ∂ X ( t ,   w ) ∂ t is the derivative with respect to t and ∂ Z ( t ,   w ) ∂ w is the derivative with respect to w.

The volume of B-spline surface of orders k₁ × k₂ is: (8) V = ∑ i = k 1 m ∑ j = k 2 n ( ∑ l 1 = 1 ( 3 × k 2 − 1 ) ∑ l 2 = 1 ( 3 × k 1 − 1 ) C i , j ( l 1 ,   l 2 ) × 1 l 2 + 1 × 1 l 1 + 1 )where C_{i, j} is the matrix of size 3k₁ × 3k₂ which is the product of the three polynomials Y(t,w).

Cardiac cycle is a very complicated physical process. Traditional researches used to divide the cycle into two major parts as systole and diastole. During systole, LV contracts thus the blood in LV can be ejected out. On the opposite, during diastole LV bulges and imbibes blood in. The function of heart is achieved by the repeatedly alternating systole and diastole. As the LV motion is not uniform neither in systole nor in diastole, this rough partition can hardly express the true feature of LV motion. In fact it is shown by anatomy knowledge that the whole cardiac cycle contains 7 CPPs based on different LV shape and function. These CPPs are Isovolumic Systolic (IS), Rapid Ejection Period (REP), Slow Down Ejection Period (SDEP), Isovolumic Relaxation Period (IRP), Rapid Filling Period (RFP), Slow Down Filling Period (SDFP) and Atrial Systole (AS) [19] where IS, REP and SDEP compose the systole and IPR, RFP, SDFP belong to the diastole.

The shape of LV shows various features in different CPP, and the changing of these shapes is the main basis of CPP partition. To divide the CPP phases, two shape factors are necessary. The first shape factor is the volume of LV (LVV). Assume that the LVV curve during whole cardiac cycle is already known and denoted with C(t). It is easy to understand that during the whole systole C(t) keeps decreasing, while in diastole it keeps increasing. Let curve C′(t) denote derivative of C(t). According to medical knowledge, the features of C(t) and C′(t) in each CPP can be listed as in the columns 3–4 of Table 1. During the IS, IRP and AS phases, the values of C(t) remain almost invariant and consequently its derivative is approximate to zero. During the REP and SDEP phases, the values of C(t) keep on reducing and C′(t) is of course negative. During the RFP and SDFP phases, the values of C(t) keep on increasing and C′(t) is positive. The IS and AS, REP and SDEP, RFP and SDFP, however, are the adjacent phases, therefore it is difficult to separate them.

Fortunately, there is another shape factor, called LV long-axis length (LVLL), that can provide the complement information. LVLL is defined as the height from the base to the apical of LV. Assuming the LVLL curve is L(t), and its derivative is L′(t). According to the anatomy priori knowledge the L(t) and L′(t) features in each CPP are listed in the columns 5–6 of Table 1. During IS and SDFP phases, L(t) keeps on decreasing and L′(t) is negative. During SDEP phase, L(t) keeps on increasing and L′(t) is positive. By compounding the shape factors, LVV and LVLL, it is now easy to divide the seven phases of cardiac cycle. Figure 2 illustrate examples of C′(t) and L′(t).

In the beginning of systole and diastole, the shape of LV sharply changes while the LVV stays invariant. These periods are called isovolumetric contraction (IC) and isovolumetric relaxation (IR). Medical research shows that the biggest stress and displacement of LV occur in these two periods. When some diseases occur, the LV would need longer time to achieve the deformation and displacement, thus the length of IC and IR are very important index for evaluating LV functions. Based on that Tei-index is raised by Japanese researcher Tei in 1995 [4]. The definition of Tei is:

Tei index is also called myocardial performance index (MPI). This new index can generally evaluate the heart function in both diastole and systole. It has been widely used in heart disease diagnosis. Based on the CPP partition, a direct method of calculating Tei index can be deduced.

IC and IR are the periods while the LV shape changes largely and LVV keeps almost invariant. According to the CPP characters listed in Table 1, it is obvious that IC is equal to IS and IR is equal to IRP. The ET is the length of systole which equals to the sum of IS, REP and SDEP.

The Tei index can therefore be calculated as: (10) Tei   index = t I S + t I R T t I S + t P R E + t S D E Pwhere the t_x is the length of time intervals of the corresponding CPP with x (x = IS, IRT, PRE, and SDEP). This equation is totally based on the partitions of CPP. Due to the accurate CPP partitions, the precise and direct calculation of Tei index can obtained.

The function of LV is achieved by cycle motion of LV wall. The motion amplitude of LV wall (LVMA) reflect the deformation capability of LV. When some disease occurs, there must be some abnormalities of the LVMA on the sick area, thus LVMA can be used as an important parameter for LV function analysis. Azhari et al. [15] have used LVMA in the detection of dysfunctional myocardium.

It is also known that the movement of LV wall is not in a uniform speed, thus the distribution of LVMA differs largely in different CPPs. For example, the LVMA in the beginning of systole and diastole are much larger than it in other time because the main deformation of LV happens in these periods. Due to these causes mentioned above, to study on the LVMA in different CPP is highly necessary.

Assuming that the point p is on the wall of LV. By tracking the position of p at each time interval t, if the time of the whole cardiac cycle is mt, a position matrix can be obtained T = [p(t) p(2t) ⋯ p(mt)](p(t) = [x_t y_t z_t]^T). Fitting each row in T with three B-spline curves M_x(t), M_y(t) and M_z(t) which stand for the trajectory of p in x, y and z axis during the whole cardiac cycle will be obtained. Through the trajectory curve of p, it is very simple to calculate the displacement of p in an arbitrary period [t₁, t₂] (0 ≤ t₁ < t₂ ≤ mt) by: (11) D 1 , 2 = ( M x ( t 2 ) − M x ( t 1 ) ) 2 + M y ( t 2 ) − M y ( t 1 ) ) 2 + M z ( t 2 ) − M z ( t 1 ) ) 2

In order to get the displacement of whole LV wall, a large amount of points should be marked and tracked. Assuming such a points set P = [p₁, p₂, ⋯, p_n] and their position matrix T are known, through Equation 11 the D_1,2 of each point in P can be calculated. The displacement vector is D = [ D 1 , 2 1 ,   D 1 , 2 2 ,   ⋯   ,   D 1 , 2 n ], where D 1 , 2 i means the displacement of ith point in P.

As an elastomer, the motion of LV is continuous and gradually variational so that the displacement of the whole LV wall can be described as a surface. Using the position information of P(t₁) (position of all points in P at t₁) and D a B-spline surface can be fitted. This surface is the displacement of whole LV wall in period [t₁, t₂] and be denoted by Df (t₁, t₂).

In Section 1 the cardiac cycle is divided into 7 CPPs (i.e., IS, REP, SDEP, IRP, RFP, SDFP, AS). The beginning and ending time of each CPP is tb_name and te_name. Then the LVMA of each CPP can be calculated by Df (tb_name, te_name).

The 3D heart model is built by the Active Shape Models (ASM) [20] which has been extended to 3D representation in our previous work. By manually labeled landmarks which form the point distribution model in training images according to the rules described in [20], the ASM can learn the variations of heart shapes. The model can then be used to segment and fit a new heart in a set of new images. Note that the model is represented by a point set. After a new 3D heart is fitted by the model, those points of this heart model are used as the control points from which the B-spline heart model can be built according to Equation 1 to Equation 5.

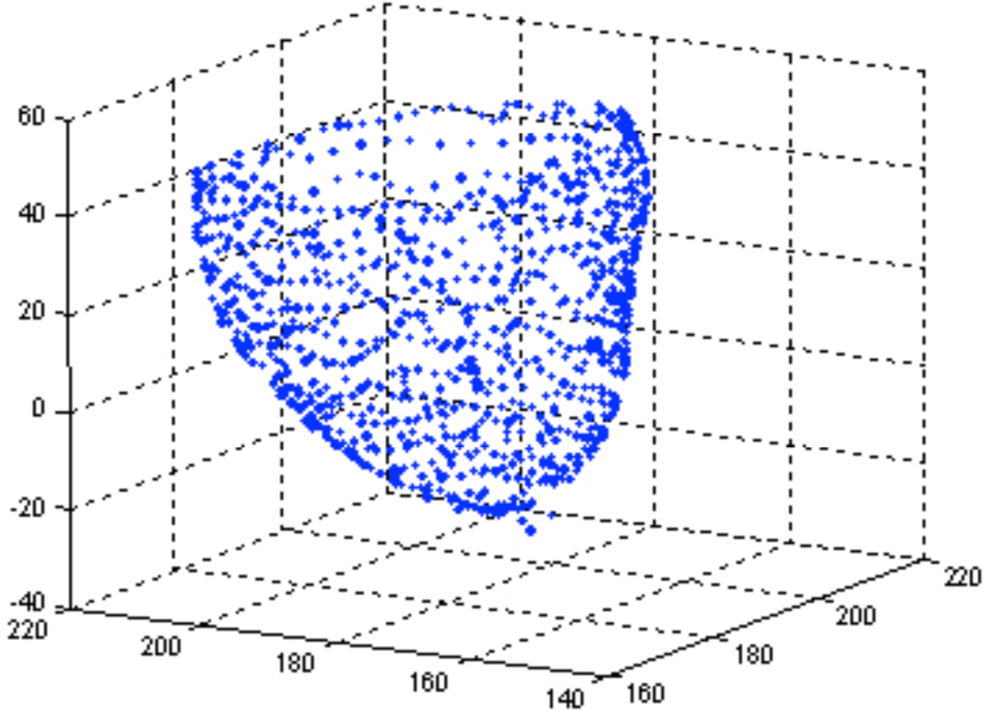
Our experiment is focused on the left ventricle, about 1000 points have been tracked, and about 400 points are distributing on inside-wall while rests are on outside-wall. These points constitute the whole motion of left ventricle in a cardiac cycle, and the points are labeled in several phases, with 0.1 second apart from each other. In the model we focus on the inside-wall surface since the LVV and LVLL is majorly decided by it. Figure 1 shows one of the point model.

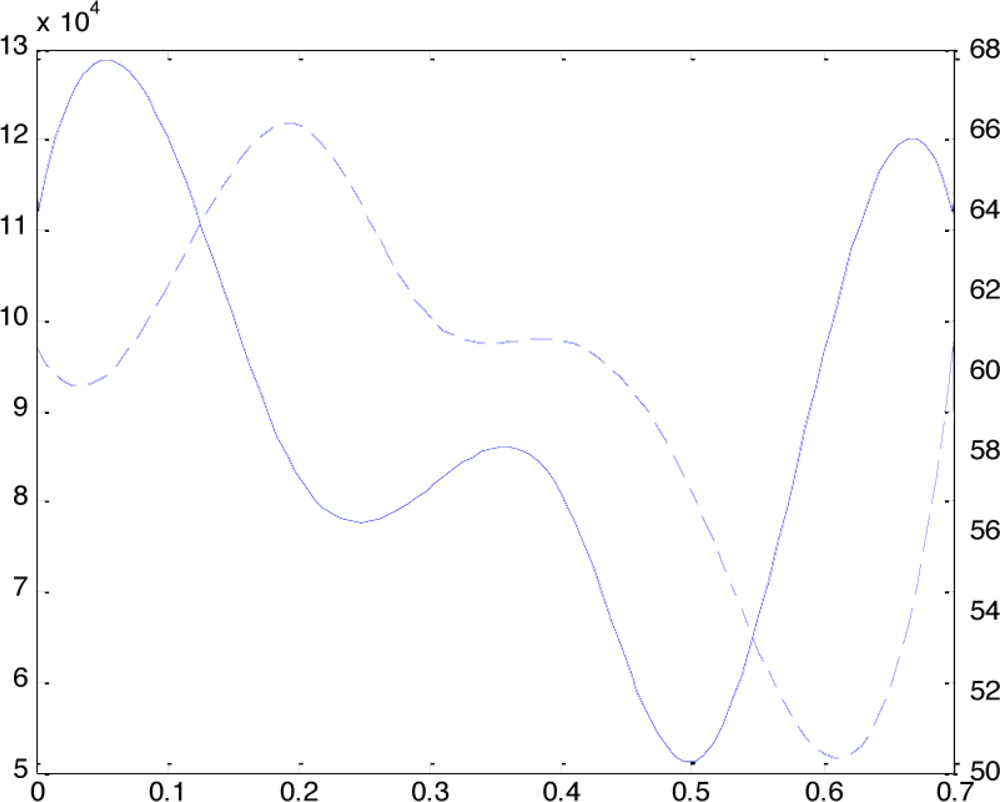
After the models in all phases are built, the LVV in each moments can be calculated by Equation 1. These LVV values are v_i where i = 1,2, ⋯,7. Using the set of v_i to interpolate with B-spline method then a LVV curve C(t) is fitted. The derivative C′(t) can also be calculated. The curve with solid line in Figure 2 is an example of the C′(t) curve. The landmarks of right Y-axis is corresponding to this curve.

In each inside-wall surface model, finding the centers at top and bottom layer, the LVLL can be calculated by the distance of these two centers. Assuming that the LVLL values are obtained from m model, l_i where i = 1,2, ⋯, m, a B-spline curve L(t) can be fitted with l_i and the derivative curve L′(t) can also be calculated. The curve with dash line in Figure 2 is an example of the L′(t) curve. The landmarks of left Y-axis is corresponding to this curve.

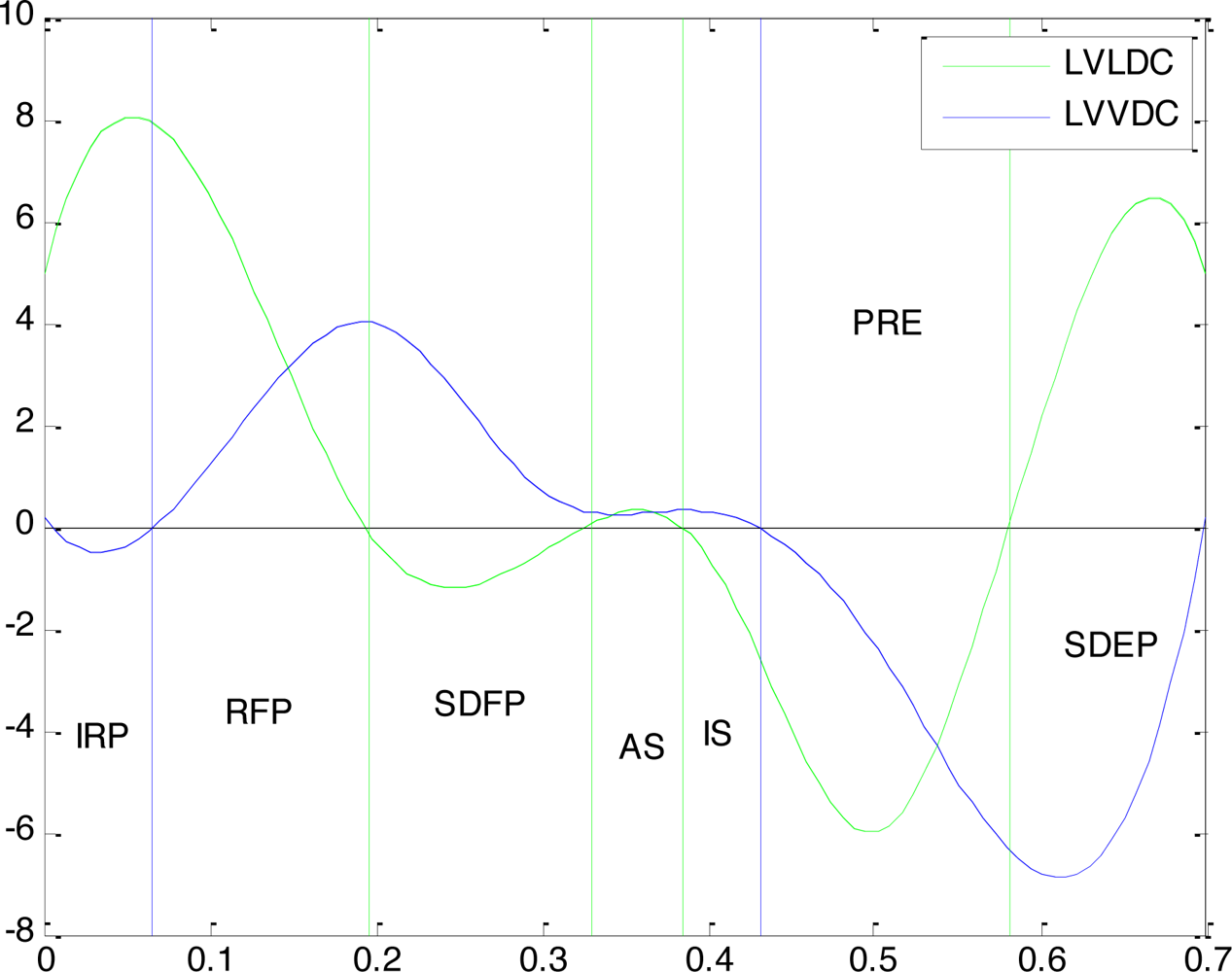
With the curves of C′(t) and L′(t), the partition of CPP can be done by following steps.

The final CPP partition result is shown in Figure 3, and the lasting time of each CPP is calculated too. The comparison of the result to the medical statistical average data decided by experts is shown in Table 2 . Obviously the experiment result is very close to the average data which can prove the validity of this partition.

The Tei index can be calculated by Equation 10. In this experiment the value of Tei is 0.3617 while the common range of Tei is 0.39±0.05 by medical statistics.

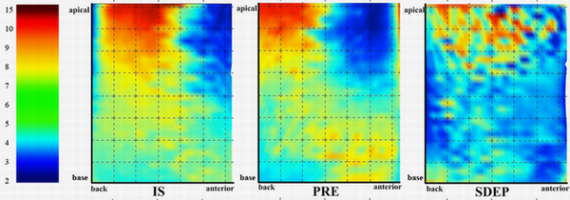
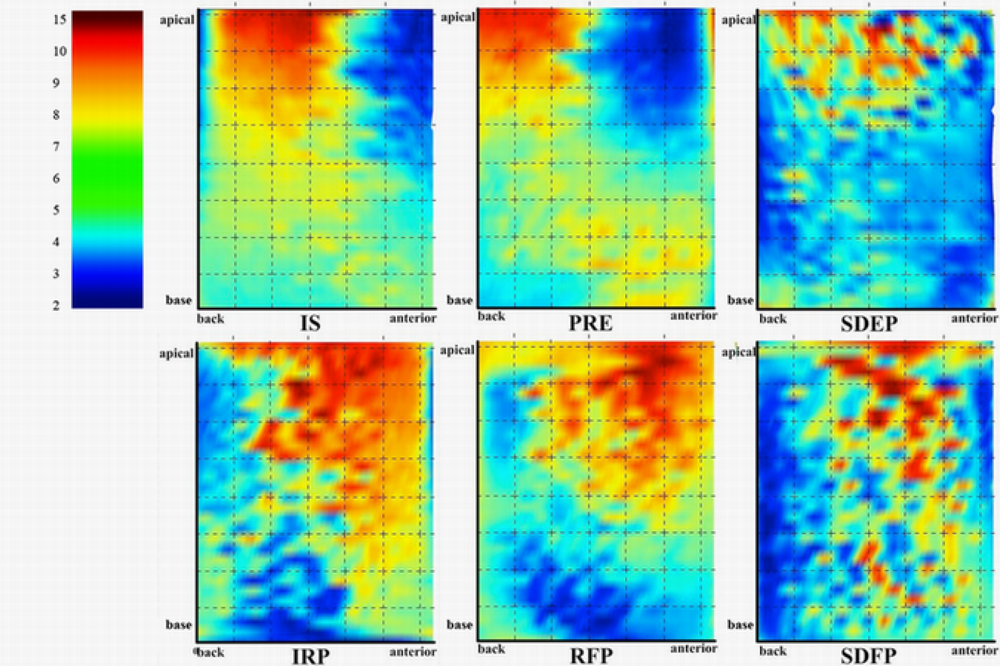
The distribution of LVMA in 6 CPPs is shown in Figure 4 (AS is neglected because in that phase the deformation of LV is inconspicuous). It can be seen that the LVMA of LV apical is much larger than that of LV base. During the systole LVMA concentrates in the back of LV while do the opposite during diastolic period. The largest LVMA occurs in IS and IRP which are the beginning of systole and diastole respectively. The result agrees with the medical statistical rule and is very closed to the result of other research [21,22].