Charge Exchange in Low-Energy H, D + C4+ Collisions with Full Account of Electron Translation
Abstract
:1 Introduction
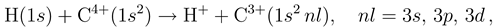
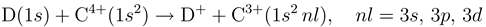
2 The theory
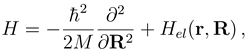
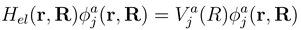
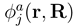
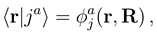
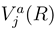 . If nonadiabatic regions are narrow, it is convenient to make a transformation to diabatic or partly diabatic basis states
. If nonadiabatic regions are narrow, it is convenient to make a transformation to diabatic or partly diabatic basis states

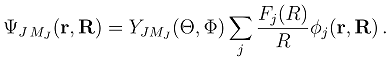
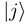 . The functions Fj(R) describe the radial motion of the nuclei. Substituting the expansion (7) into the stationary Schrödinger equation (H − Et)Ψ J M J = 0 [Et = E + V1(∞) being the total energy], multiplying it by
. The functions Fj(R) describe the radial motion of the nuclei. Substituting the expansion (7) into the stationary Schrödinger equation (H − Et)Ψ J M J = 0 [Et = E + V1(∞) being the total energy], multiplying it by  and integrating over the electronic coordinates, one obtains a set of the coupled channel equations [4]
and integrating over the electronic coordinates, one obtains a set of the coupled channel equations [4]
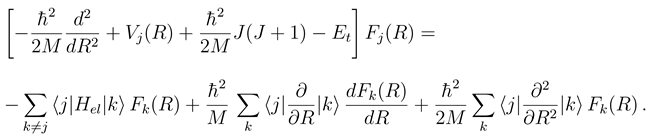
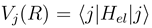 are the potentials in a choosen representation. Note, that in a partly diabatic representation not all of off-diagonal nonadiabatic matrix elements
are the potentials in a choosen representation. Note, that in a partly diabatic representation not all of off-diagonal nonadiabatic matrix elements  and
and 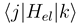 are zero.
are zero.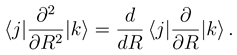
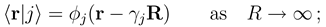

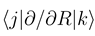 do not automatically go to zero at infinity. In the usual interpreta- tion, where Fj (R) gives the incoming and outgoing fluxes in the state
do not automatically go to zero at infinity. In the usual interpreta- tion, where Fj (R) gives the incoming and outgoing fluxes in the state 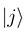 , this would indeed pre- dict inelastic transitions between atomic states at an arbitrarily large distance. We have recently shown, how the solutions of Eq. (8) should be used to derive meaningful transition probabilities even in the presence of nonzero asymptotic couplings [4,5]. One solves the coupled equations (8) numerically between a small distance and a large value Rend, where all couplings and potentials Vj are sufficiently constant, express the properties of the numerical solution at Rend by an R-matrix (R)
, this would indeed pre- dict inelastic transitions between atomic states at an arbitrarily large distance. We have recently shown, how the solutions of Eq. (8) should be used to derive meaningful transition probabilities even in the presence of nonzero asymptotic couplings [4,5]. One solves the coupled equations (8) numerically between a small distance and a large value Rend, where all couplings and potentials Vj are sufficiently constant, express the properties of the numerical solution at Rend by an R-matrix (R)
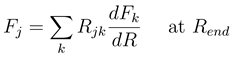
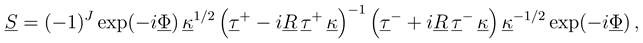
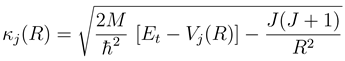
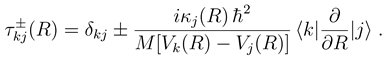
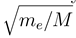 with me being the electron mass. Higher order corrections have turned out to be negligible in the examples treated so far. Eq. (13) is further based on the construction of a WKB type solution to the coupled equations beyond Rend. The WKB approximation is important only for computational convenience. It might be dropped by extending the numerical calculation to a distance, which is so large that not only variations of both the adiabatic potentials and couplings, but also the centrifugal potentials are negligible.
with me being the electron mass. Higher order corrections have turned out to be negligible in the examples treated so far. Eq. (13) is further based on the construction of a WKB type solution to the coupled equations beyond Rend. The WKB approximation is important only for computational convenience. It might be dropped by extending the numerical calculation to a distance, which is so large that not only variations of both the adiabatic potentials and couplings, but also the centrifugal potentials are negligible.3 Results and discussions
3.1 Quantum chemical data
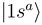 and
and 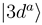 asymptotically (R → ∞) correlated to the H(1s) + C4+ and H+ + C3+(3d) states, respectively, are closely approaching each other at the internuclear distances R ≈ 4.46 a.u. and R ≈ 7.93 a.u., apparently showing two avoided crossings in these regions. Indeed the radial coupling matrix element
asymptotically (R → ∞) correlated to the H(1s) + C4+ and H+ + C3+(3d) states, respectively, are closely approaching each other at the internuclear distances R ≈ 4.46 a.u. and R ≈ 7.93 a.u., apparently showing two avoided crossings in these regions. Indeed the radial coupling matrix element 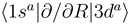 depicted in Figure 1b shows sharp peaks at the same dis- tances confirming the avoided crossing interpretation. The area under each of the peaks is close to π/2, the situation is expected to correspond closely to the Landau-Zener model. Other radial couplings are smaller by at least one order of magnitude, as shown in Figure 3 of Ref. [30].
depicted in Figure 1b shows sharp peaks at the same dis- tances confirming the avoided crossing interpretation. The area under each of the peaks is close to π/2, the situation is expected to correspond closely to the Landau-Zener model. Other radial couplings are smaller by at least one order of magnitude, as shown in Figure 3 of Ref. [30].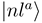 to a partly diabatic basis
to a partly diabatic basis 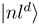 . The new diabatic electronic states
. The new diabatic electronic states 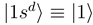 and
and 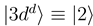 are constructed as linear combinations of
are constructed as linear combinations of 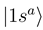 and
and  [see Eq. (6)] by the requirement
[see Eq. (6)] by the requirement 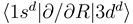 . The other states
. The other states 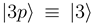 and
and 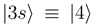 are left unchanged. The construction of the new basis is straightforward taking into account the fact that
are left unchanged. The construction of the new basis is straightforward taking into account the fact that  goes to zero at R → ∞. The avoided crossings between the adiabatic potentials become real crossings between the diabatic curves V1(R) and V2(R), the other potentials are not changed. Figure 1a shows the diabatic potentials Vj (R) obtained in this manner. The coupling between the states
goes to zero at R → ∞. The avoided crossings between the adiabatic potentials become real crossings between the diabatic curves V1(R) and V2(R), the other potentials are not changed. Figure 1a shows the diabatic potentials Vj (R) obtained in this manner. The coupling between the states  and
and 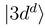 is now provided by an off-diagonal matrix element
is now provided by an off-diagonal matrix element 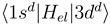 (Figure 1c, the thick solid line) of the electronic Hamiltonian, the couplings between the states
(Figure 1c, the thick solid line) of the electronic Hamiltonian, the couplings between the states 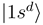 and
and  to
to 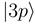 and
and 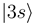 occurs by new derivative couplings (Figure 1c), the coupling between the
occurs by new derivative couplings (Figure 1c), the coupling between the  and
and 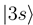 states is unchanged.
states is unchanged.
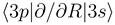 and
and  nonadiabatic matrix elements for the CD4+ quasimolecule, while the thin dashed and solid lines denote the same matrix elements for the CH4+ quasimolecule.
nonadiabatic matrix elements for the CD4+ quasimolecule, while the thin dashed and solid lines denote the same matrix elements for the CH4+ quasimolecule.3.2 Dynamics
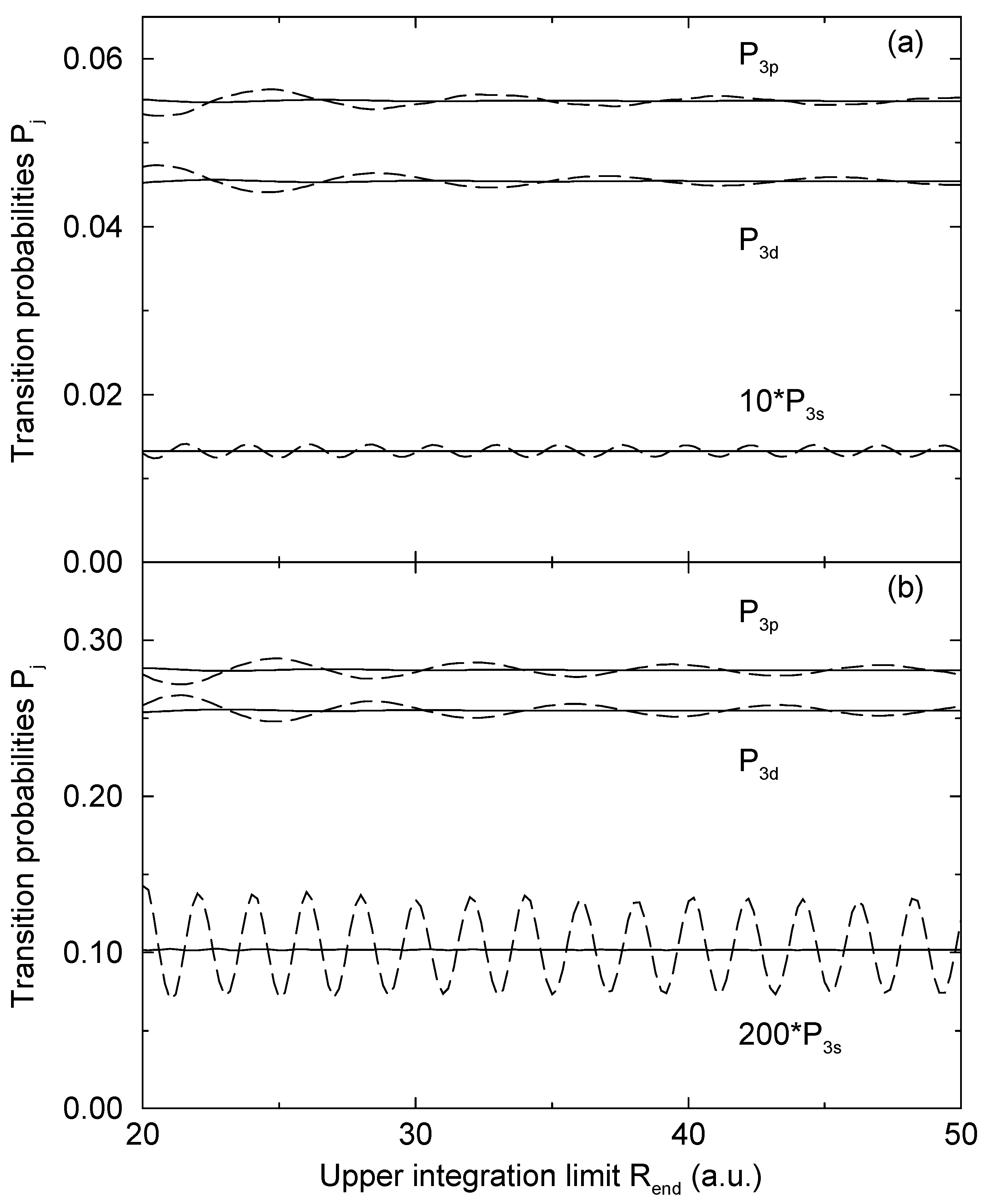
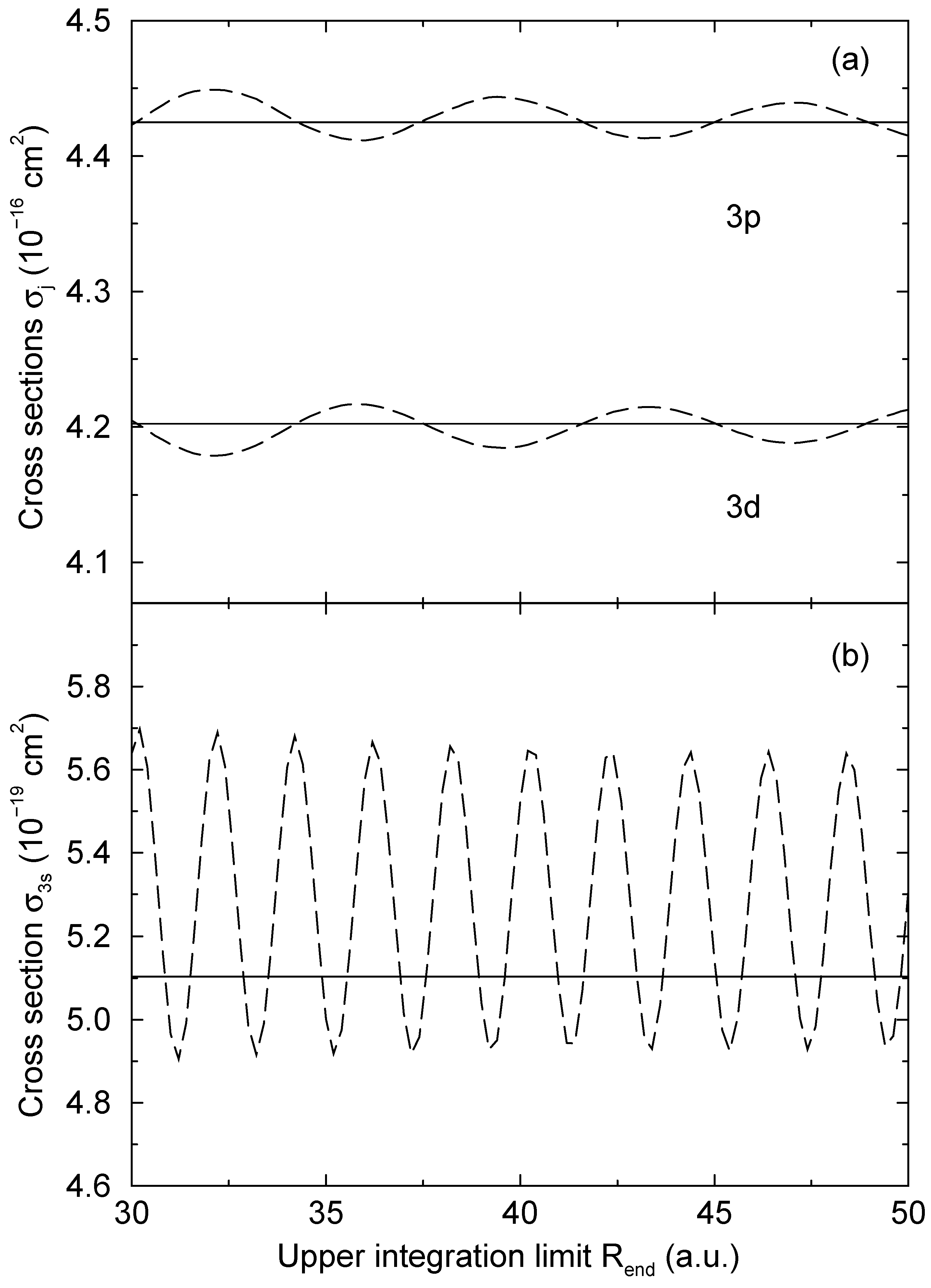
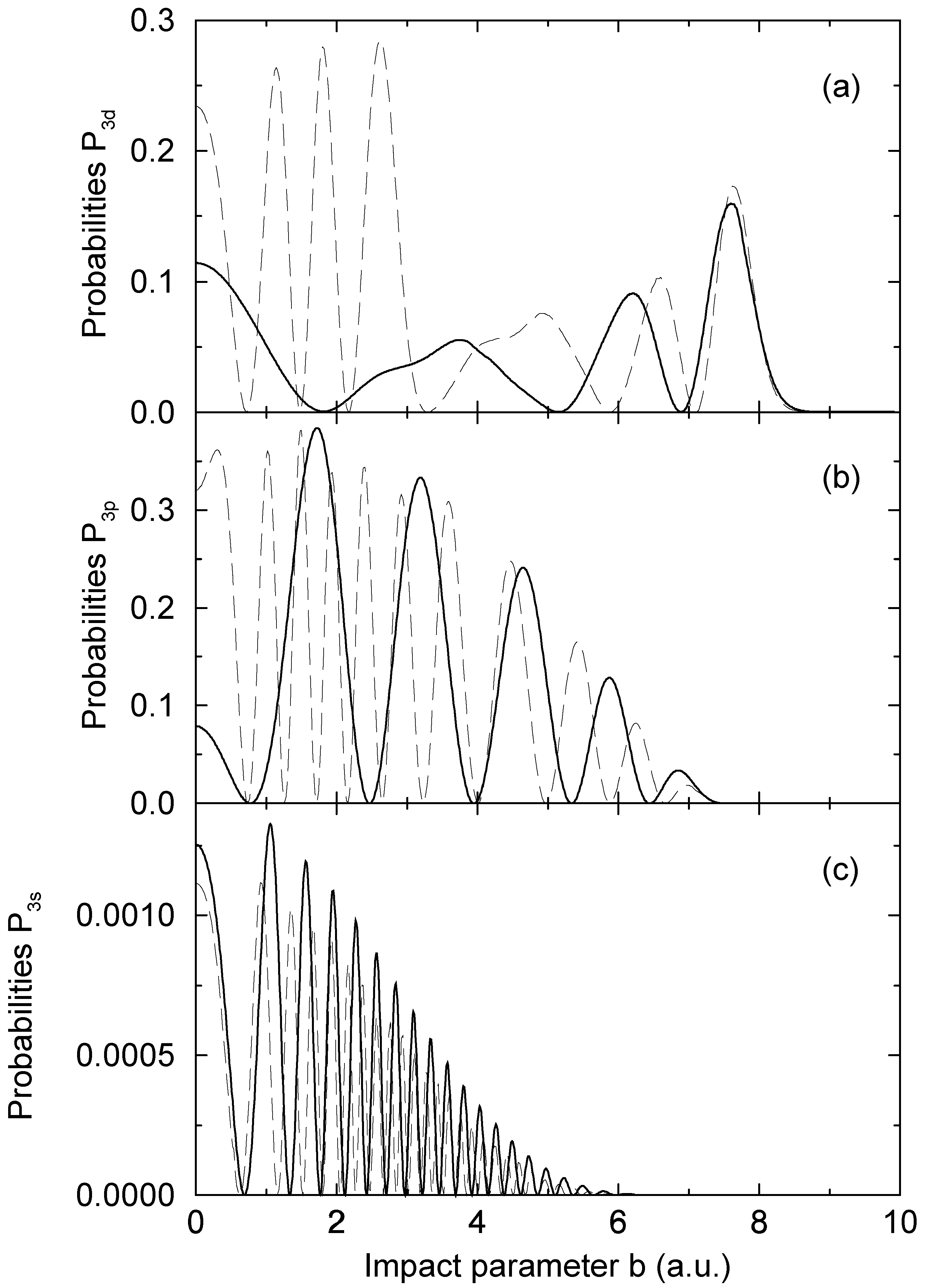
 = 1.06 a.u. (Figure 2a) and b = 1:87 a.u. (Figure 2b). The computed results are shown as functions of the upper limit Rend of the numerical integration. As long as Eq. (13) is used, the computed transition probabilities (the solid lines in Figure 2) are essentially independent from Rend, when Rend is sufficiently large. Some minor oscillations are still exist, but they are typically by more than three orders of magnitude smaller than a corresponding transition probability. We ascribe this to the neglection of second order terms in the derivation of Eq. (15), which appears to be well justified in this way. There is no other detectable variation of the computed result, supporting the use of the WKB approximation to derive Eq. (13).
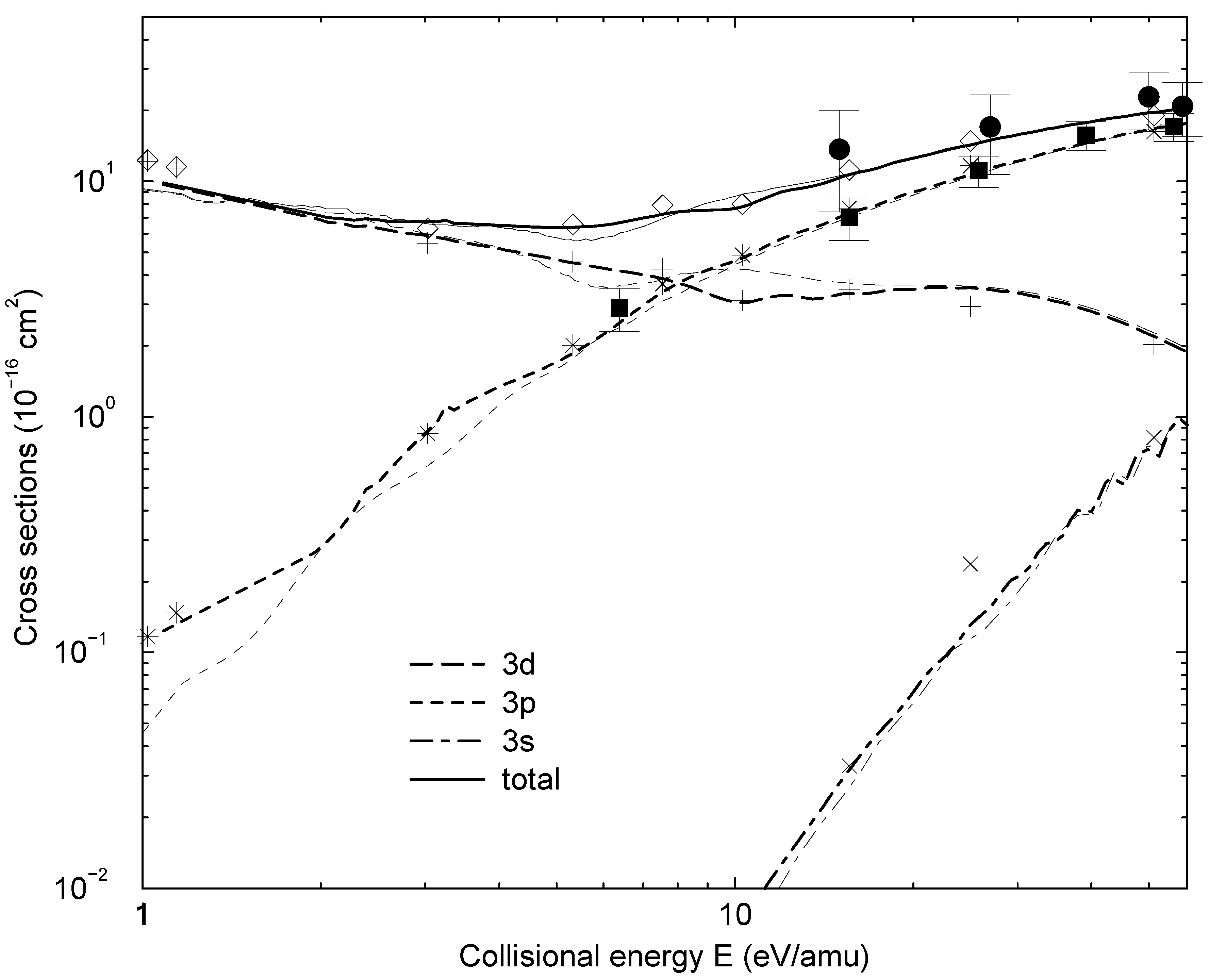
= 1.06 a.u. (Figure 2a) and b = 1:87 a.u. (Figure 2b). The computed results are shown as functions of the upper limit Rend of the numerical integration. As long as Eq. (13) is used, the computed transition probabilities (the solid lines in Figure 2) are essentially independent from Rend, when Rend is sufficiently large. Some minor oscillations are still exist, but they are typically by more than three orders of magnitude smaller than a corresponding transition probability. We ascribe this to the neglection of second order terms in the derivation of Eq. (15), which appears to be well justified in this way. There is no other detectable variation of the computed result, supporting the use of the WKB approximation to derive Eq. (13).4 Conclusion
Acknowledgment
References
- Born, M.; Oppenheimer, J.R. Ann. der Phys. 1927, 84, 457.
- Macias, A.; Riera, A. Phys. Rep. 1982, 90, 299.
- McCarroll, R.; Crothers, D.S.F. Adv. At. Mol. Opt. Phys. 1994, 32, 253.
- Grosser, J.; Menzel, T.; Belyaev, A.K. Phys. Rev. A 1999, 59, 1309.
- Belyaev, A.K.; Egorova, D.; Grosser, J.; Menzel, T. Phys. Rev. A 2001, 64, 052701.
- Bates, D.R.; McCarroll, R. Proc. R. Soc. London, Ser. A 1958, 245, 175.
- Bates, D.R.; Sprevak, D. J. Phys. B 1971, 4, L47.
- Errea, L.F.; Harel, C.; Jouin, H.; Méndez, L.; Pons, B.; Riera, A. J. Phys. B 1994, 27, 3603.
- Mittleman, M.H. Phys. Rev. 1969, 188, 221.
- Delos, J.B. Rev. Mod. Phys. 1981, 53, 287.
- Merkur’ev, S.P.; Faddeev, L.D. Quantum scattering theory for few body systems; Nauka: Moscow, 1985. [Google Scholar]
- Solov’ev, E.A.; Vinitsky, S.I. J. Phys. B 1985, 18, L557.
- Pobert, J.; Baudon, J. J. Phys. B 1986, 19, 171.
- Macek, J.; Cavagnero, M.; Jerjian, K.; Fano, U. Phys. Rev. A 1987, 35, 3940.
- Errea, L.F.; Harel, C.; Jouin, H.; Méndez, L.; Pons, B.; Riera, A. J. Phys. B 1998, 31, 3527.
- Umanskii, S.Ya.; Hadinger, G.; Aubert-Frécon, M. Phys. Rev. A 1994, 49, 2651.
- Hadinger, G.; Aubert-Frécon, M.; Umanskii, S.Ya. Chem. Phys. Rep. 2000, 18, 1255.
- Heil, T.G.; Butler, S.E.; Dalgarno, A. Phys. Rev. A 1981, 23, 1100.
- Gargaud, M.; Hanssen, J.; McCarroll, R.; Valiron, P. J. Phys. B 1981, 14, 2259.
- Gargaud, M.; McCarroll, R. J. Phys. B 1985, 18, 463.
- Mo, O.; Riera, A.; Yanez, M. Phys. Rev. A 1985, 31, 3977.
- Zygelman, B.; Dalgarno, A. Phys. Rev. A 1986, 33, 3853.
- Bransden, B.H.; McDowell, M.R.C. Charge exchange and the theory of ion - atom colli- sions; Clarendon Press: Oxford, 1992. [Google Scholar]
- Zygelman, B.; Cooper, D.L.; Ford, M.J.; Dalgarno, A.; Gerratt, J.; Raimondi, M. Phys. Rev. A 1992, 46, 3846.
- Bottrell, G.J. Nucl. Instrum. Methods. Phys. Res. B 1993, 79, 173.
- Gargaud, M.; McCarroll, R.; Valiron, P. J. Phys. B 1987, 20, 1555.
- Hoekstra, R.; Beijers, J. P. M.; Schlatmann, A. R.; Morgenstern, R.; de Heer, F. J. Phys. Rev. A 1990, 41, 4800.
- Saha, B. C. Phys. Rev. A 1995, 51, 5021.
- Tseng, H. C.; Lin, C. D. Phys. Rev. A 1998, 58, 1966.
- Vaeck, N.; Desouter-Lecomte, M.; Liévin, J. J. Phys. B 1999, 32, 409.
- Errea, L. F.; Gorfinkiel, J. D.; Harel, C.; Jouin, H.; Macias, A.; Méndez, L.; Pons, B.; Riera, A. J. Phys. B 1999, 32, L673.
- Belyaev, A. K.; Grosser, J. J. Phys. B 1996, 29, 5843.
- MOLPRO is a package of ab initio programs written by Werner, H.-J.; Knowles, P. J., with contributions from Amos, R. D.; Bernhardsson, A.; Berning, A.; Celani, P.; Cooper, D. L.; Deegan, M. J. O.; Dobbyn, A. J.; Eckert, F.; Hampel, C.; Hetzer, G.; Korona, T.; Lindh, R.; Lloyd, A. W.; McNicholas, S. J.; Manby, F. R.; Meyer, W.; Mura, M. E.; Nicklass, A.; Palmieri, P.; Pitzer, R.; Rauhut, G.; Schtz, M.; Stoll, H.; Stone, A. J.; Tarroni, R.; Thorsteinsson, T.
- Belyaev, A. K.; Grosser, J.; Hahne, J.; Menzel, T. Phys. Rev. A 1999, 60, 2151.
- Huzinaga, S. J. Chem. Phys. 1965, 42, 1293.
- Dunning, T. H. J. Chem. Phys. 1989, 90, 1007.
- Werner, H.-J.; Knowles, P.J. J. Chem. Phys. 1985, 82, 5053.
- Knowles, P.J.; Werner, H.-J. Chem. Phys. Lett. 1985, 115, 259.
- Phaneuf, R. A.; Alvarez, I.; Meyer, F.W.; Crandall, D.H. Phys. Rev. A. 1982, 26, 1892.
- Dijkkamp, D.; Ciric, D.; Vlieg, E.; de Boer, A.; de Heer, F.J. J. Phys. B 1985, 18, 4763.
- Bliek, F.W.; Hoekstra, R.; Bannister, M.E.; Havener, C.C. Phys. Rev. A. 1997, 56, 426.
- Aberle, W.; Grosser, J.; Kruger, W. J. Phys. B 1980, 13, 2083.
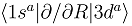 (b), and the couplings in the party diabatic representation (c). The insert in (c) shows the couplings in the enlarged scale and demonstrates that some of them do not vanish as R → ∞. The thick and thin dot-dashed lines are the
(b), and the couplings in the party diabatic representation (c). The insert in (c) shows the couplings in the enlarged scale and demonstrates that some of them do not vanish as R → ∞. The thick and thin dot-dashed lines are the 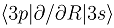 and
and 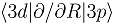 nonadiabatic matrix elements for the CD4+ quasimolecule.
nonadiabatic matrix elements for the CD4+ quasimolecule.
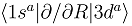 (b), and the couplings in the party diabatic representation (c). The insert in (c) shows the couplings in the enlarged scale and demonstrates that some of them do not vanish as R → ∞. The thick and thin dot-dashed lines are the
(b), and the couplings in the party diabatic representation (c). The insert in (c) shows the couplings in the enlarged scale and demonstrates that some of them do not vanish as R → ∞. The thick and thin dot-dashed lines are the 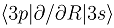 and
and 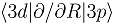 nonadiabatic matrix elements for the CD4+ quasimolecule.
nonadiabatic matrix elements for the CD4+ quasimolecule.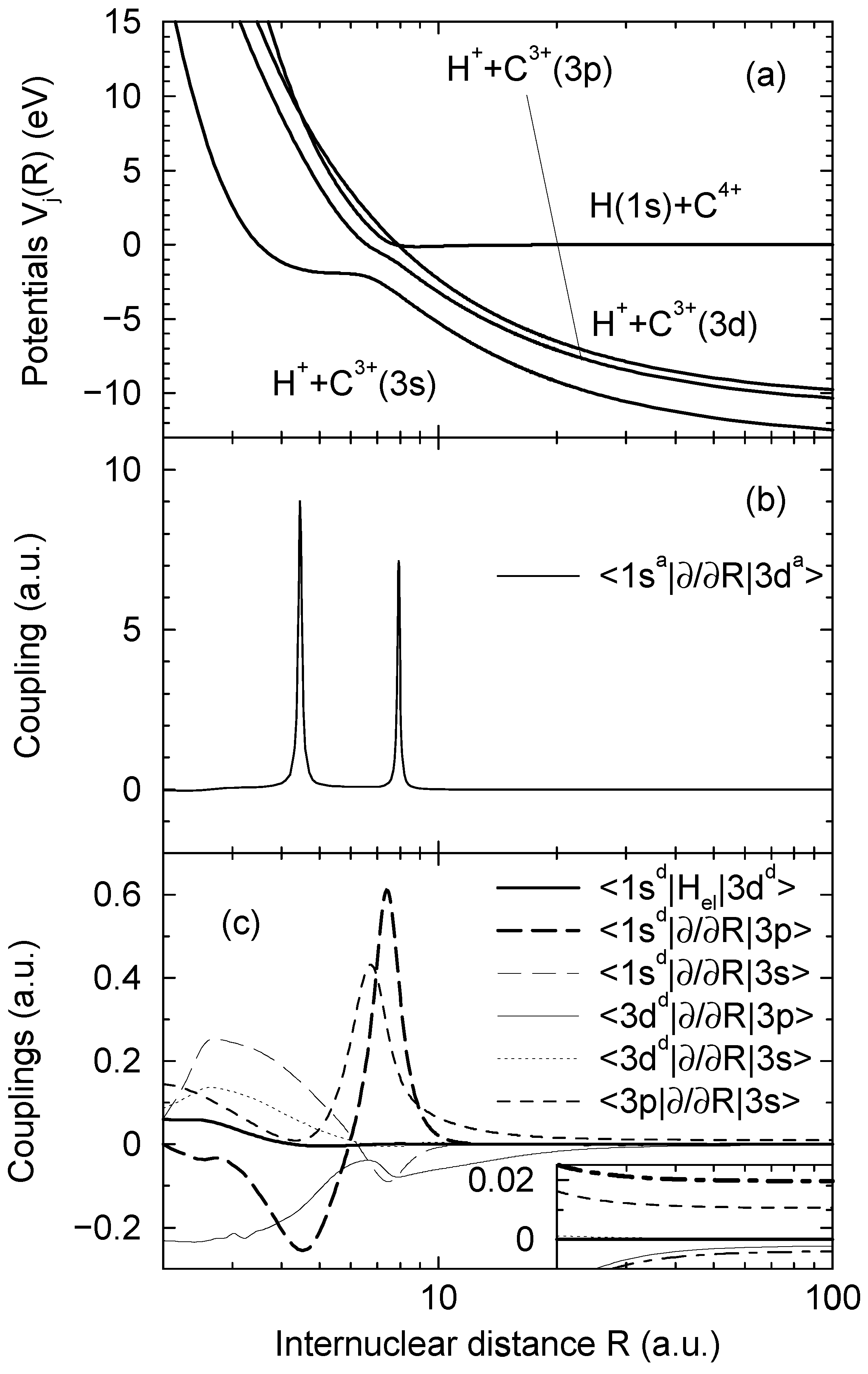
- 1For the states asymptotically corresponding to H(1s) + C4+ and H+ + C3+(3d) Figure 1a shows the diabatic potentials described below, the adiabatic potentials are not distinguishable from the diabatic ones within the figure scale.
© 2002 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Belyaev, A.K.; Grosser, J.; Liévin, J.; Vaeck, N. Charge Exchange in Low-Energy H, D + C4+ Collisions with Full Account of Electron Translation. Int. J. Mol. Sci. 2002, 3, 190-208. https://doi.org/10.3390/i3030190
Belyaev AK, Grosser J, Liévin J, Vaeck N. Charge Exchange in Low-Energy H, D + C4+ Collisions with Full Account of Electron Translation. International Journal of Molecular Sciences. 2002; 3(3):190-208. https://doi.org/10.3390/i3030190
Chicago/Turabian StyleBelyaev, A. K., J. Grosser, J. Liévin, and N. Vaeck. 2002. "Charge Exchange in Low-Energy H, D + C4+ Collisions with Full Account of Electron Translation" International Journal of Molecular Sciences 3, no. 3: 190-208. https://doi.org/10.3390/i3030190


