Automated Exploration of Free Energy Landscapes Based on Umbrella Integration
Abstract
:1. Introduction
2. Theoretical Method
2.1. Umbrella Integration Method
2.2. A New Automated Exploration Approach
- (0)
- Start from an umbrella integration (UI) calculation for a specific point in the reaction coordinate space.
- (1)
- Choose a “parent point”, which has the lowest PMF value among the points that were already sampled and exist in the border region in the reaction coordinate space.
- (2)
- Create new points around the parent point chosen in step (1).
- (3)
- Prune the points created in step (2) and if all points are rejected, the parent point is judged to not be in the border region. Then go back to step (1).
- (4)
- Choose the “child point” from among the points remaining in step (3).
- (5)
- We perform an UI calculation of the new window for the child point chosen in step (4) and added information of the distribution for the window to the list of the windows. Then, go back to step (1).
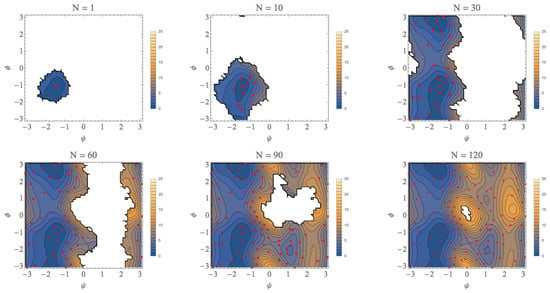
3. Computational Results
4. Discussion and Future Directions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| PMF | Potential of mean force |
| US | Umbrella sampling |
| WHAM | Weighted histogram analysis |
| UI | Umbrella integration |
| N.N. | Nearest neighboring |
| EQ | Equilibrium state |
| TS | Transition state |
Appendix A
- (A0)
- Start with the assumption that holds.
- (A1)
- Estimate , Mahalanobis distance, , and .
- (A2)
- Varying for satisfying , with minimizing .
- (A3)
- Update : , and go back to (A1).
- (A4)
- Estimate . If this value is less than a threshold, which is set to be 1.5 for the actual calculations shown in the text.
References
- Zuckerman, D.M. Statistical Physics of Biomolecules: An Introduction; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Chipot, C.; Pohorille, A. (Eds.) Theory and Applications in Chemistry and Biology. In Free Energy Calculations; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Sugita, Y.; Okamoto, Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999, 314, 141–151. [Google Scholar] [CrossRef]
- Nakajima, N.; Nakamura, H.; Kidera, A. Multicanonical Ensemble Generated by Molecular Dynamics Simulation for Enhanced Conformational Sampling of Peptides. J. Phys. Chem. B 1997, 101, 817–824. [Google Scholar] [CrossRef]
- Hansmann, U.H.E.; Okamoto, Y.; Eisenmenger, F. Molecular dynamics, Langevin and hybrid Monte Carlo simulations in a multicanonical ensemble. Chem. Phys. Lett. 1996, 259, 321–330. [Google Scholar] [CrossRef]
- Kirkwood, J.G. Statistical Mechanics of Fluid Mixtures. J. Chem. Phys. 1935, 3, 300–313. [Google Scholar] [CrossRef]
- Käster, J.; Senn, H.M.; Thiel, S.; Otte, N.; Thiel, W. QM/MM Free-Energy Perturbation Compared to Thermodynamic Integration and Umbrella Sampling: Application to an Enzymatic Reaction. J. Chem. Theory Comput. 2006, 2, 452–461. [Google Scholar] [CrossRef] [PubMed]
- Carter, E.A.; Ciccotti, G.; Hynes, J.T.; Kapral, R. Constrained reaction coordinate dynamics for the simulation of rare events. Chem. Phys. Lett. 1989, 156, 472–477. [Google Scholar] [CrossRef]
- Sprik, M.; Ciccotti, G. Free energy from constrained molecular dynamics. J. Chem. Phys. 1998, 109, 7737–7744. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J.P. Monte Carlo free energy estimates using non-Boltzmann sampling: Application to the sub-critical Lennard-Jones fluid. Chem. Phys. Lett. 1974, 28, 578–581. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J.P. Nonphysical sampling distributions in Monte Carlo free-energy estimation—Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Hooft, R.W.W.; van Eijck, B.P.; Kroon, J. An adaptive umbrella sampling procedure in conformational analysis using molecular dynamics and its application to glycol. J. Chem. Phys. 1992, 97, 6690–6694. [Google Scholar] [CrossRef]
- Kästner, J. Umbrella Sampling. WIRES Comput. Mol. Sci. 2011, 1, 932–942. [Google Scholar] [CrossRef]
- Wojtas-Niziurski, W.; Meng, Y.; Roux, B.; Bernèche, S. Self-Learning Adaptive Umbrella Sampling Method for the Determination of Free Energy Landscapes in Multiple Dimensions. J. Chem. Theory Comput. 2013, 9, 1885–1895. [Google Scholar] [CrossRef] [PubMed]
- Higo, J.; Dasgupta, B.; Mashimo, T.; Kasahara, K.; Fukunishi, Y.; Nakamura, H. Virtual-system-coupled adaptive umbrella sampling to compute free-energy landscape for flexible molecular docking. J. Comput. Chem. 2015, 36, 1489–1502. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Bouzida, D.; Swendsen, R.H.; Kollmann, P.A.; Rosenberg, J.M. The Weighted Histogram Analysis Method for Free-Energy Calculations on Biomolecules. I. The Method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Darve, E.; Pohorille, A. Calculating free energies using average force. J. Chem. Phys. 2001, 115, 9169–9183. [Google Scholar] [CrossRef]
- Darve, E.; Rodriguez-Gomez, E.; Pohorille, A. Adaptive biasing force method for scalar and vector free energy calculations. J. Chem. Phys. 2008, 128, 144120. [Google Scholar] [CrossRef] [PubMed]
- Henin, J.; Fiorin, G.; Chipot, C.; Klein, M.L. Exploring Multidimensional Free Energy Landscapes Using Time-Dependent Biases on Collective Variables. J. Chem. Theory Comput. 2010, 6, 35–47. [Google Scholar] [CrossRef] [PubMed]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef] [PubMed]
- Barducci, A.; Bonomi, M.; Parrinello, M. Metadynamics. WIRES Comput. Mol. Sci. 2011, 1, 826–843. [Google Scholar] [CrossRef]
- Kästner, J.; Thiel, W. Bridging the gap between thermodynamic integration and umbrella sampling provides a novel analysis method: “Umbrella integration”. J. Chem. Phys. 2005, 123, 144104. [Google Scholar] [CrossRef] [PubMed]
- Kästner, J.; Thiel, W. Analysis of the statistical error in umbrella sampling simulations by umbrella integration. J. Chem. Phys. 2006, 124, 234106. [Google Scholar] [CrossRef] [PubMed]
- Kästner, J. Umbrella integration in two or more reaction coordinates. J. Chem. Phys. 2009, 131, 034109. [Google Scholar] [CrossRef] [PubMed]
- Bohner, M.U.; Kästner, J. An algorithm to find minimum free-energuy paths using umbrella integration. J. Chem. Phys. 2012, 137, 034105. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Darden, T.; Perera, L.; Li, L.; Pedersen, L. New tricks for modelers from the crystallography toolkit: The particle mesh Ewald algorithm and its use in nucleic acid simulations. Structure 1999, 7, R55–R60. [Google Scholar] [CrossRef]
- Foloppe, N.; MacKerell, A.D., Jr. All-atom empirical force field for nucleic acids: I. Parameter optimization based on small molecule and condensed phase macromolecular target data. J. Comput. Chem. 2000, 21, 86–104. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, W.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [PubMed]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [PubMed]
- Bonomi, M.; Branduardi, D.; Bussi, G.; Camilloni, C.; Provasi, D.; Raiteri, P.; Donadio, D.; Marinelli, F.; Pietrucci, F.; Broglia, R.A.; et al. PLUMED: A portable plugin for free-energy calculations with molecular dynamics. Comput. Phys. Commun. 2009, 180, 1961–1972. [Google Scholar] [CrossRef]
- Grossfield, A. WHAM: The Weighted Histogram Analysis Method, Version 2.0.6. Available online: http://membrane.urmc.rochester.edu/content/wham (accessed on 20 March 2018).
- Smith, P.E. The alanine dipeptide free energy surface in solution. J. Chem. Phys. 1999, 111, 5568–5579. [Google Scholar] [CrossRef]
- Maeda, S.; Ohno, K. A New Method for Constructing Multidimensional Potential Energy Surfaces by a Polar Coordinate Interpolation Technique. Chem. Phys. Lett. 2003, 381, 177–186. [Google Scholar] [CrossRef]
- Karakasidis, T.E.; Charitidis, C.A. Multiscale modeling in nanomaterials science. Mater. Sci. Eng. C 2007, 27, 1082–1089. [Google Scholar] [CrossRef]







| φ (rad) | ψ (rad) | A (kcal/mol) | |
|---|---|---|---|
| EQ1 (αR) | −1.4 (−1.4) | −1.1 (−1.0) | 0.0 (0.0) |
| EQ2 (C7eq) | −1.5 (−1.5) | 2.9 (2.9) | 0.0 (0.0) |
| EQ3 (C7ex) | 1.1 (1.1) | −2.1 (−2.1) | 4.0 (4.0) |
| EQ4 (αL) | 1.1 (1.1) | 0.9 (0.8) | 7.0 (7.0) |
| TS1 | −1.7 (−1.7) | 0.6 (0.6) | 3.4 (3.4) |
| TS2 | 0.2 (0.2) | −1.6 (−1.6) | 6.0 (6.0) |
| TS3 | 0.2 (0.3) | 1.5 (1.4) | 8.3 (8.3) |
| TS4 | 1.3 (1.3) | −0.1 (−0.1) | 8.0 (8.0) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mitsuta, Y.; Kawakami, T.; Okumura, M.; Yamanaka, S. Automated Exploration of Free Energy Landscapes Based on Umbrella Integration. Int. J. Mol. Sci. 2018, 19, 937. https://doi.org/10.3390/ijms19040937
Mitsuta Y, Kawakami T, Okumura M, Yamanaka S. Automated Exploration of Free Energy Landscapes Based on Umbrella Integration. International Journal of Molecular Sciences. 2018; 19(4):937. https://doi.org/10.3390/ijms19040937
Chicago/Turabian StyleMitsuta, Yuki, Takashi Kawakami, Mitsutaka Okumura, and Shusuke Yamanaka. 2018. "Automated Exploration of Free Energy Landscapes Based on Umbrella Integration" International Journal of Molecular Sciences 19, no. 4: 937. https://doi.org/10.3390/ijms19040937