Insight into Conformational Change for 14-3-3σ Protein by Molecular Dynamics Simulation
Abstract
:1. Introduction
2. Results and Discussion
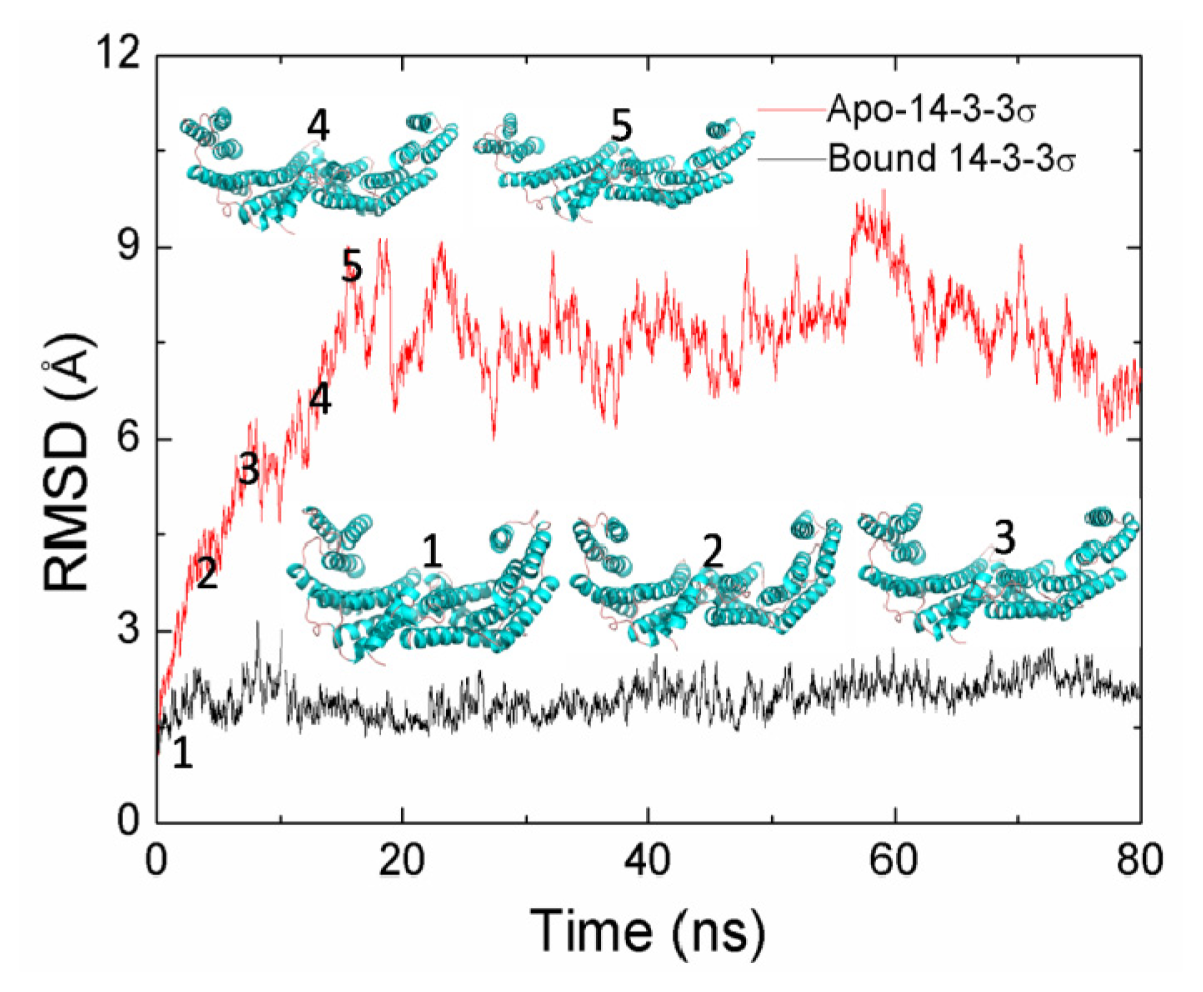
2.1. Equilibrium of the Molecular Dynamics Simulation
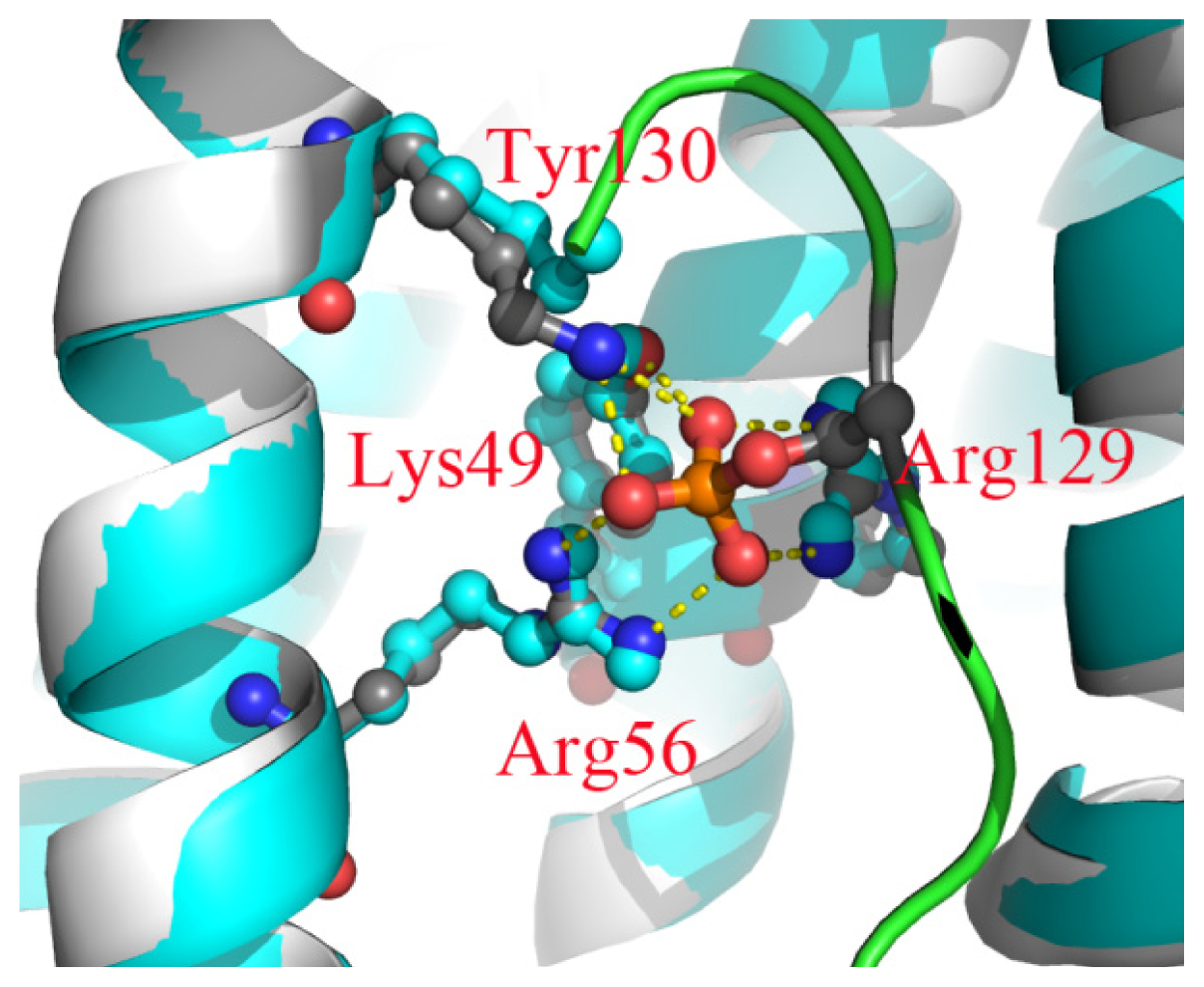
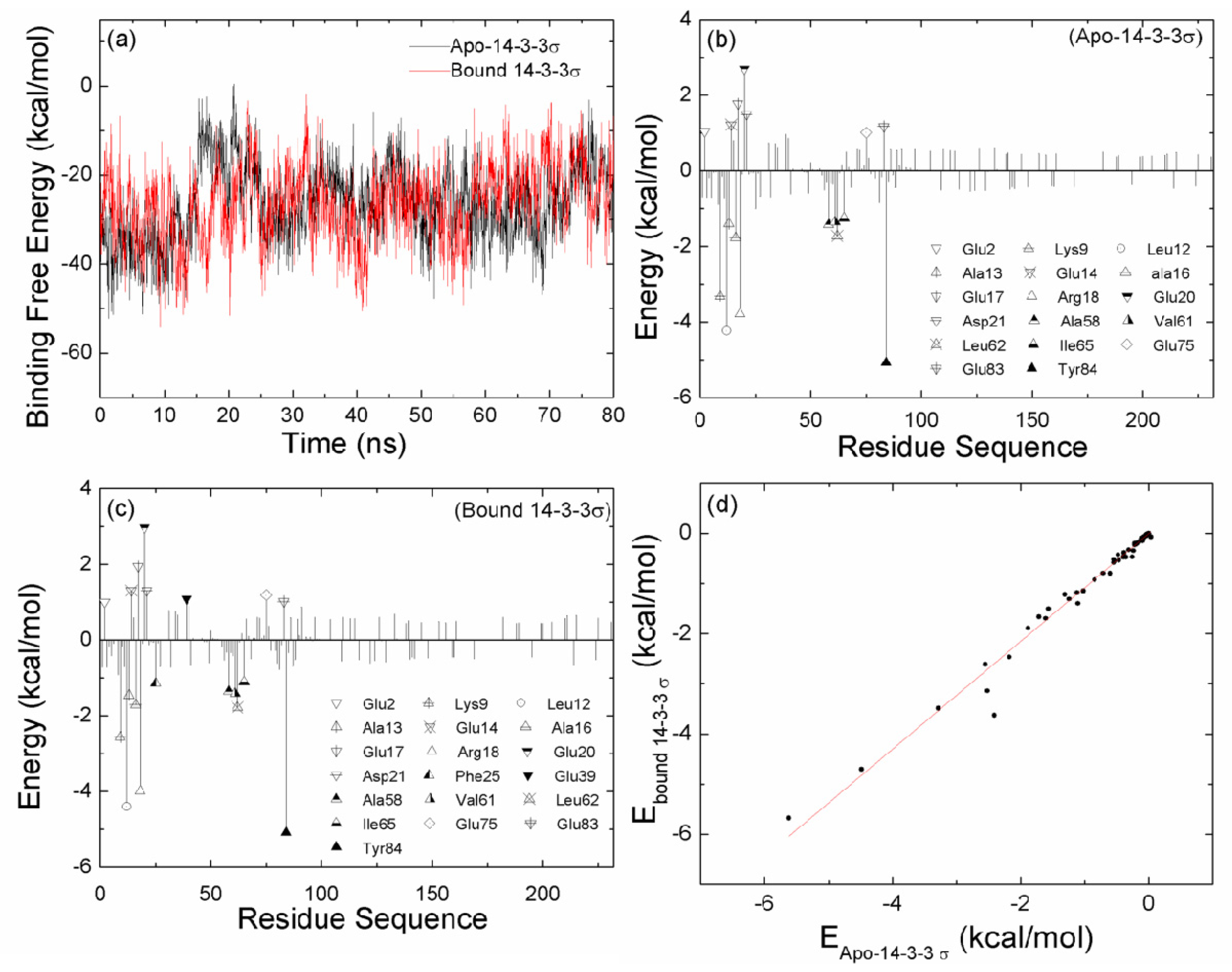
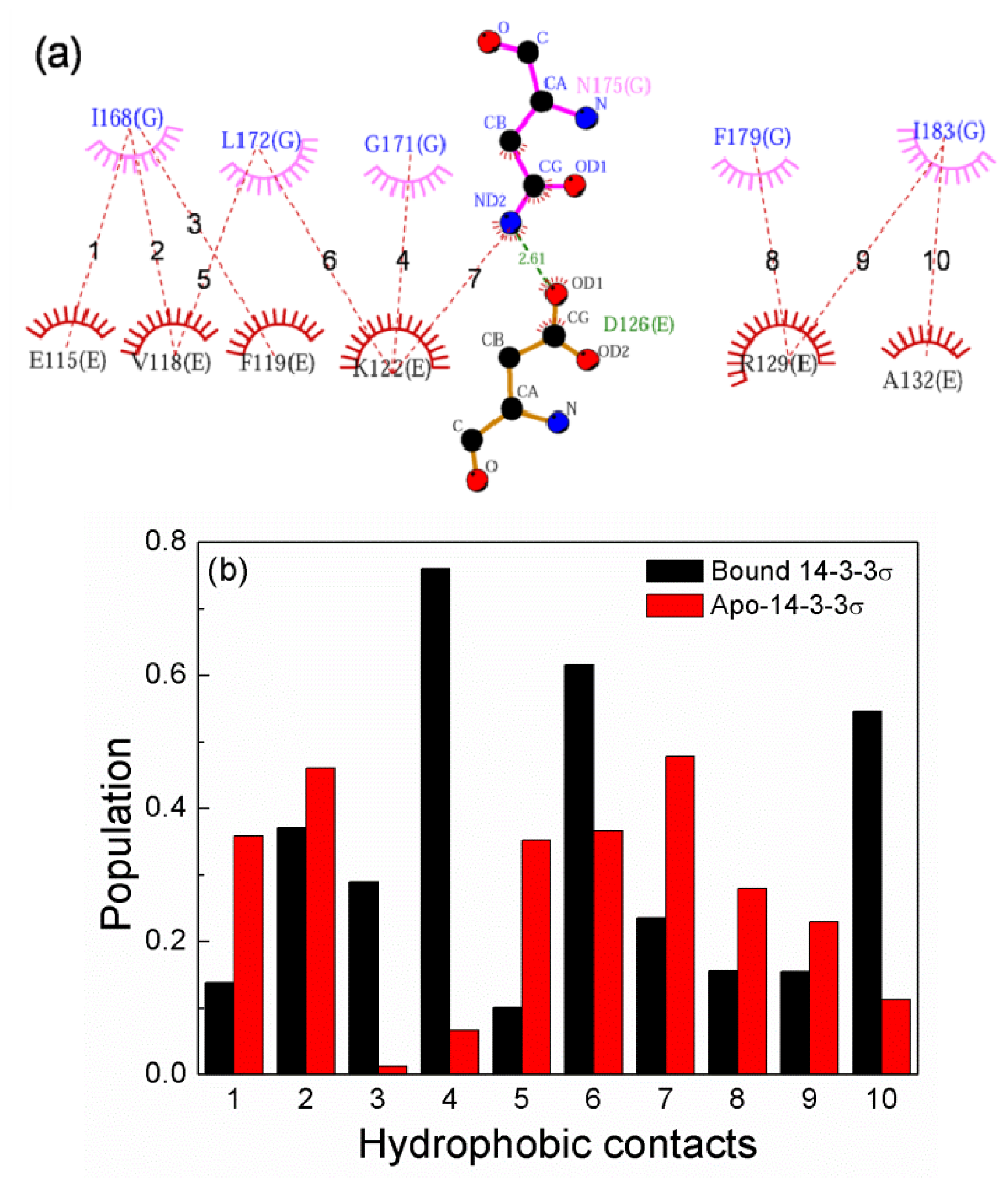
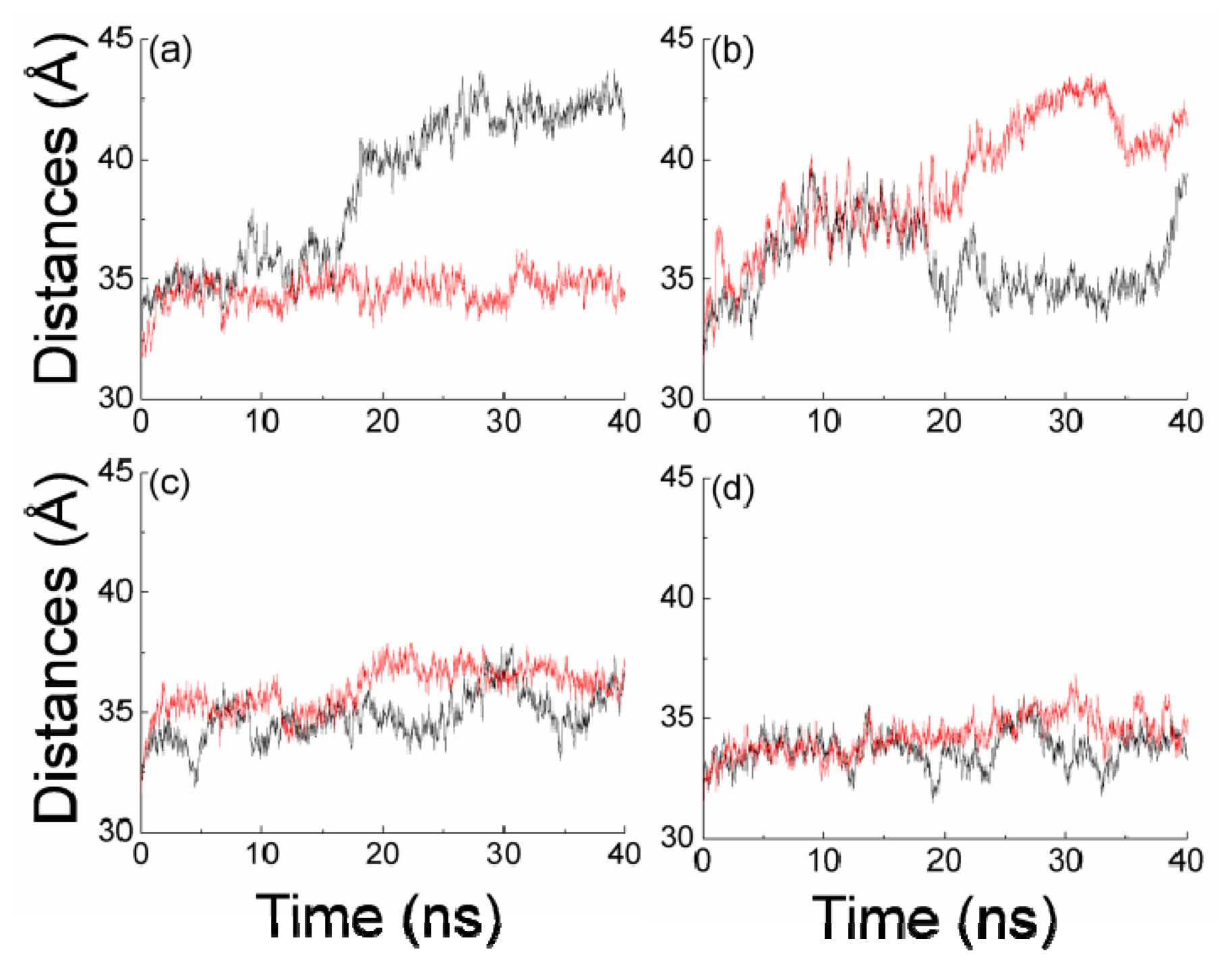
2.2. The Interaction between the Two Monomers for Apo-14-3-3σ and Bound 14-3-3σ
2.3. The Stability of the Helices A, B, C and D
2.4. The Stability of Helices G, H and I
2.5. The Conformational Change of the Helices E, F and G
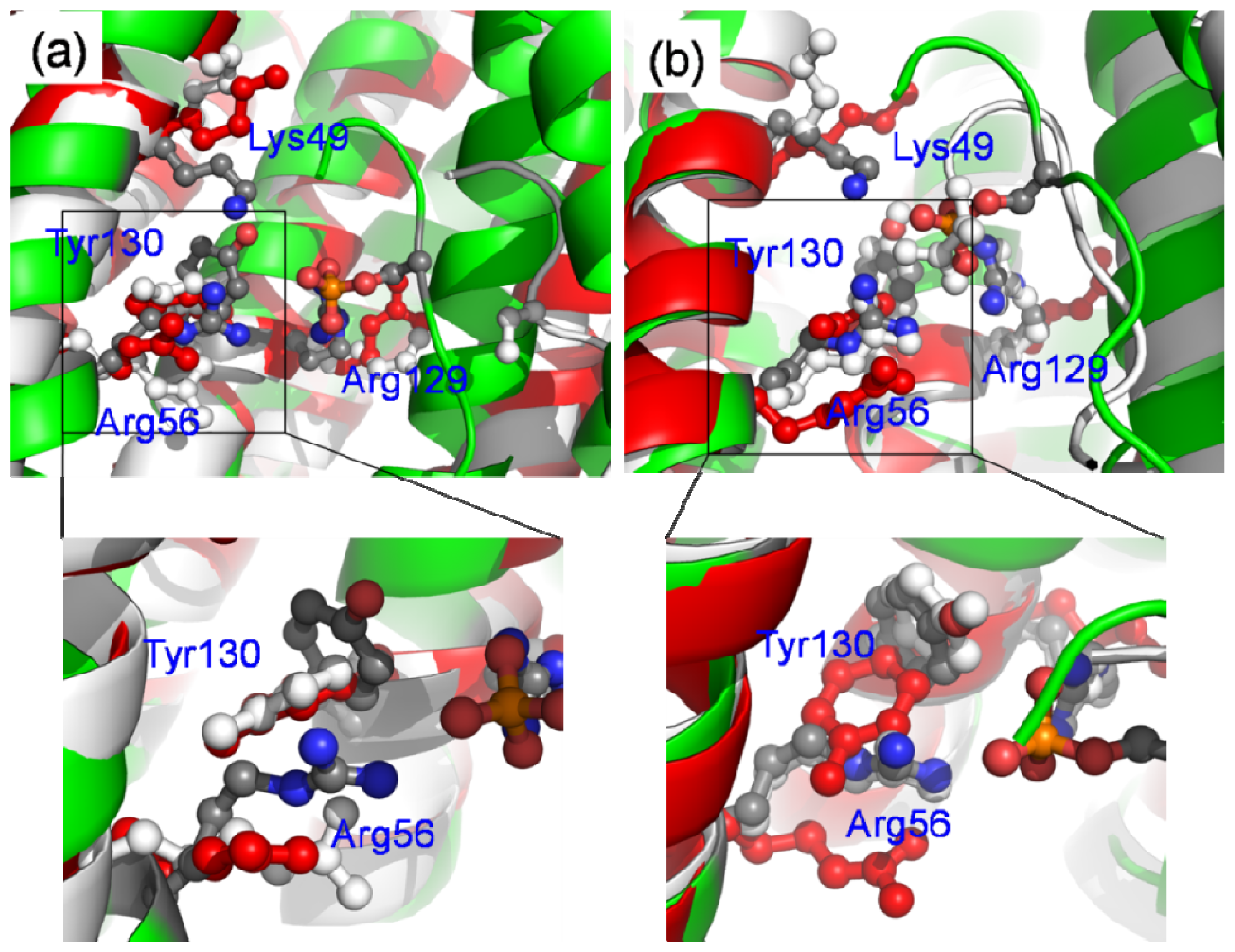
2.6. The Reason for the Conformational Change
3. Materials and Methods
3.1. System Setups
3.2. Molecular Dynamics Simulation
3.3. Free Energy Calculations
3.4. Structural Analysis
4. Conclusions
Supplementary Information
ijms-15-02794-s001.pdfAcknowledgments
Conflicts of Interest
References
- Aitken, A. 14-3-3 proteins: A historic overview. Semin. Cancer Biol 2006, 16, 162–172. [Google Scholar]
- Fu, H.; Subramanian, R.R.; Masters, S.C. 14-3-3 proteins: Structure, function, and regulation. Annu. Rev. Pharmacol. Toxicol 2000, 40, 617–647. [Google Scholar]
- Dubois, T.; Rommel, C.; Howell, S.; Steinhussen, U.; Soneji, Y.; Morrice, N.; Moelling, K.; Aitken, A. 14-3-3 is phosphorylated by casein kinase I on residue 233. Phosphorylation at this site in vivo regulates Raf/14-3-3 interaction. J. Biol. Chem 1997, 272, 28882–28888. [Google Scholar]
- Powell, D.W.; Rane, M.J.; Joughin, B.A.; Kalmukova, R.; Hong, J.H.; Tidor, B.; Dean, W.L.; Pierce, W.M.; Klein, J.B.; Yaffe, M.B.; et al. Proteomic identification of 14-3-3zeta as a mitogen-activated protein kinase-activated protein kinase 2 substrate: role in dimer formation and ligand binding. Mol. Cell. Biol 2003, 23, 5376–5387. [Google Scholar]
- Schumacher, B.; Skwarczynska, M.; Rose, R.; Ottmann, C. Structure of a 14-3-3sigma-YAP phosphopeptide complex at 1.15 A resolution. Acta Crystallogr. Sect. F 2010, 66, 978–984. [Google Scholar]
- Urano, T.; Saito, T.; Tsukui, T.; Fujita, M.; Hosoi, T.; Muramatsu, M.; Ouchi, Y.; Inoue, S. Efp targets 14-3-3 sigma for proteolysis and promotes breast tumour growth. Nature 2002, 417, 871–875. [Google Scholar]
- Chan, T.A.; Hermeking, H.; Lengauer, C.; Kinzler, K.W.; Vogelstein, B. 14-3-3sigma is required to prevent mitotic catastrophe after DNA damage. Nature 1999, 401, 616–620. [Google Scholar]
- Hermeking, H.; Benzinger, A. 14-3-3 proteins in cell cycle regulation. Semin. Cancer Biol 2006, 16, 183–192. [Google Scholar]
- Pozuelo Rubio, M.; Geraghty, K.M.; Wong, B.H.; Wood, N.T.; Campbell, D.G.; Morrice, N.; Mackintosh, C. 14-3-3-affinity purification of over 200 human phosphoproteins reveals new links to regulation of cellular metabolism, proliferation and trafficking. Biochem. J 2004, 379, 395–408. [Google Scholar]
- Yang, X.; Lee, W.H.; Sobott, F.; Papagrigoriou, E.; Robinson, C.V.; Grossmann, J.G.; Sundstrom, M.; Doyle, D.A.; Elkins, J.M. Structural basis for protein-protein interactions in the 14-3-3 protein family. Proc. Natl. Acad. Sci. USA 2006, 103, 17237–17242. [Google Scholar]
- Liu, D.; Bienkowska, J.; Petosa, C.; Collier, R.J.; Fu, H.; Liddington, R. Crystal structure of the zeta isoform of the 14-3-3 protein. Nature 1995, 376, 191–194. [Google Scholar]
- Wilker, E.W.; Grant, R.A.; Artim, S.C.; Yaffe, M.B. A structural basis for 14-3-3sigma functional specificity. J. Biol. Chem 2005, 280, 18891–18898. [Google Scholar]
- Gardino, A.K.; Smerdon, S.J.; Yaffe, M.B. Structural determinants of 14-3-3 binding specificities and regulation of subcellular localization of 14-3-3-ligand complexes: A comparison of the X-ray crystal structures of all human 14-3-3 isoforms. Semin. Cancer Biol 2006, 16, 173–182. [Google Scholar]
- Yaffe, M.B.; Rittinger, K.; Volinia, S.; Caron, P.R.; Aitken, A.; Leffers, H.; Gamblin, S.J.; Smerdon, S.J.; Cantley, L.C. The structural basis for 14-3-3:phosphopeptide binding specificity. Cell 1997, 91, 961–971. [Google Scholar]
- Rittinger, K.; Budman, J.; Xu, J.; Volinia, S.; Cantley, L.C.; Smerdon, S.J.; Gamblin, S.J.; Yaffe, M.B. Structural analysis of 14-3-3 phosphopeptide complexes identifies a dual role for the nuclear export signal of 14-3-3 in ligand binding. Mol. Cell 1999, 4, 153–166. [Google Scholar]
- Coblitz, B.; Wu, M.; Shikano, S.; Li, M. C-terminal binding: An expanded repertoire and function of 14-3-3 proteins. FEBS Lett 2006, 580, 1531–1535. [Google Scholar]
- Bustos, D.M. The role of protein disorder in the 14-3-3 interaction network. Mol. Biosyst 2012, 8, 178–184. [Google Scholar]
- Milroy, L.G.; Brunsveld, L.; Ottmann, C. Stabilization and inhibition of protein-protein interactions: The 14-3-3 case study. ACS Chem. Biol 2013, 8, 27–35. [Google Scholar]
- Liu, J.Y.; Li, Z.; Li, H.; Zhang, J.T. Critical residue that promotes protein dimerization: A story of partially exposed Phe25 in 14-3-3sigma. J. Chem. Inf. Model 2011, 51, 2612–2625. [Google Scholar]
- Li, Z.; Peng, H.; Qin, L.; Qi, J.; Zuo, X.; Liu, J.Y.; Zhang, J.T. Determinants of 14-3-3sigma protein dimerization and function in drug and radiation resistance. J. Biol. Chem 2013, 288, 31447–31457. [Google Scholar]
- Benzinger, A.; Popowicz, G.M.; Joy, J.K.; Majumdar, S.; Holak, T.A.; Hermeking, H. The crystal structure of the non-liganded 14-3-3sigma protein: Insights into determinants of isoform specific ligand binding and dimerization. Cell Res 2005, 15, 219–227. [Google Scholar]
- Scott, K.A.; Randles, L.G.; Moran, S.J.; Daggett, V.; Clarke, J. The folding pathway of spectrin R17 from experiment and simulation: Using experimentally validated MD simulations to characterize States hinted at by experiment. J. Mol. Biol 2006, 359, 159–173. [Google Scholar]
- Ji, C.G.; Zhang, J.Z. Understanding the molecular mechanism of enzyme dynamics of ribonuclease A through protonation/deprotonation of HIS48. J. Am. Chem. Soc 2011, 133, 17727–17737. [Google Scholar]
- Chen, H.F.; Luo, R. Binding induced folding in p53-MDM2 complex. J. Am. Chem. Soc 2007, 129, 2930–2937. [Google Scholar]
- Hu, G.; Chen, L.Y.; Wang, J. Insights into the mechanisms of the selectivity filter of Escherichia coli aquaporin Z. J. Mol. Model 2012, 18, 3731–3741. [Google Scholar]
- Verma, S.; Singh, A.; Mishra, A. The effect of fulvic acid on pre- and postaggregation state of Abeta17–42. Molecular dynamics simulation studies. BBA-Proteins Proteomics 2013, 1834, 24–33. [Google Scholar]
- Obsil, T.; Obsilova, V. Structural basis of 14-3-3 protein functions. Semin. Cell Dev. Biol 2011, 22, 663–672. [Google Scholar]
- Joosten, R.P.; te Beek, T.A.; Krieger, E.; Hekkelman, M.L.; Hooft, R.W.; Schneider, R.; Sander, C.; Vriend, G. A series of PDB related databases for everyday needs. Nucleic Acids Res 2011, 39, D411–D419. [Google Scholar]
- Hu, G.; Zhang, Q.; Chen, L.Y. Insights into scFv: Drug binding using the molecular dynamics simulation and free energy calculation. J. Mol. Model 2011, 17, 1919–1926. [Google Scholar]
- Gohlke, H.; Kiel, C.; Case, D.A. Insights into protein-protein binding by binding free energy calculation and free energy decomposition for the Ras-Raf and Ras-RalGDS complexes. J. Mol. Biol 2003, 330, 891–913. [Google Scholar]
- Chen, J.; Zhang, D.; Zhang, Y.; Li, G. Computational studies of difference in binding modes of peptide and non-peptide inhibitors to MDM2/MDMX based on molecular dynamics simulations. Int. J. Mol. Sci 2012, 13, 2176–2195. [Google Scholar]
- Laskowski, R.A.; Swindells, M.B. LigPlot+: Multiple ligand-protein interaction diagrams for drug discovery. J. Chem. Inf. Model 2011, 51, 2778–2786. [Google Scholar]
- Fu, H.; Coburn, J.; Collier, R.J. The eukaryotic host factor that activates exoenzyme S of Pseudomonas aeruginosa is a member of the 14-3-3 protein family. Proc. Natl. Acad. Sci. USA 1993, 90, 2320–2324. [Google Scholar]
- Henriksson, M.L.; Troller, U.; Hallberg, B. 14-3-3 proteins are required for the inhibition of Ras by exoenzyme S. Biochem. J 2000, 349, 697–701. [Google Scholar]
- Yong, D.; Chun, W.; Shibasish, C.; Mathew, C.L.; Guoming, X.; Wei, Z.; Rong, Y.; Piotr, C.; Ray, L.; Taisung, L.; et al. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J. Comput. Chem 2003, 24, 1999–2012. [Google Scholar]
- Homeyer, N.; Horn, A.H.; Lanig, H.; Sticht, H. AMBER force-field parameters for phosphorylated amino acids in different protonation states: Phosphoserine, phosphothreonine, phosphotyrosine, and phosphohistidine. J. Mol. Model 2006, 12, 281–289. [Google Scholar]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Comput. Phys 1983, 79, 926–935. [Google Scholar]
- Case, D.A.; Darden, T.A.; Cheatham, T.E., III; Simmerling, C.L.; Wang, J.; Duke, R.E.; Luo, R.; Crowley, M.; Walker, R.C.; Zhang, W.; et al. AMBER, version 10; University of California: San Francisco, CA, USA, 2008. [Google Scholar]
- Darden, T.; York, D.; Pedersen, L. Particle mesh ewald and Log(N) method for ewald sums in large systems. J. Comput. Phys 1993, 98, 10089–10092. [Google Scholar]
- Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J.C. Numerical-integration of cartesian equations of motion of a system with constraints-molecular-dynamics of N-alkanes. J. Comput. Phys 1977, 23, 327–341. [Google Scholar]
- Weiser, J.; Shenkin, P.S.; Still, W.C. Approximate atomic surfaces from linear combinations of pairwise overlaps (LCPO). J. Comput. Chem 1999, 20, 217–230. [Google Scholar]
- Onufriev, A.; Bashford, D.; Case, D.A. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins 2004, 55, 383–394. [Google Scholar]
- Case, D.A. Normal mode analysis of protein dynamics. Curr. Opin. Struct. Biol 1994, 4, 285–290. [Google Scholar]
- Case, D.A.; Cheatham, T.E., 3rd; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M., Jr.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The Amber biomolecular simulation programs. J. Comput. Chem 2005, 26, 1668–1688. [Google Scholar]


| 14-3-3σ | Enthalpic contribution | Entropic contribution | Total energy |
|---|---|---|---|
| Apo-14-3-3σ | −5532.83 ± 43.46 | 2666.32 ± 6.46 | −8199.15 |
| Bound 14-3-3σ | −5520.95 ± 43.62 | 2658.52 ± 6.90 | −8179.47 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hu, G.; Li, H.; Liu, J.-Y.; Wang, J. Insight into Conformational Change for 14-3-3σ Protein by Molecular Dynamics Simulation. Int. J. Mol. Sci. 2014, 15, 2794-2810. https://doi.org/10.3390/ijms15022794
Hu G, Li H, Liu J-Y, Wang J. Insight into Conformational Change for 14-3-3σ Protein by Molecular Dynamics Simulation. International Journal of Molecular Sciences. 2014; 15(2):2794-2810. https://doi.org/10.3390/ijms15022794
Chicago/Turabian StyleHu, Guodong, Haiyan Li, Jing-Yuan Liu, and Jihua Wang. 2014. "Insight into Conformational Change for 14-3-3σ Protein by Molecular Dynamics Simulation" International Journal of Molecular Sciences 15, no. 2: 2794-2810. https://doi.org/10.3390/ijms15022794





