1. Introduction
The prediction of ligand-protein binding affinities or binding
free energies is not only a major challenge in structure-based drug design, but also for
in silico studies on metabolism of xenobiotics. Different (drug-)metabolizing enzymes may catalyze the formation of different products. Therefore, predicting the affinity and selectivity towards these enzymes can be an important step in (drug-)metabolite prediction. Although there are many approaches available to calculate protein binding free energies [
1,
2], most of them lack either accuracy [
3–
6] or computational efficiency [
7,
8]. In the past, Å qvist and co-workers [
9] have introduced the linear interaction energy (LIE) approach as a relatively fast method for binding affinity computation with satisfactory accuracy [
5,
10].
LIE is based on linear response theory and determines ligand solvation free energies from molecular dynamics (MD) simulations at only two states,
i.e., when bound to the protein, and when being unbound (freely solvated) in water. The simplicity of this method makes it appealing to use. However, its accuracy or efficiency may be restricted by the required conformational sampling of the protein bound state, especially when calculating affinities to very flexible and malleable proteins such as Cythochrome P450s (CYPs) [
11,
12].
CYPs are able to metabolize a large variety of substrates. This ability can be attributed to the considerable flexibility and plasticity of their active site. For example, work of Ekroos and Sjögren [
13] showed that upon substrate binding, CYP 3A4 can substantially alter its conformation and it can increase the size of its active site by more than 80%. Also another drug metabolizing CYP, 2D6, is known to be able to substantially adapt its conformation upon substrate binding, depending on the size and properties of the substrate [
14,
15]. These examples are not unique in this family of enzymes, and as it is suggested in a review by Pochapsky
et al. [
16], CYP enzyme structure must be considered in four dimensions, as flexible and dynamic arrangements.
Proteins with large and flexible active sites can accommodate ligands in various orientations. Hence, the choice of the initial binding mode used to start MD simulations from is crucial for the parametrization and accuracy of the designed LIE model. To tackle this problem, we recently proposed an iterative scheme that makes it possible to include multiple independent simulations (starting from different ligand-binding modes) into a single LIE model. Using a Boltzmann-weighting approach, the relative contributions of the various simulations to the binding free energy are automatically obtained [
17]. Inclusion of different ligand poses was found to significantly increase the accuracy of a LIE model for CYP 2C9 binding, in line with recent theoretical studies of Faver
et al. [
18] highlighting the importance of local sampling to reduce errors in free energy computation. The obtained increase in accuracy showed the advantage of the iterative approach, especially in cases when binding modes have not been experimentally determined.
For flexible proteins, developing accurate LIE models is additionally challenged by difficulties in covering the protein-conformational space during MD simulations of the protein-ligand complex. Evidently, the large number of conformations available to CYPs or other flexible proteins makes full sampling and enumeration of available protein-conformational space problematic. As a remedy, we propose to extend the iterative LIE scheme to also include and combine results from multiple MD simulations starting from different protein conformations. Here, we illustrate the strength of this approach by developing LIE models for CYP 2D6, which is known for its large active-site malleability and for which distinct catalytically-active conformations were recently identified by Hritz
et al. [
14].
Cytochrome P450 2D6 accounts for only a few percent of all human CYPs but it metabolizes more than 20% of the clinical drugs on the current market [
19,
20]. The first crystal structure of CYP 2D6 (PDB code 2F9Q, 2006, Rowland
et al. [
21]) revealed an active-site cavity with an estimated volume of approximately 0.54 nm
3, which is larger than for CYPs 2A6, 2A13, 1A2 and 2E1, but smaller than for 2R1, 3A4, 2C8, and 2C9. Hritz
et al. studied the impact of the plasticity and flexibility of CYP 2D6 on the accuracy of docking-based Site-of-Metabolism (SOM) prediction [
14] and revealed that not only large conformational changes but also thermal motion can influence the reliability of structure-based SOM prediction. Interestingly, it was possible to select from MD simulations only a few CYP 2D6 structures that can be used as docking templates to obtain SOM prediction accuracies of more than 80% [
14]. Later, positional fluctuations observed during MD [
14] of side chains of active-site residues (Glu216, Phe483) could be confirmed by comparison to newly published X-ray structures (PDB codes 3QM4 [
15], 3TDA and 3TBG) [
22].
Here, we use the structures of Hritz
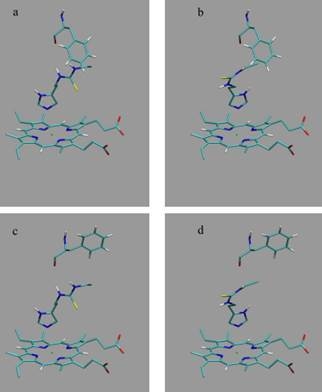
et al. as template coordinate sets to start different MD simulations of substrate-bound CYP 2D6. We will demonstrate the importance of selecting distinct protein conformations (additional to diverse ligand orientations) for the construction of an accurate LIE model, by developing a CYP 2D6 LIE model for thiourea compounds (
Table 1 and
Figure 1), for which relevant binding orientations could be selected manually. In a follow-up study [
23], we show how our iterative LIE method can be used for automated binding affinity prediction for a series of CYP 2D6 binders with a large diversity of possible binding modes, for which
a priori selection of relevant binding modes (based on visual inspection) is not possible.
2. Iterative LIE approach
According to the LIE method [
9], free energies of ligand binding are estimated from ensemble-averaged electrostatic
and van der Waals interaction energies
between the ligand and its surrounding in the protein-bound (ligand in protein) and in the free state (ligand free in water), as obtained from separate MD simulations. The binding free energy Δ
Gi for the ligand binding in pose
i to the protein is then calculated as
α and
β are empirical parameters for the van derWaals and electrostatic contribution of the nonbonded interaction energy to the free energy of binding, respectively.
β was originally set to 0.5 (according to linear response theory) and only
α was calibrated using sets of training compounds with experimentally known binding free energies [
9]. Later it was shown that coefficient
β can vary from its theoretical value [
10]. Here,
β is trained in the LIE parameterization procedure as well.
To account for the flexibility of the protein-ligand complex,
and
are in the current study obtained by performing for every ligand a series of (short) MD simulations of the protein-bound state, with each simulation starting from a different protein-ligand starting structure.
The relative contribution
Wi of an independent simulation
i to the interaction energy of the protein-bound ligand with its surrounding can be calculated [
17] as
such that the binding free energy ΔGcalc of that ligand averaged over the i independent simulations can be calculated from
The W
i’s are obtained by applying an iterative scheme, as described by Stjernschantz and Oostenbrink [
17]. After an initial guess, the LIE coefficients
α and
β are iteratively optimized until convergence is reached,
i.e., by obtaining a minimum value for the root-mean-square error between calculated and experimental values for the binding free energies. Relative experimental binding free energies Δ
Gexp for the considered thioureas were derived from inhibition data reported by Onderwater [
24] (
Table 1).
3. Results and Discussion
When calibrating LIE models using results from a single simulation per starting conformation (
i.e., using either the S1 or S2 subset of MD simulations, Section 4.3), different values were obtained for LIE parameters and for the root-mean-square errors (RMSEs) between calculated (Δ
Gcalc) and experimental binding free energies (Δ
Gexp).
Tables 2 and
3 report
α,
β and RMSE values for the different LIE models as obtained for the S1 and S2 sets of simulations, together with errors in the prediction for the compounds (outliers) for which Δ
Gcalc deviates by more than 1 kcal mol
−1 (4.184 kJ mol
−1) from Δ
Gexp.
The first four models in
Tables 2 and
3 (designated as P70-M1, P70-M2, P170-M1, and P170-M2) correspond to traditional LIE models and include per ligand results of a single MD simulation of the protein-bound state, starting from binding pose M1 (Section 4.2) in the P70 conformation (Section 4.1) in case of P70-M1,
etc. The P70 and P170 models in
Tables 2 and
3 combine results of the two simulations starting from either the M1 or M2 orientation in the corresponding protein structure, whereas the M1 and M2 models are based on the sets of two simulations starting from the M1 or M2 pose, respectively, in either of the two protein conformations. Finally, “all” in
Tables 2 and
3 refers to the LIE models that include results from simulations starting from any of the four starting configurations.
From the results presented in
Tables 2 and
3, one may conclude that inclusion of different starting configurations in the calculations does not necessarily improve the correlation between experimental and calculated values for the binding free energy. For example, when considering the S1 subset of simulations (
Table 2), the lowest RMSE value and number of outliers was obtained for the P70-M2 model, which was calibrated from single protein-ligand simulations per compound. However, the S2 subset of simulations indicates that the lowest RMSE was obtained for the M1 model instead, whereas the P70-M2 model shows the highest number of outliers of the S2-based models (
Table 3). These discrepancies suggest that interaction energies are not converged in a single MD simulation starting from a given protein-ligand conformation. This is also illustrated by the finding that from the S1 and S2 models based on one simulation per ligand, the lowest RMSE was obtained when starting MD from the P70-M2 and the P70-M1 conformation, respectively, whereas in the S1 and S2 models that combine results from all four MD runs, the simulations starting from the P70-M2 and P70-M1 conformations showed the largest contribution to Δ
Gcalc for only one (S1) or five (S2) of the ligands (see
Supplementary Material, Table S1).
To improve convergence of average ligand-protein interaction energies, results from the S1 and S2 simulation sets were combined to calibrate the LIE models presented in
Tables 4 and
5. Combination of the S1 and S2 results can be achieved in two ways. The first combination scheme was used in calibrating the LIE models in
Table 4 (referred to as S1–S2) and considers every S1 and S2 simulation separately in
Equation (3), also S1 and S2 runs that start from the same protein-thiourea configuration. As pointed out in reference [
17], use of
Equation (3) to calculate Δ
Gbind from multiple MD simulations per ligand requires that individual simulations cover different parts of protein-ligand conformational space. For several ligands, different hydrogen bond interactions with the protein were observed when comparing pairs of S1 and S2 simulations starting from the same protein-ligand conformation (see
Supplementary Material, Table S2 and
Figure S1). This can be seen as a motivation to treat S1 and S2 simulations individually, as in the calibration of the S1–S2 models. On the other hand, relatively short MD simulations were performed in this study, justified by the fact that conformational sampling is already partly achieved by including results from simulations starting from different protein conformations and ligand-binding orientations. Therefore, large conformational changes cannot be expected during a single simulation and based on this argument, pairs of S1 and S2 simulations starting from a single configuration should not be assigned separate weights
Wi in calibrating the LIE models. In the S1-S2-A models presented in
Table 5, 〈
VEL〉 and 〈
VV dW〉 obtained from pairs of S1 and S2 simulations (starting from the same protein-ligand conformation) were averaged for use in
Equation (3). Note that in the limit of infinite sampling, the ensemble averages of the interaction energies would be identical for simulations S1 and S2, leading to identical weights (
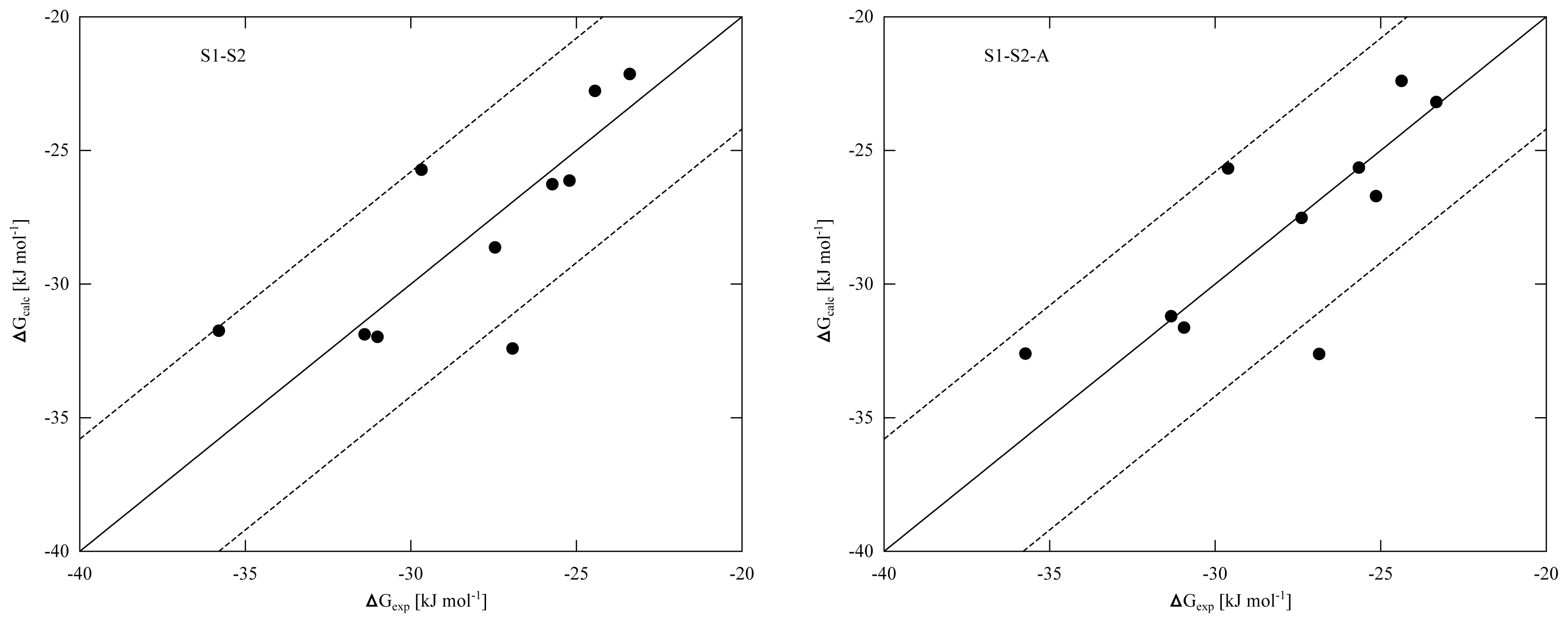
Equation 2) and the difference between models S1-S2 and S1-S2-A disappears. From the RMSEs of the S1-S2 and S1-S2-A models (
Tables 4 and
5) and the obtained correlation between calculated and experimental binding affinities (
Figure 2), we found similar performance in binding free energy prediction when using either one of the schemes, despite of the slight differences in calibrated
β values (
Tables 4 and
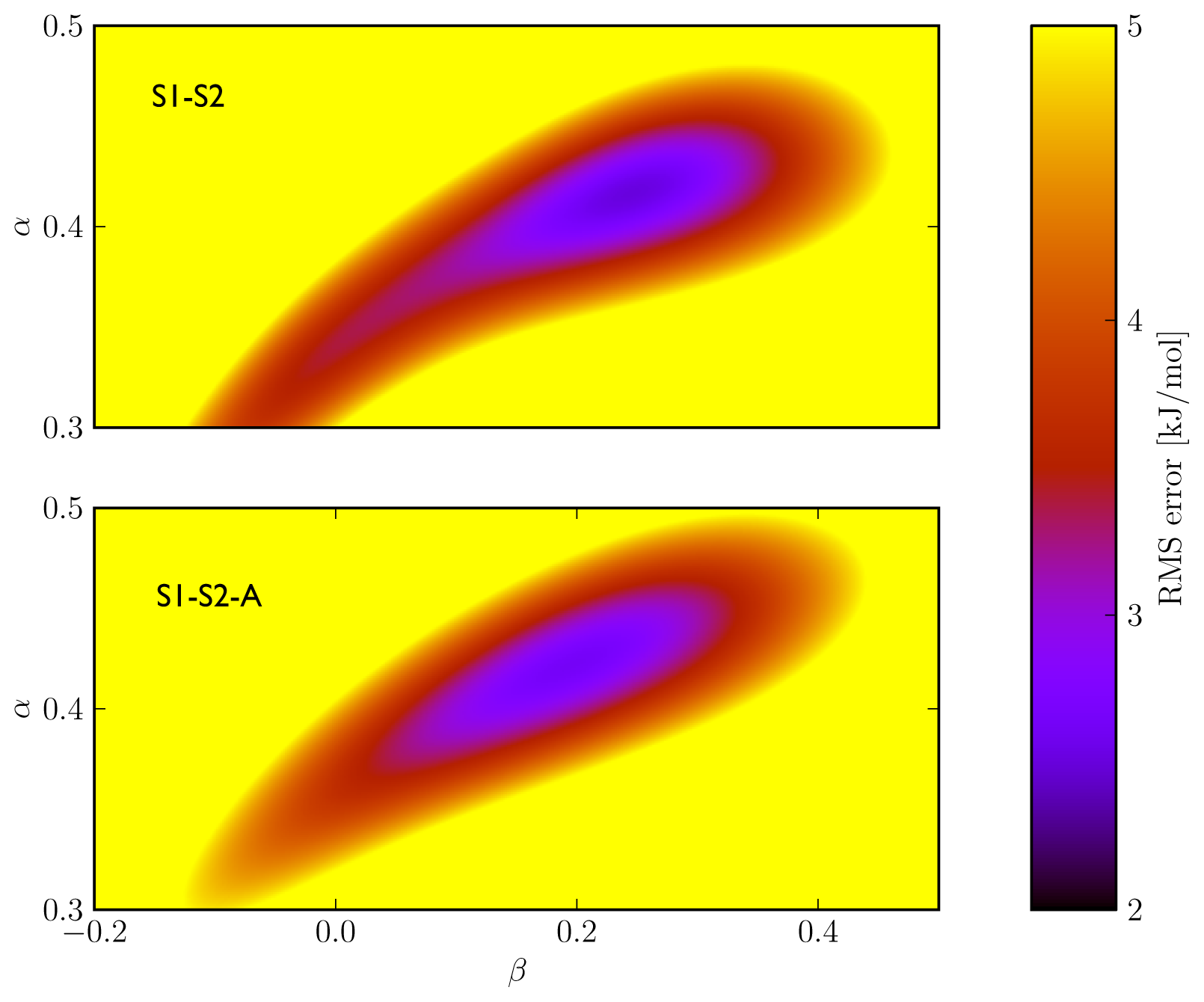
5). In addition, the S1–S2 and S1-S2-A sets demonstrate a similar profile in terms of the dependence of the model’s RMSE on the calibrated
α and
β values (
Figure 3), which also shows a larger sensitivity of the RMSE on the
α than on the
β parameter. This indicates a larger dependency of the predicted binding free energy on differences in (apolar) van der Waals interactions than on changes in electrostatic interactions between ligand and environment upon binding, in line with an earlier LIE model for CYP 1A2 as presented by Vasanthanathan
et al. [
25]. For CYP 1A2, Vasanthanathan found that the predictive accuracy of the free-energy models improved upon forcing
β to zero in
Equation (1) and introducing a constant
γ as additional off-set parameter. Here, we found for some of the models in
Tables 2–
5 a small decrease in RMSE when recalibrating our models using
α and
γ as fitting parameters (instead of
α and
β). For example, for the models in
Tables 2–
5 in which
β was found to adopt an unphysical (negative) value, RMSEs were found to decrease by 0.15 (M1/S1), 0.66 (P170/S2), 0.03 (P170/S1-S2) and 0.14 kJ mol
−1 (P170/S1-S2-A), respectively. However, when fitting a model with
α and
γ as parameters and using results from
all simulations, we found an increase in RMSE by 0.62 kJ mol
−1 (S1–S2) and 0.72 kJ mol
−1 (S1-S2-A) when compared to values in
Tables 4 and
5, indicating that the dependency of the binding free energy on electrostatic interactions should not be neglected in these cases.
When improving MD sampling by combining results from the S1 and S2 subsets of simulations using the S1–S2 scheme, the LIE model with lowest RMSE from experiment and lowest number of outliers (
1) was obtained when combining results from all simulations (
Table 4). Also when using the S1-S2-A scheme, the LIE model that includes results from all simulations shows a lower RMSE and fewer outliers than the models that were calibrated based on smaller sets of simulations. Only the S1-S2-A M2 model shows a slightly lower RMSE than the S1-S2-A ‘all’ model (by 0.26 kJ mol
−1,
Table 5), but when including simulations starting from the M1 poses as well, a
β value was obtained that is in turn slightly closer to the theoretical value of 0.5 [
9]. Moreover, when inspecting contributions from the sets of simulations included in the S1-S2 and S1-S2-A LIE models based on all MD runs (
Tables 6 and
7), significant contributions to the predicted free energies were not only obtained from simulations starting from the M2 pose, but also from those starting from M1 (with the latter even dominating for most of the ligands in case of S1-S2-A,
Table 7).
The finding that different thiourea binding orientations contribute to predicted CYP 2D6 binding affinities is in line with our earlier work [
17], in which significant contributions from multiple ligand-binding modes on the accuracy of predicting CYP 2C9 binding free energies were observed. To develop an accurate LIE model for CYP 2C9, it was found sufficient to combine results from different simulations using the same protein conformation to start MD from [
17]. Here we show that for the very flexible CYP 2D6 enzyme, predictions improve upon including simulations starting from different protein conformations, as illustrated in
Tables 4 and
5 by the decreased RMSE when comparing LIE models based on all simulations with the P70 and P170 models. It should be noted that especially for the S1-S2-A P70 model, this decrease in RMSE is relatively small (0.19 kJ mol
−1,
Table 5). On the other hand, when comparing the LIE models based on all simulations with the P170 models, improvement is also observed in terms of a significant increase in
β. In addition, both protein conformations contribute significantly to the predicted binding free energies (
Tables 6 and
7). These findings demonstrate the importance for the flexible Cytochrome P450 2D6 enzyme of including MD simulations starting from different protein-ligand conformations to obtain accurate binding affinities. Moreover, because sampling of protein-ligand conformational space is already partly accounted for by combining MD simulations starting from distinct configurations, relatively short MD simulations (1 ns) are sufficient to obtain RMSE errors well below 1 kcal mol
−1. In contrast, calculation of relative binding free energy differences between any pair of ligands by using rigorous free energy methods such as thermodynamic integration [
8] or free-energy perturbation [
7] would probably require a series of simulations on the nanosecond time scale for every perturbation of a given ligand into another one. In summary, the chosen approach does not only improve the predictive quality of the method, but also its computational attractability and efficiency. Because our approach relies on averaging over multiple independent simulations, its efficiency can be optimized by using implementations of MD software on massively parallel computing facilities that are available within e.g., the Folding@Home [
26] andWeNMR communities [
27]. An additional strength of the chosen approach is that
a priori, no knowledge is required of the dominant protein configuration. In a follow-up study [
23] we will show how our approach can be automated (e.g., for industrial application) by developing a LIE model for a different class of CYP 2D6 binders, for which pre-selection of possible ligand-binding modes (based on visual inspection of docked ligand poses) is not feasible.