Conformational Solvation Studies of LIGNOLs with Molecular Dynamics and Conductor-Like Screening Model
Abstract
:1. Introduction
2. Results and Discussion
2.1. Solvation Effects in Ab Initio Calculations
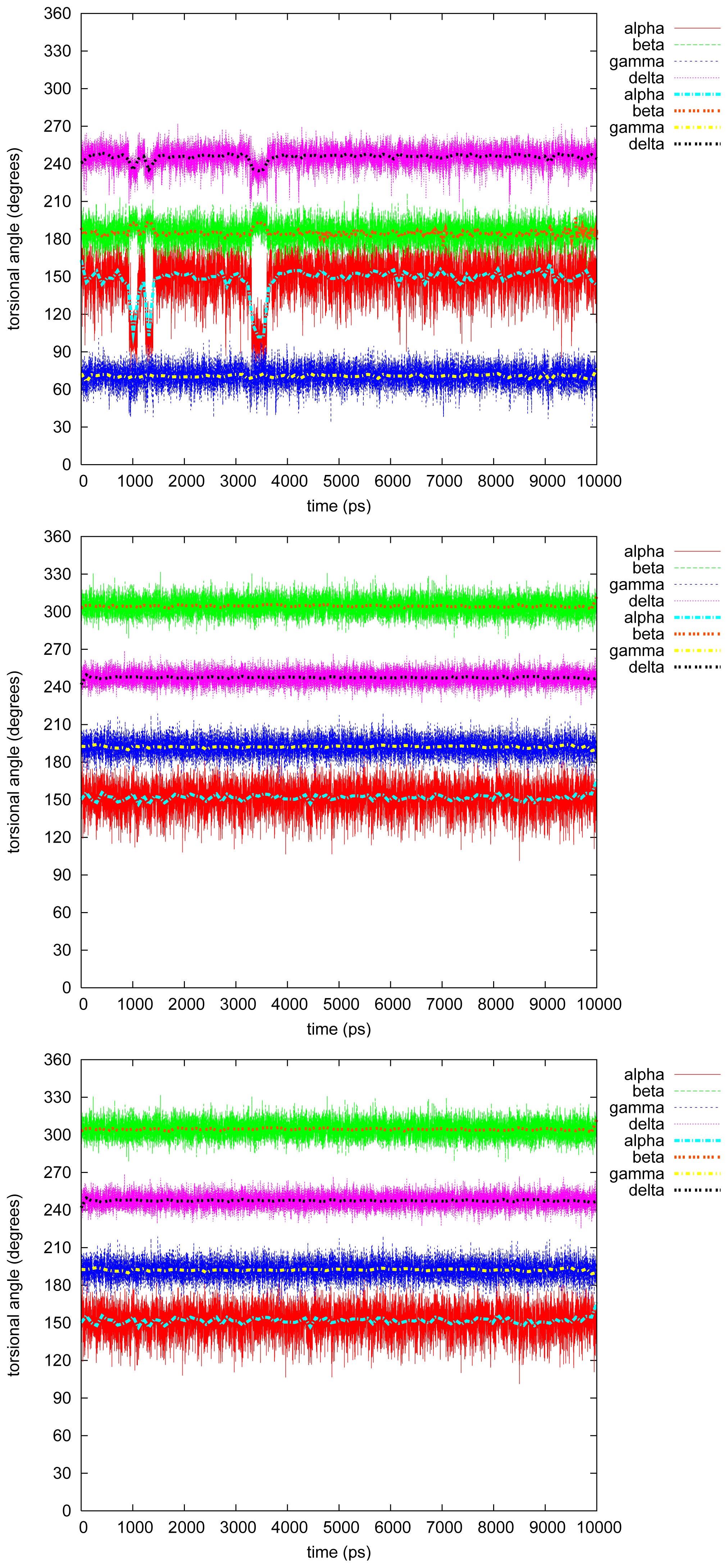
2.2. Molecular Dynamics
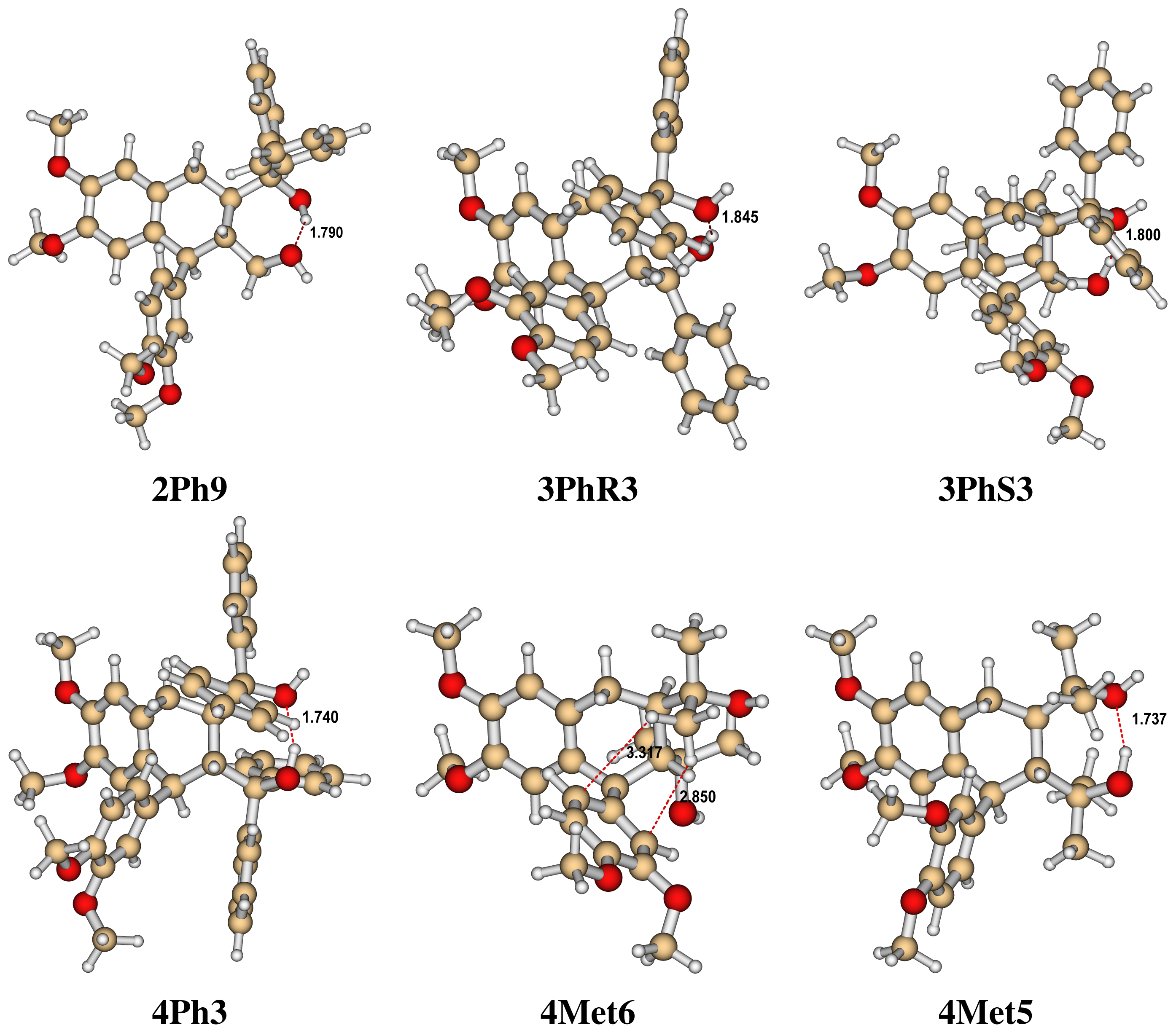
2.2.1. Diphenyl
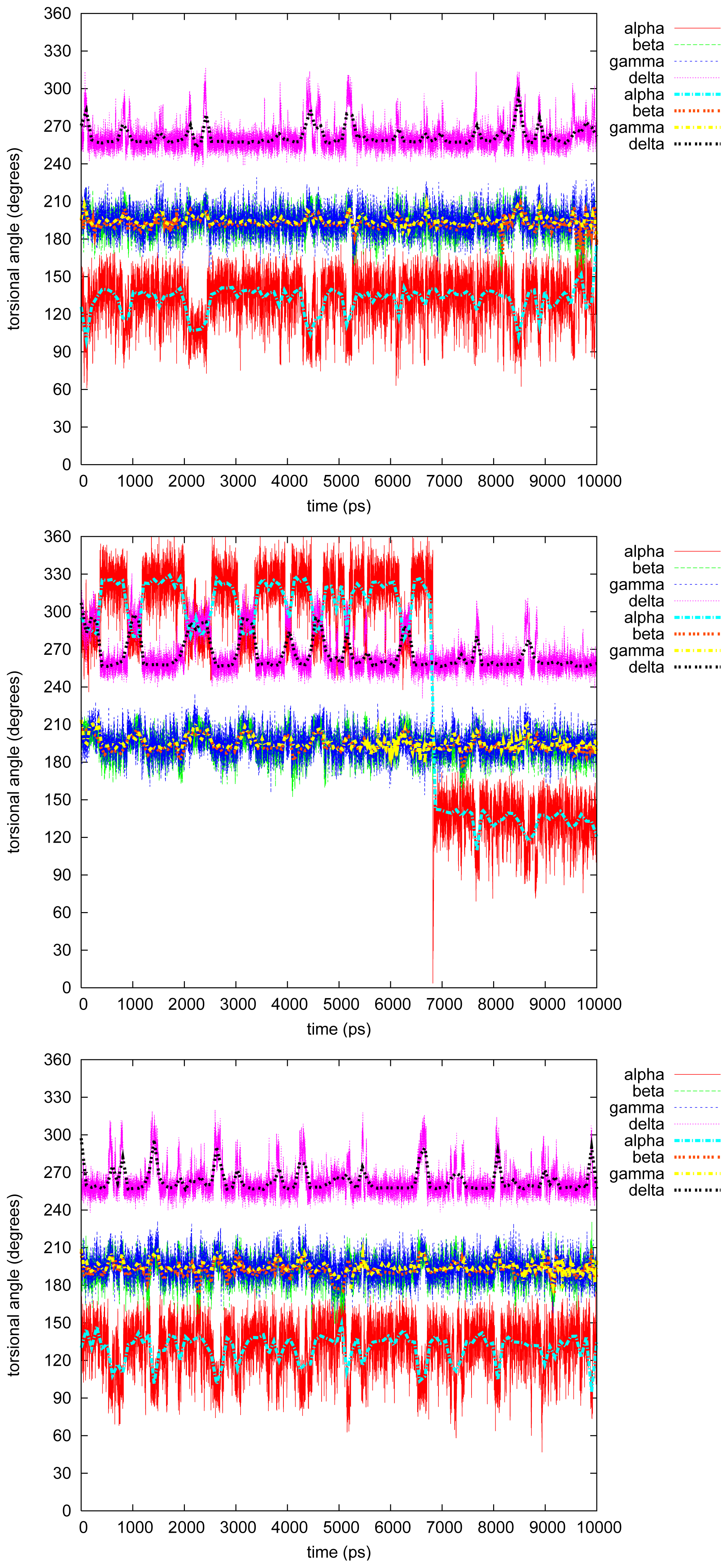
2.2.2. Triphenyl(R)
2.2.3. Triphenyl(S)
2.2.4. Tetramethyl
2.2.5. Tetraphenyl
2.2.6. Discussion on the Simulations
2.2.7. Hydration Effects
3. Computational Methods
4. Conclusions
- In MD simulations on the LIGNOLs, the conformations preferred were the energetically most favourable ones according to quantum chemical DFT calculations in gas phase, almost irrespective of the dipole moment.
- The four most relevant torsional angles α − δ, defined in Figure 2, varied during dynamics in accordance with their symmetry.
- The torsional angle δ was generally more preferred at the stabilizing value 255° than what was seen in the gas phase optimizations in [2].
- No strong correlation patterns were found, but in the last simulation of 2Ph9, α and δ changed simultaneously, while β either initialized a conformational change or lagged behind.
- In the hydration studies 2Ph1 and 2Ph2 were found to have strong hydrogen bonds from O9′, which could be very important for the application of these LIGNOLs as metal-binding agents.
- The hydration studies of the MD simulations show that several of these LIGNOLs, produced from a renewable source, have a great potential of acting as chiral catalysts.
Acknowledgments
References
- Willför, S.; Hemming, J.; Reunanen, M.; Eckerman, C.; Holmbom, B. Lignans and lipophilic extractives in Norway spruce knots and stemwood. Holzforschung 2003, 57, 27–36. [Google Scholar]
- Sandberg, T.; Brusentsev, Y.; Eklund, P.; Hotokka, M. Structural analysis of sterically hindered 1,4-diols from the naturally occurring lignan hydroxymatairesinol: A quantum chemical study. Int. J. Quantum Chem 2011, 111, 4309–4317. [Google Scholar]
- Seebach, D.; Weidmann, B.; Widler, L. Titanium and Zirconium Derivatives in Organic Synthesis. In Modern Synthetic Methods; Scheffold, R., Ed.; Salle+Sauerlnder: Aarau, Swizerland, 1983; Volume 3, pp. 217–353. [Google Scholar]
- Seebach, D.; Beck, A.K.; Schiess, M.; Widler, L.; Wonnacott, A. Some recent advances in the use of titanium reagents for organic synthesis. Pure Appl. Chem 1983, 55, 1807–1822. [Google Scholar]
- Brussee, J.; Jansen, A.C.A. A highly stereoselective synthesis of s(−)-[1,1’-binaphthalene]-2, 2’-diol. Tetrahedron Lett 1983, 24, 3261–3262. [Google Scholar]
- Taskinen, A.; Eklund, P.; Sjöholm, R.; Hotokka, M. The molecular structure and some properties of hydroxymatairesinol: An ab initio study. J. Mol. Struct 2004, 677, 113–124. [Google Scholar]
- Markus, H.; Plomp, A.J.; Sandberg, T.; Nieminen, V.; Bitter, J.H.; Murzin, D.Y. Dehydrogenation of hydroxymatairesinol to oxomatairesinol over carbon nanofibre-supported palladium catalysts. J. Mol. Cat. A 2007, 274, 42–49. [Google Scholar]
- Sandberg, T.; Hotokka, M. Conformational analysis of hydroxymatairesinol in aqueous solution with molecular dynamics. J. Comput. Chem 2009, 30, 2666–2673. [Google Scholar]
- Klamt, A.; Schüürmann, G. COSMO: A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans 1993, 2, 799–805. [Google Scholar]
- Klamt, A.; Jonas, V. Treatment of the outlying charge in continuum solvation models. J. Chem. Phys 1996, 105, 9972–9981. [Google Scholar]
- Miertus, S.; Scrocco, E.; Tomasi, J. Electrostatic interaction of a solute with a continuum: A direct utilization of ab initio molecular potentials for the prevision of solvent effects. Chem. Phys 1981, 55, 117–129. [Google Scholar]
- Tomasi, J.; Persico, M. Molecular interactions in solution: An overview of methods based on continuous distributions of the solvent. Chem. Rev 1994, 94, 2027–2094. [Google Scholar]
- Cammi, R.; Tomasi, J. Remarks on the use of the apparent surface charges (ASC) methods in solvation problems: Iterative versus matrix-inversion procedures and the renormalization of the apparent charges. J. Comput. Chem 1995, 16, 1449–1458. [Google Scholar]
- Ahlrichs, R.; Bär, M.; Häser, M.; Horn, H.; Kölmel, C. Electronic structure calculations on workstation computers: The program system turbomole. Chem. Phys. Lett 1989, 162, 165–169. [Google Scholar]
- Von Arnim, M.; Ahlrichs, R. Performance of parallel TURBOMOLE for density functional calculations. J. Comput. Chem 1998, 19, 1746–1757. [Google Scholar]
- Hehre, W.J.; Radom, L. Ab Initio Molecular Orbital Theory; John Wiley Sons: New York, NY, USA, 1986. [Google Scholar]
- Häser, M.; Ahlrichs, R. Improvements on the direct SCF method. J. Comput. Chem 1989, 10, 104–111. [Google Scholar]
- Schäfer, A.; Horn, H.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys 1992, 97, 2571–2577. [Google Scholar]
- Hehre, W.J.; Ditchfield, R.; Pople, J.A. Self-consistent molecular orbital methods. XII. Further extensions of gaussian-type basis sets for use in molecular orbital studies of organic molecules. J. Chem. Phys 1972, 56, 2257–2261. [Google Scholar]
- Hariharan, P.C.; Pople, J.A. The influence of polarization functions on molecular orbital hydrogenation energies. Theor. Chim. Acta 1973, 28, 213–222. [Google Scholar]
- Francl, M.M.; Pietro, W.J.; Hehre, W.J.; Binkley, J.S.; de Frees, D.J.; Pople, J.A.; Gordon, M.S. Self-consistent molecular orbital methods. XXIII. A polarization-type basis set for second-row elements. J. Chem. Phys 1982, 77, 3654–3665. [Google Scholar]
- Treutler, O.; Ahlrichs, R. Efficient molecular numerical integration schemes. J. Chem. Phys 1995, 102, 346. [Google Scholar]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar]
- Lee, C.; Yang, W.; Parr, R. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys 1993, 98, 5648–5652. [Google Scholar]
- Eichkorn, K.; Treutler, O.; Öhm, H.; Häser, M.; Ahlrichs, R. Auxiliary basis sets to approximate Coulomb potentials. Chem. Phys. Lett 1995, 242, 652–660. [Google Scholar]
- Eichkorn, K.; Weigend, F.; Treutler, O.; Ahlrichs, R. Auxiliary basis sets for main row atoms and transition metals and their use to approximate Coulomb potentials. Theor. Chem. Acc 1997, 97, 119–124. [Google Scholar]
- Sierka, M.; Hogekamp, A.; Ahlrichs, R. Fast evaluation of the Coulomb potential for electron densities using multipole accelerated resolution of identity approximation. J. Chem. Phys 2003, 18, 9136–9148. [Google Scholar]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys 1994, 100, 5829–5835. [Google Scholar]
- Bekker, H.; Berendsen, H.J.C.; Dijkstra, E.J.; Achterop, S.; van Drunen, R.; van der Spoel, D.; Sijbers, A.; Keegstra, H.; Reitsma, B.; Renardus, M.K.R. Gromacs: A Parallel Computer for Molecular Dynamics Simulations. In Physics Computing; Volume 92, de Groot, R.A., Nadrchal, J., Eds.; World Scientific: Singapore, 1993. [Google Scholar]
- Berendsen, H.J.C.; van der Spoel, D.; van Drunen, R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun 1995, 91, 43–56. [Google Scholar]
- Lindahl, E.; Hess, B.; van der Spoel, D. Gromacs 3.0: A package for molecular simulation and trajectory analysis. J. Mol. Mod 2001, 7, 306–317. [Google Scholar]
- Van der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, flexible and free. J. Comput. Chem 2005, 26, 1701–1718. [Google Scholar]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput 2008, 4, 435–447. [Google Scholar]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys 1983, 79, 926–935. [Google Scholar]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc 1996, 118, 11225–11236. [Google Scholar]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys 1984, 81, 3684–3690. [Google Scholar]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N-log(N) method for Ewald sums in large systems. J. Chem. Phys 1993, 98, 10089–10092. [Google Scholar]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh ewald potential. J. Chem. Phys 1995, 103, 8577–8593. [Google Scholar]




| Conformation | EHF [2] | EDFT [2] | ECOS,HF | ECOS,DFT |
|---|---|---|---|---|
| 2Ph1 | 6.1 | 7.3 | 5.7 | 9.4 |
| 2Ph2 | 5.2 | 6.7 | 4.2 | 8.1 |
| 2Ph9 | 0 | 0 | 0 | 0 |
| 3PhR3 | 21.2 | 0 | 0 | 0 |
| 3PhR4 | 20.5 | 24.5 | 28.6 | 22.5 |
| 3PhR5 | 27.8 | 36.1 | 46.2 | 44.5 |
| 3PhS3 | 35.5 | 11.6 | 22.0 | 12.7 |
| 3PhS7 | 19.6 | 11.7 | 25.2 | 12.6 |
| 3PhS10 | 0 | 12.1 | 15.9 | 17.3 |
| 4Met2 | 8.9 | 4.5 | 4.7 | 7.6 |
| 4Met3 | 0 | 4.2 | 0 | 9.2 |
| 4Met6 | 39.9 | 0 | 27.9 | 0 |
| 4Ph3 | 0 | 0 | 0 | 0 |
| 4Ph4 | 2.0 | 2.0 | 1.7 | 3.9 |
| 4Ph8 | 0.9 | 1.5 | 0.9 | 2.9 |
| Conformation | μHF | μDFT | μCOS,HF | μCOS,DFT |
|---|---|---|---|---|
| 2Ph1 | 2.19 | 2.11 | 3.88 | 4.07 |
| 2Ph2 | 1.93 | 1.56 | 3.36 | 3.38 |
| 2Ph9 | 1.79 | 2.48 | 1.87 | 2.54 |
| 3PhR3 | 6.54 | 4.40 | 6.08 | 6.44 |
| 3PhR4 | 3.46 | 3.92 | 4.22 | 5.22 |
| 3PhR5 | 2.80 | 2.09 | 3.85 | 3.77 |
| 3PhS3 | 6.61 | 6.71 | 9.29 | 9.51 |
| 3PhS7 | 6.64 | 6.67 | 8.90 | 9.50 |
| 3PhS10 | 2.22 | 2.07 | 3.57 | 3.72 |
| 4Met2 | 2.03 | 2.27 | 2.50 | 3.42 |
| 4Met3 | 1.90 | 2.09 | 3.04 | 3.55 |
| 4Met6 | 5.33 | 3.34 | 7.48 | 5.48 |
| 4Ph3 | 6.45 | 6.50 | 8.40 | 9.35 |
| 4Ph4 | 3.91 | 3.85 | 5.73 | 6.24 |
| 4Ph8 | 3.48 | 3.13 | 4.24 | 4.12 |
| Conformation | Method | α | β | γ | δ |
|---|---|---|---|---|---|
| 2Ph1 | HF | 115.9° | 49.6° | 78.3° | 314.5° |
| DFT | 115.6° | 49.5° | 78.3° | 313.5° | |
| 2Ph2 | HF | 294.9° | 48.8° | 78.2° | 315.0° |
| DFT | 294.2° | 49.7° | 78.1° | 314.4° | |
| 2Ph9 | HF | 117.1° | 198.3° | 194.8° | 311.8° |
| DFT | 117.3° | 196.7° | 195.3° | 310.8° | |
| 3PhR3 | HF | 90.0° | 190.4° | 198.8° | 285.0° |
| DFT | 348.8° | 160.3° | 180.2° | 256.8° | |
| 3PhR4 | HF | 280.5° | 190.8° | 200.3° | 285.8° |
| DFT | 270.9° | 196.3° | 198.3° | 280.9° | |
| 3PhR5 | HF | 103.5° | 206.4° | 301.1° | 302.4° |
| DFT | 101.0° | 209.8° | 303.5° | 297.9° | |
| 3PhS3 | HF | 116.7° | 224.4° | 143.9° | 305.1° |
| DFT | 170.8° | 216.4° | 185.3° | 267.6° | |
| 3PhS7 | HF | 128.6° | 208.1° | 198.8° | 299.6° |
| DFT | 171.4° | 215.6° | 186.2° | 268.3° | |
| 3PhS10 | HF | 344.0° | 64.8° | 293.3° | 260.9° |
| DFT | 344.4° | 64.5° | 292.2° | 260.5° | |
| 4Met2 | HF | 166.0° | 177.9° | 66.6° | 247.1° |
| DFT | 167.8° | 180.6° | 65.1° | 245.7° | |
| 4Met3 | HF | 163.8° | 305.8° | 187.7° | 248.2° |
| DFT | 165.6° | 307.8° | 187.3° | 247.0° | |
| 4Met6 | HF | 117.6° | 326.2° | 196.8° | 294.9° |
| DFT | 166.3° | 307.1° | 187.6° | 247.0° | |
| 4Ph3 | HF | 87.7° | 204.3° | 193.2° | 289.0° |
| DFT | 84.0° | 208.6° | 190.2° | 283.3° | |
| 4Ph4 | HF | 280.2° | 203.3° | 196.5° | 289.2° |
| DFT | 280.4° | 205.4° | 196.3° | 286.0° | |
| 4Ph8 | HF | 275.3° | 203.3° | 195.1° | 290.0° |
| DFT | 273.8° | 205.1° | 194.8° | 287.1° |
| Conformation | numO9 | numO9′ | numTot | lifeO9 | lifeO9′ | lifeTot |
|---|---|---|---|---|---|---|
| 2Ph1 | 1.24 | 0.98 | 6.23 | 3.35 | 6.18 | 1.16 |
| 2Ph2 | 1.23 | 0.98 | 6.26 | 3.26 | 5.82 | 1.15 |
| 2Ph9 | 1.41 | 0.80 | 6.08 | 2.29 | 2.24 | 1.06 |
| 3PhR3 | 1.16 | 0.71 | 5.54 | 2.03 | 1.67 | 0.97 |
| 3PhR4 | 1.11 | 0.78 | 5.53 | 1.97 | 1.72 | 0.98 |
| 3PhR5 | 1.27 | 1.15 | 6.08 | 2.88 | 3.15 | 1.11 |
| 3PhS3 | 1.25 | 0.65 | 5.58 | 2.08 | 1.58 | 0.99 |
| 3PhS7 | 1.12 | 0.80 | 5.60 | 1.96 | 1.78 | 0.98 |
| 3PhS10 | 1.10 | 1.14 | 6.51 | 3.53 | 3.35 | 1.19 |
| 4Met2 | 1.20 | 1.33 | 6.35 | 3.95 | 3.63 | 1.18 |
| 4Met3 | 1.37 | 1.24 | 7.05 | 3.57 | 3.83 | 1.27 |
| 4Met6 | 1.37 | 1.24 | 7.04 | 3.56 | 3.86 | 1.28 |
| 4Ph3 | 0.62 | 1.05 | 5.31 | 1.57 | 2.07 | 0.95 |
| 4Ph4 | 0.68 | 0.95 | 5.23 | 1.82 | 2.00 | 0.96 |
| 4Ph8 | 0.79 | 0.85 | 5.26 | 1.88 | 1.77 | 0.94 |
© 2012 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sandberg, T.; Eklund, P.; Hotokka, M. Conformational Solvation Studies of LIGNOLs with Molecular Dynamics and Conductor-Like Screening Model. Int. J. Mol. Sci. 2012, 13, 9845-9863. https://doi.org/10.3390/ijms13089845
Sandberg T, Eklund P, Hotokka M. Conformational Solvation Studies of LIGNOLs with Molecular Dynamics and Conductor-Like Screening Model. International Journal of Molecular Sciences. 2012; 13(8):9845-9863. https://doi.org/10.3390/ijms13089845
Chicago/Turabian StyleSandberg, Thomas, Patrik Eklund, and Matti Hotokka. 2012. "Conformational Solvation Studies of LIGNOLs with Molecular Dynamics and Conductor-Like Screening Model" International Journal of Molecular Sciences 13, no. 8: 9845-9863. https://doi.org/10.3390/ijms13089845




