Organic Solar Cells: Understanding the Role of Förster Resonance Energy Transfer
Abstract
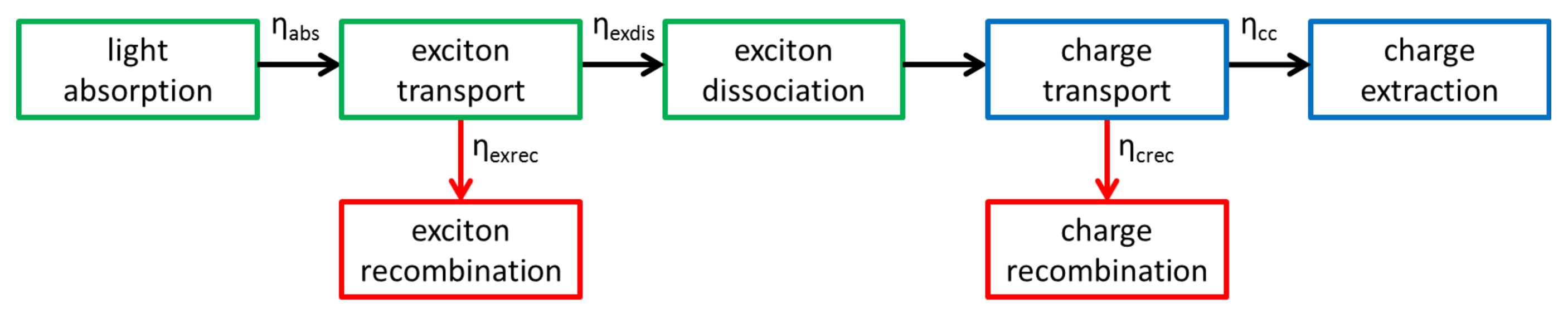
:1. Introduction
1.1. Light Absorption
1.2. Exciton Transport
1.3. Exciton Dissociation
1.4. Charge Transport
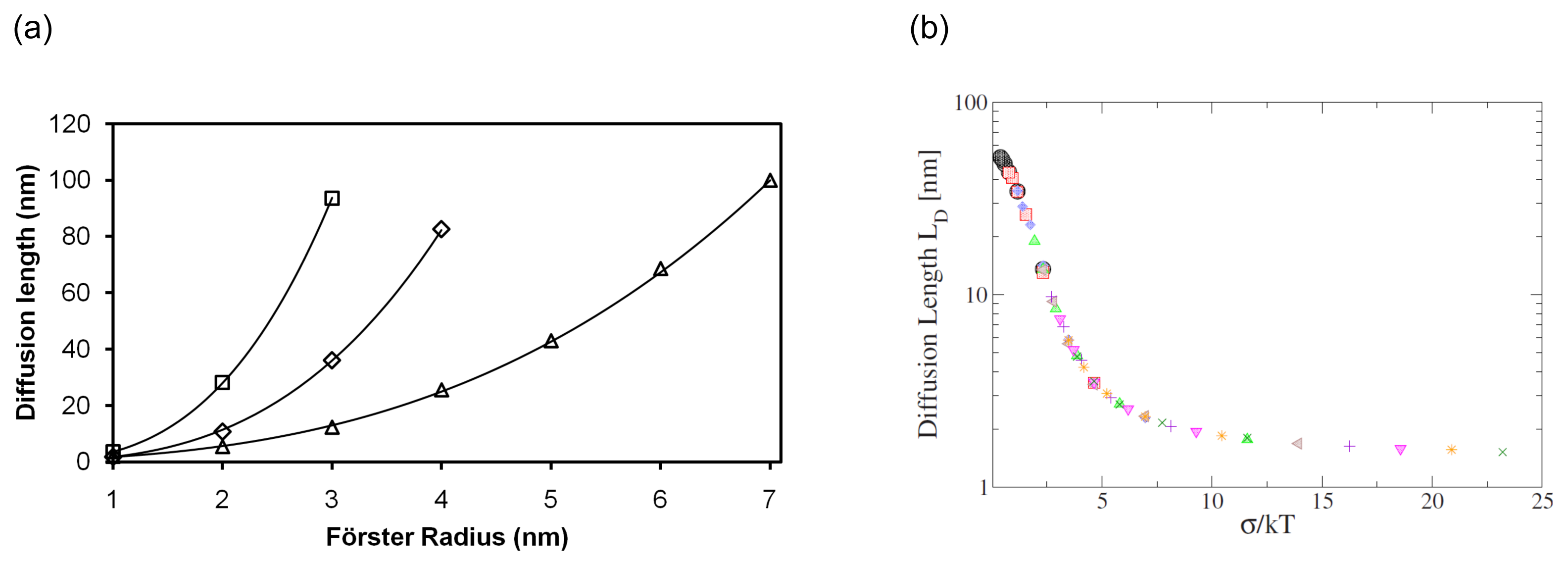
2. Exciton Transport
3. Exciton Harvesting
4. Exciton Dissociation
5. Charge Transfer States and Charge Transport
6. Energy Cascade
7. Charge Extraction
- extraction of charges at the opposite polarity electrode (reverse diffusive recombination)
- recombination of charges through defects (e.g., metal penetration into active layer) or impurity states
- formation of an energy barrier due to energy level mismatch of HOMO/LUMO and anode/cathode
- formation of an energy barrier due to electrode corrosion or other degradation effects
- exciton quenching
8. Conclusions
Acknowledgments
References
- Mishra, A.; Bäuerle, P. Small molecule organic semiconductors on the move: Promises for future solar energy technology. Angew. Chem. Int. Ed 2012, 51, 2020–2067. [Google Scholar]
- Green, M.A.; Emery, K.; Hishikawa, Y.; Warta, W.; Dunlop, E.D. Solar cell efficiency tables (version 39). Prog. Photovoltaics Res. Appl 2012, 20, 12–20. [Google Scholar]
- National Renewable Energy Laboratory. Best Research-Cell Efficiencies. Available online: http://www.nrel.gov/ncpv/images/efficiencychart.jpg accessed on 11 December 2012.
- Li, Y. Molecular design of photovoltaic materials for polymer solar cells: Toward suitable electronic energy levels and broad absorption. Acc. Chem. Res 2012, 45, 723–733. [Google Scholar]
- Li, G.; Zhu, R.; Yang, Y. Polymer solar cells. Nat. Photonics 2012, 6, 153–161. [Google Scholar]
- Deibel, C.; Dyakonov, V. Polymer-fullerene bulk heterojunction solar cells. Rep. Prog. Phys 2010, 73, 096401. [Google Scholar]
- Gregg, B.A.; Hanna, M.C. Comparing organic to inorganic photovoltaic cells: Theory, experiment, and simulation. J. Appl. Phys 2003, 93, 3605–3614. [Google Scholar]
- Günes, S.; Neugebauer, H.; Sariciftci, N.S. Conjugated polymer-based organic solar cells. Chem. Rev 2007, 107, 1324–1338. [Google Scholar]
- Borchert, H. Elementary processes and limiting factors in hybrid polymer/nanoparticle solar cells. Energy Environ. Sci 2010, 3, 1682–1694. [Google Scholar]
- Spanggaard, H.; Krebs, F.C. A brief history of the development of organic and polymeric photovoltaics. Sol. Energy Mater. Sol. Cells 2004, 83, 125–146. [Google Scholar]
- Ameri, T.; Dennler, G.; Lungenschmied, C.; Brabec, C.J. Organic tandem solar cells: A review. Energy Environ. Sci 2009, 2, 347–363. [Google Scholar]
- Kersting, R.; Lemmer, U.; Mahrt, R.F.; Leo, K.; Kurz, H.; Bässler, H.; Göbel, E.O. Femtosecond energy relaxation in π-conjugated polymers. Phys. Rev. Lett 1993, 70, 3820–3823. [Google Scholar]
- Scheidler, M.; Lemmer, U.; Kersting, R.; Karg, S.; Riess, W.; Cleve, B.; Mahrt, R.F.; Kurz, H.; Bässler, H.; Göbel, E.O.; et al. Monte Carlo study of picosecond exciton relaxation and dissociation in poly (phenylenevinylene). Phys. Rev. B 1996, 54, 5536–5544. [Google Scholar]
- Gupta, A.; Ali, A.; Bilic, A.; Gao, M.; Hegedus, K.; Singh, B.; Watkins, S.E.; Wilson, G.J.; Bach, U.; Evans, R.A. Absorption enhancement of oligothiophene dyes through the use of a cyanopyridone acceptor group in solution-processed organic solar cells. Chem. Commun 2012, 48, 1889–1891. [Google Scholar]
- Winder, C.; Sariciftci, N.S. Low bandgap polymers for photon harvesting in bulk heterojunction solar cells. J. Mater. Chem 2004, 14, 1077–1086. [Google Scholar]
- Blom, P.W.M.; Mihailetchi, V.D.; Koster, L.J.A.; Markov, D.E. Device physics of polymer: Fullerene bulk heterojunction solar cells. Adv. Mater 2007, 19, 1551–1566. [Google Scholar]
- Bian, L.; Zhu, E.; Tang, J.; Tang, W.; Zhang, F. Recent progress in the design of narrow bandgap conjugated polymers for high-efficiency organic solar cells. Prog. Polym. Sci 2012, 37, 1292–1331. [Google Scholar]
- Kroon, R.; Lenes, M.; Hummelen, J.C.; Blom, P.W.M.; de Boer, B. Small bandgap polymers for organic solar cells (polymer material development in the last 5 years). Polym. Rev 2008, 48, 531–582. [Google Scholar]
- Mikhnenko, O.V.; Azimi, H.; Scharber, M.; Morana, M.; Blom, P.W.M.; Loi, M.A. Exciton diffusion length in narrow bandgap polymers. Energy Environ. Sci 2012, 5, 6960–6965. [Google Scholar]
- Lunt, R.R.; Giebink, N.C.; Belak, A.A.; Benziger, J.B.; Forrest, S.R. Exciton diffusion lengths of organic semiconductor thin films measured by spectrally resolved photoluminescence quenching. J. Appl. Phys 2009, 105, 053711. [Google Scholar]
- Peumans, P.; Yakimov, A.; Forrest, S.R. Small molecular weight organic thin-film photodetectors and solar cells. J. Appl. Phys 2003, 93, 3693–3723. [Google Scholar]
- Scully, S.R.; McGehee, M.D. Effects of optical interference and energy transfer on exciton diffusion length measurements in organic semiconductors. J. Appl. Phys 2006, 100, 034907. [Google Scholar]
- Zhou, Y.C.; Wu, Y.; Ma, L.L.; Zhou, J.; Ding, X.M.; Hou, X.Y. Exciton migration in organic thin films. J. Appl. Phys 2006, 100, 023712. [Google Scholar]
- Feron, K.; Zhou, X.; Belcher, W.J.; Dastoor, P.C. Exciton transport in organic semiconductors: Förster resonance energy transfer compared with a simple random walk. J. Appl. Phys 2012, 111, 044510. [Google Scholar]
- Ray, B.; Alam, M.A. Random vs. regularized OPV: Limits of performance gain of organic bulk heterojunction solar cells by morphology engineering. Sol. Energy Mater. Sol. Cells 2012, 99, 204–212. [Google Scholar]
- Gregg, B.A. The photoconversion mechanism of excitonic solar cells. MRS Bull 2005, 30, 20–22. [Google Scholar]
- Im, C.; Emelianova, E.V.; Bässler, H.; Spreitzer, H.; Becker, H. Intrinsic and extrinsic charge carrier photogeneration in phenyl-substituted polyphenylenevinylene-trinitrofluorenone blend systems. J. Chem. Phys 2002, 117, 2961–2967. [Google Scholar]
- Yu, G.; Heeger, A.J. Charge separation and photovoltaic conversion in polymer composites with internal donor/acceptor heterojunctions. J. Appl. Phys 1995, 78, 4510–4515. [Google Scholar]
- McNeill, C.R. Morphology of all-polymer solar cells. Energy Environ. Sci 2012, 5, 5653–5667. [Google Scholar]
- Braun, C.L. Electric field assisted dissociation of charge transfer states as a mechanism of photocarrier production. J. Chem. Phys 1984, 80, 4157–4161. [Google Scholar]
- Clarke, T.M.; Durrant, J.R. Charge photogeneration in organic solar cells. Chem. Rev 2010, 110, 6736–6767. [Google Scholar]
- Imahori, H.; Guldi, D.M.; Tamaki, K.; Yoshida, Y.; Luo, C.; Sakata, Y.; Fukuzumi, S. Charge separation in a novel artificial photosynthetic reaction center lives 380 ms. J. Am. Chem. Soc 2001, 123, 6617–6628. [Google Scholar]
- Loi, M.A.; Toffanin, S.; Muccini, M.; Forster, M.; Scherf, U.; Scharber, M. Charge transfer excitons in bulk heterojunctions of a polyfluorene copolymer and a fullerene derivative. Adv. Funct. Mater 2007, 17, 2111–2116. [Google Scholar]
- Morteani, A.C.; Sreearunothai, P.; Herz, L.M.; Friend, R.H.; Silva, C. Exciton regeneration at polymeric semiconductor heterojunctions. Phys. Rev. Lett 2004, 92, 247402. [Google Scholar]
- Ohkita, H.; Cook, S.; Astuti, Y.; Duffy, W.; Tierney, S.; Zhang, W.; Heeney, M.; McCulloch, I.; Nelson, J.; Bradley, D.D.C.; et al. Charge carrier formation in polythiophene/fullerene blend films studied by transient absorption spectroscopy. J. Am. Chem. Soc 2008, 130, 3030–3042. [Google Scholar]
- Servaites, J.D.; Savoie, B.M.; Brink, J.B.; Marks, T.J.; Ratner, M.A. Modeling geminate pair dissociation in organic solar cells: High power conversion efficiencies achieved with moderate optical bandgaps. Energy Environ. Sci 2012, 5, 8343. [Google Scholar]
- Tvingstedt, K.; Vandewal, K.; Gadisa, A.; Zhang, F.; Manca, J.; Inganäs, O. Electroluminescence from charge transfer states in polymer solar cells. J. Am. Chem. Soc 2009, 131, 11819–11824. [Google Scholar]
- Onsager, L. Initial Recombination of Ions. Phys. Rev 1938, 54, 554–557. [Google Scholar]
- Krebs, F.C. Fabrication and processing of polymer solar cells: A review of printing and coating techniques. Sol. Energy Mater. Sol. Cells 2009, 93, 394–412. [Google Scholar]
- Dennler, G.; Scharber, M.C.; Brabec, C.J. Polymer-Fullerene Bulk-Heterojunction Solar Cells. Adv. Mater 2009, 21, 1323–1338. [Google Scholar]
- Rasmussen, S.C.; Schwiderski, R.L.; Mulholland, M.E. Thieno[3,4-b]pyrazines and their applications to low band gap organic materials. Chem. Commun 2011, 47, 11394–11410. [Google Scholar]
- Jørgensen, M.; Norrman, K.; Gevorgyan, S.A.; Tromholt, T.; Andreasen, B.; Krebs, F.C. Stability of polymer solar cells. Adv. Mater 2012, 24, 580–612. [Google Scholar]
- Shao, Y.; Yang, Y. Efficient organic heterojunction photovoltaic cells based on triplet materials. Adv. Mater 2005, 17, 2841–2844. [Google Scholar]
- Förster, T. Zwischenmolekulare energiewanderung und fluoreszenz. Ann. Phys 1948, 437, 55–75. [Google Scholar]
- Beljonne, D.; Curutchet, C.; Scholes, G.D.; Silbey, R.J. Beyond Förster resonance energy transfer in biological and nanoscale systems. J. Phys. Chem. B 2009, 113, 6583–6599. [Google Scholar]
- Westenhoff, S.; Daniel, C.; Friend, R.H.; Silva, C.; Sundström, V.; Yartsev, A. Exciton migration in a polythiophene: Probing the spatial and energy domain by line-dipole Forster-type energy transfer. J. Chem. Phys 2005, 122, 094903. [Google Scholar]
- Barford, W. Beyond Förster resonance energy transfer in linear nanoscale systems. J. Phys. Chem. A 2010, 114, 11842–11843. [Google Scholar]
- Krueger, B.P.; Scholes, G.D.; Fleming, G.R. Calculation of couplings and energy-transfer pathways between the pigments of LH2 by the ab initio transition density cube method. J. Phys. Chem. B 1998, 102, 5378–5386. [Google Scholar]
- Chang, J.C. Monopole effects on electronic excitation interactions between large molecules. I. Application to energy transfer in chlorophylls. J. Chem. Phys 1977, 67, 3901–3909. [Google Scholar]
- Hennebicq, E.; Pourtois, G.; Scholes, G.D.; Herz, L.M.; Russell, D.M.; Silva, C.; Setayesh, S.; Grimsdale, A.C.; Müllen, K.; Brédas, J.L.; et al. Exciton migration in rigid-rod conjugated polymers: An improved Förster model. J. Am. Chem. Soc 2005, 127, 4744–4762. [Google Scholar]
- Bacchiocchi, C.; Zannoni, C. Directional energy transfer in columnar liquid crystals: A computer-simulation study. Phys. Rev. E 1998, 58, 3237–3244. [Google Scholar]
- Fedchenia, I.; Westlund, P.O. Influence of molecular reorientation on electronic energy transfer between a pair of mobile chromophores: The stochastic Liouville equation combined with Brownian dynamic simulation techniques. Phys. Rev. E 1994, 50, 555–565. [Google Scholar]
- Fredrickson, G.H. Concentration depolarization of fluorescence in the presence of molecular rotation. J. Chem. Phys 1988, 88, 5291–5299. [Google Scholar]
- Jang, S.; Jung, Y.; Silbey, R.J. Nonequilibrium generalization of Förster-dexter theory for excitation energy transfer. Chem. Phys 2002, 275, 319–332. [Google Scholar]
- Gaab, K.M.; Bardeen, C.J. Wavelength and temperature dependence of the femtosecond pump-probe anisotropies in the conjugated polymer MEH-PPV: Implications for energy-transfer dynamics. J. Phys. Chem. B 2004, 108, 4619–4626. [Google Scholar]
- Fennel, F.; Lochbrunner, S. Förster-mediated spectral diffusion in disordered organic materials. Phys. Rev. B 2012, 85, 94203. [Google Scholar]
- Ullah, M.; Fishchuk, I.I.; Kadashchuk, A.; Stadler, P.; Pivrikas, A.; Simbrunner, C.; Poroshin, V.N.; Sariciftci, N.S.; Sitter, H. Dependence of MeyerCNeldel energy on energetic disorder in organic field effect transistors. Appl. Phys. Lett 2010, 96, 213306. [Google Scholar]
- Rauscher, U.; Bässler, H.; Bradley, D.D.C.; Hennecke, M. Exciton versus band description of the absorption and luminescence spectra in poly(p-phenylenevinylene). Phys. Rev. B 1990, 42, 9830–9836. [Google Scholar]
- Papadopoulos, T.A.; Muccioli, L.; Athanasopoulos, S.; Walker, A.B.; Zannoni, C.; Beljonne, D. Does supramolecular ordering influence exciton transport in conjugated systems? Insight from atomistic simulations. Chem. Sci 2011, 2, 1025–1032. [Google Scholar] [Green Version]
- Madigan, C.; Bulović, V. Modeling of exciton diffusion in amorphous organic thin films. Phys. Rev. Lett 2006, 96, 046404. [Google Scholar]
- Colby, K.A.; Burdett, J.J.; Frisbee, R.F.; Zhu, L.; Dillon, R.J.; Bardeen, C.J. Electronic energy migration on different time scales: Concentration dependence of the time-resolved anisotropy and fluorescence quenching of Lumogen Red in poly(methyl methacrylate). J. Phys. Chem. A 2010, 114, 3471–3482. [Google Scholar]
- Athanasopoulos, S.; Emelianova, E.V.; Walker, A.B.; Beljonne, D. Exciton diffusion in energetically disordered organic materials. Phys. Rev. B 2009, 80, 195209. [Google Scholar]
- Herz, L.M.; Silva, C.; Grimsdale, A.C.; Müllen, K.; Phillips, R.T. Time-dependent energy transfer rates in a conjugated polymer guest-host system. Phys. Rev. B 2004, 70, 165207. [Google Scholar]
- Faulques, E.; Ivanov, V.G.; Jonusauskas, G.; Athalin, H.; Pyshkin, O.; Wéry, J.; Massuyeau, F.; Lefrant, S. Ultrafast photoluminescence spectroscopy of exciton-exciton annihilation in oligoaniline films with nanoscale ordering. Phys. Rev. B 2006, 74, 075202. [Google Scholar]
- Ahn, T.S.; Wright, N.; Bardeen, C.J. The effects of orientational and energetic disorder on Forster energy migration along a one-dimensional lattice. Chem. Phys. Lett 2007, 446, 43–48. [Google Scholar]
- Kalinowski, J.; Stampor, W.; Di Marco, P.; Garnier, F. Photogeneration of charge in solid films of α-sexithiophene. Chem. Phys 1998, 237, 233–243. [Google Scholar]
- Mikhnenko, O.V.; Ruiter, R.; Blom, P.W.M.; Loi, M.A. Direct measurement of the triplet exciton diffusion length in organic semiconductors. Phys. Rev. Lett 2012, 108, 137401. [Google Scholar]
- Bacchiocchi, C.; Zannoni, C. Energy transfer in condensed systems: The effect of phase organization. Chem. Phys. Lett 1997, 268, 541–548. [Google Scholar]
- Mikhnenko, O.V.; Lin, J.; Shu, Y.; Anthony, J.E.; Blom, P.W.M.; Nguyen, T.Q.; Loi, M.A. Effect of thermal annealing on exciton diffusion in a diketopyrrolopyrrole derivative. PCCP 2012, 14, 14196–14201. [Google Scholar]
- Mani, A.; Schoonman, J.; Goossens, A. Photoluminescence study of sexithiophene thin films. J. Phys. Chem. B 2005, 109, 4829–4836. [Google Scholar]
- Lakowicz, J. Principles of Fluorescence Spectroscopy, 3rd ed; Plenum Press: New York, NY, USA, 1983; p. 258. [Google Scholar]
- Allegra, M.; Giorda, P. Topology and energy transport in networks of interacting photosynthetic complexes. Phys. Rev. E 2012, 85, 051917. [Google Scholar]
- Müller, J.G.; Atas, E.; Tan, C.; Schanze, K.S.; Kleiman, V.D. The role of exciton hopping and direct energy transfer in the efficient quenching of conjugated polyelectrolytes. J. Am. Chem. Soc 2006, 128, 4007–4016. [Google Scholar]
- Soos, Z.G.; Powell, R.C. Generalized random-walk model for singlet-exciton energy transfer. Phys. Rev. B 1972, 6, 4035–4046. [Google Scholar]
- Liu, Y.X.; Summers, M.A.; Scully, S.R.; McGehee, M.D. Resonance energy transfer from organic chromophores to fullerene molecules. J. Appl. Phys 2006, 99, 093521. [Google Scholar]
- Liu, Y.; Summers, M.A.; Edder, C.; Fréchet, J.M.J.; McGehee, M.D. Using resonance energy transfer to improve exciton harvesting in organic-inorganic hybrid photovoltaic cells. Adv. Mater 2005, 17, 2960–2964. [Google Scholar]
- Luhman, W.A.; Holmes, R.J. Investigation of energy transfer in organic photovoltaic cells and impact on exciton diffusion length measurements. Adv. Funct. Mater 2011, 21, 764–771. [Google Scholar]
- Gong, X.; Lim, S.H.; Ostrowski, J.C.; Moses, D.; Bardeen, C.J.; Bazan, G.C. Phosphorescence from iridium complexes doped into polymer blends. J. Appl. Phys 2004, 95, 948–953. [Google Scholar]
- Cook, S.; Katoh, R.; Furube, A. Ultrafast studies of charge generation in PCBM:P3HT blend films following excitation of the fullerene PCBM. J. Phys. Chem. C 2009, 113, 2547–2552. [Google Scholar]
- Horowitz, G.; Valat, P.; Garnier, F.; Kouki, F.; Wintgens, V. Photoinduced spontaneous and stimulated emission in sexithiophene single crystals. Opt. Mater 1998, 9, 46–52. [Google Scholar]
- Shaw, P.E.; Ruseckas, A.; Samuel, I.D.W. Exciton diffusion measurements in Poly(3-hexylthiophene). Adv. Mater 2008, 20, 3516–3520. [Google Scholar]
- Cheng, X.; Ichimura, K.; Fichou, D.; Kobayashi, T. Nanosecond time-resolved absorption spectra of thin films of α-conjugated thiophene oligomers. Chem. Phys. Lett 1991, 185, 286–291. [Google Scholar]
- Cook, S.; Ohkita, H.; Durrant, J.R.; Kim, Y.; Benson-Smith, J.J.; Nelson, J.; Bradley, D.D.C. Singlet exciton transfer and fullerene triplet formation in polymer-fullerene blend films. Appl. Phys. Lett 2006, 89, 101128. [Google Scholar]
- Brazovskii, S.; Kirova, N. Physical theory of excitons in conducting polymers. Chem. Soc. Rev 2010, 39, 2453–2465. [Google Scholar]
- Deibel, C. Chapter 9 — Photocurrent Generation in Organic Solar Cells; Volume 85, Elsevier Inc: Amsterdam, The Netherlands, 2011; pp. 297–330. [Google Scholar]
- Singh-Rachford, T.N.; Castellano, F.N. Photon upconversion based on sensitized triplet-triplet annihilation. Coord. Chem. Rev 2010, 254, 2560–2573. [Google Scholar]
- Schulze, T.F.; Cheng, Y.Y.; Fückel, B.; MacQueen, R.W.; Danos, A.; Davis, N.J.L.K.; Tayebjee, M.J.Y.; Khoury, T.; Clady, R.G.C.R.; Ekins-Daukes, N.J.; et al. Photochemical upconversion enhanced solar cells: Effect of a back reflector. Aust. J. Chem 2012, 65, 480–485. [Google Scholar]
- Smith, M.B.; Michl, J. Singlet fission. Chem. Rev 2010, 110, 6891–6936. [Google Scholar]
- Lee, J.; Jadhav, P.; Baldo, M.A. High efficiency organic multilayer photodetectors based on singlet exciton fission. Appl. Phys. Lett 2009, 95, 033301. [Google Scholar]
- Ehrler, B.; Wilson, M.W.B.; Rao, A.; Friend, R.H.; Greenham, N.C. Singlet exciton fission-sensitized infrared quantum dot solar cells. Nano Lett 2012, 12, 1053–1057. [Google Scholar]
- Reusswig, P.D.; Congreve, D.N.; Thompson, N.J.; Baldo, M.A. Enhanced external quantum efficiency in an organic photovoltaic cell via singlet fission exciton sensitizer. Appl. Phys. Lett 2012, 101, 113304. [Google Scholar]
- Howard, I.A.; Mauer, R.; Meister, M.; Laquai, F. Effect of morphology on ultrafast free carrier generation in polythiophene:fullerene organic solar cells. J. Am. Chem. Soc 2010, 132, 14866–14876. [Google Scholar]
- Koeppe, R.; Bossart, O.; Calzaferri, G.; Sariciftci, N.S. Advanced photon-harvesting concepts for low-energy gap organic solar cells. Sol. Energy Mater. Sol. Cells 2007, 91, 986–995. [Google Scholar]
- Slooff, L.H.; Veenstra, S.C.; Kroon, J.M.; Moet, D.J.D.; Sweelssen, J.; Koetse, M.M. Determining the internal quantum efficiency of highly efficient polymer solar cells through optical modeling. Appl. Phys. Lett 2007, 90, 143506. [Google Scholar]
- Albuquerque, R.Q.; Hofmann, C.C.; Köhler, J.; Köhler, A. Diffusion-limited energy transfer in blends of oligofluorenes with an anthracene derivative. J. Phys. Chem. B 2011, 115, 8063–8070. [Google Scholar]
- Stevens, A.L.; Kaeser, A.; Schenning, A.P.H.J.; Herz, L.M. Morphology-dependent energy transfer dynamics in fluorene-based amphiphile nanoparticles. ACS Nano 2012, 6, 4777–4787. [Google Scholar]
- Movaghar, B.; Grünewald, M.; Ries, B.; Bassler, H.; Würtz, D. Diffusion and relaxation of energy in disordered organic and inorganic materials. Phys. Rev. B 1986, 33, 5545–5554. [Google Scholar]
- Parkinson, P.; Aharon, E.; Chang, M.H.; Dosche, C.; Frey, G.L.; Köhler, A.; Herz, L.M. Dimensionality-dependent energy transfer in polymer-intercalated SnS2 nanocomposites. Phys. Rev. B 2007, 75, 165206. [Google Scholar]
- Bässler, H. Charge transport in disordered organic photoconductors a monte carlo simulation study. Phys. Status Solidi B 1993, 175, 15–56. [Google Scholar]
- Scully, S.R.; Armstrong, P.B.; Edder, C.; Fréchet, J.M.J.; McGehee, M.D. Long-range resonant energy transfer for enhanced exciton harvesting for organic solar cells. Adv. Mater 2007, 19, 2961–2966. [Google Scholar]
- Shaw, P.E.; Ruseckas, A.; Samuel, I.D.W. Distance dependence of excitation energy transfer between spacer-separated conjugated polymer films. Phys. Rev. B 2008, 78, 245201. [Google Scholar]
- Hesse, H.C.; Weickert, J.; Hundschell, C.; Feng, X.; Müllen, K.; Nickel, B.; Mozer, A.J.; Schmidt-Mende, L. Perylene sensitization of fullerenes for improved performance in organic photovoltaics. Adv. Energy Mater 2011, 1, 861–869. [Google Scholar]
- Banerji, N.; Wang, M.; Fan, J.; Chesnut, E.S.; Wudl, F.; Moser, J.E. Sensitization of fullerenes by covalent attachment of a diketopyrrolopyrrole chromophore. J. Mater. Chem 2012, 22, 13286–13294. [Google Scholar]
- Dang, M.T.; Hirsch, L.; Wantz, G. P3HT: PCBM, best seller in polymer photovoltaic research. Adv. Mater 2011, 23, 3597–3602. [Google Scholar]
- Nicolaidis, N.C.; Routley, B.S.; Holdsworth, J.L.; Belcher, W.J.; Zhou, X.; Dastoor, P.C. Fullerene contribution to photocurrent generation in organic photovoltaic cells. J. Phys. Chem. C 2011, 115, 7801–7805. [Google Scholar]
- Cooling, N.; Burke, K.B.; Zhou, X.; Lind, S.J.; Gordon, K.C.; Jones, T.W.; Dastoor, P.C.; Belcher, W.J. A study of the factors influencing the performance of ternary MEH-PPV: Porphyrin:PCBM heterojunction devices: A steric approach to controlling charge recombination. Sol. Energy Mater. Sol. Cells 2011, 95, 1767–1774. [Google Scholar]
- Dastoor, P.C.; McNeill, C.R.; Frohne, H.; Foster, C.J.; Dean, B.; Fell, C.J.; Belcher, W.J.; Campbell, W.M.; Officer, D.L.; Blake, I.M.; et al. Understanding and improving solid-state Polymer/C60-fullerene bulk-heterojunction solar cells using ternary porphyrin blends. J. Phys. Chem. C 2007, 111, 15415–15426. [Google Scholar]
- Honda, S.; Ohkita, H.; Benten, H.; Ito, S. Multi-colored dye sensitization of polymer/fullerene bulk heterojunction solar cells. Chem. Commun 2010, 46, 6596–6598. [Google Scholar]
- Cooling, N.A.; Zhou, X.; Sales, T.A.; Sauer, S.E.; Lind, S.J.; Gordon, K.C.; Jones, T.W.; Burke, K.B.; Dastoor, P.C.; Belcher, W.J. A study of the factors influencing the performance of ternary MEH-PPV:porphyrin: PCBM heterojunction devices: Electronic effects in porphyrinoid ternary blend bulk heterojunction photovoltaic devices. Sol. Energy Mater. Sol. Cells 2012, 98, 308–316. [Google Scholar]
- Honda, S.; Yokoya, S.; Ohkita, H.; Benten, H.; Ito, S. Light-harvesting mechanism in Polymer/Fullerene/Dye ternary blends studied by transient absorption spectroscopy. J. Phys. Chem. C 2011, 115, 11306–11317. [Google Scholar]
- Yang, F.; Lunt, R.R.; Forrest, S.R. Simultaneous heterojunction organic solar cells with broad spectral sensitivity. Appl. Phys. Lett 2008, 92, 053310. [Google Scholar]
- Scharber, M.C.; Mühlbacher, D.; Koppe, M.; Denk, P.; Waldauf, C.; Heeger, A.J.; Brabec, C.J. Design rules for donors in bulk-heterojunction solar cells—Towards 10% energy-conversion efficiency. Adv. Mater 2006, 18, 789–794. [Google Scholar]
- Lloyd, M.T.; Lim, Y.F.; Malliaras, G.G. Two-step exciton dissociation in poly(3-hexylthiophene)/fullerene heterojunctions. Appl. Phys. Lett 2008, 92, 143308. [Google Scholar]
- Eo, Y.S.; Rhee, H.W.; Chin, B.D.; Yu, J.W. Influence of metal cathode for organic photovoltaic device performance. Synth. Met 2009, 159, 1910–1913. [Google Scholar]
- Valadares, M.; Silvestre, I.; Calado, H.D.R.; Neves, B.R.A.; Guimarães, P.S.S.; Cury, L.A. BEHP-PPV and P3HT blends for light emitting devices. Mater. Sci. Eng. C 2009, 29, 571–574. [Google Scholar]
- Wang, M.; Wang, X. P3HT/TiO2 bulk-heterojunction solar cell sensitized by a perylene derivative. Sol. Energy Mater. Sol. Cells 2007, 91, 1782–1787. [Google Scholar]
- Coffey, D.C.; Ferguson, A.J.; Kopidakis, N.; Rumbles, G. Photovoltaic charge generation in organic semiconductors based on long-range energy transfer. ACS Nano 2010, 4, 5437–5445. [Google Scholar]
- Bakulin, A.A.; Hummelen, J.C.; Pshenichnikov, M.S.; van Loosdrecht, P.H.M. Ultrafast hole-transfer dynamics in Polymer/PCBM bulk heterojunctions. Adv. Funct. Mater 2010, 20, 1653–1660. [Google Scholar]
- Soon, Y.W.; Clarke, T.M.; Zhang, W.; Agostinelli, T.; Kirkpatrick, J.; Dyer-Smith, C.; McCulloch, I.; Nelson, J.; Durrant, J.R. Energy versus electron transfer in organic solar cells: A comparison of the photophysics of two indenofluorene: fullerene blend films. Chem. Sci 2011, 2, 1111–1120. [Google Scholar]
- Dimitrov, S.D.; Nielsen, C.B.; Shoaee, S.; Shakya Tuladhar, P.; Du, J.; McCulloch, I.; Durrant, J.R. Efficient charge photogeneration by the dissociation of PC 70 BM excitons in Polymer/Fullerene solar cells. J. Phys. Chem. Lett 2012, 3, 140–144. [Google Scholar]
- Segal-Peretz, T.; Leman, O.; Nardes, A.M.; Frey, G.L. On the origin of charge generation in hybrid TiO x /conjugated polymer photovoltaic devices. J. Phys. Chem. C 2012, 116, 2024–2032. [Google Scholar]
- Driscoll, K.; Fang, J.; Humphry-Baker, N.; Torres, T.; Huck, W.T.S.; Snaith, H.J.; Friend, R.H. Enhanced photoresponse in solid-state excitonic solar cells via resonant energy transfer and cascaded charge transfer from a secondary absorber. Nano Lett 2010, 10, 4981–4988. [Google Scholar]
- Goris, L.; Haenen, K.; Nesládek, M.; Wagner, P.; Vanderzande, D.; de Schepper, L.; Dhaen, J.; Lutsen, L.; Manca, J.V. Absorption phenomena in organic thin films for solar cell applications investigated by photothermal deflection spectroscopy. J. Mater. Sci 2005, 40, 1413–1418. [Google Scholar]
- Groves, C.; Blakesley, J.C.; Greenham, N.C. Effect of charge trapping on geminate recombination and polymer solar cell performance. Nano Lett 2010, 10, 1063–1069. [Google Scholar]
- Tachiya, M. Breakdown of the Onsager theory of geminate ion recombination. J. Chem. Phys 1988, 89, 6929–6935. [Google Scholar]
- Wojcik, M.; Tachiya, M. Geminate charge recombination with distance-dependent intrinsic reaction rate: Escape probability and its electric field effect. Radiat. Phys. Chem 2005, 74, 132–138. [Google Scholar]
- Koster, L.J.A.; Mihailetchi, V.D.; Blom, P.W.M. Bimolecular recombination in polymer/fullerene bulk heterojunction solar cells. Appl. Phys. Lett 2006, 88, 052104. [Google Scholar]
- Hausermann, R.; Knapp, E.; Moos, M.; Reinke, N.A.; Flatz, T.; Ruhstaller, B. Coupled optoelectronic simulation of organic bulk-heterojunction solar cells: Parameter extraction and sensitivity analysis. J. Appl. Phys 2009, 106, 104507. [Google Scholar]
- Koster, L.J.A.; Smits, E.C.P.; Mihailetchi, V.D.; Blom, P.W.M. Device model for the operation of polymer/fullerene bulk heterojunction solar cells. Phys. Rev. B 2005, 72, 085205. [Google Scholar]
- Miller, A.; Abrahams, E. Impurity conduction at low concentrations. Phys. Rev 1960, 120, 745–755. [Google Scholar]
- Marcus, R.A. On the theory of oxidation reduction reactions involving electron transfer. I. J. Chem. Phys 1956, 42, 966–978. [Google Scholar]
- Pettersson, L.A.A.; Roman, L.S.; Inganäs, O. Modeling photocurrent action spectra of photovoltaic devices based on organic thin films. J. Appl. Phys 1999, 86, 487–496. [Google Scholar]
- Marsh, R.A.; Groves, C.; Greenham, N.C. A microscopic model for the behavior of nanostructured organic photovoltaic devices. J. Appl. Phys 2007, 101, 083509. [Google Scholar] [Green Version]
- Watkins, P.K.; Walker, A.B.; Verschoor, G.L.B. Dynamical Monte Carlo modelling of organic solar cells: The dependence of internal quantum efficiency on morphology. Nano Lett 2005, 5, 1814–1818. [Google Scholar]
- Yang, F.; Forrest, S.R. Photocurrent generation in nanostructured organic solar cells. ACS Nano 2008, 2, 1022–1032. [Google Scholar]
- Groves, C.; Marsh, R.A.; Greenham, N.C. Monte Carlo modeling of geminate recombination in polymer-polymer photovoltaic devices. J. Chem. Phys 2008, 129, 114903. [Google Scholar] [Green Version]
- Meng, L.; Wang, D.; Li, Q.; Yi, Y.; Brédas, J.L.; Shuai, Z. An improved dynamic Monte Carlo model coupled with Poisson equation to simulate the performance of organic photovoltaic devices. J. Chem. Phys 2011, 134, 124102. [Google Scholar]
- Feron, K.; Fell, C.J.; Rozanski, L.J.; Gong, B.B.; Nicolaidis, N.; Belcher, W.J.; Zhou, X.; Sesa, E.; King, B.V.; Dastoor, P.C. Towards the development of a virtual organic solar cell: An experimental and dynamic Monte Carlo study of the role of charge blocking layers and active layer thickness. Appl. Phys. Lett. 2012, 101, 193306. [Google Scholar]
- Casalegno, M.; Carbonera, C.; Luzzati, S.; Raos, G. Coarse-grained kinetic modelling of bilayer heterojunction organic solar cells. Org. Electron 2012, 13, 750–761. [Google Scholar]
- Koster, L.J.A.; Shaheen, S.E.; Hummelen, J.C. Pathways to a new efficiency regime for organic solar cells. Adv. Energy Mater 2012, 2, 1246–1253. [Google Scholar]
- Tavernier, H.L.; Fayer, M.D. Distance dependence of electron transfer in DNA: The role of the reorganization energy and free energy. J. Phys. Chem. B 2000, 104, 11541–11550. [Google Scholar]
- Grampp, G. The marcus inverted region from theory to experiment. Angew. Chem. Int. Ed 1993, 32, 691–693. [Google Scholar]
- Imahori, H.; Tamaki, K.; Guldi, D.M.; Luo, C.; Fujitsuka, M.; Ito, O.; Sakata, Y.; Fukuzumi, S. Modulating charge separation and charge recombination dynamics in porphyrin-fullerene linked dyads and triads: Marcus-normal versus inverted region. J. Am. Chem. Soc 2001, 123, 2607–2617. [Google Scholar]
- Van Hal, P.A.; Meskers, S.C.J.; Janssen, R.A.J. Photoinduced energy and electron transfer in oligo(p -phenylene vinylene)-fullerene dyads. Appl. Phys. A 2004, 79, 41–46. [Google Scholar]
- Coffey, D.C.; Larson, B.W.; Hains, A.W.; Whitaker, J.B.; Kopidakis, N.; Boltalina, O.V.; Strauss, S.H.; Rumbles, G. An optimal driving force for converting excitons into free carriers in excitonic solar cells. J. Phys. Chem. C 2012, 116, 8916–8923. [Google Scholar]
- Clarke, T.M.; Ballantyne, A.M.; Nelson, J.; Bradley, D.D.C.; Durrant, J.R. Free energy control of charge photogeneration in polythiophene/fullerene solar cells: The influence of thermal annealing on p3ht/pcbm blends. Adv. Funct. Mater 2008, 18, 4029–4035. [Google Scholar]
- Ray, B.; Lundstrom, M.S.; Alam, M.A. Can morphology tailoring improve the open circuit voltage of organic solar cells? Appl. Phys. Lett 2012, 100, 013307. [Google Scholar]
- Sista, S.; Yao, Y.; Yang, Y.; Tang, M.L.; Bao, Z. Enhancement in open circuit voltage through a cascade-type energy band structure. Appl. Phys. Lett 2007, 91, 223508. [Google Scholar]
- Schlenker, C.W.; Barlier, V.S.; Chin, S.W.; Whited, M.T.; McAnally, R.E.; Forrest, S.R.; Thompson, M.E. Cascade organic solar cells. Chem. Mater 2011, 23, 4132–4140. [Google Scholar]
- Ameri, T.; Min, J.; Li, N.; Machui, F.; Baran, D.; Forster, M.; Schottler, K.J.; Dolfen, D.; Scherf, U.; Brabec, C.J. Performance enhancement of the P3HT/PCBM solar cells through NIR sensitization using a small-bandgap polymer. Adv. Energy Mater 2012, 2, 1198–1202. [Google Scholar]
- Daniel, C.; Makereel, F.; Herz, L.M.; Hoeben, F.J.M.; Jonkheijm, P.; Schenning, A.P.H.J.; Meijer, E.W.; Silva, C. Mesoscopic order and the dimensionality of long-range resonance energy transfer in supramolecular semiconductors. J. Chem. Phys 2008, 129, 104701. [Google Scholar]
- Huang, J.; Chen, L.; He, F.; Zhang, T.; Niu, G.; Pan, J.; Xiong, Z.; Song, Q. P-type sensitized organic solar cells with cascade energy alignment. J. Phys. D Appl. Phys 2012, 45, 195101. [Google Scholar]
- Steim, R.; Kogler, F.R.; Brabec, C.J. Interface materials for organic solar cells. J. Mater. Chem 2010, 20, 2499–2512. [Google Scholar]
- Gomez, E.D.; Loo, Y.L. Engineering the organic semiconductor-electrode interface in polymer solar cells. J. Mater. Chem 2010, 20, 6604–6611. [Google Scholar]
- Brabec, C.J.; Shaheen, S.E.; Winder, C.; Sariciftci, N.S.; Denk, P. Effect of LiF/metal electrodes on the performance of plastic solar cells. Appl. Phys. Lett 2002, 80, 1288–1290. [Google Scholar]
- Griffiths, D.J. Introduction to Electrodynamics; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Wagenpfahl, A.; Rauh, D.; Binder, M.; Deibel, C.; Dyakonov, V. S-shaped current-voltage characteristics of organic solar devices. Phys. Rev. B 2010, 82, 115306. [Google Scholar]
- Wagner, J.; Gruber, M.; Wilke, A.; Tanaka, Y.; Topczak, K.; Steindamm, A.; Hörmann, U.; Opitz, A.; Nakayama, Y.; Ishii, H.; et al. Identification of different origins for s-shaped current voltage characteristics in planar heterojunction organic solar cells. J. Appl. Phys 2012, 111, 054509. [Google Scholar]









© 2012 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Feron, K.; Belcher, W.J.; Fell, C.J.; Dastoor, P.C. Organic Solar Cells: Understanding the Role of Förster Resonance Energy Transfer. Int. J. Mol. Sci. 2012, 13, 17019-17047. https://doi.org/10.3390/ijms131217019
Feron K, Belcher WJ, Fell CJ, Dastoor PC. Organic Solar Cells: Understanding the Role of Förster Resonance Energy Transfer. International Journal of Molecular Sciences. 2012; 13(12):17019-17047. https://doi.org/10.3390/ijms131217019
Chicago/Turabian StyleFeron, Krishna, Warwick J. Belcher, Christopher J. Fell, and Paul C. Dastoor. 2012. "Organic Solar Cells: Understanding the Role of Förster Resonance Energy Transfer" International Journal of Molecular Sciences 13, no. 12: 17019-17047. https://doi.org/10.3390/ijms131217019



