Structural Characterization of Poly-L-lactic Acid (PLLA) and Poly(glycolic acid)(PGA) Oligomers
Abstract
:1. Introduction
2. Results and Discussions
2.1. Structural Characterization
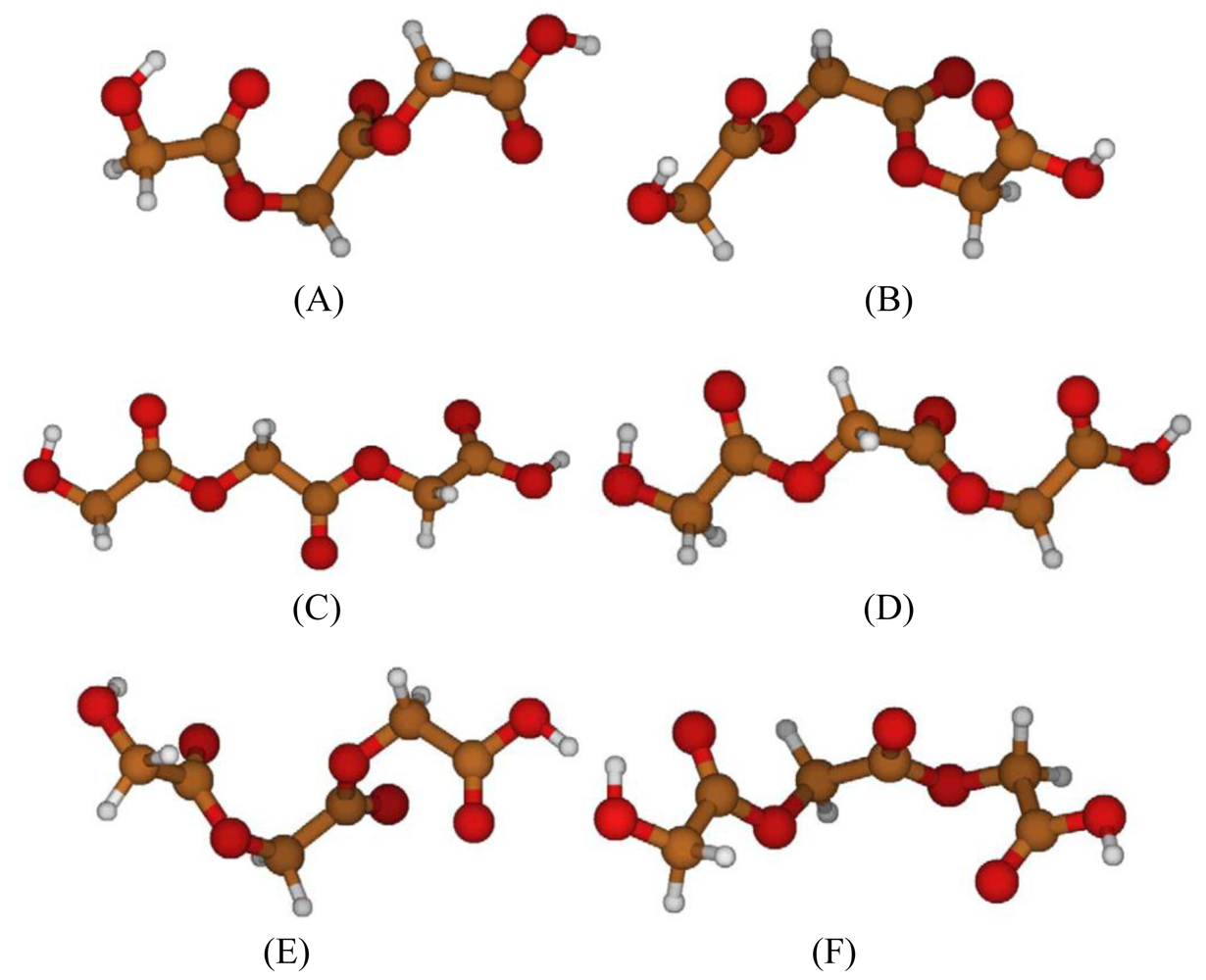
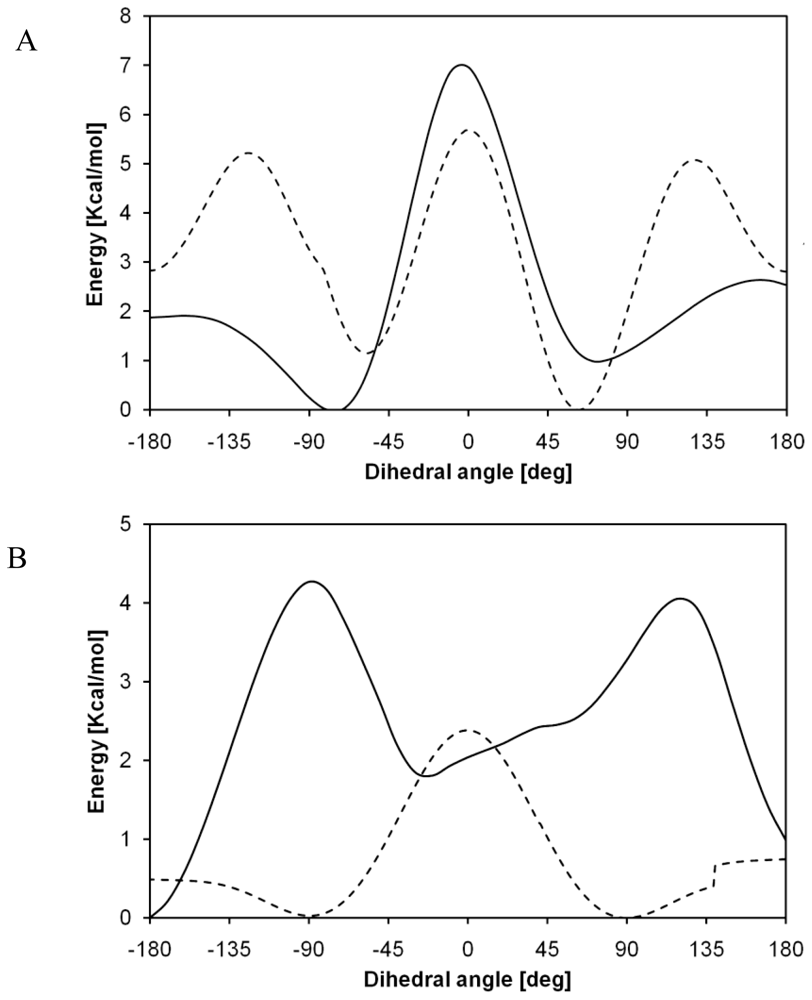
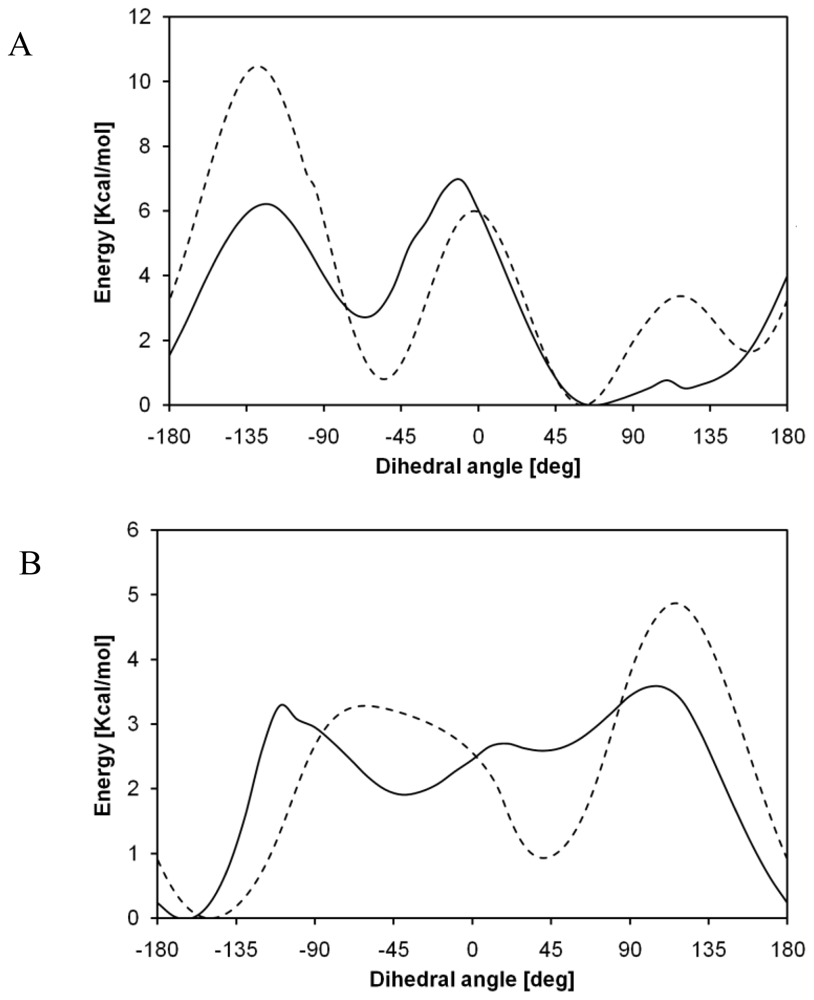
2.2. Structural Analysis of PGA
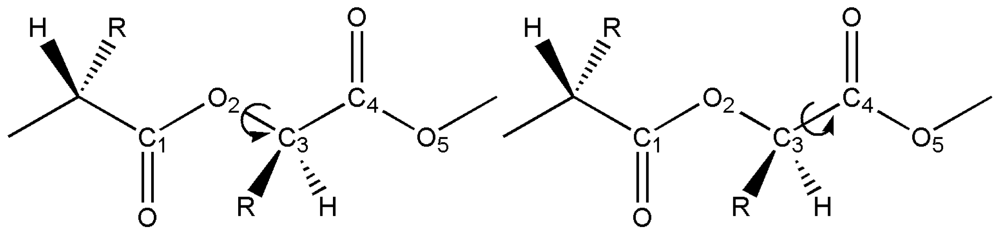
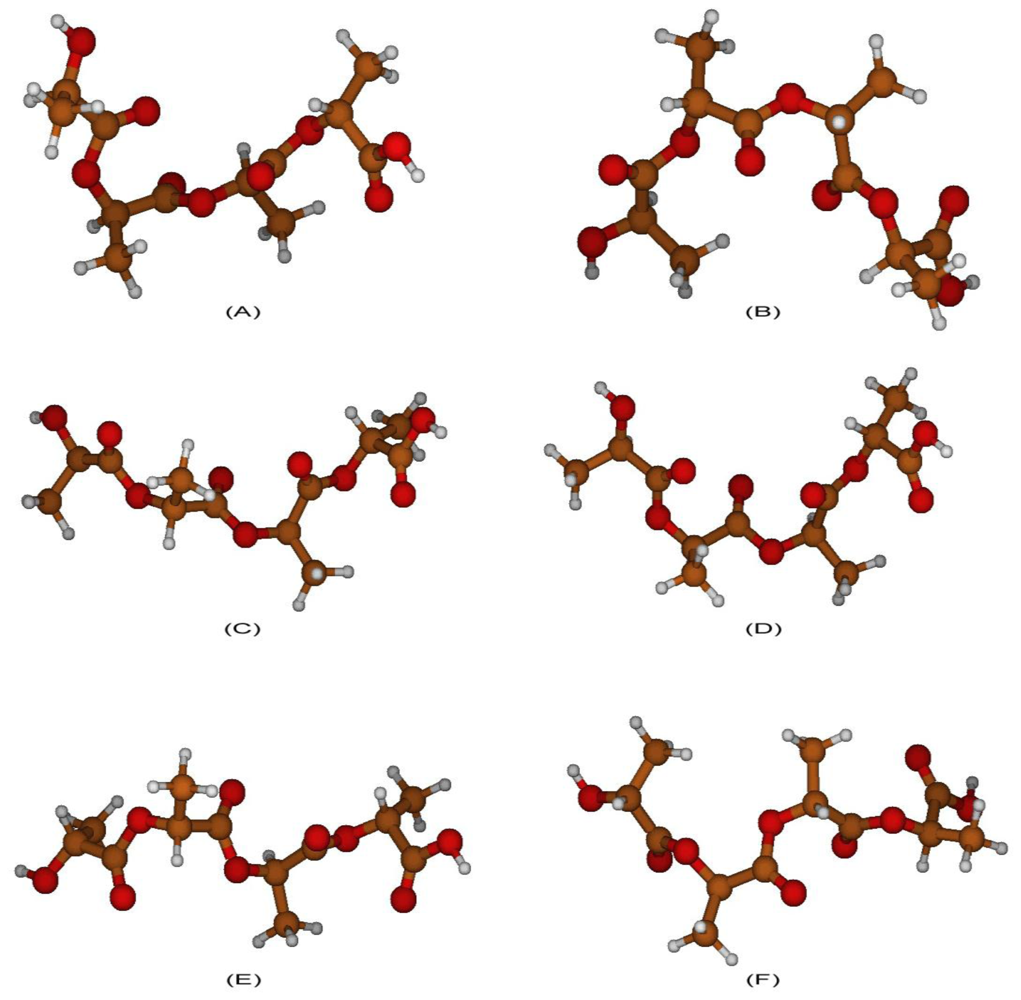
2.3. Structural Characterization of PLLA
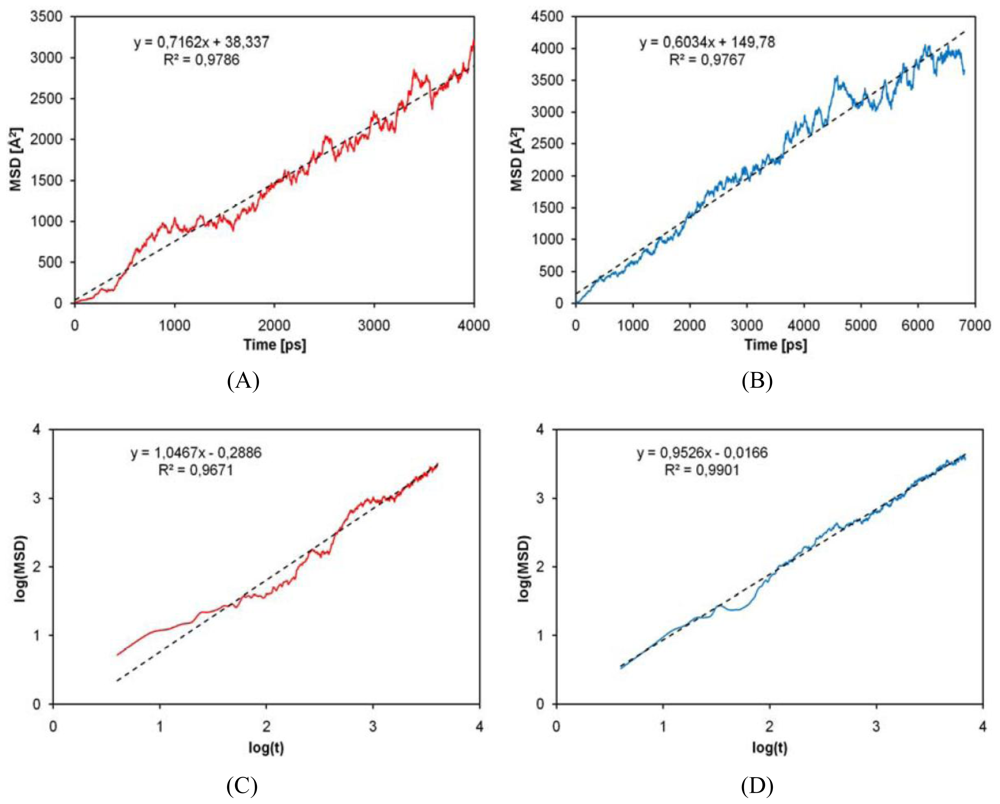
2.4. Diffusion Coefficients Computation
3. Simulation Details
3.1. Structural Characterization
3.2. Molecular Dynamics Simulations
4. Conclusions
References
- Ruhle, M; Dosch, H; Mittenmeijer, E; van der Vorde, M (Eds.) European White Book on Fundamental Research in Materials Science; Max-Planck-Institut für Metallforschung: Stuttgart, Germany, 2001.
- Ratner, BD. Biomaterials Science: An Introduction to Materials in Medicine, 2nd ed; Elsevier Academic Press: Amsterdam, The Netherland, 2004. [Google Scholar]
- Grizzi, I; Garreau, H; Li, S; Vert, M. Hydrolytic degradation of devices based on poly(DL-lactic acid) size-dependence. Biomaterials 1995, 16, 305–311. [Google Scholar]
- Alexis, F. Factors affecting the degradation and drug-release mechanism of poly(lactic acid) and poly[(lactic acid)-co-(glycolic acid)]. Polymer Int 2005, 54, 36–46. [Google Scholar]
- Nagarajan, S; Reddy, BSR. Bio-absorbable polymers in implantation—An overview. J. Sci. Ind. Res 2009, 68, 993–1009. [Google Scholar]
- Zilberman, M; Eberhart, RC. Drug-eluting bioresorbable stents for various applications. Ann. Rev. Biomed. Eng 2006, 8, 153–180. [Google Scholar]
- Tuomo, P; Matti, L; Hannu, P; Pentti, R; Henna, N; Pertti, T. Fixation of distal femoral osteotomies with self-reinforced poly(L/DL)lactide 70:30/bioactive glass composite rods. An experimental study on rats. J. Mater. Sci.-Mater. Med 2004, 15, 275–281. [Google Scholar]
- Lu, Y; Chen, SC. Micro and nano-fabrication of biodegradable polymers for drug delivery. Adv. Drug Deliv. Rev 2004, 56, 1621–1633. [Google Scholar]
- Nampoothiri, KM; Nair, NR; John, RP. An overview of the recent developments in polylactide (PLA) research. Bioresource Tech 2010, 101, 8493–8501. [Google Scholar]
- Perale, G; Casalini, T; Barri, V; Muller, M; Maccagnan, S; Masi, M. Lidocaine release from polycaprolactone threads. J. Appl. Polymer Sci 2010, 117, 3610–3614. [Google Scholar]
- Ella, V; Kellomaki, M; Tormala, P. In vitro properties of PLLA screws and novel bioabsorbable implant with elastic nucleus to replace intervertebral disc. J. Mater. Sci.-Mater. Med 2005, 16, 655–662. [Google Scholar]
- Frank, A; Rath, SK; Venkatraman, SS. Controlled release from bioerodible polymers: Effect of drug type and polymer composition. J. Contr. Release 2005, 102, 333–344. [Google Scholar]
- Liggins, RT; Burt, HM. Paclitaxel loaded poly(L-lactic acid) microspheres: Properties of microspheres made with low molecular weight polymers. Int. J. Pharm 2001, 222, 19–33. [Google Scholar]
- Bettini, R; Catellani, PL; Santi, P; Massimo, G; Peppas, NA; Colombo, P. Translocation of drug particles in HPMC matrix gel layer: Effect of drug solubility and influence on release rate. J. Control. Release 2001, 70, 383–391. [Google Scholar]
- Crow, BB; Borneman, AF; Hawkins, DL; Smith, GM; Nelson, KD. Evaluation of in vitro drug release, pH change, and molecular weight degradation of poly(l-lactic acid) and poly(d, l-lactide-co-glycolide) fibers. Tissue Eng 2005, 11, 1077–1084. [Google Scholar]
- Blomqvist, J; Ahjopalo, L; Mannfors, B; Pietila, LO. Studies on aliphatic polyesters I: Ab initio, density functional and force field studies of esters with one carboxyl group. J. Mol. Struct. Theochem 1999, 488, 247–262. [Google Scholar]
- Blomqvist, J; Mannfors, B; Pietila, LO. Studies on aliphatic polyesters. Part II. Ab initio, density functional and force field studies of model molecules with two carboxyl groups. J. Mol. Struct. Theochem 2000, 531, 359–374. [Google Scholar]
- Xiang, HZ; Wang, YL; Yang, WH; Hu, CB; Mu, YH; Li, JF. Study of the mechanical and thermal properties of poly(lactic acid) and poly(ethylene glycol) block copolymer with molecular dynamics. Int. J. Polymer Anal. Char 2010, 15, 235–244. [Google Scholar]
- Entrialgo-Castano, M; Salvucci, AE; Lendlein, A; Hofmann, D. An atomistic modeling and quantum mechanical approach to the hydrolytic degradation of aliphatic polyesters. Macromol. Symp 2008, 269, 47–64. [Google Scholar]
- Walter, J; Ermatchkov, V; Vrabec, J; Hasse, H. Molecular dynamics and experimental study of conformation change of poly(N-isopropylacrylamide) hydrogels in water. Fluid Phase Equil 2010, 296, 164–172. [Google Scholar]
- Jang, SS; Goddard, WA; Kalani, MYS. Mechanical and transport properties of the poly(ethylene oxide)-poly(acrylic acid) double network hydrogel from molecular dynamic simulations. J. Phys. Chem. B 2007, 111, 1729–1737. [Google Scholar]
- Lee, SG; Brunello, GF; Jang, SS; Bucknall, DG. Molecular dynamics simulation study of P (VP-co-HEMA) hydrogels: Effect of water content on equilibrium structures and mechanical properties. Biomaterials 2009, 30, 6130–6141. [Google Scholar]
- Chiessi, E; Cavalieri, F; Paradossi, G. Water and polymer dynamics in chemically cross-linked hydrogels of poly(vinyl alcohol): A molecular dynamics simulation study. J. Phys. Chem. B 2007, 111, 2820–2827. [Google Scholar]
- Chiessi, E; Lonardi, A; Paradossi, G. Toward modeling thermoresponsive polymer networks: A molecular dynamics simulation study of N-isopropyl acrylamide co-oligomers. J. Phys. Chem. B 2010, 114, 8301–8312. [Google Scholar]
- Codari, F; Moscatelli, D; Storti, G; Morbidelli, M. Characterization of low-molecular-weight PLA using HPLC. Macromol. Mater. Eng 2010, 295, 58–66. [Google Scholar]
- Case, DA; Darden, TA; Cheatham, TE; Simmerling, CL; Wang, J; Duke, RE; Luo, R; Merz, KM; Wang, B; Pearlman, DA; et al. Amber; p. 80. University of California: San Francisco, CA, USA, 2004. [Google Scholar]
- Wang, JM; Wolf, RM; Caldwell, JW; Kollman, PA; Case, DA. Development and testing of a general amber force field. J. Comput. Chem 2004, 25, 1157–1174. [Google Scholar]
- Frenkel, D; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications, 2nd ed; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Ribeiro, ACF; Lobo, VMM; Leaist, DG; Natividade, JJS; Verissimo, LP; Barros, MCF; Cabral, AMTDPV. Binary diffusion coefficients for aqueous solutions of lactic acid. J. Solution Chem 2005, 34, 1009–1016. [Google Scholar]
- Becke, AD. Density-functional thermochemistry. 3. The role of exact exchange. J. Chem. Phys 1993, 98, 5648–5652. [Google Scholar]
- Lee, CT; Yang, WT; Parr, RG. Development of the colle-salvetti correlation-energy formula into a functional of the electron-density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar]
- Ditchfield, R; Hehre, WJ; Pople, JA. Self consistent molecular orbital methods. IX. An extended gaussian type basis for molecular orbital studies of organic molecules. J. Chem. Phys 1971, 54, 724–728. [Google Scholar]
- Frisch, MJ; Trucks, GW; Schlegel, HB; Scuseria, GE; Robb, MA; Cheeseman, JR; Montgomery, JA; Vreven, JT; Kudin, KN; Burant, JC; et al. Gaussian 03, Revision C01; Gaussian, Inc: Pittsburgh, PA, USA, 2003. [Google Scholar]
- Bayly, CI; Cieplak, P; Cornell, WD; Kollman, PA. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges—The resp model. J. Phys. Chem 1993, 97, 10269–10280. [Google Scholar]
- Jang, SS; Blanco, M; Goddard, WA; Caldwell, G; Ross, RB. The source of helicity in perfluorinated N-alkanes. Macromolecules 2003, 36, 5331–5341. [Google Scholar]
- Cances, E; Mennucci, B; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Phys. Chem 1997, 107, 3032–3041. [Google Scholar]
- Jorgensen, WL; Chandrasekar, J; Madura, JD. Comparison of simple potential functions for simulating liquid water. J. Phys. Chem 1983, 79, 926–935. [Google Scholar]



© 2011 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Casalini, T.; Rossi, F.; Santoro, M.; Perale, G. Structural Characterization of Poly-L-lactic Acid (PLLA) and Poly(glycolic acid)(PGA) Oligomers. Int. J. Mol. Sci. 2011, 12, 3857-3870. https://doi.org/10.3390/ijms12063857
Casalini T, Rossi F, Santoro M, Perale G. Structural Characterization of Poly-L-lactic Acid (PLLA) and Poly(glycolic acid)(PGA) Oligomers. International Journal of Molecular Sciences. 2011; 12(6):3857-3870. https://doi.org/10.3390/ijms12063857
Chicago/Turabian StyleCasalini, Tommaso, Filippo Rossi, Marco Santoro, and Giuseppe Perale. 2011. "Structural Characterization of Poly-L-lactic Acid (PLLA) and Poly(glycolic acid)(PGA) Oligomers" International Journal of Molecular Sciences 12, no. 6: 3857-3870. https://doi.org/10.3390/ijms12063857



