Characterization of Doped Amorphous Silicon Thin Films through the Investigation of Dopant Elements by Glow Discharge Spectrometry: A Correlation of Conductivity and Bandgap Energy Measurements
Abstract
:1. Introduction
2. Experimental
2.1. Sample Preparation: Doped Hydrogenated Amorphous Silicon Thin Films
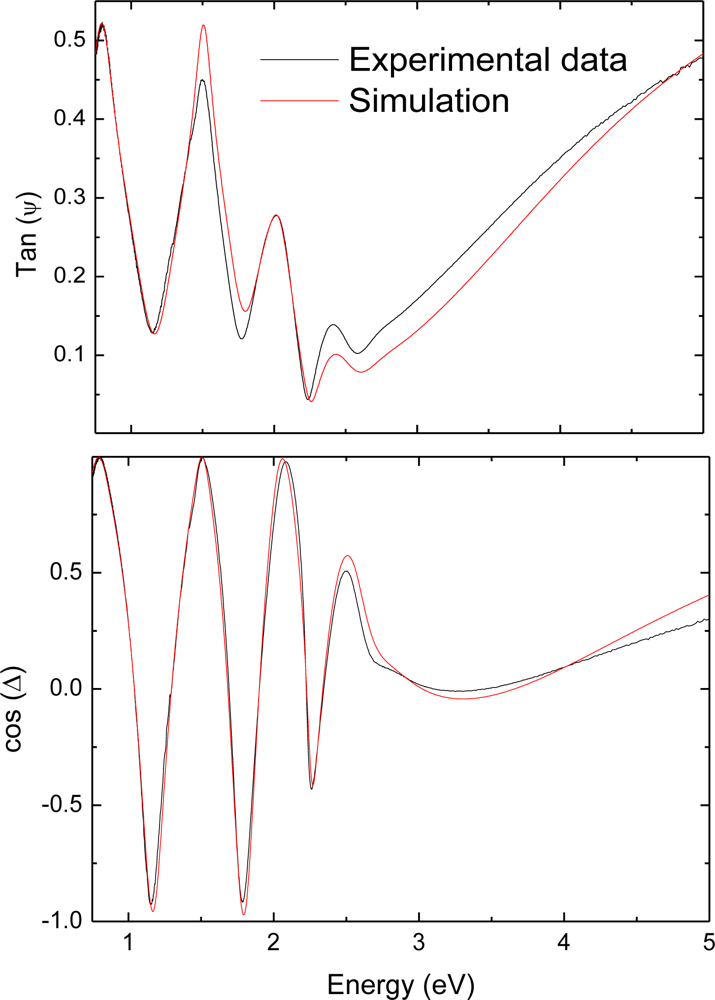
2.2. UV-NIR Spectrophotometry and Ellipsometry
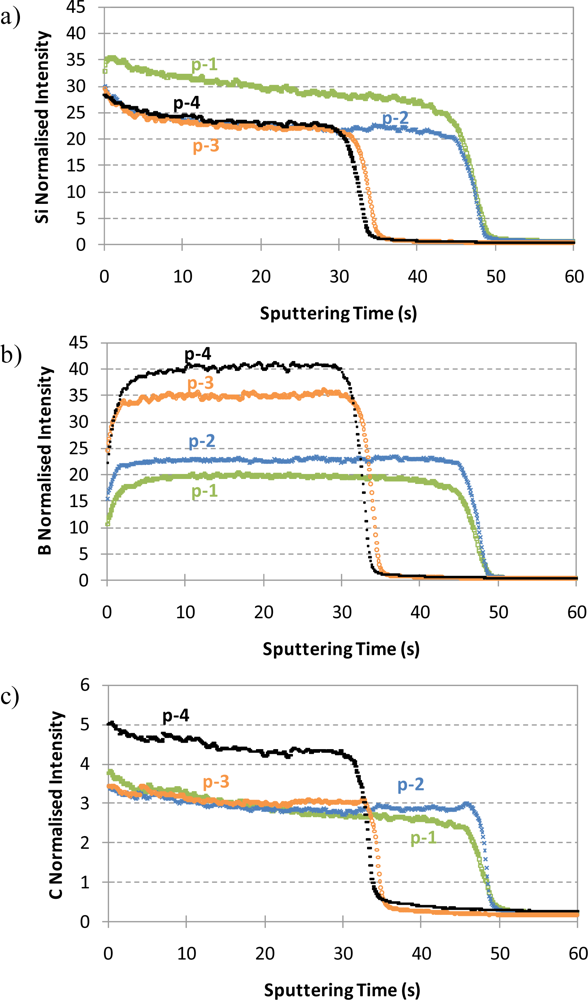
2.3. Glow Discharge—Optical Emission Spectrometry
3. Results and Discussion
3.1. UV-NIR Spectrophotometry and Ellipsometry Measurements
3.2. Depth Profiling Analysis of p-a-SiC:H Thin Films by rf-GD-OES
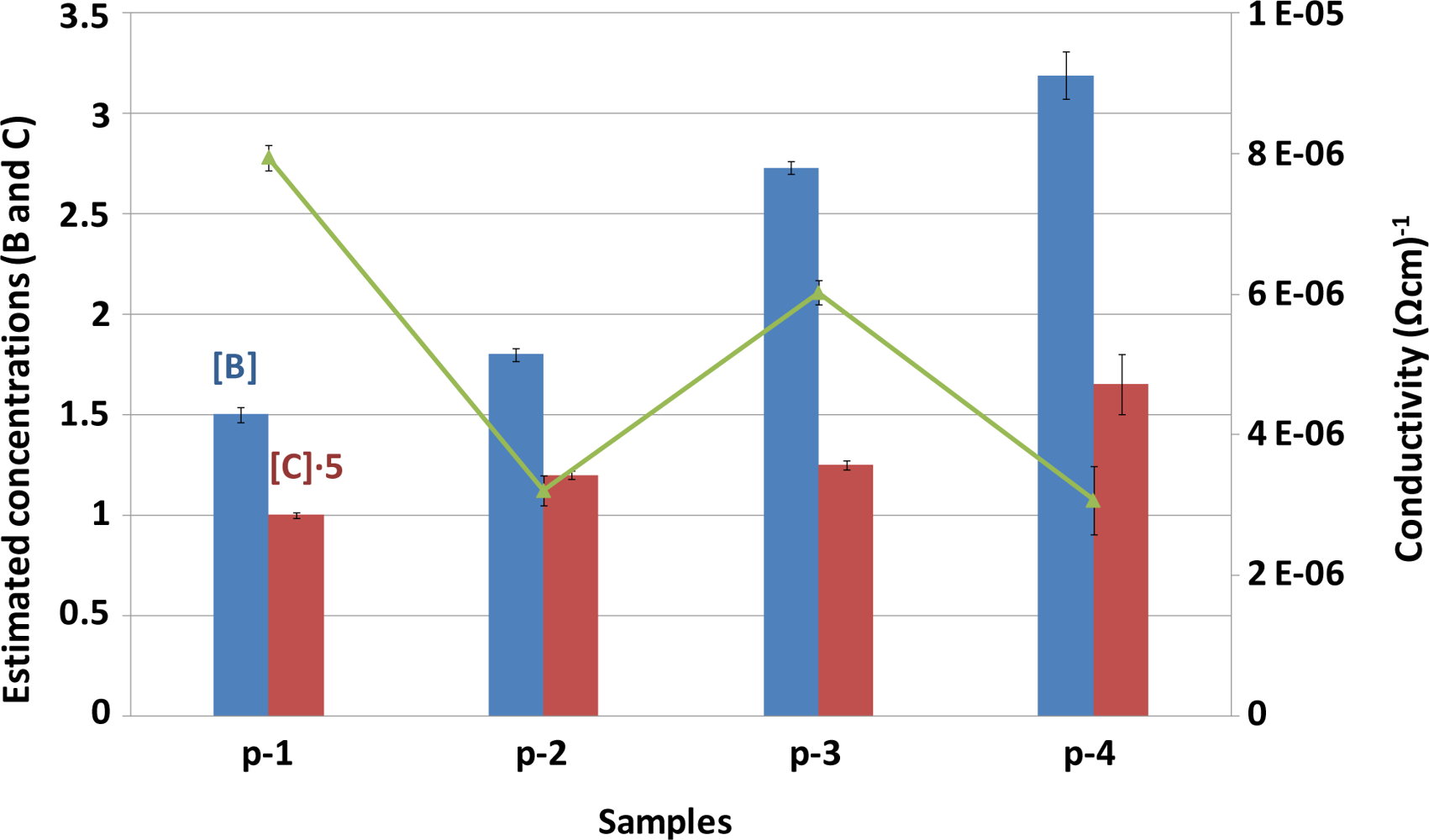
3.3. Relationship between Conductivity Measurements and Dopant Elements Concentration
4. Conclusions
Acknowledgments
References
- Cárabe, J; Gandía, JJ. Thin-film-silicon solar cells. Opto-Electron. Rev 2004, 12, 1–6. [Google Scholar]
- Markvart, T; Castañer, L. Practical Handbook of Photovoltaics: Fundamentals and Application; Elsevier Science Ltd: Kidlington, Oxford, UK, 2003; pp. 218–317. [Google Scholar]
- Mercaldo, LV; Addonizio, ML; Della Noce, M; Delli Veneri, P; Scognamiglio, A; Privato, C. Thin film silicon photovoltaics: Architectural perspectives and technological issues. Appl. Energy 2009, 86, 1836–1844. [Google Scholar]
- Hegedus, S. Progress in Photovoltaics: Research and Application; John Wiley & Sons Ltd: Chichester, UK, 2006; pp. 393–411. [Google Scholar]
- Poortmans, J; Arkhipov, V. Thin Film Solar Cells; John Wiley & Sons Ltd: Chichester, UK, 2006; pp. 194–196. [Google Scholar]
- Stapinski, K; Swatowski, B; Kluska, S; Walasek, E. Optical and structural properties of amorphous silicon-carbon films for optoelectronic applications. Appl. Surf. Sci 2004, 238, 367–374. [Google Scholar]
- Schropp, REI; Zeman, M. Amorphous and Microcrystalline Silicon Solar Cells: Modeling Material and Device Technology; Kluwer Academic Publishers: Norwell, MA, USA, 1998; pp. 41–68. [Google Scholar]
- Jellison, GE. Spectroscopic ellipsometry data analysis: measured versus calculated quantities. Thin Solid Films 1998, 313–314, 33–39. [Google Scholar]
- Centurioni, E; Desalvo, A; Pinghini, R; Rizzoli, R; Summonte, C; Zignani, F. Effect of hydrogen plasma treatments at very high frequency in p-type amorphous and microcrystalline silicon films. In Microcrystalline and Nanocrystalline Semiconductors; Sailor, MJ, Tsai, CC, Canham, LT, Tanaka, K, Eds.; Materials Research Society Symposia Proceedings: Boston, MA, USA, 1999; pp. 517–522. [Google Scholar]
- Iliopoulos, E; Adikimenakis, A; Giesen, C; Heuken, M; Georgakilas, A. Energy bandgap bowing of InAlN alloys studied by spectroscopic ellipsometry. Appl. Phys. Lett 2008, 92, 191907. [Google Scholar]
- Park, J-W; Hwan Eom, S; Lee, H; Da Silva, JLF; Kang, Y-S; Lee, T-Y; Khang, YH. Optical properties of pseudobinary GeTe, Ge2Sb2Te5, GeSb2Te4, GeSb4Te7, and Sb2Te3 from ellipsometry and density functional theory. Phys. Rev. B 2008, 80, 115209. [Google Scholar]
- Liu, C; Erdmann, J; Maj, J; Macrander, A. Thickness determination of metal thin films with spectroscopic ellipsometry for x-ray mirror and multilayer applications. J. Vac. Sci. Technol. A 1999, 17, 2741–2148. [Google Scholar]
- Ferrari, S; Modreanu, M; Scarel, G; Fanciulli, M. X-Ray reflectivity and spectroscopic ellipsometry as metrology tools for the characterization of interfacial layers in high-k materials. Thin Solid Films 2004, 450, 124–127. [Google Scholar]
- Bernhard, C; Humlicek, J; Keimer, B. Far-infrared ellipsometry using a synchrotron light source-the dielectric response of the cuprate high Tc superconductors. Thin Solid Films 2004, 455–456, 143–149. [Google Scholar]
- Pisonero, J; Fernández, B; Günther, D. Critical revision of GD-MS, LA-ICP-MS and SIMS as inorganic mass spectrometric techniques for direct solid analysis. J. Anal. Atom. Spectrom 2009, 24, 1145–1160. [Google Scholar]
- Escobar-Galindo, R; Gago, R; Lousa, A; Albella, JM. Comparative depth-profiling analysis of nanometer-metal multi-layers by ion-probing techniques. Trends Anal. Chem 2009, 28, 494–505. [Google Scholar]
- Fernández, B; Pereiro, R; Sanz-Medel, A. Glow discharge analysis of nanostructured materials and nanolayers-A review. Anal. Chim. Acta 2010, 679, 7–16. [Google Scholar]
- Pisonero, J; Fernández, B; Pereiro, R; Bordel, N; Sanz-Medel, A. Glow-discharge spectrometry for direct analysis of thin and ultra-thin solid films. Trends Anal. Chem 2006, 25, 11–18. [Google Scholar]
- Glow Discharge Plasmas in Analytical Spectroscopy; Marcus, RK; Broekaert, JAC (Eds.) John Wiley & Sons Ltd: Chichester, UK, 2003.
- Winchester, MR; Payling, R. Radio-frequency glow discharge spectrometry: A critical review. Spectrochim. Acta Part B 2004, 59, 607–666. [Google Scholar]
- Sanchez, P; Fernández, B; Menéndez, A; Pereiro, R; Sanz-Medel, A. Pulsed radiofrequency glow discharge optical emission spectrometry for the direct characterisation of photovoltaic thin film silicon solar cells. J. Anal. Atom. Spectrom 2010, 25, 370–377. [Google Scholar]
- Centurioni, E. Generalized matrix method for calculation of internal light energy flux in mixed coherent and incoherent multilayer. Appl. Optics 2005, 44, 7532–7539. [Google Scholar]
- Summonte, C; Rizzoli, R; Desalvo, A; Zignani, F; Centurioni, E; Pinghini, R; Bruno, G; Losurdo, M; Capezzuto, P; Gemmi, M. Plasma enhanced chemical vapor deposition of microcrystalline silicon: on the dynamics of the amorphous-microcrystalline interface by optical methods. Phil. Mag. B 2000, 80, 459–473. [Google Scholar]
- Summonte, C; Rizzoli, R; Desalvo, A; Zignani, F; Centurioni, E; Pinghini, R; Gemmi, M. Very high frequency hydrogen plasma treatment of growing surfaces: a study of the p-type amorphous to microcrystalline silicon transition. J Non-Crystal Solids 2000, 266–269, 624–629. [Google Scholar]
- Bruggeman, DAG. Berechung verschiedener physikalischer. Konstanten von heterogenen Substanzen. Ann. Phys 1935, 24, 636–679. [Google Scholar]
- Fernández, B; Bordel, N; Pereiro, R; Sanz-Medel, A. The effect of thin conductive layers on glass on the performance of radiofrequency glow discharge optical emission spectrometry. J. Anal. Atom. Spectrom 2005, 20, 462–466. [Google Scholar]
- Menéndez, A; Bordel, N; Pereiro, R; Sanz-Medel, A. Radiofrequency glow discharge optical emission spectrometry for the analysis of metallurgical-grade silicon. J. Anal. Atom. Spectrom 2005, 20, 233–235. [Google Scholar]
- Jellison, GE, Jr; Modine, FA. Parameterization of the optical functions of amorphous materials in interband region. Appl. Phys. Lett 1996, 69, 371–373. [Google Scholar]
- Morigaki, K. Physics of Amorphous Semiconductors; Imperial College Press and World Scientific Publishing: London, UK, 1999; pp. 137–149. [Google Scholar]
- Hoffmann, V; Dorka, R; Wilken, L; Hodoroaba, VD; Wetzig, K. Present possibilities of thin-layer analysis by GDOES. Surf. Interface Anal 2003, 35, 575–582. [Google Scholar]

| Sample | SiH4 (sccm) | CH4 (sccm) | B2H6 (sccm) | Total Flow Rate (sccm) |
|---|---|---|---|---|
| p-1 | 10 | 10 | 12 | 32 |
| p-2 | 8 | 10 | 12 | 30 |
| p-3 | 8 | 10 | 20 | 38 |
| p-4 | 6 | 10 | 20 | 36 |
| Sample | Bandgap Energy by Ellipsometry/Tauc (eV) | Bandgap Energy by Spectrophotometry # (eV) |
|---|---|---|
| p-1 | 1.77 ± 0.04 | 1.82–1.91 |
| p-2 | 1.83 ± 0.03 | 1.78–1.85 |
| p-3 | 1.82 ± 0.03 | 1.81–1.88 |
| p-4 | 1.83 ± 0.03 | 1.83–1.90 |
| Sample | Estimated (Si) | Estimated (B) | Estimated (C) |
|---|---|---|---|
| p-1 | 2.03 ± 0.05 | 1.50 ± 0.04 | 0.20 ± 0.003 |
| p-2 | 1.88 ± 0.06 | 1.80 ± 0.03 | 0.24 ± 0.004 |
| p-3 | 1.86 ± 0.03 | 2.73 ± 0.03 | 0.25 ± 0.005 |
| p-4 | 1.75 ± 0.03 | 3.19 ± 0.12 | 0.33 ± 0.03 |
| Sample | Thickness (nm) by Ellipsometry | Thickness (nm) by Profilometry |
|---|---|---|
| p-1 | 619 ± 10 | 606 ± 12 |
| p-2 | 607 ± 10 | 589 ± 14 |
| p-3 | 448 ± 6 | 426 ± 18 |
| p-4 | 435 ± 7 | 414 ± 15 |
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sánchez, P.; Lorenzo, O.; Menéndez, A.; Menéndez, J.L.; Gomez, D.; Pereiro, R.; Fernández, B. Characterization of Doped Amorphous Silicon Thin Films through the Investigation of Dopant Elements by Glow Discharge Spectrometry: A Correlation of Conductivity and Bandgap Energy Measurements. Int. J. Mol. Sci. 2011, 12, 2200-2215. https://doi.org/10.3390/ijms12042200
Sánchez P, Lorenzo O, Menéndez A, Menéndez JL, Gomez D, Pereiro R, Fernández B. Characterization of Doped Amorphous Silicon Thin Films through the Investigation of Dopant Elements by Glow Discharge Spectrometry: A Correlation of Conductivity and Bandgap Energy Measurements. International Journal of Molecular Sciences. 2011; 12(4):2200-2215. https://doi.org/10.3390/ijms12042200
Chicago/Turabian StyleSánchez, Pascal, Olaya Lorenzo, Armando Menéndez, Jose Luis Menéndez, David Gomez, Rosario Pereiro, and Beatriz Fernández. 2011. "Characterization of Doped Amorphous Silicon Thin Films through the Investigation of Dopant Elements by Glow Discharge Spectrometry: A Correlation of Conductivity and Bandgap Energy Measurements" International Journal of Molecular Sciences 12, no. 4: 2200-2215. https://doi.org/10.3390/ijms12042200





