The Solubility Parameters of Ionic Liquids
Abstract
:1. Introduction
2. Results and Discussion
3. Calculation of Solubility Parameters
3.1. Experimental Procedure
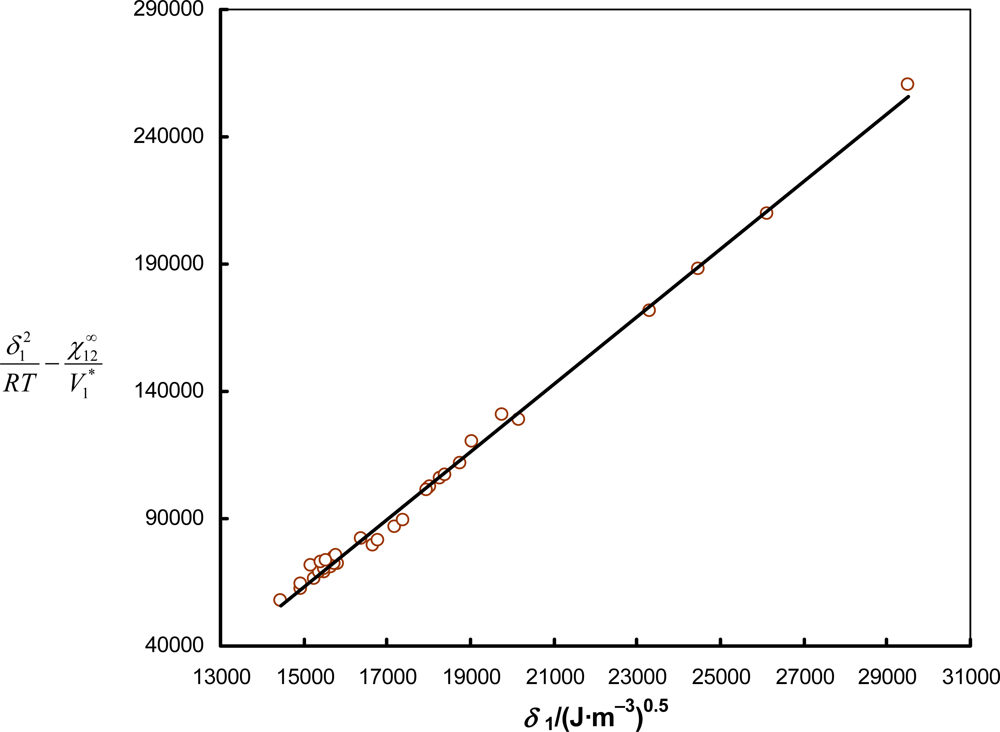
3.2. Theoretical Basis
4. Conclusions
Acknowledgments
Electronic Supporting Information
References and Notes
- Voelkel, A; Strzemiecka, B; Adamska, K; Milczewska, K. Inverse gas chromatography as a source of physiochemical data. J. Chromatogr. A 2009, 1216, 1551–1566. [Google Scholar]
- Marciniak, A. Influence of cation and anion structure of the ionic liquid on extraction processes based on activity coefficients at infinite dilution: A review. Fluid Phase Equilib 2010. [Google Scholar]
- Domańska, U; Marciniak, A. Activity coefficients at infinite dilution measurements for organic solutes and water in the ionic liquid 1-ethyl-3-methylimidazolium trifluoroacetate. J. Phys. Chem. B 2007, 111, 11984–11988. [Google Scholar]
- Domańska, U; Marciniak, A. Measurements of activity coefficients at infinite dilution of aromatic and aliphatic hydrocarbons, alcohols, and water in the new ionic liquid [EMIM][SCN] using GLC. J. Chem. Thermodyn 2008, 40, 860–866. [Google Scholar]
- Domańska, U; Laskowska, M. Measurements of activity coefficients at infinite dilution of aliphatic and aromatic hydrocarbons, alcohols, thiophene, tetrahydrofuran, MTBE, and water in ionic liquid [BMIM][SCN] using GLC. J. Chem. Thermodyn 2009, 41, 645–650. [Google Scholar]
- Domańska, U; Marciniak, A; Królikowska, M; Arasimowicz, M. Activity coefficients at infinite dilution measurements for organic solutes and water in the ionic liquid 1-hexyl-3-methylimidazolium thiocyanate. J Chem Eng Data 2010. [Google Scholar]
- Domańska, U; Królikowska, M. Measurements of activity coefficients at infinite dilution in solvent mixtures with thiocyanate-based ionic liquids using GLC technique. J Phys Chem B 2010. [Google Scholar]
- Domańska, U; Marciniak, A. Activity coefficients at infinite dilution measurements for organic solutes and water in the ionic liquid 1-butyl-3-methylimidazolium trifluoromethanesulfonate. J. Phys. Chem. B 2008, 112, 11100–11105. [Google Scholar]
- Marciniak, A; Wlazło, M. Activity coefficients at infinite dilution for organic solutes and water in the ionic liquid 1-butyl-3-methyl-pyridinium trifluoromethanesulfonate. J Chem Eng Data 2010. [Google Scholar]
- Domańska, U; Redhi, GG; Marciniak, A. Activity coefficients at infinite dilution measurements for organic solutes and water in the ionic liquid 1-butyl-1-methylpyrrolidinium trifluoromethanesulfonate using GLC. Fluid Phase Equilib 2009, 278, 97–102. [Google Scholar]
- Letcher, TM; Domańska, U; Marciniak, M; Marciniak, A. Activity coefficients at infinite dilution measurements for organic solutes in the ionic liquid 1-butyl-3-methyl-imidazolium 2-(2-methoxyethoxy) ethyl sulfate using g.l.c. at T = (298.15, 303.15, and 308.15) K. J. Chem. Thermodyn 2005, 37, 587–593. [Google Scholar]
- Letcher, TM; Marciniak, A; Marciniak, M; Domańska, U. Determination of activity coefficients at infinite dilution of solutes in the ionic liquid 1-butyl-3-methylimidazolium octyl sulfate using gas-liquid chromatography at a temperature of 298.15 K, 313.15 K, or 328.15 K. J. Chem. Eng. Data 2005, 50, 1294–1298. [Google Scholar]
- Domańska, U; Paduszyński, K. Gas-liquid chromatography measurements of activity coefficients at infinite dilution of various organic solutes and water in tri-iso-butylmethylphosphonium tosylate ionic liquid. J. Chem. Thermodyn 2010, 42, 707–711. [Google Scholar]
- Letcher, TM; Ramjugernath, D; Królikowski, M; Laskowska, M; Naidoo, P; Domańska, U. Activity coefficients at infinite dilution measurements for organic solutes in the ionic liquid N-butyl-4-methylpyridinium tosylate using GLC at T = (328.15, 333.15, 338.15, and 343.15) K. Fluid Phase Equilib 2009, 276, 31–36. [Google Scholar]
- Domańska, U; Marciniak, A. Activity coefficients at infinite dilution measurements for organic solutes and water in the ionic liquid 4-methyl-N-butyl-pyridinium bis(trifluoromethylsulfonyl)-imide. J. Chem. Thermodyn 2009, 41, 1350–1355. [Google Scholar]
- Domańska, U; Marciniak, A. Activity coefficients at infinite dilution measurements for organic solutes and water in the 1-hexyloxymethyl-3-methyl-imidazolium and 1,3-dihexyloxymethyl-imidazolium bis(trifluoromethylsulfonyl)-imide ionic liquids - The cation influence. Fluid Phase Equilib 2009, 286, 154–161. [Google Scholar]
- Domańska, U; Marciniak, A. Activity coefficients at infinite dilution measurements for organic solutes and water in the ionic liquid triethylsulphonium bis(trifluoromethylsulfonyl)imide. J. Chem. Thermodyn 2009, 41, 754–758. [Google Scholar]
- Letcher, TM; Marciniak, A; Marciniak, M; Domańska, U. Activity coefficients at infinite dilution measurements for organic solutes in the ionic liquid 1-hexyl-3-methyl-imidazolium bis(trifluoromethylsulfonyl)-imide using g.l.c. at T = (298.15, 313.15, and 333.15) K. J. Chem. Thermodyn 2005, 37, 1327–1331. [Google Scholar]
- Barton, AFM. Solubility parameters. Chem. Rev 1975, 75, 731–753. [Google Scholar]
- Hansen, CM. Hansen Solubility Parameters: A User's Handbook, 2nd ed; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Revelli, A-L; Mutelet, F; Jaubert, J-N. Partition coefficients of organic compounds in new imidazolium based ionic liquids using inverse gas chromatography. J. Chromatogr. A 2009, 1216, 4775–4786. [Google Scholar]
- Mutelet, F; Jaubert, J-N. Measurement of activity coefficients at infinite dilution in 1-hexadecyl-3-methylimidazolium tetrafluoroborate ionic liquid. J. Chem. Thermodyn 2007, 39, 1144–1150. [Google Scholar]
- Mutelet, F; Butet, V; Jaubert, J-N. Application of inverse gas chromatography and regular solution theory for characterization of ionic liquids. Ind. Eng. Chem. Res 2005, 44, 4120–4127. [Google Scholar]
- Foco, GM; Bottini, SB; Quezada, N; de la Fuente, JC; Peters, CJ. Activity coefficients at infinite dilution in 1-alkyl-3-methylimidazolium tetrafluoroborate ionic liquids. J. Chem. Eng. Data 2006, 51, 1088–1091. [Google Scholar]
- Lee, SH; Lee, SB. The Hildebrand solubility parameters, cohesive energy densities and internal energies of 1-alkyl-3-methylimidazolium-based room temperature ionic liquids. Chem Commun 2005, 3469–3471. [Google Scholar]
- Swiderski, K; McLean, A; Gordon, CM; Vaughan, DH. Estimates of internal energies of vaporisation of some room temperature ionic liquids. Chem Commun 2004, 2178–2179. [Google Scholar]
- Deyko, A; Lovelock, KRJ; Corfield, J-A; Taylor, AW; Gooden, PN; Villar-Garcia, IJ; Licence, P; Jones, RG; Krasovskiy, VG; Chernikova, EA; Kustov, LM. Measuring and predicting ΔvapH298 values of ionic liquids. Phys. Chem. Chem. Phys 2009, 11, 8544–8555. [Google Scholar]
- Sambasivarao, SV; Acevedo, O. Development of OPLS-AA force field parameters for 68 unique ionic liquids. J. Chem. Theory Comput 2009, 5, 1038–1050. [Google Scholar]
- Zaitsau, DH; Kabo, GJ; Strechan, AA; Paulechka, YU; Tschersich, A; Verevkin, SP; Heintz, A. Experimental vapor pressures of 1-alkyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imides and a correlation scheme for estimation of vaporization enthalpies of ionic liquids. J. Phys. Chem. A 2006, 110, 7303–7306. [Google Scholar]
- Rodríguez, H; Brennecke, JF. Temperature and composition dependence of the density and viscosity of binary mixtures of water + ionic liquid. J. Chem. Eng. Data 2006, 51, 2145–2155. [Google Scholar]
- Domańska, U; Królikowska, M; Królikowski, M. Phase behaviour and physico-chemical properties of the binary systems {1-ethyl-3-methylimidazolium thiocyanate, or 1-ethyl-3-methylimidazolium tosylate + water, or + an alcohol}. Fluid Phase Equilib 2010. [Google Scholar]
- Domańska, U; Laskowska, M. Temperature and composition dependence of the density and viscosity of binary mixtures of {1-butyl-3-methylimidazolium thiocyanate + 1-alcohols}. J. Chem. Eng. Data 2009, 54, 2113–2119. [Google Scholar]
- Domańska, U; Królikowska, M; Arasimowicz, M. Phase equilibria of (1-hexyl-3-methylimidazolium thiocyanate + water, alcohol, or hydrocarbon) binary systems. J. Chem. Eng. Data 2010, 55, 773–777. [Google Scholar]
- Anthony, JL; Anderson, JL; Maginn, EJ; Brennecke, JF. Anion effects on gas solubility in ionic liquids. J. Phys. Chem. B 2005, 109, 6366–6374. [Google Scholar]
- Majer, V; Svoboda, V. Enthalpies of Vaporization of Organic Compounds: A Critical Review and Data Compilation; Blackwell Scientific Publications: Oxford, UK, 1985. [Google Scholar]
- DIPPR Project 801 - Full Version; Design Institute for Physical Property Data/AIChE: New York, NY, USA, 2009.
- McGlashan, ML; Potter, DJB. An apparatus for the measurement of the second virial coefficients of vapors; the second virial coefficients of some n-alkanes and of some mixtures of n-alkanes. Proc. Roy. Soc 1951, 267, 478–500. [Google Scholar]
- Poling, BE; Prausnitz, JM. Properties of Gases and Liquids, 5th ed; McGraw-Hill Publishing: New York, NY, USA, 2001. [Google Scholar]
- Yaws, CL. Chemical Properties Handbook; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]
- Yaws, CL; Narasimhan, PK; Gabbula, C. Yaws' Handbook of Antoine Coefficients for Vapor Pressure, 2nd e- ed.; Knovel: New York, NY, USA, 2009. [Google Scholar]
- Yaws, CL. Yaws' Handbook of Thermodynamic and Physical Properties of Chemical Compounds; Knovel: New York, NY, USA, 2003. [Google Scholar]
- Dean, JA. Lange's Handbook of Chemistry, 15th ed; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]
 ) [SCN]−; (
) [SCN]−; (  ) [BF4]−; (
) [BF4]−; (  ) [NTf2]−. The lines are drawn to guide the eye.
) [NTf2]−. The lines are drawn to guide the eye.
 ) [SCN]−; (
) [SCN]−; (  ) [BF4]−; (
) [BF4]−; (  ) [NTf2]−. The lines are drawn to guide the eye.
) [NTf2]−. The lines are drawn to guide the eye.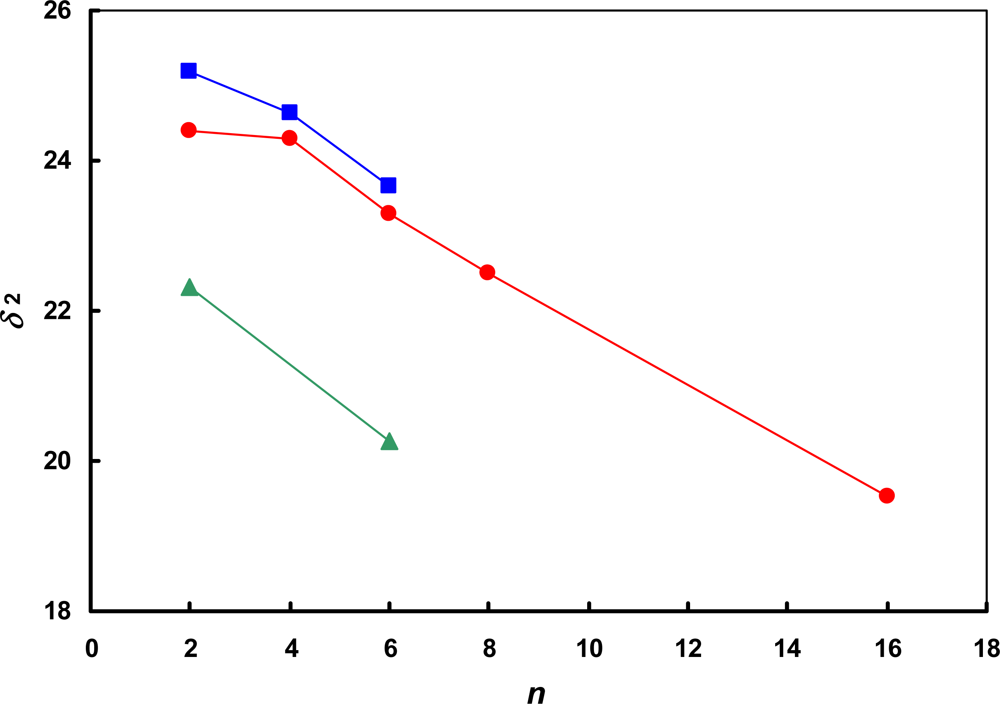
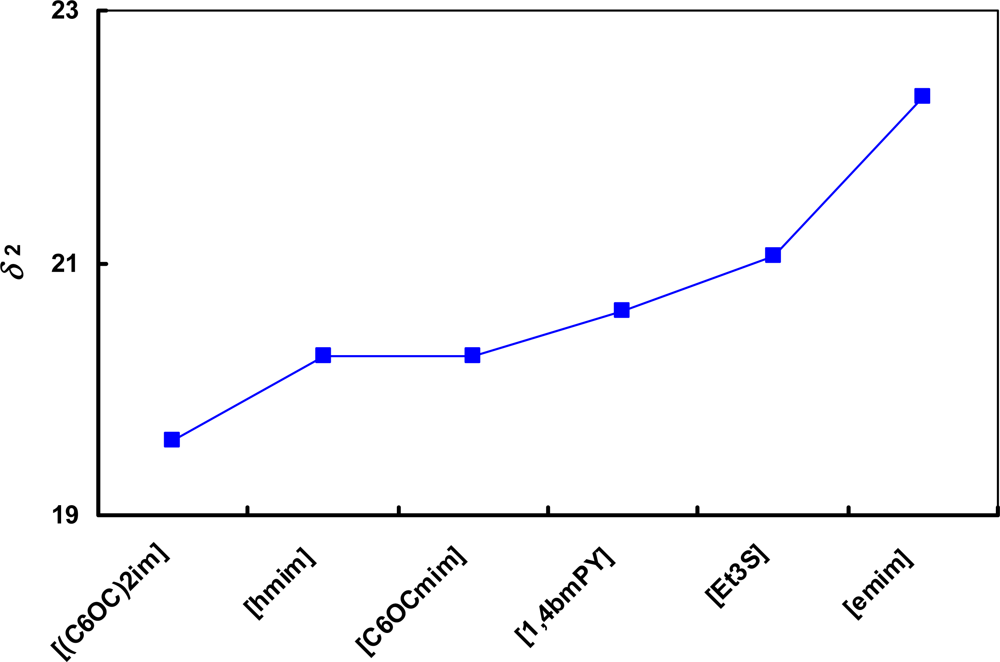
 ) [emim]+; (
) [emim]+; (  ) [bmim]+; (
) [bmim]+; (  ) [hmim]+; (
) [hmim]+; (  ) [omim]+; (
) [omim]+; (  ) [1,4bmPY]+; (
) [1,4bmPY]+; (  ) [1,3bmPY]+; (
) [1,3bmPY]+; (  ) [bmPYR]+.
) [bmPYR]+.
 ) [emim]+; (
) [emim]+; (  ) [bmim]+; (
) [bmim]+; (  ) [hmim]+; (
) [hmim]+; (  ) [omim]+; (
) [omim]+; (  ) [1,4bmPY]+; (
) [1,4bmPY]+; (  ) [1,3bmPY]+; (
) [1,3bmPY]+; (  ) [bmPYR]+.
) [bmPYR]+.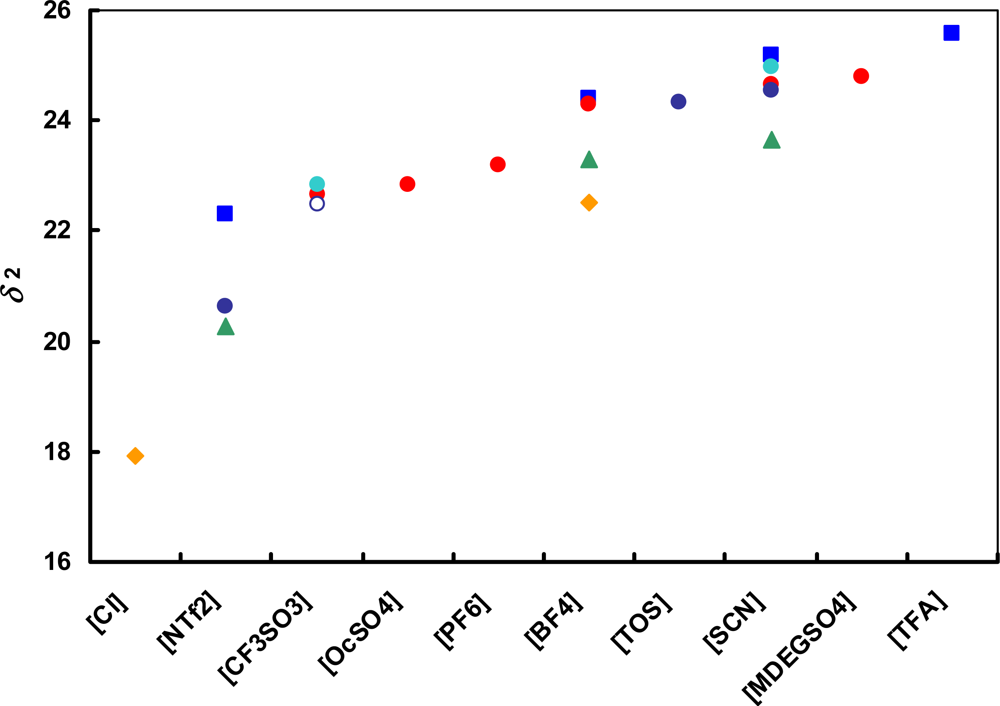
 ) [SCN]− and (
) [SCN]− and (  ) [CF3SO3]− anions. The lines are drawn to guide the eye.
) [CF3SO3]− anions. The lines are drawn to guide the eye.
 ) [SCN]− and (
) [SCN]− and (  ) [CF3SO3]− anions. The lines are drawn to guide the eye.
) [CF3SO3]− anions. The lines are drawn to guide the eye.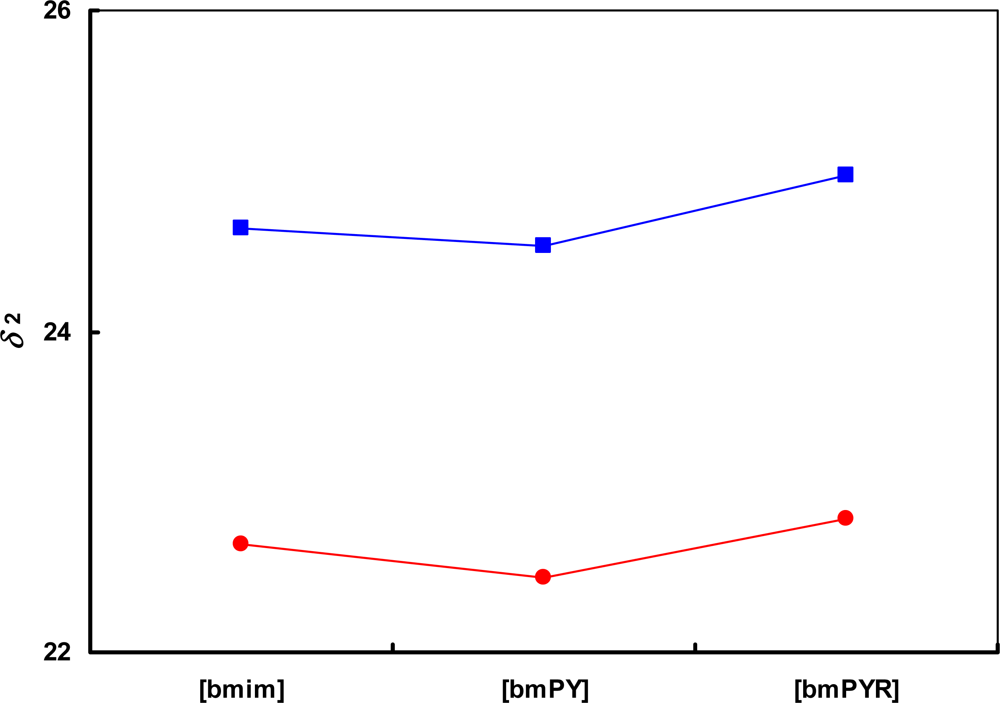
| Abbreviation | Name | Structure | Reference |
|---|---|---|---|
| [emim][TFA] | 1-Ethyl-3-methyl-imidazolium trifluoroacetate | 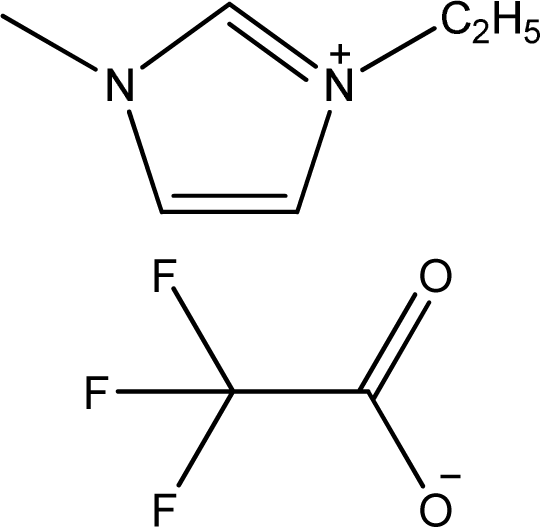 | [3] |
| [emim][SCN] | 1-Ethyl-3-methyl-imidazolium thiocyanate |  | [4] |
| [bmim][SCN] | 1-Butyl-3-methyl-imidazolium thiocyanate | 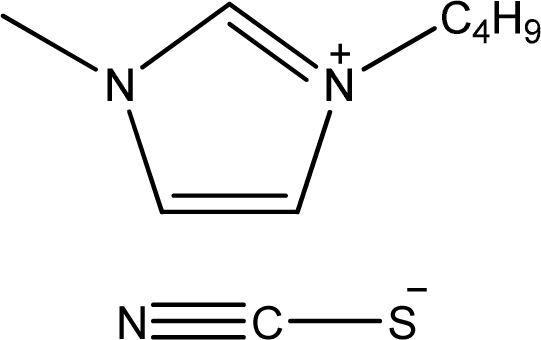 | [5] |
| [hmim][SCN] | 1-Hexyl-3-methyl-imidazolium thiocyanate |  | [6] |
| [1,4bmPY][SCN] | 1-Butyl-4-methyl-pyridinium thiocyanate |  | [7] |
| [bmPYR][SCN] | 1-Butyl-1-methyl-pyrrolidinium thiocyanate | 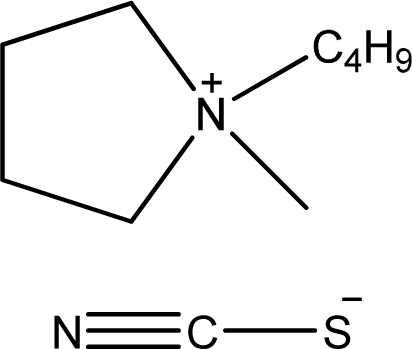 | [7] |
| [bmim][CF3SO3] | 1-Butyl-3-methyl-imidazolium trifluoromethanesulfonate |  | [8] |
| [1,3bmPY][CF3SO3] | 1-Butyl-3-methyl-pyridinium trifluoromethanesulfonate | 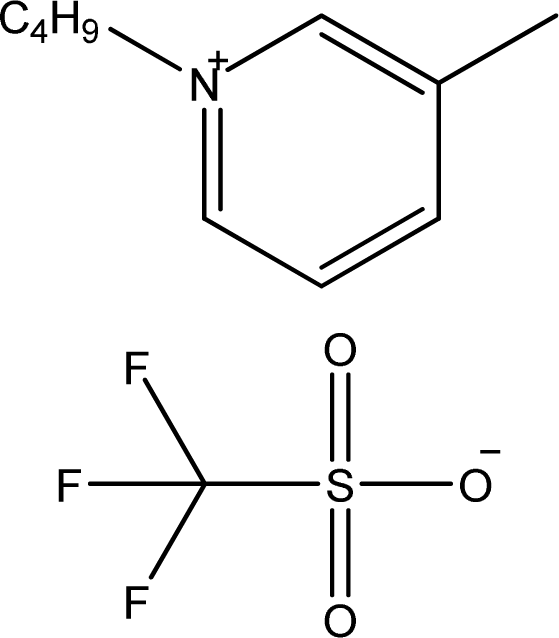 | [9] |
| [bmPYR][CF3SO3] | 1-Butyl-1-methyl-pyrrolidinium trifluoromethanesulfonate | 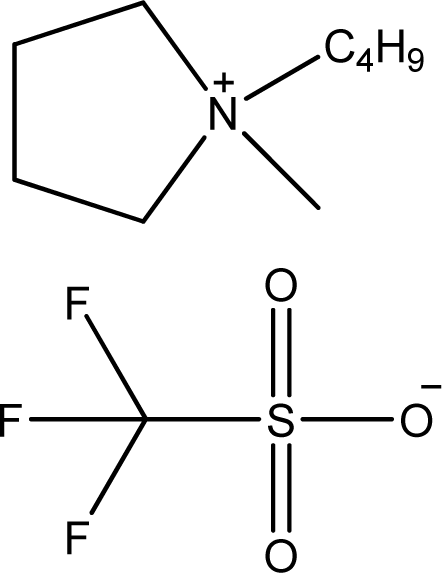 | [10] |
| [bmim][MDEGSO4] | 1-Butyl-3-methyl-imidazolium 2-(2-methoxyethoxy)ethyl sulfate | 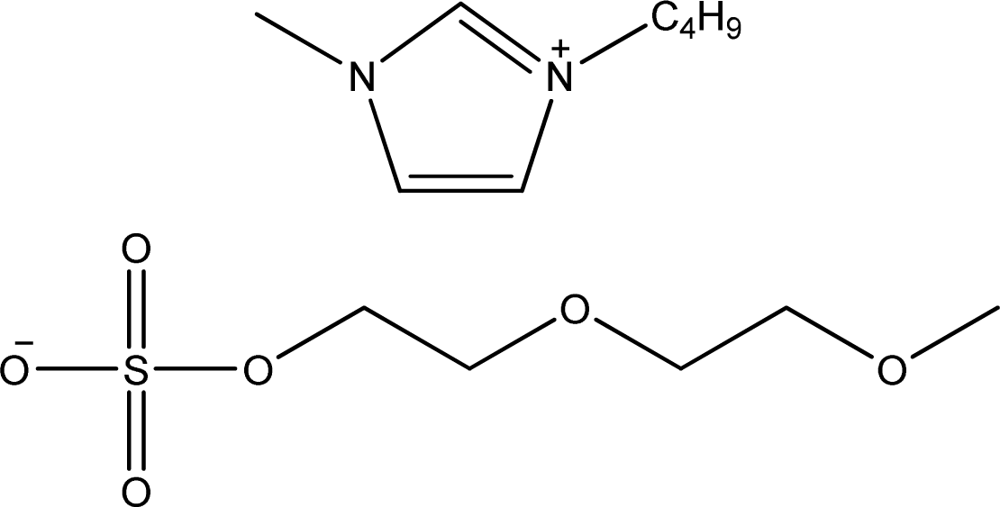 | [11] |
| [bmim][OcSO4] | 1-Butyl-3-methyl-imidazolium octyl sulfate |  | [12] |
| [P1,i4,i4,i4][TOS] | Triisobutyl-methyl-phosphonium tosylate |  | [13] |
| [1,4bmPY][TOS] | 1-Butyl-4-methyl-pyridinium tosylate | 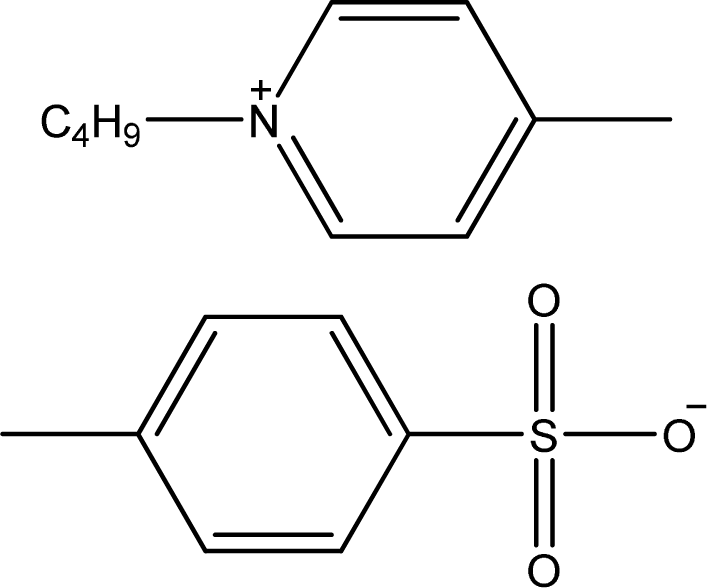 | [14] |
| [1,4bmPY][NTf2] | 1-Butyl-4-methyl-pyridinium bis(trifluoromethylsulfonyl)-amide |  | [15] |
| [C6OCmim][NTf2] | 1-Hexyloxymethyl-3-methyl-imidazolium bis(trifluoromethylsulfonyl)-amide |  | [16] |
| [(C6OC)2im][NTf2] | 1,3-Dihexyloxymethyl-imidazolium bis(trifluoromethylsulfonyl)-amide |  | [16] |
| [Et3S][NTf2] | Triethyl-sulfonium bis(trifluoromethylsulfonyl)-amide | 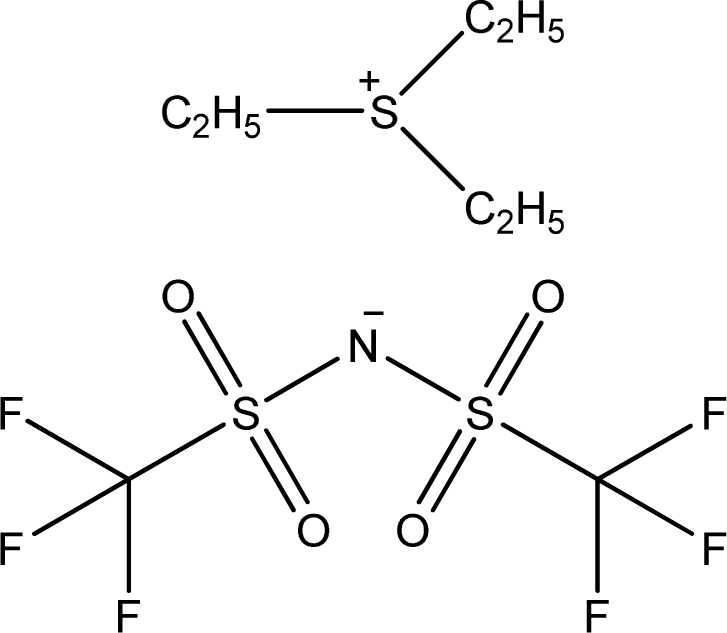 | [17] |
| [hmim][NTf2] | 1-Hexyl-3-methyl-imidazolium bis(trifluoromethylsulfonyl)-amide |  | [18] |
| Ionic liquid | T/K | δ2/MPa0.5 |
|---|---|---|
| [emim][TFA] | 298.15 | 25.561 |
| 328.15 | 25.58 | |
| 338.15 | 25.59 | |
| 348.15 | 25.60 | |
| 358.15 | 25.60 | |
| [emim][SCN] | 298.15 | 25.191 |
| 308.15 | 25.24 | |
| 318.15 | 25.33 | |
| 328.15 | 25.41 | |
| 338.15 | 25.46 | |
| 348.15 | 25.55 | |
| 358.15 | 25.57 | |
| [bmim][SCN] | 298.15 | 24.641 |
| 318.15 | 24.70 | |
| 328.15 | 24.72 | |
| 338.15 | 24.75 | |
| 348.15 | 24.77 | |
| 358.15 | 24.80 | |
| [hmim][SCN] | 298.15 | 23.651 |
| 318.15 | 23.74 | |
| 328.15 | 23.79 | |
| 338.15 | 23.84 | |
| 348.15 | 23.90 | |
| 358.15 | 23.93 | |
| 368.15 | 23.98 | |
| [1,4bmPY][SCN] | 298.15 | 24.53 |
| 308.15 | 24.57 | |
| 318.15 | 24.62 | |
| 328.15 | 24.67 | |
| 338.15 | 24.71 | |
| 348.15 | 24.74 | |
| 358.15 | 24.77 | |
| [bmPYR][SCN] | 298.15 | 24.96 |
| 308.15 | 24.98 | |
| 318.15 | 25.00 | |
| 328.15 | 25.01 | |
| 338.15 | 25.02 | |
| 348.15 | 25.04 | |
| 358.15 | 25.05 | |
| [bmPYR][SCN] | 298.15 | 24.96 |
| 308.15 | 24.98 | |
| 318.15 | 25.00 | |
| 328.15 | 25.01 | |
| 338.15 | 25.02 | |
| 348.15 | 25.04 | |
| 358.15 | 25.05 | |
| [bmim][CF3SO3] | 298.15 | 22.671 |
| 308.15 | 22.74 | |
| 318.15 | 22.81 | |
| 328.15 | 22.87 | |
| 338.15 | 22.97 | |
| 348.15 | 23.03 | |
| 358.15 | 23.09 | |
| [1,3bmPY][CF3SO3] | 298.15 | 22.471 |
| 318.15 | 22.61 | |
| 328.15 | 22.68 | |
| 338.15 | 22.75 | |
| 348.15 | 22.84 | |
| 358.15 | 22.89 | |
| [bmPYR][CF3SO3] | 298.15 | 22.831 |
| 318.15 | 22.94 | |
| 328.15 | 23.01 | |
| 338.15 | 23.06 | |
| 348.15 | 23.13 | |
| 358.15 | 23.17 | |
| 368.15 | 23.24 | |
| [bmim][MDEGSO4] | 298.15 | 24.80 |
| 303.15 | 24.80 | |
| 308.15 | 24.81 | |
| [bmim][OcSO4] | 298.15 | 22.83 |
| 313.15 | 23.00 | |
| 328.15 | 23.25 | |
| [P1,i4,i4,i4][TOS] | 298.15 | 24.331 |
| 318.15 | 24.20 | |
| 328.15 | 24.13 | |
| 338.15 | 24.05 | |
| 348.15 | 23.99 | |
| 358.15 | 23.93 | |
| [1,4bmPY][TOS] | 298.15 | 23.061 |
| 328.15 | 23.24 | |
| 333.15 | 23.27 | |
| 338.15 | 23.29 | |
| 343.15 | 23.33 | |
| [1,4bmPY][NTf2] | 298.15 | 20.611 |
| 318.15 | 20.82 | |
| 328.15 | 20.92 | |
| 338.15 | 21.05 | |
| 348.15 | 21.15 | |
| 358.15 | 21.25 | |
| 368.15 | 21.35 | |
| [C6OCmim][NTf2] | 298.15 | 20.261 |
| 318.15 | 20.48 | |
| 328.15 | 20.59 | |
| 338.15 | 20.71 | |
| 348.15 | 20.82 | |
| 358.15 | 20.93 | |
| 368.15 | 21.05 | |
| [(C6OC)2im][NTf2] | 298.15 | 19.601 |
| 318.15 | 19.81 | |
| 328.15 | 19.92 | |
| 338.15 | 20.03 | |
| 348.15 | 20.14 | |
| 358.15 | 20.25 | |
| 368.15 | 20.35 | |
| [Et3S][NTf2] | 298.15 | 21.051 |
| 308.15 | 21.13 | |
| 318.15 | 21.25 | |
| 328.15 | 21.35 | |
| 338.15 | 21.47 | |
| 348.15 | 21.55 | |
| 358.15 | 21.66 | |
| 368.15 | 21.72 | |
| [hmim][NTf2] | 298.15 | 20.25 |
| 308.15 | 20.36 | |
| 313.15 | 20.44 | |
| 328.15 | 20.58 | |
| 333.15 | 20.64 | |
| 338.15 | 20.70 | |
| 348.15 | 20.83 | |
| Solubility parameters taken from the literature | ||
| [mmim][(CH3)2PO4] [21] | 312.55 | 26.54 |
| 332.65 | 25.96 | |
| 352.75 | 25.16 | |
| [emim][(C2H5)2PO4] [21] | 312.65 | 25.81 |
| 332.55 | 25.44 | |
| 352.65 | 25.32 | |
| [emim][NTf2] [23] | 313.15 | 22.31 |
| [emim][NTf2] [25] | 298.15 | 27.6 |
| [emim][BF4] [24] | 298.15 | 24.4 |
| [bmim][BF4] [24] | 298.15 | 24.3 |
| [bmim][BF4] [25] | 298.15 | 31.6 |
| [bmim][NTf2] [25] | 298.15 | 26.7 |
| [bmim][NTf2] [26] | 298.15 | 25.5 |
| [bmim][CF3SO3] [25] | 298.15 | 24.9 |
| [bmim][CF3SO3] [26] | 298.15 | 25.4 |
| [bmim][PF6] [23] | 313.15 | 23.2 |
| 323.15 | 22.62 | |
| 333.15 | 22.05 | |
| [bmim][PF6] [25] | 298.15 | 29.8 |
| [bmim][PF6] [26] | 298.15 | 30.2 |
| [bmim][SbF6] [26] | 298.15 | 31.5 |
| [bmmim][NTf2] [26] | 298.15 | 24.2 |
| [hmim][BF4] [24] | 298.15 | 23.3 |
| [hmim][NTf2] [25] | 298.15 | 25.6 |
| [hmim][PF6] [25] | 298.15 | 28.6 |
| [omim][BF4] [24] | 298.15 | 22.5 |
| [omim][NTf2] [25] | 298.15 | 25.0 |
| [omim][PF6] [25] | 298.15 | 27.8 |
| [omim][Cl] [23] | 313.15 | 17.91 |
| [C16mim][BF4] [22] | 323.15 | 19.52 |
| 333.15 | 19.61 | |
| 343.15 | 19.60 | |
| [OH-C2mim][BF4] [21] | 302.55 | 22.77 |
| 312.65 | 22.87 | |
| 332.65 | 22.88 | |
| [OH-C2mim][PF6] [21] | 302.65 | 21.84 |
| 312.55 | 21.93 | |
| 332.45 | 22.45 | |
| Ionic liquid | Vm/cm3·mol−1 | ΔvapH298.15/kJ·mol−1 | ||||
|---|---|---|---|---|---|---|
| [emim][TFA] | 173.71 | 115.97 | ||||
| [emim][SCN] | 151.62 | 98.67 | 1518 | |||
| [bmim][SCN] | 184.43 | 114.57 | 1488 | |||
| [hmim][SCN] | 200.04 | 114.37 | ||||
| [1,4bmPY][SCN] | 196.25 | 120.5 | ||||
| [bmPYR][SCN] | 188.85 | 120.1 | ||||
| [bmim][CF3SO3] | 222.05 | 116.67 | 1398 | 130.29 | 140.110 | 145.711 |
| [1,3bmPY][CF3SO3] | 234.75 | 121.07 | ||||
| [bmPYR][CF3SO3] | 232.65 | 123.77 | ||||
| [bmim][MDEGSO4] | 284.25 | 177.6 | ||||
| [bmim][OcSO4] | 327.75 | 173.0 | ||||
| [P1,i4,i4,i4][TOS] | 363.46 | 217.67 | ||||
| [1,4bmPY][NTf2] | 304.85 | 132.07 | 1528 | |||
| [C6OCmim][NTf2] | 349.95 | 146.07 | ||||
| [(C6OC)2im][NTf2] | 460.25 | 179.27 | ||||
| [Et3S][NTf2] | 273.75 | 123.77 | ||||
| [hmim][NTf2] | 326.45 | 136.7 | 1398 | 141.612 | 216.410 | |
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Marciniak, A. The Solubility Parameters of Ionic Liquids. Int. J. Mol. Sci. 2010, 11, 1973-1990. https://doi.org/10.3390/ijms11051973
Marciniak A. The Solubility Parameters of Ionic Liquids. International Journal of Molecular Sciences. 2010; 11(5):1973-1990. https://doi.org/10.3390/ijms11051973
Chicago/Turabian StyleMarciniak, Andrzej. 2010. "The Solubility Parameters of Ionic Liquids" International Journal of Molecular Sciences 11, no. 5: 1973-1990. https://doi.org/10.3390/ijms11051973