SwarmDock and the Use of Normal Modes in Protein-Protein Docking
Abstract
:1. Introduction
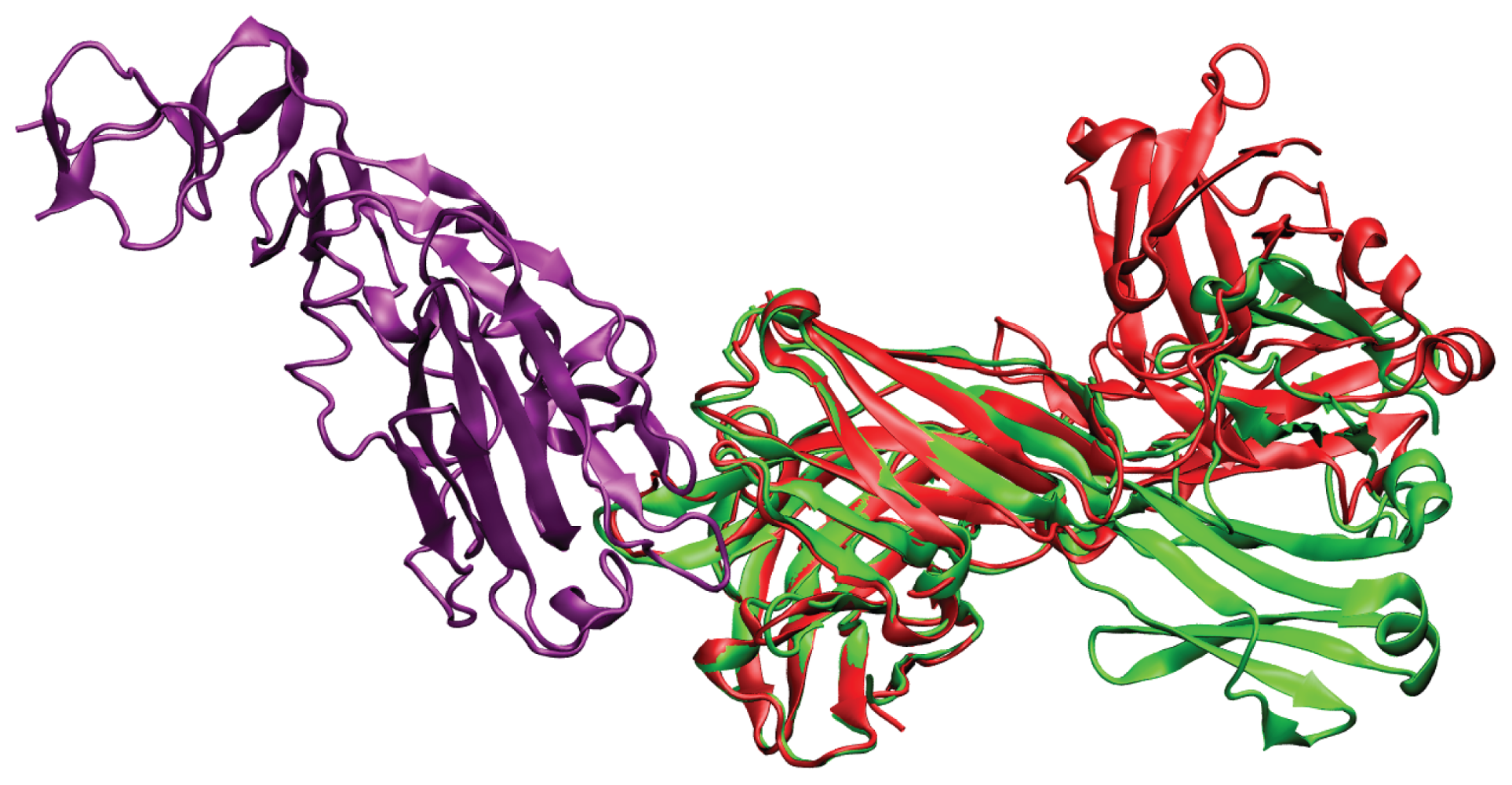
2. Results and Discussion
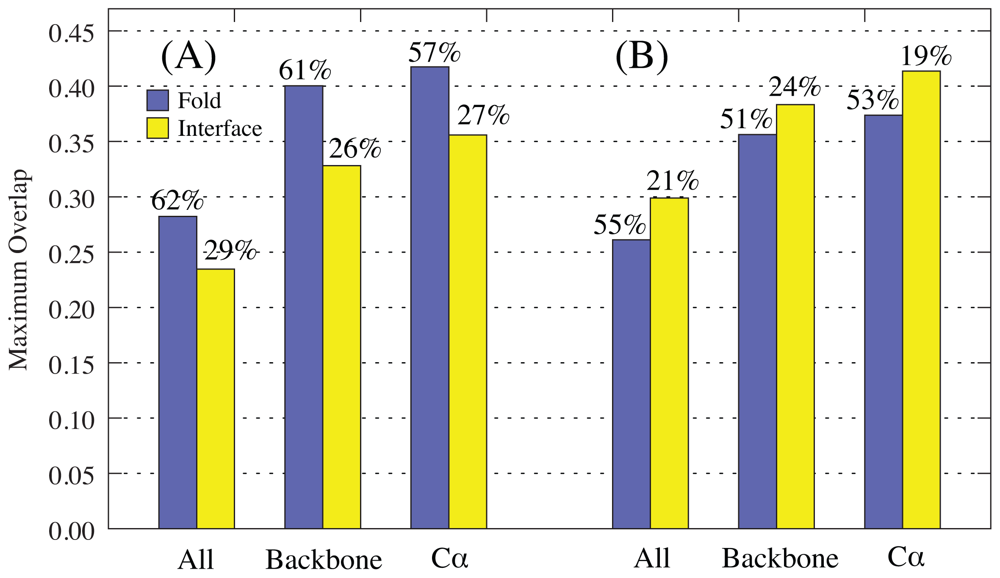
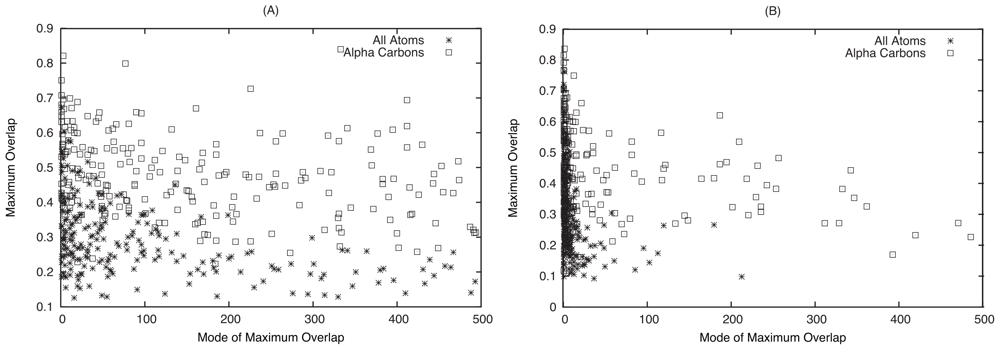
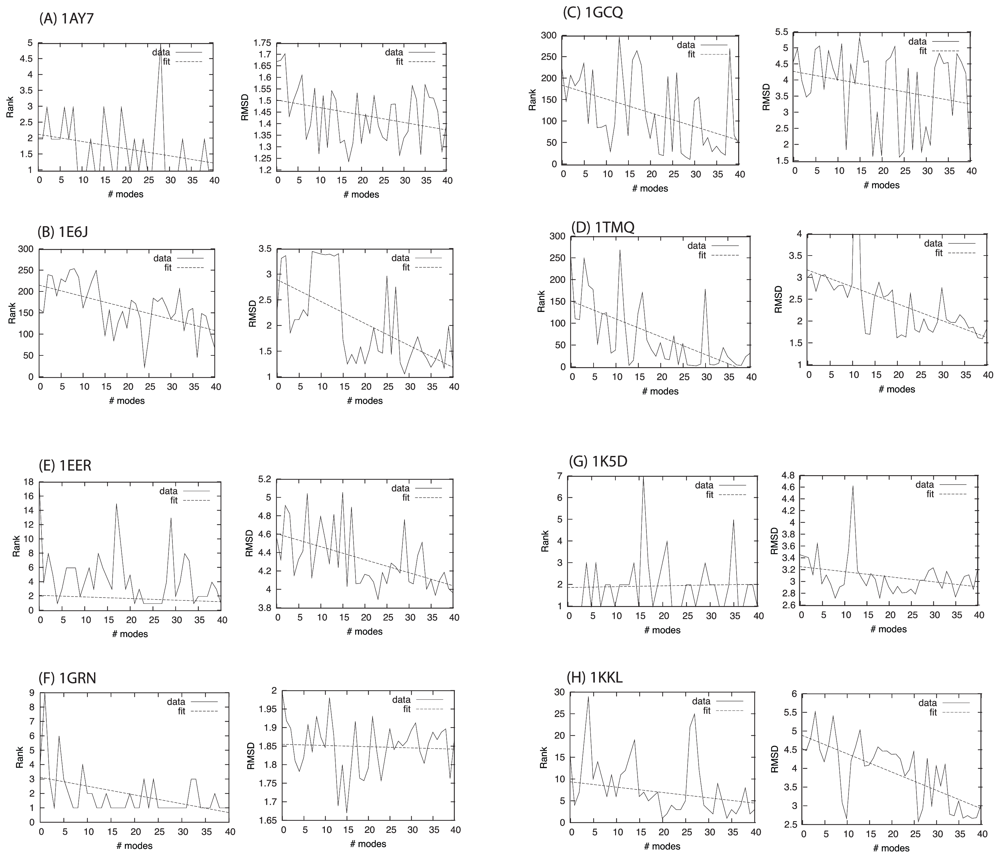
2.1. Overlap
2.1.1. Rotations-Translation-in-Blocks Method
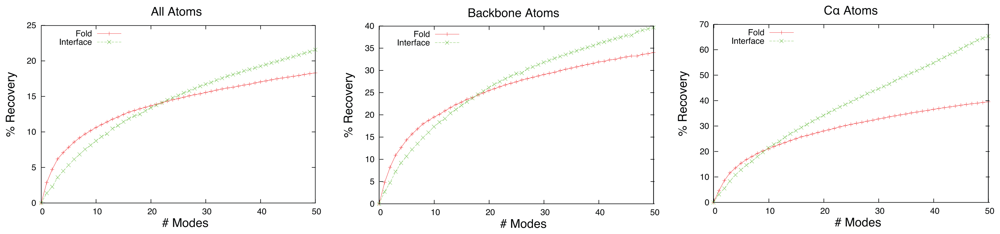
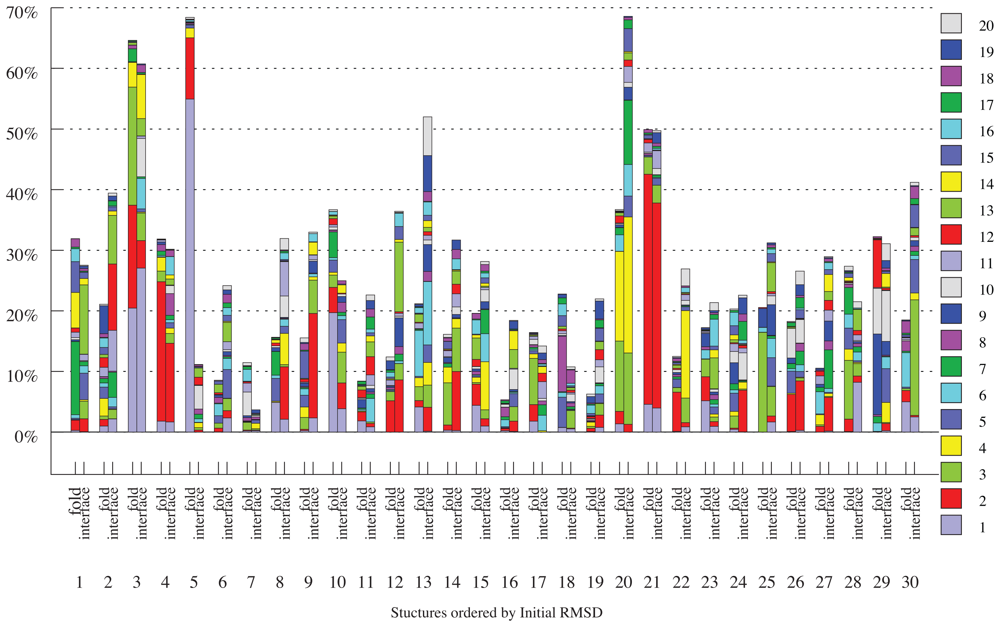
2.2. Linear Combinations of Normal Modes
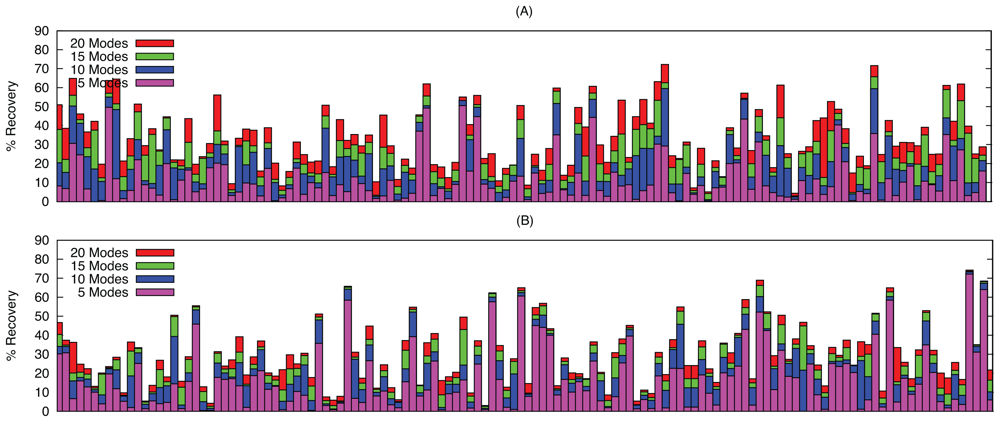
2.3. Docking as a Function of Normal Modes
3. Conclusions
4. Experimental Section
4.1. Normal Mode Analysis
4.1.1. The Rotation-Translation-of-Blocks Method
4.1.2. Overlap
4.1.3. Data Set
4.2. Analytical Mapping of Unbound to Bound
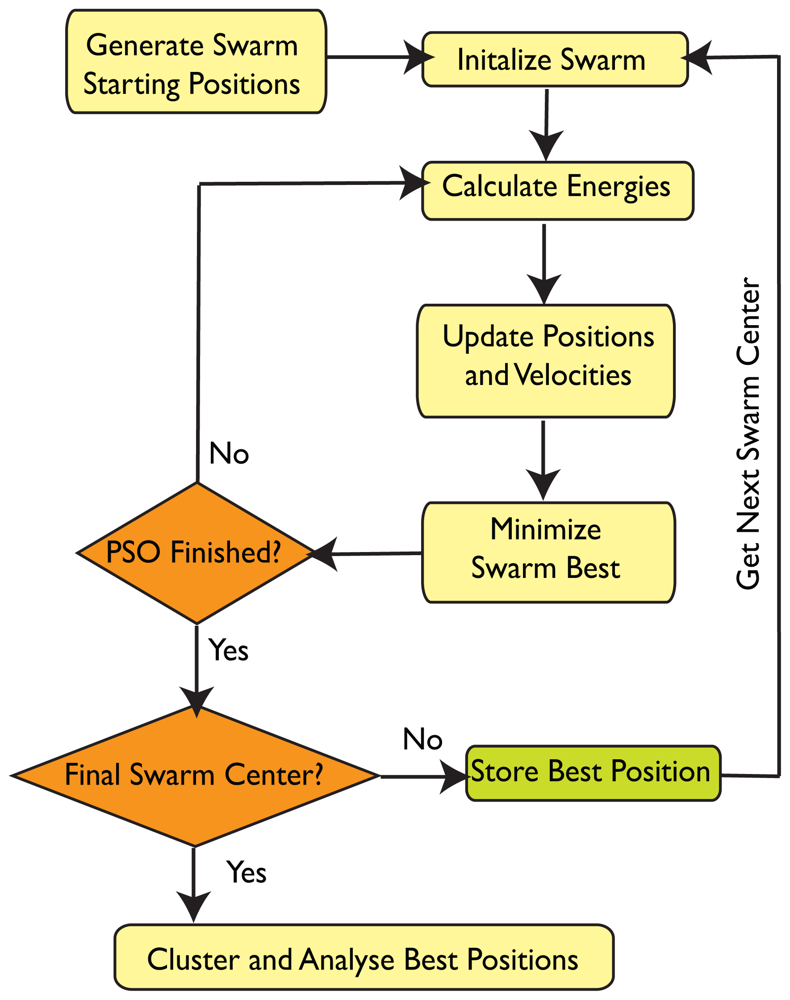
4.3. SwarmDock
4.3.1. Search Space
4.3.2. Initialisation
4.3.3. Propagation
4.3.4. Velocity Clamping
4.3.5. Local Minimisation
4.3.6. Clustering
4.3.7. Analysis of Docked poses
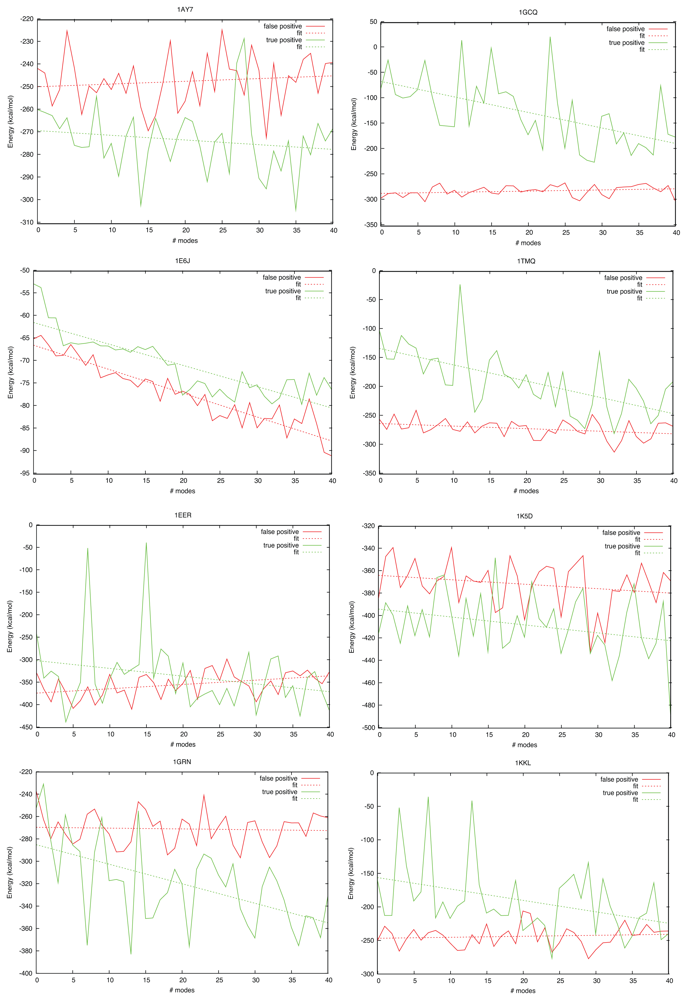
4.3.8. Energy Function
Acknowledgements
References
- Katchalski-Katzir, E; Shariv, I; Eisenstein, M; Friesem, AA; Aflalo, C; Vakser, IA. Molecular surface recognition: Determination of geometric fit between proteins and their ligands by correlation techniques. Proc. Natl. Acad. Sci. USA 1992, 89, 2195–2199. [Google Scholar]
- Chen, R; Weng, Z. Docking unbound proteins using shape complementarity, desolvation, and electrostatics. Proteins 2002, 47, 281–294. [Google Scholar]
- Schneidman-Duhovny, D; Inbar, Y; Nussinov, R; Wolfson, HJ. PatchDock and SymmDock: servers for rigid and symmetric docking. Nucleic Acids Res 2005, 33, W363–367. [Google Scholar]
- Shentu, Z; Al Hasan, M; Bystroff, C; Zaki, MJ. Context shapes: Efficient complementary shape matching for protein-protein docking. Proteins 2008, 70, 1056–1073. [Google Scholar]
- Li, N; Sun, Z; Jiang, F. SOFTDOCK application to protein-protein interaction benchmark and CAPRI. Proteins 2007, 69, 801–808. [Google Scholar]
- Jackson, RM; Gabb, HA; Sternberg, MJ. Rapid refinement of protein interfaces incorporating solvation: application to the docking problem. J. Mol. Biol 1998, 276, 265–285. [Google Scholar]
- Mandell, JG; Roberts, VA; Pique, ME; Kotlovyi, V; Mitchell, JC; Nelson, E; Tsigelny, I; Ten Eyck, LF. Protein docking using continuum electrostatics and geometric fit. Protein Eng 2001, 14, 105–113. [Google Scholar]
- Ritchie, DW; Kemp, GJ. Protein docking using spherical polar Fourier correlations. Proteins 2000, 39, 178–194. [Google Scholar]
- Tovchigrechko, A; Vakser, IA. Development and testing of an automated approach to protein docking. Proteins 2005, 60, 296–301. [Google Scholar]
- Zacharias, M. Protein-protein docking with a reduced protein model accounting for side-chain flexibility. Protein Sci 2003, 12, 1271–1282. [Google Scholar]
- Gardiner, EJ; Willett, P; Artymiuk, PJ. Protein docking using a genetic algorithm. Proteins 2001, 44, 44–56. [Google Scholar]
- Smith, GR; Sternberg, MJ; Bates, PA. The relationship between the flexibility of proteins and their conformational states on forming protein-protein complexes with an application to protein-protein docking. J. Mol. Biol 2005, 347, 1077–1101. [Google Scholar]
- Grunberg, R; Leckner, J; Nilges, M. Complementarity of structure ensembles in protein-protein binding. Structure 2004, 12, 2125–2136. [Google Scholar]
- Krol, M; Chaleil, RA; Tournier, AL; Bates, PA. Implicit flexibility in protein docking: Cross-docking and local refinement. Proteins 2007, 69, 750–757. [Google Scholar]
- Krol, M; Tournier, AL; Bates, PA. Flexible relaxation of rigid-body docking solutions. Proteins 2007, 68, 159–169. [Google Scholar]
- Dominguez, C; Boelens, R; Bonvin, AM. HADDOCK: A protein-protein docking approach based on biochemical or biophysical information. J. Am. Chem. Soc 2003, 125, 1731–1737. [Google Scholar]
- Gray, JJ; Moughon, S; Wang, C; Schueler-Furman, O; Kuhlman, B; Rohl, CA; Baker, D. Protein-protein docking with simultaneous optimization of rigid-body displacement and side-chain conformations. J. Mol. Biol 2003, 331, 281–299. [Google Scholar]
- Comeau, SR; Gatchell, DW; Vajda, S; Camacho, CJ. ClusPro: An automated docking and discrimination method for the prediction of protein complexes. Bioinformatics 2004, 20, 45–50. [Google Scholar]
- Camacho, CJ; Gatchell, DW. Successful discrimination of protein interactions. Proteins 2003, 52, 92–97. [Google Scholar]
- Li, L; Chen, R; Weng, Z. RDOCK: Refinement of rigid-body protein docking predictions. Proteins 2003, 53, 693–707. [Google Scholar]
- Andrusier, N; Nussinov, R; Wolfson, HJ. FireDock: Fast interaction refinement in molecular docking. Proteins 2007, 69, 139–159. [Google Scholar]
- Fernndez-Recio, J; Totrov, M; Abagyan, R. ICM-DISCO docking by global energy optimization with fully flexible side-chains. Proteins 2003, 52, 113–117. [Google Scholar]
- Bastard, K; Prvost, C; Zacharias, M. Accounting for loop flexibility during protein-protein docking. Proteins 2006, 62, 956–969. [Google Scholar]
- Schneidman-Duhovny, D; Inbar, Y; Nussinov, R; Wolfson, HJ. Geometry-based flexible and symmetric protein docking. Proteins 2005, 60, 224–231. [Google Scholar]
- Tirion, MM. Large Amplitude Elastic Motions in Proteins from a Single-Parameter, Atomic Analysis. Phys. Rev. Lett 1996, 77, 1905–1908. [Google Scholar]
- Bahar, I; Atilgan, AR; Erman, B. Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential. Fold Des 1997, 2, 173–181. [Google Scholar]
- Yang, LW; Eyal, E; Chennubhotla, C; Jee, J; Gronenborn, AM; Bahar, I. Insights into equilibrium dynamics of proteins from comparison of NMR and X-ray data with computational predictions. Structure 2007, 15, 741–749. [Google Scholar]
- Rueda, M; Chacon, P; Orozco, M. Thorough validation of protein normal mode analysis: A comparative study with essential dynamics. Structure 2007, 15, 565–575. [Google Scholar]
- Yang, L; Song, G; Jernigan, RL. How well can we understand large-scale protein motions using normal modes of elastic network models? Biophys. J 2007, 93, 920–929. [Google Scholar]
- Krebs, WG; Alexandrov, V; Wilson, CA; Echols, N; Yu, H; Gerstein, M. Normal mode analysis of macromolecular motions in a database framework: Developing mode concentration as a useful classifying statistic. Proteins 2002, 48, 682–695. [Google Scholar]
- Tama, F; Sanejouand, YH. Conformational change of proteins arising from normal mode calculations. Protein Eng 2001, 14, 1–6. [Google Scholar]
- Atilgan, AR; Durell, SR; Jernigan, RL; Demirel, MC; Keskin, O; Bahar, I. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J 2001, 80, 505–515. [Google Scholar]
- Dobbins, SE; Lesk, VI; Sternberg, MJ. Insights into protein flexibility: The relationship between normal modes and conformational change upon protein-protein docking. Proc. Natl. Acad. Sci. USA 2008, 105, 10390–10395. [Google Scholar]
- Cui, Q; Li, G; Ma, J; Karplus, M. A normal mode analysis of structural plasticity in the biomolecular motor F(1)-ATPase. J. Mol. Biol 2004, 340, 345–372. [Google Scholar]
- Petrone, P; Pande, VS. Can conformational change be described by only a few normal modes? Biophys. J 2006, 90, 1583–1593. [Google Scholar]
- Tama, F; Miyashita, O; Brooks, CL. Normal mode based flexible fitting of high-resolution structure into low-resolution experimental data from cryo-EM. J. Struct. Biol 2004, 147, 315–326. [Google Scholar]
- Mustard, D; Ritchie, DW. Docking essential dynamics eigenstructures. Proteins 2005, 60, 269–274. [Google Scholar]
- Andrusier, N; Mashiach, E; Nussinov, R; Wolfson, HJ. Principles of flexible protein-protein docking. Proteins 2008, 73, 271–289. [Google Scholar]
- Bonvin, AM. Flexible protein-protein docking. Curr. Opin. Struct. Biol 2006, 16, 194–200. [Google Scholar]
- May, A; Zacharias, M. Accounting for global protein deformability during protein-protein and protein-ligand docking. Biochim. Biophys. Acta 2005, 1754, 225–231. [Google Scholar]
- Rueda, M; Bottegoni, G; Abagyan, R. Consistent improvement of cross-docking results using binding site ensembles generated with elastic network normal modes. J. Chem. Inf. Model 2009, 49, 716–725. [Google Scholar]
- Zacharias, M; Sklenar, H. Harmonic modes as variables to approximately account for receptor flexibility in ligand-receptor docking simulations: Application to DNA minor groove ligand complex. J. Comp. Chem 1999, 20, 287–300. [Google Scholar]
- Lindahl, E; Delarue, M. Refinement of docked protein-ligand and protein-DNA structures using low frequency normal mode amplitude optimization. Nucleic Acids Res 2005, 33, 4496–4506. [Google Scholar]
- May, A; Zacharias, M. Protein-ligand docking accounting for receptor side chain and global flexibility in normal modes: Evaluation on kinase inhibitor cross docking. J. Med. Chem 2008, 51, 3499–3506. [Google Scholar]
- Floquet, N; Marechal, JD; Badet-Denisot, MA; Robert, CH; Dauchez, M; Perahia, D. Normal mode analysis as a prerequisite for drug design: application to matrix metalloproteinases inhibitors. FEBS Lett 2006, 580, 5130–5136. [Google Scholar]
- Sander, T; Liljefors, T; Balle, T. Prediction of the receptor conformation for iGluR2 agonist binding: QM/MM docking to an extensive conformational ensemble generated using normal mode analysis. J. Mol. Graph. Model 2008, 26, 1259–1268. [Google Scholar]
- Cavasotto, CN; Kovacs, JA; Abagyan, RA. Representing receptor flexibility in ligand docking through relevant normal modes. J. Am. Chem. Soc 2005, 127, 9632–9640. [Google Scholar]
- Kovacs, JA; Cavasotto, CN; Abagyan, R. Conformational Sampling of Protein Flexibility in Generalized Coordinates: Application to Ligand Docking. J. Comput. Theor. Nanosci 2005, 2, 354–361. [Google Scholar]
- May, A; Zacharias, M. Energy minimization in low-frequency normal modes to efficiently allow for global flexibility during systematic protein-protein docking. Proteins 2008, 70, 794–809. [Google Scholar]
- Mashiach, E; Nussinov, R; Wolfson, HJ. FiberDock: Flexible induced-fit backbone refinement in molecular docking. Proteins 2010, 78, 1503–1519. [Google Scholar]
- Hwang, H; Pierce, B; Mintseris, J; Janin, J; Weng, Z. Protein-protein docking benchmark version 3.0. Proteins 2008, 73, 705–709. [Google Scholar]
- Canutescu, AA; Shelenkov, AA; Dunbrack, RL. A graph-theory algorithm for rapid protein side-chain prediction. Protein Sci 2003, 12, 2001–2014. [Google Scholar]
- Rotkiewicz, P; Skolnick, J. Fast procedure for reconstruction of full-atom protein models from reduced representations. J. Comput. Chem 2008, 29, 1460–1465. [Google Scholar]
- Kennedy, J; Eberhart, RC. Particle Swarm Optimization. Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia; 1995; 4, pp. 1942–1948. [Google Scholar]
- Solis, FJ; Wets, RJB. Minimization by Random Search Techniques. Math. Oper. Res 1981, 6, 19–30. [Google Scholar]
- Sousa, T; Silva, A; Neves, A. Particle swarm based Data Mining Algorithms for classification tasks. Parallel Comput 2004, 30, 767–783. [Google Scholar]
- Xiao, X; Dow, ER; Eberhart, R; Miled, ZB; Oppelt, RJ. Gene Clustering Using Self-Organizing Maps and Particle Swarm Optimization. Proceedings of the International Parallel and Distributed Processing Symposium, Nice, France; 2003; p. 154b. [Google Scholar]
- Rasmussen, TK; Krink, T. Improved Hidden Markov Model training for multiple sequence alignment by a particle swarm optimization-evolutionary algorithm hybrid. BioSystems 2003, 72, 5–17. [Google Scholar]
- Namasivayam, V; Gunther, R. PSO@Autodock: A fast flexible molecular docking program based on Swarm intelligence. Chem. Biol. Drug Des 2007, 70, 475–484. [Google Scholar]
- Chen, HM; Liu, BF; Huang, HL; Hwang, SF; Ho, SY. SODOCK: Swarm optimization for highly flexible protein-ligand docking. J. Comput. Chem 2007, 28, 612–623. [Google Scholar]
- Janson, S; Merkle, S; Middendorf, M. Molecular docking with multi-objective Particle Swarm Optimization. Appl. Soft Comput 2008, 8, 666–675. [Google Scholar]
- Li, X; Moal, IH; Bates, PA. Detection and Refinement of Encounter Complexes for Protein-Protein Docking: Taking Account of Macromolecular Crowding. Proteins 2010. [Google Scholar] [CrossRef]
- Magnusson, U; Chaudhuri, BN; Ko, J; Park, C; Jones, TA; Mowbray, SL. Hinge-bending motion of D-allose-binding protein from Escherichia coli: Three open conformations. J. Biol. Chem 2002, 277, 14077–14084. [Google Scholar]
- Arnold, GE; Ornstein, RL. Protein hinge bending as seen in molecular dynamics simulations of native and M61 mutant T4 lysozymes. Biopolymers 1997, 41, 533–544. [Google Scholar]
- Boehr, DD; Nussinov, R; Wright, PE. The role of dynamic conformational ensembles in biomolecular recognition. Nat. Chem. Biol 2009, 5, 789–796. [Google Scholar]
- Isabet, T; Montagnac, G; Regazzoni, K; Raynal, B; El Khadali, F; England, P; Franco, M; Chavrier, P; Houdusse, A; Menetrey, J. The structural basis of Arf effector specificity: The crystal structure of ARF6 in a complex with JIP4. EMBO J 2009, 28, 2835–2845. [Google Scholar]
- O’Neal, CJ; Jobling, MG; Holmes, RK; Hol, WG. Structural basis for the activation of cholera toxin by human ARF6-GTP. Science 2005, 309, 1093–1096. [Google Scholar]
- Offman, MN; Tournier, AL; Bates, PA. Alternating evolutionary pressure in a genetic algorithm facilitates protein model selection. BMC Struct. Biol 2008, 8, 34. [Google Scholar]
- O’Shea, EK; Klemm, JD; Kim, PS; Alber, T. X-ray structure of the GCN4 leucine zipper, a two-stranded, parallel coiled coil. Science 1991, 254, 539–544. [Google Scholar]
- Katz, BA; Finer-Moore, J; Mortezaei, R; Rich, DH; Stroud, RM. Episelection: Novel Ki approximately nanomolar inhibitors of serine proteases selected by binding or chemistry on an enzyme surface. Biochemistry 1995, 34, 8264–8280. [Google Scholar]
- Kurkcuoglu, O; Jernigan, RL; Doruker, P. Loop motions of triosephosphate isomerase observed with elastic networks. Biochemistry 2006, 45, 1173–1182. [Google Scholar]
- Brooks, BR; Janezic, D; Karplus, M. Harmonic analysis of large systems. I. Methodology. J. Comp. Chem 1995, 16, 1522–1542. [Google Scholar]
- Tama, F; Gadea, FX; Marques, O; Sanejouand, YH. Building-block approach for determining low-frequency normal modes of macromolecules. Proteins 2000, 41, 1–7. [Google Scholar]
- Suhre, K; Sanejouand, YH. ElNemo: a normal mode web server for protein movement analysis and the generation of templates for molecular replacement. Nucleic Acids Res 2004, 32, W610–W614. [Google Scholar]
- Dongarra, J. Basic Linear Algebra Subprograms Technical Forum Standard. Int. J. High Perform. Appl. Supercomput 2002, 16, 115–199. [Google Scholar]
- Tama, F; Gadea, FX; Marques, O; Sanejouand, YH. Building-block approach for determining low-frequency normal modes of macromolecules. Proteins 2000, 41, 1–7. [Google Scholar]
- Li, G; Cui, Q. A coarse-grained normal mode approach for macromolecules: an efficient implementation and application to Ca2+-ATPase. Biophys. J 2002, 83, 2457–2474. [Google Scholar]
- Durand, P; Trinquier, G; Sanejouand, YH. A new approach for determining low-frequency normal modes in macromolecules. Biopolymers 1994, 34, 759–771. [Google Scholar]
- Durand, P. Direct determination of effective Hamiltonians by wave-operator methods. I. General formalism. Phys. Rev. A 1983, 28, 3184–3192. [Google Scholar]
- Marques, O; Sanejouand, YH. Hinge-bending motion in citrate synthase arising from normal mode calculations. Proteins 1995, 23, 557–560. [Google Scholar]
- Chen, R; Mintseris, J; Janin, J; Weng, Z. A protein-protein docking benchmark. Proteins 2003, 52, 88–91. [Google Scholar]
- Mendez, R; Leplae, R; de Maria, L; Wodak, SJ. Assessment of blind predictions of protein-protein interactions: current status of docking methods. Proteins 2003, 52, 51–67. [Google Scholar]
- MacKerell, AD; Bashford, D; Bellott; Dunbrack, RL; Evanseck, JD; Field, MJ; Fischer, S; Gao, J; Guo, H; Ha, S; Joseph-McCarthy, D; Kuchnir, L; Kuczera, K; Lau, FTK; Mattos, C; Michnick, S; Ngo, T; Nguyen, DT; Prodhom, B; Reiher, WE; Roux, B; Schlenkrich, M; Smith, JC; Stote, R; Straub, J; Watanabe, M; Wiorkiewicz-Kuczera, J; Yin, D; Karplus, M. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar]
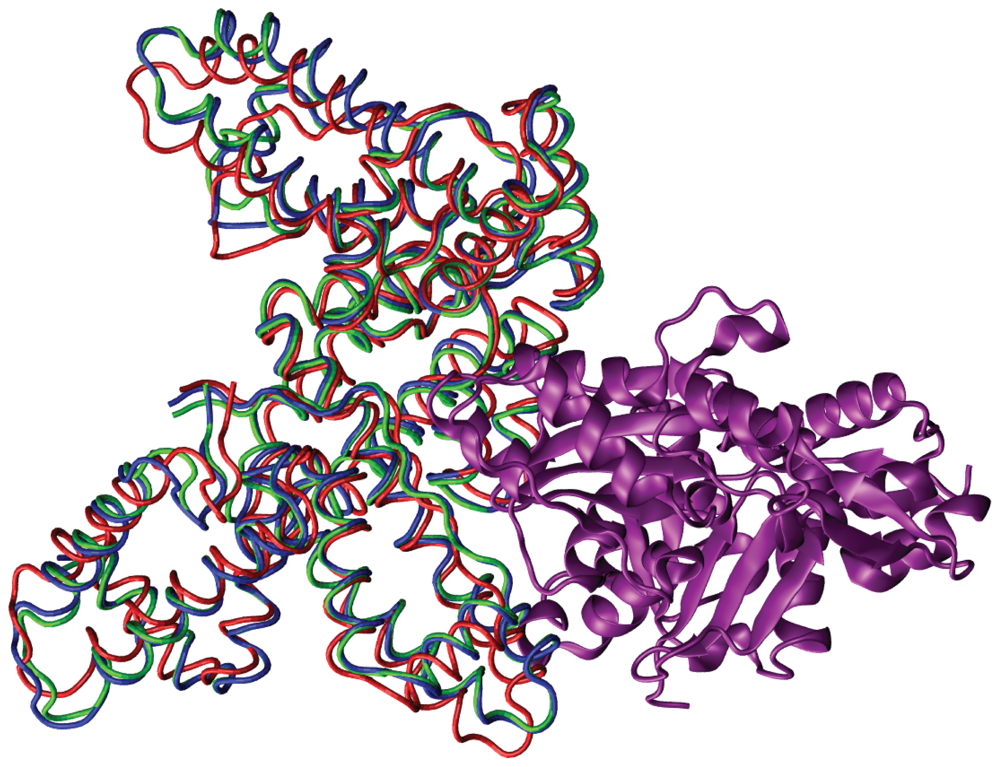
| Complex | Modes: 1–10 | 11–20 | 21–30 | 31–40 |
|---|---|---|---|---|
| 1AY7 | 15.1 | 11.2 | 12.3 | 14.3 |
| 1GCQ | 1.2 | 1.9 | 2.9 | 2.6 |
| 1E6J | 10.0 | 9.9 | 11.0 | 11.5 |
| 1TMQ | 2.1 | 2.9 | 4.7 | 2.9 |
| 1EER | 3.6 | 3.1 | 5.3 | 5.9 |
| 1K5D | 5.9 | 6.9 | 7.4 | 6.6 |
| 1GRN | 26.6 | 28.7 | 29.3 | 27.3 |
| 1KKL | 2.8 | 2.9 | 3.9 | 5.6 |
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Moal, I.H.; Bates, P.A. SwarmDock and the Use of Normal Modes in Protein-Protein Docking. Int. J. Mol. Sci. 2010, 11, 3623-3648. https://doi.org/10.3390/ijms11103623
Moal IH, Bates PA. SwarmDock and the Use of Normal Modes in Protein-Protein Docking. International Journal of Molecular Sciences. 2010; 11(10):3623-3648. https://doi.org/10.3390/ijms11103623
Chicago/Turabian StyleMoal, Iain H., and Paul A. Bates. 2010. "SwarmDock and the Use of Normal Modes in Protein-Protein Docking" International Journal of Molecular Sciences 11, no. 10: 3623-3648. https://doi.org/10.3390/ijms11103623




