The Influence of Disorder on Thermotropic Nematic Liquid Crystals Phase Behavior
Abstract
:1. Introduction
2. Liquid Crystals: A Brief Overview
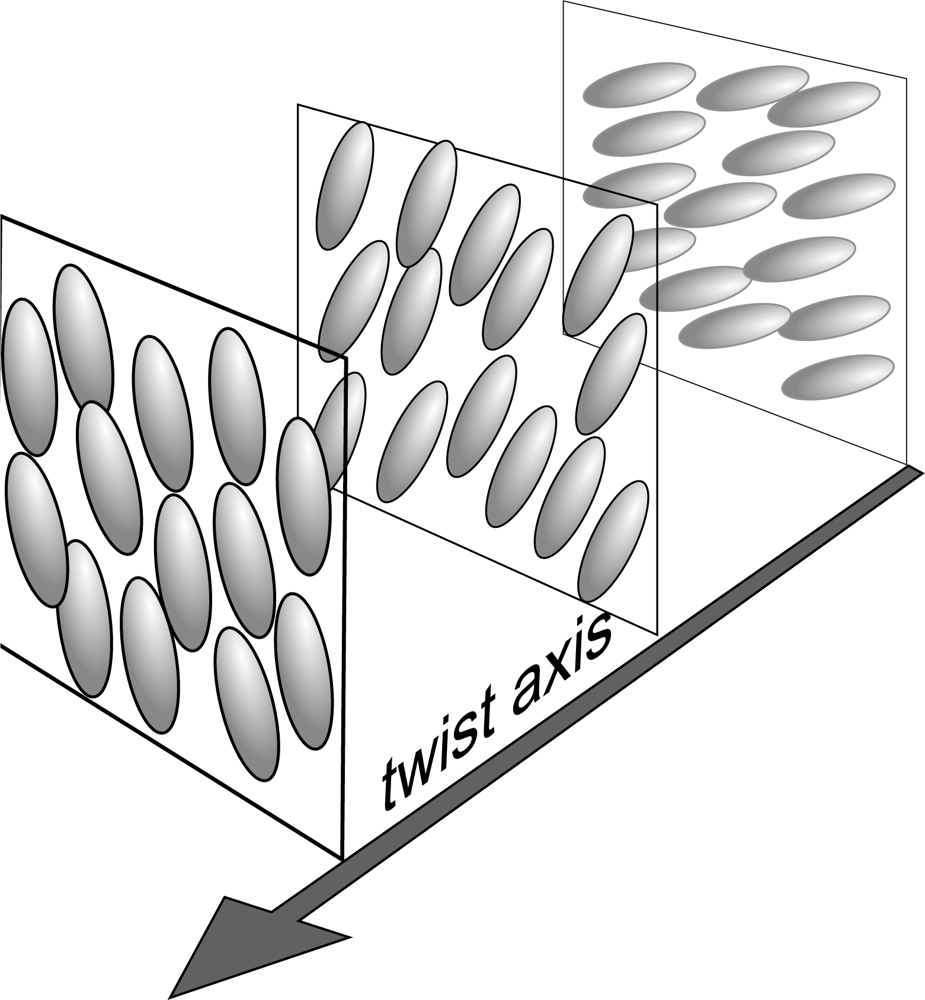
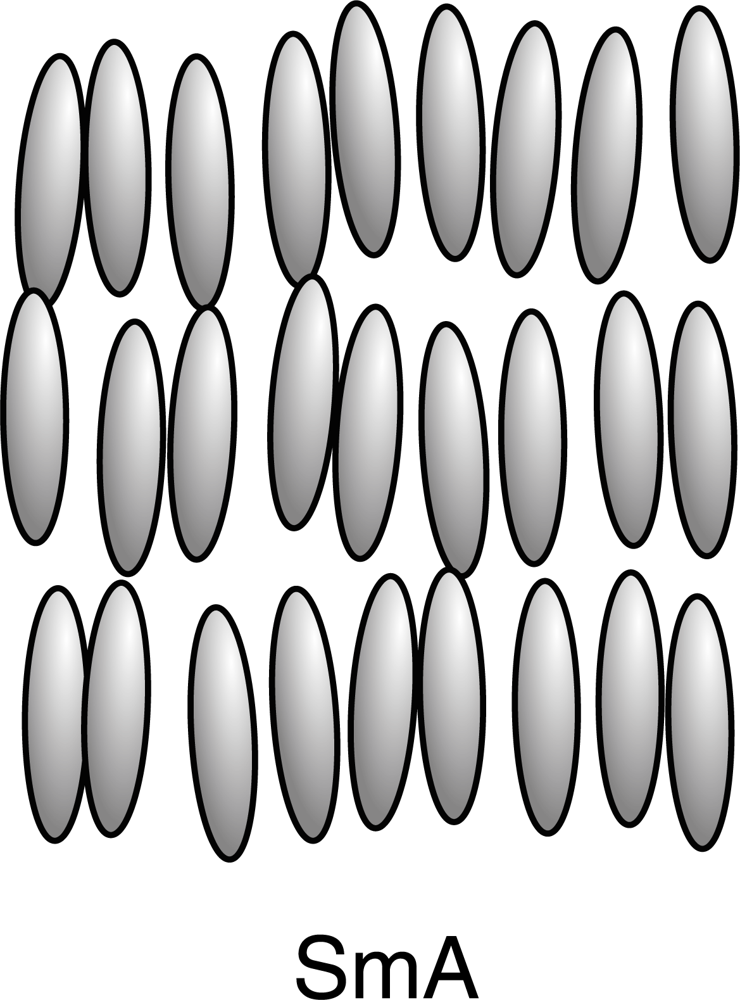
2.1. Nematic, Cholesteric and Smectic Liquid Crystals
2.2. Order Parameters
Nematic order parameter
3. Nematic-Isotropic Phase Transition: Theoretical Models
3.1. Microscopic Models
The Onsager Theory
The Maier–Saupe Model
The van der Waals (vdW) and density functional theories(DFT)
3.2. The Phenomenological Landau–de Gennes Theory
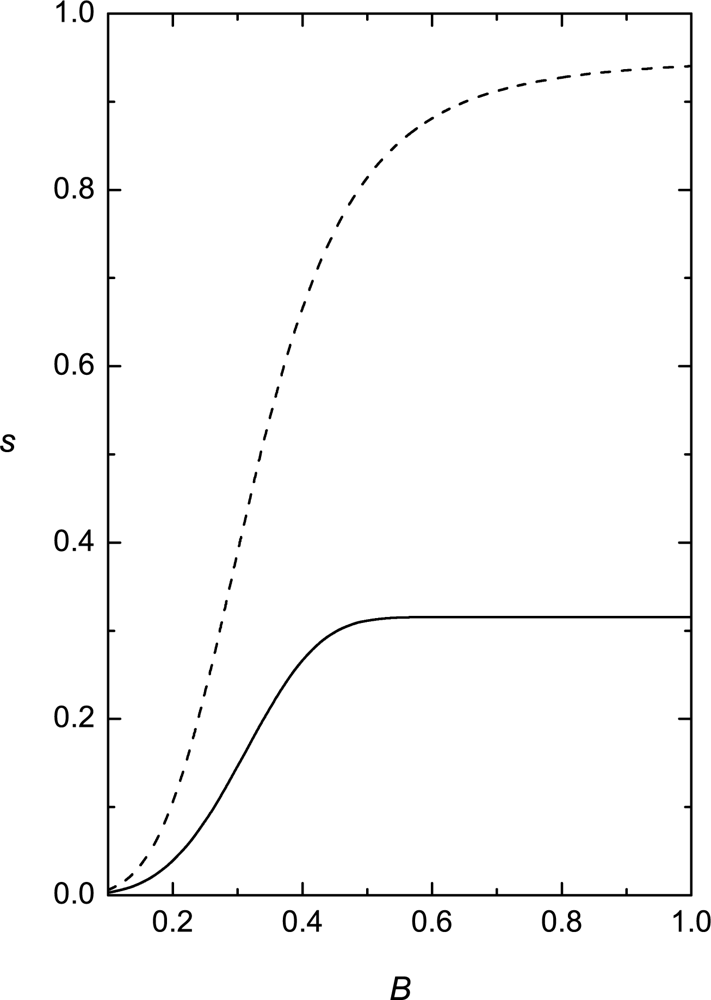
- There is no term linear in Q. This allows for the possibility of an isotropic phase (Q = 0). In the case of external fields, a linear term has to be included and the isotropic phase transforms into a paranematic phase (a phase with a very low degree of orientational order).
- If B > 0, the transition is first order (the order parameter changes discontinuous at the transition), while if B = 0 the transition is second order (the order parameter is continuous at the transition, but its first derivative with respect to temperature is discontinuous). The other possible mechanism to mimic the first order phase transition is to consider B = 0 and C < 0. In this case a stabilizing six order term with E > 0 is required.
- To ensure stability of the nematic phase, C must be positive.
3.3. Relation between Landau–de Gennes and Maier–Saupe Free Energies for Uniaxial Nematics
4. Influence of Random Field on Structural and Phase Transition Properties: A Mesoscopic Phenomenological Model
4.1. Structural Behavior : Domain-Type Patterns
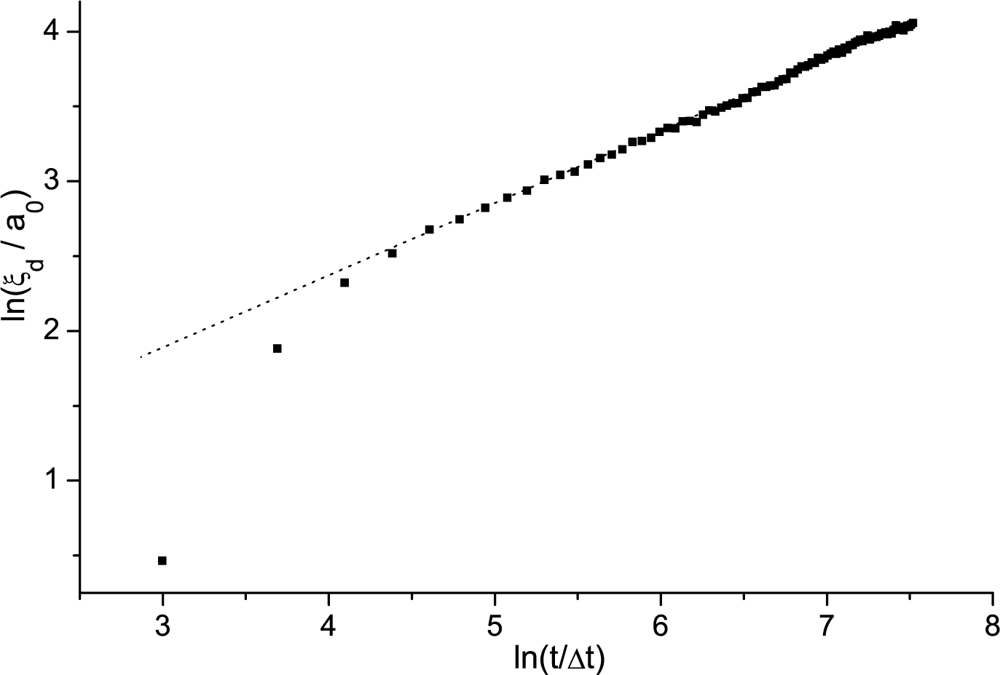
Domain Coarsening Following a Fast Enough Phase Transition
Imry-Ma Domain Pattern
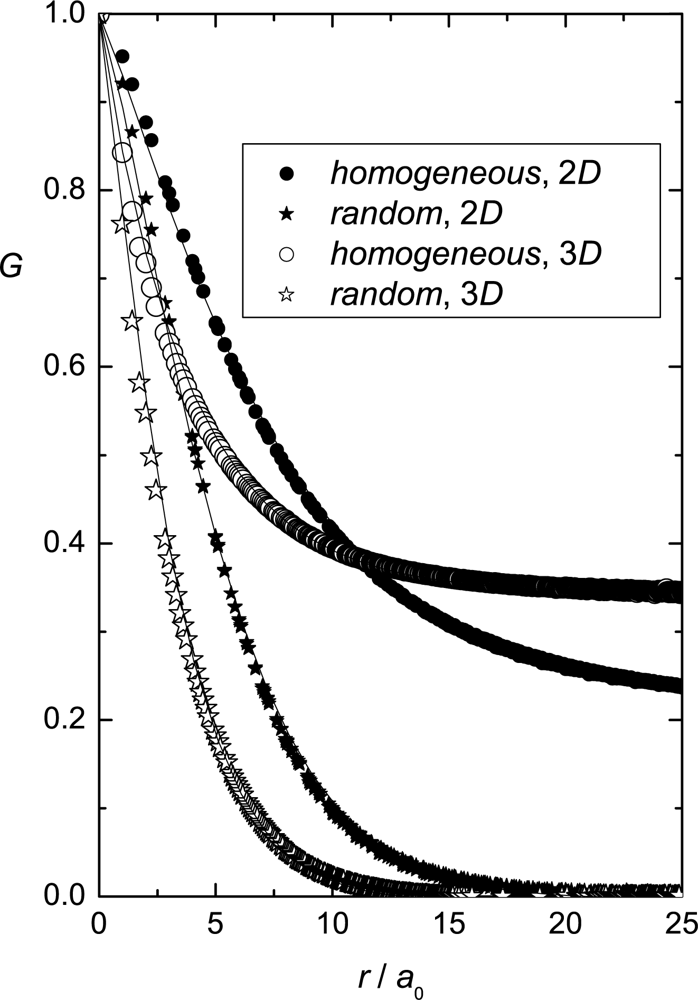
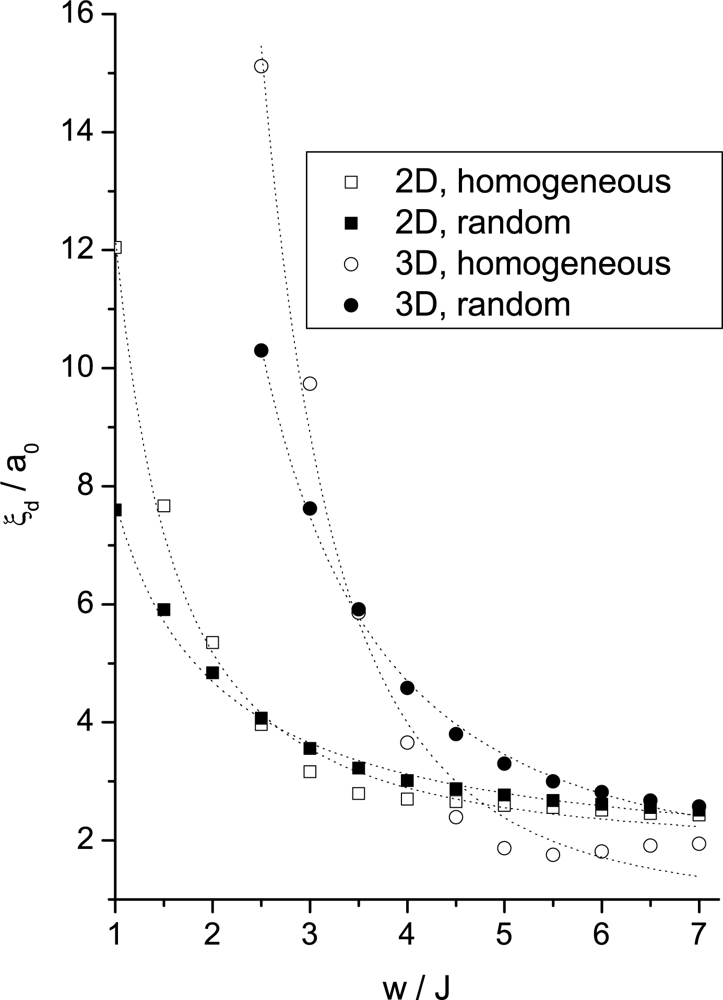
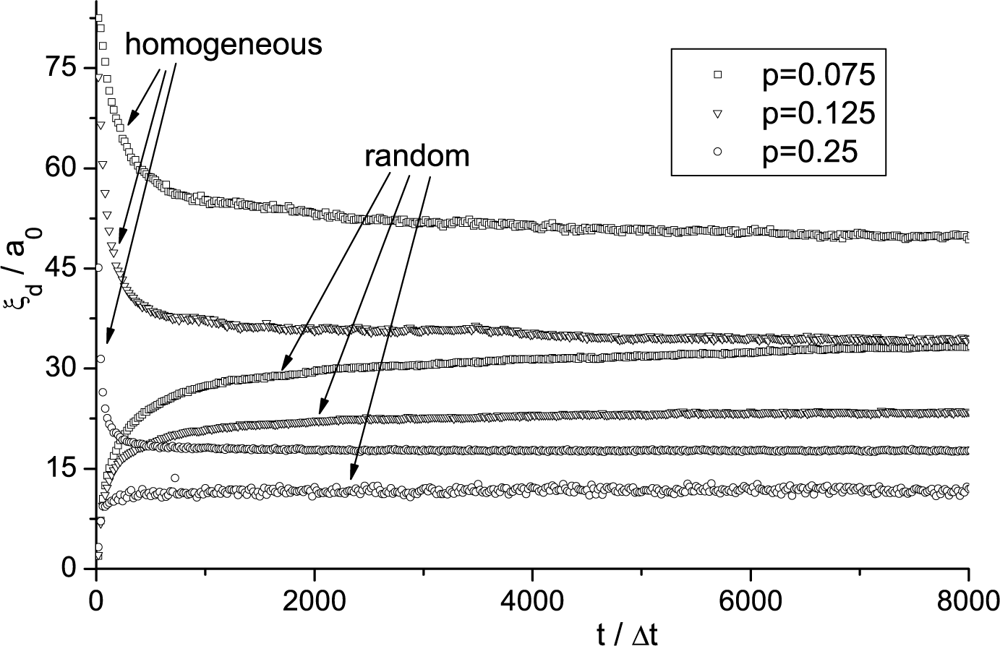
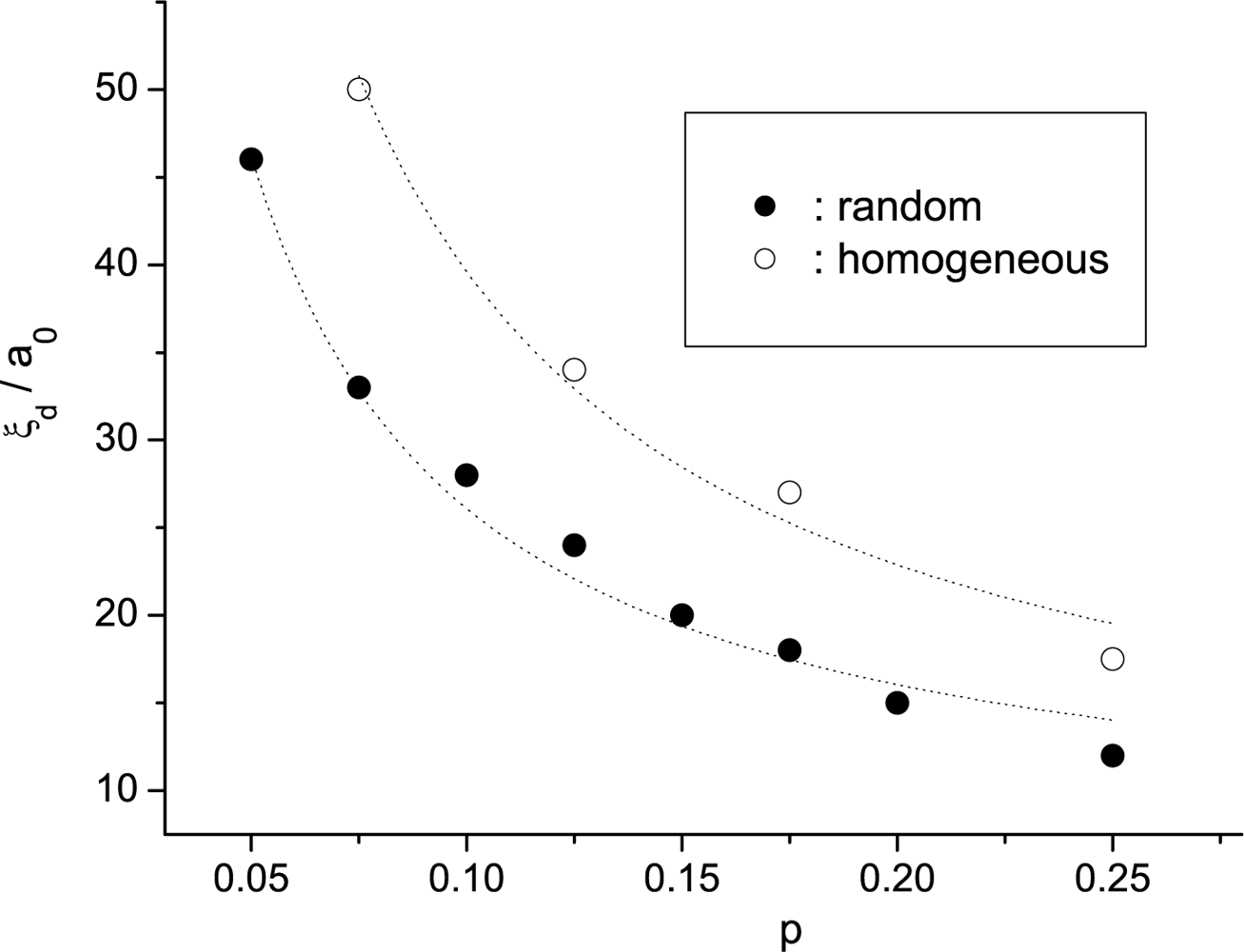
Simulation Results
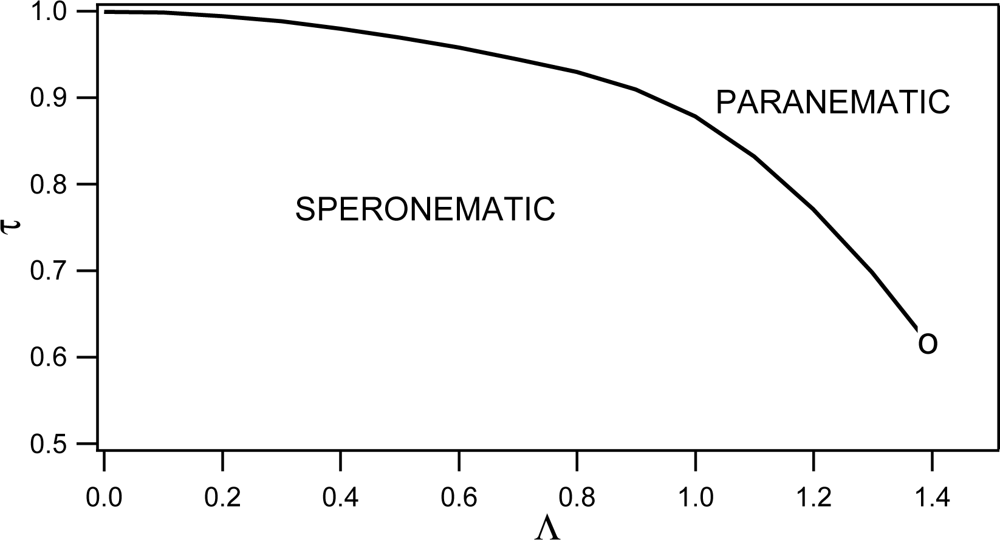
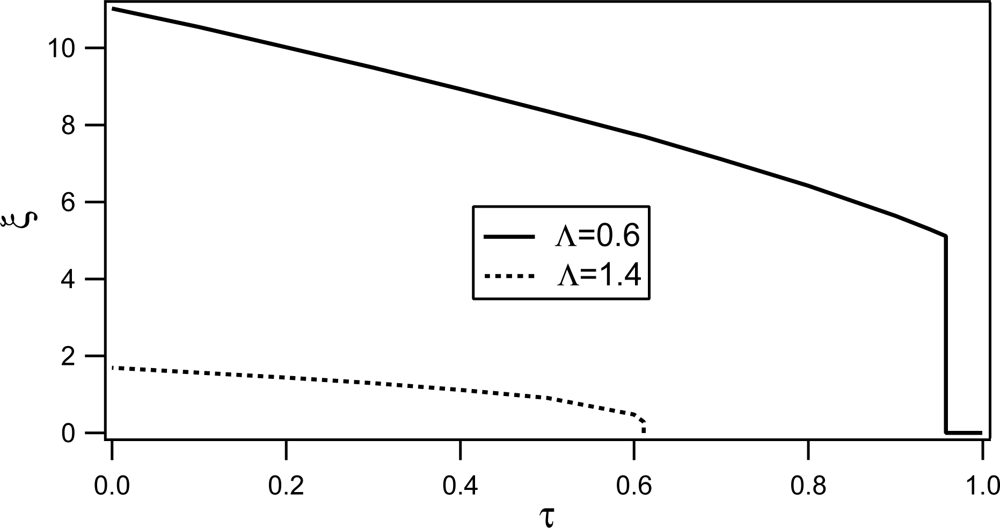
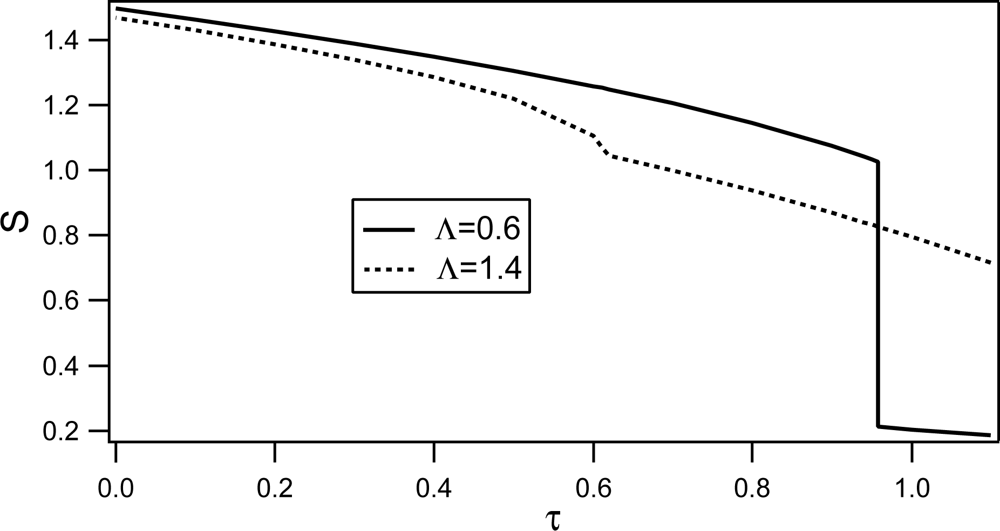
4.2. Phase Behavior
Phase behavior of RAN
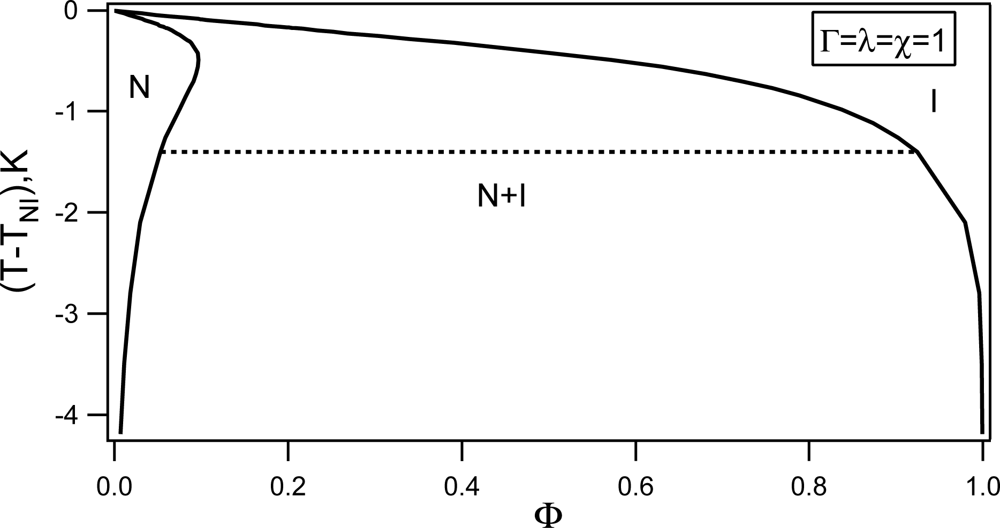
Nematic-non-Nematic Mixture
4.3. Experimental Observations
5. Concluding Remarks
Acknowledgments
References and Notes
- Fisher, DS; Grinstein, GM; Khurana, A. Theory of random magnets. Phys Today 1988, 56–67. [Google Scholar]
- Feldman, DE. Quasi-long range order in glass states of impure liquid crystals, magnets and superconductors. Int. J. Mod. Phys. B 2001, 15, 2945–2976. [Google Scholar]
- Bellini, T; Radzihovsky, L; Toner, J; Clark, NA. Universality and scaling in the disordering of a smectic liquid crystal. Science 2001, 294, 1074–1079. [Google Scholar]
- Zurek, WH. Cosmological experiments in superfluid-helium. Nature 1985, 317, 505–508. [Google Scholar]
- Aharony, A. Critical behavior of amorphous magnets. Phys. Rev. B 1975, 12, 1038–1048. [Google Scholar]
- Lubensky, TC. Critical properties of random-spin models from the epsilon expansion. Phys. Rev. B 1975, 11, 3573–3580. [Google Scholar]
- Imry, Y; Wortis, M. Influence of quenched impurities on first-order phase transitions. Phys. Rev. B 1979, 19, 3580–3585. [Google Scholar]
- Harris, AB. Effect of random defects on critical behavior of Ising models. J. Phys. C 1974, 7, 1671–1692. [Google Scholar]
- Popa-Nita, V; Kralj, S. Transformation of phase transitions driven by an anisotropic random field. Phys Rev E 2005, 71, 042701-1-4. [Google Scholar]
- Halperin, BI; Lubensky, TC; Ma, S. First-order phase transitions in superconductors and smectic-A liquid crystals. Phys. Rev. Lett 1974, 32, 292–295. [Google Scholar]
- Anisimov, MA; Cladis, PE; Gorodetskii, EE; Huse, DA; Podneks, VE; Taratuta, VG; van Saarloos, W; Voronov, VP. Experimental test of a fluctuation-induced first-order phase transition: The nematicsmectic-A transition. Phys. Rev. A 1990, 41, 6749–6762. [Google Scholar]
- Imry, Y; Ma, S. Random-field instability of the ordered state of continuous symmetry. Phys. Rev. Lett 1975, 35, 1399–1401. [Google Scholar]
- Larkin, AI. Effect of inhomogeneities on structure of mixed state of superconductors. Sov. Phys. JETP 1970, 31, 784–791. [Google Scholar]
- Aharony, A; Pytte, E. Infinite susceptibility phase in random uniaxial anisotropy magnets. Phys. Rev. Lett 1980, 45, 1583–1586. [Google Scholar]
- Giamarchi, T; Le Doussal, P. Elastic theory of flux lattices in the presence of weak disorder. Phys. Rev. B 1995, 52, 1242–1270. [Google Scholar]
- Liquid Crystals in Complex Geometries Formed by Polymer and Porous Networks; Crawford, GP; Žumer, S (Eds.) Oxford University Press (Taylor and Francis): London, UK, 1996.
- Kleman, M; Lavrentovich, OD. Soft Matter Physics; Springer: Berlin, Germany, 2002. [Google Scholar]
- Palffy-Muhoray, P. The diverse world of liquid crystals. Phys. Today 2007, 60, 54–60. [Google Scholar]
- Mermin, N. The topological theory of defects in ordered media. Rev. Mod. Phys 1979, 51, 591–648. [Google Scholar]
- Spergel, DN; Turok, NG. Textures and cosmic structure. Scient. Am 1992, 266, 52–59. [Google Scholar]
- Kibble, T. Phase-transition dynamics in the lab and the universe. Phys. Today 2007, 60, 47–52. [Google Scholar]
- Kurik, MV; Lavrentovich, OD. Defects in liquid crystals - homotopy-theory and experimental investigations. Sov Phys Usp 1988, 3–53. [Google Scholar]
- de las Heras, D; Velasco, E; Mederos, L. Capillary smectization and layering in a confined liquid crystal. Phys Rev Lett 2005, 94, 017801-1-4. [Google Scholar]
- Iannacchione, GS; Garland, CW; Mang, JT; Rieker, TP. Calorimetric and small angle X-ray scattering study of phase transitions in octylcyanobiphenyl-aerosil dispersions. Phys. Rev. E 1998, 58, 5966–5981. [Google Scholar]
- Hourri, A; Bose, TK; Thoen, J. Effect of silica aerosil dispersions on the dielectric properties of a nematic liquid crystal. Phys Rev E 2001, 63, 051702-1-6. [Google Scholar]
- Cordoyiannis, G; Kralj, S; Nounesis, G; Žumer, S; Kutnjak, Z. Soft-stiff regime crossover for an aerosil network dispersed in liquid crystals. Phys Rev E 2006, 73, 031707-1-4. [Google Scholar]
- Bellini, T; Clark, NA; Muzny, CD; Wu, L; Garland, CW; Schaefer, DW; Oliver, BJ. Phase behavior of the liquid crystal 8CB in a silica aerogel. Phys. Rev. Lett 1992, 69, 788–791. [Google Scholar]
- Kralj, S; Zidanšek, A; Lahajnar, G; Muševič, I; Žumer, S; Blinc, R; Pintar, MM. Nematic ordering in porous glasses: A deuterium NMR study. Phys. Rev. E 1996, 53, 3629–3638. [Google Scholar]
- Aliev, FM; Breganov, MN. Dielectric polarization and dynamics of molecular motion of polar liquid crystals in micropores and macropores. Sov. Phys. JETP 1989, 68, 70–86. [Google Scholar]
- Tripathi, S; Rosenblatt, C; Aliev, FM. Orientational susceptibility in porous glass near a bulk nematic-isotropic phase transition. Phys. Rev. Lett 1994, 72, 2725–2729. [Google Scholar]
- Dadmun, MD; Muthukumar, M. The nematic to isotropic transition of a liquid crystal in porous media. J. Chem. Phys 1993, 98, 4850–4852. [Google Scholar]
- Kutnjak, Z; Kralj, S; Lahajnar, G; Žumer, S. Calorimetric study of octylcyanobiphenyl liquid crystal confined to a controlled-pore glass. Phys Rev E 2003, 68, 021705-1-12. [Google Scholar]
- Reinitzer, F. Contributions to the knowledge of cholesterol. Liq. Cryst 1989, 5, 7–25. [Google Scholar]
- Lehmann, O. Űber Fliessende Krystalle. Zs. Phys. Ch 1889, 4, 462–470. [Google Scholar]
- Friedel, G. Mesomorfic states of matter. Annales de Physique 1922, 18, 273–287. [Google Scholar]
- Stephen, MJ; Straley, JP. Physics of liquid crystals. Rev. Mod. Phys 1974, 46, 617–704. [Google Scholar]
- Introduction to Liquid Crystals; Priestley, EB; Wojtowicz, PJ; Sheng, P (Eds.) Plenum Press: New York, NY, USA, 1974.
- The Molecular Physics of Liquid Crystals; Luckhurst, GR; Gray, GW (Eds.) Academic Press: New York, NY, USA, 1979.
- Vertogen, G; de Jeu, WH. Thermotropic Liquid Crystals: Fundamentals; Springer: Berlin, Germany, 1988. [Google Scholar]
- Physics of Liquid Crystalline Materials; Khoo, IC (Ed.) Gordon and Breach: Amsterdam, Holand, 1991.
- Chandrasekhar, S. Liquid Crystals; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- de Gennes, PG; Prost, J. The Physics of Liquid Crystals, 2nd ed; Oxford University Press: New York, USA, 1993. [Google Scholar]
- Handbook of Liquid Crystal Research; Collings, PJ; Patel, JS (Eds.) Oxford University Press: Oxford, NY, USA, 1997.
- Singh, S. Phase transitions in liquid crystals. Phys. Rep 2000, 324, 107–269. [Google Scholar]
- Oswald, P; Pieranski, P. Nematic and Cholesteric Liquid crystals; concepts and physical properties illustrated by experiments; Taylor and Francis Group; CRC Press: Boca Raton, FL, USA, 2005; in Liquid Crystals Book Series, Boca Raton. [Google Scholar]
- White, AM; Windle, AH. Liquid Crystal Polymers; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Collyer, AA. Liquid Crystals Polymers: From Structures to aplications; Elsevier: Oxford, UK, 1993. [Google Scholar]
- Liquid Crystals Polymers; Carfagna, C (Ed.) Pergamon Press: Oxford, UK, 1994.
- Popa-Nita, V; Sluckin, TJ; Wheeler, AA. Statics and kinetics at the nematic-isotropic interface: Effects of biaxiality. J. Phys. II France 1997, 7, 1225–1243. [Google Scholar]
- Zannoni, C. Distribution functions and order parameters. In The Molecular Physics of Liquid Crystals; Luckhurst, GR, Gray, GW, Eds.; Academic Press: New York, NY, USA, 1979; pp. 51–83. [Google Scholar]
- Onsager, L. The Effects of Shapes on the Interacti on of Colloidal Particles. Ann. N.Y. Acad. Sci 1949, 51, 627–645. [Google Scholar]
- Cotter, MA. Hard particle theories of nematics. In The Molecular Physics of Liquid Crystals; Luckhurst, GR, Gray, GW, Eds.; Academic Press: New York, NY, USA, 1979; pp. 169–180. [Google Scholar]
- Luckhurst, GR. Molecular field theories of nematics. In The Molecular Physics of Liquid Crystals; Luckhurst, GR, Gray, GW, Eds.; Academic Press: New York, NY, USA, 1979; pp. 85–118. [Google Scholar]
- Cotter, MA. The van der Waals approach to nematic liquids. In The Molecular Physics of Liquid Crystals; Luckhurst, GR, Gray, GW, Eds.; Academic Press: New York, NY, USA, 1979; pp. 181–189. [Google Scholar]
- Gelbart, WM. Molecular Theory of Nematic Liquid Crystals. J. Phys. Chem 1982, 86, 4298–4307. [Google Scholar]
- Hansen, JP; McDonald, IR. Theory of Simple Liquids; Academic Press: London, UK, 1976. [Google Scholar]
- Evans, R. The nature of the liquid-vapour interface and other topics in the statistical mechanics of non-uniform, classical fluids. Adv. Phys 1979, 28, 143–200. [Google Scholar]
- Singh, Y. Density functional theory of freezing and properties of the ordered phase. Phys. Rep 1991, 207, 351–444. [Google Scholar]
- Gramsbergen, EF; Longa, L; de Jeu, WH. Landau theory of the nematic-isotropic phase transition. Phys. Rep 1986, 135, 195–257. [Google Scholar]
- Landau, LD; Lifshitz, EM. Statistical Physics, 2nd ed; Pergamon Press: Oxford, UK, 1969. [Google Scholar]
- Katriel, J; Kventsel, GF; Luckhurst, GR; Sluckin, TJ. Free energies in the Landau and molecular field approaches. Liq. Cryst 1986, 1, 337–355. [Google Scholar]
- Kralj, S; Bradač, Z; Popa-Nita, V. The influence of nanoparticles on the phase and structural ordering for nematic liquid crystals. J Phys Condens Matter 2008, 20, 244112–244122. [Google Scholar]
- Maritan, A; Cieplak, M; Banavar, R. Nematic-isotropic transition in porous media. In Liquid Ccrystals in Complex Geometries Formed by Polymer and Porous Networks; Crawford, GP, Z̆umer, S, Eds.; Oxford University Press (Taylor and Francis): London, UK, 1996; pp. 483–496. [Google Scholar]
- Cleaver, DJ; Kralj, S; Sluckin, TJ; Allen, MP. The random anisotropy nematic spin model. In Liquid Crystals in Complex Geometries Formed by Polymer and Porous Networks; Crawford, GP, Z̆umer, S, Eds.; Oxford University Press (Taylor and Francis): London, UK, 1996; pp. 467–481. [Google Scholar]
- Radzihovsky, L; Toner, J. Smectic liquid crystals in random environments. Phys. Rev. B 1999, 60, 206–257. [Google Scholar]
- Jacobsen, B; Saunders, K; Radzihovsky, L; Toner, J. Two new topologically ordered glass phases of smectics confined in anisotropic random media. Phys. Rev. Lett 1999, 83, 1363–1366. [Google Scholar]
- Chakrabarti, J. Simulation evidence of critical behavior of isotropic-nematic phase transition in a porous medium. Phys. Rev. Lett 1998, 81, 385–388. [Google Scholar]
- Popa-Nita, V. Statics and kinetics at the nematic-isotropic interface in porous media. Eur. Phys. J. B 1999, 12, 83–90. [Google Scholar]
- Popa-Nita, V. Magnetic-field-induced isotropic-nematic phase transition in porous media. Chem. Phys 1999, 246, 247–253. [Google Scholar]
- Popa-Nita, V; Romano, S. Nematic-smectic A phase transition in porous media. Chem. Phys 2001, 264, 91–99. [Google Scholar]
- Kralj, S; Popa-Nita, V. Random anisotropy nematic model: connection with experimental systems. Eur. Phys. J. E 2004, 14, 115–125. [Google Scholar]
- Popa-Nita, V; Kralj, S. Random anisotropy nematic model: Nematicnon-nematic mixture. Phys Rev E 2006, 73, 041705-1-8. [Google Scholar]
- Popa-Nita, V; van der Schoot, P; Kralj, S. Influence of a random field on particle fractionation and solidification in liquid-crystal colloid mixtures. Eur. Phys. J. E 2006, 221, 189–199. [Google Scholar]
- Kralj, S; Virga, EG. Universal fine structure of nematic hedgehogs. J. Phys. A: Math. Gen 2001, 34, 829–838. [Google Scholar]
- Bray, AJ. THeory of phase ordering kinetics. Adv. Phys 1994, 43, 357–459. [Google Scholar]
- Bradač, Z; Kralj, S; Žumer, S. Molecular dynamics study of the isotropic-nematic quench. Phys Rev E 2002, 65, 021705-1-10. [Google Scholar]
- Volovik, GE. Topological singularities on the surface of an ordered system. JETP Lett 1978, 28, 59–63. [Google Scholar]
- Toth, G; Denniston, C; Yeomans, JM. Hydrodynamics of topological defects in nematic liquid crystals. Phys Rev Lett 2002, 88, 105504-1-4. [Google Scholar]
- Svetec, M; Bradač, Z; Kralj, S; Žumer, S. Annihilation of nematic point defects: pre-collision and post-collision evolution. Eur. Phys. J. E 2004, 19, 5–15. [Google Scholar]
- Kibble, TWB. Topology of cosmic domains and strings. J. Phys. A 1976, 9, 1387–1398. [Google Scholar]
- Karra, G; Rivers, RJ. Reexamination of Quenches in 4He (and 3He). Phys. Rev. Lett 2000, 81, 3707–3710. [Google Scholar]
- Araki, T; Tanaka, H. Colloidal Aggregation in a nematic liquid crystal: topological arrest of particles by a single-stroke disclination line. Phys Rev Lett 2006, 97, 127801-1-4. [Google Scholar]
- Bellini, T; Buscagli, M; Chiccoli, C; Mantegazza, F; Pasini, P; Zannoni, C. Nematics with quenched disorder: What is left when long range order is disrupted. Phys Rev Lett 2000, 31, 1008–1011. [Google Scholar]
- Cvetko, M; Ambrožič, M; Kralj, S. Memory effects in randomly perturbed systems exhibiting continuous symmetry breaking. Liq. Cryst 2009, 36, 33–42. [Google Scholar]
- Ambrožič, M; Sluckin, TJ; Cvetko, M; Kralj, S. Stability and metastability in nematic glasses: A computational study. In Metastable Systems under Pressure; Rzoska, S, Ed.; Springer Verlag: Berlin, Germany, 2009. [Google Scholar]
- Ermak, DL. Computer simulation of charged particles in solution. 1. Technique and equilibrium properties. J. Chem. Phys 1975, 62, 4189–4196. [Google Scholar]
- Barbero, G. Some considerations on the elastic theory for nematic liquid crystal. Mol. Cryst. Liq. Cryst 1991, 195, 199–220. [Google Scholar]
- Lebwohl, PA; Lasher, G. Nematic-liquid-crystal order-A monte carlo calculation. Phys. Rev. A 1972, 6, 426–429. [Google Scholar]
- Flory, PJ. Principles of Polymer Chemistry; Cornell University Press: Ithaca, Greece, 1953. [Google Scholar]
- Popa-Nita, V; Sluckin, TJ; Kralj, S. Waves at the nematic-isotropic interface: Thermotropic nematogen-non-nematogen mixtures. Phys Rev E 2005, 71, 061706-1-13. [Google Scholar]
- Chaikin, PM; Lubensky, TC. Principles of Condensed Matter Physics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Feldman, DE; Pelcovits, RA. Liquid crystals in random porous media: Disorder is stronger in low-density. Phys Rev E 2004, 70, 040702R-1-4. [Google Scholar]
- Fricke, J. Aerogels - highly tenous solids with fascinating properties. J. Non-Cryst. Solids 1988, 100, 169–173. [Google Scholar]
- Haga, H; Garland, CW. Effect of silica aerosil particles on liquid-crystal phase transitions. Phys. Rev. E 1997, 56, 3044–3052. [Google Scholar]
- Kutnjak, Z; Kralj, S; Lahajnar, G; Žumer, S. Influence of finite size and wetting on nematic and smectic phase behavior of liquid crystal confined to controlled-pore matrices. Phys Rev E 2004, 70, 51703-1-11. [Google Scholar]
- Kralj, S; Cordoyiannis, G; Zidanšek, A; Lahajnar, G; Amenitsch, H; Žumer, S; Kutnjak, Z. Presmectic wetting and supercritical-like phase behavior of octylcyanobiphenyl liquid crystal confined to controlled-pore glass matrices. J. Chem. Phys 2007, 127, 154905–154915. [Google Scholar]
- Leon, N; Korb, JP; Bonalde, I; Levitz, P. Universal nuclear spin relaxation and long-range order in nematics strongly confined in mass fractal silica gels. Phys Rev Lett 2004, 92, 1955-04-1-4. [Google Scholar]
- Sheng, P. Boundary-layer phase transition in nematic liquid crystals. Phys. Rev. A 1982, 26, 1610–1617. [Google Scholar]


© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Popa-Nita, V.; Gerlič, I.; Kralj, S. The Influence of Disorder on Thermotropic Nematic Liquid Crystals Phase Behavior. Int. J. Mol. Sci. 2009, 10, 3971-4008. https://doi.org/10.3390/ijms10093971
Popa-Nita V, Gerlič I, Kralj S. The Influence of Disorder on Thermotropic Nematic Liquid Crystals Phase Behavior. International Journal of Molecular Sciences. 2009; 10(9):3971-4008. https://doi.org/10.3390/ijms10093971
Chicago/Turabian StylePopa-Nita, Vlad, Ivan Gerlič, and Samo Kralj. 2009. "The Influence of Disorder on Thermotropic Nematic Liquid Crystals Phase Behavior" International Journal of Molecular Sciences 10, no. 9: 3971-4008. https://doi.org/10.3390/ijms10093971



