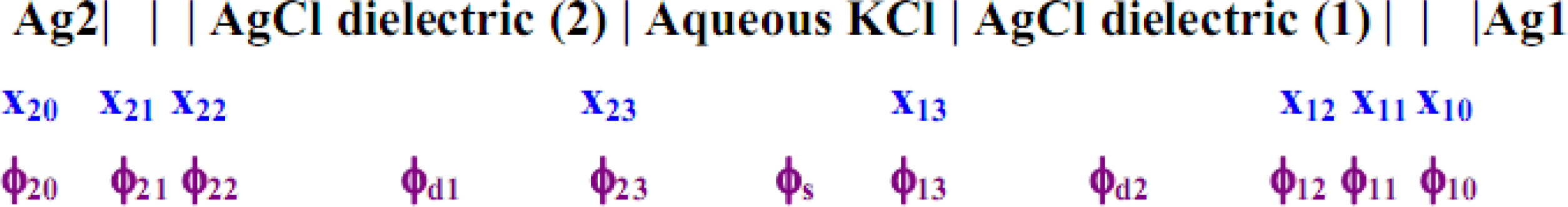5.1. Computational Method for Cell E.M.F
For cell (1a), the e.m.f. E is given by (2a-b) as:
where E
ø is the standard potential of the cell concerned, and which is deemed to cancel in practical applications, leading to zero net potential; for what follows, γ
– refers to the single ionic activity coefficient which is calculated from the Pitzer equation[
37], where for simple 1-1 electrolytes, these equations are symmetrical in the single activity coefficients of both anion and cation and is numerically the same as the mean ionic activity of the salt concerned and may be reduced to the general form:
where F, B
mx and C
mx are rather complicated functions[
37] of the ionic strength I, and m is the (molality) concentration for the species concerned. Since E
ø = (−μ(Ag) – μ
o(Cl
−) + μ(e) + μ(AgCl))/F and μ
l (e) is assumed invariant in μ(e) = μ
F(e) + μ
l (e), (7) becomes by virtue of subtraction at fixed (25 °C) temperature:
where the subscripts in μ
F refer to the electronic chemical potential of the cell concerned. If A is the total surface area of the electrode then:
from (3), where δN appears in (4). Since ΔΨ
d = ℑ
AgCl|Cl − (RT/F)ln m.γ
– (where ℑ
AgCl|Cl = ℑ
o), then for any fixed m, ΔΨ
d = ΔΨ
d (γ
–). From (3a,b,d), we may write:
F
gen is a generic function that is utilized to determine the charge Q on the electrode; the forms utilized here are given in 3(a,b,d), so that for fixed m, Q = Q(γ
–). Further, we note that at 0.1 N, we wrote:
Since ℑ
o = (−μ(Ag) – μ
o(Cl
−) + μ(e) + μ(AgCl))/F where ℑ|
neutral refers to the neutral state when Q = 0, we write:
where δℑ
o = δμ(e)/F is due to the change of ℑ
o due to charge transfer. At 0.1 N ℑ
o is known precisely (the value 0.394031V is used here for the theoretical calculations), so that Q|
m = 0.1 may be calculated, and δℑ
o may be determined from (4) and (5). Hence:
Since δℑ
o = δℑ
o (Q) and the functional form δℑ
o may be determined, then for any other value of m (other than 0.1 N where N refers to Normality units of concentration), δℑ
o(mγ) may be computed from (50c). Thus, Q = Q(γ
–) even if ℑ
o is allowed to vary and clearly, μ
F,2 = μ
F,2(γ
–).
The above sub-iterations are used to solve the following equation derived from
(48) by the secant method:
It will be noted that for each secant iteration in (37), the charge Q must be known, and this information is obtained by solving one of
equations (3), depending on electrode choice by a loop utilizing the secant method, and this value of the charge Q is substituted into
equations (50) and
(51).
Equation (45) is solved in exactly the same way irrespective of the type of dielectric model that is used below.
5.2. Theoretical Aspects of The Electrode Electrical Double Layer and the AgCl Dielectric
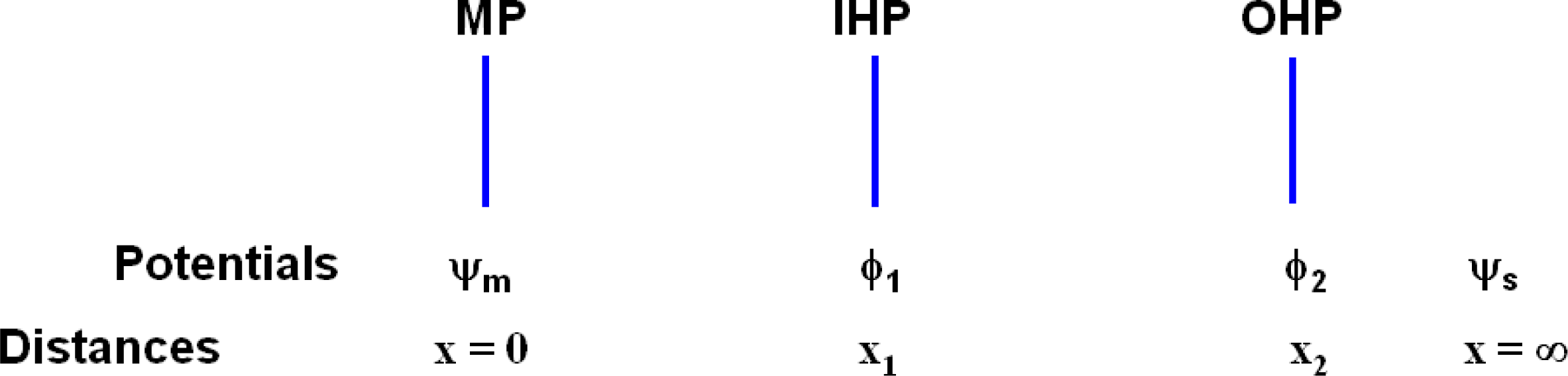
The entire cell may be characterized as having the following potentials for the entire surface perpendicular to the line direction x (from the surface of the metal substrate of the electrode concerned) as depicted in
Figure 7.
In
Figure 7, x
ij represents the interfacial distances of phase boundary j of electrode i, and the ϕ′s are the corresponding potentials at these interfaces; ϕ
s, ϕ
d1 and ϕ
d2 are the bulk solution potentials of the respective regions. Each of the above electrodes i consists of the Ag substrate coated with the AgCl dielectric, which shares a boundary at x
i3 with the aqueous KCl solution; x
i1,2 are the inner and outer Helmholtz planes within the dielectric matrix. The model (abbreviated M1) that is favored here and described immediately below focuses on the net electrode reaction:
where we envisage the Cl
− ions which are freed from the Ag-AgCl interface (x
j0) to distribute themselves according to the usual Debye-Huckel and Gouy-Chapman assumption of the Boltzmann energy distribution, where Φ, the potential within the dielectric obeys the limit Φ → 0 and dΦ/dx→ 0 as x → ∞. Furthermore, there is overall electroneutrality in (52) because the charge on the Ag metal interface equals the charge of the freed Cl
− ions; the actual mechanism of ionic migration of Cl
− ions is of no concern here, although it is of central importance in kinetic studies when various defect mechanisms (eg. Frenkel defects) [
23,
38] are mooted for solid state ionic migrations. In (M1), we do not postulate the free flow of ions from the solution to the AgCl layer treated as a pure dielectric with no strain energy associated with ionic migration, which is the assumption made in for instance the Debye-Huckel theory of ionic activity coefficients. Barring defects, the interstitial distances between fairly rigidly held Ag and Cl atoms is of the order of ~2.77 Å, whilst non-hydrated ionic radii are typically ~1.5Å, which seems to imply that free migration based on strainless movement is not favored and so there is a justified skepticism in utilizing
equations (35) and
(39) to solve for ionic concentrations within the dielectric in equilibrium with the aqueous salt.
It was discovered that for concentrations from 0.01 – 0.1 M KCl, and ℑ
o ~ 0.39 – 0.5 V, the symmetrical neutral electrolyte M
+Cl
− electrode charge
equation(3b) and that for the single anion (3c), which describes model M1 and the mechanism in (52) gave (surprisingly) almost the same charge densities σ
m, i.e.:
for x
d ranging from 3.5 to 10
–7 Å, with a maximum % deviation of ~ 0.8% at high σ
m (~ 20,000 μCcm
–2). Hence these two electrode types are practically indistinguishable for the same single ion concentration
no and permittivity ε. (The cell e.m.f. would differ by 0.01 mV maximum.) Furthermore, no assumptions involving unknown quantities are required to utilize the single-ion electrode
equation (3d), apart from the boundary conditions specified by the Uniqueness Theorem which in this case corresponds to a known physical situation. This is less true for
Equations (35) and
(39) where the activity coefficients must be known, and where it is assumed that no strain energy accompanies ionic migration from the aqueous to the dielectric phase. In
Figure 7 we assume ϕ
i = ϕ
s = ϕ
i2. This accords with normal expectation since the average potential at a long distances from a system of dipoles is zero and also with the analysis of Grimley [
39] where the potential drop of the solution V
s(l) to the dielectric given by Λ + V
c(l) = V
s(l) (his
Figure 1) is negligible, and the net charge per unit area (the actual units used is not specified explicitly) is of the order of 10
–7 μC (his
Figure 2) which is negligible compared to the magnitudes used here (200 – 20 KμCcm
–2).
In order to utilize M1, by the Uniqueness Theorem a boundary condition must be specified. Here we state that within the AgCl dielectric, when x → ∞, the concentration of the Cl
− ions must correspond to that at the AgCl-Aqueous interface, implying analytical continuity of the chloride ion concentration; hence we set [Cl
−] ≡ [Cl
−]
aq with the dielectric constant value of that for AgCl at this interfacial region, and we also set the potential gradient ∂φ/∂
ni = 0 (
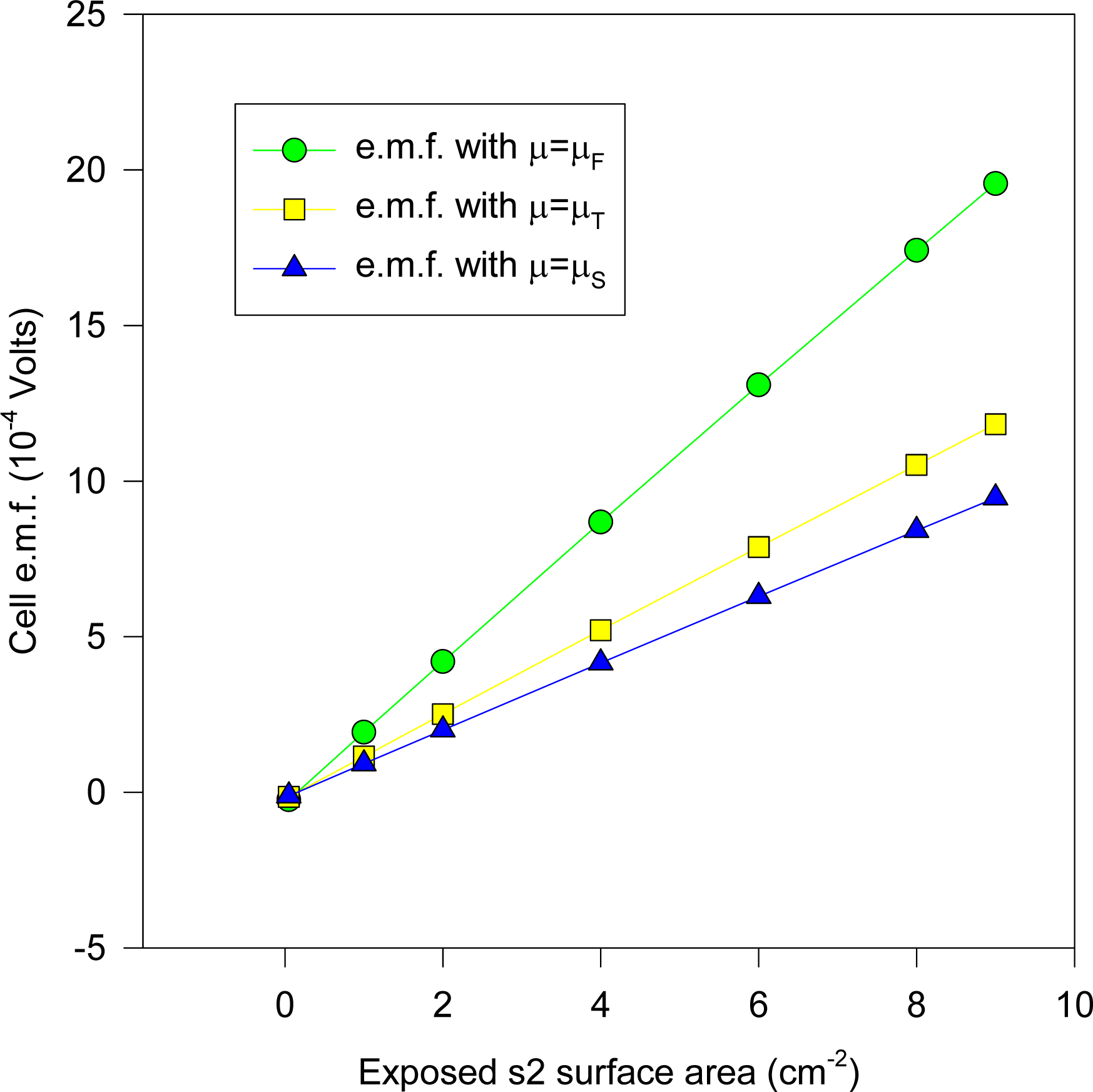
ni is the normal unit vector to the interfacial surface). Clearly, the exact concentration and potential profile is very complicated (being a function of defect concentration etc.), but is of no concern here since we are utilizing the Uniqueness Theorem, to uniquely determine the metal charge density if the potential difference and ionic concentration is specified at one surface of the system. The computed e.m.f.’s for cell (1a) for M1 for x
d = 0 (corresponding to x
i2 = x
i1 = 0) is given in
Figure 8 for ε = ε
AgCl and for the three chemical potentials mentioned here μ
F [
Equation (5)], μ
T [
Equation (7)] and μ
S [
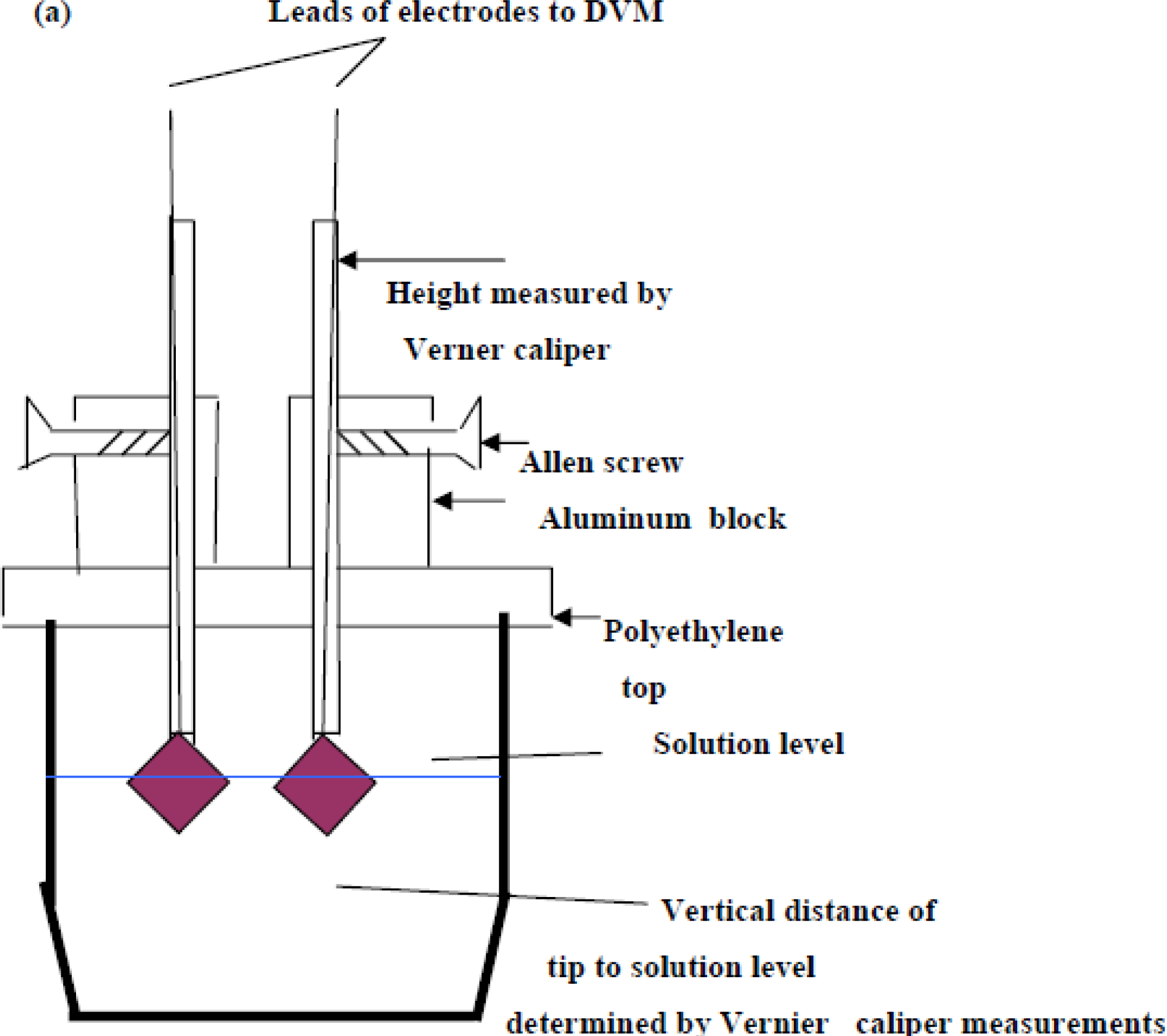
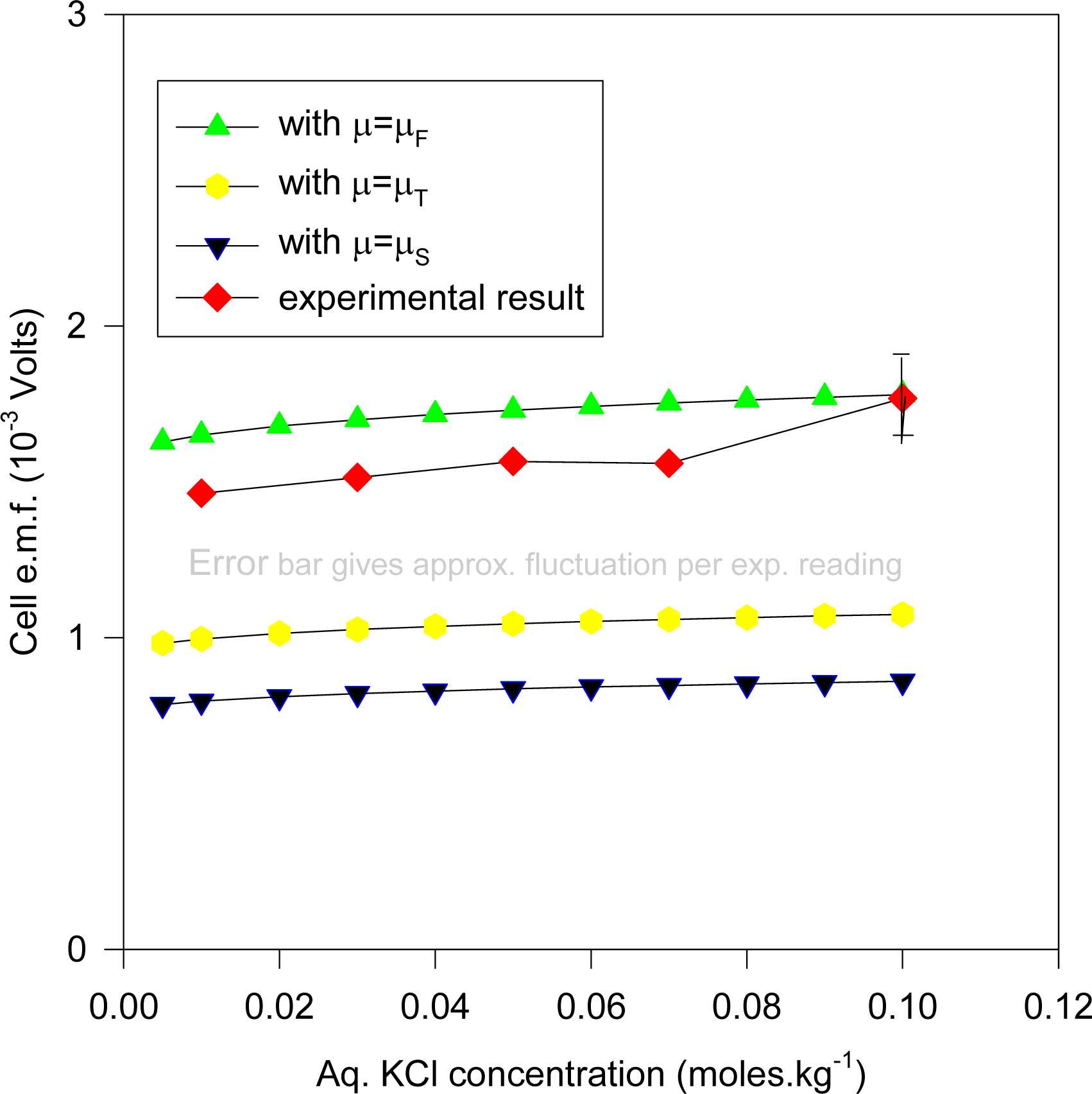
Equation (16)], together with the experimental result where the e.m.f. values are plotted against the KCl molality. The computations are for sizes of electrodes 2 × 2 cm square, with s2 having thickness 0.0225 mm, whilst s1 has thickness 1mm. It was found that comparable theoretical results (up to 0.01 mV maximum) obtain if s1 varied from 0.5 to 1mm, since at such thicknesses the chemical potentials for s1 would remain fairly constant for the different ionic concentrations.
It will be observed that the experimental results depicted in
Figure 8 lie approximately on the curve whose electronic chemical potential is between μ
T and μ
F (but closer to μ
F). This result would accord with the low-temperature specific heat ratio γ (
Equation (6)) which matches experiment almost exactly in the special case of Ag. It may be reasonably argued that the AgCl dielectric does not play a prominent role (despite its occluding the Ag substrate surface) in determining the cell e.m.f., apart from providing a reservoir for Ag
+ and Cl
− ions.
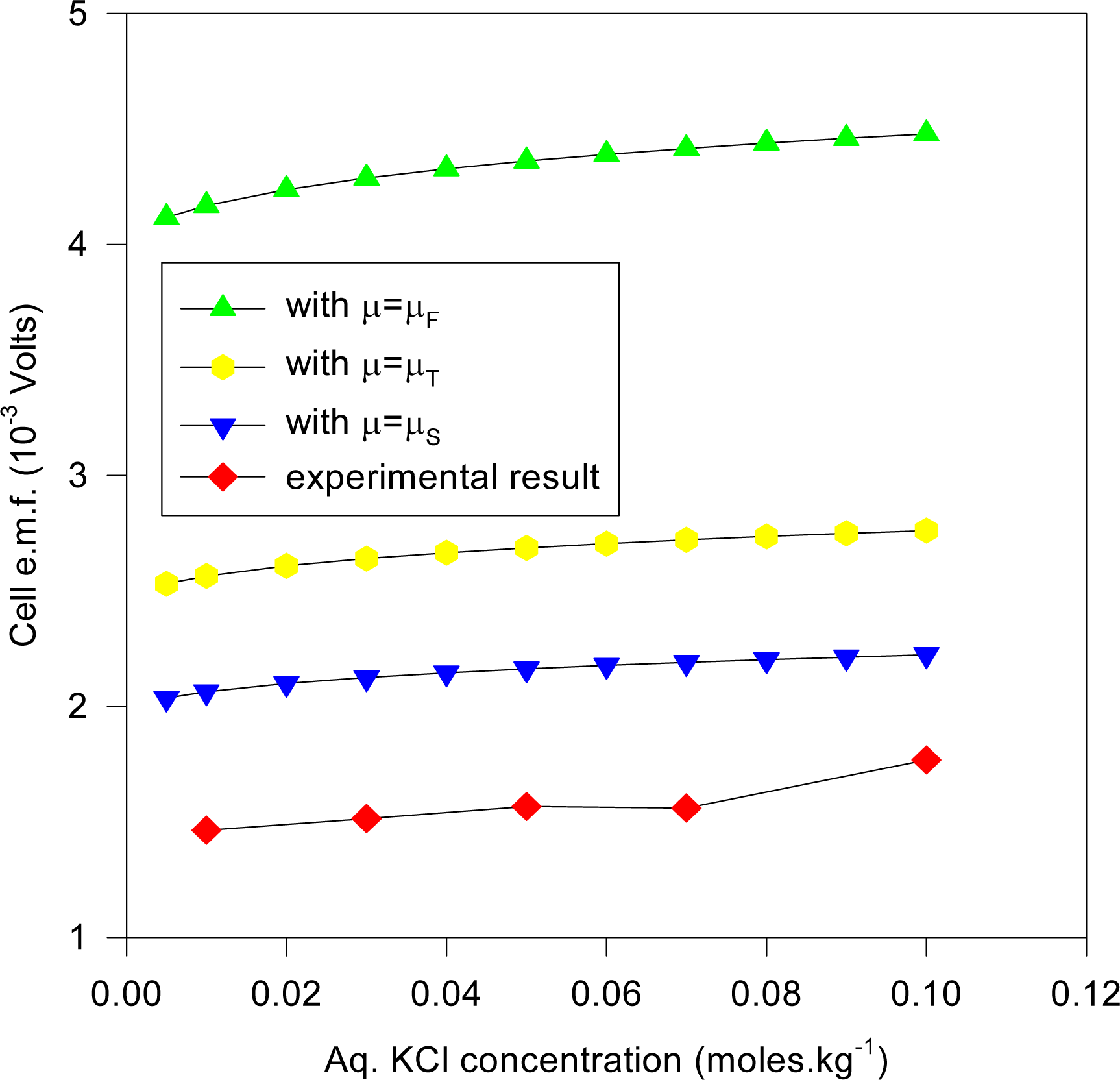
It may be reasonably argued that the AgCl dielectric does not play a prominent role (despite its occluding the Ag substrate surface) in determining the cell e.m.f., apart from providing a reservoir for Ag and Cl
− ions. This situation corresponds to solving for the cell e.m.f. with the H
2O dielectric constant (ε = 78.54) at the vicinity of Cl
− exchange at the electrode, the results of which are presented in
Figure 9 with the same axis variables as for
Figure 8 for the three aforementioned chemical potentials.
The types of electrode reactions that are applicable to the results presented in
Figure 9 include:
with the ions in the aqueous (aq) phase.
It is clear that the computed values are far in excess of the experimental results and so it is safe to infer that AgCl does play a prominent role in distributing the Cl− ions within the dielectric to produce the observed e.m.f. apart from its role as a dielectric ionic reservoir.
It is well known that the Stern modification (GCS systems) with x
d ≠ 0 is widely utilized as a refinement to the Gouy-Chapman theory [
21,
40]. In all these cases, the fundamental assumption is that of thermodynamical equilibrium. Recently, a replica of the current method was applied in a non-equilibrium study[
13] where it was concluded that the Stern modification (non-zero x
i2 of atomic radii dimension in
Figure 7) best explained the results of experiments. It is of course questionable to apply equilibrium theoretical models to non-equilibrium situations.
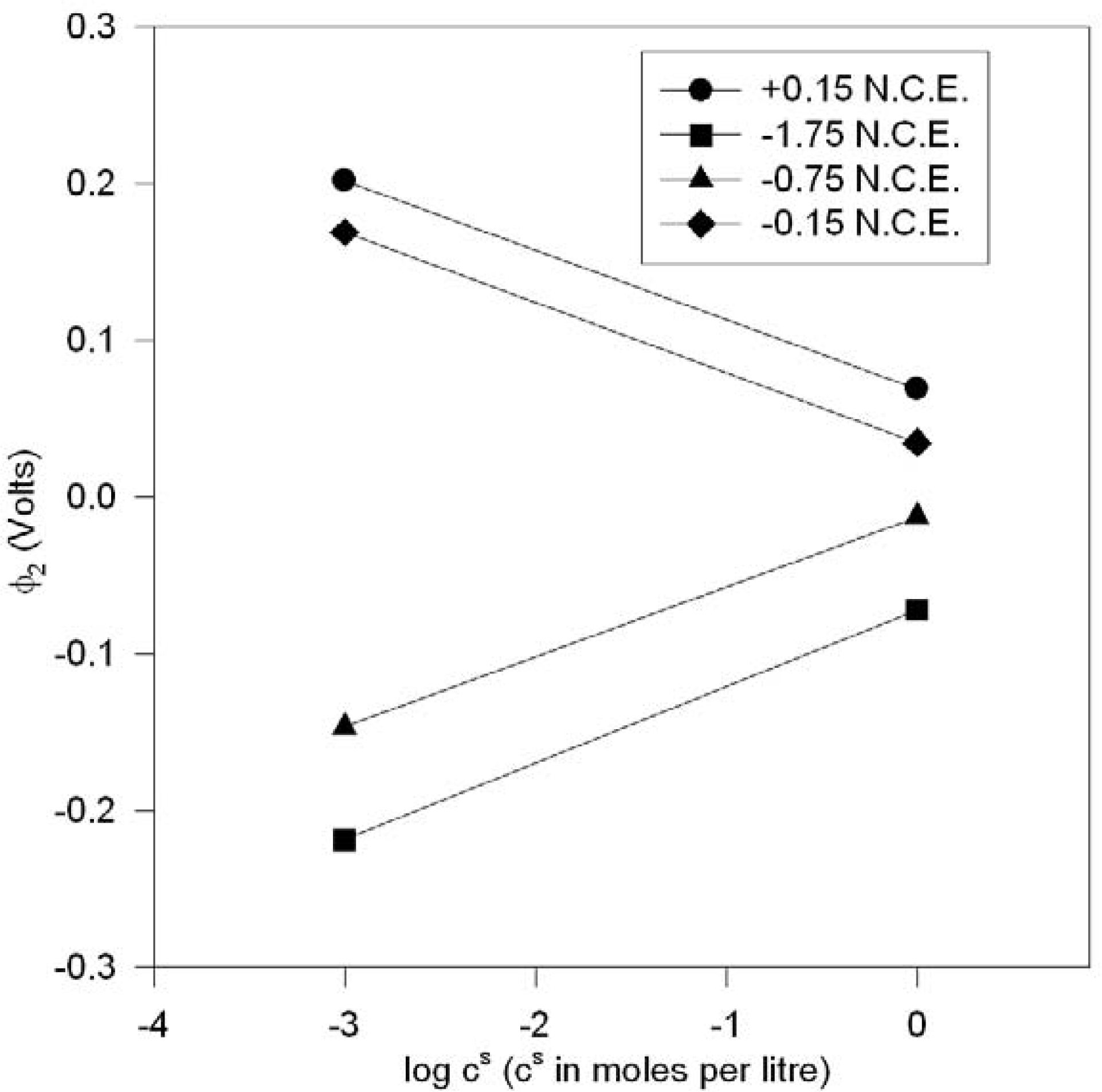
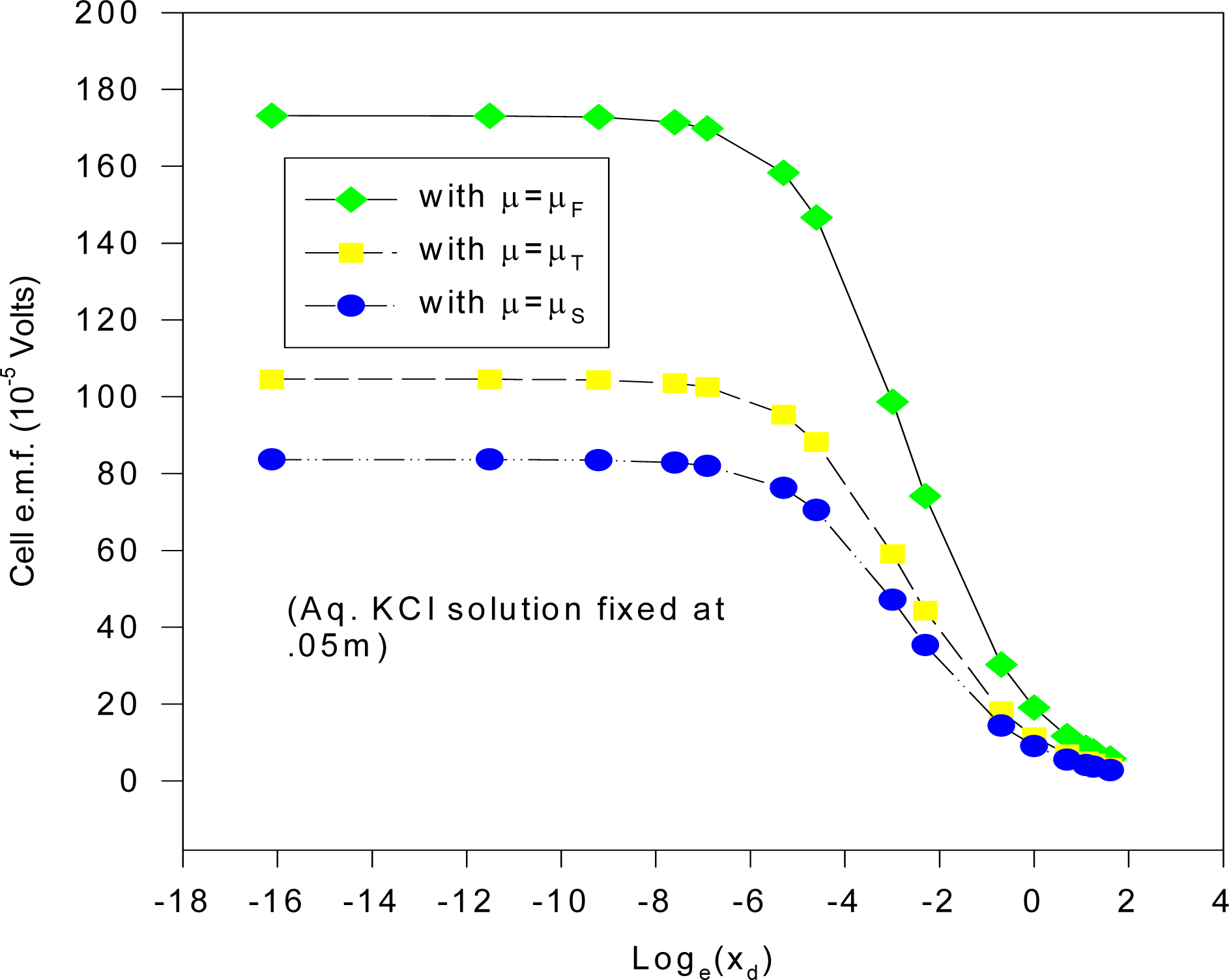
The results of using the Stern model for the electrode processes in our equilibrium electrochemical system (1a) with ε = ε
AgCl, written:
is given in
Figure 10 for the chemical potentials as mentioned before, where the cell e.m.f. is plotted against log
e(x
d) (where x
d = x
i1), the plane of closest approach in the electrode systems for fixed aqueous KCl ionic concentration (0.05 m) ; x
d must correspond to atomic (radius) dimensions (~ 3.5 Å for the hydrated chloride ion).
It is clear from
Figure 10 that x
d must be much less than 10
–3 Å, (between 10
–3 – 10
–7 Å) for there to be fair agreement with experiment; i.e. x
d is far below atomic (or even electron-nuclear atomic core) dimensions, implying that the GC double layer certainly appears more appropriate for our equilibrium study, which incidentally yields good agreement (to at least order of magnitude accuracy) with experimental values for model M1. We can conclude that in those schemes which replicated the present methodology, non-equilibrium effects may well have perturbed the steady-state ionic distribution to such an extent that the GCS equilibrium electrode model appeared to be the most appropriate one, since when we applied this model to a true equilibrium system, the results were not compatible with the experimental results where atomic dimensions are concerned. Although tentative physical considerations might rule out ionic penetrants for the case of the AgCl dielectric, theories have been successfully developed [
41,
42] to account for ionic penetrants in disordered and other media such as zeolites, with typically large pore sizes of ~ 4.5 Å diameter, where the Debye-Huckel theories apply. There is reason therefore to believe that for electrodes that are coated with such materials [
41,
42], one may use the methods of Lemma 6 to derive ionic concentration distribution functions for ions in equilibrium between two dielectrics.
In order to illustrate the feasibility of the method (even if it is not very applicable here) we solve
Equations (35) and
Equations (36) to derive estimated values of the KCl concentration within the AgCl dielectric in equilibrium with the aqueous KCl solution in the case of pure dielectric induced interactions without any lattice strain energy interactions. Unfortunately, little has been developed concerning solid-state ionic activities. As such, we make use of the extended Debye-Huckel expression as the simplest approximation for computing activities γ
±,2 in the AgCl dielectric (phase 2) relative to parameters from the aqueous phase 1, given by:
With the above (56) activity coefficient,
Equation(35) yields two branches of solution of order ~ 2 × 10
–3 and ~ 2 × 10
–4 molal KCl present in the AgCl phase, for aqueous KCl concentration in the range 0.01 – 0.1 m. The average branches from these two branches were taken, because it was noted that by slight adjustment of the ionic radii, a unique solution could be attained by any one fixed concentration of the aqueous KCl. The average solution was monotonically increasing and was linearized to yield the form c = 0.3342 m (c is the KCl concentration in moles L
–1 in the dielectric layer, m is the aqueous molality). The corresponding values for the ionic radii (Å units) were derived by scaling from Shanon’s crystallographic data [
43] and the dimensions for the AgCl unit cell; two values of the radii were used, that for the free aqueous ion (in parenthesis) and the scaled value in the AgCl dielectric, given as 1.6965 (1.81) for Cl
−, and 1.29357 (1.38) for K
+. By a process of trial and error, (36) was solved (no bifurcations were observed at low aqueous molalities < 0.05 m) yielding a monotonically increasing function with increasing aqueous concentration, and it was linearized to c = 0.064246 m (again c is the KCl concentration in moles L
–1 in the dielectric layer, and m is the aqueous molality) ; the ionic radii used was 1.6966 (1.81) for Cl
−, and 1.3077 (1.38) for K
+ for the aqueous concentration range 0.01 – 0.1m KCl. We then use these concentrations in the AgCl phase to predict the cell e.m.f. where the bulk ionic concentration corresponds to that in the AgCl dielectric layer, and where the electrode used is either of the kind described by
equations (3a) or
(3d), corresponding to the electrode equilibria (54) in the dielectric (non-aqueous) phase. The results of the computation are shown in
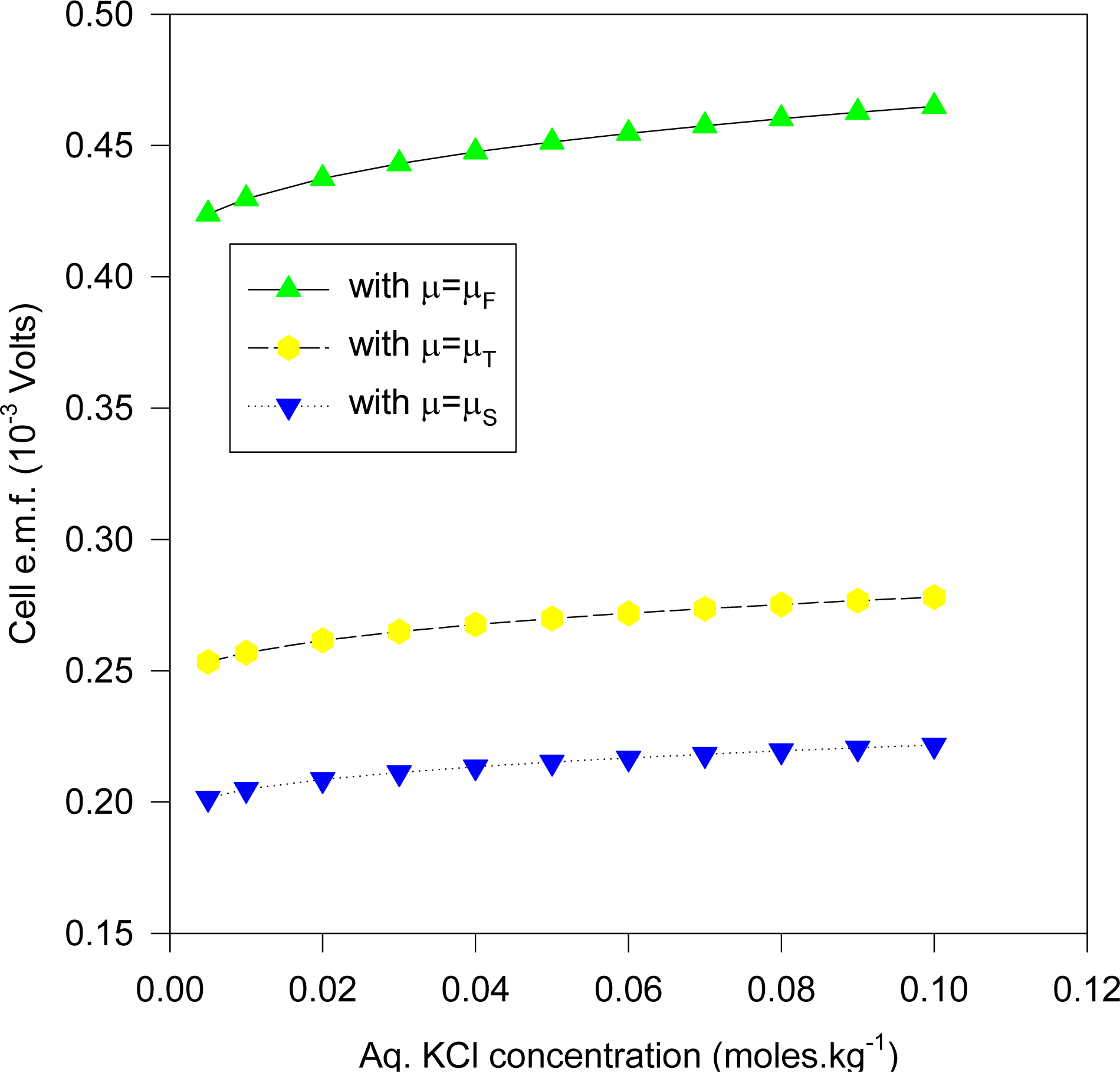
Figures 11 and
12.
Figure 11 plots the cell e.m.f. variation with the aqueous KCl concentration, where the KCl concentration in the dielectric is given by solving (35), whereas
Figure 12 is for the same cell system, but with the KCl dielectric concentration derived by solving (36). It is evident that the predicted e.m.f values are somewhat lower than that expected from the experiment, and may be due to the inadequacy of the model, and/or the imprecisely known values of the ionic radii. In cases (such as zeolites) where normal diffusion of ions into the dielectric is a feasible model for ionic migration in electrochemical electrodes, the above results emphasize the need for more precise theories from which accurate ionic radii and activity coefficients may be derived. We note that the results for the Stern modification would show even greater diminution of the predicted cell e.m.f. than those given in
Figure 10.
We may conclude from the above discussion that the so-called standard potentials E
iø for the various half-cells used to compute the overall cell e.m.f. E with standard E
sø written:
where Q is the overall equilibrium factor [
8], and c
i the stoichiometric coefficient for each half-cell reaction must be modified for a net z-electron reaction to:
where δE
ø (p,
m,γ) is the modifying function for the substrate thinfilm or micro-electrode; p refers to the particular arrangement of the electrodes in a cell relative to the standard electrode state where δE
ø = 0 and
m and
γ are the concentration and activities of the respective electrolyte constituents. The above proposal (including
Equation (58)) would account for the “uncertainty in the value of E
o ” as reported by Bates and Macaskill in their extensive tabulation and derivation of standard potential values, especially for the Ag/AgCl electrode [
44]. They attribute the variation in the reported values of the standard potentials to possible variation in preparative techniques, (and not directly to substrate size which affects the electronic chemical potential), and recommended a standardization procedure which would be abandoned once the “ cases of variability had been identified and eliminated ”. They notice standard e.m.f. differences of up to 0.2 mV amongst different workers; here we observe differences of up to ten times of what the authors quote by exaggerating the dimensions of one of the electrodes by approximately 40 times. The above computations when based on the simple Gouy-Chapman theory seem to yield values closest to experiment; it is noticed that the computational results differ with the choices of the chemical potentials with the Seitz potential registering the greatest difference. Severe discrepancies would possibly arise if one were to connect the Gouy-Chapman theory with the Gibbs adsorption isotherm, which is a standard technique in electrochemical surface analysis [
27], where finite size of ions is an extra condition imposed on the equations, leading to the utilization of the GCS model which we have demonstrated to be inadequate. No such attempts are made here to apply such Gibbsian models for 2-dimensional structures to our essentially 3-dimensional models.
Having observed the rough magnitude of the cell e.m.f. which is incompatible with the predictions made on the basis of the GCS interfacial model, we may perhaps attempt to understand why this is so from the point of view of charge accumulation on the electrodes. For the electrode reaction AgCl + e
−(Met.) ↔ Ag + Cl
− (aq) (where we assume that the AgCl dielectric is only a reservoir for ions with no other effect) the charged species in solution includes the cation, Cl
− and electrons which are able to percolate through a pathway to the substrate Ag electrode, whereas the Gouy-Chapman (and Stern modification) assumes the ions being the only charge carriers (with finite size for the Stern modification of the Helmholtz double layer). This process pathway still obtains even if we should choose model M1 (but the charges on the electrode would be scaled down by a factor of approximately two, due to the lower value of the dielectric constant for AgCl). For purposes of calculation and comparison, if the (theoretical) substrate-solution potential were fixed at ℑ
o = 0.394031 V, then for model M1, the charge per unit area on the electrode may be computed for distances x
2 = 3.5 Å (GCS model) and x
2 = 10
–9 Å (effective GC model). For the For the ordered set of KCl normalities {0.001; 0.005; 0.01; 0.05} with activity coefficients set to unity, the corresponding charge density (μCcm
–2) for the electrode at x
2 = 3.5 Å and x
2 = 10
–9 Å are the respective ordered sets with values {27.32, 33.46, 36.19, 42.70} and {398.37, 890.77, 1,259.74, 2,816.87}. If it is maintained that at very low concentrations, the Gouy-Chapman model may be accepted as fairly accurate [
9,
45–
47] then at these low concentrations, the integral capacitance is of order ~ 3,000 μCV
–1cm
–2, which differs from the Stern model prediction of ~ 100 μCcm
–2V, which is ~ 30 times less than the value predicted by the simple GC theory at its regime of validity. Hence we can expect from these observations that the Stern theory may not be a suitable description for these types of electrodes, even at low concentrations.
From a strictly theoretical angle, there appears to be a (subtle) and probably minor peculiarity which is assumed in using the GCS model as an ideal polarized electrode. By definition, no charge transfer is envisaged with change of potential, yet there is a constant setting4 of σm = –σs in order to determine the charge on the electrode (σm) where –σs = –εεo(dϕ/dx)x = x2, where ϕ is the solution potential at x2 (x2 = 0 for the GC model). The reason is attributed to total charge neutrality; if this were the case then one must allow for charge transfer. On the other hand, if there were absolutely no charge transfer then a counter-electrode would have to be placed in the solution for electroneutrality, which would negate the model boundary conditions. As discussed below, this charge neutrality between electrode and solution is accounted for directly in the ideal self-polarizing electrode. These secondary considerations, in addition to those derived from experiment, make us choose the simplified Gouy-Chapman model of the interface because the electrode reaction mentioned above provides an electronic pathway across the interface for charging the electrode; the electronic factor is not considered in the Stern modification, which could lead to a much smaller x2 than predicted for an electrode system not reacting with the fluid ions.
For instance, consider the component electrode reactions for the AgCl|Cl electrode:
where on one hand a’ alone would suggest an OHP at distance x
2 averaged between the hydration radii of Ag
+(s) and Cl
−(s). On the other hand, b’ shows that this static OHP cannot exist at x
2 because of the transfer of charge from the Ag
+(s) ion to the lattice, implying a smearing of charge between x
2 and the metal substrate which is precluded in the standard treatment of the OHP layer, which serves as a capacitance layer with no charge distribution between them (when there is no specific adsorption, i.e. x
1 = 0 in
Figure 1). Thus, it would appear that the interfacial region would resemble more to the simple GC model with x
2 = 0; also, the σ
m = –σ equation would obtain here without a need for a counterbalancing electrode since it is assumed that the charges separate in thermodynamical equilibrium from a neutral (electrode plus solution) combination, i.e. σ
m+σ
s = 0 at all times up to equilibrium. Lastly, according to Sparnaay [
45–
47] the corrections due to finite ion size and the excluded volume tend to cancel in some systems, where it is stated [
47]: “It is now generally accepted [
48] (that the corrections tend to cancel and that the original Poisson-Boltzmann equation leads to a fairly (
eg. within 20% of the uncorrected potential value) reliable distribution law of the ions near a charged wall.” We postulate that Sparnaay’s observation may well be due to the above smearing-out effect of the charge which would obliterate a static OHP surface. The following theoretical form is proposed for extensions of the Gouy model; since the relative permittivity ε(x) can be calculated from ionic concentrations which vary from the distance x of the electrode surface, we integrate the following Gauss expression from the surface of the electrode to infinity as follows. Since the field strength ξ = dϕ/dx, where ϕ is the potential function, the charge –Q on unit area of the planar electrode is:
where a > 0 for the Stern - type modification, where a is the closest approach distance to the electrode surface, and ε
o is the permittivity of free space. Further modifications to this would follow along similar lines as for previous discussions on this topic such as excluded volume effects and the finite size of ions, but it is anticipated that the ε(x) term would partially account for some of these factors.