Uncovering the Properties of Energy-Weighted Conformation Space Networks with a Hydrophobic-Hydrophilic Model
Abstract
:1. Introduction
2. Model and Method
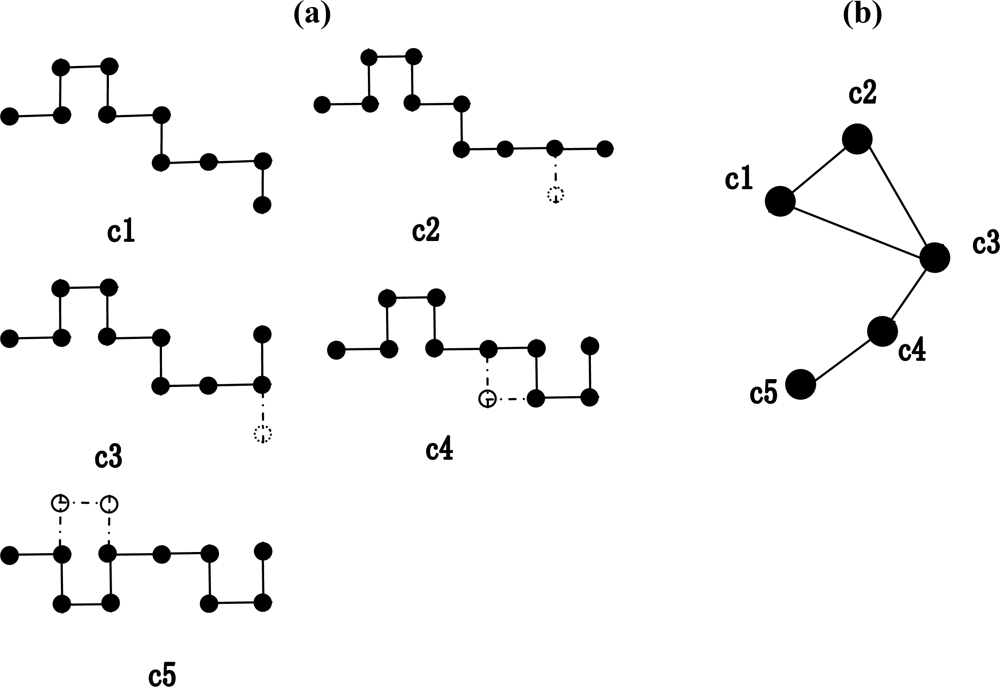
2.1. Construction of the weighted conformation space network
2.2. Folding dynamics and the power-law property of the weighted CSNs
2.3. Modularity-detection algorithm
3. Results and Discussion
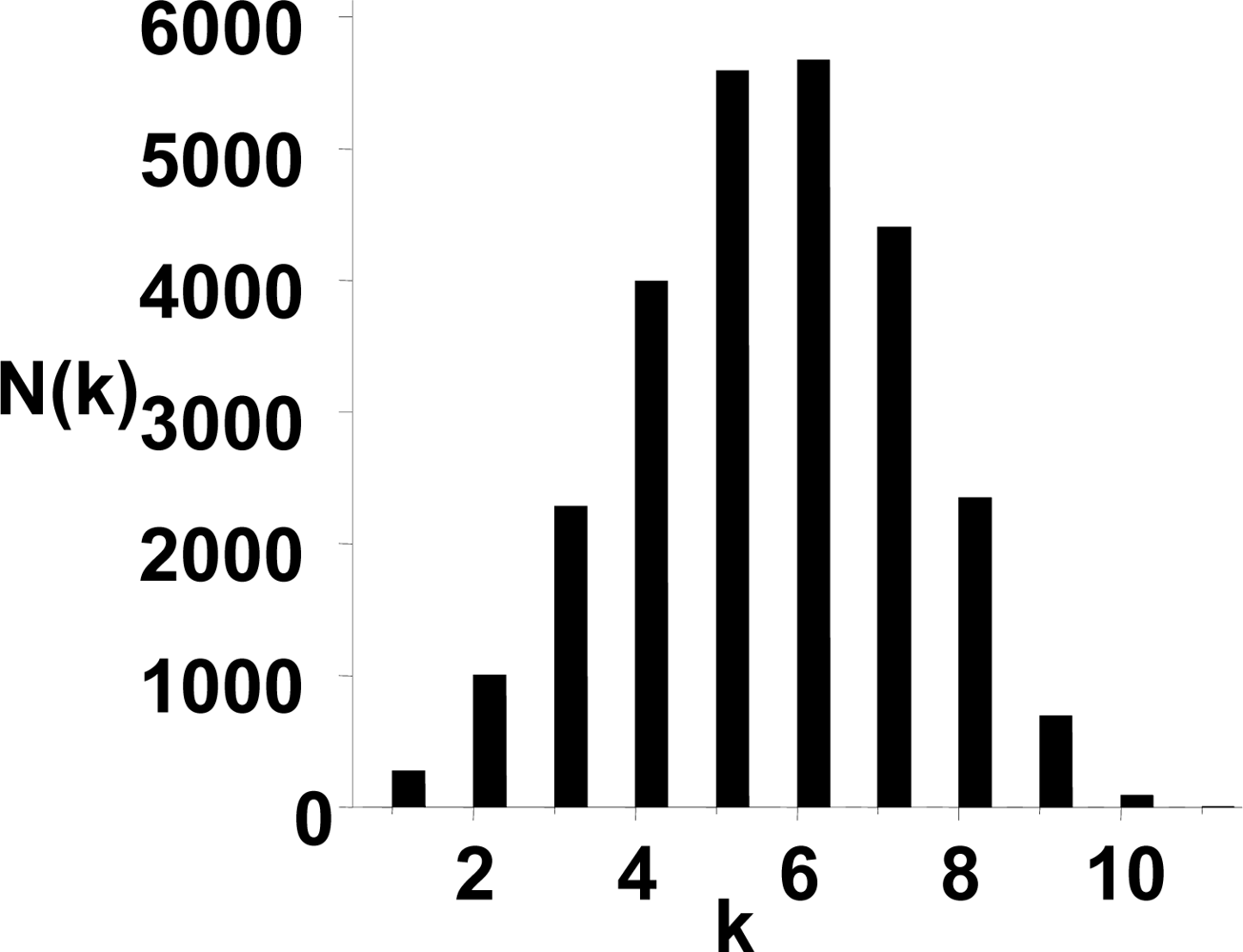
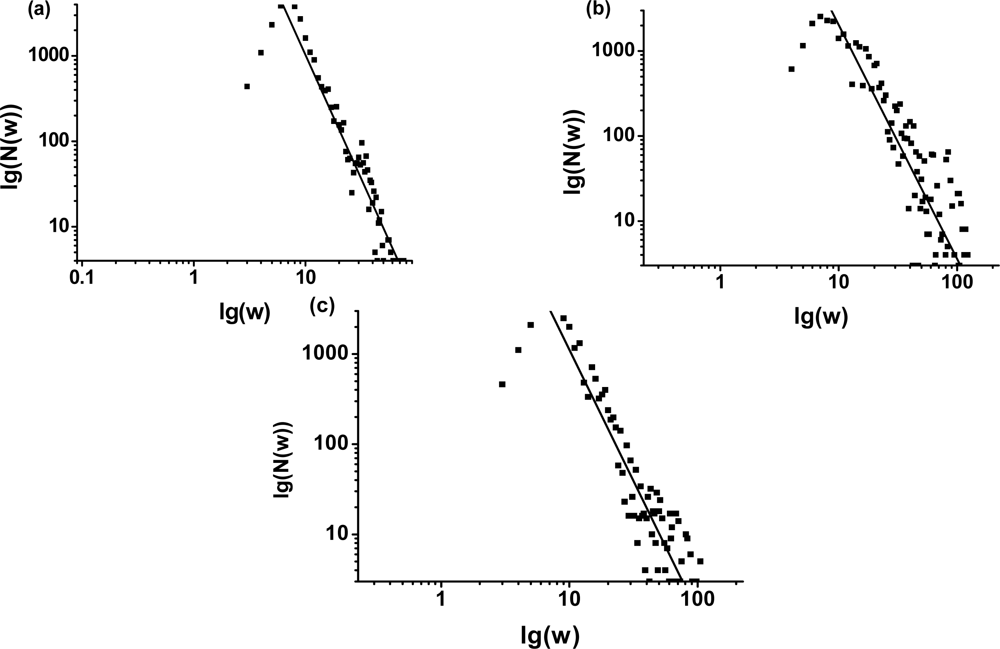
3.1. The power-law property of the weighted CSN
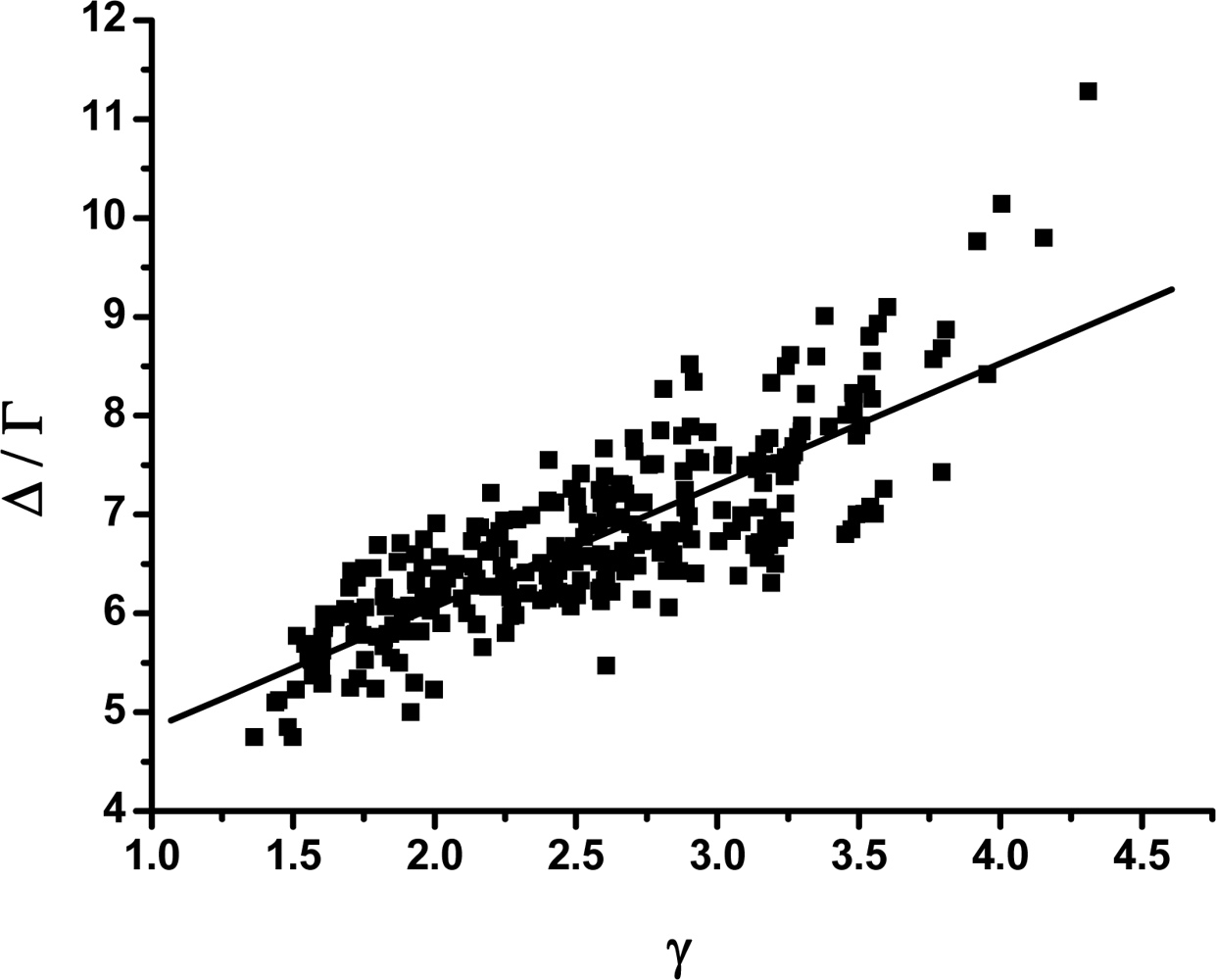
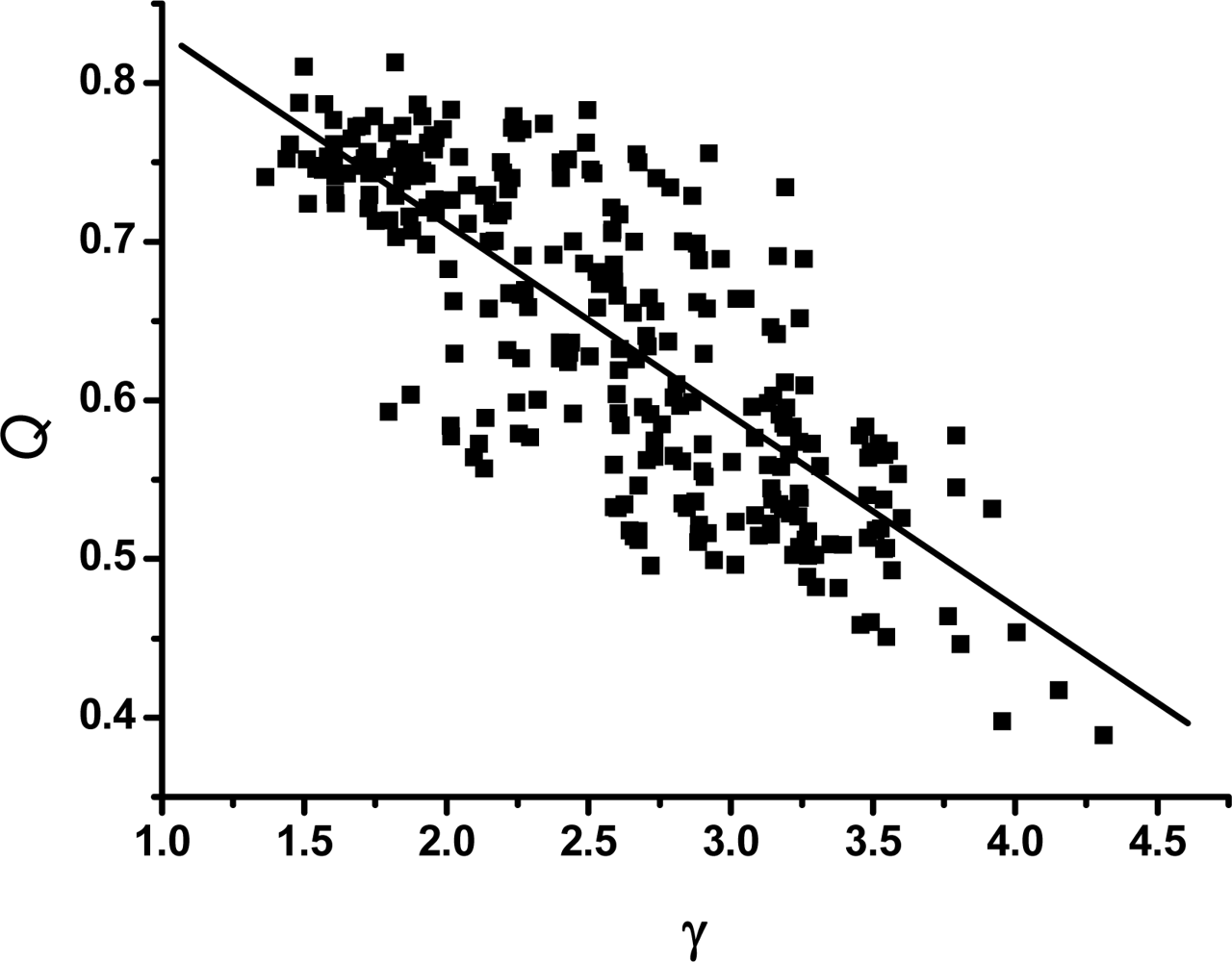
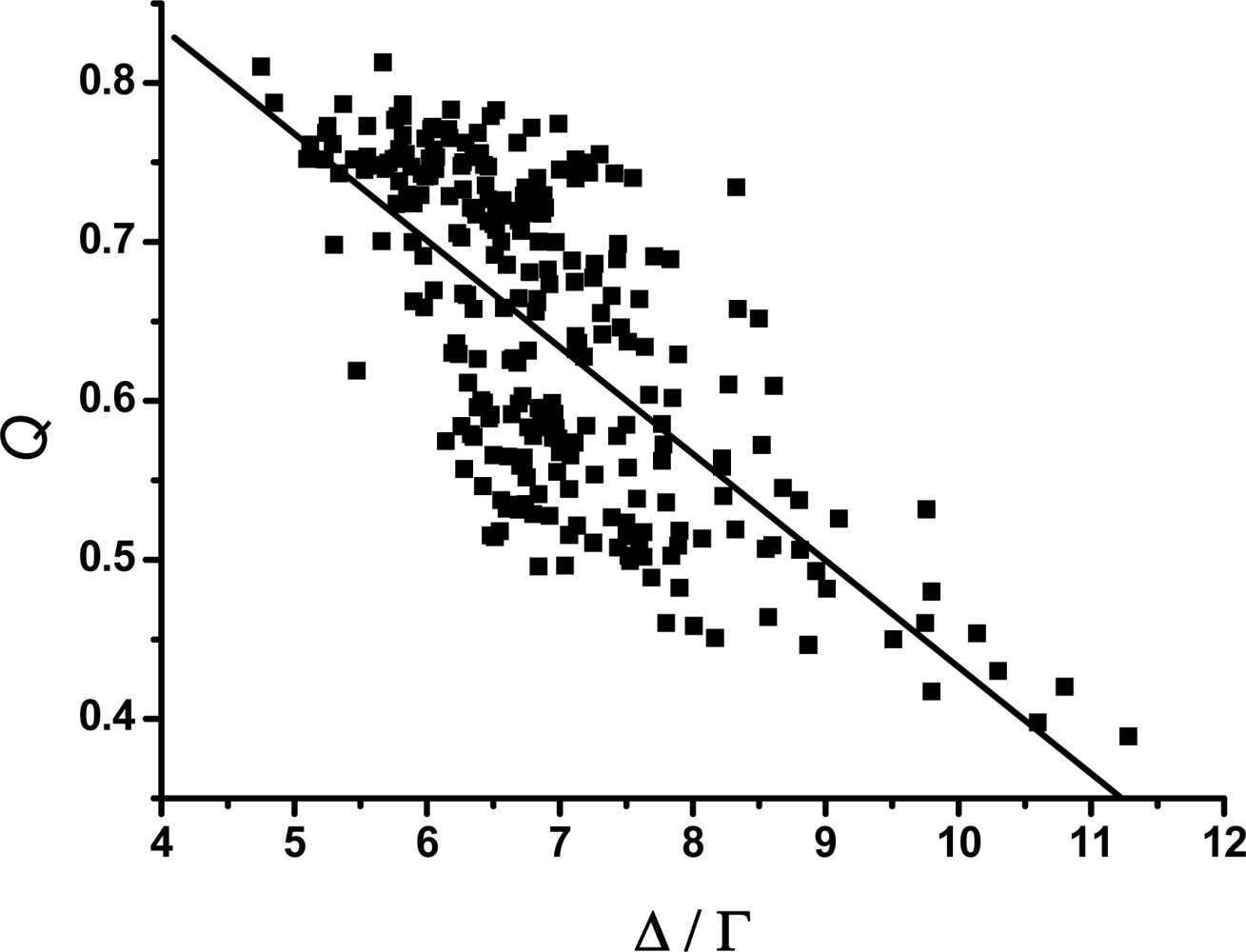
3.2. The scaling exponent γ s versus the ratio Δ/Γ
3.3. The modularity of the weighted CSNs
4. Conclusions
Acknowledgments
References and Notes
- Dorogovtsev, SN; Mendes, JFF. Evolution of networks. Adv. Phys 2002, 51, 1079–1187. [Google Scholar]
- Watts, DJ; Strogatz, SH. Collective dynamics of ’small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar]
- Barabasi, AL; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar]
- Albert, R; Barabasi, AL. Statistical mechanics of complex networks. Rev. Mod. Phys 2002, 74, 47–94. [Google Scholar]
- Doye, JPK. The network topology of a potential energy landscape: A static scale-free network. Phys. Rev. Lett 2002, 88, 238701–238704. [Google Scholar]
- Rao, F; Caflisch, A. The protein folding network. J Mol Biol 2004, 342, 299–306. [Google Scholar]
- Garlaschelli, D; Capocci, A; Caldarelli, G. Self-organized network evolution coupled to extremal dynamics. Nature Phys 2007, 3, 813–817. [Google Scholar]
- Bryngelson, JD; Onuchic, JN; Socci, ND; Wolynes, PG. Funnels, pathways, and the energy landscape of protein folding: A synthesis. Proteins 1995, 21, 167–195. [Google Scholar]
- Chahine, J; Nymeyer, H; Leite, VBP; Socci, ND; Onuchic, JN. Specific and nonspecific collapse in protein folding funnels. Phys. Rev. Lett 2002, 88, 168101. [Google Scholar]
- Stillinger, FH. A topographic view of supercooled liquids and glass formation. Science 1995, 267, 1935–1939. [Google Scholar]
- Frauenfelder, H; Sligar, SG; Wolynes, PG. The energy landscapes and motions of proteins. Science 1991, 254, 1598–1603. [Google Scholar]
- Doye, JPK; Massen, CP. Characterizing the network topology of the energy landscapes of atomic clusters. J. Chem. Phys 2005, 122, 084105. [Google Scholar]
- Krivov, SV; Karplus, M. Free energy disconnectivity graphs: Application to peptide models. J. Chem. Phys 2002, 117, 10894. [Google Scholar]
- Krivov, SV; Karplus, M. Hidden complexity of free energy surfaces for peptide (protein) folding. Proc. Natl. Acad. Sci. USA 2004, 101, 14766–14770. [Google Scholar]
- Scala, A; Amaral, LAN; Barthélémy, M. Small-world networks and the conformation space of a lattice polymer chain. Europhys. Lett 2001, 55, 594–600. [Google Scholar]
- Gfeller, D; de Los Rios, P; Caflish, A; Rao, F. complex network analysis of free-energy landscapes. Proc. Natl. Acad. Sci. USA 2007, 104, 1817–1822. [Google Scholar]
- Gfeller, D; de Lachapelle, DM; de Los Rios, P; Caldarelli, G; Rao, F. Uncovering the topology of configuration space networks. Phys. Rev. E 2007, 76, 026113. [Google Scholar]
- Dima, RI; Banavar, JR; Cieplak, M; Maritan, A. Statistical mechanics of protein-like heteropolymers. Proc. Natl. Acad. Sci. USA 1999, 96, 4904–4907. [Google Scholar]
- Melin, R; Li, H; Wingreen, NS; Tang, C. Designability, thermodynamic stability, and dynamics in protein folding: A lattice model study. J Chem Phys 1999, 110, 1252–1262. [Google Scholar]
- Kubelka, J; Hofrichter, J; Eaton, WA. The protein folding ‘speed limit’. Curr. Opin. Struct. Biol 2004, 14, 76–88. [Google Scholar]
- Mirny, LA; Abkevich, VI; Shakhnovich, EI. How evolution makes proteins fold quickly. Proc. Natl. Acad. Sci. USA 1998, 95, 4976–4981. [Google Scholar]
- Bowie, JU; Luthy, R; Eisenberg, D. A method to identify protein sequences that fold into a known three dimensional structure. Science 1991, 253, 164–170. [Google Scholar]
- Seno, F; Vendruscolo, M; Maritan, A; Banavar, JR. An optimal protein design procedure. Phys. Rev. Lett 1996, 77, 1901–1904. [Google Scholar]
- Tang, C. Simple models of the protein folding problem. Phys. A 2000, 288, 31–48. [Google Scholar]
- Newman, MEJ. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar]
- Ma, H; Zeng, AP. Reconstruction of metabolic networks from genome data and analysis of their global structure for various organisms. Bioinformatics 2003, 19, 270–277. [Google Scholar]
- Muff, S; Rao, F; Caflisch, A. Local modularity measure for network clusterizations. Phys. Rev. E 2005, 72, 056107. [Google Scholar]
- Williams, RJ; Martinez, ND. Simple rules yield complex food webs. Nature 2000, 404, 180–183. [Google Scholar]
- Albert, R; Jeong, H; Barabasi, AL. Diameter of the world wide web. Nature 1999, 401, 130–131. [Google Scholar]
- Clauset, A; Newman, MEJ; Moore, C. Finding community structure in very large networks. Phys. Rev. E 2004, 70, 066111. [Google Scholar]
- Schuetz, P; Caflisch, A. Efficient modularity optimization by multi-step greedy algorithm and vertex mover refinement. Phys. Rev. E 2008, 77, 046112. [Google Scholar]
- Schuetz, P; Caflisch, A. Multistep greedy algorithm identifies community structure in real-world and computer-generated networks. Phys. Rev. E 2008, 78, 026112. [Google Scholar]
- Holme, P; Huss, M; Jeong, H. Subnetwork hierarchies of biochemical pathways. Bioinformatics 2003, 19, 532–538. [Google Scholar]
- Das, P; Moll, M; Stamati, H; Kavraki, LE; Clementi, C. Low-dimensional, free-energy landscapes of protein-folding reactions by nonlinear dimensionality reduction. Proc. Natl. Acad. Sci. USA 2006, 103, 9885–9890. [Google Scholar]
- Lau, KF; Dill, KA. A lattice statistical mechanics model of the conformation and sequence spaces of proteins. Macromolecules 1989, 22, 3986–3997. [Google Scholar]
- Dill, KA; Bromberg, S; Yue, K; Fiebig, KM; Yee, DP; Thomas, PD; Chan, HS. Principles of protein folding – a perspective from simple exact models. Protein Sci 1995, 4, 561–602. [Google Scholar]
- Miller, R; Danko, CA; Fasolka, MJ; Balazs, AC; Chan, HS; Dill, KA. Folding kinetics of proteins and copolymers. J. Chem. Phys 1992, 96, 768–780. [Google Scholar]
- Li, H; Helling, R; Tang, C; Wingreen, N. Emergence of preferred structures in a simple model of protein folding. Science 1996, 273, 666–669. [Google Scholar]
- Gutin, AM; Abkevich, VI; Shakhnovich, EI. Chain length scaling of protein folding time. Phys. Rev. Lett 1996, 77, 5433. [Google Scholar]
- Plaxco, KW; Simons, KT; Baker, D. Contact order, transition placement and the refolding rates of single domain proteins. J. Mol. Biol 1998, 277, 985–994. [Google Scholar]
- Yue, K; Dill, KA. Forces of tertiary structural organization in globular proteins. Proc. Natl. Acad. Sci. USA 1995, 92, 146–150. [Google Scholar]
- Li, H; Tang, C; Wingreen, NS. Designability of protein structures: a lattice model study using the Miyazawa-Jernigan matrix. Proteins: Struct. Funct. Genet 2002, 49, 403–412. [Google Scholar]
- Shahrezaei, V; Hamedani, N; Ejtehadi, MR. Protein ground state candidates in a simple model: An enumeration study. Phys. Rev. E 1999, 60, 4629–36. [Google Scholar]
- Barrat, A; Barthelemy, M; Pastor-Satorras, R; Vespignani, A. The architecture of complex weighted networks. Proc. Natl. Acad. Sci. USA 2004, 101, 3747–3752. [Google Scholar]
- Wang, WX; Wang, BH; Hu, B; Yan, G; Ou, Q. General dynamics of topology and traffic on weighted technological networks. Phys. Rev. Lett 2005, 94, 188702. [Google Scholar]
- Fu, RW; Li, G; Feng, KC. Physics of polymer; Chemical Industry Press: Beijing, China, 2005; pp. 162–203. [Google Scholar]
- Bromberg, S; Dill, KA. Side-chain entropy and packing in proteins. Protein Sci 1994, 3, 997–1007. [Google Scholar]
- Kolinski, A; Gront, D; Pokarowski, P; Skolnick, J. A simple lattice model that exhibits a protein-like cooperative all-or-none folding transition. Biopolymers 2003, 69, 399–405. [Google Scholar]
- Vasquez, M; Nemethy, G; Scheraga, HA. Conformation energy calculations on polypeptides and proteins. Chem. Rev 1994, 94, 2183–2239. [Google Scholar]
- Atilgan, AR; Akan, P; Baysal, C. Small-world communication of residues and significance for protein dynamics. Biophys. J 2004, 86, 85–91. [Google Scholar]
- Stillinger, FH; Weber, TA. Packing structures and transitions in liquids and solids. Science 1984, 225, 983–989. [Google Scholar]
- Tavernelli, I; Cotesta, S; Di lorio, EE. Protein dynamics, thermal stability, and free-energy landscapes: A molecular dynamics investigation. Biophys. J 2003, 85, 2641–2649. [Google Scholar]
- Camacho, CJ; Thirumalai, D. Kinetics and thermodynamics of folding in model proteins. Proc. Natl. Acad. Sci. USA 1993, 90, 6369–6372. [Google Scholar]
- Leopold, PE; Montal, M; Onuchic, JN. Protein folding funnels: a kinetic approach to the sequence-structure relationship. Proc. Natl. Acad. Sci. USA 1992, 89, 8721–8725. [Google Scholar]
- Dinner, AR; Abkevich, V; Shakhnovich, E; Karplus, M. Factors that affect folding ability of proteins. Proteins-Struct. Funct. Genet 1999, 35, 34–40. [Google Scholar]
- Gillespie, B; Plaxco, KW. Using protein folding rates to test protein folding theories. Ann. Rev. Biochem 2004, 73, 837–859. [Google Scholar]
- Gutin, AM; Abkevich, VI; Shakhnovich, EI. Evolution-like selection of fast-folding model proteins. Proc. Natl. Acad. Sci. USA 1995, 92, 1282–1286. [Google Scholar]
- Abkevich, VI; Gutin, AM; Shakhnovich, EI. Free-energy landscape for protein-folding kinetics-intermediates, traps, and multiple pathways in theory and lattice model simulations. J. Chem. Phys 1994, 101, 6052–6062. [Google Scholar]
- Zhang, ZS. Mathematical Analysis; Peking University Press: Beijing, China, 2005; pp. 149–186. [Google Scholar]
- Wang, J; Verkhivker, GM. Energy landscape theory, funnels, specificity and optimal criterion of biomolecular binding. Phys. Rev. Lett 2003, 90, 188101. [Google Scholar]
- Wang, J; Huang, B; Xia, XF; Sun, ZR. funneled landscape leads to robustness of cellular networks. Biophys. J 2006, 91, L54–L57. [Google Scholar]
- Wang, J; Huang, B; Xia, XF; Sun, ZR. Funneled landscape leads to robustness of cell networks. PloS Comput. Biol 2006, 2, 1385–1394. [Google Scholar]
- Dahiyat, BI; Mayo, SL. Protein design automation. Protein Sci 1996, 5, 895–903. [Google Scholar]
- Vizcarra, CL; Mayo, SL. Electrostatics in computational protein design. Curr. Opin. Chem. Biol 2005, 9, 622–626. [Google Scholar]
- Bryngelson, JD; Wolynes, PG. Spin glasses and the statistical mechanics of protein folding. Proc. Natl. Acad. Sci. USA 1987, 84, 7524–7528. [Google Scholar]
- Abkevich, VI; Gutin, AM; Shakhnovich, EI. Theory of kinetic partitioning in protein folding with possible applications to prions. Proteins-Struct. Funct. Genet 1998, 31, 335–344. [Google Scholar]
- Shakhnovich, EI. Protein design: a perspective from simple tractable models. Fold. Design 1998, 3, R45–R48. [Google Scholar]
- Dokholyan, NV. What is the protein design alphabet? Proteins-Struct. Funct. Genet 2004, 54, 622–628. [Google Scholar]
- Bode, C; Kovacs, IA; Szalay, MS; Palotai, R; Korcsmaros, T; Csermely, P. Networks aanlysis of protein dynamics. FEBS Lett 2007, 581, 2776–82. [Google Scholar]
- Guimerà, R; Sales-Pardo, M; Amaral, LAN. Modularity from fluctuations in random graphs and complex networks. Phys. Rev. E 2004, 70, 025101. [Google Scholar]
- Krause, AE; Frank, KA; Mason, DM; Ulanowicz, RE; Taylor, WW. Compartments revealed in food web structure. Nature 2003, 426, 282–285. [Google Scholar]
- Parter, M; Kashtan, N; Alon, U. Environmental variability and modularity of bacterial metabolic networks. BMC Evol. Biol 2007, 7, 169–195. [Google Scholar]
- Doye, JPK; Massen, CP. Characterizing the network topology of the energy landscapes of atomic clusters. Phys. Rev. E 2005, 71, 016128. [Google Scholar]
- Massen, CP; Doye, JPK. Exploring the origins of the power-law properties of energy landscapes: an egg-box model. Phys. Rev. E 2007, 75, 037101. [Google Scholar]
- Scalley, ML; Baker, D. Protein folding kinetics exhibit an Arrhenius temperature dependence when corrected for the temperature dependence of protein stability. Proc. Natl. Acad. Sci. USA 1997, 94, 10636–10640. [Google Scholar]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lai, Z.; Su, J.; Chen, W.; Wang, C. Uncovering the Properties of Energy-Weighted Conformation Space Networks with a Hydrophobic-Hydrophilic Model. Int. J. Mol. Sci. 2009, 10, 1808-1823. https://doi.org/10.3390/ijms10041808
Lai Z, Su J, Chen W, Wang C. Uncovering the Properties of Energy-Weighted Conformation Space Networks with a Hydrophobic-Hydrophilic Model. International Journal of Molecular Sciences. 2009; 10(4):1808-1823. https://doi.org/10.3390/ijms10041808
Chicago/Turabian StyleLai, Zaizhi, Jiguo Su, Weizu Chen, and Cunxin Wang. 2009. "Uncovering the Properties of Energy-Weighted Conformation Space Networks with a Hydrophobic-Hydrophilic Model" International Journal of Molecular Sciences 10, no. 4: 1808-1823. https://doi.org/10.3390/ijms10041808



