Grunwald-Winstein Analysis - Isopropyl Chloroformate Solvolysis Revisited
Abstract
:1. Introduction
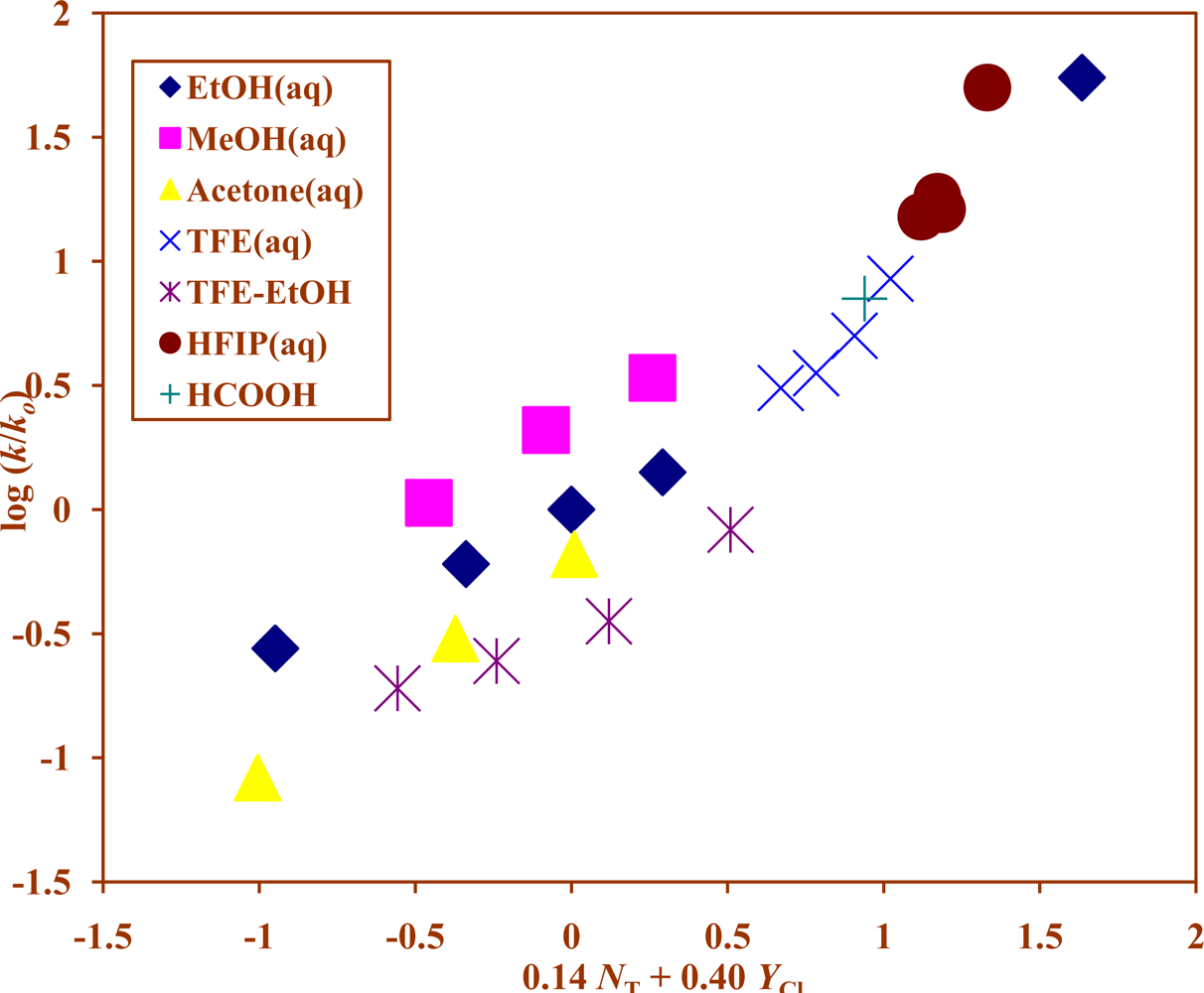
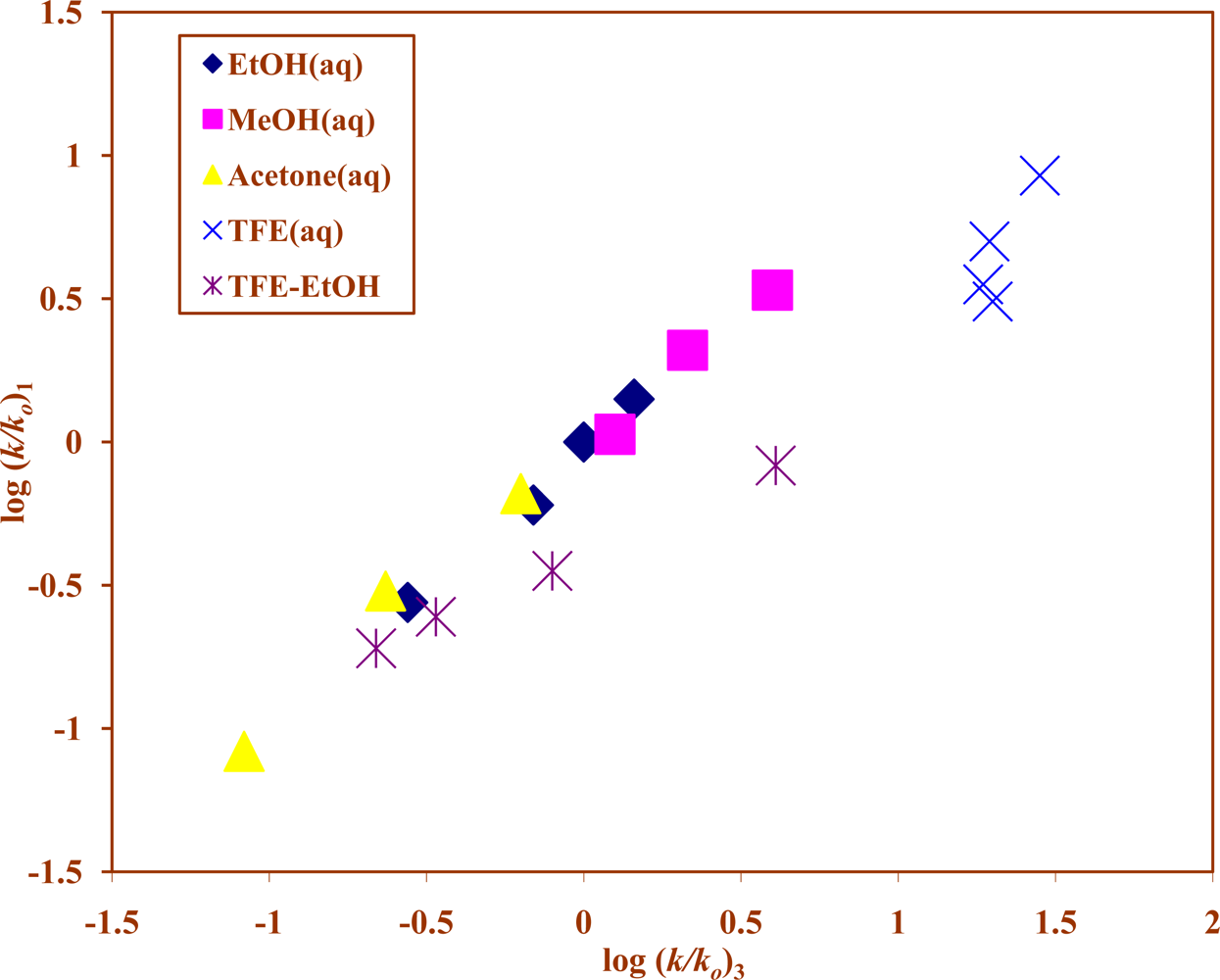
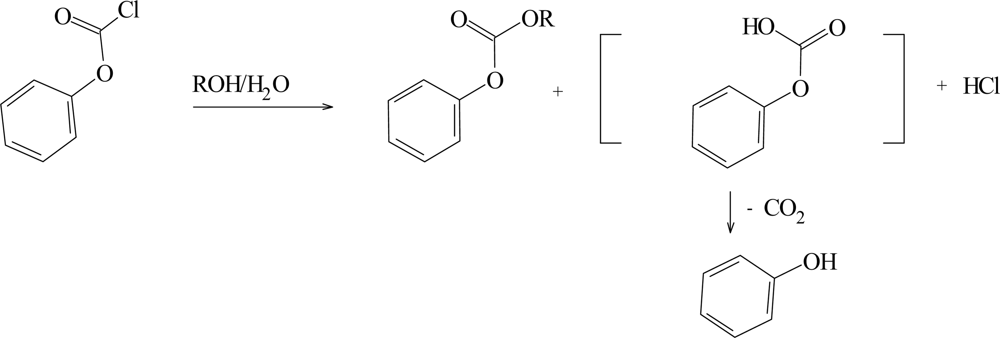
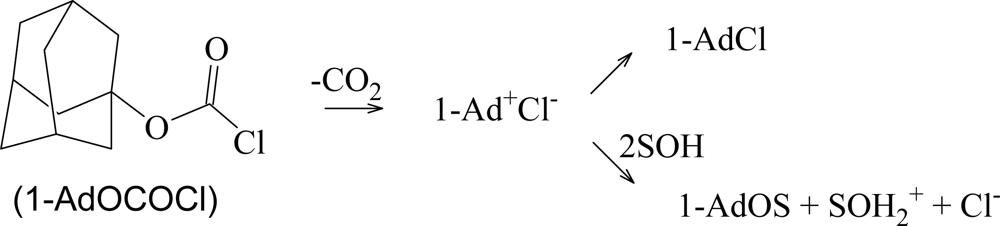
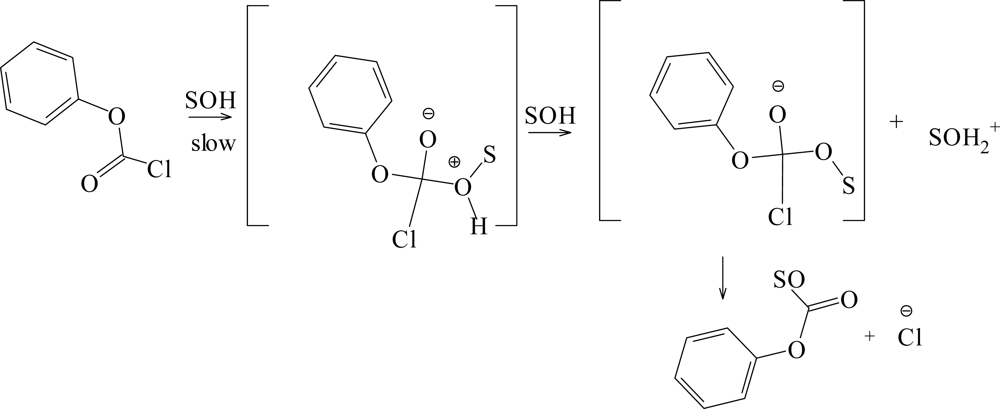
2. Results and Discussion
3. Conclusions
4. Experimental
Acknowledgments
References and Notes
- Kevill, DN; D’Souza, MJ. Sixty Years of the Grunwald-Winstein Equation: Development and Recent Applications. J Chem Res 2008, 61–66. [Google Scholar]
- Winstein, S; Grunwald, E; Jones, HW. The Correlation of Solvolyses Rates and the Classification of Solvolysis Reactions into Mechanistic Categories. J. Am. Chem. Soc 1951, 73, 2700–2707. [Google Scholar]
- Grunwald, E; Winstein, S. The Correlation of Solvolysis Rates. J. Am. Chem. Soc 1948, 70, 846–854. [Google Scholar]
- Kevill, DN; Kyong, JB; Weitl, FL. Solvolysis-Decomposition of 1-Adamantyl Chloroformate: Evidence for Ion Pair Return in 1-Adamantyl Chloride Solvolysis. J. Org. Chem 1990, 55, 4304–4311. [Google Scholar]
- Kyong, JB; Suk, YJ; Kevill, DN. Solvolysis-Decomposition of 2-Adamantyl Chloroformate: Evidence for Two Reaction Pathways. J. Org. Chem 2003, 68, 3425–3432. [Google Scholar]
- Koo, IS; Yang, K; Kang, K; Oh, HK; Lee, I. Stoichiometric Solvation Effects. Product-Rate Correlation for the Solvolyses of Phenyl Chloroformate in Alcohol-Water Mixtures. Bull. Korean Chem. Soc 1996, 17, 520–524. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Correlation of the Rates of Solvolysis of Phenyl Chloroformate. J Chem Soc., Perkin Trans 1997, 2, 1721–1724. [Google Scholar]
- Koo, IS; Yang, K; Koo, JC; Park, J–K; Lee, I. Stoichiometric Solvation Effects. Part 4. Product–rate Correlations for Solvolyses of p-Methoxyphenyl Chloroformate in Alcohol–Water Mixtures. Bull. Korean Chem. Soc 1997, 18, 1017–1021. [Google Scholar]
- Koo, IS; Yang, K; Kang, K; Lee, I; Bentley, TW. Stoichiometric Solvation Effects. Part 3. Product–rate Correlations for Solvolyses of p-Nitrophenyl Chloroformate in Alcohol–Water Mixtures. J Chem Soc., Perkin Trans 1998, 2, 1179–1183. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Concerning the Two Reaction Channels for the Solvolyses of Ethyl Chloroformate and Ethyl Chlorothioformate. J. Org. Chem 1998, 63, 2120–2124. [Google Scholar]
- Koo, IS; Yang, K; Kang, K; Lee, I. Transition-State Variation in the Solvolyses of para-Substituted Phenyl Chloroformates in Alcohol-Water Mixtures. Bull. Korean Chem. Soc 1998, 19, 968–973. [Google Scholar]
- Kevill, DN; Kim, JC; Kyong, JB. Correlation of the Rates of Methyl Chloroformate with Solvent Properties. J Chem Res Synop 1999, 150–151. [Google Scholar]
- Kyong, JB; Kim, YG; Kim, DK; Kevill, DN. Dual Pathways in the Solvolyses of Isopropyl Chloroformate. Bull. Korean Chem. Soc 2000, 21, 662–664. [Google Scholar]
- Park, KH; Kyong, JB; Kevill, DN. Nucleophilic Substitution Reactions of p-Nitrobenzyl Chloroformate. Bull. Korean Chem. Soc 2000, 21, 1267–1270. [Google Scholar]
- Kyong, JB; Park, B-C; Kim, C-B; Kevill, DN. Rate and Product Studies with Benzyl and p-Nitrobenzyl Chloroformates under Solvolytic Conditions. J. Org. Chem 2000, 65, 8051–8058. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Correlation of the Rates of Solvolyses of n-Octyl Fluoroformate and a Comparison with n-Octyl Chloroformate Solvolyses. J Chem Soc., Perkin Trans 2002, 2, 240–243. [Google Scholar]
- Castro, EA; Ruiz, MG; Salinas, S; Santos, JG. Kinetics and Mechanism of the Aminolysis of Phenyl and 4-Nitrophenyl Chloroformates in Aqueous Solution. J. Org. Chem 1999, 64, 4817–4820. [Google Scholar]
- Kyong, JB; Won, H; Kevill, DN. Application of the Extended Grunwald-Winstein Equation to Solvolyses of n-Propyl Chloroformate. Int. J. Mol. Sci 2005, 6, 87–96. [Google Scholar]
- Bentley, TW; Harris, HC; Zoon, H-R; Gui, TL; Dae, DS; Szajda, SR. Mechanisms of Solvolyses of Acid Chlorides and Chloroformates. Chloroacetyl and Phenylacetyl Chloride as Similarity Models. J. Org. Chem 2005, 70, 8963–8970. [Google Scholar]
- Ryu, ZH; Lee, YH; Oh, Y. Stoichiometric Effects. Correlation of the Rates of Solvolysis of Isopropenyl Chloroformate. Bull. Korean Chem. Soc 2005, 26, 1761–1766. [Google Scholar]
- Kevill, DN; Koyoshi, F; D’Souza, MJ. Correlation of the Specific Rates of Solvolysis of Aromatic Carbamoyl Chlorides, Chloroformates, Chlorothionoformates, and Chlorodithioformates Revisited. Int. J. Mol. Sci 2007, 8, 346–352. [Google Scholar]
- D’Souza, MJ; Reed, D; Koyoshi, F; Kevill, DN. Consideration of the Factors Influencing the Specific Rates of Solvolysis of p-Methoxyphenyl Chloroformate. Int. J. Mol. Sci 2007, 8, 788–796. [Google Scholar]
- D’Souza, MJ; Shuman, KE; Carter, SE; Kevill, DN. Extended Grunwald-Winstein Analysis -LFER Used to Gauge Solvent Effects in p-Nitrophenyl Chloroformate Solvolysis. Int. J. Mol. Sci 2008, 9, 2231–2242. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Correlation of the Rates of Solvolysis of Phenyl Chlorothionoformate and Phenyl Chlorodithioformate. Can. J. Chem 1999, 77, 1118–1122. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Dual Pathways in the Solvolyses of Phenyl Chlorothioformate. J. Org. Chem 1997, 62, 7869–7871. [Google Scholar]
- Koo, IS; Yang, K; Kang, DH; Park, HJ; Kang, K; Lee, I. Transition-State Variation in the Solvolyses of Phenyl Chlorothionoformate in Alcohol-Water Mixtures. Bull. Korean Chem. Soc 1999, 20, 577. [Google Scholar]
- An, SK; Yang, JS; Cho, JM; Yang, K; Lee, PL; Bentley, TW; Lee, I; Koo, IS. Correlation of the Rates of Solvolysis of Phenyl Chlorodithioformate. Bull. Korean Chem. Soc 2002, 23, 1445. [Google Scholar]
- Bentley, TW. Structural Effects on the Solvolytic Reactivity of Carboxylic and Sulfonic Acid Chlorides. Comparisons with Gas-Phase Data for Cation Formation. J. Org. Chem 2008, 73, 6251–6257. [Google Scholar]
- Bentley, TW; Garley, MS. Correlations and Predictions of Solvent Effects on Reactivity: Some Limitations of Multi-Parameter Equations and Comparisons with Similarity Models Based on One Solvent Parameter. J. Phys. Org. Chem 2006, 19, 341–349. [Google Scholar]
- Bentley, TW; Llewellyn, G. Yx Scales of Solvent Ionizing Power. Prog. Phys. Org. Chem 1990, 17, 121–158. [Google Scholar]
- Schadt, FL; Bentley, TW; Schleyer, PvR. The SN2-SN1 Spectrum. 2. Quantitative Treatments of Nucleophilic Solvent Assistance. A Scale of Solvent Nucleophilicities. J. Am. Chem. Soc 1976, 98, 7667–7674. [Google Scholar]
- Kevill, DN; Anderson, SW. An Improved Scale of Solvent Nucleophilicity Based on the Solvolysis of the S-Methyldibenzothiophenium Ion. J. Org. Chem 1991, 56, 1845–1850. [Google Scholar]
- Kevill, DN. Development and Uses of Scales of Solvent Nucleophilicity. In Advances in Quantitative Structure-Property Relationships; Charton, M, Ed.; JAI Press: Greenwich, CT, 1996; Volume 1, pp. 81–115. [Google Scholar]
- D’Souza, MJ; Ryu, ZH; Park, B-C; Kevill, DN. Correlation of the Rates of Solvolysis of Acetyl Chloride and α-Substituted Derivatives. Can. J. Chem 2008, 86, 359–367. [Google Scholar]
- Castro, EA; Ruiz, MG; Santos, JG. Structure-Reactivity Correlations in the Aminolysis of Aryl Chloroformates. Int J Chem Kinetics 2001, 281–287. [Google Scholar]
- Choppin, AR; Rodgers, JW. The Preparation of Di-t-butyl Carbonate and t-Butyl Chlorocarbonate. J. Am. Chem. Soc 1948, 70, 2967. [Google Scholar]
- Kevill, DN; Weitl, FL. Competing Solvolysis-Decomposition of 1-Adamantyl Chloroformate. Tetrahedron Lett 1971, 707–710. [Google Scholar]
- 18 January 2009.
- Husek, P. Chloroformates in Gas Chromatography as General Purpose Derivatizing Agents. J. Chromatogr. B Biomed Sci. Appl 1998, 17, 57–91. [Google Scholar]
- Kaspi, J; Rappoport, Z. Nucleophilicity and Ionizing Power in Binary Solvent Mixtures. Tetrahedron Lett 1977, 2035. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Additional YCl Values and Correlation of the Specific Rates of Solvolysis of tert-Butyl Chloride in Terms of NT and YCl Scales. J Chem Res Synop 1993, 174–175. [Google Scholar]
- Kevill, DN; Park, B-C; Park, K-H; D’Souza, MJ; Yaakoubd, L; Mlynarski, SL; Kyong, JB. Rate and Product Studies in the Solvolyses of N,N-Dimethylsulfamoyl and 2-Propanesulfonyl Chlorides. Org. Biomol. Chem 2006, 4, 1580–1586. [Google Scholar]
- Kevill, DN; Ryu, ZH. Additional Solvent Ionizing Power Values for Binary Water – 1,1,1,3,3,3,-Hexafluoro-2-propanol Solvents. Int. J. Mol. Sci 2006, 7, 451–455. [Google Scholar]
- Kevill, DN; Ryu, ZH; Niedermeyer, MA; Koyoshi, F; D’Souza, MJ. Rate and Product Studies in the Solvolyses of Methanesulfonic Anhydride and a Comparison with Methanesulfonyl Chloride Solvolysis. J. Phys. Org. Chem 2007, 20, 431–438. [Google Scholar]
- Ryu, ZH; Lee, SW; D’Souza, MJ; Yaakoubd, L; Feld, SE; Kevill, DN. Correlation of the Rates of Solvolysis of Two Arenesulfonyl Chlorides and of trans-β-Styrenesulfonyl Chloride — Precursors in the Development of New Pharmaceuticals. Int. J. Mol. Sci 2008, 9, 2639–2657. [Google Scholar]
- Queen, A. Kinetics of the Hydrolysis of Acyl Chlorides in Pure Water. Can. J. Chem 1967, 45, 1619–1629. [Google Scholar]
- Crunden, EW; Hudson, RF. The Mechanism of Hydrolysis of Acid Chlorides. Part VII. Alkyl Chloroformates. J Chem Soc 1961, 3748–3755. [Google Scholar]
- Bentley, TW; Carter, GE. The SN2-SN1 Spectrum. 4. Mechanism for Solvolyses of tert-Butyl Chloride: A Revised Y Scale of Solvent Ionizing Power based on Solvolyses of 1-Adamantyl Chloride. J. Am. Chem. Soc 1982, 104, 5741–5747. [Google Scholar]
- Lomas, JS; D’Souza, MJ; Kevill, DN. Extremely Large Acceleration of the Solvolysis of 1-Adamantyl Chloride Upon Incorporation of a Spiro Adamantane Substituent: Solvolysis of 1-Chlorospiro[adamantane-2, 2′-adamantane]. J. Am. Chem. Soc 1995, 117, 5891–5892. [Google Scholar]
- Leimu, R. Reaction Velocity of Aliphatic Acid Halides. Chem. Ber 1937, 70 B, 1040–1053. [Google Scholar]
- Orlov, SI; Chimishkyan, AL; Grabarnik, MS. Kinetic Relationships Governing the Ethanolysis of Halogenoformates. J. Org. Chem. USSR (Engl. Transl.) 1983, 19, 1981–1987. [Google Scholar]
- Kevill, DN; Kyong, JB. Multiple Pathways in the Solvolysis of 1-Adamantyl Fluoroformate. J. Org. Chem 1992, 57, 258–265. [Google Scholar]
- Kyong, JB; Ryu, SH; Kevill, DN. Rate and Product Studies of the Solvolyses of Benzyl Fluoroformate. Int. J. Mol. Sci 2006, 7, 186–196. [Google Scholar]
- Lee, SH; Rhu, CJ; Kyong, JB; Kim, DK; Kevill, DN. Correlation of the Rates of Solvolysis of Isopropyl Fluoroformate Using the Extended Grunwald-Winstein Equation. Bull. Korean Chem. Soc 2007, 28, 657–661. [Google Scholar]
- Seong, MH; Kyong, JB; Kim, DK; Kevill, DN. Application of the Extended Grunwald-Winstein Equation to Solvolyses of n-Propyl Fluoroformate and a Consideration of Leaving Group Effects. Bull. Korean Chem. Soc 2008, 29, 1747–1751. [Google Scholar]
- Green, M; Hudson, RF. The Mechanism of Hydrolysis of Acid Chlorides. Part VIII. Chloroformates of Secondary Alcohols. J Chem Soc 1962, 1076–1080. [Google Scholar]
- Brown, HC; Ham, G. The Effect of Ring Size on the Rate of Acetolysis of the Cycloalkyl p-Toluene and p-Bromobenzenesulfonates. J. Am. Chem. Soc 1956, 78, 2735–2739. [Google Scholar]
- Conner, JK; Haider, J; Stuart Hill, MN; Maskill, H; Pestman, M. The Mechanism of Solvolysis of 2-Adamantyl Azoxytosylate: Isotopic Labelling, Medium Effect, and Attempted Deoxygenation Studies. Can. J. Chem 1998, 76, 862–868. [Google Scholar]
- Frost, AA; Pearson, RG. Kinetics and Mechanism-a Study of Homogeneous Chemical Reactions, 2nd Ed ed; Wiley: New York, 1961; pp. 49–50. [Google Scholar]
- Kevill, DN; Abduljaber, MH. Correlation of the Rates of Solvolysis of Cyclopropylcarbinyl and Cyclobutyl Bromides Using the Extended Grunwald-Winstein Equation. J. Org. Chem 2000, 65, 2548–2554. [Google Scholar]

| Solvent (%)b | 1 @ 25.0 °C; 105k, s−1c,d | 1 @ 40.0 °C; 105k, s−1e | NTe | YClf | % Acidc,f |
|---|---|---|---|---|---|
| 100% MeOH | 4.19 ± 0.10g | 15.4 ± 0.1 | 0.17 | −1.2 | 96 ± 2 |
| 90% MeOH | 8.28 ± 0.09 | 30.7 ± 0.6 | −0.01 | −0.20 | 97 ± 1 |
| 80% MeOH | 13.4 ± 0.4 | 49.7 ± 0.6 | −0.06 | 0.67 | 88 ± 3 |
| 70% MeOH | 76.6 ± 0.8 | −0.40 | 1.46 | 94 ± 2 | |
| 60% MeOH | 120 ± 6 | −0.54 | 2.07 | 91 ± 2 | |
| 100% EtOH | 1.09 ± 0.04h | 5.41 ± 0.01 | 0.37 | −2.50 | 93 ± 3 |
| 90% EtOH | 2.36 ± 0.09 | 10.8 ± 0.1 | 0.16 | −0.90 | 91 ± 2 |
| 80% EtOH | 3.92 ± 0.14 | 18.6 ± 0.2 | 0.00 | 0.00 | 91 ± 1 |
| 70% EtOH | 5.53 ± 0.26 | 31.3 ± 0.1 | −0.20 | 0.80 | 89 ± 2 |
| 60% EtOH | 51.3 ± 0.1 | −0.39 | 1.38 | 87 ± 5 | |
| 50% EtOH | 96.5 ± 0.3 | −0.58 | 2.02 | 90 ± 2 | |
| 90% Acetone | 0.331 ± 0.025 | 1.08 ± 0.03 | −0.35 | −2.39 | 78 ± 3 |
| 80% Acetone | 1.19 ± 0.04 | 4.27 ± 0.03 | −0.37 | −0.80 | 86 ± 5 |
| 70% Acetone | 2.59 ± 0.08 | 11.8 ± 0.2 | −0.42 | 0.17 | 81 ± 2 |
| 60% Acetone | 28.8 ± 0.2 | −0.52 | 1.00 | 85 ± 1 | |
| 97% TFE (w/w) | 12.3 ± 0.3 | 71.6 ± 0.7 | −3.30 | 2.83 | 67 ± 1 |
| 90% TFE (w/w) | 13.9 ± 0.4 | 74.7 ± 0.8 | −2.55 | 2.85 | 72 ± 1 |
| 70% TFE (w/w) | 19.7 ± 0.7 | 117 ± 3 | −1.98 | 2.96 | 80 ± 3 |
| 50% TFE (w/w) | 33.5 ± 0.04 | −1.73 | 3.16 | ||
| 80T-20E | 3.26 ± 0.07 | 21.3 ± 0.7 | −1.76 | 1.89 | 68 ± 1 |
| 60T-40E | 1.41 ± 0.10 | 7.87 ± 0.06 | −0.94 | 0.63 | 72 ± 1 |
| 40T-60E | 0.964 ± 0.023 | 3.76 ± 0.03 | −0.34 | −0.48 | |
| 20T-80E | 0.757 ± 0.014 | 3.16 ± 0.06 | 0.08 | −1.42 | |
| 100% H2O | 218 ± 1i | 1622 ± 4i | −1.38 | 4.57 | 98j |
| 99.3% HCOOH | 28.2 ± 0.1k | 172 ± 2k | −2.44l | 3.20l | |
| 97%HFIP (w/w) | 146 ± 2 | 563 ± 16d,m | −5.26 | 5.17 | |
| 90%HFIP (w/w) | 63.2 ± 2.9 | 246 ± 12d,m | −3.84 | 4.41 | |
| 70%HFIP (w/w) | 60.1 ± 2.4 | −2.94 | 3.83 | ||
| 50%HFIP (w/w) | 71.0 ± 3.0 | −2.49 | 3.8 |
| Solvent (%)a | 105k, s−1b | 105 ki, s−1c | 105 (k–ki), s−1 | 105k, s−1e | 105 ki, s−1f | 105 (k–ki), s−1 |
|---|---|---|---|---|---|---|
| 100% MeOH | 15.4 | 1.5 | 13.9d | 4.19 | 0.12 | 4.07g |
| 90% MeOH | 30.7 | 5.1 | 25.6d | 8.28 | 0.46 | 7.82g |
| 80% MeOH | 49.7 | 16.2 | 33.5d | 13.4 | 1.53 | 11.9g |
| 70% MeOH | 76.6 | 39.5 | 37.1 | |||
| 60% MeOH | 120 | 83.2 | 36.8 | |||
| 100% EtOH | 5.41 | 0.29 | 5.1d | 1.09 | 0.021 | 1.07g |
| 90% EtOH | 10.8 | 2.2 | 8.6d | 2.36 | 0.18 | 2.18g |
| 80% EtOH | 18.6 | 6.8 | 11.9d | 3.92 | 0.61 | 3.31g |
| 70% EtOH | 31.3 | 17.8 | 13.5 | 5.53 | 1.73 | 3.8 |
| 60% EtOH | 51.3 | 35.5 | 15.8 | |||
| 50% EtOH | 96.5 | 76.1 | 20.4 | |||
| 90% Acetone | 1.08 | 0.30 | 0.78d | 0.33 | 0.020 | 0.31g |
| 80% Acetone | 4.27 | 1.93 | 2.34d | 1.19 | 0.18 | 1.01g |
| 70% Acetone | 11.8 | 6.9 | 4.9d | 2.59 | 0.680 | 1.91g |
| 60% Acetone | 28.8 | 19.9 | 8.9 | |||
| 97% TFE (w/w) | 71.6 | 60.4 | 12.3 | 12.2 | ||
| 90% TFE (w/w) | 74.7 | 87.6 | 13.9 | 15.4 | ||
| 70% TFE (w/w) | 117 | 134 | 19.7 | 21.1 | ||
| 50% TFE (w/w) | 33.5 | 29.6 | ||||
| 80T-20E | 21.3 | 36.0 | 3.26 | 5.08 | ||
| 60T-40E | 7.87 | 9.9 | 1.41 | 1.12 | ||
| 40T-60E | 3.76 | 3.03 | 0.7 | 0.96 | 0.280 | 0.68 |
| 20T-80E | 3.16 | 1.07 | 2.1 | 0.757 | 0.088 | 0.67 |
| 100% H2O | 1622 | 1514 | 218 | 229 | ||
| 99.3% HCOOH | 172 | 150 | 28.2 | 25.7 | ||
| 97%HFIP (w/w) | 563 | 523 | 146 | 179 | ||
| 90%HFIP (w/w) | 246 | 331 | 63.2 | 80.0 | ||
| 70%HFIP (w/w) | 60.1 | 54.1 | ||||
| 50%HFIP (w/w) | 71.0 | 58.1 |
| Substrate | na | lb | mb | cc | Rd | Fe |
|---|---|---|---|---|---|---|
| 1; 40.0 °C | 26f | 0.33 ± 0.03 | −0.11 ± 0.07 | 0.919 | 130 | |
| 0.21 ± 0.06 | 0.44 ± 0.04 | −0.02 ± 0.06 | 0.947 | 100 | ||
| 7g | 0.44 ± 0.12 | −0.56 ± 0.44 | 0.861 | 14 | ||
| 0.21 ± 0.04 | 0.58 ± 0.05 | −0.44 ± 0.16 | 0.987 | 74 | ||
| 11h | 0.41 ± 0.04 | −0.45 ± 0.12 | 0.964 | 117 | ||
| 0.20 ± 0.06 (0.014)i | 0.53 ± 0.05 | −0.33 ± 0.09 | 0.984 | 121 | ||
| 10j | 0.37 ± 0.02 | −0.43 ± 0.07 | 0.983 | 232 | ||
| 0.05 ± 0.11 (0.67)i | 0.41 ± 0.08 | −0.41 ± 0.10 | 0.984 | 105 | ||
| 9k | 0.36 ± 0.10 | 0.04 ± 0.14 | 0.803 | 13 | ||
| 1.05 ± 0.17 | 0.44 ± 0.04 | 0.15 ± 0.06 | 0.976 | 61 | ||
| 9k,l | 0.31 ± 0.13 | 0.03 ± 0.17 | 0.661 | 5 | ||
| 1.35 ± 0.22 | 0.40 ± 0.05 | 0.18 ± 0.07 | 0.960 | 35 | ||
| 16m | 0.38 ± 0.05 | −0.28 ± 0.13 | 0.911 | 69 | ||
| 0.28 ± 0.04 | 0.59 ± 0.04 | −0.32 ± 0.06 | 0.982 | 176 | ||
| 1; 25.0 °C | 24f | 0.31 ± 0.03 | −0.10 ± 0.07 | 0.923 | 127 | |
| 0.14 ± 0.08 (0.10)i | 0.40 ± 0.05 | −0.02 ± 0.08 | 0.933 | 71 | ||
| 10g | 0.52 ± 0.06 | −0.83 ± 0.22 | 0.952 | 78 | ||
| 0.12 ± 0.02 | 0.60 ± 0.03 | −0.81 ± 0.10 | 0.991 | 203 | ||
| 14h | 0.41 ± 0.03 | −0.48 ± 0.10 | 0.967 | 175 | ||
| 0.11 ± 0.07 (0.14)i | 0.48 ± 0.05 | −0.41 ± 0.10 | 0.973 | 99 | ||
| 13j | 0.40 ± 0.03 | −0.46 ± 0.09 | 0.970 | 176 | ||
| 0.05 ± 0.10 (0.66)i | 0.43 ± 0.08 | −0.44 ± 0.11 | 0.971 | 82 | ||
| 9k | 0.36 ± 0.10 | 0.10 ± 0.13 | 0.812 | 14 | ||
| 0.92 ± 0.23 | 0.42 ± 0.06 | 0.20 ± 0.08 | 0.953 | 30 | ||
| 9k,l | 0.34 ± 0.11 | 0.11 ± 0.14 | 0.765 | 10 | ||
| 1.01 ± 0.26 | 0.41 ± 0.06 | 0.22 ± 0.08 | 0.940 | 23 | ||
| Substrate | na | lb | mb | cc | Rd | Fe |
|---|---|---|---|---|---|---|
| EtOCOClf | 28 | 1.56 ± 0.09 | 0.55 ± 0.03 | 0.19 ± 0.24 | 0.967 | 179 |
| 7 | 0.69 ± 0.13 | 0.82 ± 0.16 | −2.40 ± 0.27 | 0.946 | 17 | |
| MeOCOClg | 19 | 1.59 ± 0.09 | 0.58 ± 0.05 | 0.16 ± 0.07 | 0.977 | |
| 4h | 49 | 1.66 ± 0.05 | 0.56 ± 0.03 | 0.15 ± 0.07 | 0.980 | 568 |
| PhSCSCli | 31 | 0.69 ± 0.05 | 0.95 ± 0.03 | 0.18 ± 0.05 | 0.987 | 521 |
| 2j | 11 | 0.57 ± 0.03 | 0.05 ± 0.08 | 0.985 | 294 | |
| 11 | 0.08 ± 0.20 (0.71)i | 0.59 ± 0.05 | 0.06 ± 0.08 | 0.985 | 133 | |
| 3k | 19 | 0.47 ± 0.03 | −0.11 ± 0.19 | 0.970 | 274 | |
| 19 | 0.03 ± 0.07 (0.70)i | 0.48 ± 0.04 | −0.10 ± 0.19 | 0.971 | 130 |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/). This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
D’Souza, M.J.; Reed, D.N.; Erdman, K.J.; Kyong, J.B.; Kevill, D.N. Grunwald-Winstein Analysis - Isopropyl Chloroformate Solvolysis Revisited. Int. J. Mol. Sci. 2009, 10, 862-879. https://doi.org/10.3390/ijms10030862
D’Souza MJ, Reed DN, Erdman KJ, Kyong JB, Kevill DN. Grunwald-Winstein Analysis - Isopropyl Chloroformate Solvolysis Revisited. International Journal of Molecular Sciences. 2009; 10(3):862-879. https://doi.org/10.3390/ijms10030862
Chicago/Turabian StyleD’Souza, Malcolm J., Darneisha N. Reed, Kevin J. Erdman, Jin Burm Kyong, and Dennis N. Kevill. 2009. "Grunwald-Winstein Analysis - Isopropyl Chloroformate Solvolysis Revisited" International Journal of Molecular Sciences 10, no. 3: 862-879. https://doi.org/10.3390/ijms10030862




