Chaperonin Structure - The Large Multi-Subunit Protein Complex
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.2. “Fuzzy-oil-drop” Model
- the geometric centre of the molecule shall be localized in the center of coordinate system.
- the longest distance between two residues (represented by the effective atom – geometric centre of side chain of the amino acid) shall overlap one of the axes (say the X-axis).
- the molecule shall be rotated around the X-axis to orient the longest inter-projections (on the YZ plane) distance along the Y-axis.
- the linear size (the maximum inter-atomic distance along the X, Y, and Z axes) increased by 9 Å in each direction (the cutoff distance for hydrophobic interaction) makes possible calculation of σx,σy,σz
2.3. Protein Partitioning
- The complete molecule was treated as one uniform “drop” – the orientation of molecule was according to its 7-fold symmetry axis (the X-axis).
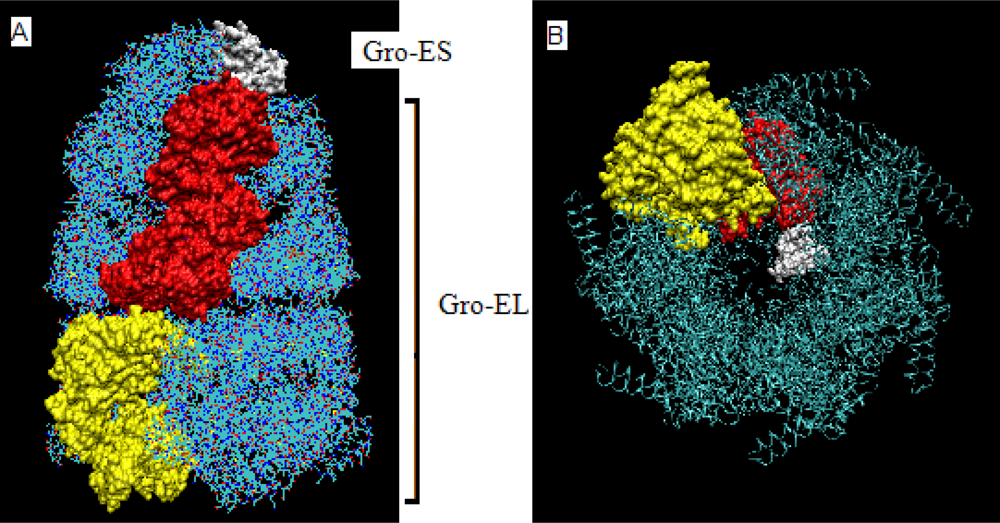
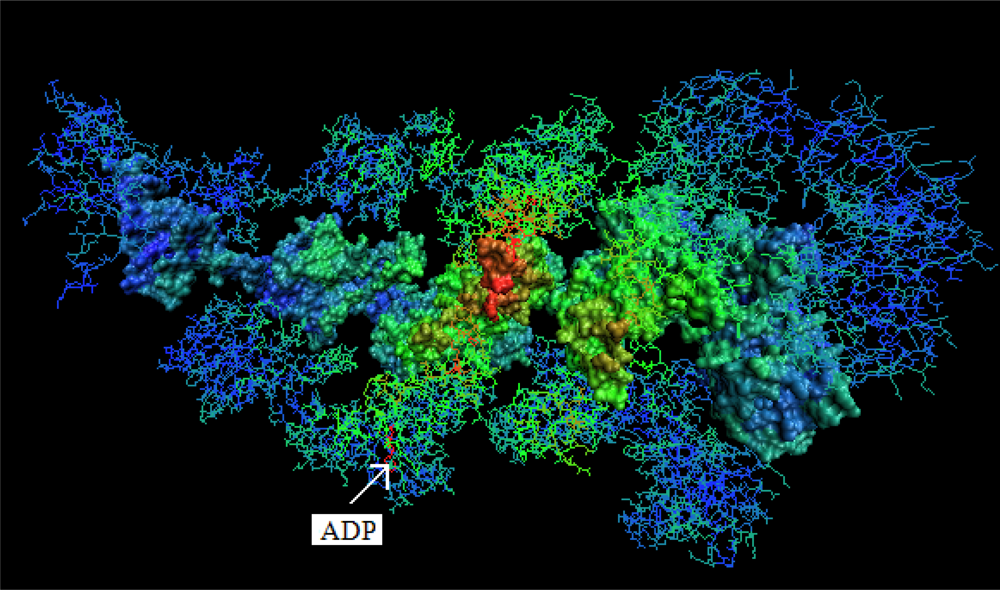
- The chaperonin molecule represents three levels organization: two stacked rings (Gro-EL) with the third one (Gro-ES) as “cap”.
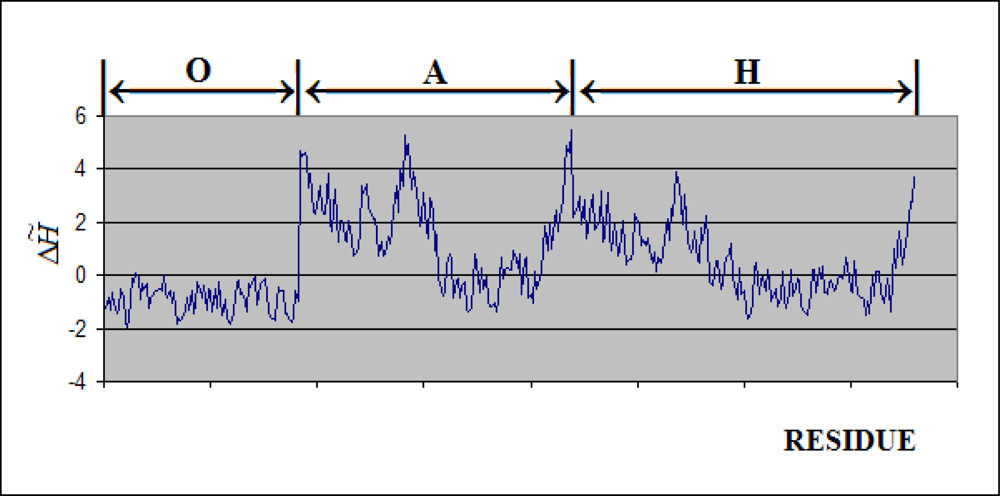
- Each ring (Gro-EL) and the “cap” (Gro-ES) is composed of seven identical polypeptide chains which are also treated as structural units (chains A-H, G-N and O-U).
- The polypeptide chains belonging to Gro-EL evidently represent the two-domain construction. This is why each such domain is treated as independent individual part and treated as a “drop”.
2.4. Identification of the Non-Bonding Interactions
2.5. Implementation
2.6. Clustering Analysis
3. Results
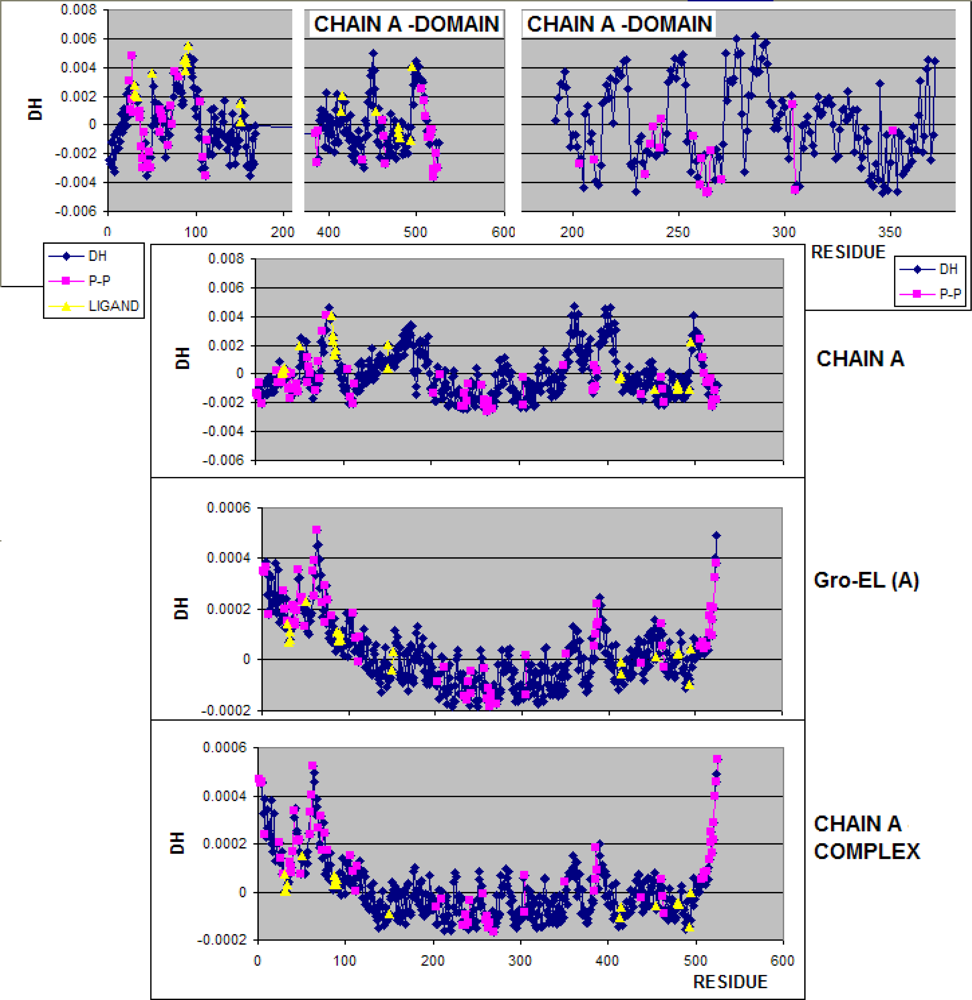
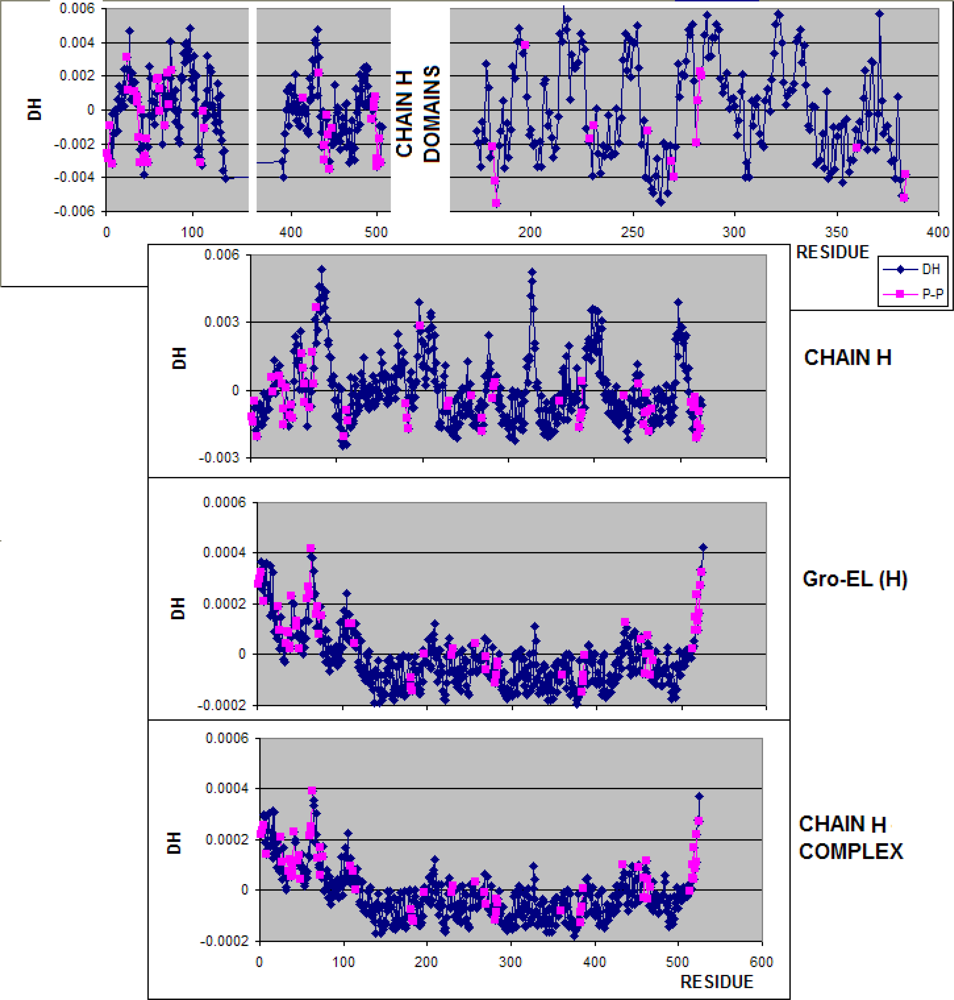
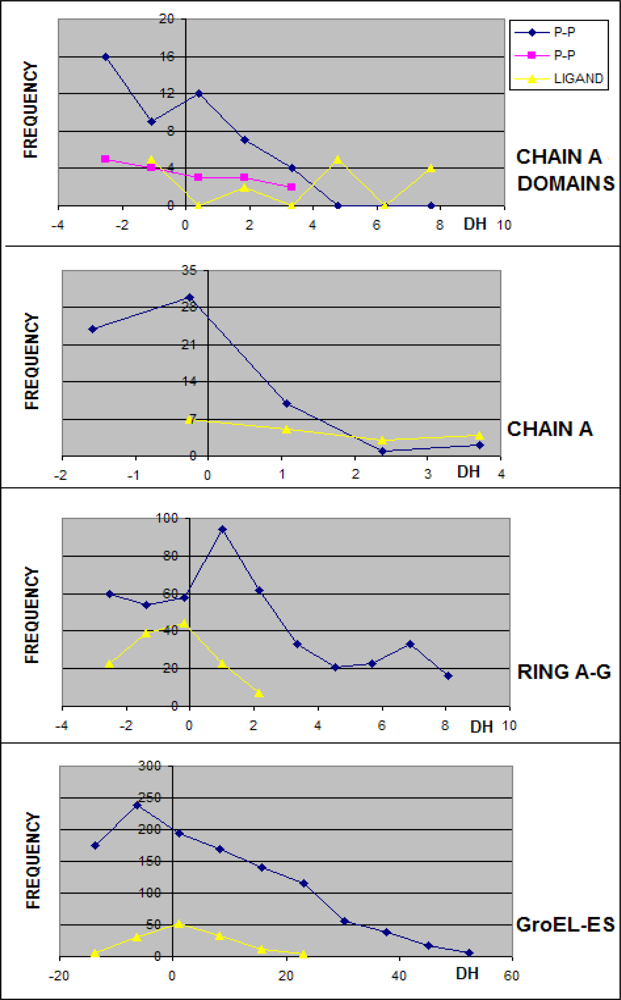
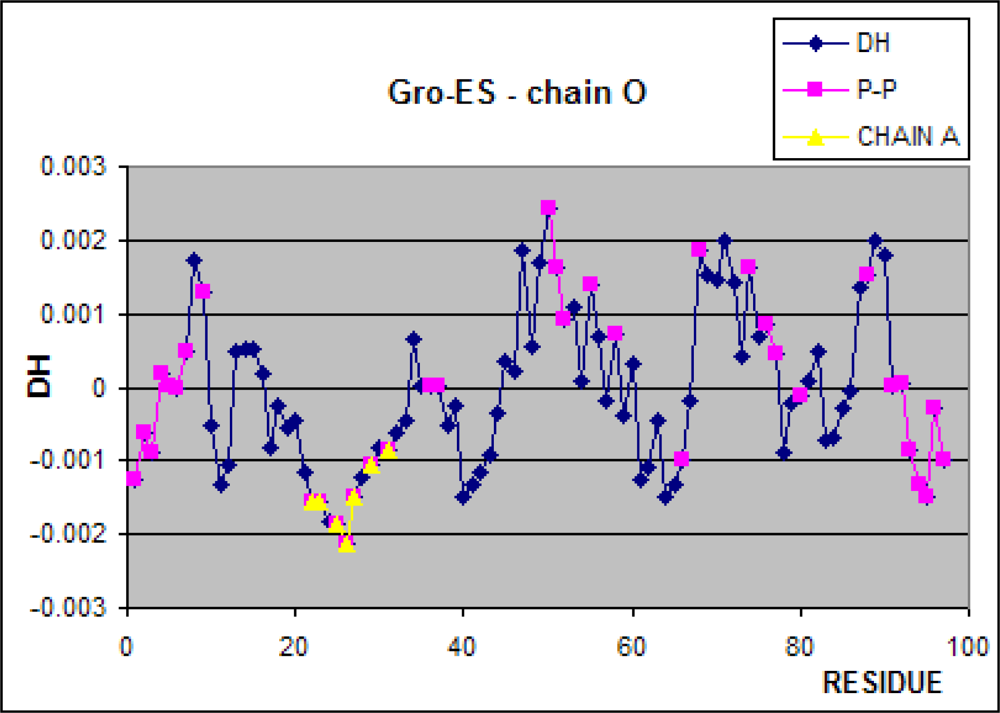
3.1. Hydrophobicity Density Irregularity in Chaperonin Molecule
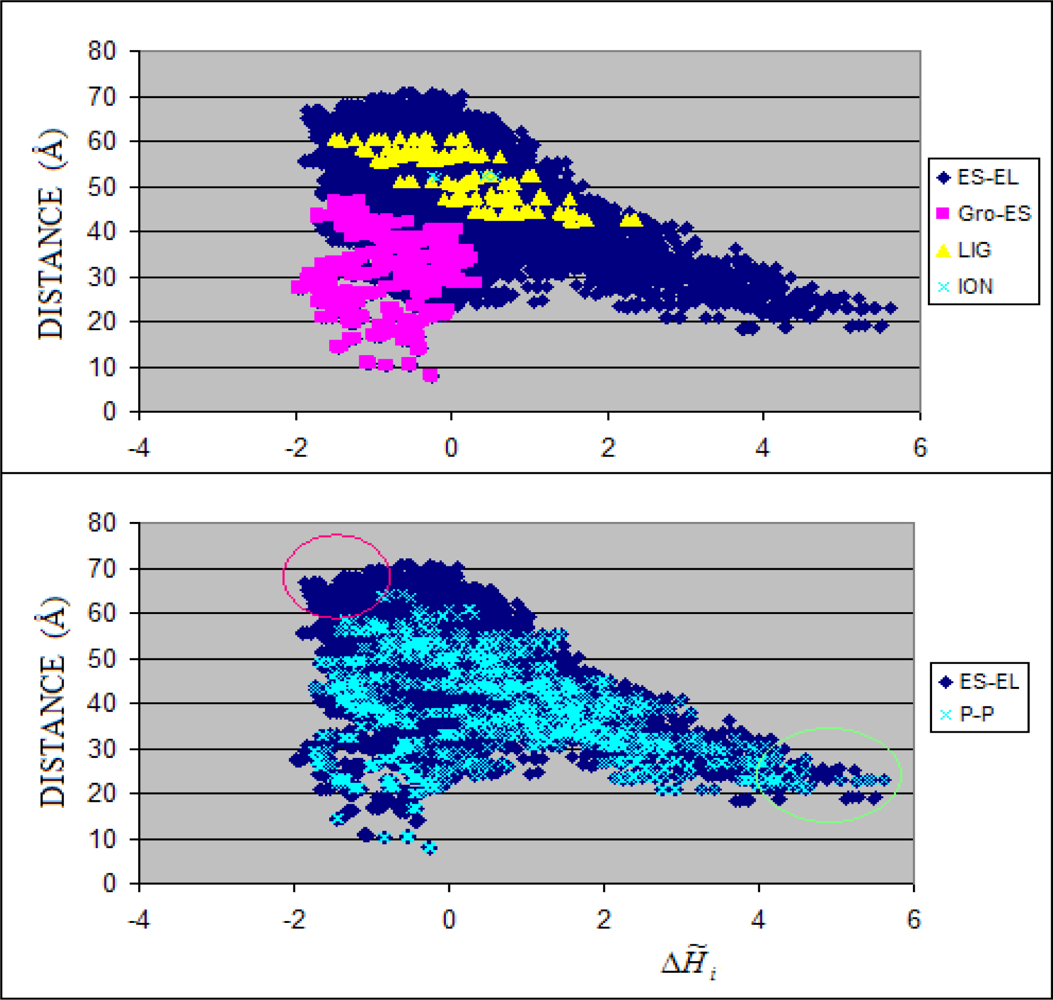
3.2. Clustering
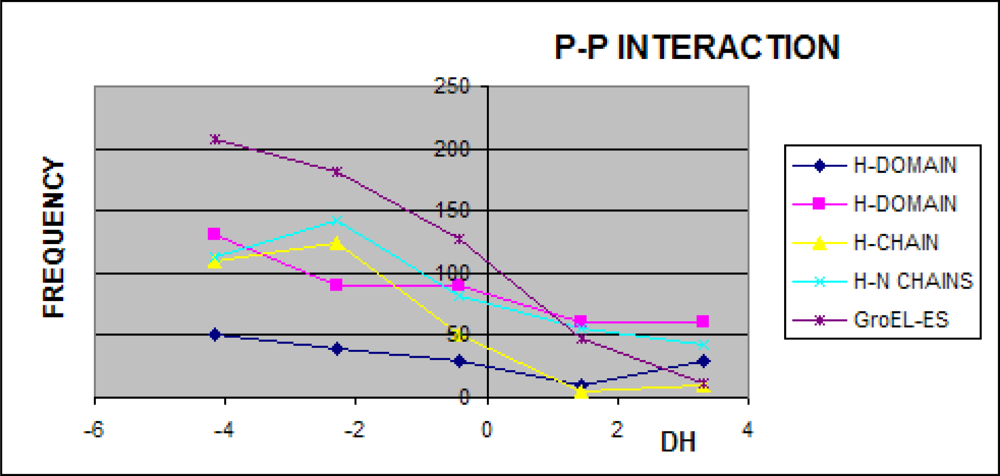
3.3. Structure-to-function Characteristics
4. Conclusions
References
- Motojima, F; Chaudhry, C; Fenton, WA; Farr, GW; Horwich, AL. Substrate polypeptide presents a load on the apical domains of the chaperonin GroEL. Proc. Natl. Acad. Sci. USA 2004, 101, 15005–15012. [Google Scholar]
- Rye, HS; Roseman, AM; Chen, S; Furtak, K; Fenton, WA; Saibil, HR; Horwich, AL. GroEL-GroES cycling: ATP and nonnative polypeptide direct alternation of folding-active rings. Cell 1999, 97, 325–338. [Google Scholar]
- Xu, Z; Sigler, PB. GroEL/GroES: Structure and function of a two-stroke folding machine. J. Struct. Biol 1998, 124, 129–141. [Google Scholar]
- Fenton, WA; Horwich, AL. GroEL-mediated protein folding. Protein Sci 1997, 6, 743–760. [Google Scholar]
- Konieczny, L; Brylinski, M; Roterman, I. Gauss-function-Based model of hydrophobicity density in proteins. Silico Biol 2006, 6, 15–22. [Google Scholar]
- Brylinski, M; Konieczny, L; Roterman, I. Hydrophobic collapse in late-stage folding (in silico) of bovine pancreatic trypsin inhibitor. Biochimie 2006, 88, 1229–1239. [Google Scholar]
- Brylinski, M; Konieczny, L; Roterman, I. Fuzzy oil drop hydrophobic force field - a model to represent late-stage folding (in silico) of lysozyme. J. Biomol. Struct. Dyn 2006, 23, 519–528. [Google Scholar]
- Brylinski, M; Konieczny, L; Roterman, I. Hydrophobic collapse in (in silico) protein folding. Comput. Biol. Chem 2006, 30, 255–267. [Google Scholar]
- Brylinski, M; Konieczny, L; Roterman, I. Is the protein folding an aim-oriented process? Human haemoglobin as example. Int. J. Bioinform. Res. Appl 2007, 3, 234–260. [Google Scholar]
- Brylinski, M; Prymula, K; Jurkowski, W; Kochanczyk, M; Stawowczyk, E; Konieczny, L; Roterman, I. Prediction of functional sites based on the fuzzy oil drop model. PLoS Comput. Biol 2007, 3, e94. [Google Scholar]
- Brylinski, M; Kochanczyk, M; Broniatowska, E; Roterman, I. Localization of ligand binding site in proteins identified in silico. J. Mol. Model 2007, 13, 665–675. [Google Scholar]
- Brylinski, M; Konieczny, L; Roterman, I. Ligation site in proteins recognized in silico. Bioinformation 2006, 1, 127–129. [Google Scholar]
- Brylinski, M; Kochanczyk, M; Konieczny, L; Roterman, I. Sequence-structure-function relation characterized in silico. In Silico Biol 2006, 6, 589–600. [Google Scholar]
- Taguchi, H. Chaperonin GroEL meets the substrate protein as a “load” of the rings. J. Biochem 2005, 137, 543–549. [Google Scholar]
- Xu, Z; Horwich, AL; Sigler, PB. The crystal structure of the asymmetric GroEL-GroES-(ADP)7 chaperonin complex. Nature 1997, 388, 741–750. [Google Scholar]
- Levitt, M. A simplified representation of protein conformations for rapid simulation of protein folding. J. Mol. Biol 1976, 104, 59–107. [Google Scholar]
- Kyte, J; Doolittle, RF. A simple method for displaying the hydropathic character of a protein. J. Mol. Biol 1982, 157, 105–132. [Google Scholar]
- Engelman, DM; Steitz, TA; Goldman, A. Identifying nonpolar transbilayer helices in amino acid sequences of membrane proteins. Annu. Rev. Biophys. Biophys. Chem 1986, 15, 321–353. [Google Scholar]
- Hopp, TP; Woods, KR. Prediction of protein antigenic determinants from amino acid sequences. Proc. Natl. Acad. Sci. USA 1981, 78, 3824–3828. [Google Scholar]
- Rose, GD; Geselowitz, AR; Lesser, GJ; Lee, RH; Zehfus, MH. Hydrophobicity of amino acid residues in globular proteins. Science 1985, 229, 834–838. [Google Scholar]
- Wolfenden, R; Andersson, L; Cullis, PM; Southgate, CC. Affinities of amino acid side chains for solvent water. Biochemistry 1981, 20, 849–855. [Google Scholar]
- .
- .
- .
- .
- .
- .
- Jain, AK; Dubes, RC. Algorithms for clustering data; Prentice Hall: Englewood Cliffs NJ, USA, 1988. [Google Scholar]
- Clare, DK; Bakkes, PJ; van Heerikhuizen, H; van der Vies, SM; Saibil, HR. Chaperonin complex with a newly folded protein encapsulated in the folding chamber. Nature 2009, 457, 107–110. [Google Scholar]
- .
- Anil, B; Sato, S; Cho, J-H; Raleigh, DP. Fine structure analysis of a protein folding transition state; Distinguishing between hydrophobic stabilization and specific packing. J. Mol. Biol 2005, 354, 693–705. [Google Scholar]
| PROTEIN | METHOD | ACCORDANCE | |
|---|---|---|---|
| P-P versus all others | P-P versus not complexed | ||
| A-domain 1–191 371–524 | HIERARCHY DMIN
HIERARCHY DMAX HIERARCHY AVG | 0.8404 0.7590 0.6254 | 0.8293 0.7422 0.5993 |
| A-domain 192–371 | HIERARCHY DMIN
HIERARCHY DMAX HIERARCHY AVG | 0.9000 0.7167 0.7667 | 0.9000 0.7167 0.7667 |
| Chain A | HIERARCHY DMIN
HIERARCHY DMAX HIERARCHY AVG | 0.8702 0.5553 0.5668 | 0.8651 0.5377 0.5496 |
| Chains ABCDEFG | HIERARCHY DMIN
HIERARCHY DMAX HIERARCHY AVG | 0.8760 0.5461 0.5774 | 0.8710 0.5445 0.5808 |
| Chain O | HIERARCHY DMIN
HIERARCHY DMAX HIERARCHY AVG | 0.6598
0.5773 0.5979 | 0.6598
0.5773 0.5979 |
| COMPLEX | HIERARCHY DMIN
HIERARCHY DMAX HIERARCHY AVG | 0.8404 0.5145 0.5062 | 0.8554 0.5069 0.5563 |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/). This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Banach, M.; Stąpor, K.; Roterman, I. Chaperonin Structure - The Large Multi-Subunit Protein Complex. Int. J. Mol. Sci. 2009, 10, 844-861. https://doi.org/10.3390/ijms10030844
Banach M, Stąpor K, Roterman I. Chaperonin Structure - The Large Multi-Subunit Protein Complex. International Journal of Molecular Sciences. 2009; 10(3):844-861. https://doi.org/10.3390/ijms10030844
Chicago/Turabian StyleBanach, Mateusz, Katarzyna Stąpor, and Irena Roterman. 2009. "Chaperonin Structure - The Large Multi-Subunit Protein Complex" International Journal of Molecular Sciences 10, no. 3: 844-861. https://doi.org/10.3390/ijms10030844





