Theoretical Study of ClOO + NO Reaction: Mechanism and Kinetics
Abstract
:1. Introduction
2. Calculation Methods
3. Results and Discussion
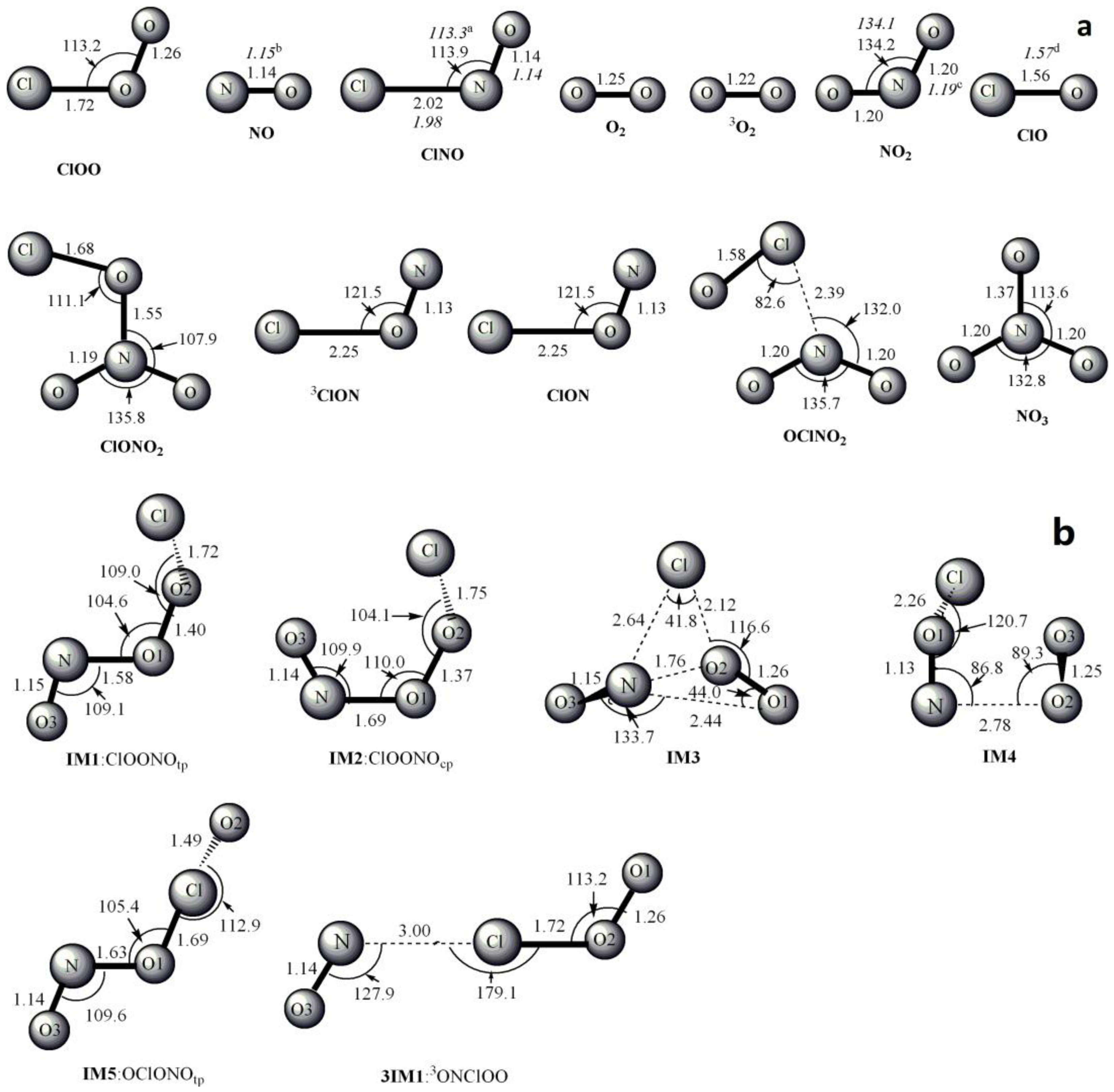
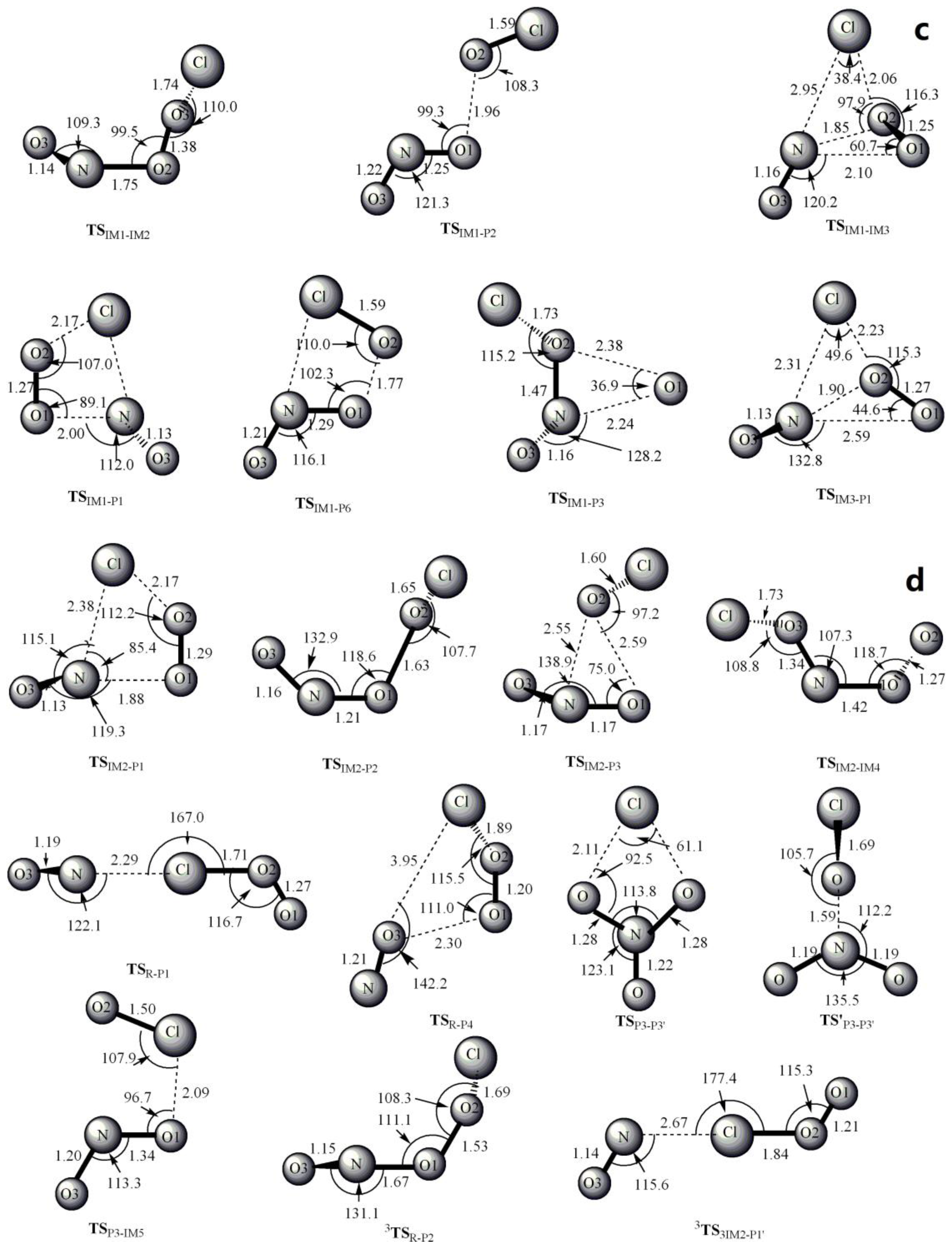
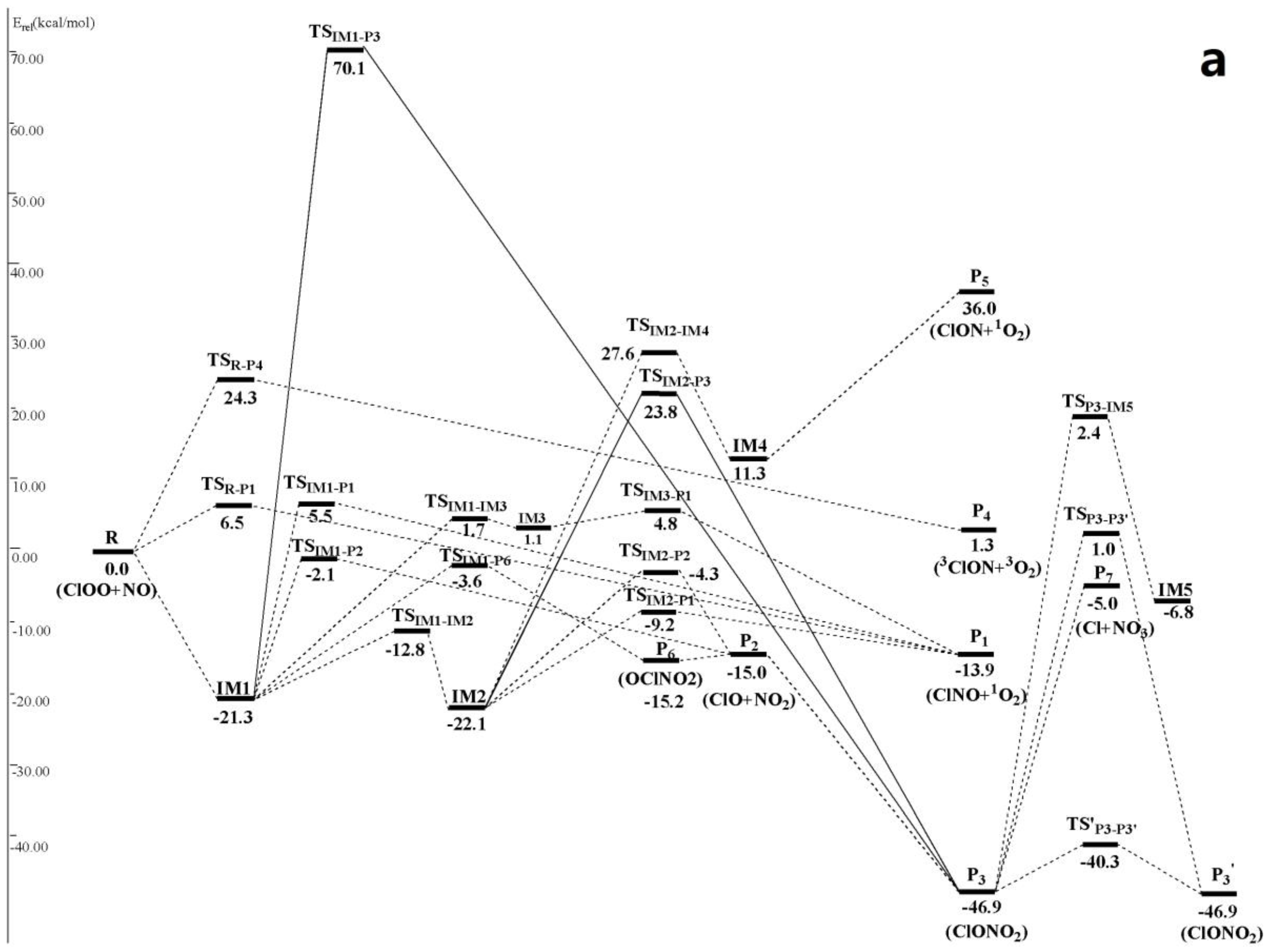
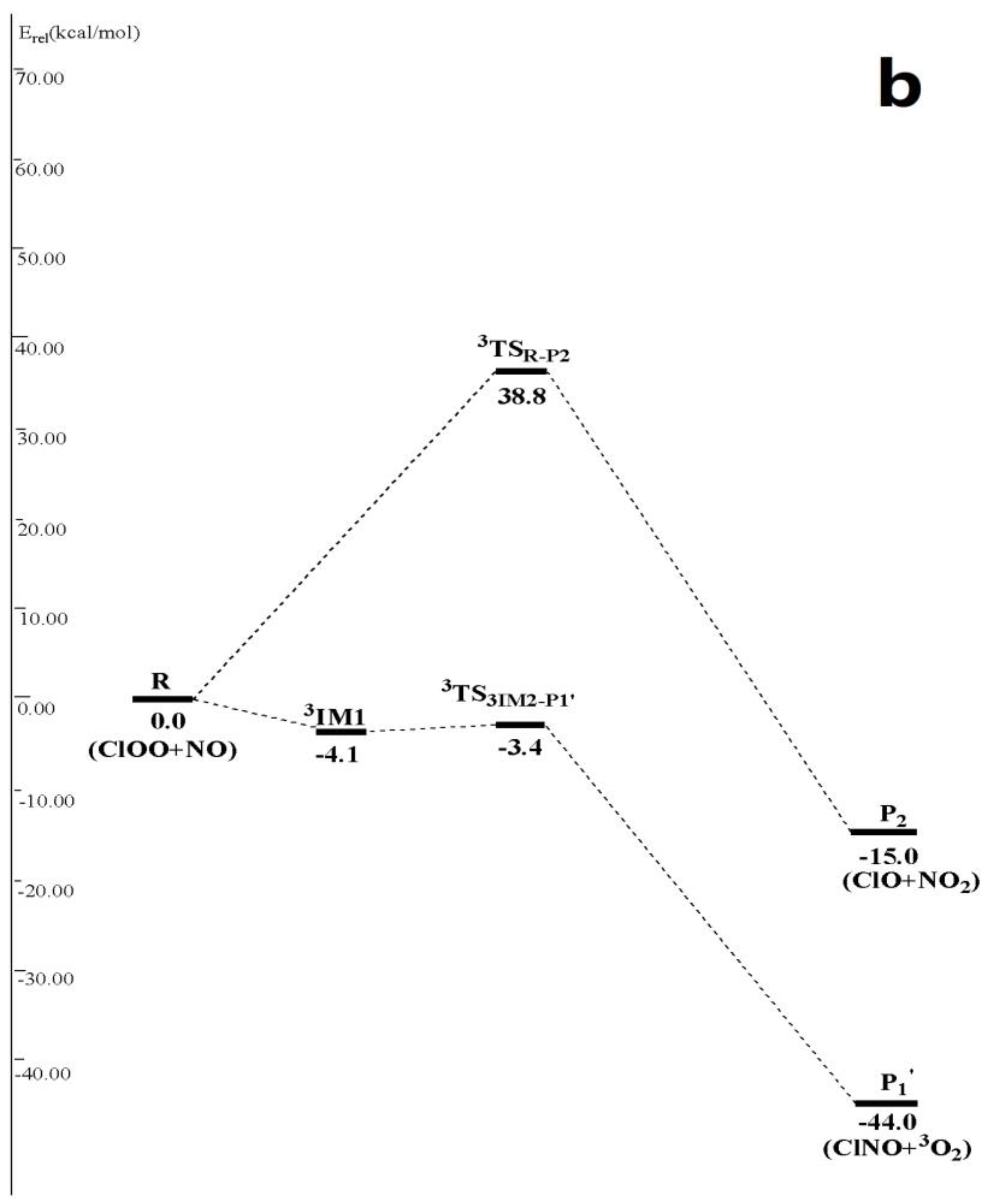
3.1. Potential Energy Surface and Reaction Mechanism
3.1.1. Addition Reaction Channels
3.1.2. Abstraction Reaction Channels
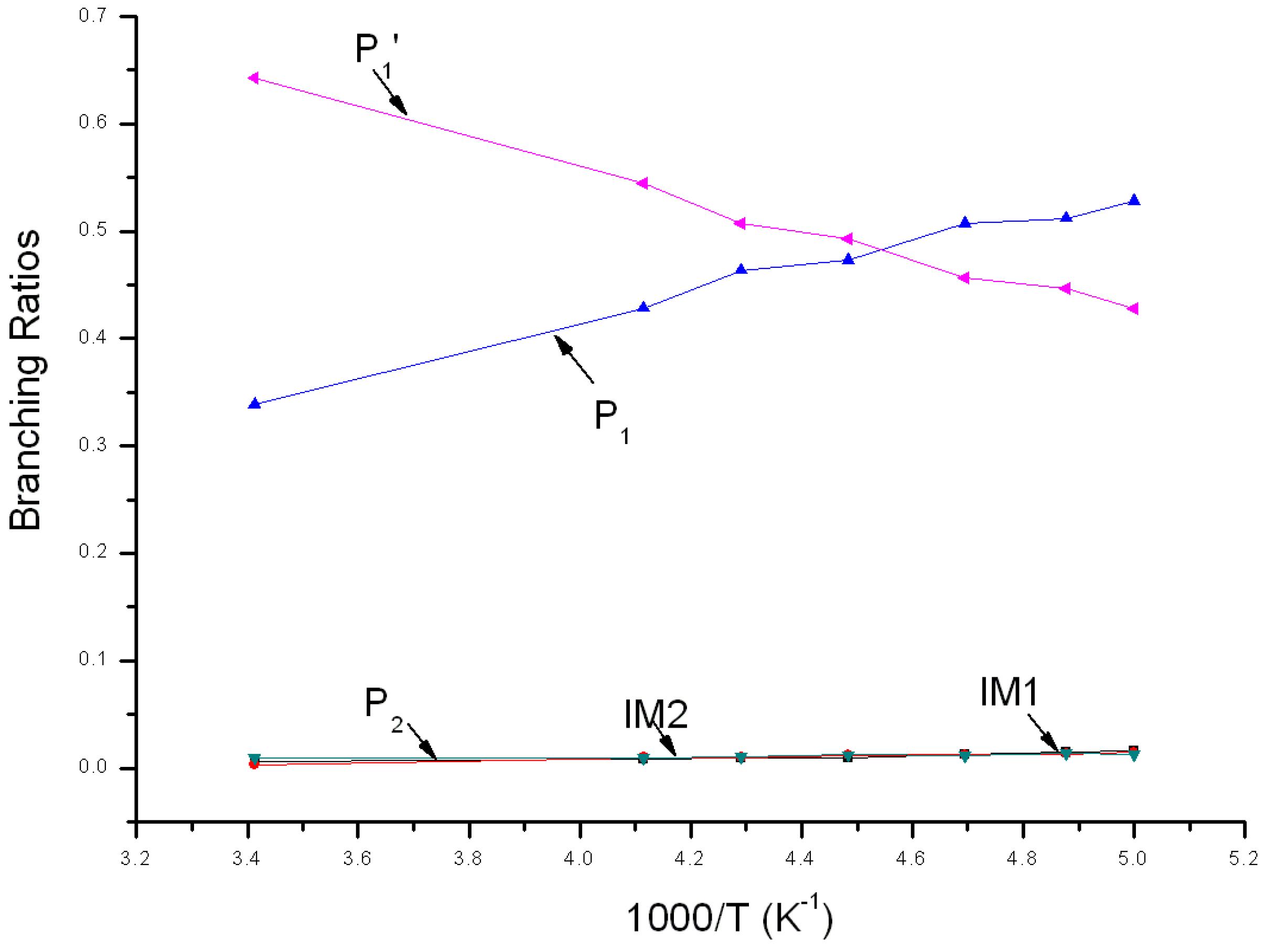
3.2. Kinetic Calculations
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Finalyson-Pitts, B.J.; Pitts, J.N., Jr. Atmospheric Chemistry; Wiley Interscience: New York, NY, USA, 1986; Part 9. [Google Scholar]
- Rowland, F.S. Stratospheric Ozone Depletion. Phys. Chem. 1994, 32, 769–790. [Google Scholar]
- Sander, S.P.; Friedl, R.R.; Yung, Y.L. Quantum yield of chlorine-atom formation in the photodissociation of chlorine peroxide (ClOOCl) at 308 nm. Science 2013, 589, 52–55. [Google Scholar]
- Katz, A.; Narkis, N. Removal of chlorine dioxide disinfection by-products by ferrous salts. Water Res. 2001, 35, 101–108. [Google Scholar] [CrossRef]
- Hart, P.W.; Hsieh, J.S. Competing Parallel Reaction of Chlorine and Chlorine Dioxide during Kraft Pulp Bleaching. Chem. Eng. Commun. 1993, 126, 27–41. [Google Scholar] [CrossRef]
- Tsai, L.S.; Huxsoll, C.C.; Robertson, G.J. Prevention of Potato Spoilage during Storage by Chlorine Dioxide. Food Sci. 2001, 66, 472–477. [Google Scholar] [CrossRef]
- Ritter, S.K. Publication Ethics: Rights and Wrongs. Chem. Eng. News 2001, 79, 24–26. [Google Scholar] [CrossRef]
- Arkell, A.; Schwager, I. Matrix infrared study of the chlorine superoxide radical. J. Am. Chem. Soc. 1967, 89, 5999–6006. [Google Scholar] [CrossRef]
- Abramowitz, S.; Chase, M.W. Thermodynamic properties of gas phase species of importance to ozone depletion. Pure Appl. Chem. 1991, 63, 1449–1454. [Google Scholar] [CrossRef]
- Baer, S.; Hippler, H.; Rahn, R.; Siefke, M.; Seitzinger, N.; Troe, J. Thermodynamic and kinetic properties of the reaction Cl + O2 + M = ClOO + M in the range 160–300 K and 1–1000 bar. J. Chem. Phys. 1991, 95, 6463–6470. [Google Scholar] [CrossRef]
- Nicovich, J.M.; Krufter, K.D.; Shockolford, C.J.; Wine, P.H. Thermochemistry and kinetics of the Cl + O2 association reaction. Chem. Phys. Lett. 1991, 179, 367–373. [Google Scholar] [CrossRef]
- Mueller, H.S.P.; Willner, H. Vibrational and electronic spectra of chlorine dioxide, OClO, and chlorine superoxide ClOO, isolated in cryogenic matrixes. J. Phys. Chem. 1993, 97, 10589–10598. [Google Scholar] [CrossRef]
- Chase, M.W. NIST-JANAF Thermochemical Tables for the Bromine Oxides. J. Phys. Chem. Ref. Data 1996, 25, 1069–1111. [Google Scholar] [CrossRef]
- Wang, X.-B.; Wang, L.-S. The electronic structure and electron affinities of higher chlorine oxide radicals ClOx (x = 2–4) from photoelectron spectroscopy of ClO−x anions. J. Chem. Phys. 2000, 113, 10928–10933. [Google Scholar] [CrossRef]
- Distelrath, V.; Boesl, U. Mass selective gas phase study of ClO, OClO, ClOO and ClAr by anion-ZEKE-photoelectron spectroscopy. Faraday Discuss. 2000, 115, 161–174. [Google Scholar] [CrossRef]
- Kopitzky, R.; Grothe, H.; Willner, H. Chlorine Oxide Radicals ClOx (x = 1–4) Studied by Matrix Isolation Spectroscopy. Chem. Eur. J. 2002, 8, 5601–5621. [Google Scholar] [CrossRef]
- Elder, T. Reactions of Lignin Model Compounds with Chlorine Dioxide. Mol. Orbital Calc. Holzforsch. 1998, 52, 371–384. [Google Scholar] [CrossRef]
- Aloisio, S.; Francisco, J.S. Radical-Water Complexes in Earth’s Atmosphere. Acc. Chem. Res. 2000, 33, 825–830. [Google Scholar] [CrossRef] [PubMed]
- Peterson, K.A.; Werner, H.J. Multireference configuration interaction calculations of the low-lying electronic states of ClO2. J. Chem. Phys. 1992, 96, 8948–8961. [Google Scholar] [CrossRef]
- Alcami, M.; Cooper, I.L. Ab initio calculations on bromine oxide and dioxides and their corresponding anions. J. Chem. Phys. 1998, 108, 9414–9424. [Google Scholar] [CrossRef]
- Alcami, M.; Mó, O.; Yáñez, M.; Cooper, I.L. The performance of density-functional theory in challenging cases: Halogen oxides. J. Chem. Phys. 2000, 112, 6131–6140. [Google Scholar] [CrossRef]
- Filatov, M.; Cremer, D. Bonding in the ClOO(2A’’) and BrOO(2A’’) radical: Nonrelativistic single-reference versus relativistic multi-reference descriptions in density functional theory. Phys. Chem. Chem. Phys. 2003, 5, 2320–2326. [Google Scholar] [CrossRef]
- Jafri, J.A.; Iii, B.H.L.; Bauschlicher, C.W., Jr.; Phillips, D.H. The lower electronic states of ClOO: A computational investigation. J. Chem. Phys. 1985, 83, 1693–1701. [Google Scholar] [CrossRef]
- Wood, S.C. Select the Right NOx Control Technology—Consider the Degree of Emission Reduction Needed, the Type of Fuel, Combustion Device Design, and Operational Factors. Chem. Eng. Prog. 1994, 90, 32–38. [Google Scholar]
- Brunet, S.M.K.; Guo, J.Z.; Carrington, T.; Filseth, S.V.; Sadowski, C.M. State-to-state and total rotational energy transfer rate constants for CN(B2Σ+, v = 0, N) + H2, CN(X2Σ+, v = 2, N) + H2, D2, and CN(X2Σ+, v = 3, N) + NO. J. Chem. Phys. 2002, 116, 3617. [Google Scholar] [CrossRef]
- Zhang, J.-X.; Li, Z.-S.; Liu, J.-Y.; Sun, C.-C. Theoretical Study on Reaction Mechanism of the Cyanogen Radical with Nitrogen Dioxide. J. Phys. Chem. A 2005, 109, 10307–10313. [Google Scholar] [CrossRef] [PubMed]
- Baren, R.E.; Hershberger, J.F. Kinetics of the NCN Radical. J. Phys. Chem. A 2002, 106, 11093–11097. [Google Scholar] [CrossRef]
- Huang, C.-L.; Tseng, S.-Y.; Wang, T.-Y.; Wang, N.-S.; Xu, Z.-F.; Lin, M.-C. Reaction mechanism and kinetics of the NCN + NO reaction: Comparison of theory and experiment. J. Chem. Phys. 2005, 122. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.-T.; Ho, J.-J. Theoretical Investigation of the Mechanisms of Reaction of NCN with NO and NS. J. Phys. Chem. A 2005, 109, 2564. [Google Scholar] [CrossRef] [PubMed]
- Wei, Z.-G.; Li, Q.-S.; Zhang, S.-W.; Sun, Y.-B.; Sun, C.-C. Quantum mechanical studies on the potential energy surface of the reactions 3NCN/3CNN + NO, 1NNO + CN and 2N3 + CO. J. Mol. Struct. THEOCHEM 2005, 722, 139–146. [Google Scholar] [CrossRef]
- Jin, L.; Ding, Y.-H.; Wang, J.; Sun, C.-C. Reaction mechanism of the CCN radical with nitric oxide. J. Comput. Chem. 2006, 27, 883–893. [Google Scholar] [CrossRef] [PubMed]
- Baren, R.E.; Hershberger, J.F. Kinetics of the NCS Radical. J. Phys. Chem. A 1999, 103, 11340–11344. [Google Scholar] [CrossRef]
- Wei, Z.-G.; Huang, X.-R.; Sun, Y.-B.; Sun, C.-C. On the Theoretical Study of the Potential Energy Surface for the C2H + NO2 Reaction. Chem. J. Chin. Univ. 2003, 24, 2224–2226. [Google Scholar]
- Chen, H.-L.; Wu, C.-W.; Ho, J.-J. Theoretical Investigation of the Mechanisms of Reactions of H2CN and H2SiN with NO. J. Phys. Chem. A 2006, 110, 8893–8900. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.-L.; Ho, J.-J. Computational investigation of the reaction of NO with imine, silanimine, and its substituted derivatives. J. Mol. Struct. THEOCHEM 2006, 772, 93–102. [Google Scholar] [CrossRef]
- Enami, S.; Hoshino, Y.; Ito, Y.; Hashimoto, S.; Kawasaki, M. Kinetic Study of the ClOO + NO Reaction Using Cavity Ring-Down Spectroscopy. J. Phys. Chem. A 2006, 110, 3546–3551. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Sun, M. Theoretical study of the mechanism for the ClOO + NO reaction on the singlet potential energy surface. Struct. Chem. 2012, 23, 107–114. [Google Scholar] [CrossRef]
- Ou-Yang, S.-L.; Wu, N.-N.; Liu, J.-Y.; Han, X.-G. Theoretical mechanism study on the reaction of FOO radical with NO. J. Chem. 2016, 2016. [Google Scholar] [CrossRef]
- Holbrook, K.A.; Pilling, M.J.; Robertson, S.H. Unimolecular Reactions; Wiley: Chichester, UK, 1972; Volume 15, pp. 357–362. [Google Scholar]
- Hehre, W.J.; Radom, L.; Schleyer, P.v.R.; Pople, J. AB INITIO Molecular Orbital Theory; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1986; Volume 9, pp. 399–406. [Google Scholar]
- Fukui, K. The path of chemical reactions—The IRC approach. Acc. Chem. Res. 1981, 14, 471–476. [Google Scholar] [CrossRef]
- Doubleday, C., Jr.; Page, M.; Mclver, J.W., Jr. Singlet biradicals as intermediates. Canonical variational transition-state theory results for trimethylene. J. Chem. Phys. 2002, 92, 4367–4371. [Google Scholar] [CrossRef]
- Gonzalez, C.; Schlegel, H.B. An improved algorithm for reaction path following. J. Chem. Phys. 1989, 90, 2154–2161. [Google Scholar] [CrossRef]
- Gonzalez, C.; Schlegel, H.B. Reaction path following in mass-weighted internal coordinates. J. Phys. Chem. 1990, 94, 5523–5527. [Google Scholar] [CrossRef]
- Frisch, M.J.; Truck, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Zakrzewski, V.G.; Montgomery, J.A., Jr.; Stratmann, R.E.; Burant, J.C.; et al. GAUSSIAN 03, Revision A.1; Guassian, Inc.: Pittsburgh, PA, USA, 2003. [Google Scholar]
- Barker, J.R. Multiple-Well, multiple-path unimolecular reaction systems. I. MultiWell computer program suite. Int. J. Chem. Kinet. 2001, 33, 232–245. [Google Scholar] [CrossRef]
- Barker, J.R.; Ortiz, N.F.; Preses, J.M.; Lohr, L.L.; Maranzana, A.; Stimac, P.J. MultiWell-2011 Software; University of Michigan: Ann Arbor, MI, USA, 2007; Available online: http://aoss.engin.umich.edu/multiwell/ (accessed on 1 January 2011).
- Hellwege, K.H.; Hellwege, A.M. (Eds.) Landolt-Bornstein: Group II: Atomic and Molecular Physics Volume 7: Structure Data of Free Polyatomic Molecule; Springer: Berlin/Heidelberg, Germany, 1976. [Google Scholar]
- Huber, K.P.; Herzberg, G. Molecular Spectra and Molecular Structure. IV. Constants of Diatomic Molecules; Van Nostrand Reinhold Co.: New York, NY, USA, 1979. [Google Scholar]
- Herzberg, G. Electronic Spectra and Electronic Structure of Polyatomic Molecules; Van Nostrand: New York, NY, USA, 1966; pp. 273–283. [Google Scholar]
- Irikura, K.K. Experimental Vibrational Zero-Point Energies: Diatomic Molecules. J. Phys. Chem. Ref. Data 2007, 36, 389–397. [Google Scholar] [CrossRef]
- Klippenstein, S.J. An Efficient Procedure for Evaluating the Number of Available States within a Variably Defined Reaction Coordinate Framework. J. Phys. Chem. 1994, 98, 11459–11464. [Google Scholar] [CrossRef]
- Klippenstein, S.J. A bond length reaction coordinate for unimolecular reactions. II. Microcanonical and canonical implementations with application to the dissociation of NCNO. J. Chem. Phys. 1991, 94, 6469–6482. [Google Scholar] [CrossRef]
- Francisco, J.S. An ab initio investigation of the significance of the HOOF intermediate in coupling reactions involving FOOx and HOx species. J. Chem. Phys. 1993, 98, 2198–2207. [Google Scholar] [CrossRef]
- Francisco, J.S.; Su, Y. An ab initio study of the reaction between FO radicals and H2O. Chem. Phys. Lett. 1993, 215, 58–62. [Google Scholar] [CrossRef]
Sample Availability: Not available. |
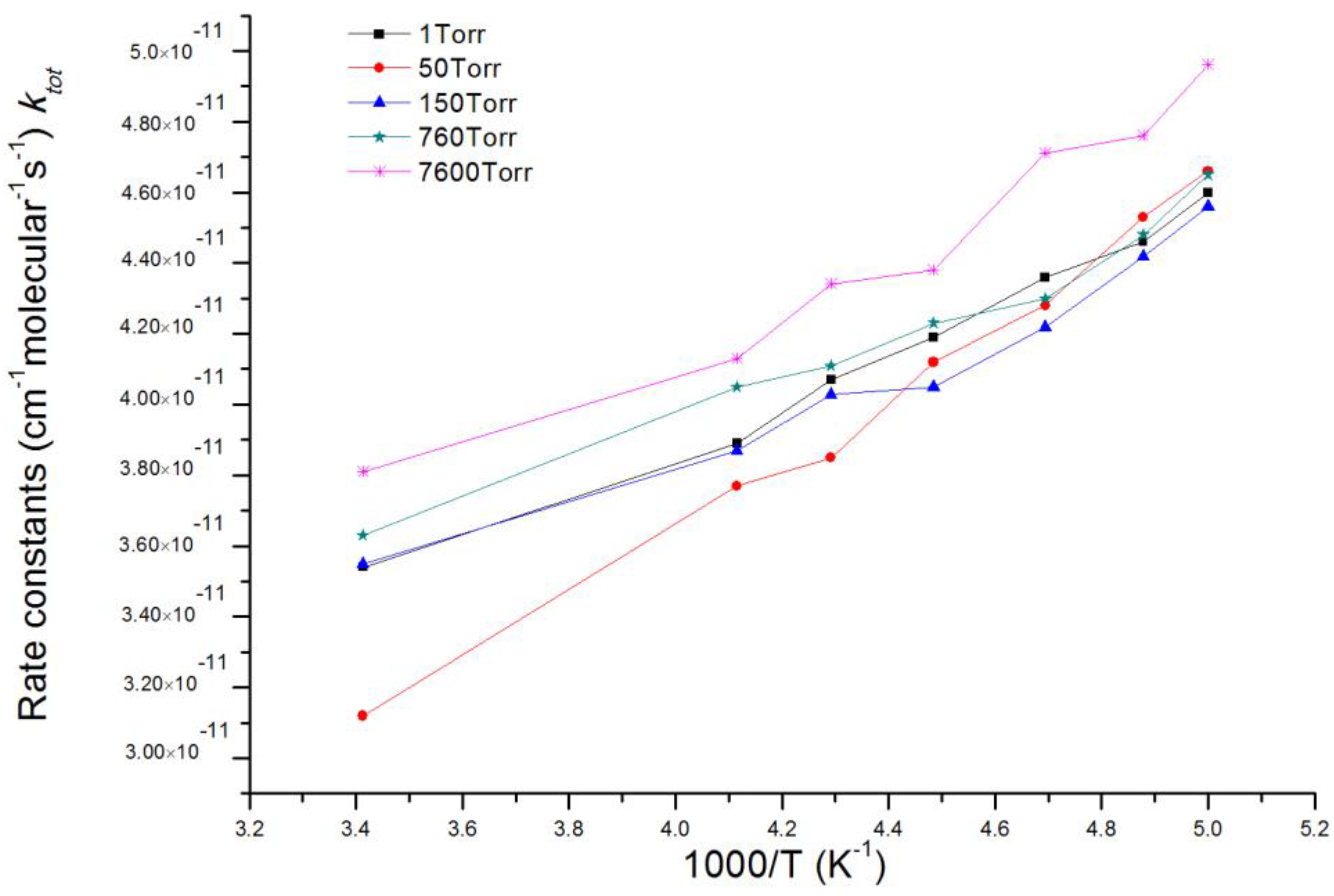
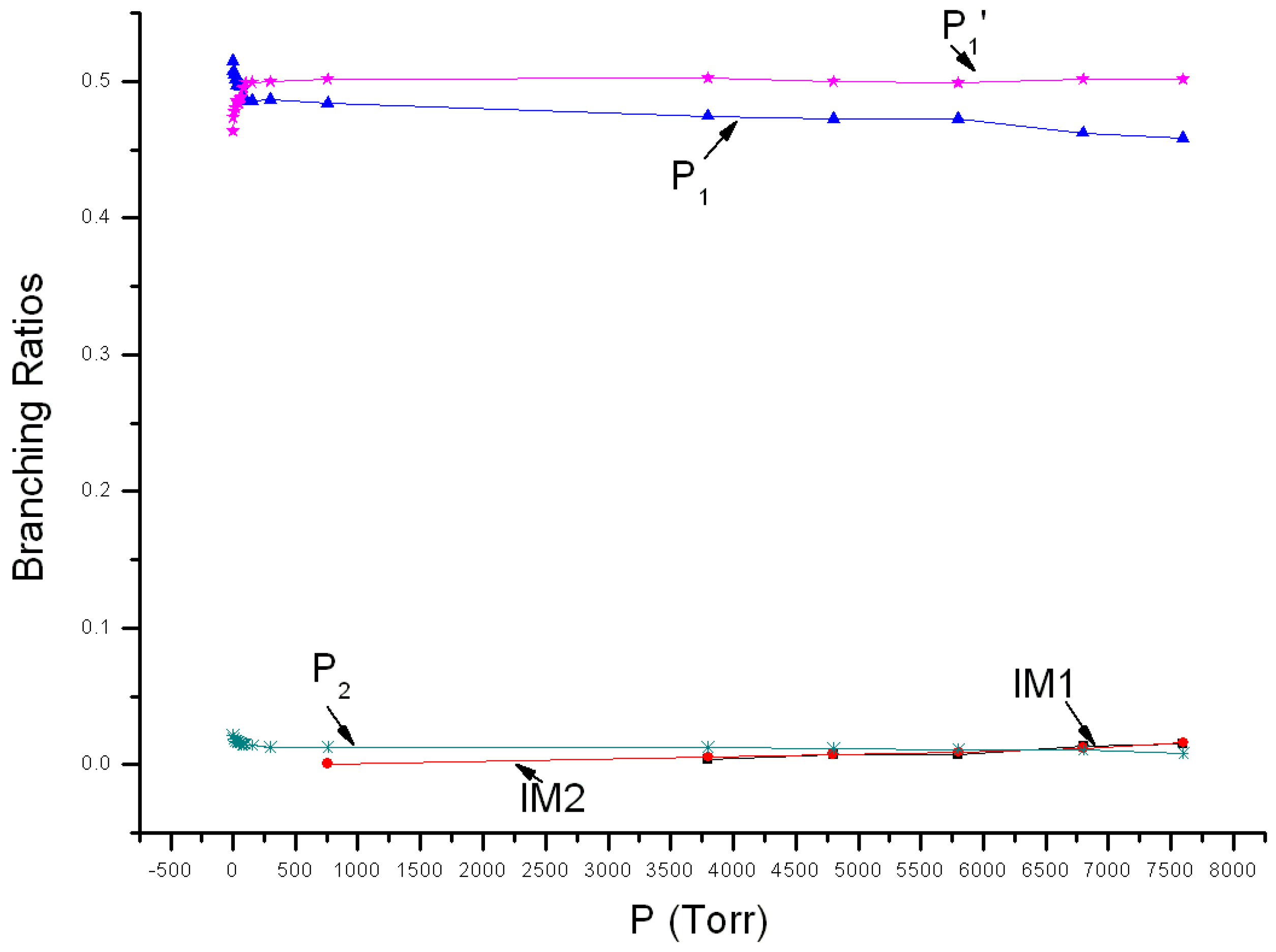
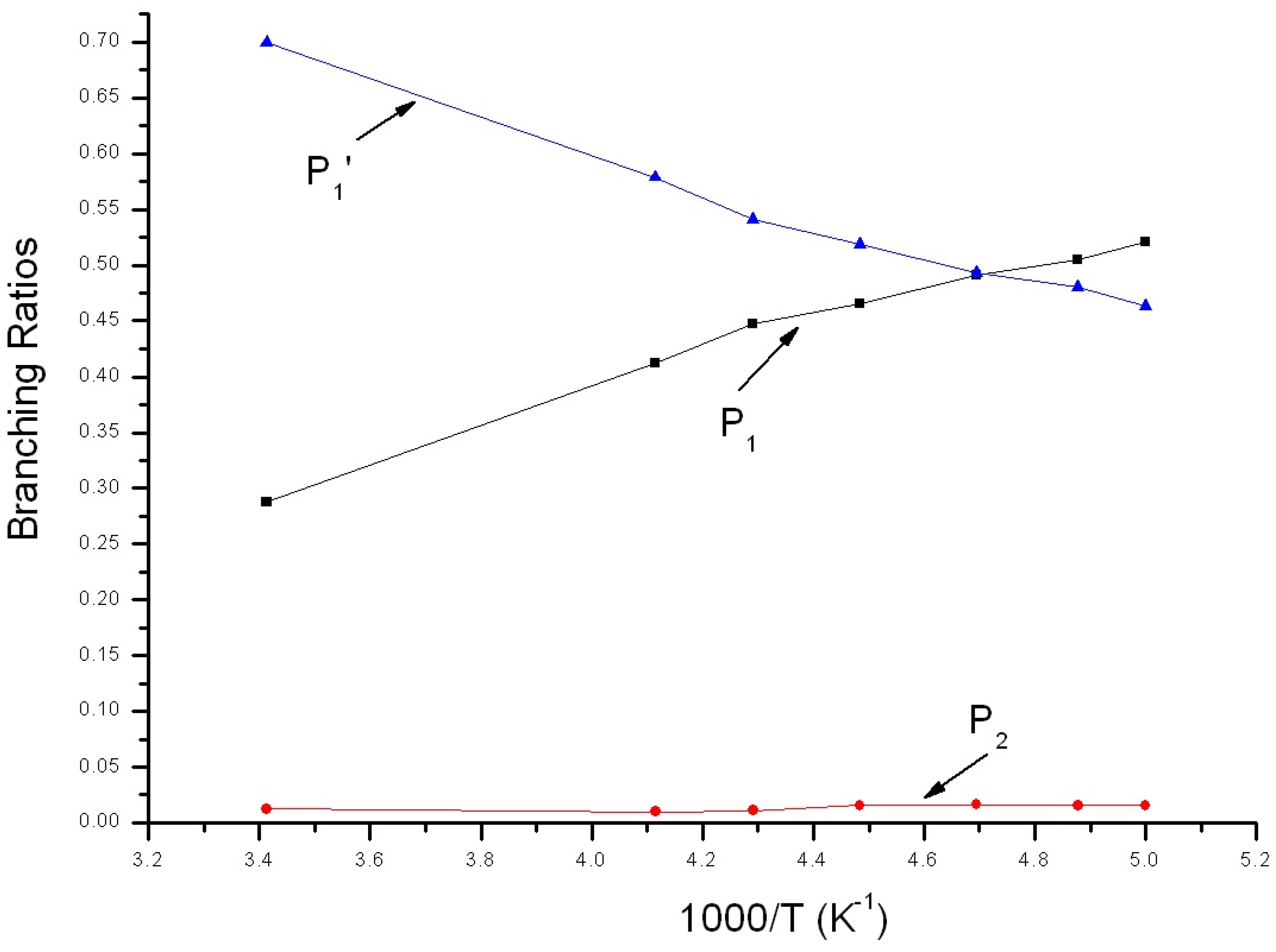
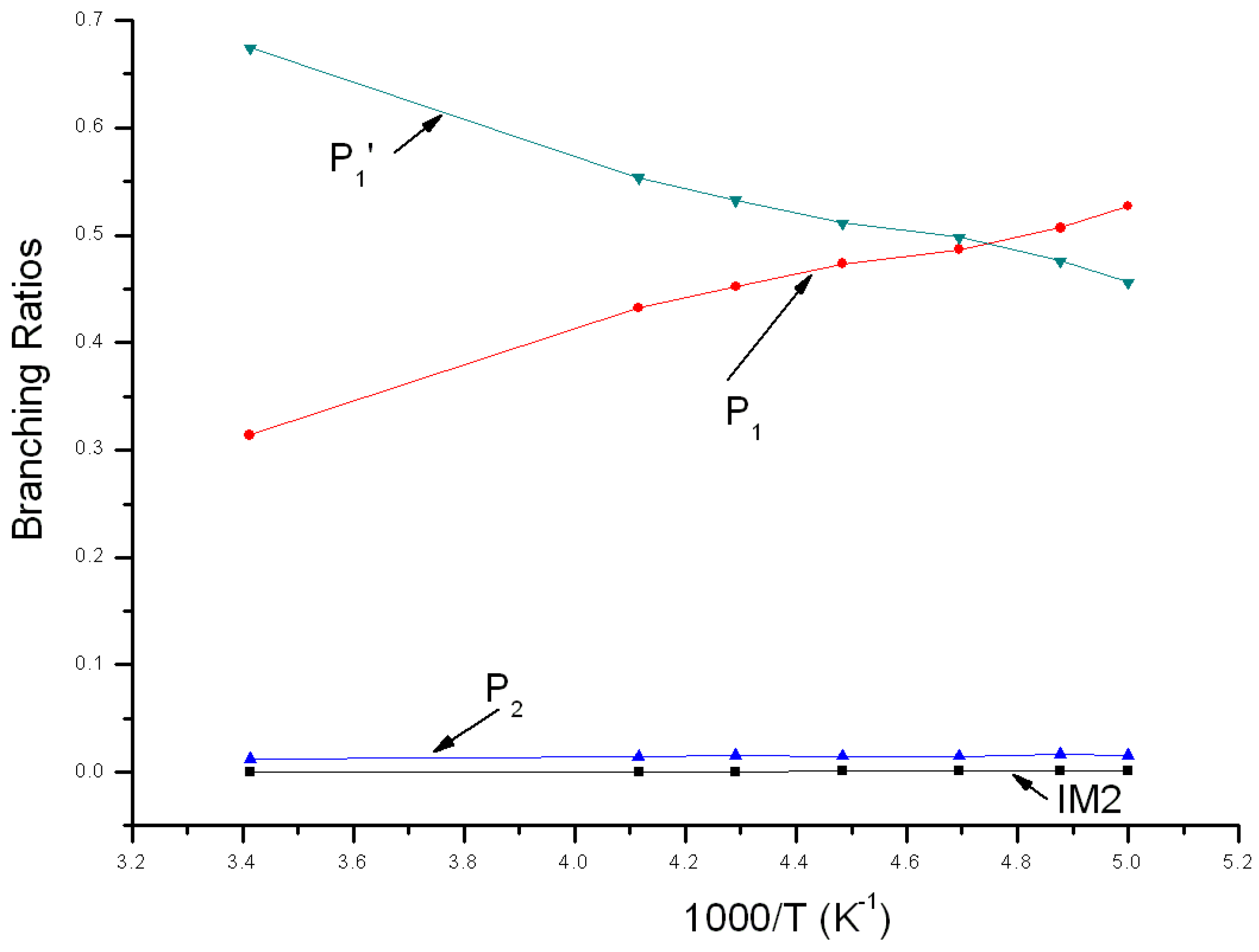
| T(K)/ktot (×10−11 cm3 mol−1 s−1) | 205 | 213 | 223 | 233 | 243 |
|---|---|---|---|---|---|
| Experimental data a | 4.3 ± 0.8 | 4.5 ± 0.9 | 4.2 ± 0.8 | 4.9 ± 1.0 | 5.5 ± 1.2 |
| Theoretical calculation results (RRKM) | 4.4 | 4.2 | 4.1 | 4.0 | 3.9 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, N.-N.; Ou-Yang, S.-L.; Li, L. Theoretical Study of ClOO + NO Reaction: Mechanism and Kinetics. Molecules 2017, 22, 2121. https://doi.org/10.3390/molecules22122121
Wu N-N, Ou-Yang S-L, Li L. Theoretical Study of ClOO + NO Reaction: Mechanism and Kinetics. Molecules. 2017; 22(12):2121. https://doi.org/10.3390/molecules22122121
Chicago/Turabian StyleWu, Nan-Nan, Shun-Li Ou-Yang, and Liang Li. 2017. "Theoretical Study of ClOO + NO Reaction: Mechanism and Kinetics" Molecules 22, no. 12: 2121. https://doi.org/10.3390/molecules22122121





