Identification of DNA–protein Binding Sites through Multi-Scale Local Average Blocks on Sequence Information
Abstract
:1. Introduction
2. Materials and Methods
2.1. Feature Extraction via Position Specific Scoring Matrix
2.2. Predicted Solvent Accessibility
2.3. Weighted Sparse Representation Based Classifier
2.4. Ensemble Classifier and Random Under-Sampling
3. Results
3.1. Datasets of DNA–Protein Binding Sites
3.2. Evaluation Measurements
3.3. Predicted Results on the PDNA-543 Dataset
3.3.1. Selecting Optimal Size of Sliding Window and Number of Base Classifiers
3.3.2. Performance of Different Features
3.3.3. Selecting Optimal Score Function of Base WSRC
3.3.4. Comparison with Existing Predictors on PDNA-543
3.4. Predicted Results on the Independent Test Set of PDNA-41
3.5. Predicted Results on the PDNA-316 Dataset
3.6. Predicted Results on PDNA-335 and PDNA-52 Datasets
3.7. Significance Analysis
3.8. Case of Prediction
3.9. Running Time
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Si, J.; Zhao, R.; Wu, R. An Overview of the Prediction of Protein DNA-Binding Sites. Int. J. Mol. Sci. 2015, 16, 5194–5215. [Google Scholar] [CrossRef] [PubMed]
- Miao, Z.; Westhof, E. A Large-Scale Assessment of Nucleic Acids Binding Site Prediction Programs. PLoS Comput. Biol. 2015, 11, e1004639. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Brown, S.J. BindN: A web-based tool for efficient prediction of DNA and RNA binding sites in amino acid sequences. Nucleic Acid Res. 2006, 34, 243–248. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Yang, M.Q.; Yang, J.Y. Prediction of DNA-binding residues from protein sequence information using random forests. BMC Genom. 2009, 10, 961–964. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Huang, C.; Yang, M.Q.; Yang, J.Y. BindN+ for accurate prediction of DNA and RNA-binding residues from protein sequence features. BMC Syst. Biol. 2010, 4, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Yan, C.; Terribilini, M.; Wu, F.; Jernigan, R.L.; Dobbs, D.; Honavar, V. Predicting DNA-binding sites of proteins from amino acid sequence. BMC Bioinform. 2006, 7, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, S.; Gromiha, M.M.; Sarai, A. Analysis and prediction of DNA-binding proteins and their binding residues based on composition, sequence and structural information. Bioinformatics 2004, 20, 477–486. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, S.; Sarai, A. PSSM-based prediction of DNA binding sites in proteins. BMC Bioinform. 2005, 6, 33–38. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chu, W.-Y.; Huang, Y.-F.; Huang, C.-C.; Cheng, Y.-S.; Huang, C.-K.; Oyang, Y.-J. ProteDNA: A sequence-based predictor of sequence-specific DNA-binding residues in transcription factors. Nucleic Acid Res. 2009, 37, 396–401. [Google Scholar] [CrossRef] [PubMed]
- Hwang, S.; Gou, Z.K.; Kuznetsov, I.B. DP-Bind: A web server for sequence-based prediction of DNA-binding residues in DNA-binding proteins. Bioinformatics 2007, 23, 634–636. [Google Scholar] [CrossRef] [PubMed]
- Ofran, Y.; Mysore, V.; Rost, B. Prediction of dna-binding residues from sequence. Bioinformatics 2007, 23, i347–i353. [Google Scholar] [CrossRef] [PubMed]
- Si, J.; Zhang, Z.; Lin, B.; Huang, B. MetaDBSite: A meta approach to improve protein DNA-binding sites prediction. BMC Syst. Biol. 2011, 5, S7. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Li, Y.; Zhang, M.; Yang, X.; Shen, H.B.; Yu, D.J. Predicting Protein-DNA Binding Residues by Weightedly Combining Sequence-based Features and Boosting Multiple SVMs. IEEE/ACM Trans. Comput. Biol. Bioinform. 2016, 99, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Georgiou, D.N.; Karakasidis, T.E.; Nieto, J.J.; Torres, A. A study of entropy/clarity of genetic sequences using metric spaces and fuzzy sets. J. Theor. Biol. 2010, 267, 95–105. [Google Scholar] [CrossRef] [PubMed]
- Buenrostro, J.D.; Giresi, P.G.; Zaba, L.C. Transposition of native chromatin for fast and sensitive epigenomic profiling of open chromatin, DNA-binding proteins and nucleosome position. Nat. Methods 2013, 10, 1213–1218. [Google Scholar] [CrossRef] [PubMed]
- Shanahan, H.P.; Garcia, M.A.; Jones, S.; Thornton, J.M. Identifying DNA-binding proteins using structural motifs and the electrostatic potential. Nucleic Acid Res. 2004, 32, 4732–4741. [Google Scholar] [CrossRef] [PubMed]
- Gao, M.; Skolnick, J. DBD-Hunter: A knowledge-based method for the prediction of DNA-protein interactions. Nucleic Acid. Res. 2008, 36, 3978–3992. [Google Scholar] [CrossRef] [PubMed]
- Wong, K.C.; Yue, L.; Peng, C.B.; Moses, A.M.; Zhang, Z.L. Computational Learning on Specificity-Determining Residue-Nucleotide Interactions. Nucleic Acid Res. 2015, 43, 10180–10189. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.D.; Li, T.H.; Sun, J.M.; Li, D.P.; Xiong, W.W.; Wang, W.Y.; Tang, S.N. Shape string: A new feature for prediction of DNA-binding residues. Biochimie 2013, 95, 354–358. [Google Scholar] [CrossRef] [PubMed]
- Li, B.Q.; Feng, K.Y.; Ding, J.; Cai, Y.D. Predicting DNA-binding sites of proteins based on sequential and 3D structural information. Mol. Genet. Genom. 2014, 289, 489–499. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Song, N.Y.; Yan, H. Chapter 2: Identification of Genes and their Regulatory Regions Based on Multiple Physical and Structural Properties of a DNA Sequence. Biol. Data Min. Appl. Healthc. 2014, 33–65. [Google Scholar]
- Ison, R.E.; Hovmoller, S.; Kretsinger, R.H. Predicting DNA-binding sites of proteins based on sequential and 3D structural information. IEEE Eng. Med. Biol. Mag. 2005, 24, 41–49. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Tang, S.; Xiong, W.; Cong, P.; Li, T. DSP: A protein shape string and its profile prediction server. Nucleic Acid Res. 2012, 40, 298–302. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Li, Q.Z.; Liu, S.; Fan, G.; Zuo, Y.C.; Peng, Y. PreDNA: Accurate prediction of DNA-binding sites in proteins by integrating sequence and geometric structure information. Bioinformatics 2013, 29, 678–685. [Google Scholar] [CrossRef] [PubMed]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wang, Y.B.; You, Z.H.; Li, X.; Chen, X.; Jiang, T.H.; Zhang, J.T. PCVMZM: Using the Probabilistic Classification Vector Machines Model Combined with a Zernike Moments Descriptor to Predict Protein-Protein Interactions from Protein Sequences. Int. J. Mol. Sci. 2017, 18, 1029. [Google Scholar] [CrossRef] [PubMed]
- Babak, A.; Andrew, D.; Matthew, T.W.; Brendan, J.F. Predicting the sequence specificities of DNA-and RNA-binding proteins by deep learning. Nat. Biotechnol. 2015, 33, 831–838. [Google Scholar]
- Wang, Y.; Ding, Y.J.; Guo, F.; Wei, L.Y.; Tang, J.J. Improved detection of DNA-binding proteins via compression technology on PSSM information. PLoS ONE 2017, 12, e0185587. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.Y.; Tang, J.J.; Zou, Q. Local-DPP: An Improved DNA-binding Protein Prediction Method by Exploring Local Evolutionary Information. Inf. Sci. 2017, 384, 135–144. [Google Scholar] [CrossRef]
- Shen, C.; Ding, Y.J.; Tang, J.J.; Xu, X.; Guo, F. An ameliorated prediction of drug-target interactions based on multi-scale discrete wavelet transform and network features. Int. Mol. Sci. 2017, 18, 1781. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.J.; Tang, J.J.; Guo, F. Identification of drug-target interactions via multiple information integration. Inf. Sci. 2017, 418, 546–560. [Google Scholar] [CrossRef]
- Ding, Y.J.; Tang, J.J.; Guo, F. Identification of Protein-Protein Interactions via a Novel Matrix-Based Sequence Representation Model with Amino Acid Contact Information. Int. J. Mol. Sci. 2017, 17, 1623. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.J.; Tang, J.J.; Fei, G. Predicting protein-protein interactions via multivariate mutual information of protein sequences. BMC Bioinform. 2017, 17, 398. [Google Scholar] [CrossRef] [PubMed]
- Zou, Q.; Li, J.J.; Hong, Q.Q.; Lin, Z.Y.; Wu, Y.; Shi, H.; Ju, Y. Prediction of microRNA-disease associations based on social network analysis methods. BioMed Res. Int. 2015, 2015, 810514. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Tang, J.; Du, P.F. Predicting protein lysine phosphoglycerylation sites by hybridizing many sequence based features. Mol. BioSyst. 2017, 13, 874–882. [Google Scholar] [CrossRef] [PubMed]
- Buenrostro, J.D.; Giresi, P.G.; Zaba, L.C.; Chang, H.Y.; Greenleaf, W.J. Transposition of native chromatin for fast and sensitive epigenomic profiling of open chromatin, dna-binding proteins and nucleosome position. Nat. Methods 2013, 10, e153. [Google Scholar] [CrossRef] [PubMed]
- Lei, G.C.; Tang, J.J.; Du, P.F. Predicting S-sulfenylation Sites Using Physicochemical Properties Differences. Lett. Organ. Chem. 2017, 14, 665–672. [Google Scholar] [CrossRef]
- Zou, Q.; Zeng, J.C.; Cao, L.J.; Ji, R. A Novel Features Ranking Metric with Application to Scalable Visual and Bioinformatics Data Classification. Neurocomputing 2016, 173, 346–354. [Google Scholar] [CrossRef]
- Zou, Q.; Wan, S.X.; Ju, Y.; Tang, J.J.; Zeng, X. Pretata: Predicting TATA binding proteins with novel features and dimensionality reduction strategy. BMC Syst. Biol. 2016, 10 (Suppl 4), 114. [Google Scholar] [CrossRef] [PubMed]
- Altschul, S.F.; Madden, T.L.; Schäffer, A.A.; Zhang, J.H.; Zhang, Z.; Miller, W.; Lipman, D.J. Gapped BLAST and PSI-BLAST: A new generation of protein database search programs. Nucleic Acid Res. 1997, 25, 3389–3402. [Google Scholar] [CrossRef] [PubMed]
- Camacho, C.; Coulouris, G.; Avagyan, V.; Ma, N.; Papadopoulos, J.; Bealer, K.; Madden, T.L. BLAST+: Architecture and applications. BMC Bioinform. 2009, 10, 421–429. [Google Scholar] [CrossRef] [PubMed]
- Jeong, J.C.; Lin, X.; Chen, X.W. BLAST+: Architecture and applications. IEEE/ACM Trans. Comput. Biol. Bioinform. 2011, 8, 308–315. [Google Scholar] [PubMed]
- Pan, G.F.; Tang, J.J.; Guo, F. Analysis of Co-Associated Transcription Factors via Ordered Adjacency Differences on Motif Distribution. Sci. Rep. 2017, 7, 43597. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, S.; Gromiha, M.M.; Sarai, A. Real value prediction of solvent accessibility from amino acid sequence. Proteins Struct. Funct. Genet. 2003, 50, 629–635. [Google Scholar] [CrossRef] [PubMed]
- Joo, K.; Lee, S.J.; Lee, J. Sann: Solvent accessibility prediction of proteins by nearest neighbor method. Proteins Struct. Funct. Bioinform. 2012, 80, 1791–1797. [Google Scholar] [CrossRef] [PubMed]
- Wright, J.; Yang, A.Y.; Ganesh, A.; Sastry, S.S.; Ma, Y. Robust Face Recognition via Sparse Representation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 210–227. [Google Scholar] [CrossRef] [PubMed]
- Wright, J.; Ganesh, A.; Zhou, Z.; Wagner, A. Demo: Robust face recognition via sparse representation. IEEE Int. Conf. Autom. Face Gesture Recognit. 2008, 31, 1–2. [Google Scholar]
- Liao, B.; Jiang, Y.; Yuan, G.; Zhu, W.; Cai, L.J.; Cao, Z. Learning a weighted meta-sample based parameter free sparse representation classification for microarray data. PLoS ONE 2014, 9, e104314. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.A.; You, Z.H.; Chen, X.; Chan, K.; Luo, X. Sequence-based prediction of protein-protein interactions using weighted sparse representation model combined with global encoding. BMC Bioinform. 2016, 17, 184–194. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.A.; You, Z.H.; Gao, X.; Wong, L.; Wang, L. Using Weighted Sparse Representation Model Combined with Discrete Cosine Transformation to Predict Protein-Protein Interactions from Protein Sequence. BioMed Res. Int. 2015, 2015, e902198. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.Y.; Min, H.; Gui, J.; Zhu, L.; Lei, Y.K. Face recognition via Weighted Sparse Representation. J. Vis. Commun. Image Represent. 2013, 24, 111–116. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap Methods: Another Look at the Jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Tao, D.; Tang, X.; Li, X.; Wu, X. Asymmetric Bagging and Random Subspace for Support Vector Machines-Based Relevance Feedback in Image Retrieval. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1088–1099. [Google Scholar] [PubMed]
- Rose, P.W.; Prlić, A.; Bi, C.; Bluhm, W.F.; Christie, C.H.; Dutta, S.; Green, R.K.; Goodsell, D.S.; Westbrook, J.D.; Woo, J.; et al. The RCSB Protein Data Bank: views of structural biology for basic and applied research and education. Nucleic Acid Res. 2015, 43, 345–356. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Godzik, A. Cd-hit: A fast program for clustering and comparing large sets of protein or nucleotide sequences. Bioinformatics 2006, 22, 1658–1659. [Google Scholar] [CrossRef] [PubMed]
- Yu, D.J.; Hu, J.; Yang, J.; Shen, H.B.; Tang, J.H.; Yang, J.Y. Designing Template-Free Predictor for Targeting Protein-Ligand Binding Sites with Classifier Ensemble and Spatial Clustering. IEEE/ACM Trans. Comput. Biol. Bioinform. 2013, 10, 994–1008. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Roy, A.; Zhang, Y. BioLiP: A semi-manually curated database for biologically relevant ligand-protein interactions. Nucleic Acid Res. 2013, 41, 1096–1103. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Dunbrack, R.L. PISCES: A protein sequence culling server. Bioinformatics 2003, 19, 1589–1591. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, I.B.; Gou, Z.K.; Li, R.; Hwang, S. Using evolutionary and structural information to predict DNA-binding sites on DNA-binding proteins. Proteins Struct. Funct. Bioinform. 2006, 64, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.C.; Lin, C.J. LIBSVM: A Library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 389–396. [Google Scholar] [CrossRef]
- Koh, K.; Kim, S.; Boyd, S. An Interior-Point Method for Large-Scale l 1 -Regularized Logistic Regression. J. Mach. Learn. Res. 2008, 1, 606–617. [Google Scholar]
- Tipping, M.E. Sparse bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Ma, X.; Guo, J.; Liu, H.D.; Xie, J.M. Sequence-Based Prediction of DNA-Binding Residues in Proteins with Conservation and Correlation Information. IEEE/ACM Trans. Comput. Biol. Bioinform. 2012, 9, 1766–1775. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Chen, W.; Qiu, C.; Wu, Y.; Krishnan, S.; Zou, Q. LibD3C: Ensemble classifiers with a clustering and dynamic selection strategy. Neurocomputing 2014, 123, 424–435. [Google Scholar] [CrossRef]
- Lin, C.; Zou, Y.; Qin, J.; Liu, X.; Jiang, Y.; Ke, C.; Zou, Q. Hierarchical classification of protein folds using a novel ensemble classifier. PLoS ONE 2013, 8, e56499. [Google Scholar] [CrossRef] [PubMed]
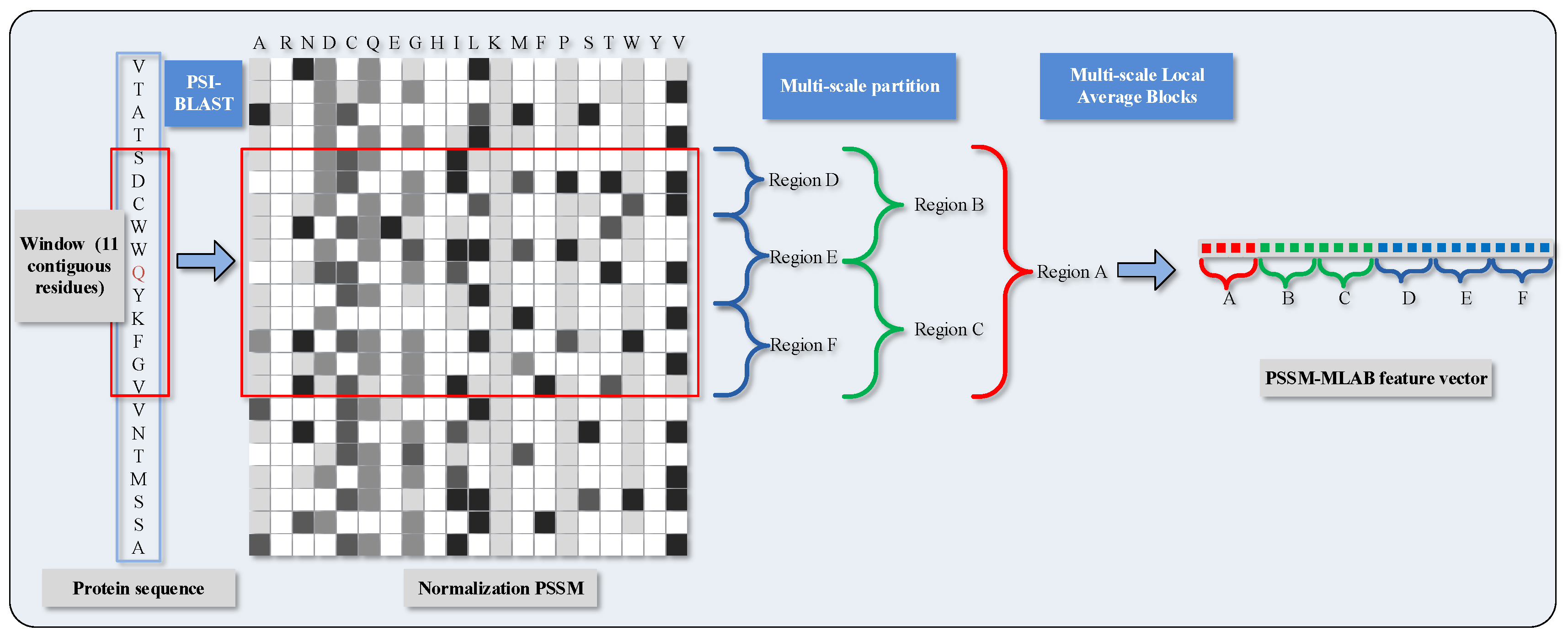

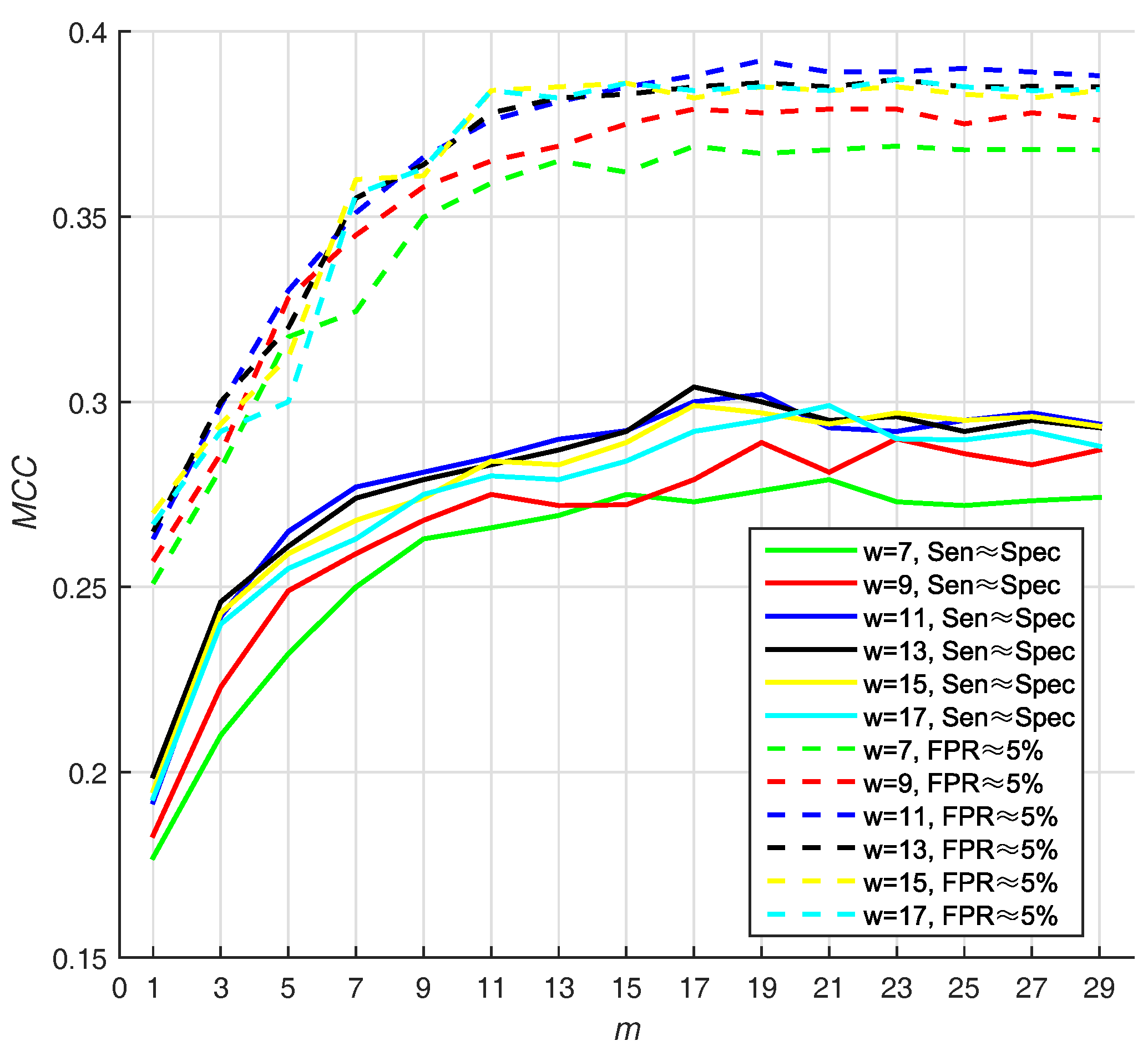

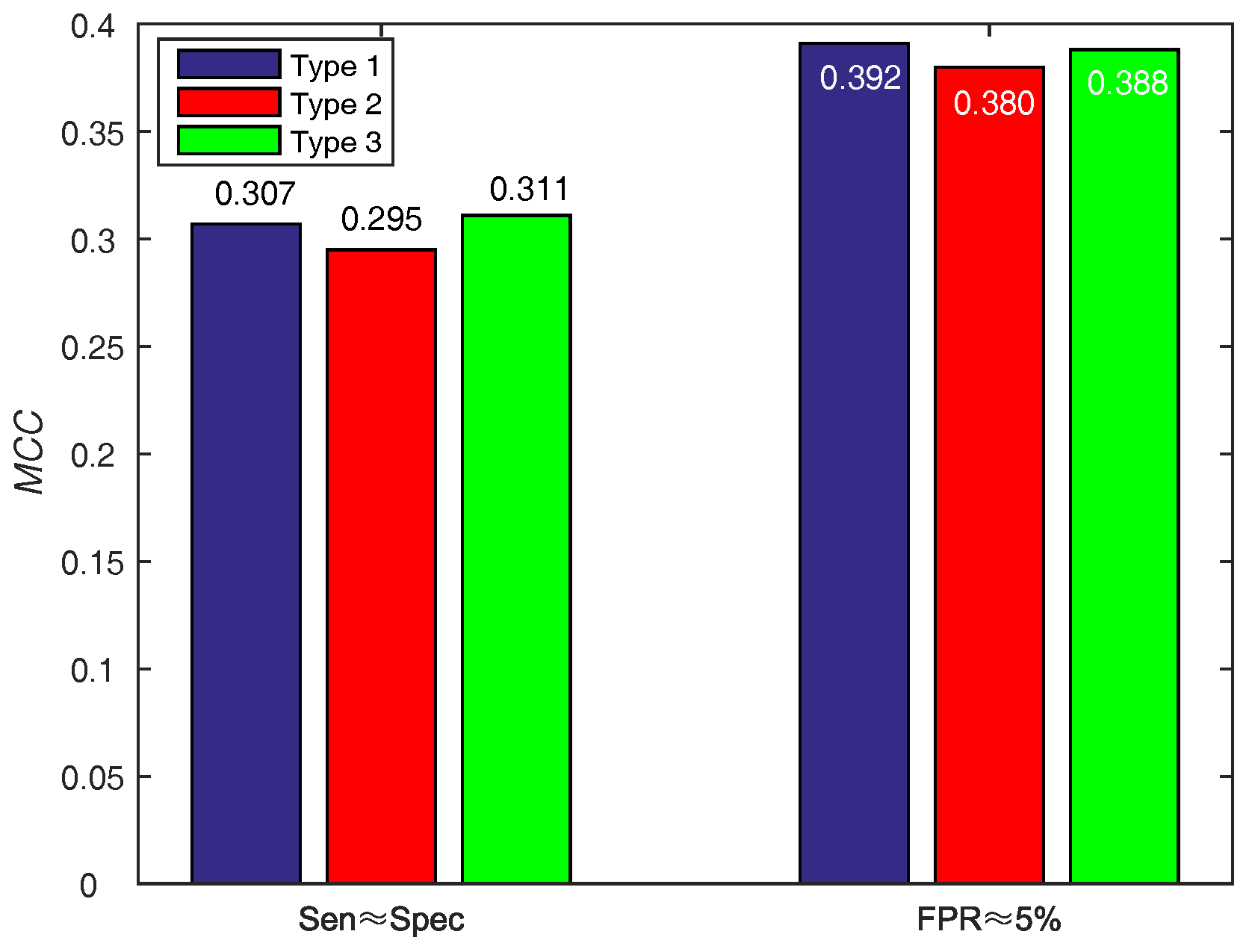

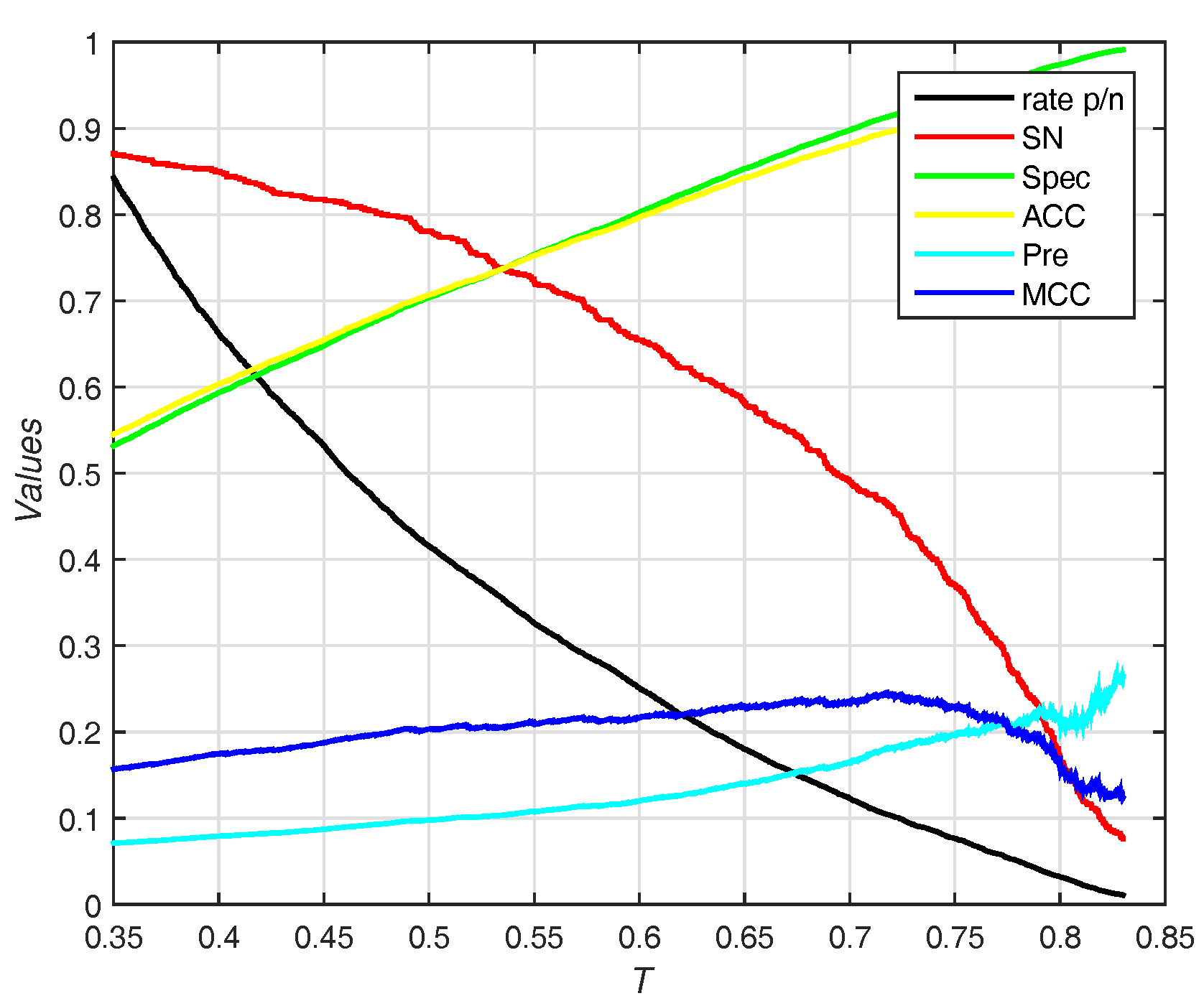
| Dataset | No. of Sequences | No. of Binding | No. of Non-Binding | Ratio |
|---|---|---|---|---|
| PDNA(Protein and DNA)-543 | 543 | 9549 | ||
| PDNA-41 | 41 | 734 | ||
| PDNA-335 | 335 | 6461 | ||
| PDNA-52 | 52 | 973 | ||
| PDNA-316 | 316 | 5609 |
| Feature | ||||||
|---|---|---|---|---|---|---|
| PSSM () | 0.7738 | 0.7570 | 0.7581 | 0.1844 | 0.294 | 0.843 |
| PSSM () | 0.4377 | 0.9500 | 0.9160 | 0.3832 | 0.364 | 0.843 |
| PSSM + PSA () | 0.7850 | 0.7590 | 0.7607 | 0.1874 | 0.302 | 0.851 |
| PSSM + PSA () | 0.4541 | 0.9494 | 0.9166 | 0.3886 | 0.375 | 0.851 |
| PSSM-MLAB () | 0.7744 | 0.7599 | 0.7609 | 0.1864 | 0.297 | 0.848 |
| PSSM-MLAB () | 0.4516 | 0.9510 | 0.9178 | 0.3955 | 0.378 | 0.848 |
| PSSM-MLAB + PSA () | 0.7894 | 0.7629 | 0.7646 | 0.1907 | 0.307 | 0.855 |
| PSSM-MLAB + PSA () | 0.4762 | 0.9492 | 0.9180 | 0.3991 | 0.392 | 0.855 |
| Methods | ||||||
|---|---|---|---|---|---|---|
| TargetDNA () [13] | 0.7698 | 0.7705 | 0.7704 | 0.1918 | 0.304 | 0.845 |
| TargetDNA () [13] | 0.4060 | 0.9500 | 0.9140 | 0.3647 | 0.339 | 0.845 |
| Our method () | 0.7894 | 0.7629 | 0.7646 | 0.1907 | 0.307 | 0.855 |
| Our method () | 0.4762 | 0.9492 | 0.9180 | 0.3991 | 0.392 | 0.855 |
| Methods | |||||
|---|---|---|---|---|---|
| BindN | 0.143 | 0.4564 | 0.8090 | 0.7915 | 0.1112 |
| ProteDNA | 0.160 | 0.0477 | 0.9984 | 0.9511 | 0.6030 |
| BindN+ () | 0.178 | 0.2411 | 0.9511 | 0.9158 | 0.2051 |
| BindN+ () | 0.213 | 0.5081 | 0.8541 | 0.8369 | 0.1542 |
| MetaDBSite | 0.221 | 0.3420 | 0.9335 | 0.9041 | 0.2122 |
| DP-Bind | 0.241 | 0.6172 | 0.8243 | 0.8140 | 0.1553 |
| DNABind (structure based) | 0.264 | 0.7016 | 0.8028 | 0.7978 | 0.1570 |
| TargetDNA () | 0.269 | 0.6022 | 0.8579 | 0.8452 | 0.1816 |
| TargetDNA () | 0.300 | 0.4550 | 0.9327 | 0.9089 | 0.2613 |
| EC-RUS (WSRC) () | 0.193 | 0.6104 | 0.7725 | 0.7644 | 0.1231 |
| EC-RUS (WSRC) () | 0.315 | 0.2725 | 0.9731 | 0.9458 | 0.4292 |
| EC-RUS (SVM) () | 0.261 | 0.6975 | 0.8032 | 0.7972 | 0.1567 |
| EC-RUS (SVM) () | 0.302 | 0.3787 | 0.9577 | 0.9281 | 0.3092 |
| EC-RUS (RF) () | 0.234 | 0.6785 | 0.7818 | 0.7767 | 0.1401 |
| EC-RUS (RF) () | 0.261 | 0.3351 | 0.9524 | 0.9217 | 0.2691 |
| EC-RUS (L1-LR) () | 0.228 | 0.6199 | 0.8084 | 0.7991 | 0.1449 |
| EC-RUS (L1-LR) () | 0.246 | 0.3120 | 0.9541 | 0.9221 | 0.2623 |
| EC-RUS (SBL) () | 0.219 | 0.7084 | 0.7434 | 0.7416 | 0.1263 |
| EC-RUS (SBL) () | 0.247 | 0.3202 | 0.9521 | 0.9206 | 0.2591 |
| Methods | ||||
|---|---|---|---|---|
| DBS-PRED (structure based) | 0.5300 | 0.7600 | 0.7500 | 0.170 |
| BindN | 0.5400 | 0.8000 | 0.7800 | 0.210 |
| DNABindR | 0.6600 | 0.7400 | 0.7300 | 0.230 |
| DISIS | 0.1900 | 0.9800 | 0.9200 | 0.250 |
| DP-Bind | 0.6900 | 0.7900 | 0.7800 | 0.290 |
| BindN-RF | 0.6700 | 0.8300 | 0.8200 | 0.320 |
| MetaDBSite [12] | 0.7700 | 0.7700 | 0.7700 | 0.320 |
| TargetDNA () [13] | 0.7796 | 0.7803 | 0.7802 | 0.339 |
| TargetDNA () [13] | 0.4302 | 0.9500 | 0.9099 | 0.375 |
| EC-RUS (WSRC) () | 0.8067 | 0.7818 | 0.7837 | 0.356 |
| EC-RUS (WSRC) () | 0.5108 | 0.9499 | 0.9161 | 0.439 |
| EC-RUS (SVM) () | 0.8011 | 0.7969 | 0.7973 | 0.369 |
| EC-RUS (SVM) () | 0.4935 | 0.9500 | 0.9150 | 0.426 |
| EC-RUS (RF) () | 0.7989 | 0.7542 | 0.7576 | 0.326 |
| EC-RUS (RF) () | 0.4521 | 0.9502 | 0.9118 | 0.394 |
| EC-RUS (L1-LR) () | 0.7347 | 0.7659 | 0.7635 | 0.300 |
| EC-RUS (L1-LR) () | 0.3523 | 0.9498 | 0.9037 | 0.319 |
| EC-RUS (SBL) () | 0.7453 | 0.7540 | 0.7533 | 0.295 |
| EC-RUS (SBL) () | 0.3562 | 0.9480 | 0.9023 | 0.317 |
| Methods | |||||
|---|---|---|---|---|---|
| TargetS [57] | 0.413 | 0.965 | 0.933 | 0.377 | 0.836 |
| MetaDBSite [12] | 0.580 | 0.764 | 0.752 | 0.192 | - |
| DNABR [64] | 0.407 | 0.873 | 0.846 | 0.185 | - |
| alignment-based | 0.266 | 0.943 | 0.905 | 0.190 | - |
| EC-RUS (WSRC) | 0.467 | 0.913 | 0.896 | 0.245 | 0.808 |
| EC-RUS (SVM) | 0.528 | 0.835 | 0.823 | 0.185 | 0.756 |
| EC-RUS (RF) | 0.561 | 0.773 | 0.764 | 0.152 | 0.741 |
| EC-RUS (L1-LR) | 0.594 | 0.811 | 0.803 | 0.201 | 0.787 |
| EC-RUS (SBL) | 0.635 | 0.782 | 0.776 | 0.192 | 0.786 |
| Methods | p-Value |
|---|---|
| Our method-MetaDBSite | 0.2667 |
| Our method-TargetDNA | 0.4610 |
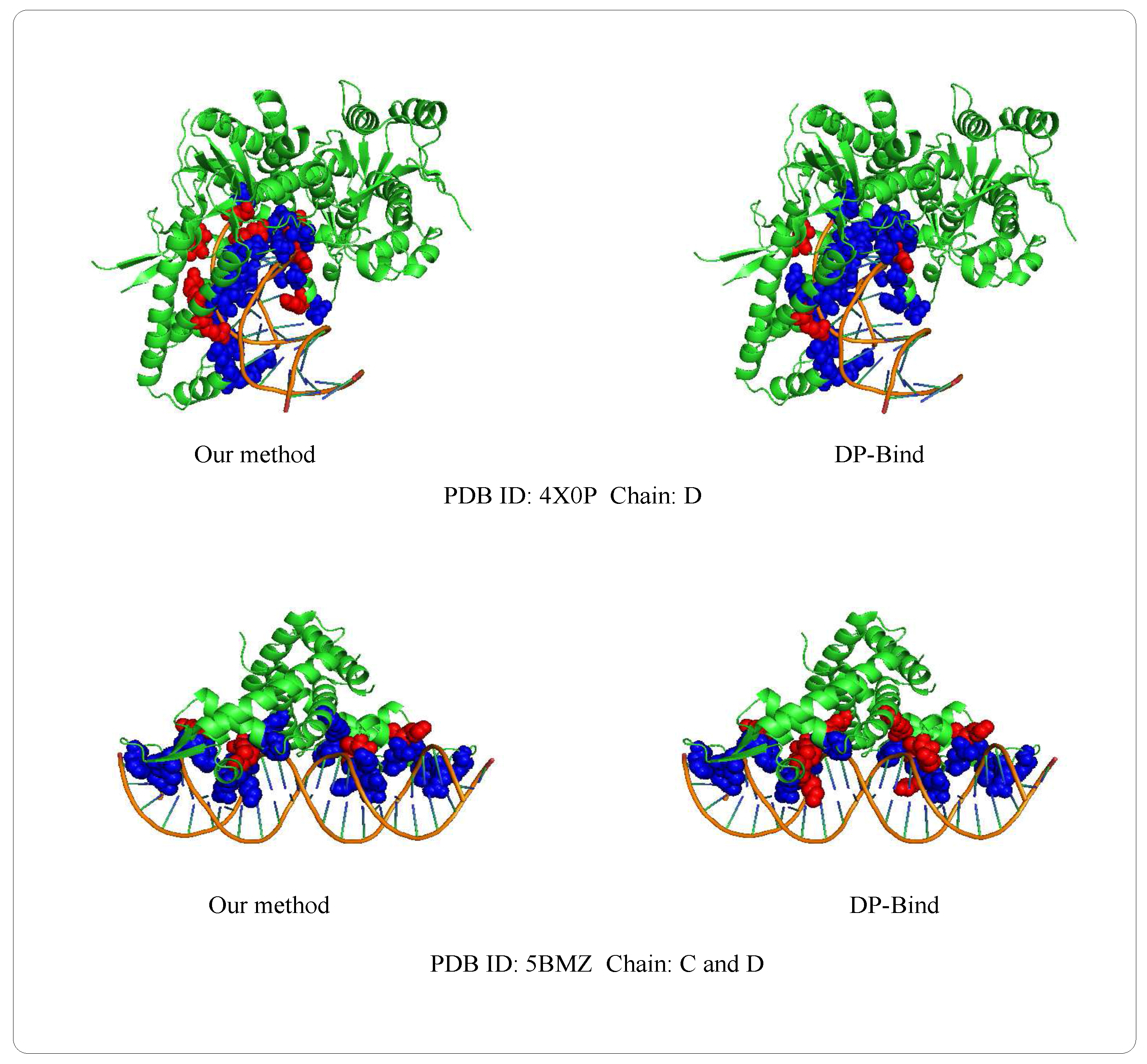
| PDB (Protein Data Bank) ID | Method | ||||
|---|---|---|---|---|---|
| 4X0P-D | our method | 24 | 559 | 34 | 8 |
| DP-Bind | 29 | 439 | 154 | 3 | |
| 5BMZ-D | our method | 14 | 110 | 9 | 3 |
| DP-Bind | 10 | 103 | 16 | 7 |
| Classifier | PDNA-41 | PDNA-52 |
|---|---|---|
| EC-RUS (WSRC) | 9227 | 14,407 |
| EC-RUS (L1-LR) | 705 | 232 |
| EC-RUS (RF) | 3778 | 1632 |
| EC-RUS (SBL) | 136,241 | 40,121 |
| EC-RUS (SVM) | 27,210 | 2043 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, C.; Ding, Y.; Tang, J.; Song, J.; Guo, F. Identification of DNA–protein Binding Sites through Multi-Scale Local Average Blocks on Sequence Information. Molecules 2017, 22, 2079. https://doi.org/10.3390/molecules22122079
Shen C, Ding Y, Tang J, Song J, Guo F. Identification of DNA–protein Binding Sites through Multi-Scale Local Average Blocks on Sequence Information. Molecules. 2017; 22(12):2079. https://doi.org/10.3390/molecules22122079
Chicago/Turabian StyleShen, Cong, Yijie Ding, Jijun Tang, Jian Song, and Fei Guo. 2017. "Identification of DNA–protein Binding Sites through Multi-Scale Local Average Blocks on Sequence Information" Molecules 22, no. 12: 2079. https://doi.org/10.3390/molecules22122079





