Molecules and the Eigenstate Thermalization Hypothesis
Abstract
:1. Introduction
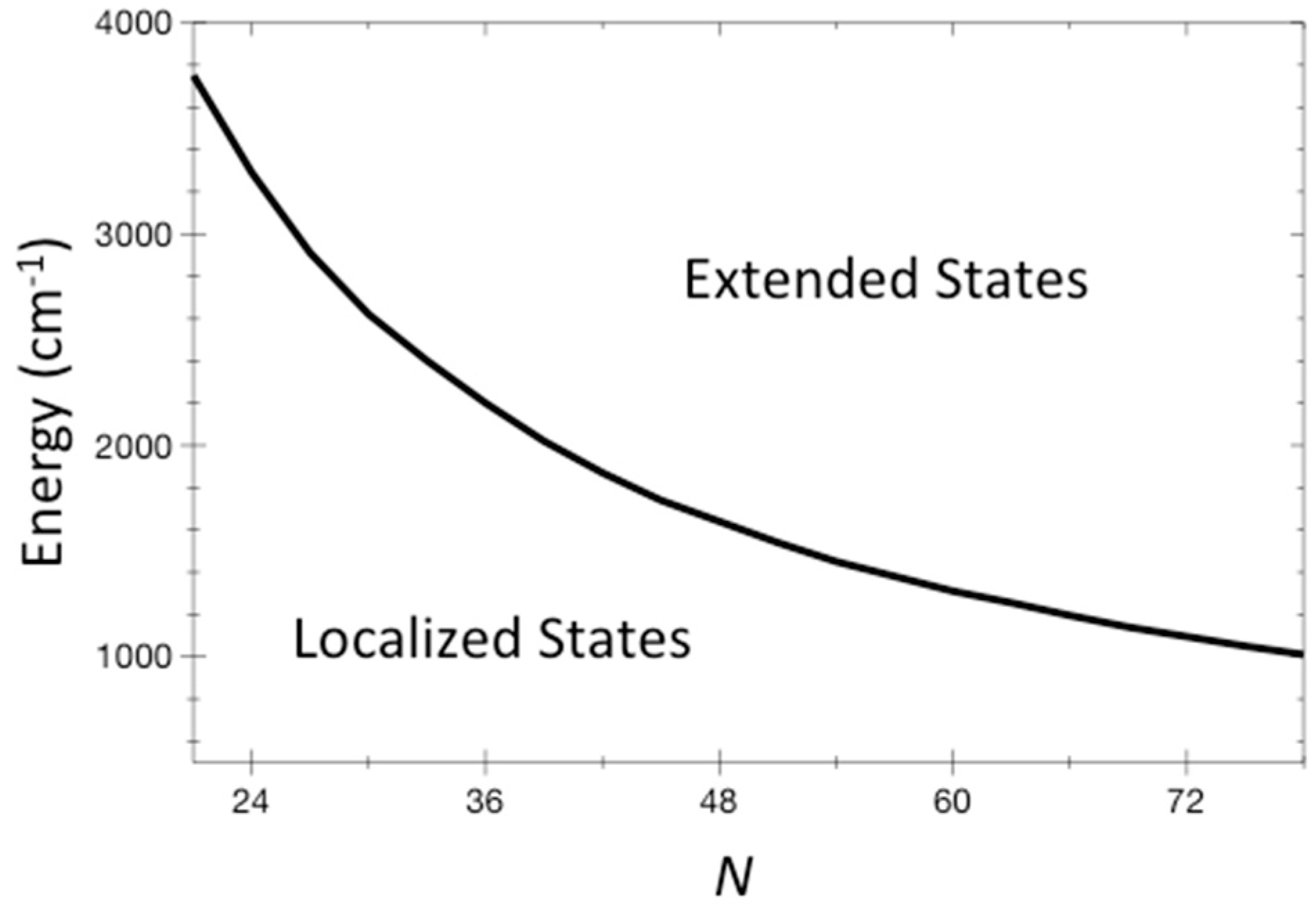
2. Criteria for Quantum Ergodicity in Molecules
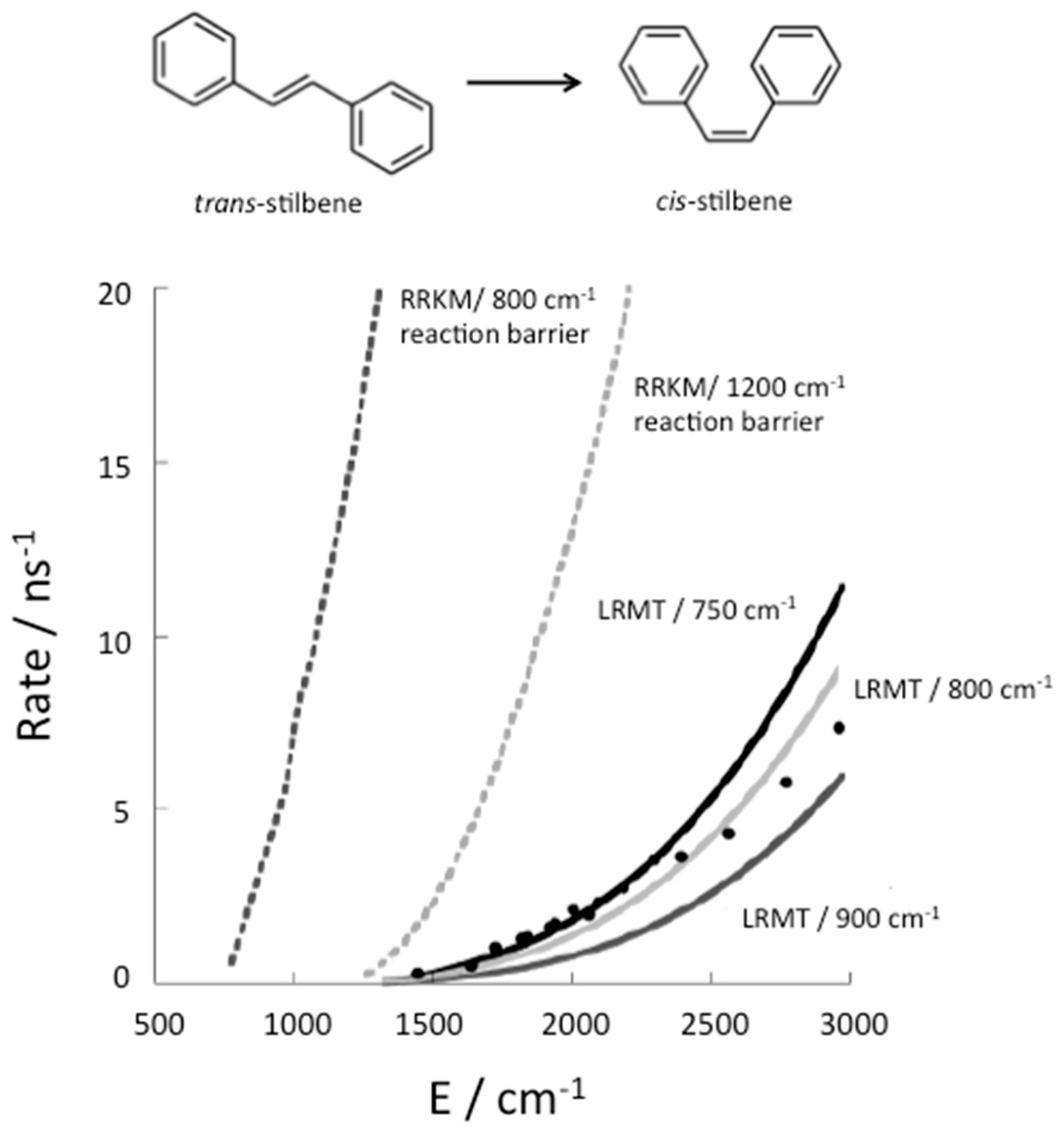
3. Quantum Ergodicity and the Kinetics of Conformational Change
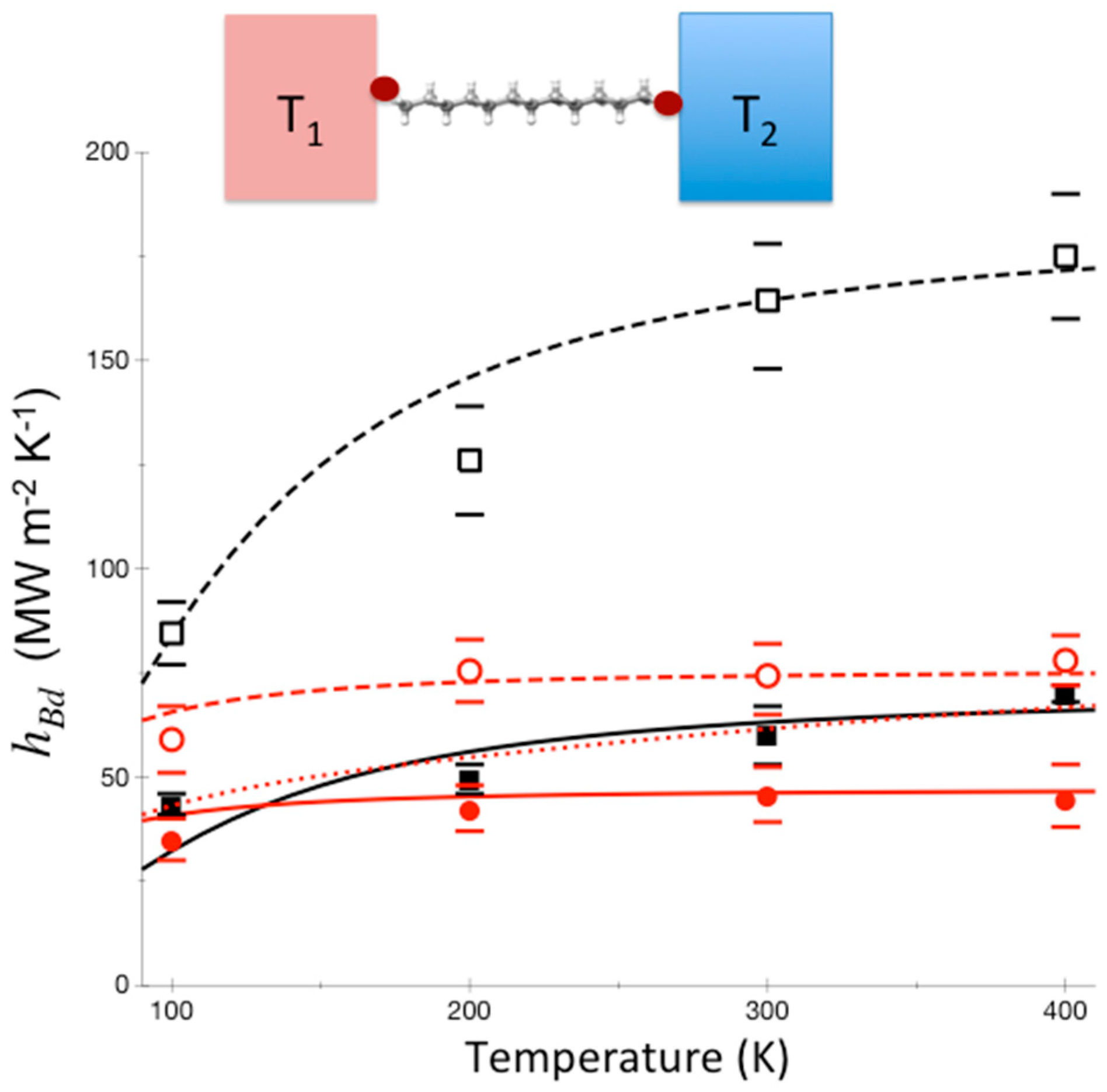
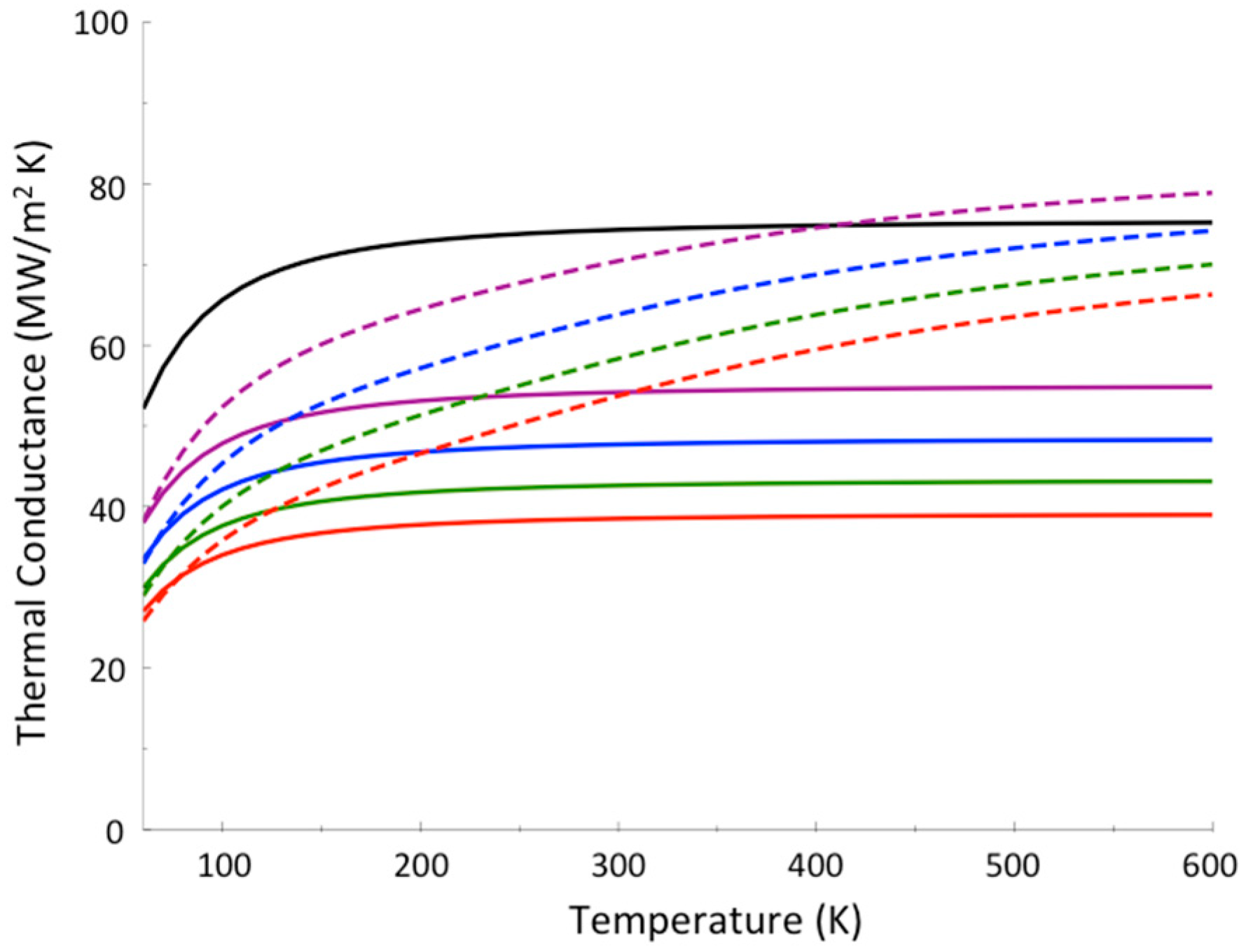
4. Thermalization and Thermal Transport in Molecules
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Deutsch, J.M. Quantum statistical mechanics in a closed system. Phys. Rev. A 1991, 43, 2046–2049. [Google Scholar] [CrossRef] [PubMed]
- Srednicki, M. Chaos and quantum thermalization. Phys. Rev. E 1994, 50, 888–901. [Google Scholar] [CrossRef] [Green Version]
- Rigol, M.; Dunjko, V.; Olshanii, M. Thermalization and its mechanism for generic isolated quantum systems. Nature 2008, 452, 854–858. [Google Scholar] [CrossRef] [PubMed]
- D’Alessio, L.; Kafri, Y.; Polkovnikov, A.; Rigol, M. From quantum chaos and eigenstate thermalization to statistical mechanics and thermodynamics. Adv. Phys. 2016, 65, 239–362. [Google Scholar] [CrossRef] [Green Version]
- Rice, O.K. Several remarks on the energy exchange within molecules and between molecules during collisions. Z. Phys. Chem. B 1930, 7, 226–233. [Google Scholar]
- Kuzmin, M.V.; Letokhov, V.S.; Stuchebrukhov, A.A. Threshold energy dependence of the intramolecular vibrational relaxation rate for an isolated polyatomic molecule. Zh. Eksp. Teor. Fiz. 1986, 90, 458–470. [Google Scholar]
- Logan, D.E.; Wolynes, P.G. Quantum localization and energy flow in many-dimensional Fermi resonant systems. J. Chem. Phys. 1990, 93, 4994–5012. [Google Scholar] [CrossRef]
- Uzer, T. Theories of intramolecular vibrational energy transfer. Phys. Rep. 1991, 199, 73–146. [Google Scholar] [CrossRef] [Green Version]
- Leitner, D.M. Quantum ergodicity and energy flow in molecules. Adv. Phys. 2015, 64, 445–517. [Google Scholar] [CrossRef]
- Nandkishore, R.; Huse, D.A. Many-body localization and thermalization in quantum statistical mechanics. Annu. Rev. Cond. Mat. Phys. 2015, 6, 15–38. [Google Scholar] [CrossRef]
- Campbell, D.M.; Mackowiak, M.; Jonas, J. Cyclohexane revisited: High pressure nuclear magnetic resonance rotating frame relaxation study of the dynamical solvent effects on the conformational isomerization of cyclohexane. J. Chem. Phys. 1992, 96, 2717–2723. [Google Scholar] [CrossRef]
- Hasha, D.L.; Eguchi, T.; Jonas, J. Dynamical effects on conformational isomerization of cyclohexane. J. Chem. Phys. 1981, 75, 1571–1572. [Google Scholar] [CrossRef]
- Felker, P.M.; Zewail, A.H. Rates of photoisomerization of trans-stilbene in isolated and solvated molecules-experiments on the deuterium-isotope effect and RRKM behavior. J. Phys. Chem. 1985, 89, 5402–5411. [Google Scholar] [CrossRef]
- Leitner, D.M. Heat transport in molecules and reaction kinetics: The role of quantum energy flow and localization. In Geometric Structures of Phase Space in Multidimensional Chaos: Applications to Chemical Reaction Dynamics in Complex Systems; Toda, M., Komatsuzaki, T., Konishi, T., Berry, R.S., Rice, S.A., Eds.; Advances in Chemical Physics; John Wiley & Sons: New York, NY, USA, 2005; Volume 130, pp. 205–256. [Google Scholar]
- Leitner, D.M.; Levine, B.; Quenneville, J.; Martinez, T.J.; Wolynes, P.G. Quantum energy flow and trans stilbene photoisomerization: An example of a non-RRKM reaction. J. Phys. Chem. 2003, 107, 10706–10716. [Google Scholar] [CrossRef]
- Leitner, D.M.; Wolynes, P.G. Quantum energy flow during molecular isomerization. Chem. Phys. Lett. 1997, 280, 411–418. [Google Scholar] [CrossRef]
- Nordholm, S. Photoisomerization of stilbene-a theoretical study of deuteration shifts and limited internal vibrational redistribution. Chem. Phys. 1989, 137, 109–120. [Google Scholar] [CrossRef]
- Leitner, D.M.; Gruebele, M. A quantum model of restricted vibrational energy flow on the way to the transition state in unimolecular reactions. Mol. Phys. 2008, 106, 433–442. [Google Scholar] [CrossRef]
- Leitner, D.M. Influence of quantum energy flow and localization on molecular isomerization in gas and condensed phases. Int. J. Quantum Chem. 1999, 75, 523–531. [Google Scholar] [CrossRef]
- McWhorter, D.A.; Hudspeth, E.; Pate, B.H. The rotational spectra of single molecular eigenstates of 2-fluoroethanol: Measurement of the conformational isomerization rate at 2980 cm−1. J. Chem. Phys. 1999, 110, 2000–2009. [Google Scholar] [CrossRef]
- Balk, M.W.; Fleming, G.R. Unimolecular reactions in isolated and collisional systems: Is the transition-state rate an upper limit for the isomerization of stilbene. J. Phys. Chem. 1986, 90, 3975–3983. [Google Scholar] [CrossRef]
- Marcus, R.A. Unimolecular dissociations and free radical recombination reactions. J. Chem. Phys. 1952, 20, 359–364. [Google Scholar] [CrossRef]
- Robinson, P.J.; Holbrook, K.A. Unimolecular Reactions; Wiley Interscience: New York, NY, USA, 1972. [Google Scholar]
- Forst, W. Theory of Unimolecular Reactions; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Forst, W. Unimolecular Reactions: A Concise Introduction; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Leitner, D.M.; Wolynes, P.G. Vibrational relaxation and energy localization in polyatomics: Effects of high-order resonances on flow rates and the quantum ergodicity transition. J. Chem. Phys. 1996, 105, 11226–11236. [Google Scholar] [CrossRef]
- Leitner, D.M.; Wolynes, P.G. Statistical properties of localized vibrational eigenstates. Chem. Phys. Lett. 1996, 258, 18–24. [Google Scholar] [CrossRef]
- Leitner, D.M.; Wolynes, P.G. Many-dimensional quantum energy flow at low energy. Phys. Rev. Lett. 1996, 76, 216–219. [Google Scholar] [CrossRef] [PubMed]
- Leitner, D.M.; Wolynes, P.G. Predictions of local random matrix theory for vibrational mixing and energy flow in polyatomics. ACH-Models Chem. 1997, 134, 663–677. [Google Scholar] [CrossRef]
- Leitner, D.M.; Wolynes, P.G. Vibrational mixing and energy flow in polyatomics: Quantitative prediction using local random matrix theory. J. Phys. Chem. A 1997, 101, 541–548. [Google Scholar] [CrossRef]
- Altshuler, B.L.; Gefen, Y.; Kamenev, A.; Levitov, L.S. Quasiparticle lifetime in a finite system: A nonperturbative approach. Phys. Rev. Lett. 1997, 78, 2803–3806. [Google Scholar] [CrossRef]
- Feingold, M.; Leitner, D.M.; Piro, O. Semiclassical structure of Hamiltonians. Phys. Rev. A 1989, 39, 6507–6514. [Google Scholar] [CrossRef]
- Wilkinson, M.; Feingold, M.; Leitner, D.M. Localization and spectral statistics in a banded random matrix ensemble. J. Phys. A Math. Gen. 1991, 24, 175–181. [Google Scholar] [CrossRef]
- Feingold, M.; Leitner, D.M.; Wilkinson, M. Spectral statistics in semiclassical random matrix ensembles. Phys. Rev. Lett. 1991, 66, 986–989. [Google Scholar] [CrossRef] [PubMed]
- Burin, A. Localization and chaos in a quantum spin glass model in random longitudinal fields: Mapping to the localization problem in a Bethe lattice with a correlated disorder. Ann. Phys. 2017, 529, 1600292. [Google Scholar] [CrossRef]
- Burin, A.L. Many-body localization in a strongly disordered system with long-range interactions: Finite-size scaling. Phys. Rev. B 2015, 91, 094202. [Google Scholar] [CrossRef]
- Basko, D.M.; Aleiner, I.L.; Altshuler, B.L. Possible experimental manifestations of the many-body localization. Phys. Rev. Lett. 2007, 76, 052203. [Google Scholar] [CrossRef]
- Lev, Y.B.; Reichman, D.R. Dynamics of many-body localization. Phys. Rev. B 2014, 89, 220201. [Google Scholar] [Green Version]
- Khripkov, C.; Vardi, A.; Cohen, D. Semiclassical theory of strong localization for quantum thermalization. Phys. Rev. E 2018, 97, 022127. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tikhonenkov, I.; Vardi, A.; Anglin, J.R.; Cohen, D. Minimal Fokker-Planck theory for the thermalization of mesoscopic subsystems. Phys. Rev. Lett. 2013, 110, 050401. [Google Scholar] [CrossRef] [PubMed]
- Giannoni, M.-J.; Voros, A.; Zinn-Justin, J. Chaos and Quantum Physics; North Holland Publishing: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Porter, C.E. Statistical Theories of Spectra: Fluctuations; Academic Press: New York, NY, USA, 1965. [Google Scholar]
- Chirikov, B.V. A universal instability of many-dimensional oscillator systems. Phys. Rep. 1979, 52, 263. [Google Scholar] [CrossRef]
- Manikandan, P.; Keshavamurthy, S. Dynamical traps lead to the slowing down of intramolecular vibrational energy flow. Proc. Natl. Acad. Sci. USA 2014, 111, 14354–14359. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Patra, S.; Keshavamurthy, S. Classical-quantum correspondence in a model for conformational dynamics: Connecting phase space reactive islands with rare events sampling. Chem. Phys. Lett. 2015, 634, 1–10. [Google Scholar] [CrossRef]
- Bigwood, R.; Gruebele, M.; Leitner, D.M.; Wolynes, P.G. The vibrational energy flow transition in organic molecules: Theory meets experiment. Proc. Natl. Acad. Sci. USA 1998, 95, 5960–5964. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leitner, D.M. Dynamical tunneling from the edge of vibrational state space of large molecules. In Dynamical Tunneling: Theory and Experiment; Keshavamurthy, S., Schlagheck, P., Eds.; CRC Press: Boca Raton, FL, USA, 2011; pp. 211–224. [Google Scholar]
- Baer, T.; Hase, W.L. Unimolecular Reaction Dynamics: Theory and Experiment; Oxford University Press: New York, NY, USA, 1996. [Google Scholar]
- Leitner, D.M.; Wolynes, P.G. Quantum theory of enhanced unimolecular reaction rates below the ergodicity threshold. Chem. Phys. 2006, 329, 163–167. [Google Scholar] [CrossRef]
- Waldeck, D.H. Photoisomerization dynamics of stilbenes. Chem. Rev. 1991, 91, 415–436. [Google Scholar] [CrossRef]
- Syage, J.A.; Lambert, W.R.; Felker, P.M.; Zewail, A.H.; Hochstrasser, R.M. Picosecond excitation and trans-cis isomerization of stilbene in a supersonic jet: Dynamics and spectra. Chem. Phys. Lett. 1982, 88, 266–270. [Google Scholar] [CrossRef]
- Khundkar, L.R.; Marcus, R.A.; Zewail, A.H. Unimolecular reactions at low energies and RRKM behavior: Isomerization and dissociation. J. Phys. Chem. 1983, 87, 2473–2476. [Google Scholar] [CrossRef]
- Weston, R.E.; Barker, J.R. On modeling the pressure-dependent photoisomerization of trans-stilbene by including slow intramolecular vibrational energy redistribution. J. Phys. Chem. A 2006, 110, 7888–7897. [Google Scholar] [CrossRef] [PubMed]
- Losego, M.D.; Grady, M.E.; Sottow, N.R.; Cahill, D.G.; Braun, P.V. Effects of chemical bonding on heat transport across interfaces. Nat. Mater. 2012, 11, 502–506. [Google Scholar] [CrossRef] [PubMed]
- Majumdar, S.; Sierra-Suarez, J.A.; Schiffres, S.N.; Ong, W.-L.; Higgs, C.F.; McGaughey, A.J.H.; Malen, J.A. Vibrational mismatch of metal leads controls thermal conductance of self-assembled monolayer junctions. Nano. Lett. 2015, 15, 2985–2991. [Google Scholar] [CrossRef] [PubMed]
- Galperin, M.; Nitzan, A.; Ratner, M.A. Heat conduction in molecular transport junctions. Phys. Rev. B 2007, 75, 155312. [Google Scholar] [CrossRef]
- Lee, W.; Kim, K.; Jeong, W.; Zotti, L.A.; Pauly, F.; Cuevas, J.C.; Reddy, P. Heat dissipation in atomic-scale junctions. Nature 2013, 498, 209–213. [Google Scholar] [CrossRef] [PubMed]
- Segal, D.; Nitzan, A.; Hänggi, P. Thermal conductance through molecular wires. J. Chem. Phys. 2003, 119, 6840–6855. [Google Scholar] [CrossRef]
- Segal, D.; Agarwalla, B.K. Vibrational heat transport in molecular junctions. Ann. Rev. Phys. Chem. 2016, 67, 185–209. [Google Scholar] [CrossRef] [PubMed]
- Gaskins, J.T.; Bulusu, A.; Giordano, A.J.; Duda, J.C.; Graham, S.; Hopkins, P.E. Thermal conductance across phosphonic acid molecules and interfaces: Ballistic versus diffusive vibrational transport in molecular monolayers. J. Phys. Chem. C 2015, 119, 20931–20939. [Google Scholar] [CrossRef]
- Leitner, D.M. Thermal boundary conductance and rectification in molecules. J. Phys. Chem. B 2013, 117, 12820–12828. [Google Scholar] [CrossRef] [PubMed]
- Craven, G.T.; Nitzan, A. Electron transfer across a thermal gradient. Proc. Natl. Acad. Sci. USA 2016, 113, 9421–9429. [Google Scholar] [CrossRef] [PubMed]
- O’Brien, P.J.; Shenogin, S.; Liu, J.; Chow, P.K.; Laurencin, D.; Mutin, P.H.; Yamaguchi, M.; Keblinski, P.; Ramanath, G. Bonding-induced thermal conductance enhancement at inorganic heterointerfaces using nanomolecular monolayers. Nat. Mater. 2012, 12, 118–122. [Google Scholar] [CrossRef] [PubMed]
- Cui, L.; Miao, R.; Jiang, C.; Meyhofer, E.; Reddy, P. Perspective: Thermal and thermoelectric transport in molecular junctions. J. Chem. Phys. 2017, 146, 092201. [Google Scholar] [CrossRef] [Green Version]
- Pandey, H.D.; Leitner, D.M. Small saccharides as a blanket around proteins: A computational study. J. Phys. Chem. B 2018, 122, 7277–7285. [Google Scholar] [CrossRef] [PubMed]
- Pandey, H.D.; Leitner, D.M. Influence of thermalization on thermal conduction through molecular junctions: Computational study of PEG oligomers. J. Chem. Phys. 2017, 147, 084701. [Google Scholar] [CrossRef] [PubMed]
- Pandey, H.D.; Leitner, D.M. Vibrational energy transport in molecules and the statistical properties of vibrational modes. Chem. Phys. 2017, 482, 81–85. [Google Scholar] [CrossRef]
- Pandey, H.D.; Leitner, D.M. Thermalization and thermal transport in molecules. J. Phys. Chem. Lett. 2016, 7, 5062–5067. [Google Scholar] [CrossRef] [PubMed]
- Craven, G.T.; Nitzan, A. Electron transfer at thermally heterogeneous molecule-metal interfaces. J. Chem. Phys. 2017, 146, 092305. [Google Scholar] [CrossRef]
- Chen, R.; Craven, G.T.; Nitzan, A. Electron-transfer-induced and phononic heat transport in molecular environments. J. Chem. Phys. 2017, 147, 124101. [Google Scholar] [CrossRef] [PubMed]
- He, D.; Thingna, J.; Cao, J. Interfacial thermal transport with strong system-bath coupling: A phonon delocalization effect. Phys. Rev. B 2018, 97, 195437. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Hsieh, C.-Y.; Wu, C.; Cao, J. Frequency-dependent current noise in quantum heat transfer with full counting statistics. J. Chem. Phys. 2018, 148, 234104. [Google Scholar] [CrossRef] [PubMed]
- Leitner, D.M. Energy Relaxation and Thermal Transport in Molecules. In Handbook of Materials Modeling; Andreoni, W., Yip, S., Eds.; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Buldum, A.; Leitner, D.M.; Ciraci, S. Thermal conduction through a molecule. Europhys. Lett. 1999, 47, 208–212. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Wang, J. Vibrational and coherence dynamics of molecules. Phys. Chem. Chem. Phys. 2015, 17, 23754–23760. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Z.; Wang, J. Landscape, kinetics, paths and statistics of curl flux, coherence, entanglement and energy transfer in non-equilibrium quantum systems. New J. Phys. 2015, 17, 043053. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Leitner, D.M. Heat flow in proteins: Computation of thermal transport coefficients. J. Chem. Phys. 2005, 122, 054902. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Leitner, D.M. Vibrational energy transfer and heat conduction in a protein. J. Phys. Chem. B 2003, 107, 1698–1707. [Google Scholar] [CrossRef]
- Leitner, D.M. Energy flow in proteins. Ann. Rev. Phys. Chem. 2008, 59, 233–259. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Carter, J.A.; Lagutchev, A.; Koh, Y.K.; Seong, N.-H.; Cahill, D.G.; Dlott, D.D. Ultrafast flash thermal conductance of molecular chains. Science 2007, 317, 787–790. [Google Scholar] [CrossRef] [PubMed]
- Leitner, D.M. Vibrational energy transfer in helices. Phys. Rev. Lett. 2001, 87, 188102. [Google Scholar] [CrossRef]
- Leitner, D.M. Vibrational energy transfer and heat conduction in a one-dimensional glass. Phys. Rev. B 2001, 64, 094201. [Google Scholar] [CrossRef]
- Leitner, D.M.; Straub, J.E. Proteins: Energy, Heat and Signal Flow; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Leitner, D.M. Frequency resolved communication maps for proteins and other nanoscale materials. J. Chem. Phys. 2009, 130, 195101. [Google Scholar] [CrossRef] [PubMed]
- Gnanasekaran, R.; Xu, Y.; Leitner, D.M. Dynamics of water clusters confined in proteins: A molecular dynamics simulation study of interfacial waters in a dimeric hemoglobin. J. Phys. Chem. B 2010, 114, 16989–16996. [Google Scholar] [CrossRef] [PubMed]
- Gnanasekaran, R.; Agbo, J.K.; Leitner, D.M. Communication maps computed for homodimeric hemoglobin: Computational study of water-mediated energy transport in proteins. J. Chem. Phys. 2011, 135, 08B610. [Google Scholar] [CrossRef] [PubMed]
- Leitner, D.M.; Yamato, T. Mapping energy transport networks in proteins. arXiv, 2018; arXiv:1805.03715. [Google Scholar]
- Botan, V.; Backus, E.H.G.; Pfister, R.; Moretto, A.; Crisma, M.; Toniolo, C.; Nguyen, P.H.; Stock, G.; Hamm, P. Energy transport in peptide helices. Proc. Natl. Acad. Sci. USA 2007, 104, 12749–12754. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, X.; Varshney, V.; Lee, J.; Pang, Y.; Roy, A.K.; Luo, T. How to characterize thermal transport capability of 2D materials fairly?–Sheet thermal conductance and the choice of thickness. Chem. Phys. Lett. 2017, 669, 233–237. [Google Scholar] [CrossRef]
- Luo, T.; Chen, G. Nanoscale heat transfer–from computation to experiment. Phys. Chem. Chem. Phys. 2013, 15, 3389–3412. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stocker, K.M.; Neidhart, S.M.; Gezelter, J.D. Interfacial thermal conductance of thiolate-protected gold nanospheres. J. Appl. Phys. 2016, 119, 025106. [Google Scholar] [CrossRef] [Green Version]
- Cahill, D.G.; Ford, W.K.; Goodson, K.E.; Mahan, G.D.; Majumdar, A.; Maris, H.J.; Merlin, R.; Phillpot, S.R. Nanoscale thermal transport. J. Appl. Phys. 2003, 93, 793–818. [Google Scholar] [CrossRef]
- Cahill, D.G.; Braun, P.V.; Chen, G.; Clarke, D.R.; Fan, S.; Goodson, K.E.; Keblinski, P.; King, W.P.; Mahan, G.D.; Majumdar, A.; et al. Nanoscale thermal transport. II. 2003–2012. Appl. Phys. Rev. 2014, 1, 011305. [Google Scholar] [CrossRef] [Green Version]
- Cao, X.-H.; Zhou, W.-X.; Chen, C.-Y.; Tang, L.-M.; Long, M.; Chen, K.-Q. Excellent thermoelectric properties induced by different contact geometries in phenalenyl-based single-molecule devices. Sci. Rep. 2017, 7, 10842. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Luo, T. Giant thermal rectification from polyethylene nanofiber thermal diodes. Small 2015, 11, 4657–4665. [Google Scholar] [CrossRef] [PubMed]
- Segal, D.; Nitzan, A. Heat rectification in molecular junctions. J. Chem. Phys. 2005, 122, 194704. [Google Scholar] [CrossRef] [PubMed]
- Leitner, D.M.; Pandey, H.D. Quantum bottlenecks and unidirectional energy flow in molecules. Ann. Phys. 2015, 527, 601–609. [Google Scholar] [CrossRef]
- Leitner, D.M.; Pandey, H.D. Asymmetric energy flow in liquid alkylbenzenes: A computational study. J. Chem. Phys. 2015, 143, 144301. [Google Scholar] [CrossRef] [PubMed]
- Pein, B.C.; Sun, Y.; Dlott, D.D. Unidirectional vibrational energy flow in nitrobenzene. J. Phys. Chem. A 2013, 117, 6066–6072. [Google Scholar] [CrossRef] [PubMed]
- Pein, B.C.; Sun, Y.; Dlott, D.D. Controlling vibrational energy flow in liquid alkylbenzenes. J. Phys. Chem. B 2013, 117, 10898–10904. [Google Scholar] [CrossRef] [PubMed]
- Kang, H.; Yang, F.; Urban, J.J. Thermal rectification via heterojunctions of solid-state phase-change materials. Phys. Rev. Appl. 2018, 10, 024034. [Google Scholar] [CrossRef]
- Rubtsova, N.I.; Qasim, L.N.; Kurnosov, A.A.; Burin, A.L.; Rubtsov, I.V. Ballistic energy transport in oligomers. Acc. Chem. Res. 2015, 48, 2547–2555. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Rubtsov, I.V. Constant-speed vibrational signaling along polyethyleneglycol chain up to 60 Å distance. Proc. Natl. Acad. Sci. USA 2012, 109, 1413–1418. [Google Scholar] [CrossRef] [PubMed]
- Rubtsova, N.I.; Rubtsov, I.V. Vibrational energy transport in molecules studied by relaxation-assisted two-dimensional infrared spectroscopy. Ann. Rev. Phys. Chem. 2015, 66, 717–738. [Google Scholar] [CrossRef] [PubMed]
- Meier, T.; Menges, F.; Nirmalraj, P.; Hölscher, H.; Riel, H.; Gotsmann, B. Length-dependent thermal transport along molecular chains. Phys. Rev. Lett. 2014, 113, 060801. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, P.E. Thermal transport across solid interfaces with nanoscale imperfections: Effects of roughness, disorder, dislocations and bonding on thermal boundary conductance. ISRN Mech. Eng. 2013, 2013, 682586. [Google Scholar] [CrossRef]
- Li, Q.; Duchemin, I.; Xiong, S.; Solomon, G.C.; Donadio, D. Mechanical tuning of thermal transport in a molecular junction. J. Phys. Chem. C 2015, 119, 24636–24642. [Google Scholar] [CrossRef]
- Li, Q.; Strange, M.; Duchemin, I.; Donadio, D.; Solomon, G.C. A strategy to suppress phonon transport in molecular junctions using π-stacked systems. J. Phys. Chem. C 2017, 121, 7175–7182. [Google Scholar] [CrossRef]
- Datta, S. Electronic Transport in Mesoscopic Systems; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Bohigas, O.; Tomsovic, S.; Ullmo, D. Manifestations of classical phase space structures in quantum mechanics. Phys. Rep. 1993, 223, 43–133. [Google Scholar] [CrossRef]
- Leitner, D.M. Real-symmetric random matrix ensembles of Hamiltonians with partial symmetry-breaking. Phys. Rev. E 1993, 48, 2536–2546. [Google Scholar] [CrossRef]
- Leitner, D.M.; Köppel, H.; Cederbaum, L.S. Effects of symmetry breaking on spectra of chaotic Hamiltonian systems. Phys. Rev. Lett. 1994, 73, 2970–2973. [Google Scholar] [CrossRef] [PubMed]
- Leitner, D.M.; Wolynes, P.G. Semiclassical quantization of the stochastic pump model of Arnold diffusion. Phys. Rev. Lett. 1997, 79, 55–58. [Google Scholar] [CrossRef]
- Mauguiere, F.A.L.; Collins, P.; Ezra, G.S.; Farantos, S.C.; Wiggins, S. Multiple transition states and roaming in ion-molecule reactions: A phase space perspective. Chem. Phys. Lett. 2014, 592, 282–287. [Google Scholar] [CrossRef]
- Revuelta, F.; Bartsch, T.; Benito, R.M.; Borondo, F. Communication: Transition state theory for dissipative systems without a dividing surface. J. Chem. Phys. 2012, 136, 091102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Collins, P.; Kramer, Z.C.; Carpenter, B.K.; Ezra, G.S.; Wiggins, S. Nonstatistical dynamics on the caldera. J. Chem. Phys. 2014, 141, 034111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kawaiand, S.; Komatsuzaki, T. Quantum reaction boundary to mediate reactions in laser fields. J. Chem. Phys. 2011, 134, 024317. [Google Scholar] [Green Version]
- Uzer, T.; Jaffe, C.; Palacián, J.; Yanguas, P.; Wiggins, S. The geometry of reaction dynamics. Nonlinearity 2002, 15, 957–992. [Google Scholar] [CrossRef] [Green Version]
- Teramoto, H.; Toda, M.; Komatsuzaki, T. Breakdown mechanisms of normally hyperbolic invariant manifolds in terms of unstable periodic orbits and homoclinic/heteroclinic orbits in Hamiltonian systems. Nonlinearity 2015, 28, 2677–2698. [Google Scholar] [CrossRef]
- Yadava, P.K.; Keshavamurthy, S. Breaking a bond: When is it statistical? Faraday Discuss. 2015, 177, 21–32. [Google Scholar] [CrossRef] [PubMed]
- Komatsuzaki, T.; Berry, R.S.; Leitner, D.M. Advancing Theory for Kinetics and Dynamics of Complex, Many-Dimensional Systems: Clusters and Proteins; Advances in Chemical Physics; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 145. [Google Scholar]
- Keshavamurthy, S. Eigenstates of thiophosgene near the dissociation threshold: Deviations from ergodicity. J. Phys. Chem. A 2013, 117, 8729–8736. [Google Scholar] [CrossRef] [PubMed]
- Leitner, D.M.; Matsunaga, Y.; Li, C.-B.; Komatsuzaki, T.; Shojiguchi, A.; Toda, M. Non-Brownian Phase Space Dynamics of Molecules, the Nature of Their Vibrational States, and Non-RRKM Kinetics. Adv. Chem. Phys. 2011, 145, 83–122. [Google Scholar]
- Leitner, D.M.; Wolynes, P.G. Intramolecular energy flow in the condensed phase: Effects of dephasing on localization in the quantum stochastic pump model. Chem. Phys. Lett. 1997, 276, 289–295. [Google Scholar] [CrossRef]
- Leitner, D.M. Quantum localization and protein-assisted vibrational energy flow in cofactors. New J. Phys. 2010, 12, 085004. [Google Scholar] [CrossRef] [Green Version]
- Agbo, J.K.; Leitner, D.M.; Evans, D.A.; Wales, D.J. Influence of vibrational energy flow on isomerization of flexible molecules: Incorporating non-RRKM kinetics in the simulation of dipeptide isomerization. J. Chem. Phys. 2005, 123, 124304. [Google Scholar] [CrossRef] [PubMed]
- Agbo, J.K.; Leitner, D.M.; Myshakin, E.M.; Jordan, K.D. Quantum energy flow and the kinetics of water shuttling between hydrogen bonding sites on trans-formanilide (TFA). J. Chem. Phys. 2007, 127, 064315. [Google Scholar] [CrossRef] [PubMed]
- Patra, S.; Keshavamurthy, S. Detecting reactive islands using Lagrangian descriptors and the relevance to transition path sampling. Phys. Chem. Chem. Phys. 2018, 20, 4970–4981. [Google Scholar] [CrossRef] [PubMed]
- Leitner, D.M. Mode damping rates in a protein chromophore. Chem. Phys. Lett. 2012, 530, 102–106. [Google Scholar] [CrossRef]
- Perez, J.B.; Arce, J.C. Quantum dynamics of the intramolecular vibrational energy redistribution in OCS: From localization to quasi-thermalization. J. Chem. Phys. 2018, 148, 214302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schofield, S.A.; Wyatt, R.E.; Wolynes, P.G. Computational study of many-dimensional quantum energy flow: From action diffusion to localization. Phys. Rev. Lett. 1995, 74, 3720–3723. [Google Scholar] [CrossRef] [PubMed]
- Schofield, S.A.; Wolynes, P.G. Picturing quantized intramolecular vibrational energy flow: Action diffusion, localization, and scaling. In Dynamics of Molecules and Chemical Reactions; Wyatt, R.E., Zhang, J.Z.H., Eds.; Marcel Dekker: New York, NY, USA, 1996. [Google Scholar]
- Krems, R.V. Ultracold controlled chemistry. Physics 2010, 3, 10. [Google Scholar] [CrossRef]
- Tariq, N.; Taisan, N.A.; Singh, V.; Weinstein, J.D. Spectroscopic detection of the LiHe molecule. Phys. Rev. Lett. 2013, 110, 153201. [Google Scholar] [CrossRef] [PubMed]
- Lemeshko, M.; Krems, R.V.; Doyle, J.M.; Kais, S. Manipulation of molecules with electromagnetic fields. Mol. Phys. 2013, 111, 1648–1682. [Google Scholar] [CrossRef]
- Patterson, D.; Tsikata, E.; Doyle, J.M. Cooling and collisions of large gas phase molecules. Phys. Chem. Chem. Phys. 2010, 12, 9736–9741. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Patterson, D.; Doyle, J.M. Cooling molecules in a cell for FTMW spectroscopy. Mol. Phys. 2012, 110, 1757–1766. [Google Scholar] [CrossRef]
- Patterson, D.; Doyle, J.M. A slow, continuous beam of cold benzonitrile. Phys. Chem. Chem. Phys. 2015, 17, 5372–5375. [Google Scholar] [CrossRef] [PubMed]
- Frisch, A.; Mark, M.; Aikawa, K.; Ferlaino, F.; Bohn, J.L.; Makrides, C.; Petrov, A.; Kotochigova, S. Quantum chaos in ultracold collisions of gas phase erbium atoms. Nature 2014, 507, 475–479. [Google Scholar] [CrossRef] [PubMed]
- Cui, J.; Li, Z.; Krems, R.V. Collision lifetimes of polyatomic molecules at low temperatures: Benzene–benzene vs benzene–rare gas atom collisions. J. Chem. Phys. 2014, 141, 164315. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Krems, R.V.; Heller, E.J. Collision dynamics of polyatomic molecules containing carbon rings at low temperatures. J. Chem. Phys. 2014, 141, 104317. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Zhang, P.; Wang, X.; Stancil, P.C.; Bowman, J.M.; Balakrishnan, N.; Forrey, R.C. Quantum dynamics of CO-H2 in full dimensionality. Nat. Comm. 2015, 6, 6629. [Google Scholar] [CrossRef] [PubMed]
- Kendrick, B.K.; Hazra, J.; Balakrishnan, N. The geometric phase controls ultracold chemistry. Nat. Comm. 2015, 6, 7918. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stuhl, B.K.; Hummon, M.T.; Ye, J. Cold State-Selected Molecular Collisions and Reactions. Ann. Rev. Phys. Chem. 2014, 65, 501–518. [Google Scholar] [CrossRef] [PubMed]
- Quéméner, G.; Julienne, P.S. Ultracold molecules under control! Chem. Rev. 2012, 112, 4949–5011. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Byrd, J.N.; Simbotin, I.; Côté, R. Tuning ultracold chemical reactions via Rydberg-dressed interactions. Phys. Rev. Lett. 2014, 113, 025302. [Google Scholar] [CrossRef] [PubMed]
- Côté, R. Ultracold molecules: Their formation and application to quantum computing. Adv. Chem. Phys. 2014, 154, 403–448. [Google Scholar]
- Quiros, N.; Tariq, N.; Tscherbul, T.V.; Weinstein, J.D. Cold anisotropically interacting van der waals molecule: TiHe. Phys. Rev. Lett. 2017, 118, 213401. [Google Scholar] [CrossRef] [PubMed]
- Vieira, D.; Krems, R.V.; Tscherbul, T.V. Molecular collisions and reactive scattering in external fields: Are field-induced couplings important at short range? J. Chem. Phys. 2017, 146, 024102. [Google Scholar] [CrossRef] [PubMed]
- Eibenberger, S.; Doyle, J.; Patterson, D. Enantiomer-Specific State Transfer of Chiral Molecules. Phys. Rev. Lett. 2017, 118, 123002. [Google Scholar] [CrossRef] [PubMed]
- Shyshlov, D.; Berrios, E.; Gruebele, M.; Babikov, D. On readout of vibrational qubits using quantum beats. J. Chem. Phys. 2014, 141, 224306. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cederbaum, L.S. Efficient non-resonant intermolecular vibrational energy transfer. Mol. Phys. 2018, 2018, 1–6. [Google Scholar] [CrossRef]
- Bohn, J.L.; Rey, A.M.; Ye, J. Cold molecules: Progress in quantum engineering of chemistry and quantum matter. Science 2017, 357, 1002–1010. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sous, J.; Grant, E. Many-body physics with ultracold plasmas: Quenched randomness and localization. arXiv, 2018; arXiv:1808.07479. [Google Scholar]
- Sous, J.; Grant, E. Possible many-body localization in a long-lived finite-temperature ultracold quasineutral molecular plasma. Phys. Rev. Lett. 2018, 120, 110601. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leitner, D.M. Molecules and the Eigenstate Thermalization Hypothesis. Entropy 2018, 20, 673. https://doi.org/10.3390/e20090673
Leitner DM. Molecules and the Eigenstate Thermalization Hypothesis. Entropy. 2018; 20(9):673. https://doi.org/10.3390/e20090673
Chicago/Turabian StyleLeitner, David M. 2018. "Molecules and the Eigenstate Thermalization Hypothesis" Entropy 20, no. 9: 673. https://doi.org/10.3390/e20090673




