Information-Length Scaling in a Generalized One-Dimensional Lloyd’s Model
Abstract
:1. Introduction
2. Results
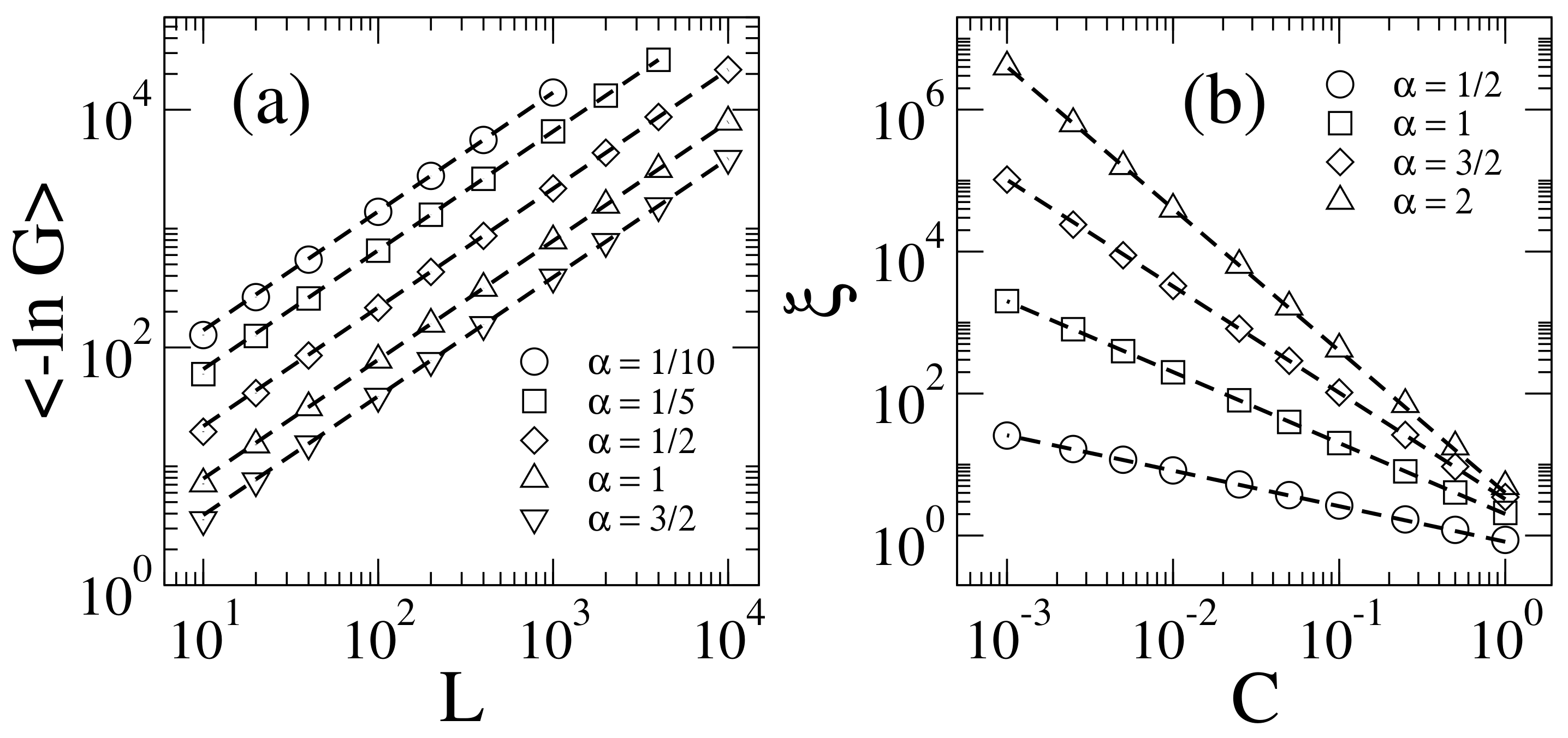
2.1. Extraction of the Localization Length
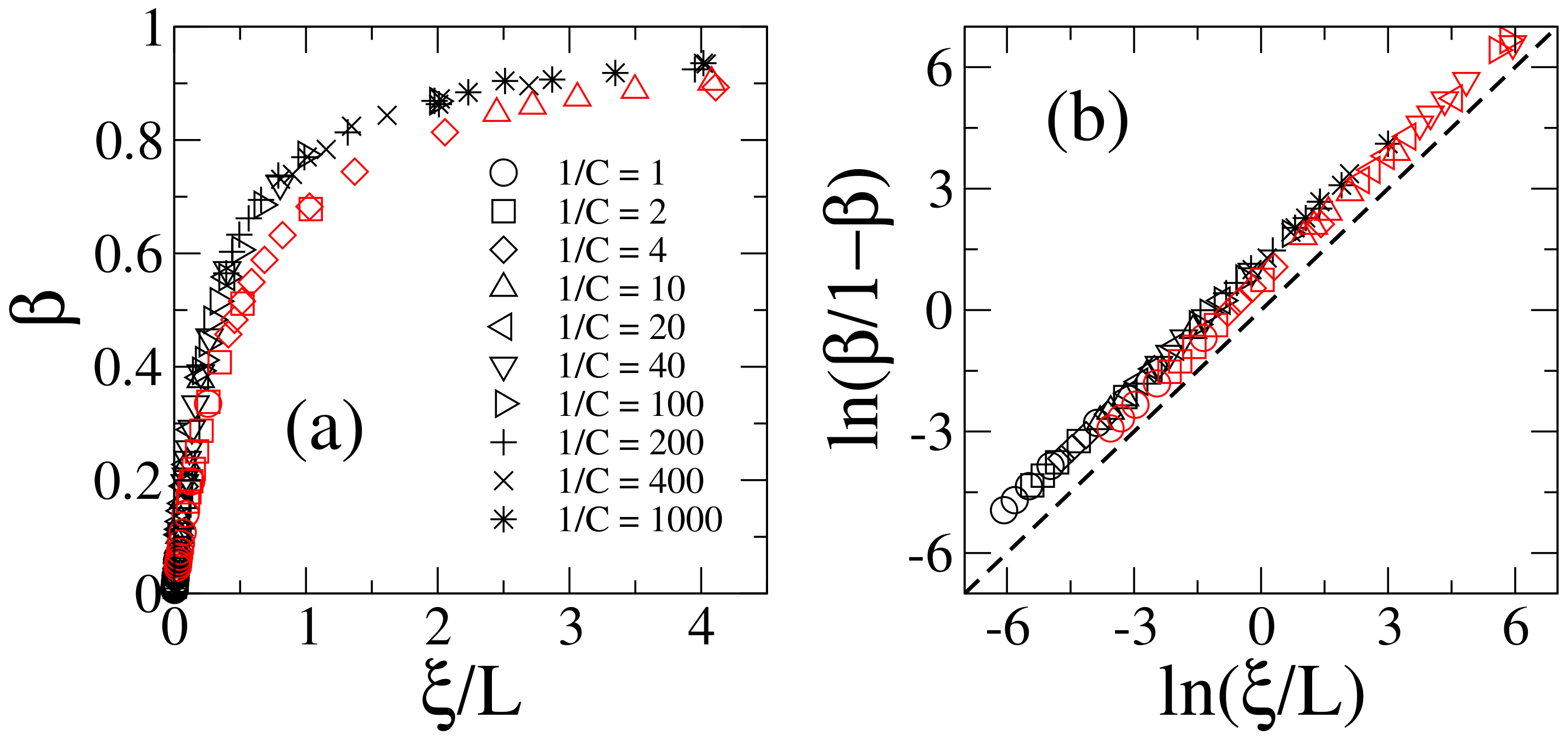
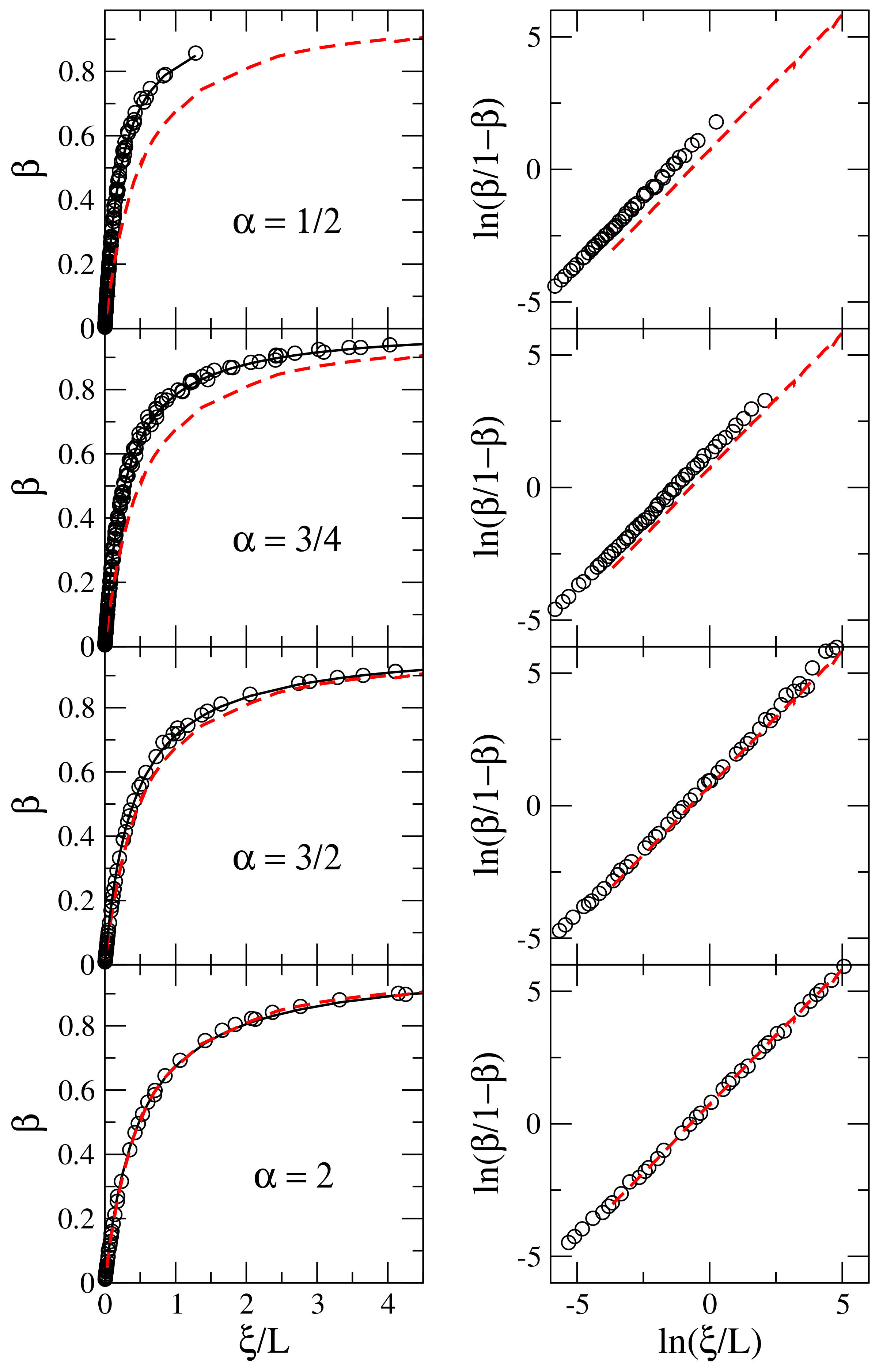
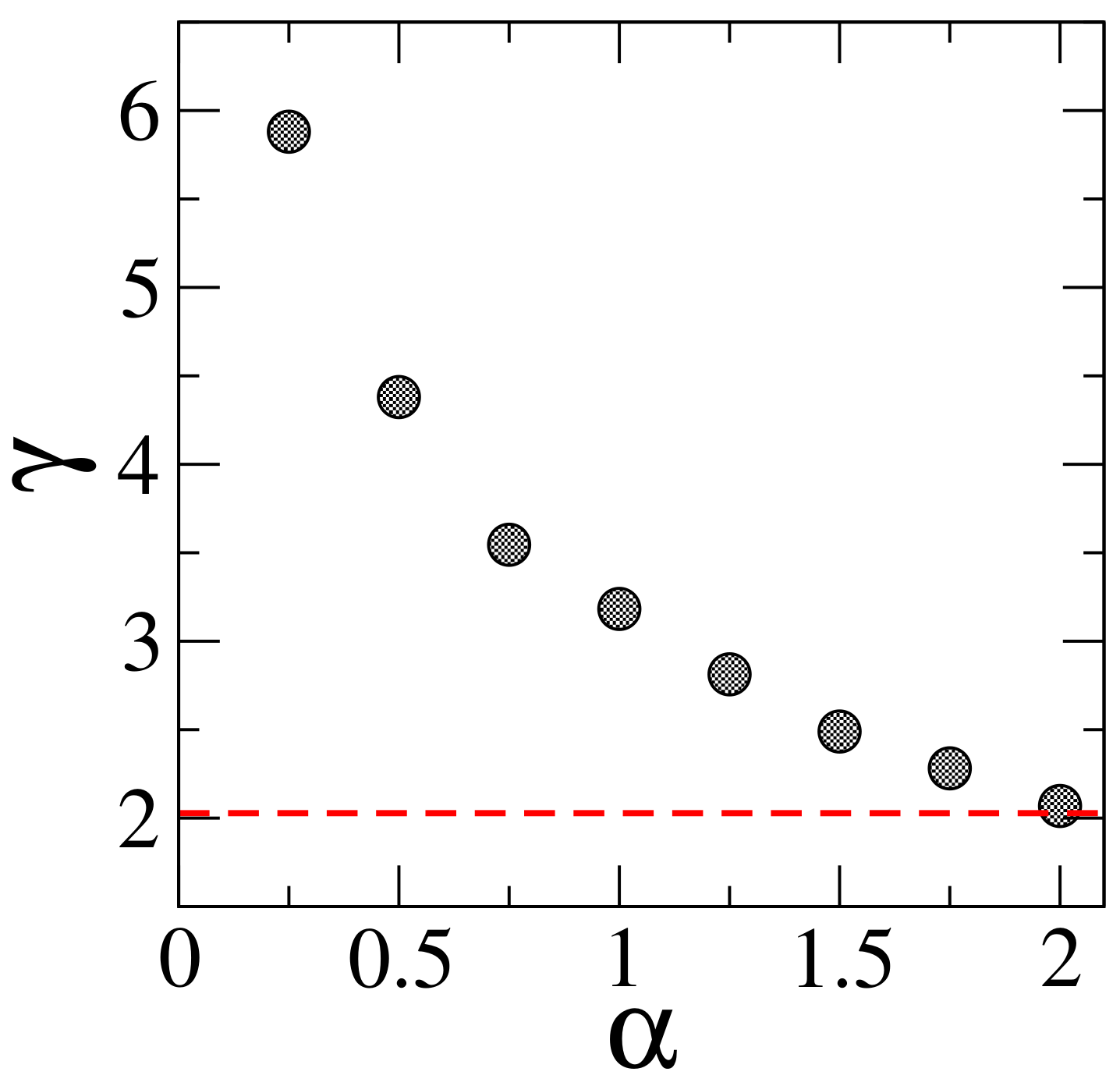
2.2. Calculation of the Information Length
3. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lloyd, P. Exactly solvable model of electronic states in a three-dimensional disordered Hamiltonian: non-existence of localized states. J. Phys. C 1969, 2, 1717–1725. [Google Scholar] [CrossRef]
- Saitoh, M. Existence of localization in Lloyd’s disordered lattice model. Phys. Lett. A 1970, 33, 44–45. [Google Scholar] [CrossRef]
- Saitoh, M. Electric Conductivity for Lloyd’s Disordered Lattice Model. Progr. Theor. Phys. 1971, 45, 746–755. [Google Scholar] [CrossRef]
- Kumar, A.P.; Baskaran, G. Coherent potential approximation, averaged T-matrix approximation and Lloyd’s model. J. Phys. C 1973, 6, L399–L401. [Google Scholar] [CrossRef]
- Hoshino, K. Electrical conductivity and electron localization for the Lloyd model. Phys. Lett. A 1976, 56, 133–134. [Google Scholar] [CrossRef]
- Bandy, W.R.; Glick, A.J. Tight-binding Green’s-function calculations of electron tunneling. II. Diagonal disorder in the one-dimensional two-band model. Phys. Rev. B 1977, 16, 2346–2349. [Google Scholar] [CrossRef]
- Kivelson, S.; Gelatt, C.D. Impurity states in a disordered insulator: The Lloyd model. Phys. Rev. B 1979, 20, 4167–4170. [Google Scholar] [CrossRef]
- Simon, B. Equality of the density of states in a wide class of tight-binding Lorentzian random models. Phys. Rev. B 1983, 27, 3859–3860. [Google Scholar] [CrossRef]
- Rodrigues, D.E.; Weisz, J.F. Generalization of the Lloyd model for calculation of electronic structure at disordered interfaces. Phys. Rev. B 1986, 34, 2306–2310. [Google Scholar] [CrossRef]
- Kolley, E.; Kolley, W. Conductivity in Anderson-type models: a comparative study of critical disorder. J. Phys. C 1988, 21, 6099–6109. [Google Scholar] [CrossRef]
- Johnston, R.; Kunz, H. A method for calculating the localisation length, with an analysis of the Lloyd model. J. Phys. C 1983, 16, 4565–4580. [Google Scholar] [CrossRef]
- Rodrigues, D.E.; Pastawski, H.M.; Weisz, J.F. Localization and phase coherence length in the Lloyd model. Phys. Rev. B 1986, 34, 8545–8549. [Google Scholar] [CrossRef]
- Thouless, D.J. A relation between the density of states and range of localization for one dimensional random systems. J. Phys. C 1972, 5, 77–81. [Google Scholar] [CrossRef]
- Ishii, K. Localization of eigenstates and transport phenomena in the one-dimensional disordered system. Suppl. Progr. Theor. Phys. 1973, 53, 77–138. [Google Scholar] [CrossRef]
- Abou-Chacra, R.; Thouless, D.J. Self-consistent theory of localization. II. Localization near the band edges. J. Phys. C 1974, 7, 65–75. [Google Scholar] [CrossRef]
- Thouless, D.J. Localisation in the Lloyd model. J. Phys. C 1983, 16, L929–L931. [Google Scholar] [CrossRef]
- MacKinnon, A. Localisation in the Lloyd model of a disordered solid. J. Phys. C 1984, 17, L289–L291. [Google Scholar] [CrossRef]
- Robbins, M.O.; Koiller, B. Localization properties of random and partially ordered one-dimensional systems. Phys. Rev. B 1985, 32, 4576–4583. [Google Scholar] [CrossRef]
- Shepelyansky, D.L. Localization of quasienergy eigenfunctions in action space. Phys. Rev. Lett. 1986, 56, 677–680. [Google Scholar] [CrossRef] [PubMed]
- Fishman, S.; Prange, R.E.; Griniasty, M. Scaling theory for the localization length of the kicked rotor. Phys. Rev. A 1989, 39, 1628–1633. [Google Scholar] [CrossRef]
- Murdy, C.; Brouwer, P.W.; Halperin, B.I.; Gurarie, V.; Zee, A. Density of states in the non-Hermitian Lloyd model. Phys. Rev. B 1998, 58, 13539–13543. [Google Scholar] [CrossRef]
- Deych, L.I.; Lisyansky, A.A.; Altshuler, B.L. Single parameter scaling in one-dimensional localization revisited. Phys. Rev. Lett. 2000, 84, 2678–2681. [Google Scholar] [CrossRef] [PubMed]
- Deych, L.I.; Lisyansky, A.A.; Altshuler, B.L. Single-parameter scaling in one-dimensional Anderson localization: Exact analytical solution. Phys. Rev. B 2001, 64, 224202. [Google Scholar] [CrossRef]
- Gangardt, D.M.; Fishman, S. Localization of eigenstates in a modified Tomonaga-Luttinger model. Phys. Rev. B 2001, 63, 045106. [Google Scholar] [CrossRef]
- Fuchs, C.; Baltz, R.V. Optical properties of quantum wires: Disorder scattering in the Lloyd model. Phys. Rev. B 2001, 63, 085318. [Google Scholar] [CrossRef]
- Titov, M.; Schomerus, H. Anomalous wave function statistics on a one-dimensional lattice with power-law disorder. Phys. Rev. Lett. 2003, 91, 176601. [Google Scholar] [CrossRef] [PubMed]
- Mendez-Bermudez, J.A.; Martinez-Mendoza, A.J.; Gopar, V.A.; Varga, I. Lloyd-model generalization: Conductance fluctuations in one-dimensional disordered systems. Phys. Rev. E 2016, 93, 012135. [Google Scholar] [CrossRef] [PubMed]
- Roy, D.; Kumar, N. Random-phase reservoir and a quantum resistor: The Lloyd model. Phys. Rev. B 2007, 76, 092202. [Google Scholar] [CrossRef]
- Kozlov, G.G. Spectral dependence of the localization degree in the one-dimensional disordered Lloyd model. Theor. Math. Phys. 2012, 171, 531–540. [Google Scholar] [CrossRef]
- Casati, G.; Guarneri, I.; Izrailev, F.M.; Fishman, S.; Molinari, L. Scaling of the information length in 1D tight-binding models. J. Phys. Condens. Matter 1992, 4, 149–156. [Google Scholar] [CrossRef]
- Barthelemy, P.; Bertolotti, J.; Wiersma, D.S. A Levy flight for light. Nature 2008, 453, 495–498. [Google Scholar] [CrossRef] [PubMed]
- Fernandez-Marin, A.A.; Mendez-Bermudez, J.A.; Carbonell, J.; Cervera, F.; Sanchez-Dehesa, J.; Gopar, V.A. Beyond anderson localization in 1D: Anomalous localization of microwaves in random waveguides. Phys. Rev. Lett. 2014, 113, 233901. [Google Scholar] [CrossRef] [PubMed]
- Fernandez-Marin, A.A.; Mendez-Bermudez, J.A.; Carbonell, J.; Cervera, F.; Sanchez-Dehesa, J.; Gopar, V.A. Beyond Anderson localization: Anomalous transmission of waves through media with Levy disorder. In Proceedings of the 9th International Congress on Advanced Electromagnetic Materials in Microwaves and Optics (Metamaterials 2015), Oxford, UK, 7–12 September 2015; pp. 409–411. [Google Scholar]
- Beenakker, C.W.J.; Groth, C.W.; Akhmerov, A.R. Nonalgebraic length dependence of transmission through a chain of barriers with a Levy spacing distribution. Phys. Rev. B 2009, 79, 024204. [Google Scholar] [CrossRef]
- Burioni, R.; Caniparoli, L.; Vezzani, A. Levy walks and scaling in quenched disordered media. Phys. Rev. E 2010, 81, 060101(R). [Google Scholar] [CrossRef] [PubMed]
- Eisfeld, A.; Vlaming, S.M.; Malyshev, V.A.; Knoester, J. Excitons in molecular aggregates with Levy-type disorder: Anomalous localization and exchange broadening of optical spectra. Phys. Rev. Lett. 2010, 105, 137402. [Google Scholar] [CrossRef] [PubMed]
- Bertolotti, J.; Vynck, K.; Pattelli, L.; Barthelemy, P.; Lepri, S.; Wiersma, D.S. Engineering disorder in superdiffusive Levy glasses. Adv. Funct. Mater. 2010, 20, 965–968. [Google Scholar] [CrossRef]
- Barthelemy, P.; Bertolotti, J.; Vynck, K.; Lepri, S.; Wiersma, D.S. Role of quenching on superdiffusive transport in two-dimensional random media. Phys. Rev. E 2010, 82, 011101. [Google Scholar] [CrossRef] [PubMed]
- Burresi, M.; Radhalakshmi, V.; Savo, R.; Bertolotti, J.; Vynck, K.; Wiersma, D.S. Weak localization of light in superdiffusive random systems. Phys. Rev. Lett. 2012, 108, 110604. [Google Scholar] [CrossRef] [PubMed]
- Groth, C.W.; Akhmerov, A.R.; Beenakker, C.W.J. Transmission probability through a Levy glass and comparison with a Levy walk. Phys. Rev. E 2012, 85, 021138. [Google Scholar] [CrossRef] [PubMed]
- Burioni, R.; diSanto, S.; Lepri, S.; Vezzani, A. Scattering lengths and universality in superdiffusive Levy materials. Phys. Rev. E 2012, 86, 031125. [Google Scholar] [CrossRef] [PubMed]
- Vlaming, S.M.; Malyshev, V.A.; Eisfeld, A.; Knoester, J. Subdiffusive exciton motion in systems with heavy-tailed disorder. J. Chem. Phys. 2013, 138, 214316. [Google Scholar] [CrossRef] [PubMed]
- Burioni, R.; Ubaldi, E.; Vezzani, A. Superdiffusion and transport in two-dimensional systems with Levy-like quenched disorder. Phys. Rev. E 2014, 89, 022135. [Google Scholar] [CrossRef] [PubMed]
- Bernabo, P.; Burioni, R.; Lepri, S.; Vezzani, A. Anomalous transmission and drifts in one-dimensional Levy structures. Chaos Solitons Fractals 2014, 67, 11–19. [Google Scholar] [CrossRef]
- Zakeri, S.S.; Lepri, S.; Wiersma, D.S. Localization in one-dimensional chains with Levy-type disorder. Phys. Rev. E 2015, 91, 032112. [Google Scholar] [CrossRef] [PubMed]
- Ardakani, A.G.; Nezhadhaghighi, M.G. Controlling Anderson localization in disordered heterostrctures with Levy-type distribution. J. Opt. 2015, 17, 105601. [Google Scholar] [CrossRef]
- Falceto, F.; Gopar, V.A. Conductance through quantum wires with Levy-type disorder: Universal statistics in anomalous quantum transport. Europhys. Lett. 2010, 92, 57014. [Google Scholar] [CrossRef]
- Fernandez-Marin, A.A.; Mendez-Bermudez, J.A.; Gopar, V.A. Photonic heterostructures with Levy-type disorder: Statistics of coherent transmission. Phys. Rev. A 2012, 85, 035803. [Google Scholar] [CrossRef]
- Amanatidis, I.; Kleftogiannis, I.; Falceto, F.; Gopar, V.A. Conductance of one-dimensional quantum wires with anomalous electron wave-function localization. Phys. Rev. B 2012, 85, 235450. [Google Scholar] [CrossRef]
- Amanatidis, I.; Kleftogiannis, I.; Falceto, F.; Gopar, V.A. Coherent wave transmission in quasi-one-dimensional systems with Lévy disorder. Phys. Rev. E 2017, 96, 062141. [Google Scholar] [CrossRef] [PubMed]
- Anderson, P.W. Absence of diffusion in certain random lattices. Phys. Rev. 1958, 109, 1492–1505. [Google Scholar] [CrossRef]
- Abrahams, E. (Ed.) 50 Years of Anderson Localization; World Scientific: Singapore, 2010. [Google Scholar]
- Anderson, P.W.; Thouless, D.J.; Abrahams, E.; Fisher, D.S. New method for a scaling theory of localization. Phys. Rev. B 1980, 22, 3519–3526. [Google Scholar] [CrossRef]
- Landauer, R. Spatial variation of currents and fields due to localized scatterers in metallic conduction. IBM J. Res. Dev. 1957, 1, 223–231. [Google Scholar] [CrossRef]
- Landauer, R. Spatial variation of currents and fields due to localized scatterers in metallic conduction. IBM J. Res. Dev. 1988, 32, 306–316. [Google Scholar] [CrossRef]
- Buttiker, M. Four-terminal phase-coherent conductance. Phys. Rev. Lett. 1986, 57, 1761–1764. [Google Scholar] [CrossRef] [PubMed]
- Buttiker, M. Symmetry of electrical conduction. IBM J. Res. Dev. 1988, 32, 317–334. [Google Scholar] [CrossRef]
- Lifshits, I.M.; Gredeskul, S.A.; Pastur, L.A. Introduction to the Theory of Disordered Systems; Willey: New York, NY, USA, 1988. [Google Scholar]
- Varga, I.; Pipek, J. Information length and localization in one dimension. J. Phys. Condens. Matter 1994, 6, L115–L122. [Google Scholar] [CrossRef]
- Mendez-Bermudez, J.A.; deOliveira, J.A.; Leonel, E.D. Two-dimensional nonlinear map characterized by tunable Levy fights. Phys. Rev. E 2014, 90, 042138. [Google Scholar] [CrossRef] [PubMed]
- Mahaux, C.; Weidenmüller, H.A. Shell Model Approach in Nuclear Reactions; North-Holland Pub. Co.: Amsterdam, The Netherlands, 1969. [Google Scholar]
- Verbaarschot, J.J.M.; Weidenmüller, H.A.; Zirnbauer, M.R. Grassmann integration in stochastic quantum physics: The case of compound-nucleus scattering. Phys. Rep. 1985, 129, 367–438. [Google Scholar] [CrossRef]
- Rotter, I. A continuum shell model for the open quantum mechanical nuclear system. Rep. Prog. Phys. 1991, 54, 635–682. [Google Scholar] [CrossRef]
- Auerbach, N.; Zelevinsky, V. Super-radiant dynamics, doorways and resonances in nuclei and other open mesoscopic systems. Rep. Prog. Phys. 2011, 74, 106301. [Google Scholar] [CrossRef]
- Izrailev, F.M. Simple models of quantum chaos: Spectrum and eigenfunctions. Phys. Rep. 1990, 196, 299–392. [Google Scholar] [CrossRef]
- Metha, M.L. Random Matrices; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Fyodorov, Y.F.; Mirlin, A.D. Analytical derivation of the scaling law for the inverse participation ratio in quasi-one-dimensional disordered systems. Phys. Rev. Lett. 1992, 69, 1093–1096. [Google Scholar] [CrossRef] [PubMed]
- Casati, G.; Molinari, L.; Izrailev, F.M. Scaling properties of band random matrices. Phys. Rev. Lett. 1990, 64, 1851–1854. [Google Scholar] [CrossRef] [PubMed]
- Evangelou, S.N.; Economou, E.N. Eigenvector statistics and multifractal scaling of band random matrices. Phys. Lett. A 1990, 151, 345–348. [Google Scholar] [CrossRef]
- Fyodorov, Y.F.; Mirlin, A.D. Scaling properties of localization in random band matrices: A σ-model approach. Phys. Rev. Lett. 1991, 67, 2405–2409. [Google Scholar] [CrossRef] [PubMed]
- Izrailev, F.M. Scaling properties of spectra and eigenfunctions for quantum dynamical and disordered systems. Chaos Solitons Fractals 1995, 5, 1219–1234. [Google Scholar] [CrossRef]
- Mirlin, A.D.; Fyodorov, Y.F. The statistics of eigenvector components of random band matrices: Analytical results. J. Phys. A Math. Gen. 1993, 26, L551–L558. [Google Scholar] [CrossRef]
- Fyodorov, Y.F.; Mirlin, A.D. Level-to-level fluctuations of the inverse participation ratio in finite quasi 1D disordered systems. Phys. Rev. Lett. 1993, 71, 412–415. [Google Scholar] [CrossRef] [PubMed]
- Fyodorov, Y.F.; Mirlin, A.D. Statistical properties of eigenfunctions of random quasi 1D one-particle Hamiltonians. Int. J. Mod. Phys. B 1994, 8, 3795–3842. [Google Scholar] [CrossRef]
- Casati, G.; Guarneri, I.; Izrailev, F.M.; Scharf, R. Scaling behavior of localization in quantum chaos. Phys. Rev. Lett. 1990, 64, 5–8. [Google Scholar] [CrossRef] [PubMed]
- Mendez-Bermudez, J.A.; Ferraz de Arruda, G.; Rodrigues, F.A.; Moreno, Y. Diluted banded random matrices: scaling behavior of eigenfunction and spectral properties. J. Phys. A Math. Theor. 2017, 50, 495205. [Google Scholar] [CrossRef]
- Mendez-Bermudez, J.A.; Ferraz de Arruda, G.; Rodrigues, F.A.; Moreno, Y. Scaling properties of multilayer random networks. Phys. Rev. E 2017, 96, 012307. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Méndez-Bermúdez, J.A.; Aguilar-Sánchez, R. Information-Length Scaling in a Generalized One-Dimensional Lloyd’s Model. Entropy 2018, 20, 300. https://doi.org/10.3390/e20040300
Méndez-Bermúdez JA, Aguilar-Sánchez R. Information-Length Scaling in a Generalized One-Dimensional Lloyd’s Model. Entropy. 2018; 20(4):300. https://doi.org/10.3390/e20040300
Chicago/Turabian StyleMéndez-Bermúdez, J. A., and R. Aguilar-Sánchez. 2018. "Information-Length Scaling in a Generalized One-Dimensional Lloyd’s Model" Entropy 20, no. 4: 300. https://doi.org/10.3390/e20040300




