Quantum Nonlocality and Quantum Correlations in the Stern–Gerlach Experiment
Abstract
:1. Introduction
2. Quantum Nonlocality
3. The SGE in A Complete Quantum Treatment
4. Quantum Correlations and Nonlocality in the Stern–Gerlach Experiment
4.1. A Pure State
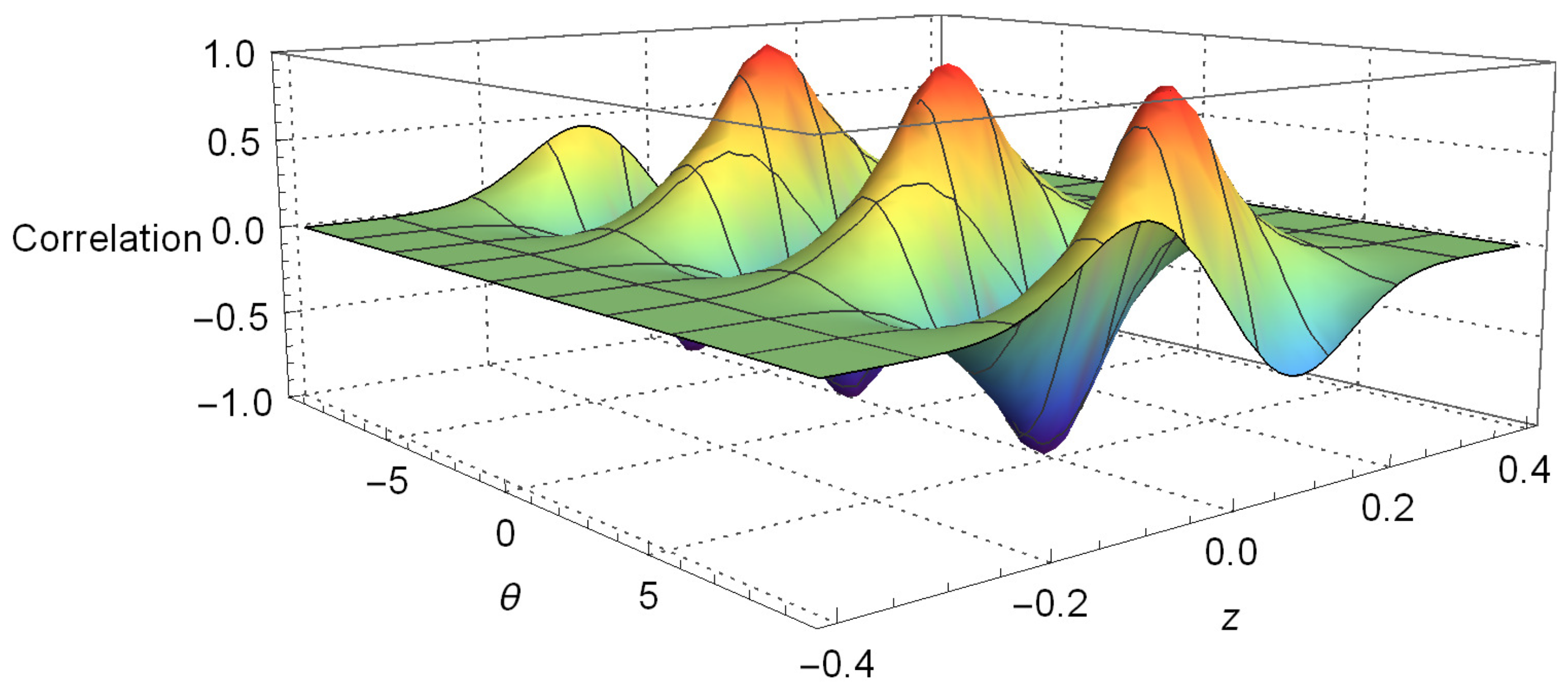
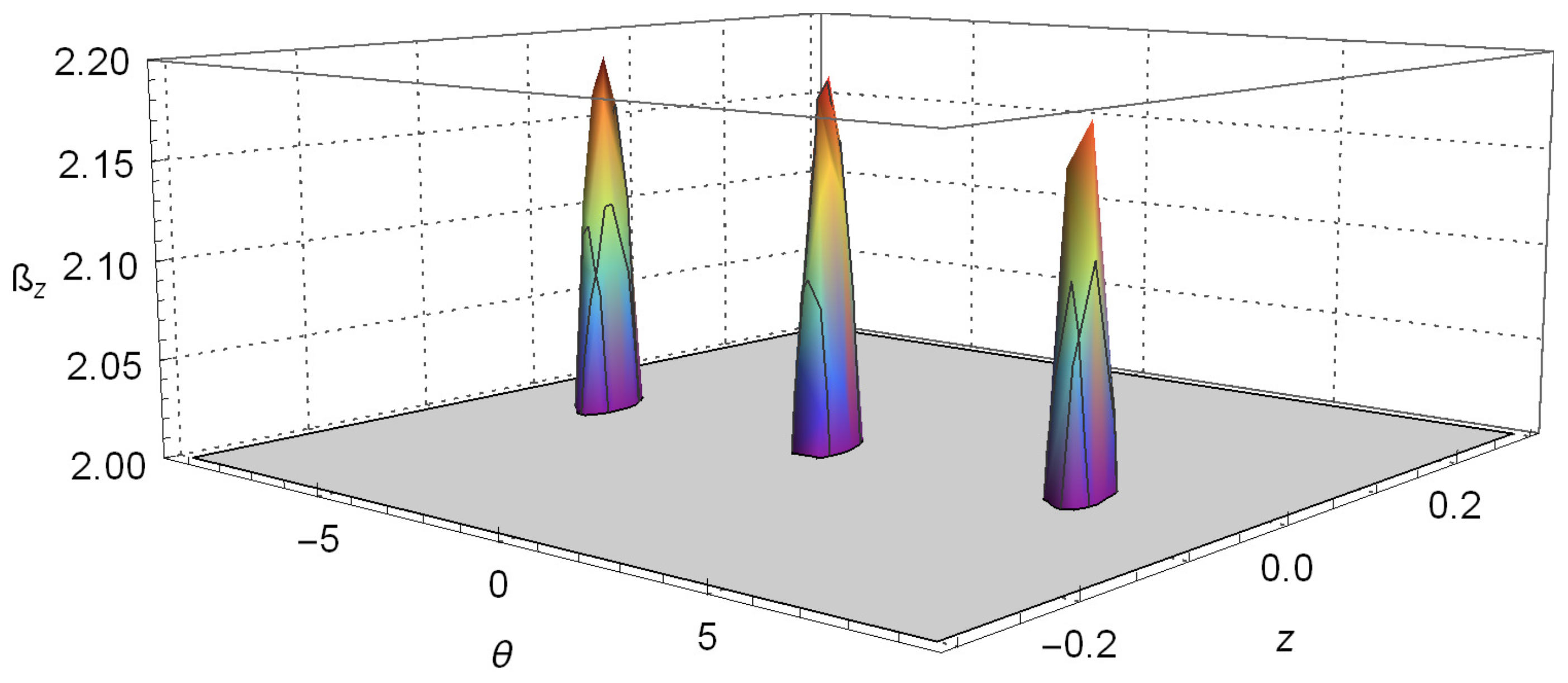
4.2. Violation of Bell’s Inequalities
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Friedrich, B.; Herschbach, D. Space Quantization: Otto Stern’s Lucky Star. Daedalus 1998, 127, 165–191. [Google Scholar]
- Friedrich, B.; Herschbach, D. Stern and Gerlach: How a bad cigar helped reorient atomic physics. Phys. Today 2003, 56, 53–59. [Google Scholar] [CrossRef]
- Schmidt-Böcking, H.; Schmidt, L.; Lüdde, H.J.; Trageser, W.; Templeton, A.; Sauer, T. The Stern–Gerlach experiment revisited. Eur. Phys. J. H 2016, 41, 327–364. [Google Scholar] [CrossRef]
- Weinert, F. Wrong theory-Right experiment: The significance of the Stern–Gerlach experiments. Stud. Hist. Phil. Mod. Phys. 1995, 26, 75–86. [Google Scholar] [CrossRef]
- Rodríguez, E.B.; Aguilar, L.A.; Martínez, E.P. A full quantum analysis of the Stern–Gerlach experiment using the evolution operator method: Analyzing current issues in teaching quantum mechanics. Eur. J. Phys. 2017, 38, 025403. [Google Scholar] [CrossRef]
- Rodríguez, E.B.; Aguilar, L.A.; Martínez, E.P. Corrigendum: A full quantum analysis of the Stern–Gerlach experiment using the evolution operator method: Analysing current issues in teaching quantum mechanics. Eur. J. Phys. 2017, 38, 069501. [Google Scholar] [CrossRef]
- Home, D.; Pan, A.K.; Ali, M.M.; Majumdar, A.S. Aspects of nonideal Stern–Gerlach experiment and testable ramifications. J. Phys. A: Math. Theor. 2007, 40, 13975. [Google Scholar] [CrossRef]
- Roston, G.B.; Casas, M.; Plastino, A.; Plastino, A.R. Quantum entanglement, spin-1/2 and the Stern–Gerlach experiment. Eur. J. Phys. 2005, 26, 657–672. [Google Scholar] [CrossRef]
- Scully, M.O.; Lamb, W.E.; Barut, A. On the theory of the Stern–Gerlach apparatus. Found. Phys. 1987, 17, 575–583. [Google Scholar] [CrossRef]
- Platt, D.E. A modern analysis of the Stern–Gerlach experiment. Am. J. Phys. 1992, 60, 306–308. [Google Scholar] [CrossRef]
- Hsu, B.C.; Berrondo, M.; Van Huele, J.F.S. Stern–Gerlach dynamics with quantum propagators. Phys. Rev. A 2011, 83, 012109. [Google Scholar] [CrossRef]
- Sparaciari, C.; Paris, M.G. Canonical Naimark extension for generalized measurements involving sets of Pauli quantum observables chosen at random. Phys. Rev. A 2013, 87, 012106. [Google Scholar] [CrossRef]
- Potel, G.; Barranco, F.; Cruz-Barrios, S.; Gómez-Camacho, J. Quantum mechanical description of Stern–Gerlach experiments. Phys. Rev. A 2005, 71, 052106. [Google Scholar] [CrossRef]
- Sparaciari, C.; Paris, M.G. Probing qubit by qubit: Properties of the POVM and the information/disturbance tradeoff. Int. J. Quantum Inf. 2014, 12, 1461012. [Google Scholar] [CrossRef]
- Fratini, F.; Safari, L. Quantum mechanical evolution operator in the presence of a scalar linear potential: Discussion on the evolved state, phase shift generator and tunneling. Phys. Scr. 2014, 89, 085004. [Google Scholar] [CrossRef] [Green Version]
- Wennerström, H.; Westlund, P.O. A Quantum Description of the Stern–Gerlach Experiment. Entropy 2017, 19, 186. [Google Scholar] [CrossRef]
- Rossi, M.A.; Benedetti, C.; Paris, M.G. Engineering decoherence for two-qubit systems interacting with a classical environment. Int. J. Quantum Inf. 2014, 12, 1560003. [Google Scholar] [CrossRef]
- Boustimi, M.; Bocvarski, V.; de Lesegno, B.V.; Brodsky, K.; Perales, F.; Baudon, J.; Robert, J. Atomic interference patterns in the transverse plane. Phys. Rev. A 2000, 61, 033602. [Google Scholar] [CrossRef]
- Larson, J.; Garraway, B.M.; Stenholm, S. Transient effects on electron spin observation. Phys. Rev. A 2004, 69, 032103. [Google Scholar] [CrossRef]
- Machluf, S.; Japha, Y.; Folman, R. Coherent Stern–Gerlach momentum splitting on an atom chip. Nat. Commun. 2013, 4, 2424. [Google Scholar] [CrossRef] [PubMed]
- Quijas, P.G.; Aguilar, L.A. Factorizing the time evolution operator. Phys. Scr. 2007, 75, 185–194. [Google Scholar] [CrossRef]
- Quijas, P.G.; Aguilar, L.A. Overcoming misconceptions in quantum mechanics with the time evolution operator. Eur. J. Phys. 2007, 28, 147–159. [Google Scholar] [CrossRef]
- Aguilar, L.A.; Quijas, P.G. Reply to Comment on “Overcoming misconceptions in quantum mechanics with the time evolution operator”. Eu. J. Phys. 2013, 34, L77. [Google Scholar] [CrossRef]
- Aguilar, L.A.; Luna, F.V.; Robledo-Sánchez, C.; Arroyo-Carrasco, M.L. The infinite square well potential and the evolution operator method for the purpose of overcoming misconceptions in quantum mechanics. Eur. J. Phys. 2014, 35, 025001. [Google Scholar] [CrossRef]
- Quijas, P.C.; Aguilar, L.M. A quantum coupler and the harmonic oscillator interacting with a reservoir: Defining the relative phase gate. Quantum Inf. Comput. 2010, 10, 190–200. [Google Scholar]
- Toyama, F.M.; Nogami, Y. Comment on ‘Overcoming misconceptions in quantum mechanics with the time evolution operator’. Eur. J. Phys. 2013, 34, L73. [Google Scholar] [CrossRef]
- Amaku, M.; Coutinho, F.A.; Masafumi Toyama, F. On the definition of the time evolution operator for time-independent Hamiltonians in non-relativistic quantum mechanics. Am. J. Phys. 2017, 85, 692–697. [Google Scholar] [CrossRef]
- Singh, C.; Belloni, M.; Christian, W. Improving students’ understanding of quantum mechanics. Phys. Today 2006, 59, 43–49. [Google Scholar] [CrossRef]
- Chhabra, M.; Das, R. Quantum mechanical wavefunction: Visualization at undergraduate level. Eur. J. Phys. 2017, 38, 015404. [Google Scholar] [CrossRef]
- Cataloglu, E.; Robinett, R.W. Testing the development of student conceptual and visualization understanding in quantum mechanics through the undergraduate career. Am. J. Phys. 2002, 70, 238–251. [Google Scholar] [CrossRef]
- Emigh, P.J.; Passante, G.; Shaffer, P.S. Student understanding of time dependence in quantum mechanics. Phys. Rev. ST Phys. Educ. Res. 2015, 11, 020112. [Google Scholar] [CrossRef]
- Dini, V.; Hammer, D. Case study of a successful learner’s epistemological framings of quantum mechanics. Phys. Rev. Phys. Educ. Res. 2017, 13, 010124. [Google Scholar] [CrossRef]
- Zhu, G.; Singh, C. Improving students understanding of quantum mechanics via the Stern–Gerlach experiment. Am. J. Phys. 2011, 79, 499–507. [Google Scholar] [CrossRef]
- Carr, L.D.; McKagan, S.B. Graduate quantum mechanics reform. Am. J. Phys. 2009, 77, 308–319. [Google Scholar] [CrossRef]
- Passante, G.; Emigh, P.J.; Shaffer, P.S. Examining student ideas about energy measurements on quantum states across undergraduate and graduate levels. Phys. Rev. Spec. Top. Phys. Educ. Res. 2015, 11, 020111. [Google Scholar] [CrossRef]
- Passante, G.; Emigh, P.J.; Shaffer, P.S. Student ability to distinguish between superposition states and mixed states in quantum mechanics. Phys. Rev. Spec. Top. Phys. Educ. Res. 2015, 11, 020135. [Google Scholar] [CrossRef]
- Greca, I.M.; Freire, O. Meeting the Challenge: Quantum Physics in Introductory Physics Courses. In International Handbook of Research in History, Philosophy and Science Teaching; Springer: Dordrecht, The Netherlands, 2014; pp. 183–209. [Google Scholar]
- Kohnle, A.; Bozhinova, I.; Browne, D.; Everitt, M.; Fomins, A.; Kok, P.; Kulaitis, G.; Prokopas, M.; Raine, D.; Swinbank, E. A new introductory quantum mechanics curriculum. Eur. J. Phys. 2014, 35, 015001. [Google Scholar] [CrossRef]
- Singh, C. Students understanding of quantum mechanics at the beginning of graduate instruction. Am. J. Phys. 2008, 76, 277–287. [Google Scholar] [CrossRef]
- Singh, C.; Marshman, E. Review of student difficulties in upper-level quantum mechanics. Phys. Rev. Spec. Top. Phys. Educ. Res. 2015, 11, 020117. [Google Scholar] [CrossRef]
- Johansson, A.; Andersson, S.; Salminen-Karlsson, M.; Elmgren, M. “Shut up and calculate”: The available discursive positions in quantum physics courses. Cult. Stud. Sci. Educ. 2016, 13, 205–226. [Google Scholar] [CrossRef]
- Greca, I.M.; Freire, O. Teaching introductory quantum physics and chemistry: Caveats from the history of science and science teaching to the training of modern chemists. Chem. Educ. Res. Pract. 2014, 15, 286–296. [Google Scholar] [CrossRef]
- Coto, B.; Arencibia, A.; Suárez, I. Monte Carlo method to explain the probabilistic interpretation of atomic quantum mechanics. Comput. Appl. Eng. Educ. 2016, 24, 765–774. [Google Scholar] [CrossRef]
- Marshman, E.; Singh, C. Investigating and improving student understanding of the expectation values of observables in quantum mechanics. Eur. J. Phys. 2017, 38, 045701. [Google Scholar] [CrossRef]
- Siddiqui, S.; Singh, C. How diverse are physics instructors’ attitudes and approaches to teaching undergraduate level quantum mechanics? Eur. J. Phys. 2017, 38, 035703. [Google Scholar] [CrossRef]
- Marshman, E.; Singh, C. Investigating and improving student understanding of quantum mechanical observables and their corresponding operators in Dirac notation. Eur. J. Phys. 2018, 39, 015707. [Google Scholar] [CrossRef]
- Kohnle, A.; Baily, C.; Campbell, A.; Korolkova, N.; Paetkau, M.J. Enhancing student learning of two-level quantum systems with interactive simulations. Am. J. Phys. 2015, 83, 560–566. [Google Scholar] [CrossRef] [Green Version]
- Baily, C.; Finkelstein, N.D. Teaching quantum interpretations: Revisiting the goals and practices of introductory quantum physics courses. Phys. Rev. Spec. Top. Phys. Educ. Res. 2015, 11, 020124. [Google Scholar] [CrossRef]
- McKagan, S.B.; Perkins, K.K.; Wieman, C.E. Design and validation of the Quantum Mechanics Conceptual Survey. Phys. Rev. Spec. Top. Phys. Educ. Res. 2010, 6, 020121. [Google Scholar] [CrossRef]
- Sadaghiani, H.R.; Pollock, S.J. Quantum mechanics concept assessment: Development and validation study. Phys. Rev. Spec. Top. Phys. Educ. Res. 2015, 11, 010110. [Google Scholar] [CrossRef]
- Wuttiprom, S.; Sharma, M.D.; Johnston, I.D.; Chitaree, R.; Soankwan, C. Development and Use of a Conceptual Survey in Introductory Quantum Physics. Int. J. Sci. Educ. 2009, 31, 631–654. [Google Scholar] [CrossRef]
- Bao, L.; Redish, E.F. Understanding probabilistic interpretations of physical systems: A prerequisite to learning quantum physics. Am. J. Phys. 2002, 70, 210–217. [Google Scholar] [CrossRef]
- Archer, R.; Bates, S. Asking the right questions: Developing diagnostic tests in undergraduate physics. New Dir. Teach. Phys. Sci. 2009, 5, 22–25. [Google Scholar]
- Clauser, J.F.; Shimony, A. Bell’s theorem. Experimental tests and implications. Rep. Prog. Phys. 1978, 41, 1881–1927. [Google Scholar] [CrossRef]
- Gisin, N. Quantum Chance: Nonlocality, Teleportation and Other Quantum Marvels; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Augusiak, R.; Demianowicz, M.; Acín, A. Local hidden variable models for entangled quantum states. J. Phys. A Math. Theor. 2014, 47, 424002. [Google Scholar] [CrossRef]
- Gisin, N. Bell’s inequality holds for all non-product states. Phys. Lett. A 1991, 154, 201–202. [Google Scholar] [CrossRef]
- Popescu, S.; Rohrlich, D. Generic quantum nonlocality. Phys. Lett. A 1992, 166, 293–297. [Google Scholar] [CrossRef]
- Popescu, S. Bell’s inequalities versus teleportation: What is nonlocality? Phys. Rev. Lett. 1994, 72, 797–799. [Google Scholar] [CrossRef] [PubMed]
- Brunner, N.; Gisin, N.; Scarani, V. Entanglement and non-locality are different resources. New J. Phys. 2005, 7, 88. [Google Scholar] [CrossRef]
- Bennett, C.H.; DiVincenzo, D.P.; Fuchs, C.A.; Mor, T.; Rains, E.; Shor, P.W.; Smolin, J.A.; Wootters, W.K. Quantum nonlocality without entanglement. Phys Rev A 1999, 59, 1070–1091. [Google Scholar] [CrossRef]
- Jammer, M. The Philosophy of Quantum Mechanics; John Wiley & Sons: New York, NY, USA, 1974. [Google Scholar]
- Fine, A. The Shaky Game; The University of Chicago Press: London, UK, 1986. [Google Scholar]
- Norsen, T. Einstein’s boxes. Am. J. Phys. 2005, 73, 164–176. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Gallego, R.; Würflinger, L.E.; Acín, A.; Navascués, M. Operational Framework for Nonlocality. Phys. Rev. Lett. 2012, 109, 070401. [Google Scholar] [CrossRef] [PubMed]
- Forster, M.; Winkler, S.; Wolf, S. Distilling Nonlocality. Phys. Rev. Lett. 2009, 102, 120401. [Google Scholar] [CrossRef] [PubMed]
- Wódkiewicz, K. Nonlocality of the Schrödinger cat. New J. Phys. 2000, 2, 21. [Google Scholar] [CrossRef]
- Banaszek, K.; Wódkiewicz, K. Testing Quantum Nonlocality in Phase Space. Phys. Rev. Lett. 1999, 82, 2009–2013. [Google Scholar] [CrossRef]
- Haug, F.; Freyberger, M.; Wódkiewicz, K. Nonlocality of a free atomic wave packet. Phys. Lett. A 2004, 321, 6–13. [Google Scholar] [CrossRef]
- Agarwal, G.; Home, D.; Schleich, W. Einstein-Podolsky-Rosen correlation—Parallelism between the Wigner function and the local hidden variable approaches. Phys. Lett. A 1992, 170, 359–362. [Google Scholar] [CrossRef]
- Ben-Benjamin, J.S.; Kim, M.B.; Schleich, W.P.; Case, W.B.; Cohen, L. Working in phase-space with Wigner and Weyl. Fortschr. Phys. 2017, 65, 1600092. [Google Scholar] [CrossRef]
- Case, W.B. Wigner functions and Weyl transforms for pedestrians. Am. J. Phys. 2008, 76, 937–946. [Google Scholar] [CrossRef]
- Royer, A. Wigner function as the expectation value of a parity operator. Phys. Rev. A 1977, 15, 449–450. [Google Scholar] [CrossRef]
- Hillery, M.O.S.M.; O’Connell, R.F.; Scully, M.O.; Wigner, E.P. Distribution functions in physics: Fundamentals. Phys. Rep. 1984, 106, 121–167. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence and the Transition from Quantum to Classical. Phys. Today 1991, 44, 36. [Google Scholar] [CrossRef]
- Gerry, C.C.; Knight, P.L. Quantum superpositions and Schrödinger cat states in quantum optics. Am. J. Phys. 1997, 65, 964–974. [Google Scholar] [CrossRef]
- Ballentine, L.E. Quantum Mechanics: A Modern Development; World Scientific Publishing: Singapore, 1998. [Google Scholar]
- Jeong, H.; Son, W.; Kim, M.S.; Ahn, D.; Brukner, Č. Quantum nonlocality test for continuous-variable states with dichotomic observable. Phys. Rev. A 2003, 67, 012106. [Google Scholar] [CrossRef]
- Chen, Z.B.; Pan, J.W.; Hou, G.; Zhang, Y.D. Maximal Violation of Bell’s Inequalities for Continuous Variable Systems. Phys. Rev. Lett. 2002, 88, 040406. [Google Scholar] [CrossRef] [PubMed]
- Zukowski, M. Bell’s Theorem Tells Us Not What Quantum Mechanics Is, but What Quantum Mechanics Is Not. In Quantum [Un]Speakables II; Bertlmann, R., Zeilinger, A., Eds.; Springer: Cham, Switzerland, 2017; pp. 175–185. [Google Scholar] [CrossRef]
- Ferraro, A.; Paris, M.G.A. Nonlocality of two- and three-mode continuous variable systems. J. Opt. B Quantum Semiclassical Opt. 2005, 7, 174–182. [Google Scholar] [CrossRef]
- Ferrie, C. Quasi-probability representations of quantum theory with applications to quantum information science. Rep. Prog. Phys. 2011, 74, 116001. [Google Scholar] [CrossRef]
- Vourdas, A. Quantum systems with finite Hilbert space. Rep. Prog. Phys. 2004, 67, 267–320. [Google Scholar] [CrossRef]
- Hinarejos, M.; Bañuls, M.C.; Pérez, A. Wigner formalism for a particle on an infinite lattice: dynamics and spin. New J. Phys. 2015, 17, 013037. [Google Scholar] [CrossRef]
- Gomis, P.; Pérez, A. Decoherence effects in the Stern–Gerlach experiment using matrix Wigner Functions. Phys. Rev. A 2016, 94, 012103. [Google Scholar] [CrossRef]
- Clauser, J.F.; Horne, M.A. Shimony A and Holt R A Proposed Experiment to Test Local Hidden-Variable Theories. Phys. Rev. Lett. 1969, 23, 880–884. [Google Scholar] [CrossRef]
- Rodríguez, E.B.; Aguilar, L.A. Disturbance-disturbance uncertainty relation: The statistical distinguishability of quantum states determines disturbance. Sci. Rep. 2018, 8, 4010. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piceno Martínez, A.E.; Benítez Rodríguez, E.; Mendoza Fierro, J.A.; Méndez Otero, M.M.; Arévalo Aguilar, L.M. Quantum Nonlocality and Quantum Correlations in the Stern–Gerlach Experiment. Entropy 2018, 20, 299. https://doi.org/10.3390/e20040299
Piceno Martínez AE, Benítez Rodríguez E, Mendoza Fierro JA, Méndez Otero MM, Arévalo Aguilar LM. Quantum Nonlocality and Quantum Correlations in the Stern–Gerlach Experiment. Entropy. 2018; 20(4):299. https://doi.org/10.3390/e20040299
Chicago/Turabian StylePiceno Martínez, Alma Elena, Ernesto Benítez Rodríguez, Julio Abraham Mendoza Fierro, Marcela Maribel Méndez Otero, and Luis Manuel Arévalo Aguilar. 2018. "Quantum Nonlocality and Quantum Correlations in the Stern–Gerlach Experiment" Entropy 20, no. 4: 299. https://doi.org/10.3390/e20040299




