Shannon Entropy of Binary Wavelet Packet Subbands and Its Application in Bearing Fault Extraction
Abstract
:1. Introduction
2. The Limitation of the Kurtosis Index
3. Proposed Method
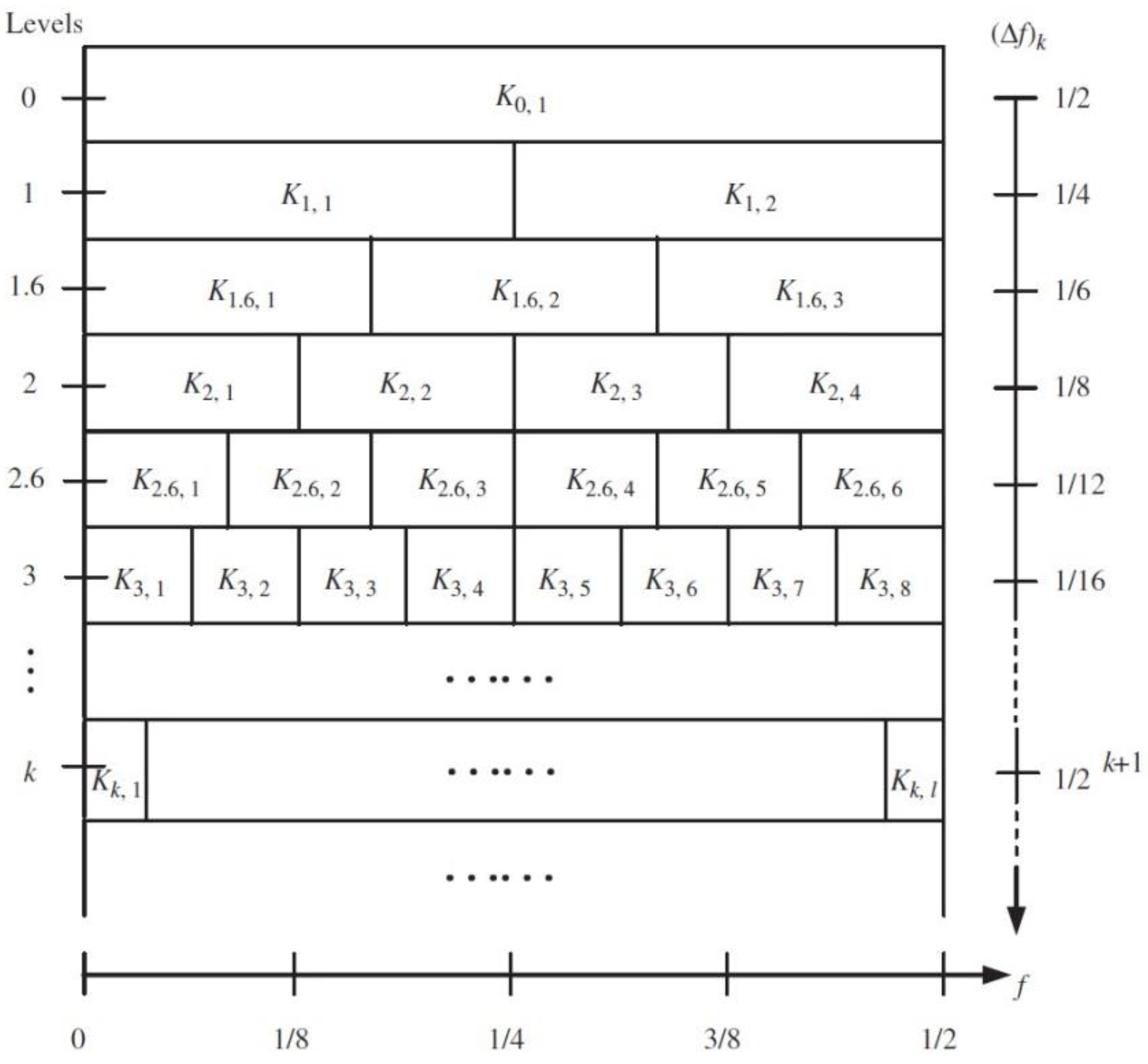
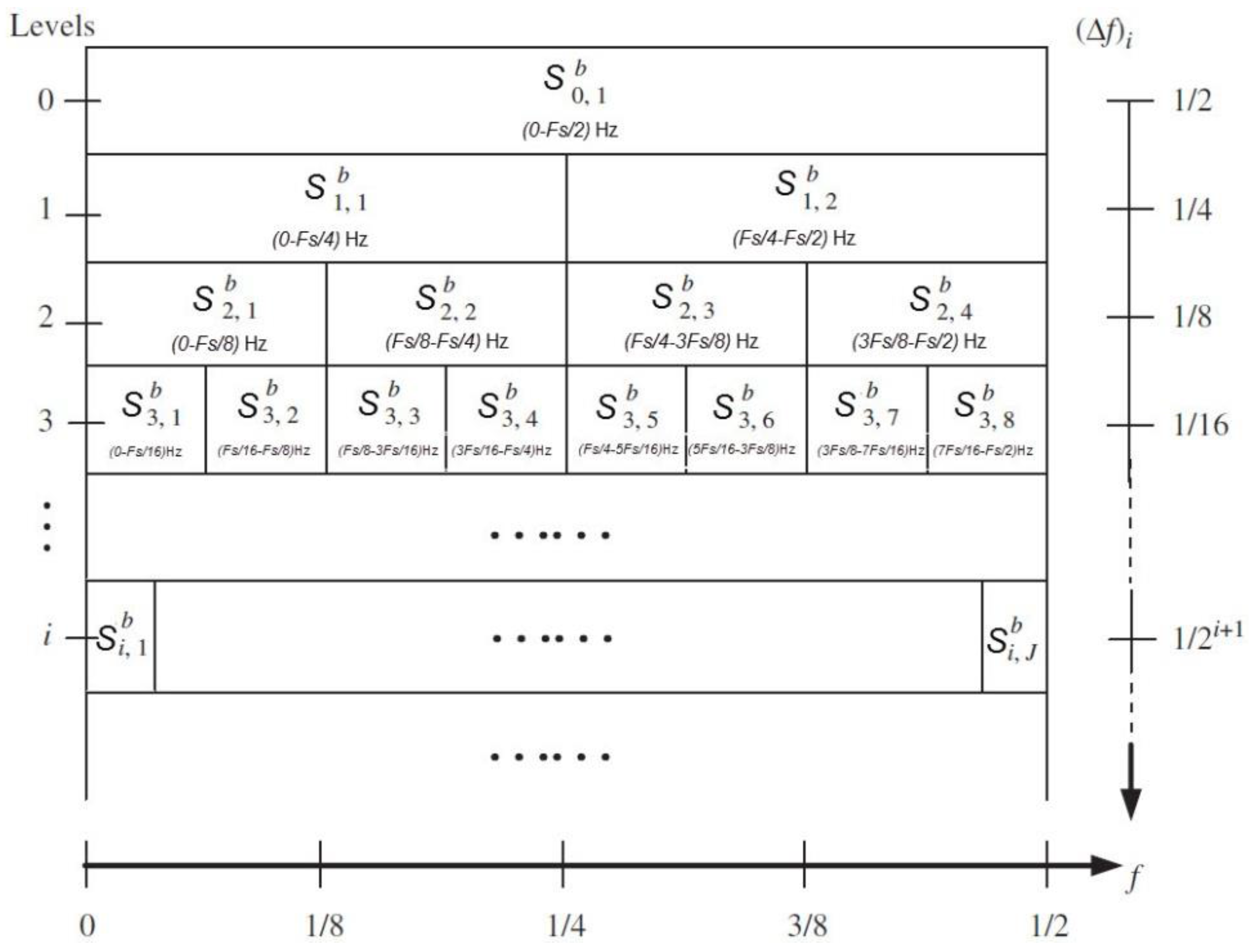
3.1. Binary Wavelet Packet Transform
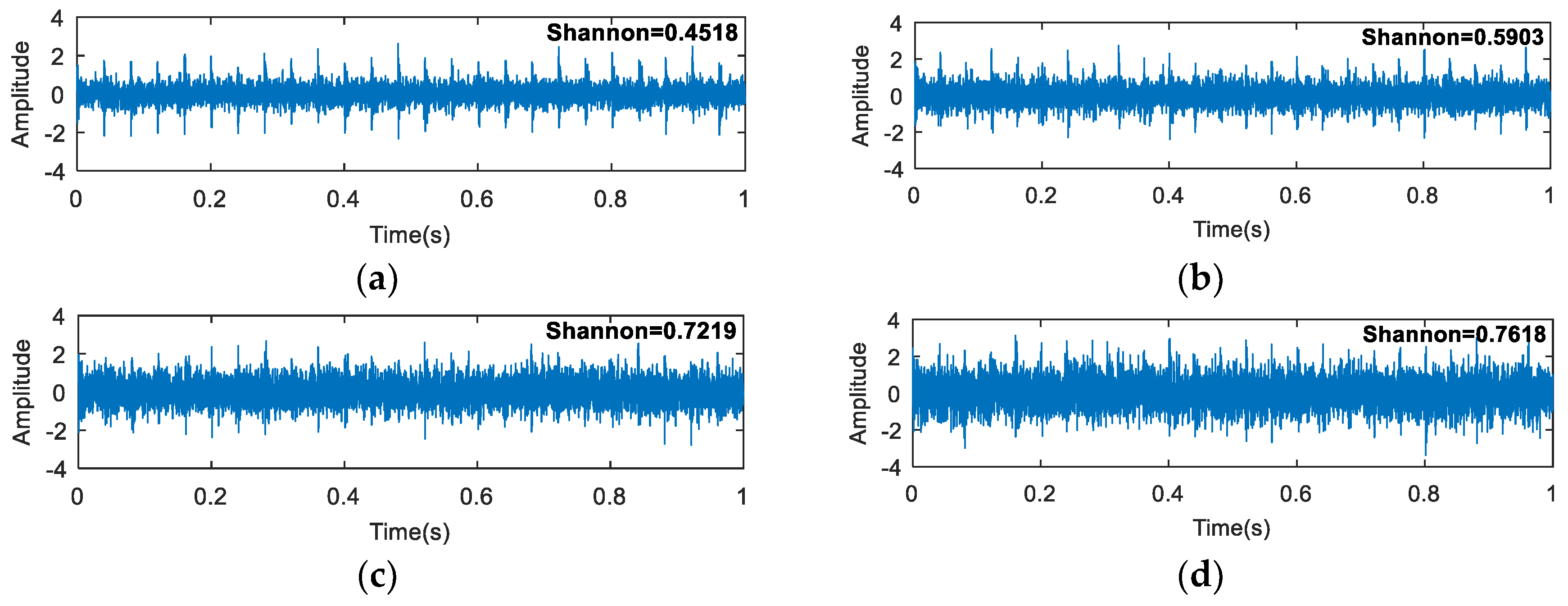
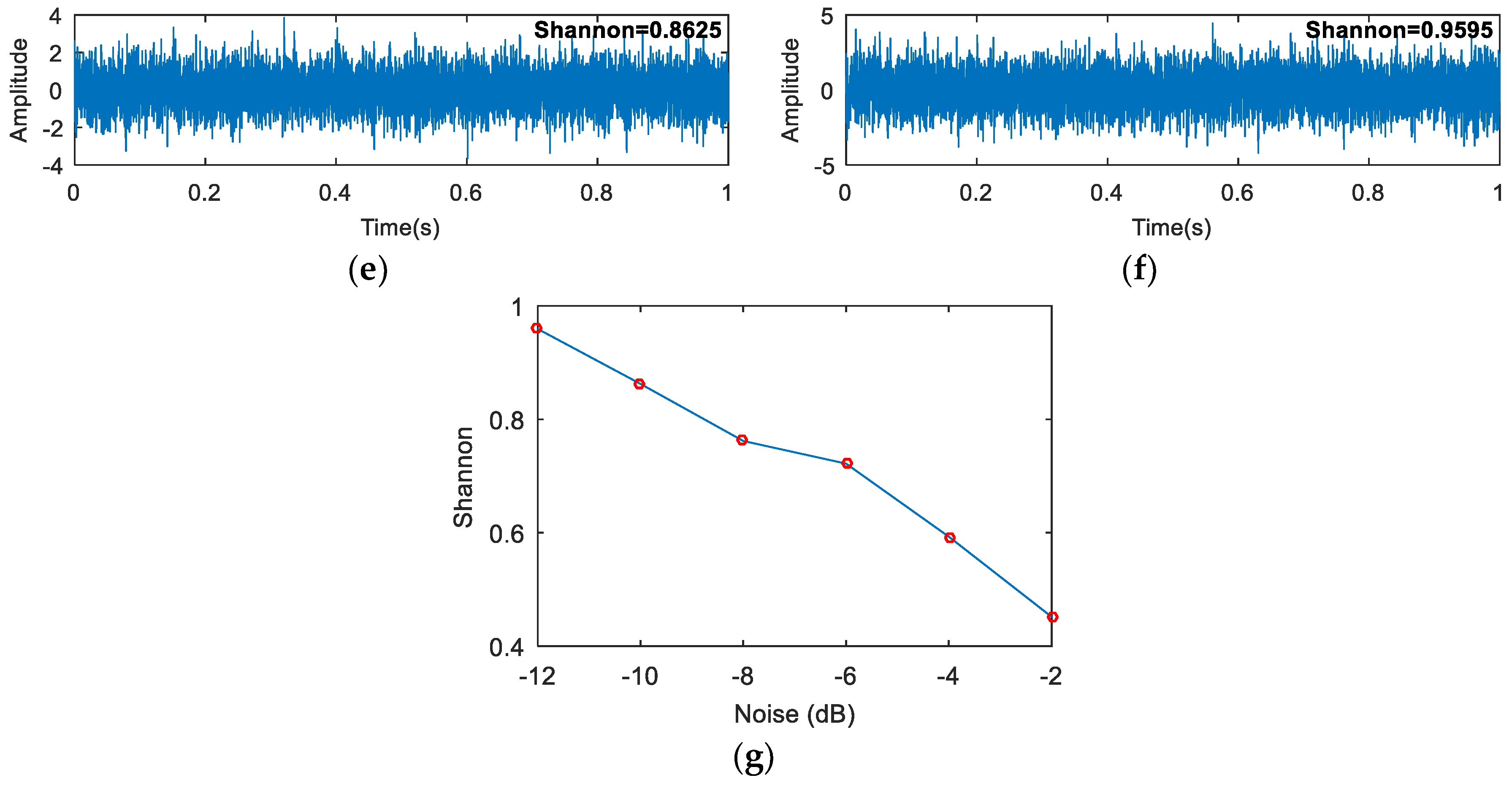
3.2. Shannon Entropy
3.3. Process of the Proposed Method
- I
- The theoretical characteristic frequency of the bearing fault is calculated according to the parameter of the bearing. The empirical formula is as follows:where , , , and respectively represent the inner ring fault, outer ring fault, rolling body element fault, and cage fault. is the number of the ball element, is the diameter of the rolling element, is the pitch diameter, is the spindle speed, and is the pressure angle.
- II
- The vibration signal is decomposed by binary wavelet packet transform (BWPT), and the Shannon entropy () of each subband after BWPT is calculated. After this, the inverse of each subband Shannon entropy value is taken as Equation (4):
- III
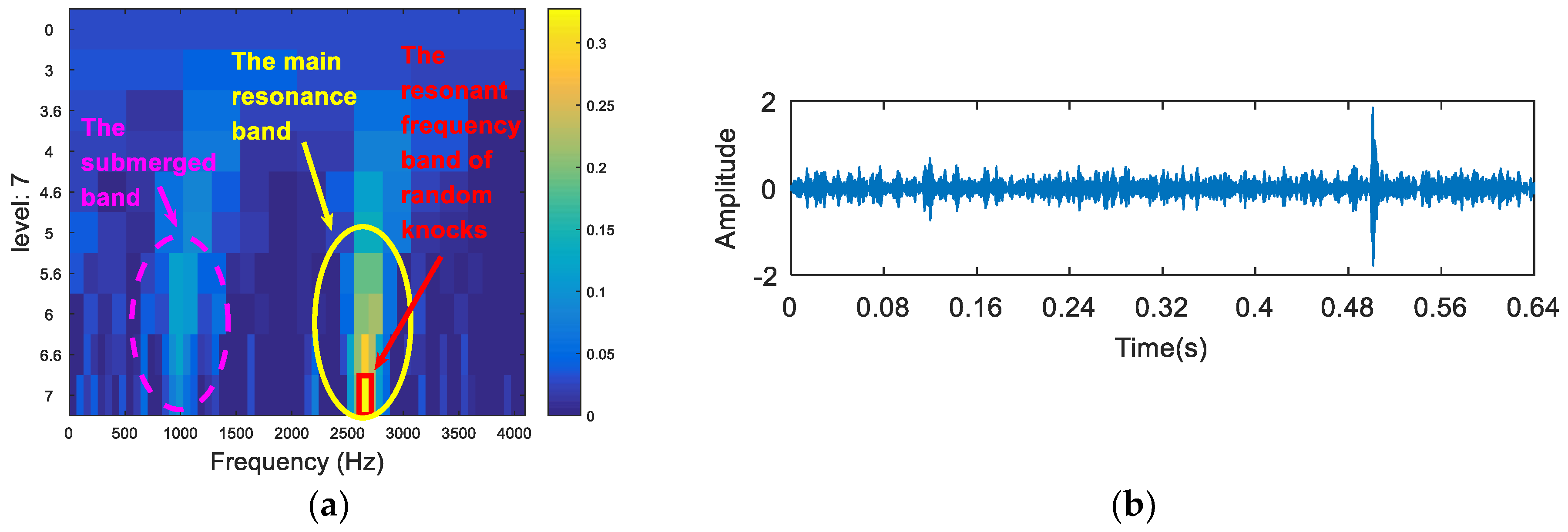
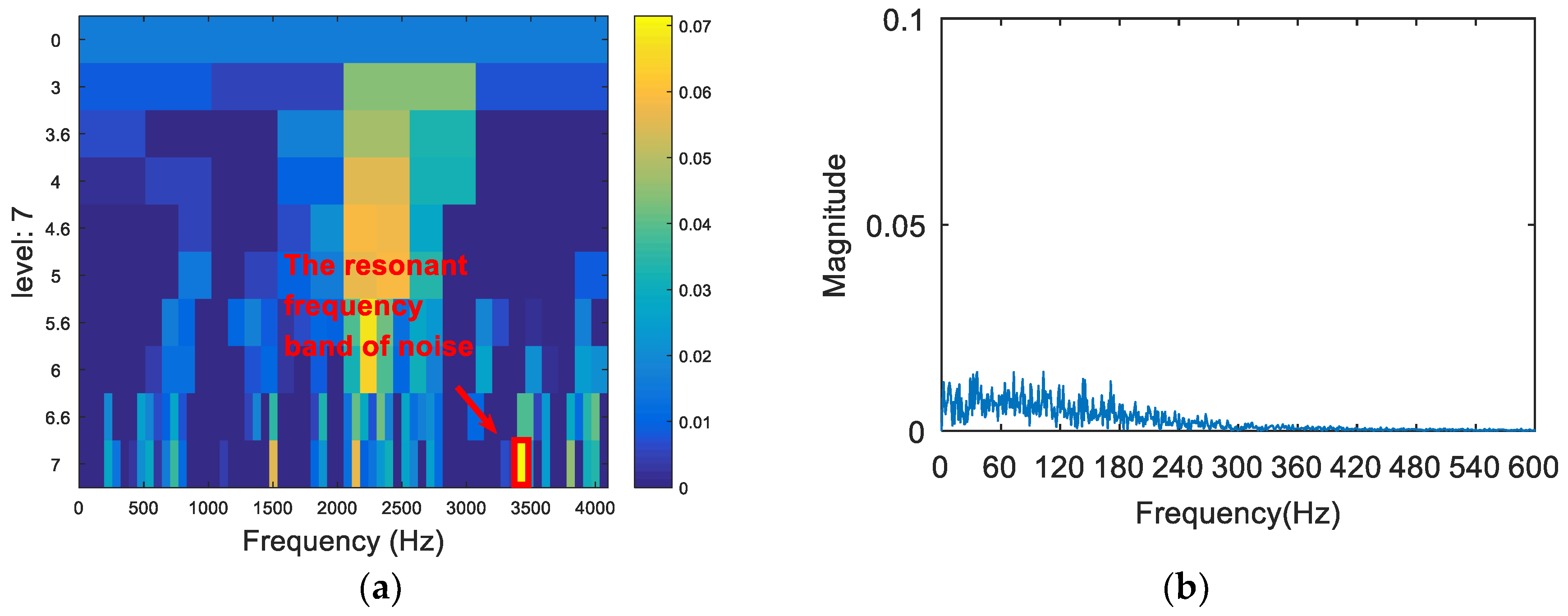
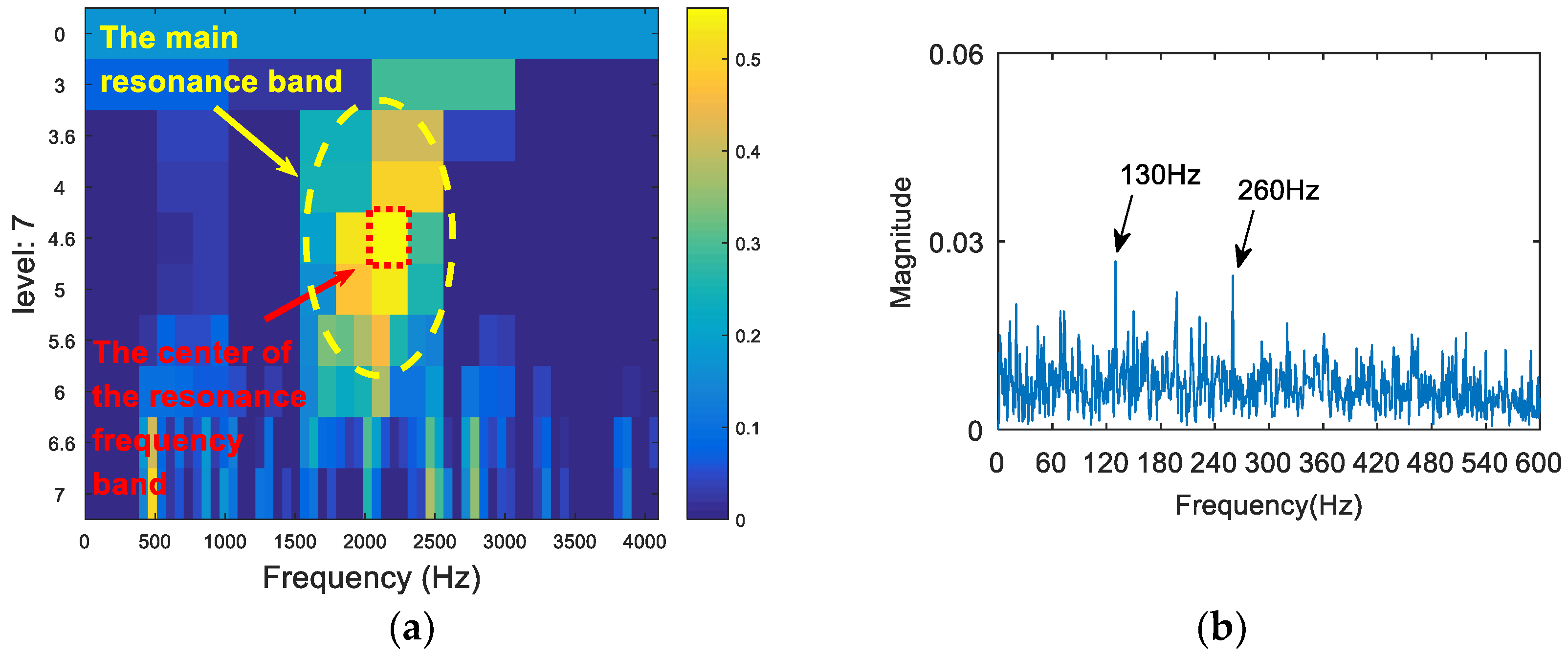
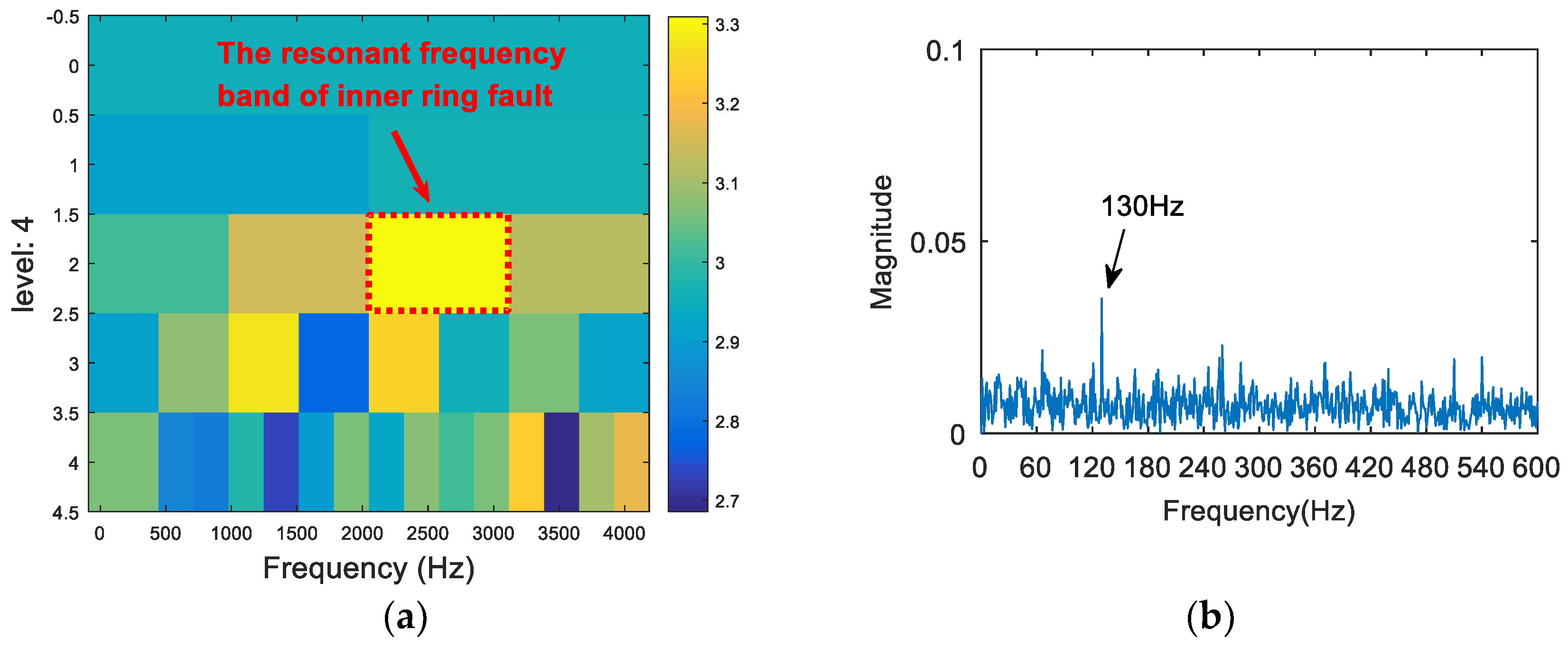
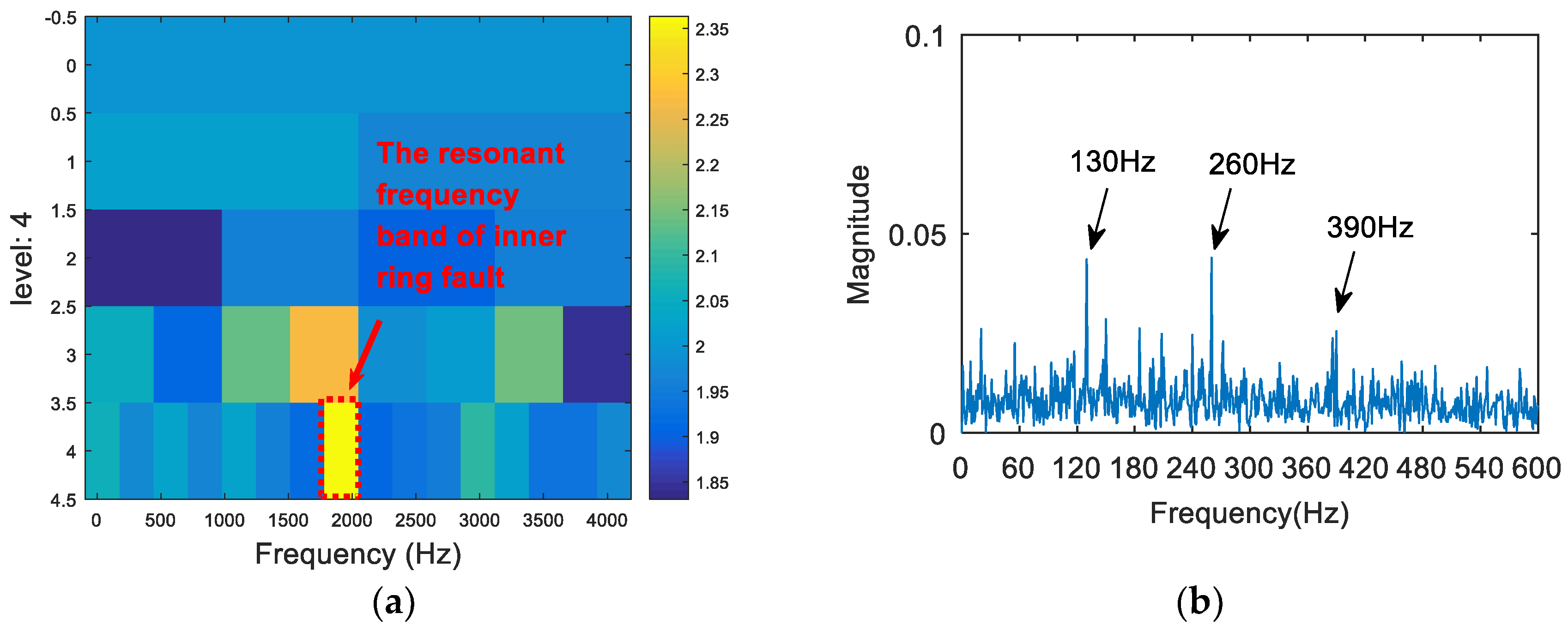
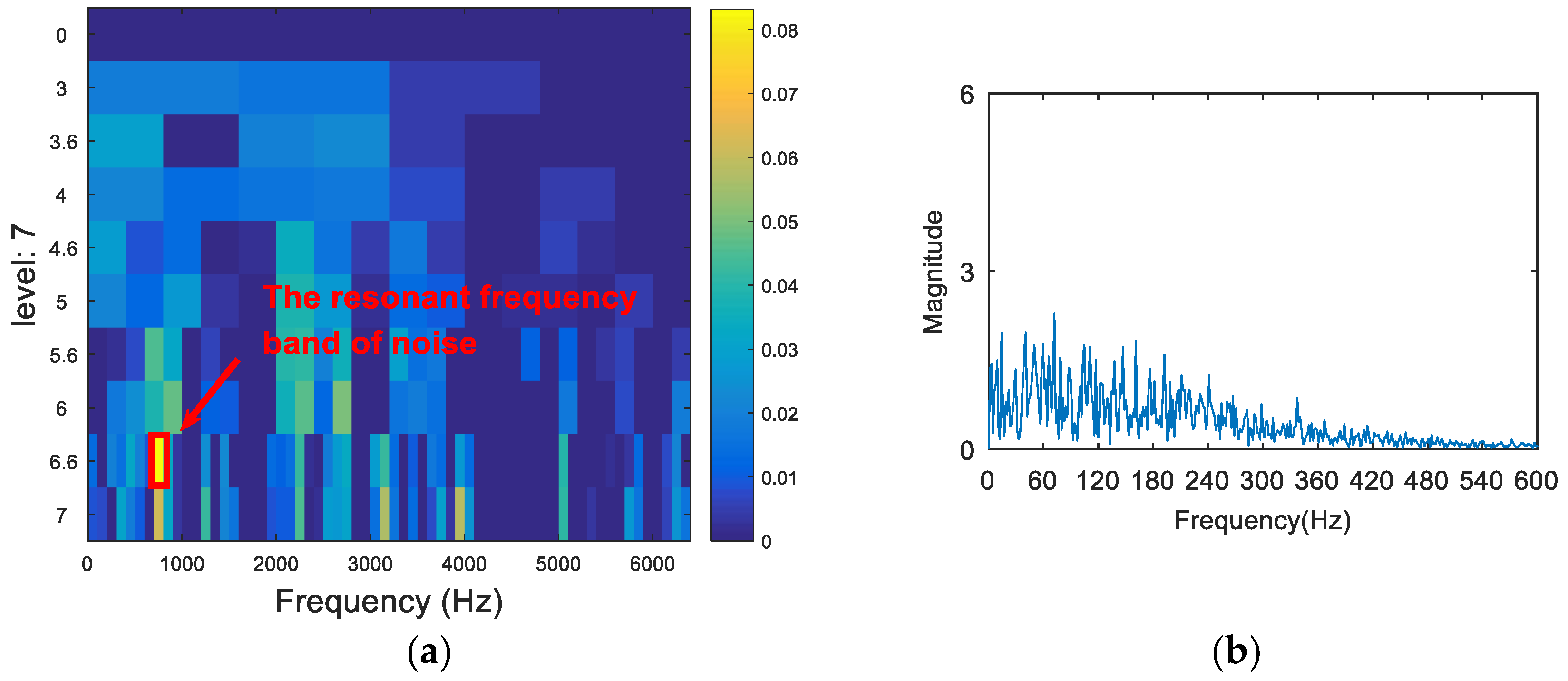
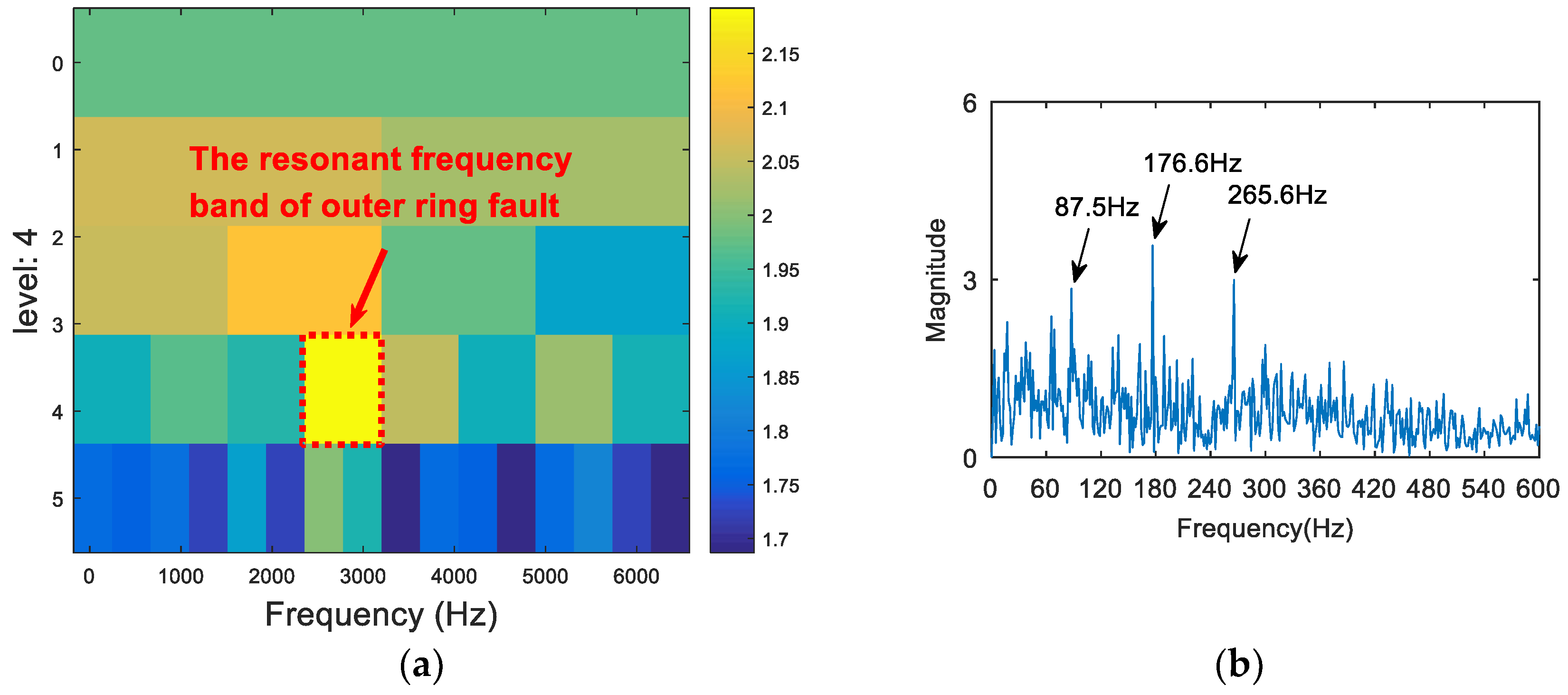
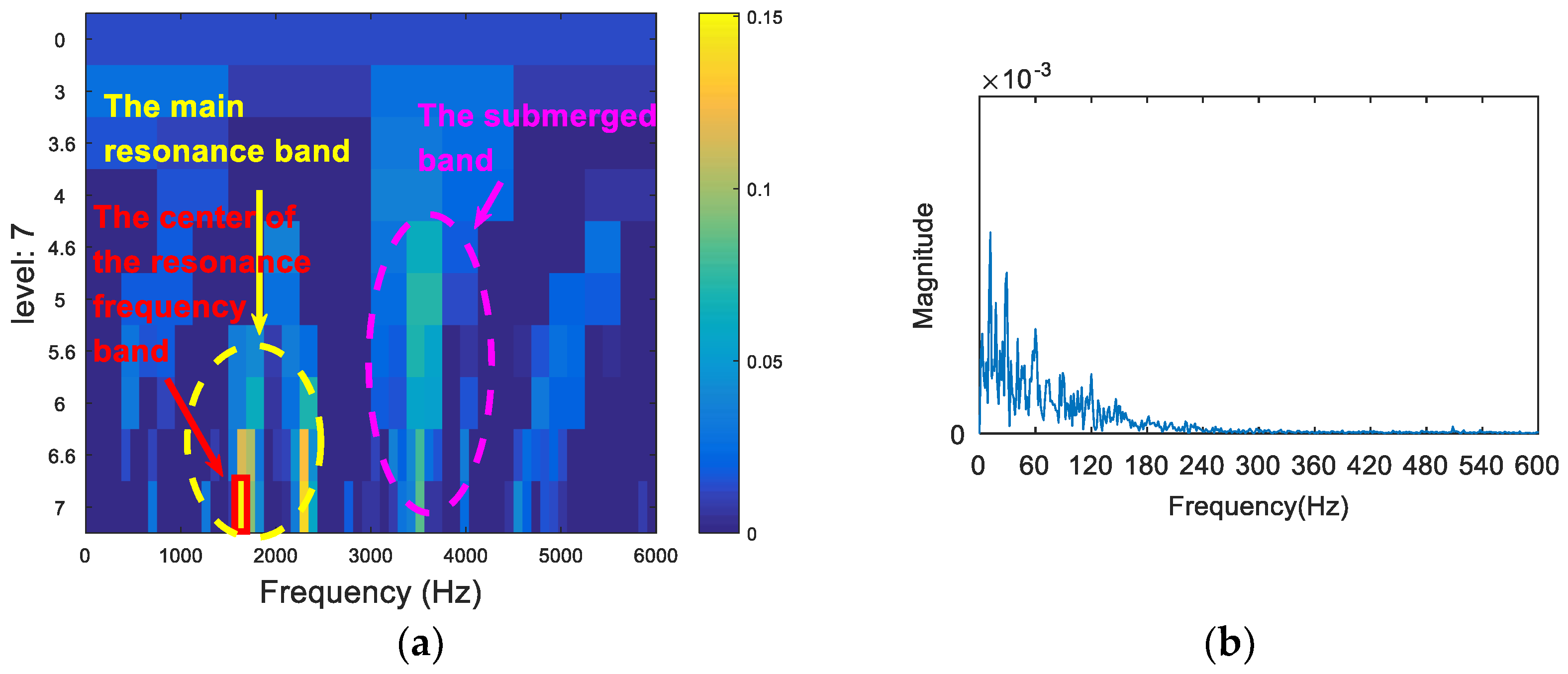
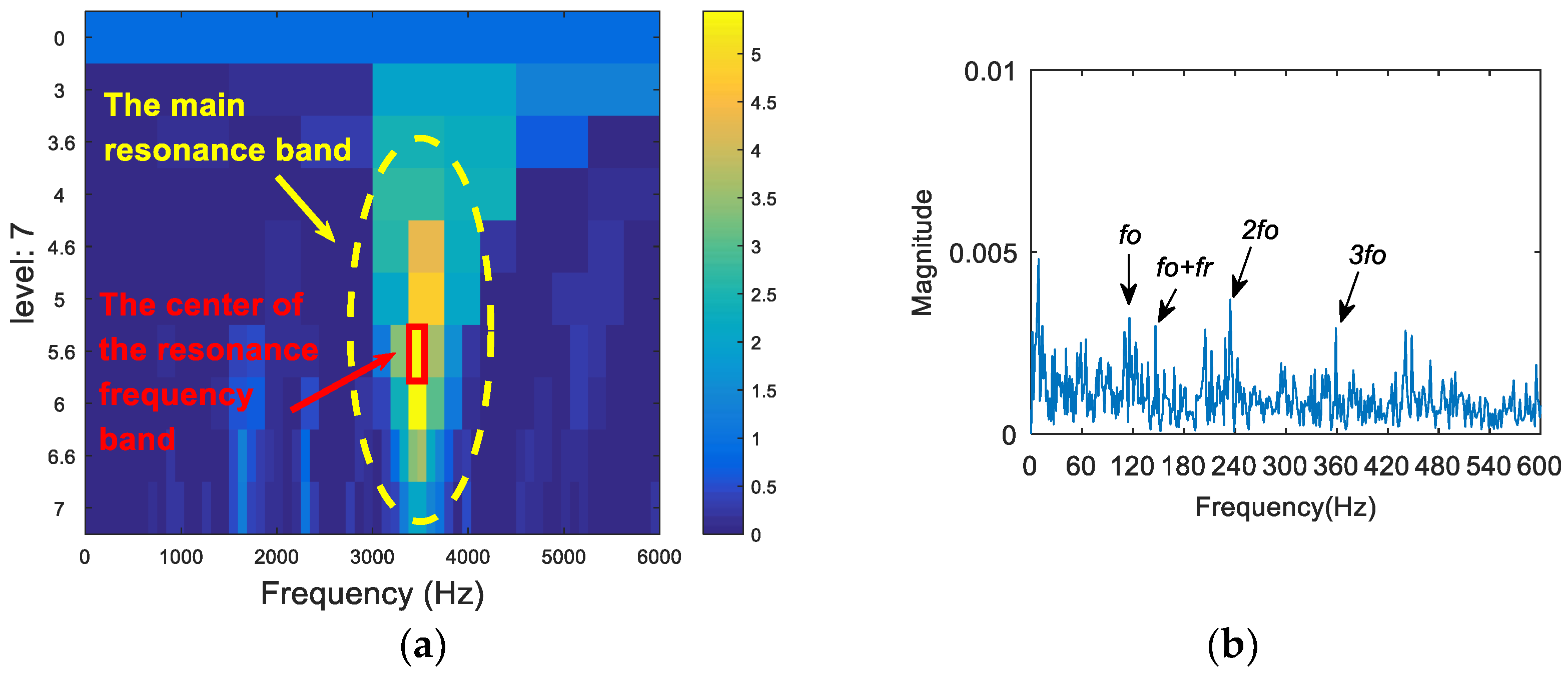
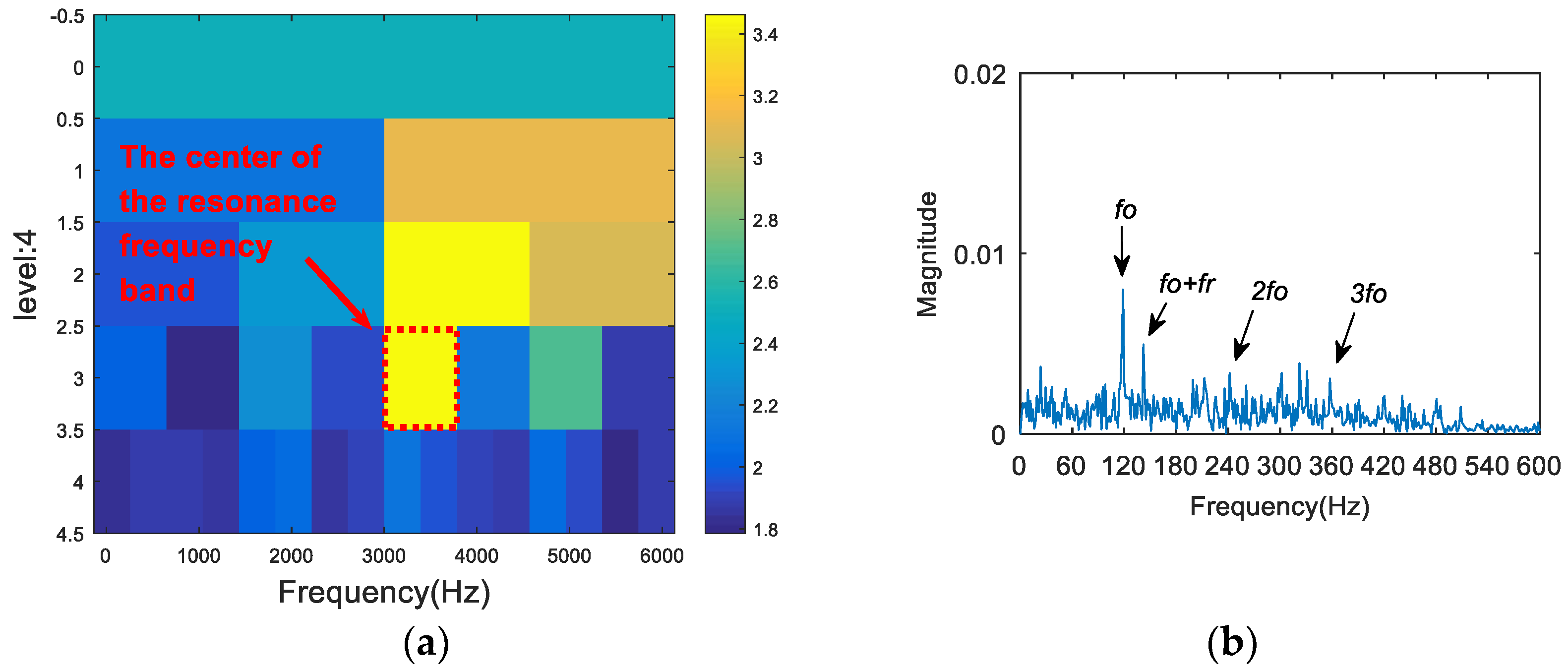
- We then generate an entropy spectrum with the inverse value () of the Shannon entropy of each wavelet packet. The subband of the maximum S value (the minimum Shannon entropy) is selected as the optimal resonance frequency band.
- IV
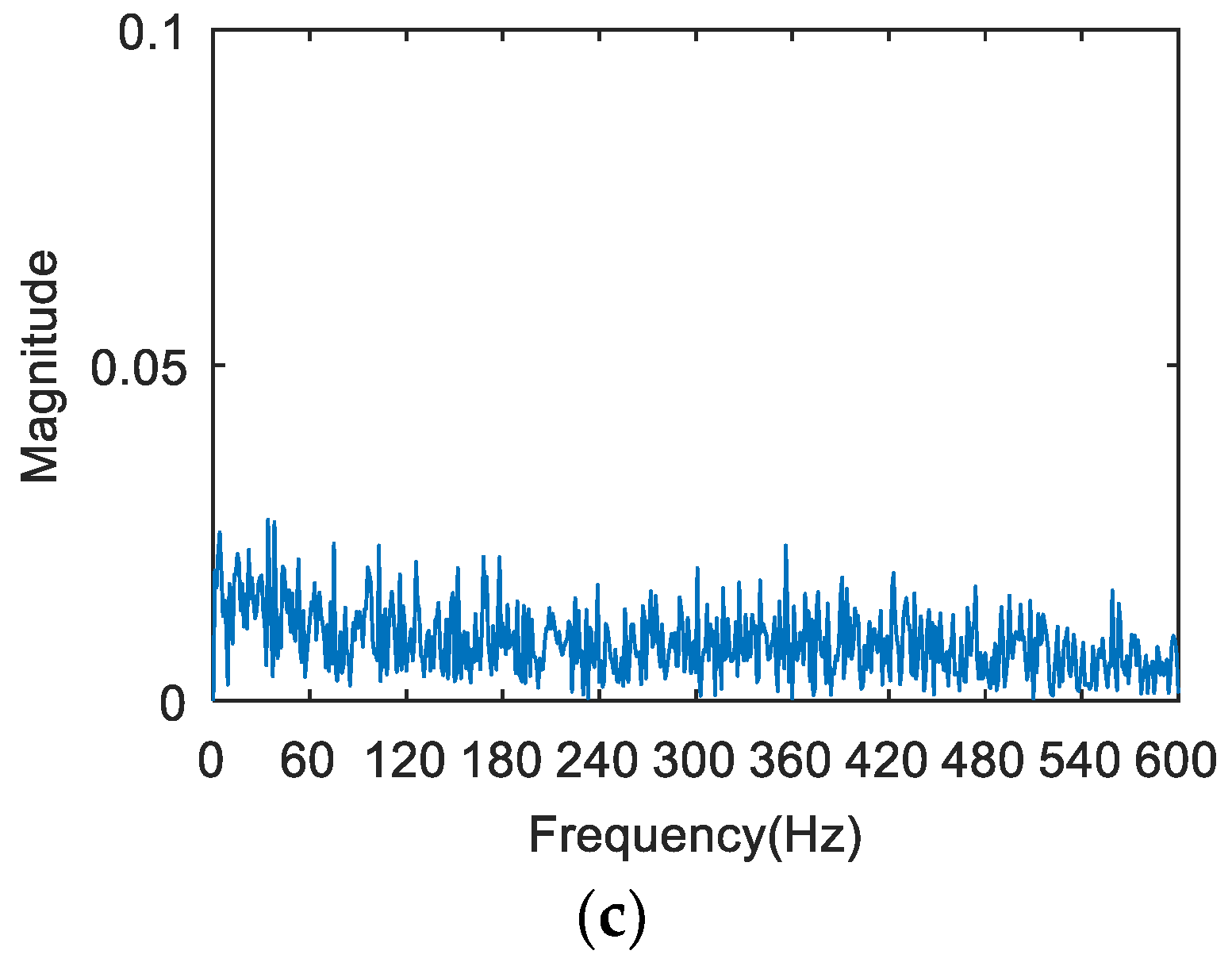
- The appropriate central frequency and bandwidth are selected to filter the resonance frequency band determined in (III). The envelope spectrum of the filtered signal is analyzed. Then, the characteristic spectral lines in the spectrum are compared with the theoretical frequency from (I), and the type of the fault is determined.
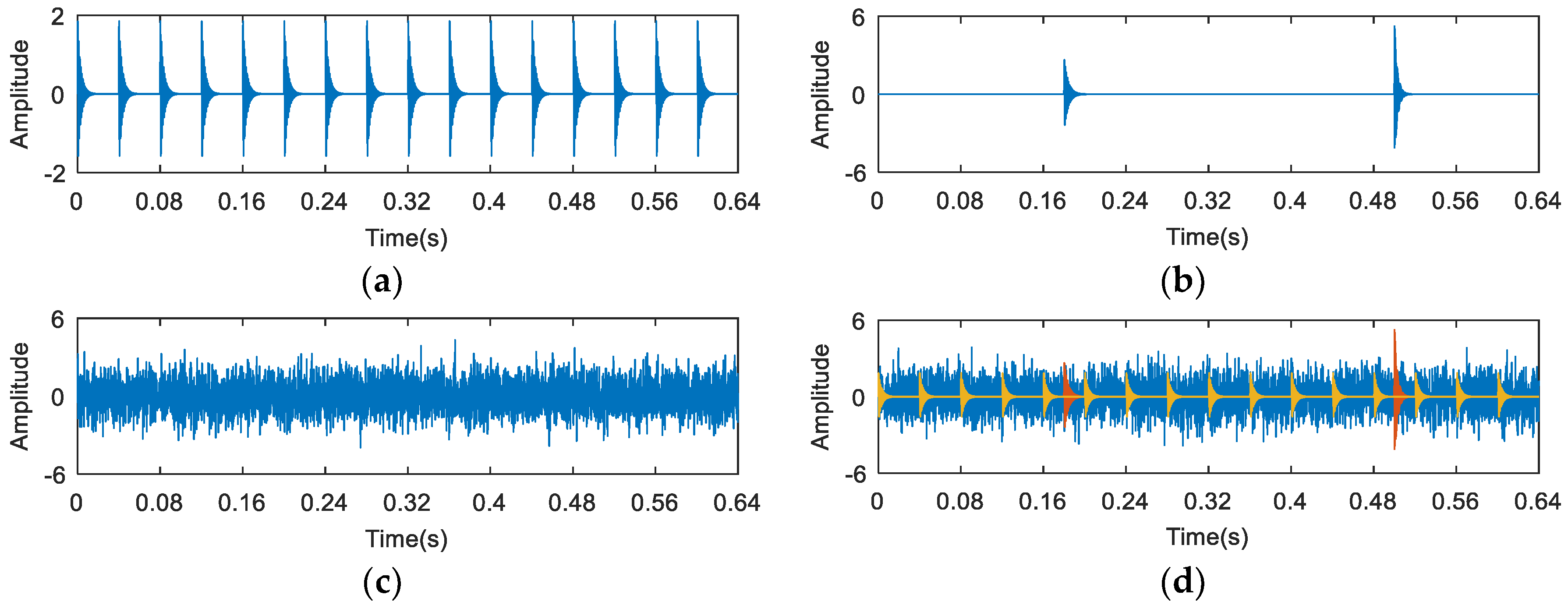
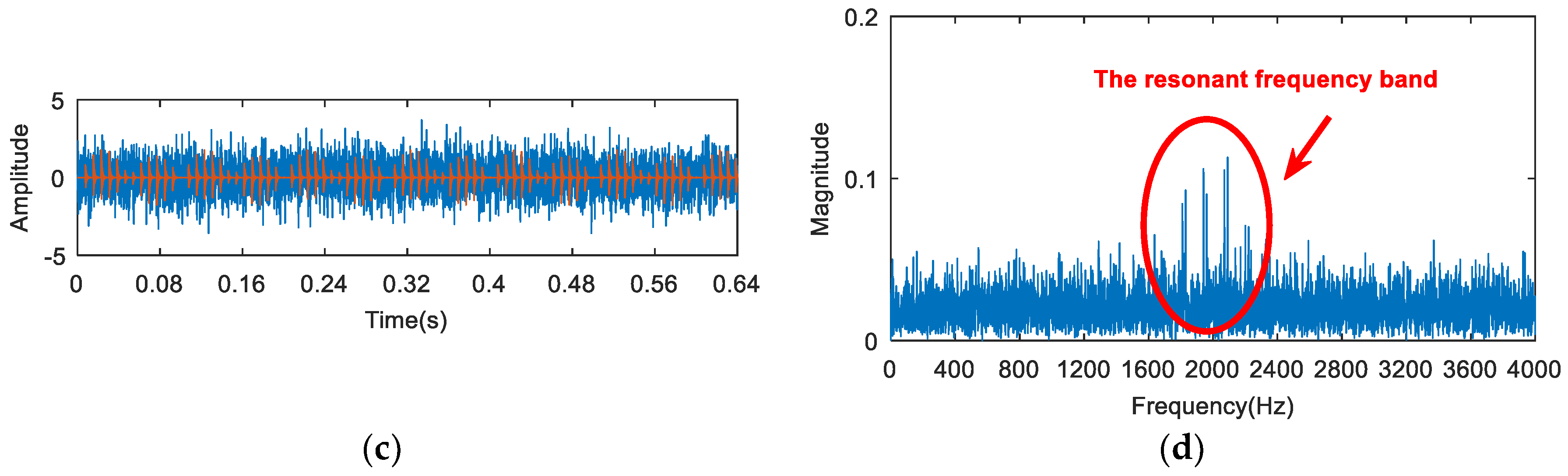
4. Simulation Analysis
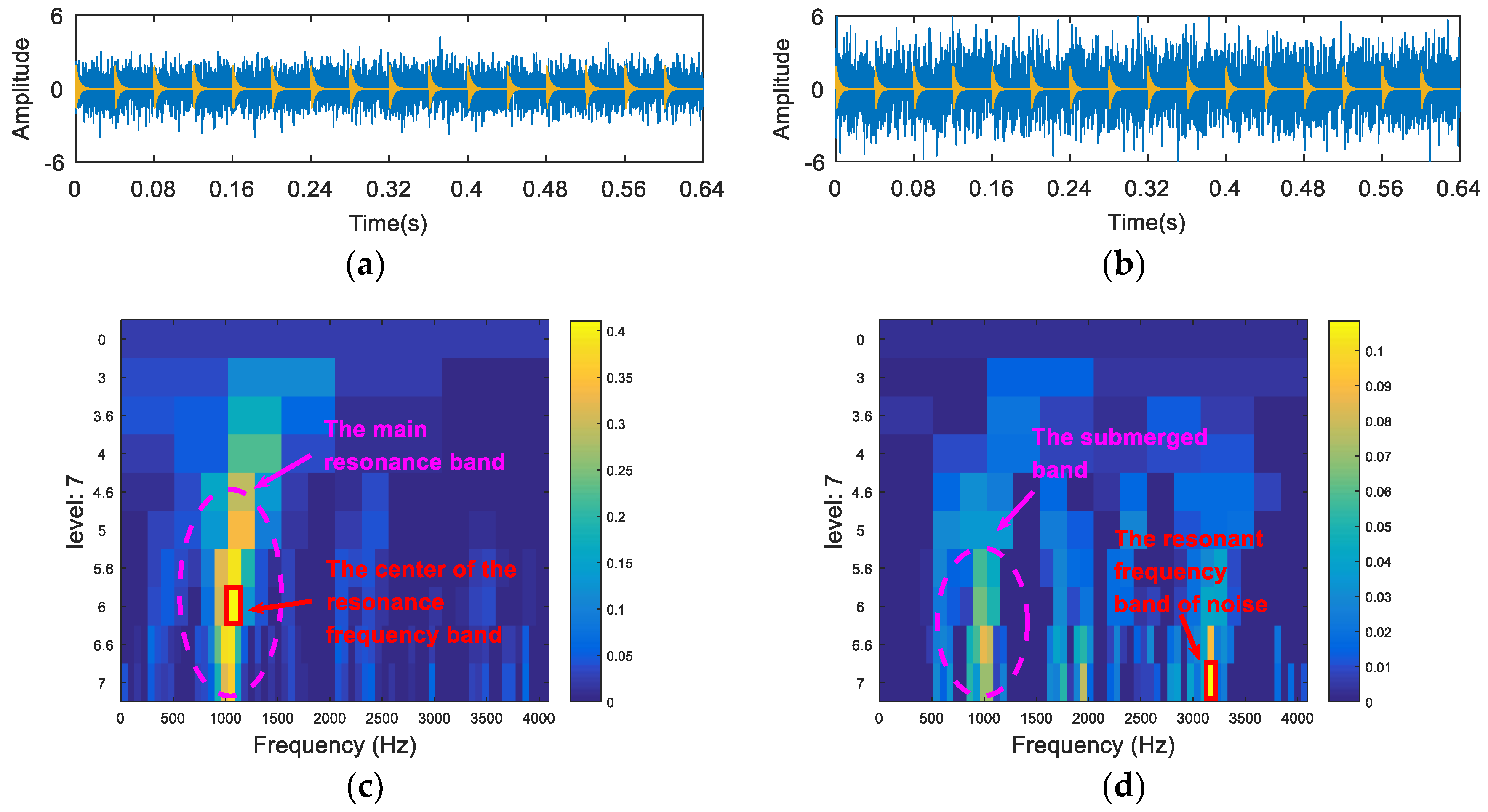
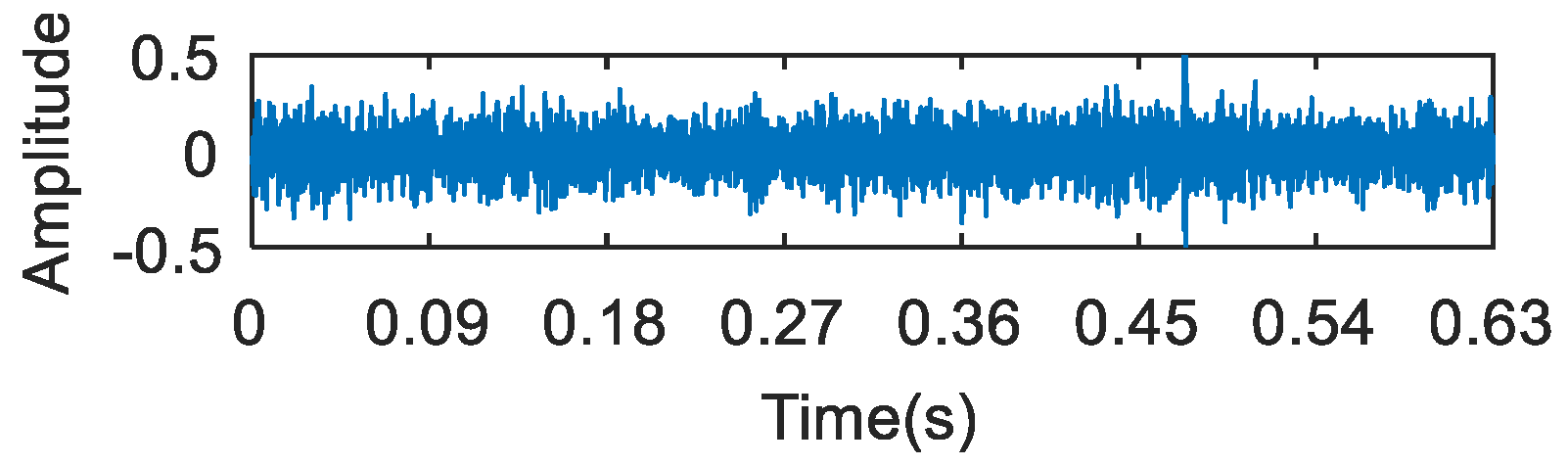
5. Experimental Analysis
5.1. Experiment 1
5.2. Experiment 2
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Antoni, J. The spectral kurtosis: A useful tool for characterising non-stationary signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Antoni, J.; Randall, R.B. The spectral kurtosis: Application to the vibratory surveillance and diagnostics of rotating machines. Mech. Syst. Signal Process. 2006, 20, 308–331. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, M. An adaptive SK technique and its application for fault detection of rolling element bearings. Mech. Syst. Signal Process. 2011, 25, 1750–1764. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; He, Z.; Zi, Y. Application of an improved kurtogram method for fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2011, 25, 1738–1749. [Google Scholar] [CrossRef]
- Wang, D.; Tse, P.W.; Tsui, K.L. An enhanced Kurtogram method for fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2013, 35, 176–199. [Google Scholar] [CrossRef]
- Tse, P.W.; Wang, D. The design of a new sparsogram for fast bearing fault diagnosis: Part 1 of the two related manuscripts that have a joint title as “Two automatic vibration-based fault diagnostic methods using the novel sparsity measurement—Parts 1 and 2”. Mech. Syst. Signal Process. 2013, 40, 499–519. [Google Scholar] [CrossRef]
- Tse, P.W.; Wang, D. The automatic selection of an optimal wavelet filter and its enhancement by the new sparsogram for bearing fault detection. Mech. Syst. Signal Process. 2013, 40, 520–544. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, Z.; Zi, Y.; He, Z.; Sun, C. Detecting of transient vibration signatures using an improved fast spatial–spectral ensemble kurtosis kurtogram and its applications to mechanical signature analysis of short duration data from rotating machinery. Mech. Syst. Signal Process. 2013, 40, 1–37. [Google Scholar] [CrossRef]
- Borghesani, P.; Pennacchi, P.; Chatterton, S. The relationship between kurtosis- and envelope-based indexes for the diagnostic of rolling element bearings. Mech. Syst. Signal Process. 2014, 43, 25–43. [Google Scholar] [CrossRef]
- Barszcz, T.; JabŁoński, A. A novel method for the optimal band selection for vibration signal demodulation and comparison with the Kurtogram. Mech. Syst. Signal Process. 2011, 25, 431–451. [Google Scholar] [CrossRef]
- Wang, D. Spectral L2/L1 norm: A new perspective for spectral kurtosis for characterizing non-stationary signals. Mech. Syst. Signal Process. 2018, 104, 290–293. [Google Scholar] [CrossRef]
- Villecco, F.; Pellegrino, A. Entropic Measure of Epistemic Uncertainties in Multibody System Models by Axiomatic Design. Entropy 2017, 19, 291. [Google Scholar] [CrossRef]
- Villecco, F.; Pellegrino, A. Evaluation of Uncertainties in the Design Process of Complex Mechanical Systems. Entropy 2017, 19, 475. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Ge, M.; Xiao, H.; Yu, X. Tensor Singular Spectrum Decomposition Algorithm Based on Permutation Entropy for Rolling Bearing Fault Diagnosis. Entropy 2017, 19, 139. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H.; Cheng, J. Rolling bearing fault detection and diagnosis based on composite multiscale fuzzy entropy and ensemble support vector machines. Mech. Syst. Signal Process. 2017, 85, 746–759. [Google Scholar] [CrossRef]
- Lei, M.; Meng, G.; Dong, G. Fault Detection for Vibration Signals on Rolling Bearings Based on the Symplectic Entropy Method. Entropy 2017, 19, 607. [Google Scholar] [CrossRef]
- Gao, Y.; Villecco, F.; Li, M.; Song, W. Multi-Scale Permutation Entropy Based on Improved LMD and HMM for Rolling Bearing Diagnosis. Entropy 2017, 19, 176. [Google Scholar] [CrossRef]
- Antoni, J. The infogram: Entropic evidence of the signature of repetitive transients. Mech. Syst. Signal Process. 2016, 74, 73–94. [Google Scholar] [CrossRef]
- Li, C.; Cabrera, D.; de Oliveira, J.V.; Sanchez, R.-V.; Cerrada, M.; Zurita, G. Extracting repetitive transients for rotating machinery diagnosis using multiscale clustered grey infogram. Mech. Syst. Signal Process. 2016, 76–77, 157–173. [Google Scholar] [CrossRef]
- Xu, X.; Qiao, Z.; Lei, Y. Repetitive transient extraction for machinery fault diagnosis using multiscale fractional order entropy infogram. Mech. Syst. Signal Process. 2018, 103, 312–326. [Google Scholar] [CrossRef]
- Wang, D. An extension of the infograms to novel Bayesian inference for bearing fault feature identification. Mech. Syst. Signal Process. 2016, 80, 19–30. [Google Scholar] [CrossRef]
- Wang, H.; Chen, J.; Dong, G. Fault diagnosis method for rolling bearing’s weak fault based on minimum entropy deconvolution and sparse decomposition. J. Mech. Eng. 2013, 49, 88–94. (In Chinese) [Google Scholar] [CrossRef]
- Bearing Data Center-Case Western Reserve University, Cleveland, OH, USA. Available online: http://www.eecs.case.edu/laboratory/ bearing (accessed on 15 July 2013).





| Parameter Type | Parameter Values |
|---|---|
| Amplitude A | 2 |
| Rotating frequency (Hz) | 20 |
| Natural frequency (Hz) | 1000 |
| Sampling frequency (Hz) | 8192 |
| Sampling points (Hz) | 8192 |
| Fault frequency (Hz) | 50 |
| Parameter Type | Parameter Values |
|---|---|
| Amplitude A | 1 |
| Rotating frequency (Hz) | 20 |
| Natural frequency (Hz) | 2000 |
| Sampling frequency (Hz) | 8192 |
| Sampling points (Hz) | 8192 |
| Fault frequency (Hz) | 130 |
| Parameter Type | Parameter Values |
|---|---|
| Inside Diameter (mm) | 25 |
| Outside Diameter (mm) | 52 |
| Ball Diameter (mm) | 7.9 |
| Pitch Diameter (mm) | 39 |
| Number of balls | 9 |
| Contact angle (°) | 0 |
| Parameter Type | Parameter Values |
|---|---|
| Inside Diameter (mm) | 17 |
| Outside Diameter (mm) | 40 |
| Ball Diameter (mm) | 6.7 |
| Pitch Diameter (mm) | 28.5 |
| Number of balls | 8 |
| Contact angle (°) | 0 |
| Types of Failures | Outer Ring | Inner Ring | Rolling Element |
|---|---|---|---|
| Defect frequencies (Hz) | 90 | 145 | 118 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, S.; Zhang, X.; Dou, L. Shannon Entropy of Binary Wavelet Packet Subbands and Its Application in Bearing Fault Extraction. Entropy 2018, 20, 260. https://doi.org/10.3390/e20040260
Wan S, Zhang X, Dou L. Shannon Entropy of Binary Wavelet Packet Subbands and Its Application in Bearing Fault Extraction. Entropy. 2018; 20(4):260. https://doi.org/10.3390/e20040260
Chicago/Turabian StyleWan, Shuting, Xiong Zhang, and Longjiang Dou. 2018. "Shannon Entropy of Binary Wavelet Packet Subbands and Its Application in Bearing Fault Extraction" Entropy 20, no. 4: 260. https://doi.org/10.3390/e20040260





