Performance Features of a Stationary Stochastic Novikov Engine
Abstract
:1. Introduction
2. Novikov Engine with Fluctuating Temperature of the Hot Bath
2.1. Classical Novikov Engine
2.2. Stochastic Novikov Engine
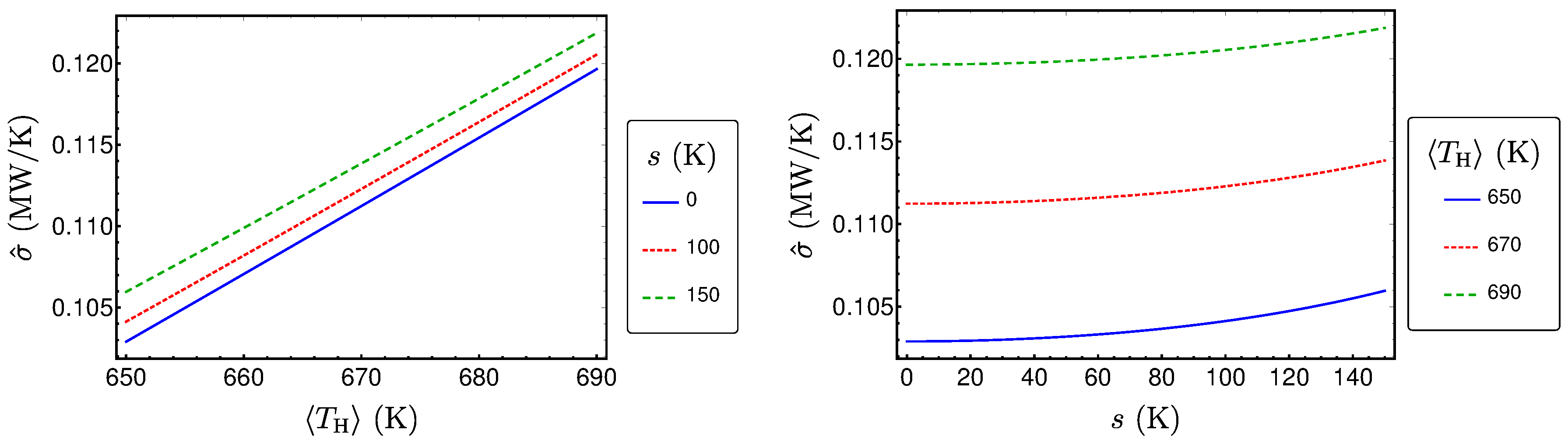
2.3. Reference Example
- The reference example is a heat engine working between a hot bath with temperature and a cold heat bath with temperature .
- has a mean value of .
- has a fixed value of .
- , so the power output is approximately at .
3. Influence of the Temperature Distribution
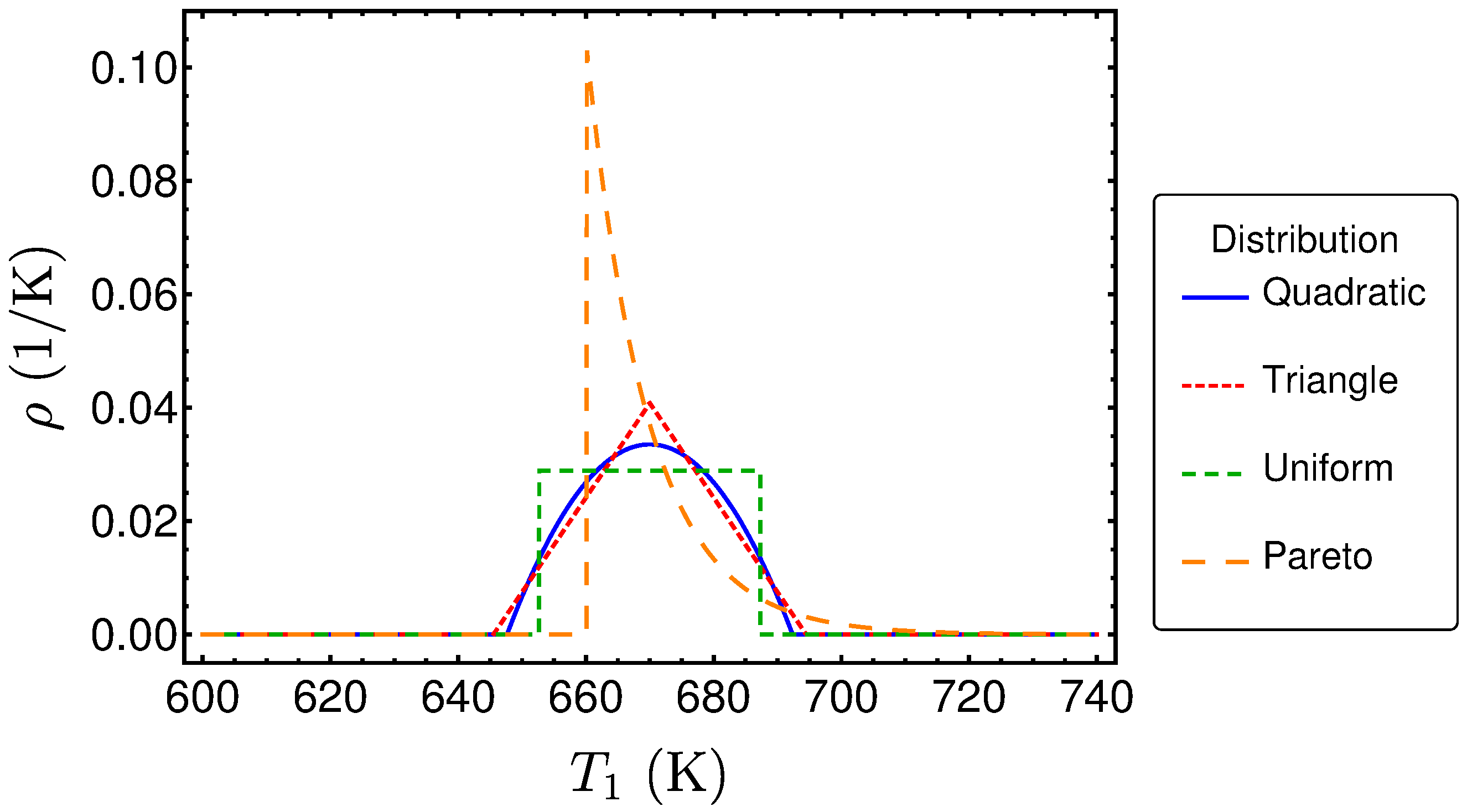
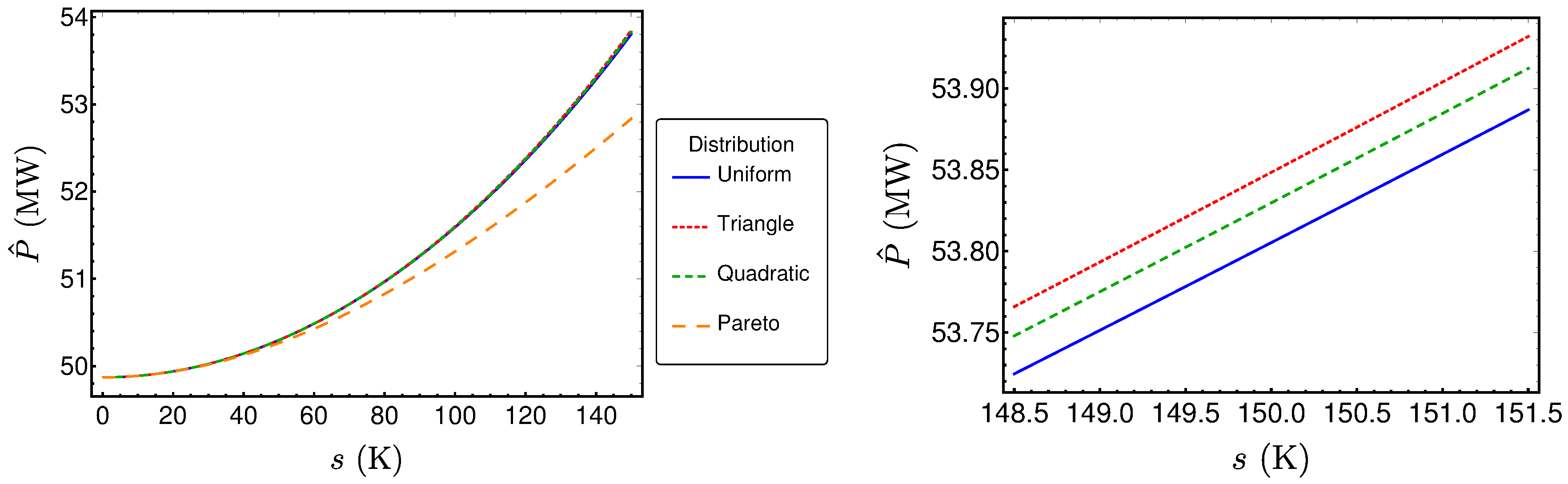
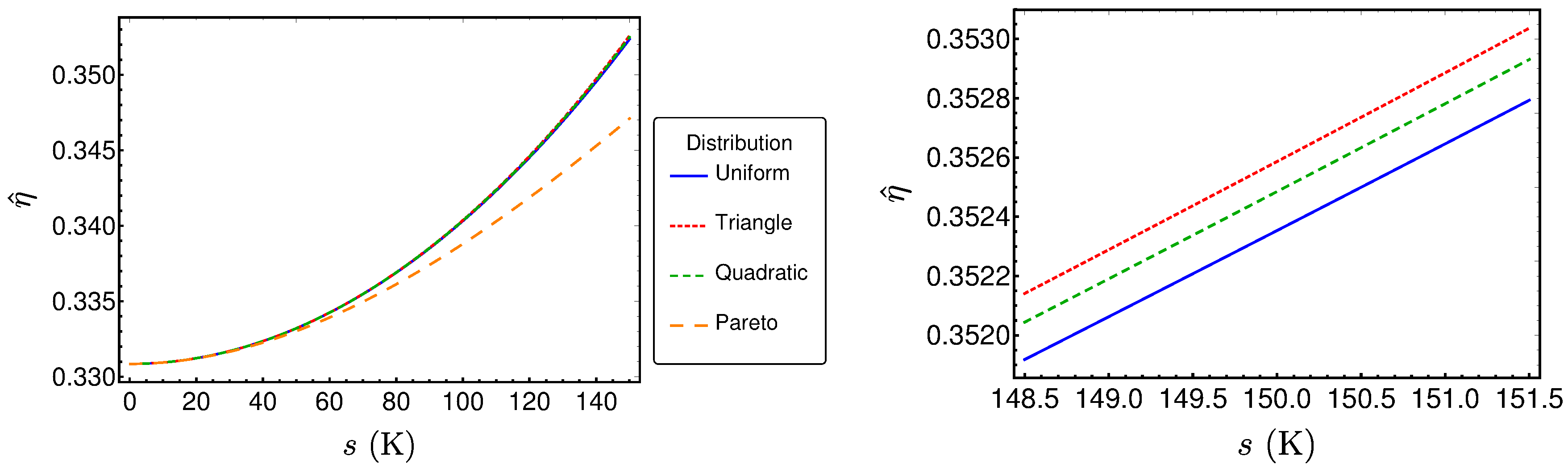
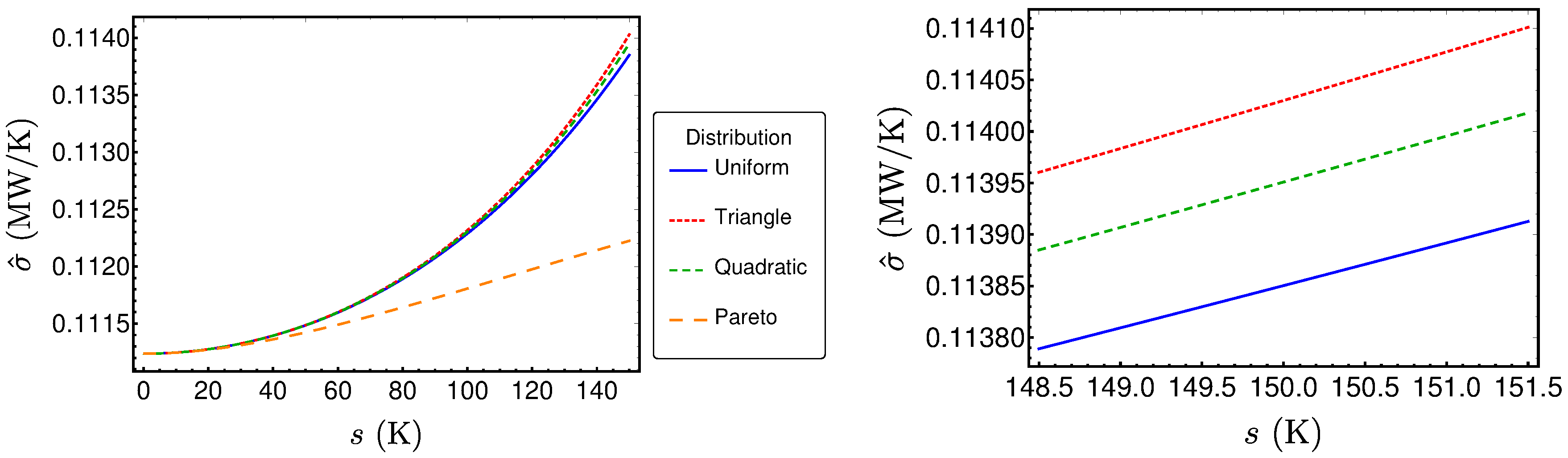
3.1. The Considered Distributions
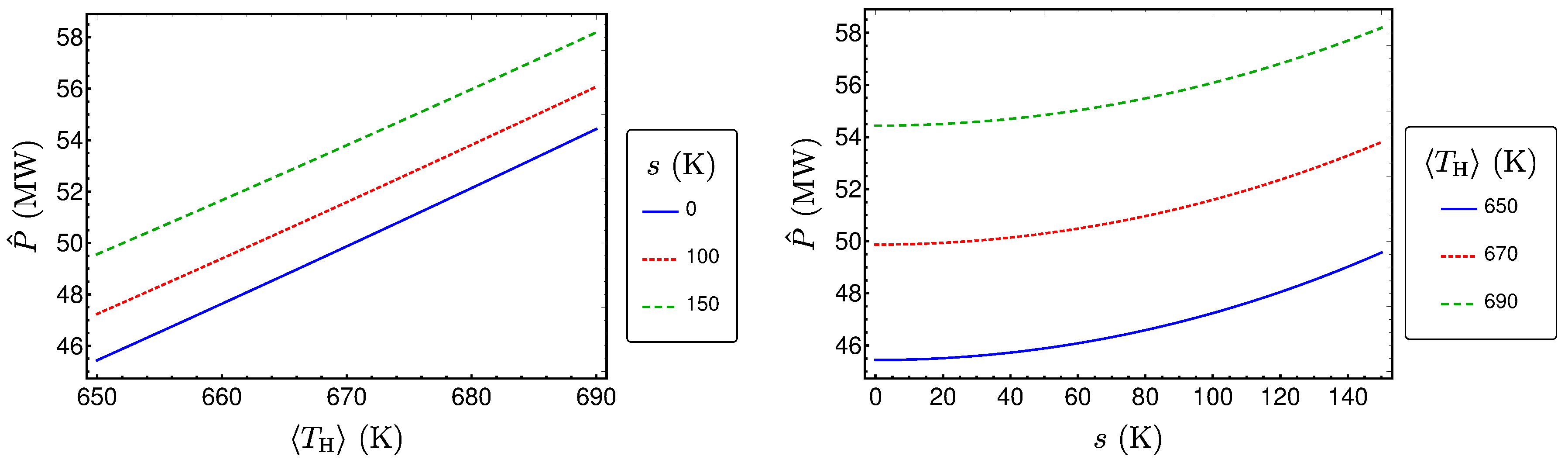
3.2. Performances Measures for the Uniform Distribution
3.3. Comparison of the Performance Measures for Different Distribution Shapes
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Reitlinger, H.B. Sur L’utilisation de la Chaleur Dans Les Machines á feu; Vaillant-Carmanne: Liége, Belgium, 1929. [Google Scholar]
- Chambadal, P. Le choix du cycle thermique dans une usine generatrice nucleaire. Rev. Gén. Électr. 1958, 67, 332–345. [Google Scholar]
- Novikov, I.I. The Efficiency of Atomic Power Stations. At. Energy 1957, 3, 409–412. (In Russian) [Google Scholar] [CrossRef]
- Novikov, I.I. The Efficiency of Atomic Power Stations. J. Nuclear Energy 1958, 7, 125–128. [Google Scholar]
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot Engine at Maximum Power Output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Hoffmann, K.H.; Burzler, J.M.; Fischer, A.; Schaller, M.; Schubert, S. Optimal Process Paths for Endoreversible Systems. J. Non-Equilib. Thermodyn. 2003, 28, 233–268. [Google Scholar] [CrossRef]
- Hoffmann, K.H.; Burzler, J.M.; Schubert, S. Endoreversible Thermodynamics. J. Non-Equilib. Thermodyn. 1997, 22, 311–355. [Google Scholar]
- De Vos, A. Endoreversible Thermodynamics of Solar Energy Conversion; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Fischer, A.; Hoffmann, K.H. Can a quantitative simulation of an Otto engine be accurately rendered by a simple Novikov model with heat leak? J. Non-Equilib. Thermodyn. 2004, 29, 9–28. [Google Scholar] [CrossRef]
- Bădescu, V. On the Theoretical Maximum Efficiency of Solar-Radiation Utilization. Energy 1989, 14, 571–573. [Google Scholar] [CrossRef]
- Bejan, A.; Kearney, D.W.; Kreith, F. Second Law Analysis and Synthesis of Solar Collector Systems. J. Sol. Energy Eng. 1981, 103, 23–28. [Google Scholar] [CrossRef]
- Carmago, M.C. Bases fisicas del aprovechamiento de la energia solar. Rev. Geophys. 1976, 35, 227–239. (In Spanish) [Google Scholar]
- Chen, J.; Andresen, B. The Maximum Coefficient of Performance of Thermoelectric Heat Pumps. Int. J. Ambient Energy 1996, 17, 22–28. [Google Scholar] [CrossRef]
- Chen, J.; Andresen, B. New bounds on the performance parameters of a thermoelectric generator. Int. J. Power Energy Syst. 1996, 16, 23–27. [Google Scholar]
- Chen, J. Thermodynamic Analysis of a Solar-Driven Thermoelectric Generator. J. Appl. Phys. 1996, 79, 2717–2721. [Google Scholar] [CrossRef]
- Gordon, J.M. Generalized Power Versus Efficiency Characteristics of Heat Engines: The Thermoelectric Generator as an Instructive Illustration. Am. J. Phys. 1991, 59, 551–555. [Google Scholar] [CrossRef]
- Müser, H. Thermodynamische Behandlung von Elektronenprozessen in Halbleiterrandschichten. Z. Phys. 1957, 148, 380–390. (In German) [Google Scholar] [CrossRef]
- Schwalbe, K.; Fischer, A.; Hoffmann, K.H.; Mehnert, J. Applied endoreversible thermodynamics: Optimization of powertrains. In Proceedings of the 27th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, Turku, Finland, 15–19 June 2014; Zevenhouen, R., Ed.; Åbo Akademi University: Turku, Finland, 2014; pp. 45–55. [Google Scholar]
- De Vos, A. Reflections on the power delivered by endoreversible engines. J. Phys. D Appl. Phys. 1987, 20, 232–236. [Google Scholar] [CrossRef]
- De Vos, A. Endoreversible Thermodynamics and Chemical Reactions. J. Chem. Phys. 1991, 95, 4534–4540. [Google Scholar] [CrossRef]
- De Vos, A. Is a solar cell an edoreversible engine? Sol. Cells 1991, 31, 181–196. [Google Scholar] [CrossRef]
- Wu, C. Performance of solar-pond thermoelectric power generators. Int. J. Ambient Energy 1995, 16, 59–66. [Google Scholar] [CrossRef]
- Wu, C. Analysis of Waste-Heat Thermoelectric Power Generators. Appl. Therm. Eng. 1996, 16, 63–69. [Google Scholar] [CrossRef]
- Kojima, S. Maximum Work of Free-Piston Stirling Engine Generators. J. Non-Equilib. Thermodyn. 2017, 42, 169–186. [Google Scholar] [CrossRef]
- Kojima, S. Theoretical Evaluation of the Maximum Work of Free-Piston Engine Generators. J. Non-Equilib. Thermodyn. 2017, 42, 31–58. [Google Scholar] [CrossRef]
- Páez-Hernández, R.T.; Portillo-Díaz, P.; Ladino-Luna, D.; Ramírez-Rojas, A.; Pacheco-Paez, J.C. An analytical study of the endoreversible Curzon-Ahlborn cycle for a non-linear heat transfer law. J. Non-Equilib. Thermodyn. 2016, 41, 19–27. [Google Scholar] [CrossRef]
- Özel, G.; Açıkkalp, E.; Savaş, A.F.; Yamık, H. Comparative Analysis of Thermoeconomic Evaluation Criteria for an Actual Heat Engine. J. Non-Equilib. Thermodyn. 2016, 41, 225–235. [Google Scholar] [CrossRef]
- Wagner, K.; Hoffmann, K.H. Endoreversible modeling of a PEM fuel cell. J. Non-Equilib. Thermodyn. 2015, 40, 283–294. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, J.; Lin, G.; Chen, J. Universal Optimization Efficiency for Nonlinear Irreversible Heat Engines. J. Non-Equilib. Thermodyn. 2017, 42, 253–263. [Google Scholar] [CrossRef]
- Kowalski, G.J.; Zenouzi, M.; Modaresifar, M. Entropy production: Iintegrating renewable energy sources into sustainable energy solutions. In Proceedings of the 12th Joint European Thermodynamics Conference, JETC 2013, Brescia, Italy, 1–5 July 2013; Pilotelli, M., Beretta, G.P., Eds.; Cartolibreria SNOOPY s.n.c.: Brescia, Italy, 2013; pp. 25–32. [Google Scholar]
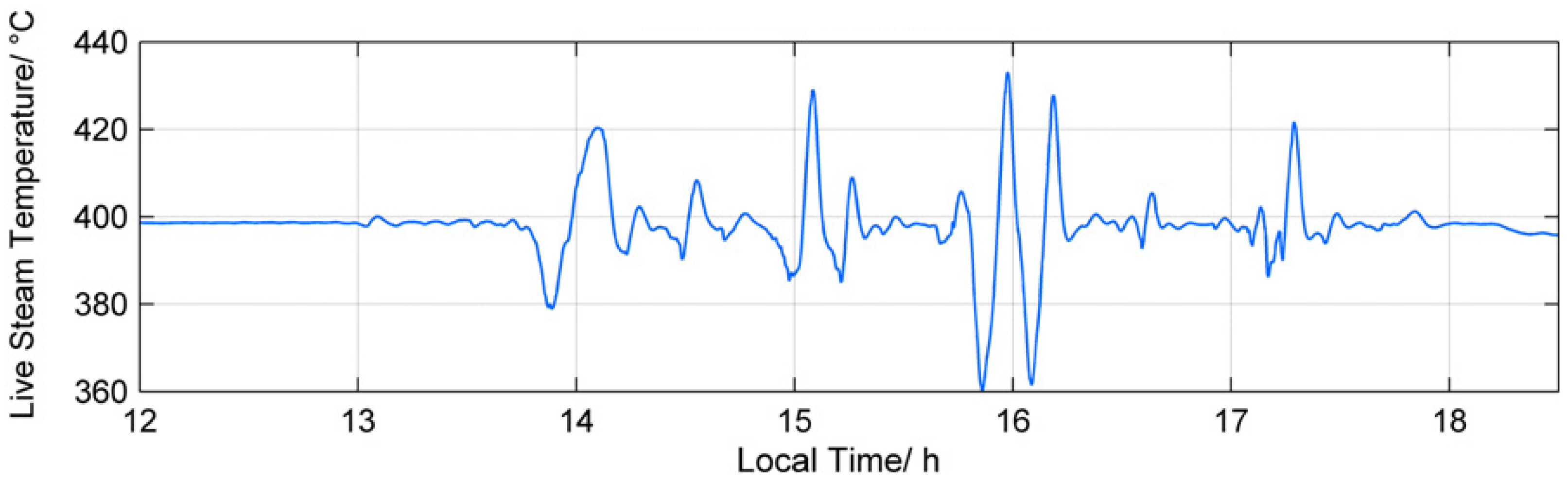
- Birnbaum, J.; Feldhoff, J.F.; Fichtner, M.; Hirsch, T.; Jöcker, M.; Pitz-Paal, R.; Zimmermann, G. Steam temperature stability in a direct steam generation solar power plant. Sol. Energy 2011, 85, 660–668. [Google Scholar] [CrossRef] [Green Version]
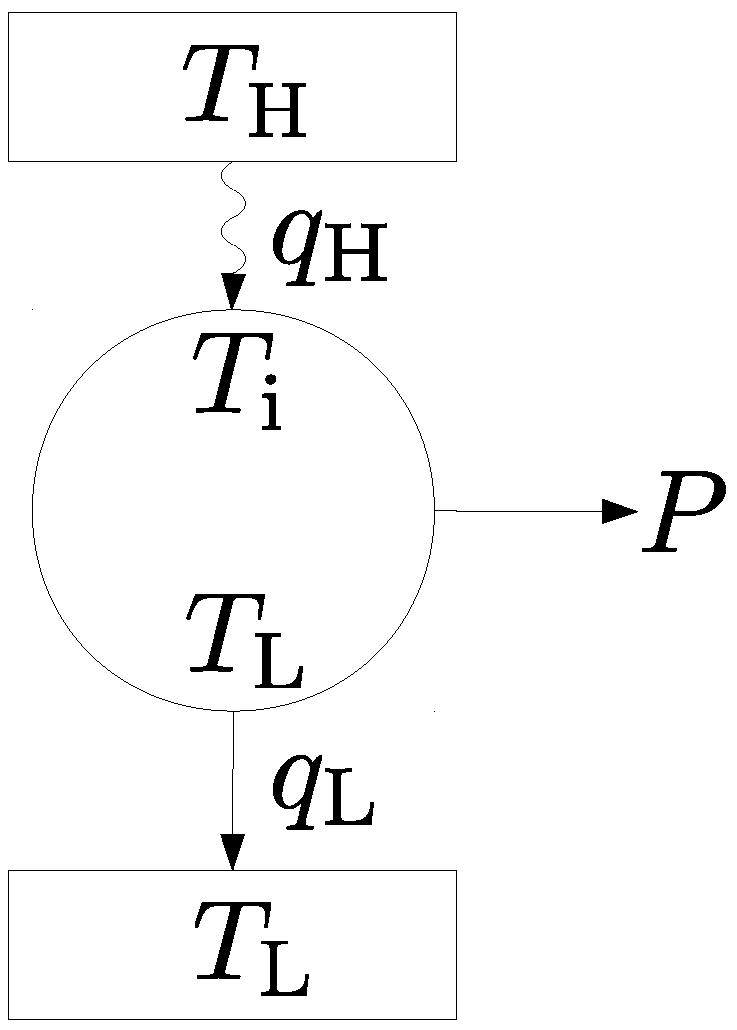

| Degree | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Uniform | 0 | 0 | |||
| Triangle | 0 | 0 | |||
| Quadratic | 0 | 0 | |||
| Pareto | 0 |
| Degree | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Uniform | 0 | 0 | |||
| Triangle | 0 | 0 | |||
| Quadratic | 0 | 0 | |||
| Pareto | 0 | * | * |
| Degree | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Uniform | 0 | 0 | |||
| Triangle | 0 | 0 | |||
| Quadratic | 0 | 0 | |||
| Pareto | 0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schwalbe, K.; Hoffmann, K.H. Performance Features of a Stationary Stochastic Novikov Engine. Entropy 2018, 20, 52. https://doi.org/10.3390/e20010052
Schwalbe K, Hoffmann KH. Performance Features of a Stationary Stochastic Novikov Engine. Entropy. 2018; 20(1):52. https://doi.org/10.3390/e20010052
Chicago/Turabian StyleSchwalbe, Karsten, and Karl Heinz Hoffmann. 2018. "Performance Features of a Stationary Stochastic Novikov Engine" Entropy 20, no. 1: 52. https://doi.org/10.3390/e20010052




