Content Delivery in Fog-Aided Small-Cell Systems with Offline and Online Caching: An Information—Theoretic Analysis
Abstract
:1. Introduction
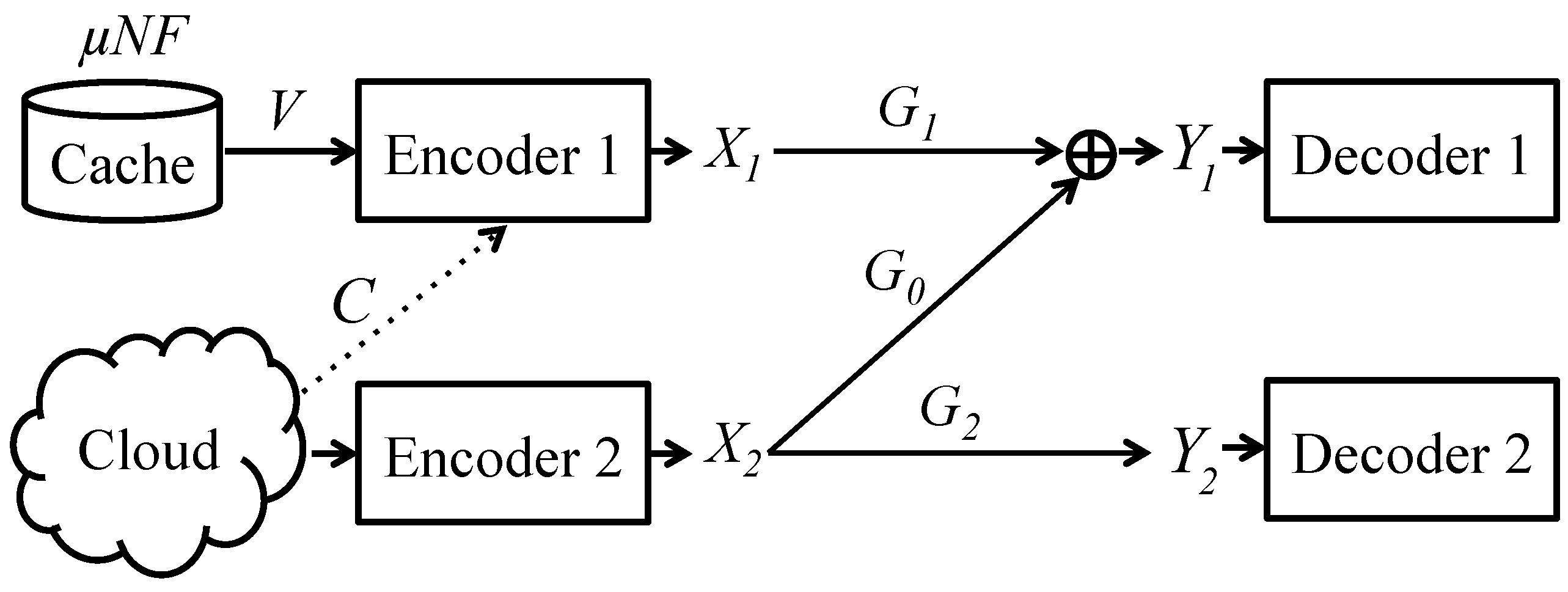
- An information-theoretic formulation for the analyses of the system in Figure 1 is presented that centers on the characterization of the minimum delivery coding latency measured in terms of the Delivery Time per Bit (DTB), for both offline and online caching. The system model is based on a one-sided interference channel.
- Assuming a fixed set of popular contents, the minimum DTB for the system in Figure 1 is obtained as a function of the cache capacity at Encoder 1 and the capacity of the backhaul link that connects the cloud to Encoder 1 in the offline setting.
- Online caching and delivery schemes based on both reactive and proactive caching principles (see, e.g., [2]) are proposed in the presence of a time-varying set of popular files, and bounds on the corresponding achievable long-term DTBs are derived.
- A lower bound on the achievable long-term DTB is obtained, which is a function of the time-variability of the set of popular files. The lower bound is then utilized to compare the achievable DTBs under offline and online caching.
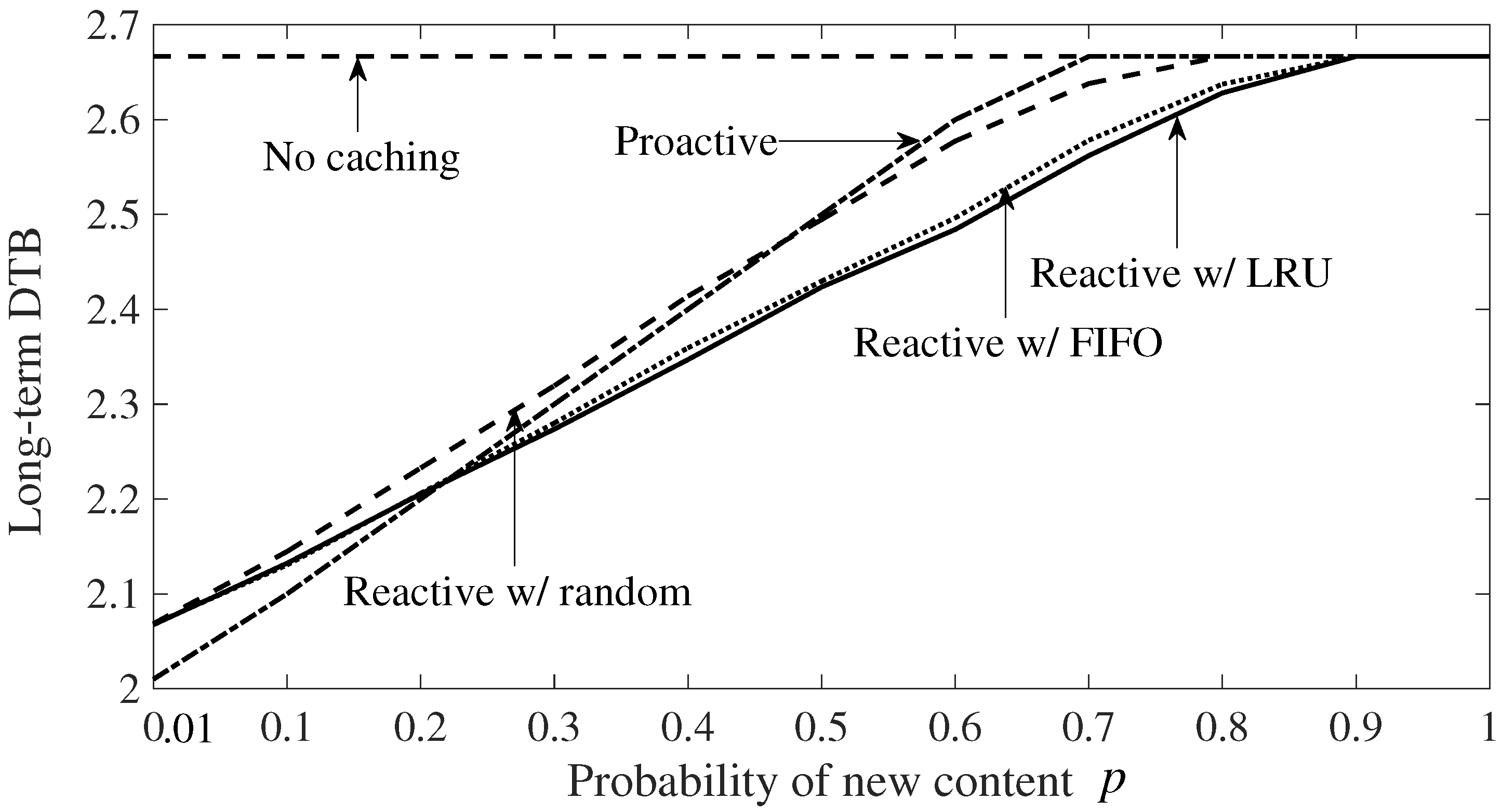
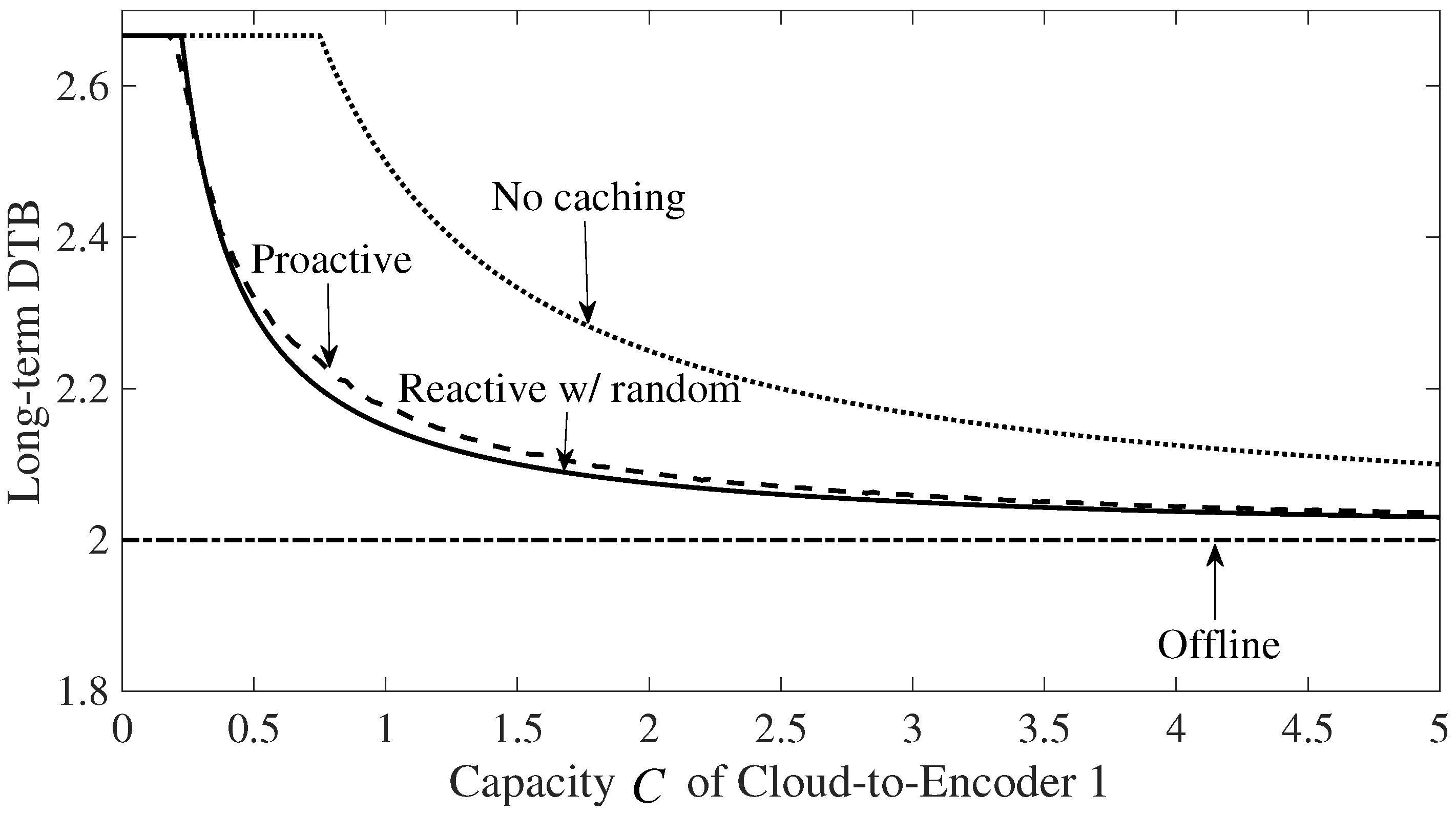
- Numerical results are provided in which the DTB performance of reactive and proactive online caching schemes is compared with offline caching. In addition, different eviction mechanisms, such as random eviction, Least Recently Used (LRU) and First In First Out (FIFO) (see, e.g., [24]), are evaluated.
2. System Model for Offline Caching
2.1. Edge-Aided Offline Caching
- (1)
- Placement phase: The placement phase is defined by functions , at Encoder 1, which maps each file to its cached versionTo satisfy cache storage constraint, it is required thatThe total cache content at Encoder 1 is given byNote that, as in [5,11], we concentrate on caching strategies that allow for arbitrary intra-file coding but not for inter-file coding as per (2). Furthermore, the caching policy is kept fixed over multiple transmission intervals and is thus independent of the receivers’ requests and of the channel realizations in the transmission intervals.
- (2)
- Delivery phase: The delivery phase is in charge of satisfying the given request vector in each transmission interval given the current channel realization. We assume the availability of full Channel State Information (CSI) throughout the transmission block for simplicity of exposition, although this is not required by achievable schemes that will be proven to be optimal (see Remark 1). Note that in practice non-causal CSI for the coding block can be justified for multi-carrier transmission schemes, such as OFDM, in which index t runs over the subcarriers. It is defined by the following two functions.
- Encoding: Encoder 1 uses the encoding functionwhich maps the cached content V, the demand vector and the CSI sequence to the transmitted codeword . Note that T represents the duration of transmission in channel uses. Encoder 2 uses the following encoding functionwhich maps the library of all files, the demand vector , and the CSI vector to the transmitted codeword .
- Decoding: Each decoder is defined by the following mappingwhich outputs the detected message where is the received signal (1) at receiver j.
2.2. Cloud and Edge-Aided Offline Caching
3. Minimum DTB under Offline Caching
3.1. Edge-Aided System ()
Proof of Achievability
- No Caching : We first consider the corner point . In this setting, in which Encoder 1 has no caching capabilities, the model reduces to a broadcast erasure channel from Encoder 2 to both decoders. The worst-case demand vector is any one in which the decoders request different files. In fact, if the same file is requested, it can always be treated as two distinct files achieving the same latency as for a scenario with distinct files. Focusing on this worst-case scenario, we adopt the following delivery policy.Encoder 1 always transmits . Encoder 2 transmits 1 bit of information to Decoder 1 in the states and , in which the channel from Encoder 2 to Decoder 1 is on while the channel to Decoder 2 is off. It transmits 1 bit of information to Decoder 2 in the states and , in which the channel to Decoder 2 is on while the channel to decoder 1 is off. Instead, in states and , in which both channels to Decoder 1 and Decoder 2 are on, Encoder 2 transmits 1 bit of information to Decoder 1 or to Decoder 2 with equal probability.Consider now the time required for Decoder 1 to decode successfully F bits. We can write this random variable aswhere denotes the number of channel uses required to transmit the kth bit. Given the discussion above, the variables are independent for and have a Geometric distribution with mean (Pr+ Pr + Pr + Pr. By the strong law of large numbers we now have the limitwith probability 1. In a similar manner, the resulting delivery time for Decoder 2 for any given bit has a Geometric distribution with mean (Pr + Pr + Pr + Pr; and, by the strong law of large numbers, we obtain that the time needed to transmit F bits to Decoder 2 satisfies the limit almost surely. Using this limit along with (17) allows to conclude that there exists a sequence of policies with for any arbitrarily small probability of error.
- Partial Caching with : Next, we consider the corner point under the condition . In this case, in which Encoder 1 has a better channel than Decoder 2 in the average sense discussed above, our findings show that Encoder 2 should communicate to Decoder 1 only in the channel states in which the channel to Decoder 2 is off. Using these states, Encoder 2 sends bits to Decoder 1. Encoder 1 cache a fraction of each file in the library and delivers bits of the requested file to Decoder 1. For this purpose, coordination between Encoder 1 and Encoder 2 is needed to manage interference in the state in which all links are on.A detailed description of the transmission strategy is provided below as a function of the channel state .
- (1)
- : Only the channel between Encoder 2 and Decoder 2 is active, and Encoder 2 transmits 1 bit of information to Decoder 2.
- (2)
- : The only active channel is between Encoder 1 and Decoder 1, and Encoder 1 transmits 1 information bit to Decoder 1.
- (3)
- : The cross channel is off, and each encoder transmits 1 bit of information to its decoder.
- (4)
- : Only the channel between Encoder 2 and Decoder 1 is active, and Encoder 2 transmits 1 bit of information to Decoder 1.
- (5)
- : The direct channel between Encoder 1 and Decoder 1 is off, while two other channels are on. Encoder 2 transmits 1 bit of information to Decoder 2.
- (6)
- : Both channels from Encoder 1 and Encoder 2 to Decoder 1 are on. Encoder 1 transmits and Encoder 2 transmits 1 bit of information to Decoder 1.
- (7)
- : Encoder 2 transmits 1 bit of information to Decoder 2. Encoder 1 transmits , where is an information bit for Decoder 1. This form of coordination is enabled by the fact that Encoder 1 knows the bit , since it is part of the cached bits from the file requested by Decoder 2. In this way, interference from Encoder 2 is cancelled at Decoder 1.
From the discussion above, Encoder 2 transmits 1 bit of information to Decoder 2 in the states (1), (3), (5) and (7). For large F, the normalized transmission delay for transmitting the requested file to Decoder 2 is then equal toFurthermore, Encoder 2 transmits bits to decoder 1 in the states at (4) and (6). The required normalized time for large F is henceFinally, Encoder 1 transmits bits to Decoder 1 in the states at (2), (3) and (7). The required time is thusIt can be shown that under the given condition , and hence the DTB is given by max . - Partial Caching () with : Finally, we consider the corner point under the complementary condition , in which Encoder 2 has better channels to the decoders. In this case, as above, Encoder 1 caches a fraction of all files. Transmission take place as described in the previous case except for state (5) which is modified as follows: (5) : Encoder 2 transmits 1 bit of information to either Decoder 1 or Decoder 2 with probabilities and , respectively.
3.2. Cloud and Edge-Aided System ()
Proof of Achievability
4. Online Caching
4.1. System Model
4.2. Proactive Online Caching
4.3. Reactive Online Caching
4.4. Lower Bound on the Minimum Long-Term DTB
5. Comparison between Online and Offline Caching
6. Numerical Results
7. Conclusions
Author Contributions
Conflicts of Interest
Appendix A. Proof of Converse for Proposition 1
Appendix B. Proof of Converse for Proposition 2
- For , the bound (A10), directly yields
Appendix C. Proof of Proposition 5
- For , the bound (A14), directly yields
Appendix D. Proof of Proposition 6
- Low capacity regime (): In this regime, using Propositions 2 and 5, the lower bound isTo prove the upper bound, we consider the following two sub-regimes
- −
- Low cache regime (): In this case, using Proposition 2 and (A21), we haveUsing Proposition 2, the minimum offline DTB is and therefore we havewhere follows from and follows from .
- −
Appendix E. Proof for Lemma A1
- Medium-cache Regime (): Using (24), we have the following upper boundwhere is obtained by omitting the negative terms.
References
- Shanmugam, K.; Golrezaei, N.; Dimakis, A.G.; Molisch, A.F.; Caire, G. Femtocaching: Wireless content delivery through distributed caching helpers. IEEE Trans. Inf. Theory 2013, 59, 8402–8413. [Google Scholar] [CrossRef]
- Bastug, E.; Bennis, M.; Debbah, M. Living on the edge: The role of proactive caching in 5G wireless networks. IEEE Commun. Mag. 2014, 52, 82–89. [Google Scholar] [CrossRef] [Green Version]
- Maddah-Ali, M.A.; Niesen, U. Cache Aided Interference Channels. 2015. Available online: http://arxiv.org/abs/1510.06121 (accessed on 21 October 2015).
- Maddah-Ali, M.A.; Niesen, U. Cache aided interference channels. In Proceedings of the 2015 IEEE International Symposium on Information Theory (ISIT), Hong Kong, China, 7–12 July 2015; pp. 809–813. [Google Scholar]
- Sengupta, A.; Tandon, R.; Simeone, O. Cache-aided wireless networks: Tradeoffs between storage and latency. In Proceedings of the Annual Conference on Information Science and Systems (CISS), Princeton, NJ, USA, 16–18 March 2016; pp. 320–325. [Google Scholar]
- Naderializadeh, N.; Maddah-Ali, M.A.; Avestimehr, A.S. Fundamental limits of cache-aided interference management. IEEE Trans. Inf. Theory 2017, 63, 3092–3107. [Google Scholar] [CrossRef]
- Xu, F.; Liu, K.; Tao, M. Cooperative Tx/Rx caching in interference channels: A storage-latency tradeoff study. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 7–12 July 2016; pp. 2034–2038. [Google Scholar]
- Roig, J.S.P.; Gunduz, D.; Tosato, F. Interference Networks with Caches at Both Ends. 2017. Available online: http://arxiv.org/abs/1703.04349 (accessed on 13 March 2017).
- Naderializadeh, N.; Maddah-Ali, M.A.; Niesen, U. On the Optimality of Separation between Caching and Delivery in General Cache Networks. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 1–5. [Google Scholar]
- Cao, Y.; Tao, M.; Xu, F.; Liu, K. Fundamental Storage-Latency Tradeoff in Cache-Aided MIMO Interference Networks. Available online: http://arxiv.org/abs/1609.01826 (accessed on 7 September 2016).
- Tandon, R.; Simeone, O. Cloud aided wireless networks with edge caching: Fundamental latency trade offs in Fog radio access networks. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 7–12 July 2016; pp. 2029–2033. [Google Scholar]
- Sengupta, A.; Tandon, R.; Simeone, O. Fog-Aided Wireless Networks for Content Delivery: Fundamental Latency Trade-Offs. 2016. Available online: http://arxiv.org/abs/1605.01690 (accessed on 5 May 2016).
- Koh, J.; Simeone, O.; Tandon, R.; Kang, J. Cloud-aided edge caching with wireless multicast fronthauling in fog radio access networks. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar]
- Girgis, M.; Ercetiny, O.; Nafie, M.; ElBatt, T. Decentralized coded caching in wireless networks: Trade-off between storage and latency. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 1–5. [Google Scholar]
- Goseling, J.; Simeone, O.; Popovski, P. Delivery Latency Regions in Fog-RANs with Edge Caching and Cloud Processing. 2017. Available online: http://arxiv.org/abs/1701.06303 (accessed on 23 January 2017).
- Azimi, S.M.; Simeone, O.; Tandon, R. Online Edge Caching in Fog-Aided Wireless Network. 2017. Available online: http://arxiv.org/abs/1701.06188 (accessed on 22 January 2017).
- Azimi, S.M.; Simeone, O.; Tandon, R. Fundamental limits on latency in small-cell caching systems: An information-theoretic analysis. In Proceedings of the IEEE Global Communication Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Kakar, J.; Gherekhloo, S.; Sezgin, A. Fundamental Limits on Delivery Time in Cloud- and Cache-Aided Heterogeneous Networks. 2017. Available online: http://arxiv.org/abs/1706.07627 (accessed on 23 June 2017).
- Peng, X.; Shen, J.C.; Zhang, J.; Kang, J.; Letaief, K.B. Joint data assignment and beamforming for backhaul limited caching networks. In Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Washington, DC, USA, 2–5 September 2014; pp. 1370–1374. [Google Scholar]
- Park, S.-H.; Simeone, O.; Shamai, S. Joint optimization of cloud and edge processing for Fog radio access networks. IEEE Trans. Wirel. Commun. 2016, 15, 7621–7632. [Google Scholar] [CrossRef]
- Tao, M.; Chen, E.; Zhou, H.; Yu, W. Content-Centric Sparse Multicast Beamforming for Cache-Enabled Cloud RAN. IEEE Trans. Wirel. Commun. 2016, 15, 6118–6131. [Google Scholar] [CrossRef]
- Azari, B.; Simeone, O.; Spagnolini, U.; Tulino, A.M. Hypergraph-based analysis of clustered cooperative beamforming with application to edge caching. IEEE Wirel. Commun. Lett. 2016, 5, 84–87. [Google Scholar] [CrossRef]
- Park, S.H.; Simeone, O.; Shamai, S. Joint cloud and edge processing for latency minimization in fog radio access networks. In Proceedings of the IEEE International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Edinburgh, UK, 3–6 July 2016; pp. 1–5. [Google Scholar]
- Martina, V.; Garetto, M.; Leonardi, E. A unified approach to the performance analysis of caching systems. In Proceedings of the IEEE Conference on Computer Communications (INFOCOM), Toronto, CA, Canada, 27 May–2 April 2014; pp. 2040–2048. [Google Scholar]
- Zhu, Y.; Guo, D. Ergodic fading Z-interference channels without state information at transmitters. IEEE Trans. Inf. Theory 2011, 57, 2627–2647. [Google Scholar] [CrossRef]
- Vahid, A.; Maddah-Ali, A.S.; Avestimehr, A.S. Capacity results for binary fading interference channels with delayed CSIT. IEEE Trans. Inf. Theory 2014, 60, 6093–6130. [Google Scholar] [CrossRef]
- Avestimehr, A.S.; Diggavi, S.N.; Tse, D.N.C. Wireless Network Information Flow: A Deterministic Approach. IEEE Trans. Inf. Theory 2011, 57, 1872–1905. [Google Scholar] [CrossRef]
- Tse, D.N.C.; Yates, R.D. Fading Broadcast Channels With State Information at the Receivers. IEEE Trans. Inf. Theory 2012, 58, 3453–3471. [Google Scholar] [CrossRef]
- Pedarsani, R.; Maddah-Ali, M.A.; Niesen, U. Online coded caching. IEEE Trans. Inf. Theory 2016, 24, 836–845. [Google Scholar] [CrossRef]
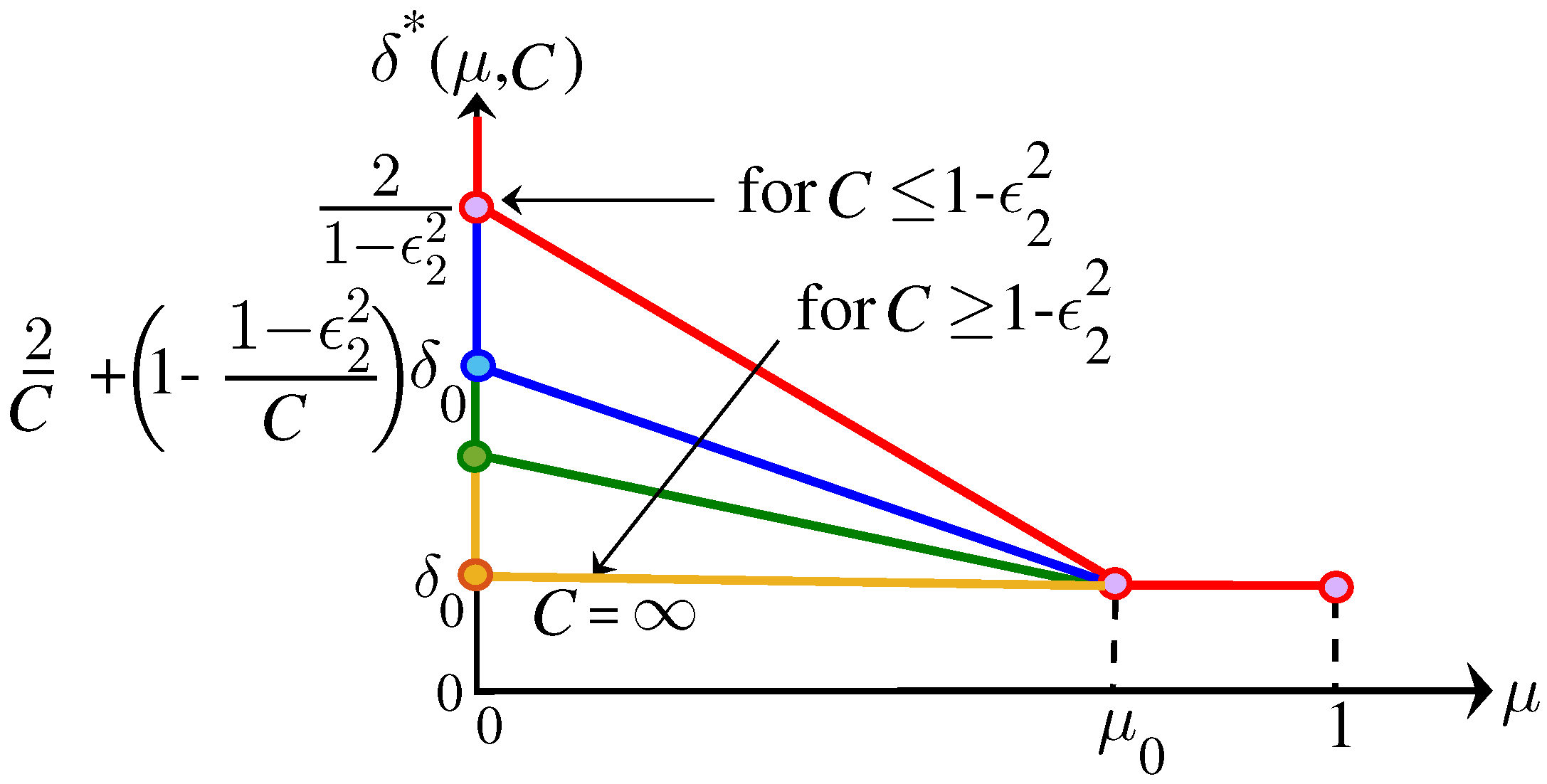
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azimi, S.M.; Simeone, O.; Tandon, R. Content Delivery in Fog-Aided Small-Cell Systems with Offline and Online Caching: An Information—Theoretic Analysis. Entropy 2017, 19, 366. https://doi.org/10.3390/e19070366
Azimi SM, Simeone O, Tandon R. Content Delivery in Fog-Aided Small-Cell Systems with Offline and Online Caching: An Information—Theoretic Analysis. Entropy. 2017; 19(7):366. https://doi.org/10.3390/e19070366
Chicago/Turabian StyleAzimi, Seyyed Mohammadreza, Osvaldo Simeone, and Ravi Tandon. 2017. "Content Delivery in Fog-Aided Small-Cell Systems with Offline and Online Caching: An Information—Theoretic Analysis" Entropy 19, no. 7: 366. https://doi.org/10.3390/e19070366