Entropic Measure of Epistemic Uncertainties in Multibody System Models by Axiomatic Design
Abstract
:1. Introduction
- {FR} = vector of functional domain
- {DP} = vector of physical domain
- {PV} = vector of process domain
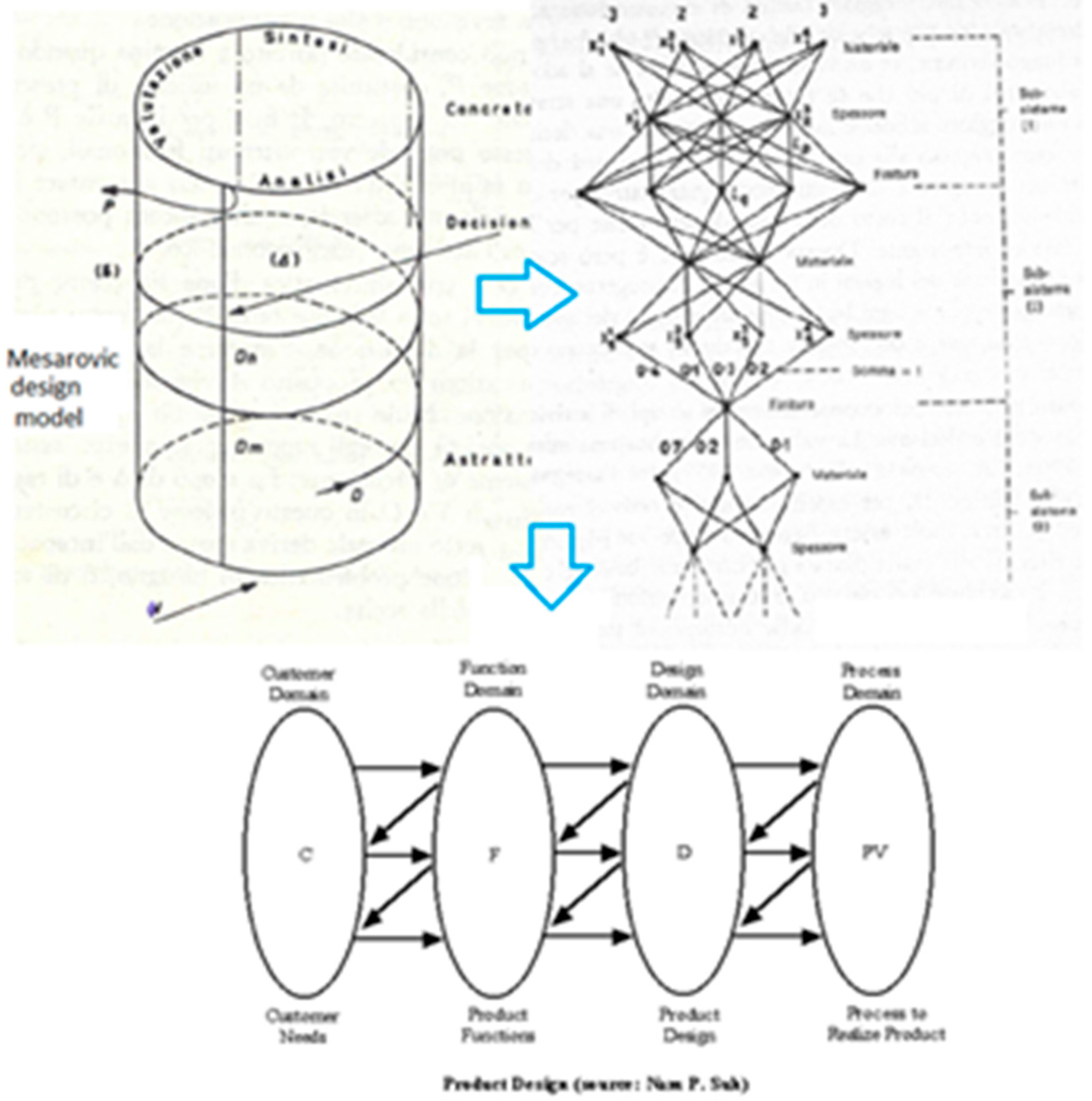
2. Classical Design
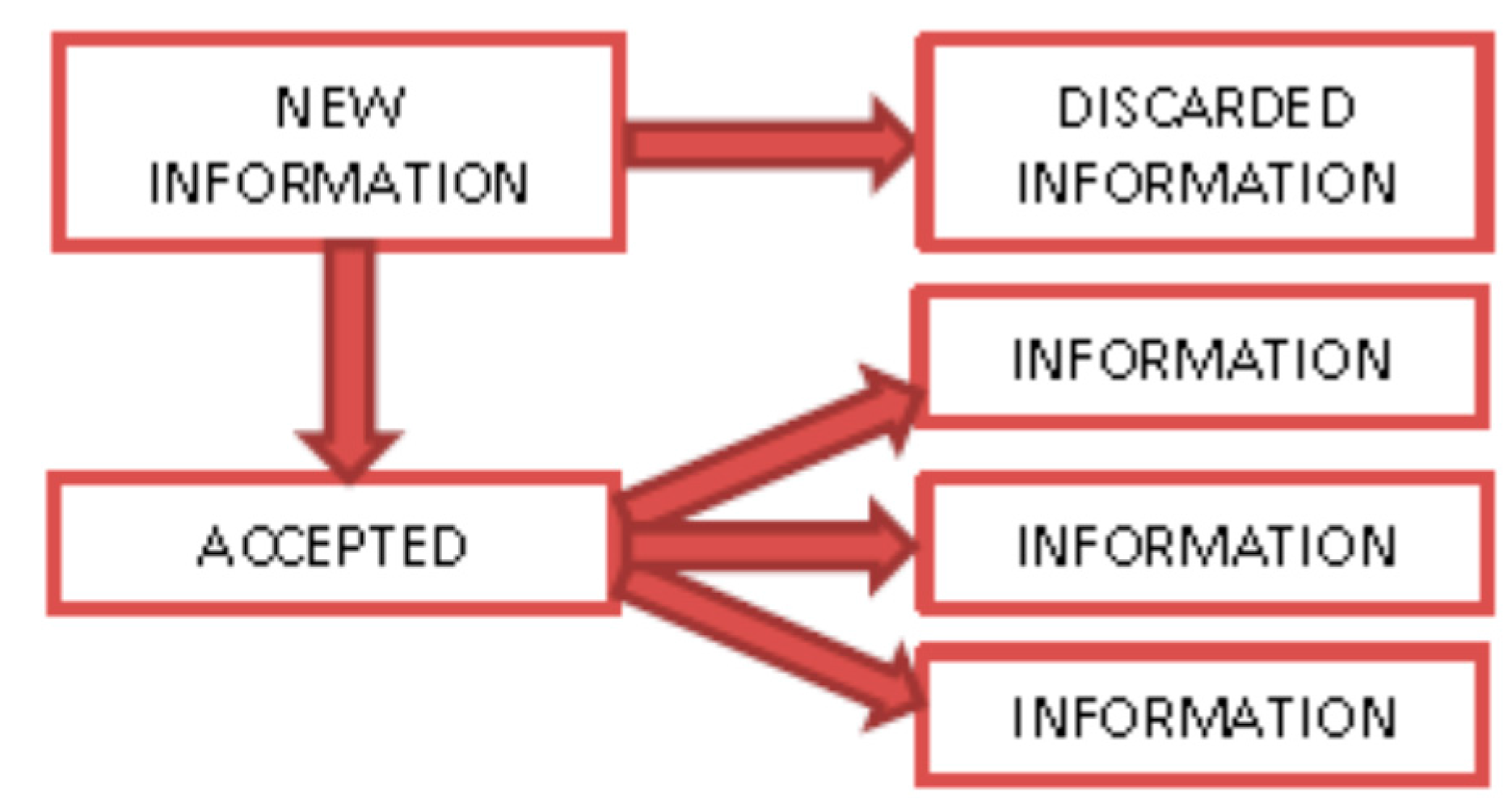
3. Non-Probabilistic Information in Metric Space
4. Entropic Analysis of Matrix
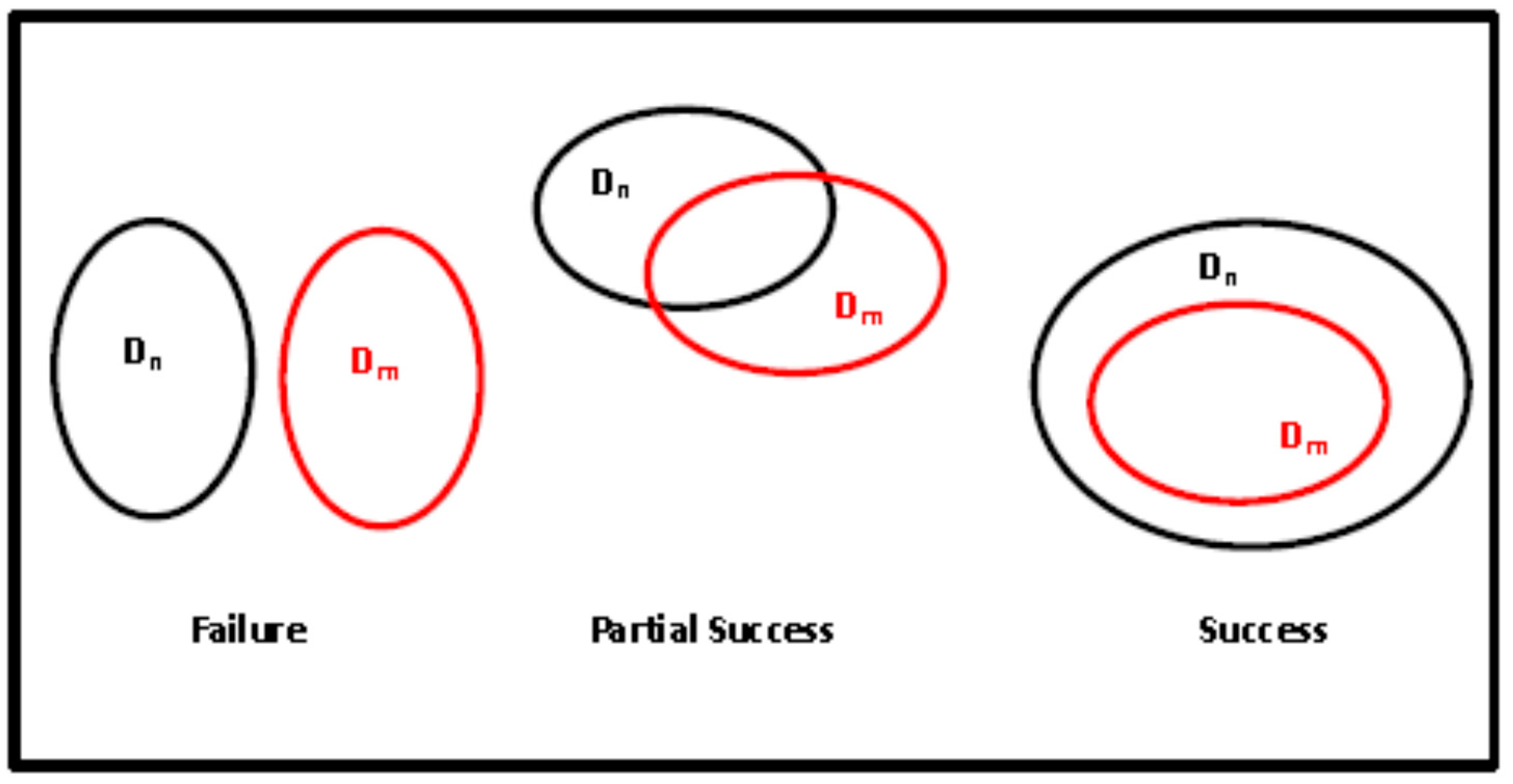
5. Numerical Example
- is the probability of satisfying with
- is the probability of satisfying with
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Ruggiero, A.; De Simone, M.C.; Russo, D.; Guida, D. Sound Pressure Measurement of Orchestral Instruments in the Concert Hall of a Public School. Int. J. Circuits Syst. Signal Process. 2016, 10, 75–81. [Google Scholar]
- Batou, A.; Soize, C. Rigid multibody system dynamics with uncertain rigid bodies. Multibody Syst. Dyn. 2012, 27, 285–319. [Google Scholar] [CrossRef]
- De Simone, M.C.; Guida, D. Dry Friction Influence on Structure Dynamics. In Proceedings of the COMPDYN 2015—5th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete, Greece, 25–27 May 2015; pp. 4483–4491. [Google Scholar]
- Guida, D.; Pappalardo, C.M. A New Control Algorithm for Active Suspension Systems Featuring Hysteresis. FME Trans. 2013, 41, 285–290. [Google Scholar]
- Borelli, D.; Devia, F.; Lo Cascio, E.; Schenone, C.; Spoladore, A. Combined production and conversion of energy in an urban integrated system. Energies 2016, 9, 817. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Wang, T.; Shabana, A.A. On the Formulation of the Planar ANCF Triangular Finite Elements. Nonlinear Dyn. 2017. [Google Scholar] [CrossRef]
- Chung, W.-H.; Kremer, G.E.O.; Wysk, R.A. A dynamic programming method for product upgrade planning incorporating technology development and end-of-life decision. J. Ind. Prod. Eng. 2017, 34, 30–41. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Guida, D. Adjoint-based Optimization Procedure for Active Vibration Control of Nonlinear Mechanical Systems. J. Dyn. Syst. Meas. Control 2017, 139, 081010. [Google Scholar] [CrossRef]
- Kulkarni, S.; Pappalardo, C.M.; Shabana, A.A. Pantograph/Catenary Contact Formulations. J. Vib. Acoust. 2017, 139, 011010. [Google Scholar] [CrossRef]
- Frimpong, S.; Thiruvengadam, M. Multibody Dynamic Stress Simulation of Rigid-Flexible Shovel Crawler Shoes. Minerals 2016, 6, 61. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Wallin, M.; Shabana, A.A. A New ANCF/CRBF Fully Parametrized Plate Finite Element. J. Comput. Nonlinear Dyn. 2017, 12, 031008. [Google Scholar] [CrossRef]
- Torres-Moreno, J.L.; Blanco-Claraco, J.L.; Giménez-Fernández, A.; Sanjurjo, E.; Naya, M.Á. Kinematic and Dynamic-State Estimation for Constrained Multibody Systems Based on IMUs. Sensors 2016, 16, 333. [Google Scholar] [CrossRef] [PubMed]
- Pappalardo, C.M.; Guida, D. Control of Nonlinear Vibrations using the Adjoint Method. Meccanica 2016. [Google Scholar] [CrossRef]
- Park, K.; Kremer, G.E.O. Assessment of static complexity in design and manufacturing of a product family and its impact on manufacturing performance. Int. J. Prod. Econ. 2015, 169, 215–232. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Yu, Z.; Zhang, X.; Shabana, A.A. Rational ANCF Thin Plate Finite Element. J. Comput. Nonlinear Dyn. 2016, 11, 051009. [Google Scholar] [CrossRef]
- Wagner, C.; Krinner, A.; Thümmel, T.; Rixen, D. Full Dynamic Ball Bearing Model with Elastic Outer Ring for High Speed Applications. Lubricants 2017, 5, 17. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Patel, M.D.; Tinsley, B.; Shabana, A.A. Contact Force Control in Multibody Pantograph/Catenary Systems. Proc. Inst. Mech. Eng. Part K J. Multibody Dyn. 2016, 230, 307–328. [Google Scholar] [CrossRef]
- Mathijssen, G.; Cherelle, P.; Lefeber, D.; Vanderborght, B. Concept of a Series-Parallel Elastic Actuator for a Powered Transtibial Prosthesis. Actuators 2013, 2, 59–73. [Google Scholar] [CrossRef]
- Pappalardo, C.M. A Natural Absolute Coordinate Formulation for the Kinematic and Dynamic Analysis of Rigid Multibody Systems. Nonlinear Dyn. 2015, 81, 1841–1869. [Google Scholar] [CrossRef]
- Guida, D.; Pappalardo, C.M. Control Design of an Active Suspension System for a Quarter-Car Model with Hysteresis. J. Vib. Eng. Technol. 2015, 3, 277–299. [Google Scholar]
- Guo, Z.; Liu, H.; Zhang, D.; Yang, J. Green Supplier Evaluation and Selection in Apparel Manufacturing Using a Fuzzy Multi-Criteria Decision-Making Approach. Sustainability 2017, 9, 650. [Google Scholar]
- Guida, D.; Pappalardo, C.M. Forward and Inverse Dynamics of Nonholonomic Mechanical Systems. Meccanica 2014, 49, 1547–1559. [Google Scholar] [CrossRef]
- Li, M.; Yuan, M. An Approach to the Match between Experts and Users in a Fuzzy Linguistic Environment. Information 2016, 7, 22. [Google Scholar] [CrossRef]
- Guida, D.; Nilvetti, F.; Pappalardo, C.M. Instability Induced by Dry Friction. Int. J. Mech. 2009, 3, 44–51. [Google Scholar]
- Guida, D.; Nilvetti, F.; Pappalardo, C.M. Dry Friction Influence on Cart Pendulum Dynamics. Int. J. Mech. 2009, 3, 31–38. [Google Scholar]
- Guida, D.; Nilvetti, F.; Pappalardo, C.M. Parameter Identification of a Two Degrees of Freedom Mechanical System. Int. J. Mech. 2009, 3, 23–30. [Google Scholar]
- Guida, D.; Pappalardo, C.M. Sommerfeld and Mass Parameter Identification of Lubricated Journal Bearing. WSEAS Trans. Appl. Theor. Mech. 2009, 4, 205–214. [Google Scholar]
- Pappalardo, C.M.; Patel, M.; Tinsley, B.; Shabana, A.A. Pantograph/Catenary Contact Force Control. In Proceedings of the ASME 2015 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference IDETC/CIE 2015, Boston, MA, USA, 2–5 August 2015; pp. 1–11. [Google Scholar]
- Pappalardo, M. Information in Metric Space. J. Mater. Process. Technol. 2004, 157, 228–231. [Google Scholar] [CrossRef]
- Wiener, N. Cybernetics. Sci. Am. 1948, 179, 14–18. [Google Scholar] [CrossRef] [PubMed]
- Suh, N.P. The Principles of Design; Oxford University Press: New York, NY, USA, 1990. [Google Scholar]
- Pahl, G.; Beitz, W.; Feldhusen, J.; Grote, K.H. Engineering Design; Springer: London, UK, 2007. [Google Scholar]
- Formato, A.; Ianniello, D.; Villecco, F.; Lenza, T.L.L.; Guida, D. Design Optimization of the Plough Working Surface by Computerized Mathematical Model. Emir. J. Food Agric. 2017, 29, 36–44. [Google Scholar] [CrossRef]
- Sena, P.; d’Amore, M.; Pappalardo, M.; Pellegrino, A.; Fiorentino, A.; Villecco, F. Studying the Influence of Cognitive Load on Driver’s Performances by a Fuzzy Analysis of Lane Keeping in a Drive Simulation. IFAC Proc. Vol. 2013, 46, 151–156. [Google Scholar] [CrossRef]
- Sena, P.; Attianese, P.; Pappalardo, M.; Villecco, F. FIDELITY: Fuzzy Inferential Diagnostic Engine for on-LIne supporT to phYsicians. In Proceedings of the 4th International Conference on the Development of Biomedical Engineering (IFMBE Proceedings), Ho Chi Minh City, Vietnam, 8–10 January 2012; Springer: Berlin, Germany, 2013; pp. 396–400. [Google Scholar]
- Sena, P.; Attianese, P.; Carbone, F.; Pellegrino, A.; Pinto, A.; Villecco, F. A Fuzzy Model to Interpret Data of Drive Performances from Patients with Sleep Deprivation. Comput. Math. Methods Med. 2012, 2012, 868410. [Google Scholar] [CrossRef] [PubMed]
- Sansone, F.; Picerno, P.; Mencherini, T.; Villecco, F.; D’Ursi, A.M.; Aquino, R.P.; Lauro, M.R. Flavonoid Microparticles by Spray-drying: Influence of Enhancers of the Dissolution Rate on Properties and Stability. J. Food Eng. 2011, 103, 188–196. [Google Scholar] [CrossRef]
- Pellegrino, A.; Villecco, F. Design Optimization of a Natural Gas Substation with Intensification of the Energy Cycle. Math. Probl. Eng. 2010, 2010, 294102. [Google Scholar] [CrossRef]
- Zhai, Y.; Liu, L.; Lu, W.; Li, Y.; Yang, S.; Villecco, F. The Application of Disturbance Observer to Propulsion Control of Sub-mini Underwater Robot. In Proceedings of the ICCSA 2010 International Conference on Computational Science and Its Applications, Fukuoka, Japan, 23–26 March 2010; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2010; pp. 590–598. [Google Scholar]
- Ghomshei, M.; Villecco, F.; Porkhial, S.; Pappalardo, M. Complexity in Energy Policy: A Fuzzy Logic Methodology. In Proceedings of the 6th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD 2009), Tianjin, China, 14–16 August 2009; IEEE: Los Alamitos, CA, USA; Volume 7, pp. 128–131. [Google Scholar]
- Ghomshei, M.; Villecco, F. Energy Metrics and Sustainability. In Proceedings of the ICCSA 2009 International Conference on Computational Science and Its Applications, Seoul, Korea, 29 June–2 July 2009; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2009; pp. 693–698. [Google Scholar]
- Zhang, Y.; Li, Z.; Gao, J.; Hong, J.; Villecco, F.; Li, Y. A method for designing assembly tolerance networks of mechanical assemblies. Math. Probl. Eng. 2012, 2012, 513958. [Google Scholar] [CrossRef]
- Gao, Y.; Villecco, F.; Li, M.; Song, W. Multi-Scale Permutation Entropy Based on Improved LMD and HMM for Rolling Bearing Diagnosis. Entropy 2017, 19, 176. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villecco, F.; Pellegrino, A. Entropic Measure of Epistemic Uncertainties in Multibody System Models by Axiomatic Design. Entropy 2017, 19, 291. https://doi.org/10.3390/e19070291
Villecco F, Pellegrino A. Entropic Measure of Epistemic Uncertainties in Multibody System Models by Axiomatic Design. Entropy. 2017; 19(7):291. https://doi.org/10.3390/e19070291
Chicago/Turabian StyleVillecco, Francesco, and Arcangelo Pellegrino. 2017. "Entropic Measure of Epistemic Uncertainties in Multibody System Models by Axiomatic Design" Entropy 19, no. 7: 291. https://doi.org/10.3390/e19070291






