A Distribution Family Bridging the Gaussian and the Laplace Laws, Gram–Charlier Expansions, Kurtosis Behaviour, and Entropy Features

Abstract

The paper devises a family of leptokurtic bell-shaped distributions which is based on the hyperbolic secant raised to a positive power, and bridges the Laplace and Gaussian laws on asymptotic arguments. Moment and cumulant generating functions are then derived and represented in terms of polygamma functions. The behaviour of shape parameters, namely kurtosis and entropy, is investigated. In addition, Gram–Charlier-type (GCT) expansions, based on the aforementioned distributions and their orthogonal polynomials, are specified, and an operational criterion is provided to meet modelling requirements in a possibly severe kurtosis and skewness environment. The role played by entropy within the kurtosis ranges of GCT expansions is also examined.

1. Introduction

The paper specifies the family of power-raised hyperbolic secant (PHS) distributions obtained by raising the hyperbolic secant function to an arbitrary positive power n, duly normalized.

Moment-generating functions arise directly from a classical integral representation of Euler’s Beta function, clearing the way for closed-form expressions of cumulants and moments in terms of polygamma functions. In particular, the kurtosis varies with n within a range of values, bounded by 6, from above, and by 3, from below, as n tends to 0 and to ∞, respectively.

The PHS family includes the hyperbolic secant and the logistic laws as special cases by taking n = 1 and n = 2, respectively. Both distributions have been widely investigated and variously generalized in the literature (see, e.g., [1,2,3,4]). The PHS family is not meant to be one of such generalizations, and is devised to encompass a whole category of bell-shaped distributions whose moment characterizations paves the way to wide-ranging extensions in the form of Gram–Charlier-type (GCT) expansions.

Leptokurtosis turns out to be inherent in these distributions, insofar as their limit laws prove to correspond to the Laplace and Gaussian densities, on asymptotic arguments, as n → 0 and n → ∞, respectively.

The behaviour of shape parameters, namely kurtosis and entropy, is examined from a specular standpoint.

It results that simple PHS specifications can be unsuitable to deal with severe kurtosis. However, as the paper shows, this hurdle can, nonetheless, be largely overcome. This is achieved by moving from PHS distributions to GCT expansions, using an argument similar to that used to alter the moments of a Gaussian via a Gram–Charlier series (see, e.g., [5] and more recently [6]). A first approach to the issue, with reference to logistic and hyperbolic secant laws, can be found in [7].

For an arbitrary PHS density, the paper specifies a GCT expansion based on the fourth and third degree polynomials associated with the parent density—making allowances for extra-kurtosis and skewness as required.

Both the feasible set of kurtosis values and the feasible region in the kurtosis-skewness plane, for which the aforementioned GCT expansions are positive definite functions are ascertained by algebraic argument. The admissible values of kurtosis span the range 3–24. As for asymmetry, the opportunity set crucially depends on the extra-kurtosis with the absolute skewness possibly attaining values around one.

The behaviour of entropy within the ranges of values taken by kurtosis of GCT expansions is investigated and some light is shed on their dual role as shape parameters.

The characteristics of the power-raised hyperbolic secant family of distributions and their GCT expansions prove useful in several contexts, such as financial time series analysis, where there is evidence of possibly severe leptokurtosis.

For practical purposes and possible applications of the analytic toolkit here developed, a (reverse) sigmoid curve is envisaged across the domain of GCT positive definiteness in the plane of the kurtosis vs. the PHS exponent, thus establishing a one-to-one correspondence between a given kurtosis level and the parent PHS density of the intended GCT expansion. Still looking at possible application requirements, it should be pointed out that, for levels of kurtosis within the range 5–21, the GCT expansions so obtained also allow for significant asymmetry, the admissible absolute skewness resulting being >0.8.

The paper is organized as follows: The power-raised hyperbolic secant distributions are introduced in Section 2, and their moments, kurtosis, and limit laws established. The issue of entropy in PHS distributions is addressed in Section 3. Section 4 specifies GCT expansions of the aforementioned distributions. The positive-definiteness requirement on excess-kurtosis and skewness are established on precise algebraic arguments, and the opportunity sets for kurtosis and skewness determined accordingly. Section 5 sheds light on the behaviour of entropy within the admissible kurtosis ranges of GCT expansions. Section 6 provides an operational criterion which permits the selection of an appropriate parent PHS density and GCT expansion to tailor to excess-kurtosis and skewness evidence. A few concluding remarks complete the article.

2. A Family of Distributions

Let us first establish the following:

Theorem 1.

Consider the family of functions:

$$f(x,a,b,n)=a{\left(sech(bx)\right)}^{n}a,b,n>0$$

(1)

Let:

$$a=a(b)=b{B}^{-1}\left(\frac{n}{2},\frac{1}{2}\right)$$

(2)

where B(.,.) is the Euler Beta function. Then, the expression:

$$f(x,b,n)=b{B}^{-1}\left(\frac{n}{2},\frac{1}{2}\right){\left(sech\left(bx\right)\right)}^n$$

(3)

where $f(x,b,n)$ is written for $f(x,a(b),b,n)$, defines the family of the power raised hyperbolic secant (PHS) distributions whose even moments:

$${\mu }_{2j}(n)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{x}^{\begin{array}{l}2j\end{array}}}f(x,n)dx,j=\mathit{1},\mathit{2},\dots$$

(4)

obey the recursion rule:

$${\mu }_{2j}(n)=2^{1-j}{\left({\psi }^{(1)}\left(\frac{n}{2}\right)\right)}^{-j}{\psi }^{(2j-1)}\left(\frac{n}{2}\right)+{\displaystyle \sum _{i=1}^{j-1}{2}^{-i+1}\left(\begin{array}{c}2j-1\\ 2i-1\end{array}\right)}{\psi }^{(1)}{\left(\frac{n}{2}\right)}^{-i}{\psi }^{(2i-1)}\left(\frac{n}{2}\right){\mu }_{2j-2i}(n)$$

(5)

where ${\psi }^{(i)}(.)$ is the polygamma function of order i.

Proof. 

See Appendix A.

As the effect of standardization is to multiply the cumulants (see Equation (A8) in Appendix A):

$${\kappa }_{2j}(b,n)=2^{1-2j}{b}^{-2j}{\psi }^{(2j-1)}\left(\frac{n}{2}\right)$$

(6)

by ${\kappa }_{{}_2}^{-1}(b,n)$ (see, e.g., [5]), the moments of $f(x,n)$ will be modified accordingly, yielding the reduced moments $m_{2i}(n)$ $=\frac{{\mu }_{2i}(b,n)}{{\mu }_2^i(b,n)}$.

In particular, $m_4(n)=\frac{{\mu }_4(b,n)}{{\mu }_2^2(b,n)}$ measures the kurtosis $K(n)$.

In this connection we have the following.

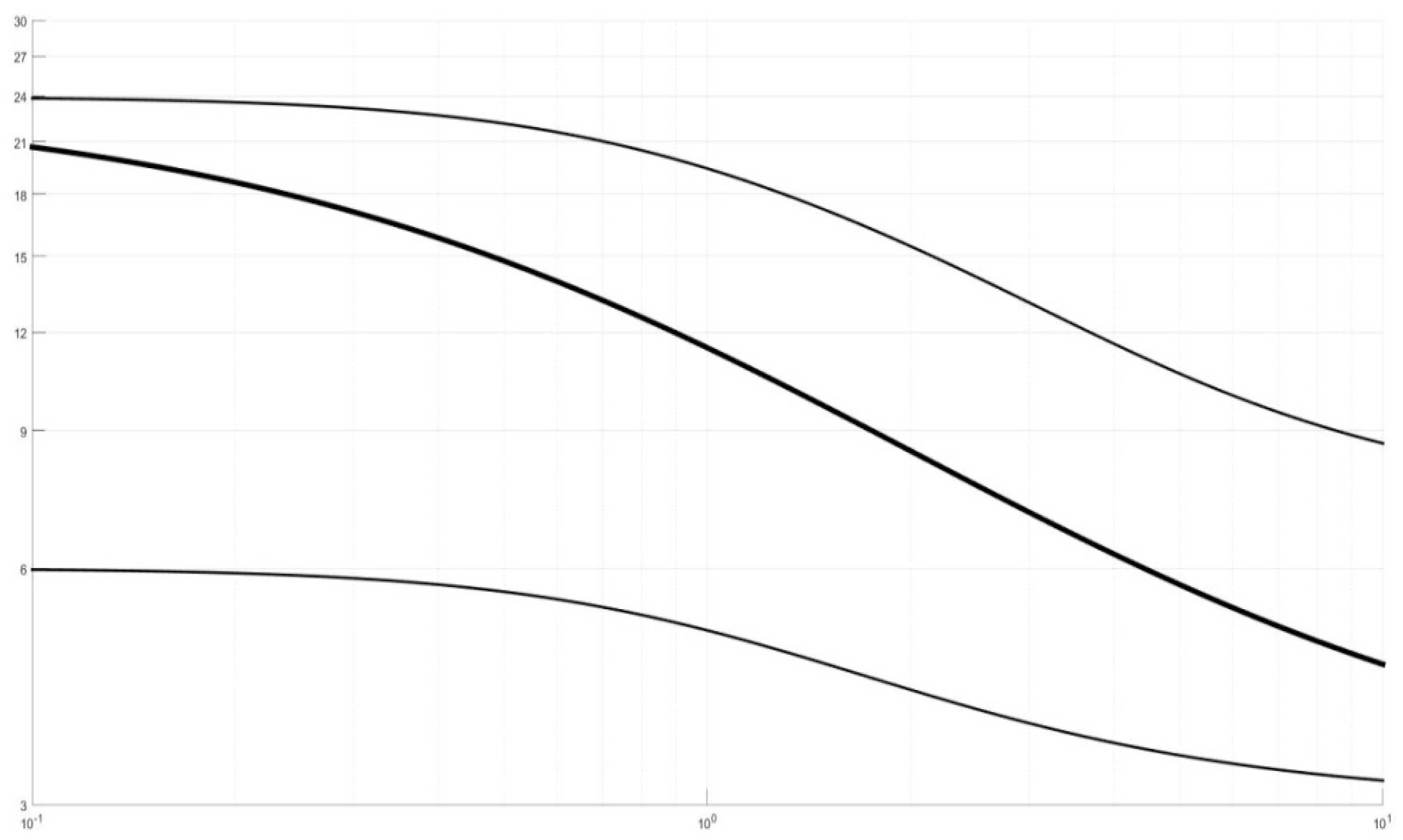
Theorem 2.

The PHS distributions Equation (3) are leptokurtic. The kurtosis $K(n)$ is given by:

$$K(n)=3+\frac{1}{2}\frac{\left({\psi }^{(3)}(n/2)\right)}{{\left({\psi }^{(1)}(n/2)\right)}^2}$$

(7)

The following properties of : $K(n)$

$$\mathit{\left(}i\mathit{\right)}K(n)\mathit{tends}\mathit{to}\mathit{6}\mathit{as}n\to \mathit{0}$$

(8)

$$\mathit{\left(}\mathit{ii}\mathit{\right)}K(n)\mathit{tends}\mathit{to}\mathit{3}\mathit{as}n\to \mathit{\infty }$$

(9)

prove true.

Proof. 

See Appendix A.

Figure 1 shows the behaviour of the index $K(n)$ as n varies from 0.1 to 10.

In fact, the asymptotic implications of PHS functions, far from being confined to kurtosis, are essential from the distribution stand-point as the following theorem proves. The latter shows that the family of PHS distributions bridges the Laplace and Gaussian laws.

Theorem 3.

The standardized PHS density functions $f(x,n)$ specified as follows (see proof of Theorem 1 in Appendix A)

$$f(x,n)={\left(\frac{1}{2}{\psi }^{(1)}\left(\frac{n}{2}\right)\right)}^{1/2}{B}^{-1}\left(\frac{n}{2},\frac{1}{2}\right){\left(sech\left({\left(\frac{1}{2}{\psi }^{(1)}\left(\frac{n}{2}\right)\right)}^{1/2}x\right)\right)}^n$$

(10)

enjoy the following limit properties,

(i) 

$f(x,n)$ approaches the normed Laplace law as n → 0, that is

$$\underset{n\to 0}{lim}f(x,n)=\frac{1}{\sqrt{2}}{e}^{-\sqrt{2}\left|x\right|}$$

(11)

(ii) 

$f(x,n)$ approaches the standard Gaussian law as n → ∞, that is

$$\underset{n\to \infty }{lim}f(x,n)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{x^2}{2}}$$

(12)

Proof. 

See Appendix A.

3. Entropy vs. Kurtosis of Power-Raised Hyperbolic Secant Distributions

The entropy $H_f$ of an absolutely continuous distribution with density function $f(x)$ is given by the integral:

$$H_f=-{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(x)log(f(x))dx}$$

(13)

where use is made of natural logarithms for convenience. The entropy from Equation (13) assumes its largest value in the case of a normal distribution (see [8], pp. 367–368).

Simple computations show that:

$$H_{Gaussian}=log{(2\pi e)}^{1/2}$$

(14)

$$H_{Laplace}=log(e\sqrt{2})$$

(15)

The Gaussian and Laplace distributions, being the limits as n → 0 and as n → ∞ respectively, of the PHS family of distributions, the more general question of the values taken by $H_f$ as n moves from 0 to ∞ naturally arises. In this connection we have the following

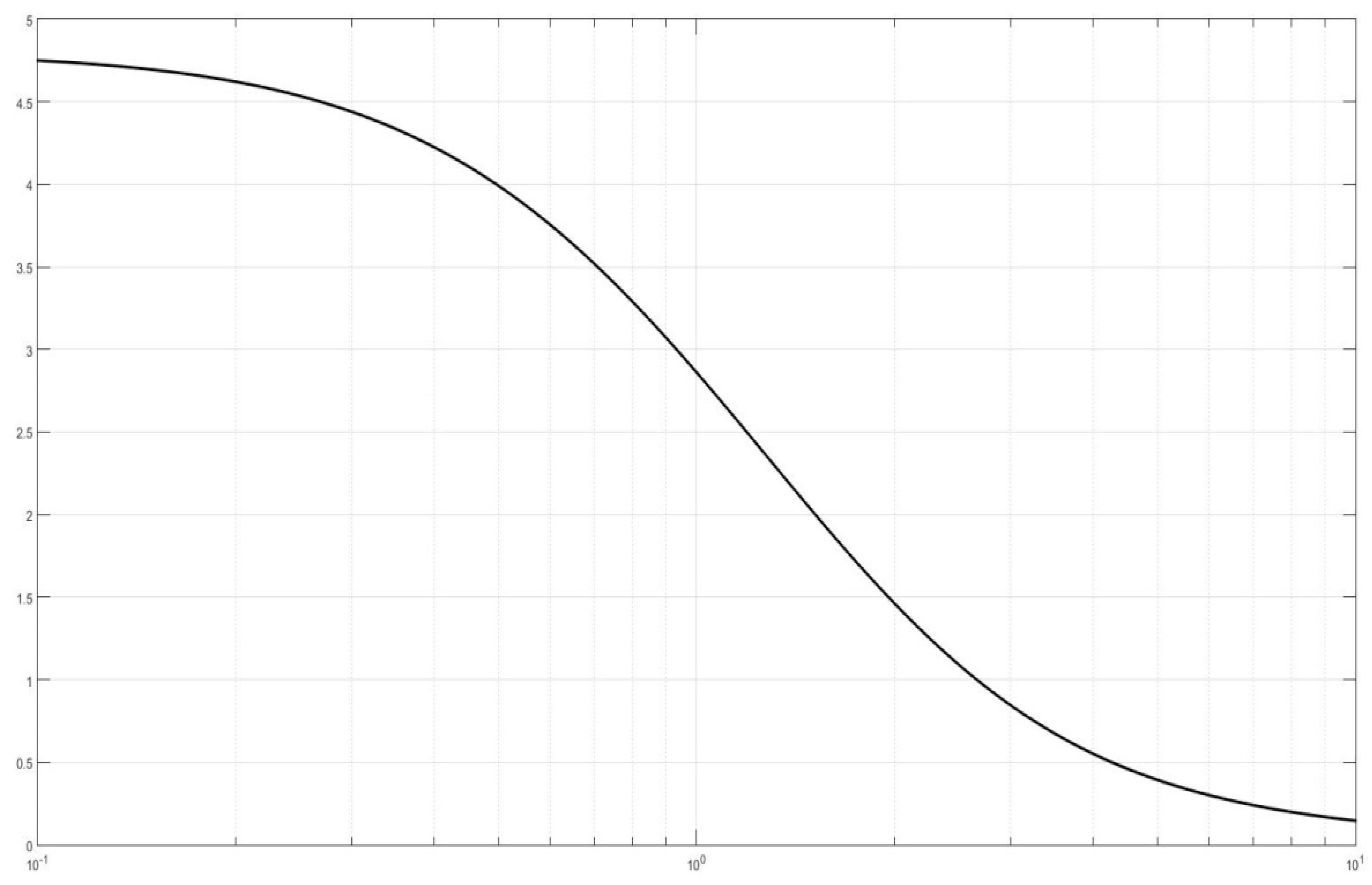
Theorem 4.

The entropy $H_{PHS}$ of the PHS distribution family is given by:

$$H_{PHS}(n)=-{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(x,n)ln(f(x,n))dx=ln}B\left(\begin{array}{cc}\frac{n}{2},& \frac{1}{2}\end{array}\right)-n\frac{\partial lnB\left(\begin{array}{cc}\frac{n}{2},& \frac{1}{2}\end{array}\right)}{dn}-lnb$$

(16)

with $f(x,n)$ and b given by Equations (10) and (A11) in Appendix A, respectively.

Proof. 

See Appendix A.

The following graph shows the behaviour of the entropy $H_{PHS}(n)$ as n varies from 0.1 to 10.

Inspecting Figure 2 above and Figure 1 of Section 2, we note how the entropy is an increasing function of n (see Figure 2), whereas the kurtosis K is a decreasing function of n (see Figure 1).

Thus, as far as PHS distributions are concerned, a drop in entropy, as compared with the Gaussian case, is accompanied by leptokurtosis, and vice versa. Consequently, for this family of distributions, an entropy loss is an indicator of excess kurtosis.

4. GCT Expansions of PHS Distributions

In this section we conceive a GCT expansion of PHS distributions by assigning to the fourth degree polynomial orthogonal with respect to $f(x,n)$ in Equation (10) the role once played by the fourth degree Hermite polynomial (see, e.g., [9], p. 28). The following GCT expansion shaped on extra-kurtosis β, is specified as:

$$\phi (x,n,\beta )=\left(1+\frac{\beta }{{\upsilon }_4(n)}{p}_4(x,n)\right)f(x,n),\beta >\mathit{0}$$

(17)

where $p_4(x,n)$ is the fourth-degree monic polynomial, orthogonal with respect to the density function $f(x,n)$, ${\upsilon }_4(n)$ is the squared norm of the aforementioned polynomial, and β is a shape parameter subject to $\phi (x,n,\beta )$ being positive definite.

As a by-product of Theorem 3, p(x,0) and p(x,∞), respectively, turn out to be the Laguerre and Hermite polynomials. More generally, (see, e.g., [10,11]), the monic polynomial $p_h(x,n)$ orthogonal with respect to the function $f(x,n)$ can be expressed in determinantal form as follows:

$$p_k(x,n)=det{(M_{\begin{array}{l}h\end{array}}(n))}^{-1}det\left[\begin{array}{cc}{M}_{\begin{array}{l}h\end{array}}(n)& \begin{array}{c}{\mu }_h(n)\\ \begin{array}{l}{\mu }_{h+1}(n)\\ ⋮\end{array}\\ {\mu }_{2h-1}(n)\end{array}\\ \begin{array}{cccc}1& x& \cdots & x^{h-1}\end{array}& x^h\end{array}\right]$$

(18)

where $M_h(n)$ is the Hankel moment matrix:

$$\underset{(h,h)}{M_h(n)}=\left[\begin{array}{cccc}{m}_0(n)& m_1(n)& \cdots & m_{h-1}(n)\\ m_1(n)& m_2(n)& \cdots & m_h(n)\\ ⋮& ⋮& \cdots & ⋮\\ m_{h-1}(n)& m_h(n)& \cdots & m_{2h-2}(n)\end{array}\right]$$

(19)

With $m_0(n)$ = $m_2(n)$ = 1, $m_4(n)=K(n)$ as specified in Equation (7), and $m_{2i+1}(n)$ = 0.

The scalar ${\upsilon }_h(n)$ can be expressed in determinantal form as well, that is:

$${\upsilon }_h(n)=det{(M_{\begin{array}{l}h\end{array}}(n))}^{-1}det{M}_{\begin{array}{l}h+1\end{array}}(n)$$

(20)

In particular, for h = 4 simple computations show that:

$$p_4(x)=x^4-e(n)x^2+d(n)$$

(21)

$${\upsilon }_4(n)=m_8(n)-e(n)m_6(n)+d(n)K(n)$$

(22)

where:

$$d(n)=(m_6(n)-K^2(n)){(K(n)-1)}^{-1}$$

(23)

$$e(n)=d(n)+K(n)$$

(24)

with p(x) standing for p(x,n).

Equation (17) provides the intended GCT expansion of $f(x,n)$ subject to being positive definite, which occurs whenever the polynomial factor in the right-hand side is itself positive definite.

First we shall prove a lemma needed for the theorem we are primarily interested in.

Lemma 1.

The biquadratic polynomial:

$$\vartheta (x,n,\beta )=1+\beta {\upsilon }_4^{-1}(n)p_4(x,n),\beta >\mathit{0}$$

(25)

parametric in β is positive definite if β satisfies:

$$\beta <4{\upsilon }_4(n){(e^2(n)-4d(n))}^{-1}$$

(26)

Proof. 

Since $p_4(x,n)$ attains its minimum at $x=\pm {\left(\frac{e(n)}{2}\right)}^{1/2}$ where it takes the value $d(n)-\frac{e^2(n)}{4}<0$, $\vartheta (x,\beta ,n)$ is bounded from below by $\vartheta \left({\left(\frac{e(n)}{2}\right)}^{1/2},\beta ,n\right)$. Hence, the former is positive definite provided the latter is a positive number, which occurs when β satisfies Equation (26), as shown by simple computation.

At this point we can prove the following.

Theorem 5.

The GCT expansion:

$$\phi (x,n,\beta )=\vartheta (x,n,\beta )f(x,n),\beta >\mathit{0}$$

(27)

where f(x,n) is the standardized distribution in (10), $\vartheta (x,\beta ,n)$ is the biquadratic polynomial of Lemma 1, and β satisfies Equation (26), provides a family of leptokurtic distribution functions.

The kurtosis $K(n,\beta )$ varies linearly with β, that is:

$$K(n,\beta )=K(n)+\beta$$

(28)

within the range of values:

$$K(n)<K(n,\beta )<K^{*}(n)$$

(29)

where:

$$K^{*}(n)=K(n)+4{\upsilon }_4(n){(e^2(n)-4d(n))}^{-1}$$

(30)

Here K(n) is the kurtosis of the PHS distributions as specified in Theorem 2, and $K^{*}(n)$ is such that:

$$\underset{n\to 0}{lim}{K}^{*}(n)=23.9518$$

(31)

$$\underset{n\to \infty }{lim}{K}^{*}(n)=7$$

(32)

Proof. 

The polynomials $p_k(x,n)$ enjoy the orthogonality property (see, e.g., [11]):

$${\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{x}^h}{p}_k(x,n)f(x,n)dx=\{\begin{array}{l}0if0\le h\le k+1,h\ne k\\ {\upsilon }_k(n)ifh=k\end{array}$$

(33)

Applying this to Equation (27) while bearing in mind Equation (25), yields Equation (28). As for Equation (29), the double inequality arises from Lemma 1 as a by-product, upon the argument previously used.

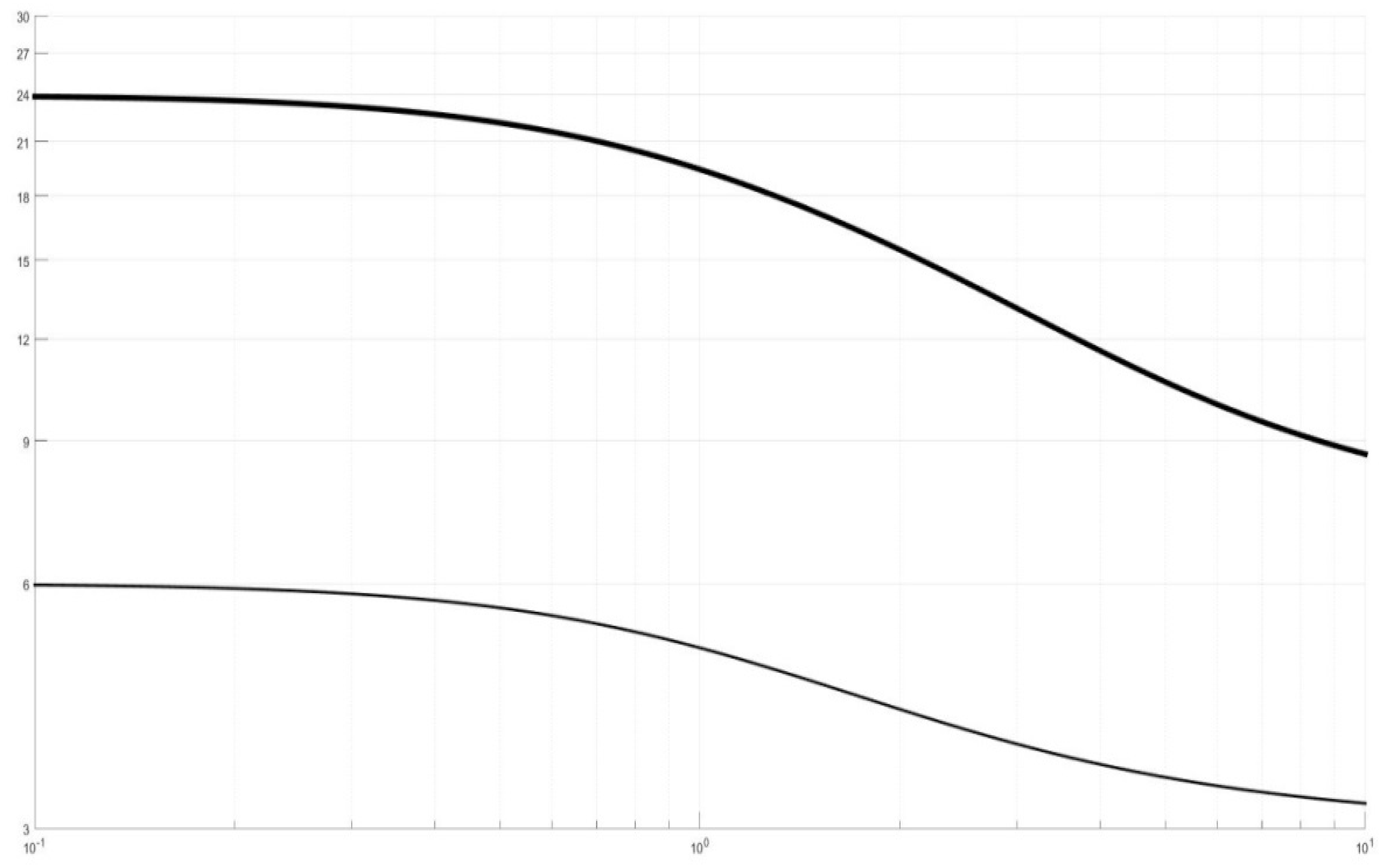
Figure 3 shows the behavior of the upper and lower bounds, indicated in Equation (29), of the kurtosis $K(n,\beta )$ of the GCT expansions $\phi (x,n,\beta )$ as n varies from 0.1 to 10 (see Figure 1 for comparison).

We now move to a GCT expansion of PHS distributions shaped on skewness accompanied by leptokurtosis. The intended density is specified as follows:

$$\varphi (x,n,\alpha ,\beta )=\left(1+\frac{\alpha }{{\upsilon }_3(n)}{p}_3(x,n)+\frac{\beta }{{\upsilon }_4(n)}{p}_4(x,n)\right)f(x,n)$$

(34)

where $p_h(x,n)$ is the monic polynomial of degree h, orthogonal with respect to the density function $f(x,n)$, ${\upsilon }_h(n)$ is the squared norm of the aforementioned polynomial, and β and α are shape parameters subject to $\varphi (x,n,\alpha ,\beta )$ being non-negative definite.

Here $p_4(x,n)$ and ${\upsilon }_4(n)$ are as in Equations (21) and (22) and $p_3(x,n)$ and ${\upsilon }_3(n)$ are given by:

$$p_3(x)=x^3-K(n)x$$

(35)

$${\upsilon }_3(n)=m_6(n)-K^2(n)$$

(36)

As usual p(x) stands for p(x,n).

Equation (34) provides the intended GCT expansion of $f(x,n)$ subject to being positive definite, which occurs whenever the polynomial factor in the right-hand side is positive definite itself.

First we shall prove a lemma needed for proving the theorem we are primarily interested in.

Lemma 2.

With β as in Equation (26) of Lemma 1, the quartic polynomial:

$$\theta (x,n,\alpha ,\beta )=\vartheta (x,n,\beta )+\frac{\alpha }{{\upsilon }_3(n)}{p}_3(x,n)=\left(1+\frac{\alpha }{{\upsilon }_3(n)}{p}_3(x,n)+\frac{\beta }{{\upsilon }_4(n)}{p}_4(x,n)\right)$$

(37)

parametric in α and β, is positive definite if α satisfies:

$$\left|\alpha \right|<\overline{\alpha }$$

(38)

where $\overline{\alpha }=\overline{\alpha }(n,\beta )$ is the smallest positive number for which the determinant of the Sylvester matrix:

$$\begin{array}{l}\underset{(7,7)}{S(n,\alpha ,\beta )}=\left[\begin{array}{ccccccc}\beta {\upsilon }_{{}_4}^{-1}& \overline{\alpha }{\upsilon }_{{}_3}^{-1}& -\beta e{\upsilon }_{{}_4}^{-1}& -\overline{\alpha }K{\upsilon }_{{}_3}^{-1}& 1+\beta d{\upsilon }_{{}_4}^{-1}& 0& 0\\ 0& \beta {\upsilon }_{{}_4}^{-1}& \overline{\alpha }{\upsilon }_{{}_3}^{-1}& -\beta e{\upsilon }_{{}_4}^{-1}& -\overline{\alpha }K{\upsilon }_{{}_3}^{-1}& 1+\beta d{\upsilon }_{{}_4}^{-1}& 0\\ 0& 0& \beta {\upsilon }_{{}_4}^{-1}& \overline{\alpha }{\upsilon }_{{}_3}^{-1}& -\beta e{\upsilon }_{{}_4}^{-1}& -\overline{\alpha }K{\upsilon }_{{}_3}^{-1}& 1+\beta d{\upsilon }_{{}_4}^{-1}\\ 4\beta {\upsilon }_{{}_4}^{-1}& 3\overline{\alpha }{\upsilon }_{{}_3}^{-1}& -2\beta e{\upsilon }_{{}_4}^{-1}& -\overline{\alpha }K{\upsilon }_{{}_3}^{-1}& 0& 0& 0\\ 0& 4\beta {\upsilon }_{{}_4}^{-1}& 3\overline{\alpha }{\upsilon }_{{}_3}^{-1}& -2\beta e{\upsilon }_{{}_4}^{-1}& -\overline{\alpha }K{\upsilon }_{{}_3}^{-1}& 0& 0\\ 0& 0& 4\beta {\upsilon }_{{}_4}^{-1}& 3\overline{\alpha }{\upsilon }_{{}_3}^{-1}& -2\beta e{\upsilon }_{{}_4}^{-1}& -\overline{\alpha }K{\upsilon }_{{}_3}^{-1}& 0\\ 0& 0& 0& 4\beta {\upsilon }_{{}_4}^{-1}& 3\overline{\alpha }{\upsilon }_{{}_3}^{-1}& -2\beta e{\upsilon }_{{}_4}^{-1}& -\overline{\alpha }K{\upsilon }_{{}_3}^{-1}\end{array}\right]\end{array}$$

(39)

vanishes. Here, υ, e, K, and d are written for υ(n), e(n), K(n), and d(n) for the simplicity of notation.

Proof. 

With β as in Lemma 1, the property of positive definiteness once established for $\vartheta (x,n,\beta )$ is maintained as we move to $\theta (x,n,\alpha ,\beta )$ provided $\left|\alpha \right|$ is small enough. It follows, on the one hand, that as long as $\left|\alpha \right|$ is small enough the quartic in Equation (37) has two pairs of complex conjugate roots, and on the other hand that increasing $\left|\alpha \right|$ will eventually attain a critical value $\left|\overline{\alpha }\right|$ at which positive definiteness no longer holds since one pair (at least) of complex conjugate roots collapses into a real double root. This marks the passage from definiteness to indefiniteness. Once the quartic in Equation (37) has a real double root, the determinant of the Sylvester matrix in Equation (39) associated with the polynomial $\theta (x,n,\alpha ,\beta )$ vanishes, as well as its derivative (see, e.g., [12]). The foregoing argument leads to bound $\left|\alpha \right|$ by the smallest $\overline{\alpha }>0$ at which such vanishing occurs.

Using Lemma 2 we can prove the main theorem.

Theorem 6.

The GCT expansion of the form

$$\varphi (x,n,\alpha ,\beta )=\theta (x,n,\alpha ,\beta )f(x,n),\beta >\mathit{0}$$

(40)

where $f(x,n)$ is the standardized PHS distribution in Equation (10), $\theta (x,n,\alpha ,\beta )$ is the quartic polynomial of Lemma 2 and α and β satisfy Equations (26) and (38), respectively, provide a family of leptokurtic skewed distribution functions.

The kurtosis $K(n,\beta )$ is given by Equation (29), according to Theorem 5.

The skewness $s(n,\alpha )$ varies linearly with α, that is:

$$s(n,\alpha )=\alpha$$

(41)

within the range of values:

$$-\overline{\alpha }(n,\beta )<s(n,\alpha )<\overline{\alpha }(n,\beta )$$

(42)

where $\overline{\alpha }(n,\beta )$ is as defined in Lemma 2.

Proof. 

The proof follows the same lines as in the previous theorem and the argument of Lemma 2.

5. Entropy vs. Kurtosis of GCT Expansions

This section aims at shedding light on the behaviour of the entropy of the GCT expansion of Equation (17) as the extra-kurtosis parameter β runs from 0 to the upper bound specified in Equation (30).

To this end, we have to examine the integral:

$$H(n,\beta )_{GCT}=-{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\phi (x,n,\beta )log(}\phi (x,n,\beta ))dx$$

(43)

where $\phi (x,n,\beta )$ is as specified in Equation (17). In order to establish if the entropy $H_{GCT}$ decreases, as expected, as the extra-kurtosis parameter β moves upwards, we can look at the signature of its derivative with respect to β.

Simple computations show that:

$$\begin{array}{ll}\frac{\partial H_{GCT}(n,\beta )}{\partial \beta }=& -\frac{2}{{\upsilon }_4(n)}{\displaystyle \underset{0}{\overset{\infty }{\int }}{p}_4(x,n)f(x,n)log(f(x,n))}dx\\ & -\frac{2}{{\upsilon }_4(n)}{\displaystyle \underset{0}{\overset{\infty }{\int }}{p}_4(x,n)f(x,n)}dx\\ & -\frac{2}{{\upsilon }_4(n)}{\displaystyle \underset{0}{\overset{\infty }{\int }}{p}_4(x,n)f(x,n)}log(1+\frac{\beta }{{\upsilon }_4(n)}{p}_4(x,n))dx\end{array}$$

(44)

First note that:

$${\displaystyle (\mathrm{i})\underset{0}{\overset{\infty }{\int }}{p}_4(x,n)f(x,n)}dx=0$$

(45)

by the properties of orthogonal polynomials:

$$(\mathrm{ii}){\displaystyle \underset{0}{\overset{\infty }{\int }}{p}_4(x,n)f(x,n)}log(1+\frac{\beta }{{\upsilon }_4(n)}{p}_4(x,n))dx>0$$

(46)

as the first and third factors under the integral sign turn out to be either both positive or both negative quantities.

Then, we need only look at the first term in the right-hand side of Equation (44) and examine the (sign of) the integral:

$$Q(n,\beta )={\displaystyle \underset{0}{\overset{\infty }{\int }}{p}_4(x,n)f(x,n)log(f(x,n))}dx$$

(47)

whose non-negativeness would provide a sufficient condition for the negativeness of the whole derivative of Equation (44), in light of Equations (45) and (46).

Some computations prove the intended result in the Laplace and Gaussian cases, namely:

$$\underset{n\to 0}{lim}Q(n,\beta )=9.6$$

(48)

$$\underset{n\to \infty }{lim}Q(n,\beta )=0$$

(49)

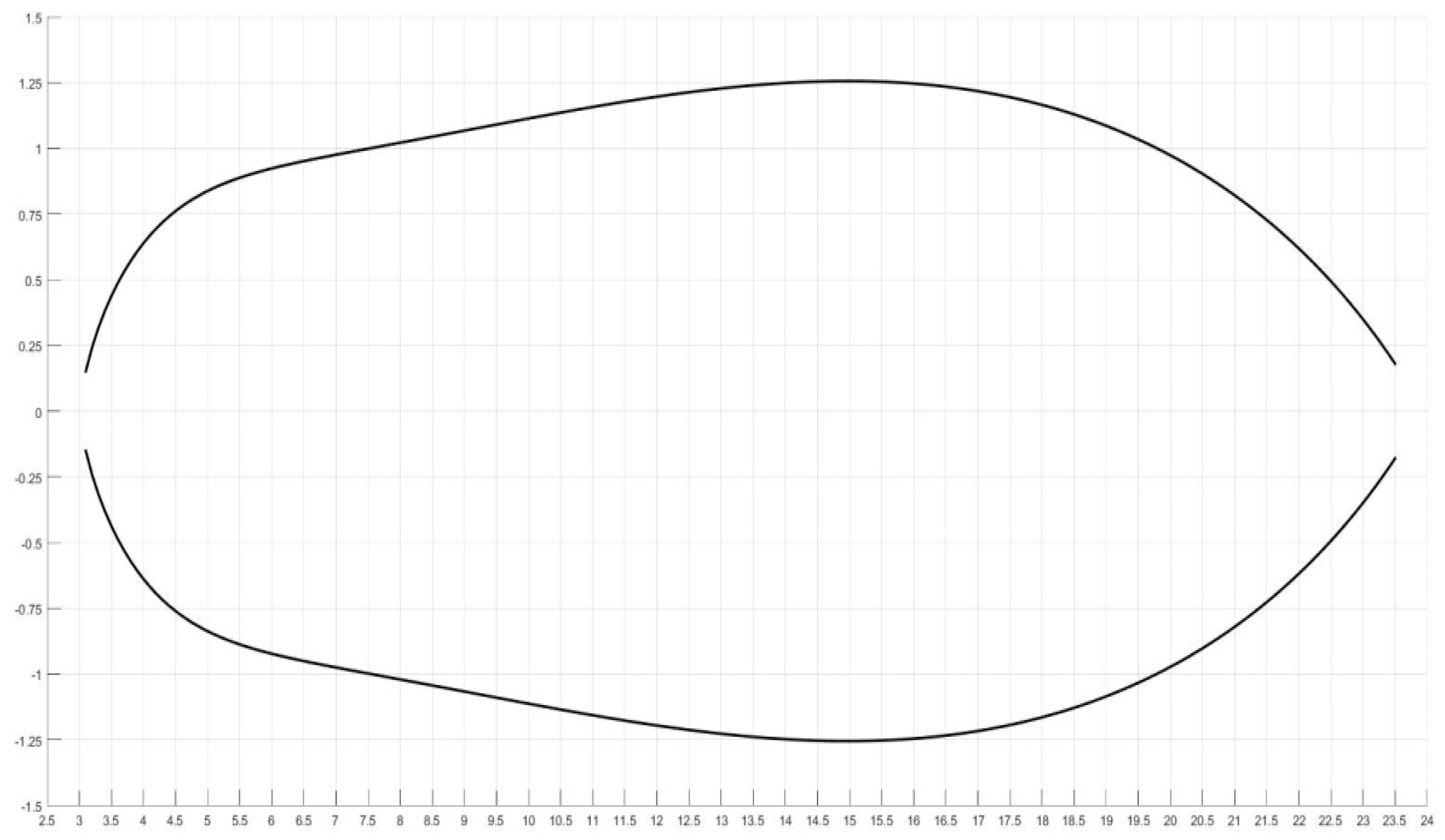
As for the behaviour of $Q(n,\beta )$ as n runs from 0 to ∞, a closed-form representation of the right-hand side of Equation (47) in terms of moment can be obtained by following an argument similar to that used in the proof of Theorem 4. However, analytic elegance aside, the closed-form so obtained would not prove of much interest. Thus, the behaviour of $Q(n,\beta )$ is given a graphic representation as shown in the chart here below.

Examining Figure 4 and given Equations (45) and (46), we realize that $H_{GCT}(n,\beta )$ is a decreasing function of β: the entropy of GCT expansions drops as the excess-kurtosis grows.

The result provides further evidence of the (inverse) relation between entropy and kurtosis formerly recognized in Section 3.

6. GCT Expansions vs. Kurtosis: The Other Way Round

Figure 3 in Section 4 shows the feasibility region in the (K, n) plane, bounded by K and $K^{*}$, where the GCT expansions of Equation (27) are definite positive.

Looking at the potential applications of the range of GCT distributions, the possibility of tracing a path across the aforesaid region is worth considering. This would entail joining the upper bound on the left (as n → 0) to the lower bound on the right (as n → ∞), which puts the level $K^{\ne }$ of kurtosis to be matched upon an empirical evidence argument, or a similar one, in a one-to-one correspondence with the parameter n identifying the PHS density and the intended GCT expansion, in turn.

From inspection of the aforesaid figure, the path across the positive-definitiveness region can be conceived as a reversed sigmoid curve, with inflection point at n = 2, in $lo{g}_{10}-lo{g}_{10}$ coordinates. The choice of the hyperbolic tangent as sigmoid function can be justified for analytic convenience by a heuristic argument. This leads to specifying the intended curve across the feasibility set as follows:

$$lo{g}_{10}{K}^{\ne }=lo{g}_{10}3+\left\{1-tanh\left(lo{g}_{10}\frac{n}{2}\right)\right\}lo{g}_{10}{\left(\frac{K_{{}_0}^{*}}{K_{\infty }}\right)}^{1/2}$$

(50)

where:

$$K_{{}_0}^{*}=\underset{n\to 0}{lim}{K}_{}^{*}(n)=23.9518$$

(51)

$$K_{\infty }=\underset{n\to \infty }{lim}K(n)=3$$

(52)

Solving Equation (50) with respect to $K^{\ne }$, as a function of n, yields:

$$K^{\ne }=K^{\ne }(n)=3\exp \left(3.793135{(n^{0.8686}+1.83)}^{-1}\right)$$

(53)

as simple computations shows. In Figure 5 the graph of $K^{\ne }$ is superimposed on those of the boundary curves $K^{*}$ and K (see Figure 3 of Section 4).

Solving Equation (50) with respect to n as a function of $K^{\ne }$ gives:

$$n=n(K^{\ne })={\left(\frac{5.799062-1.825878ln{K}^{\ne }}{ln{K}^{\ne }-ln3}\right)}^{1.1512951}$$

(54)

This formula clears the way to bridging the potential of GCT expansions to model observed data under possibly severe condition of kurtosis, and the urge from of an empirical argument if this is the case.

In fact, in order to find the properly shaped distribution for a known or an estimated value $K^{\ne }$ of kurtosis, Equation (54) allows to establish the design parameter $n(K^{\ne })$ of the parent PHS density of the target GCT expansion $f^{\ne }(x,K^{\ne })$ to be determined.

To sum up, given a value of $K^{\ne }$ the required value of n is provided by Equation (54), which leads to specifying the intended density $f^{\ne }(x,K^{\ne })$ as follows:

$$f^{\ne }(x,K^{\ne })={\left(\frac{1}{2}{\psi }^{(1)}\left(\frac{n}{2}\right)\right)}^{1/2}{B}^{-1}{}_{\left(\frac{n}{2},\frac{1}{2}\right)}\left(1+\frac{\beta (n)}{{\upsilon }_4(n)}{p}_4(x,n)\right){\left(sech\left({\left(\frac{1}{2}{\psi }^{(1)}\left(\frac{n}{2}\right)\right)}^{1/2}x\right)\right)}^n$$

(55)

where:

$$\beta \left(n\right)=K^{\ne }-K\left(n\right)$$

(56)

and the other symbols have the usual meaning. Figure 6 shows the graphs of f(x, $K^{\ne }$) for $K^{\ne }$ = 20, $K^{\ne }$ = 15, $K^{\ne }$ = 10 and $K^{\ne }$ = 5, in turn.

At this point, it is worth investigating to what extent a piece of information on skewness (α) can possibly be embodied into a GCT specification. To this end, we can follow an argument similar to that of Lemma 2 which leads to determining the feasibility region between the curves $\overline{\alpha }=\overline{\alpha }(K^{\ne })$ and $-\overline{\alpha }=-\overline{\alpha }(K^{\ne })$, of the $(\alpha ,K^{\ne })$ plane where the suitable GCT expansions are meaningful expressions. The locus of the $\alpha$, $K^{\ne }$ pairs for which positive definiteness of the intended GCT expressions is maintained, is depicted below in Figure 7.

Table 1. Values of n and bounds of skewness for $K^{\ne }$ = 4–23.

${\mathit{K}}^{\mathbf{\ne }}$	n	$\overline{\mathit{\alpha }}$
4	16.407	0.639183439
5	7.267	0.837626059
6	4.4349	0.923283996
7	3.0721	0.975361836
8	2.2741	1.021018199
9	1.751	1.066996287
10	1.3822	1.113102509
11	1.1084	1.157085560
12	0.8974	1.196177300
13	0.7301	1.227518579
14	0.5944	1.248241505
15	0.4824	1.255447821
16	0.3886	1.246145088
17	0.3092	1.217143588
18	0.2415	1.164894037
19	0.1833	1.085226615
20	0.1331	0.972914475
21	0.0899	0.820895356
22	0.0529	0.618745392
23	0.0220	0.349248618

summarizes the previous results by showing the values of the design parameter n for the integer kurtosis level $K^{\ne }$ within the range $4\le K^{\ne }\le 23$, along with the maximum admissible skewness $\overline{\alpha }$ for meaningfulness of GCT expansions.

7. Concluding Remarks

The family of power-raised hyperbolic secant (PHS) distributions $f(x,n)$ dealt with in this paper is characterized by a departure from normality as n increases. This is mirrored by both a growing kurtosis and a falling entropy. Cases of moderate leptokurtosis, which occur in several economic time series, are covered by the PHS family, but these distributions are unsuitable for these cases of severe excess kurtosis and asymmetry which are often found in financial data.

However, as the paper shows, this can be coped with Gram–Charlier-type (GCT) expansions based on orthogonal polynomials of f(x,n). This is, again, accompanied by a rise in the kurtosis along with a drop in entropy. The PHS family, and in particular its GCT expansions, provides an effective reference frame for modelling data whose departure from normality is evidenced by a thickness of the empirical distribution tails. Extensions to skewness effects clear the way to further applications, especially in financial econometrics.