Unsupervised Symbolization of Signal Time Series for Extraction of the Embedded Information
Abstract
:1. Introduction
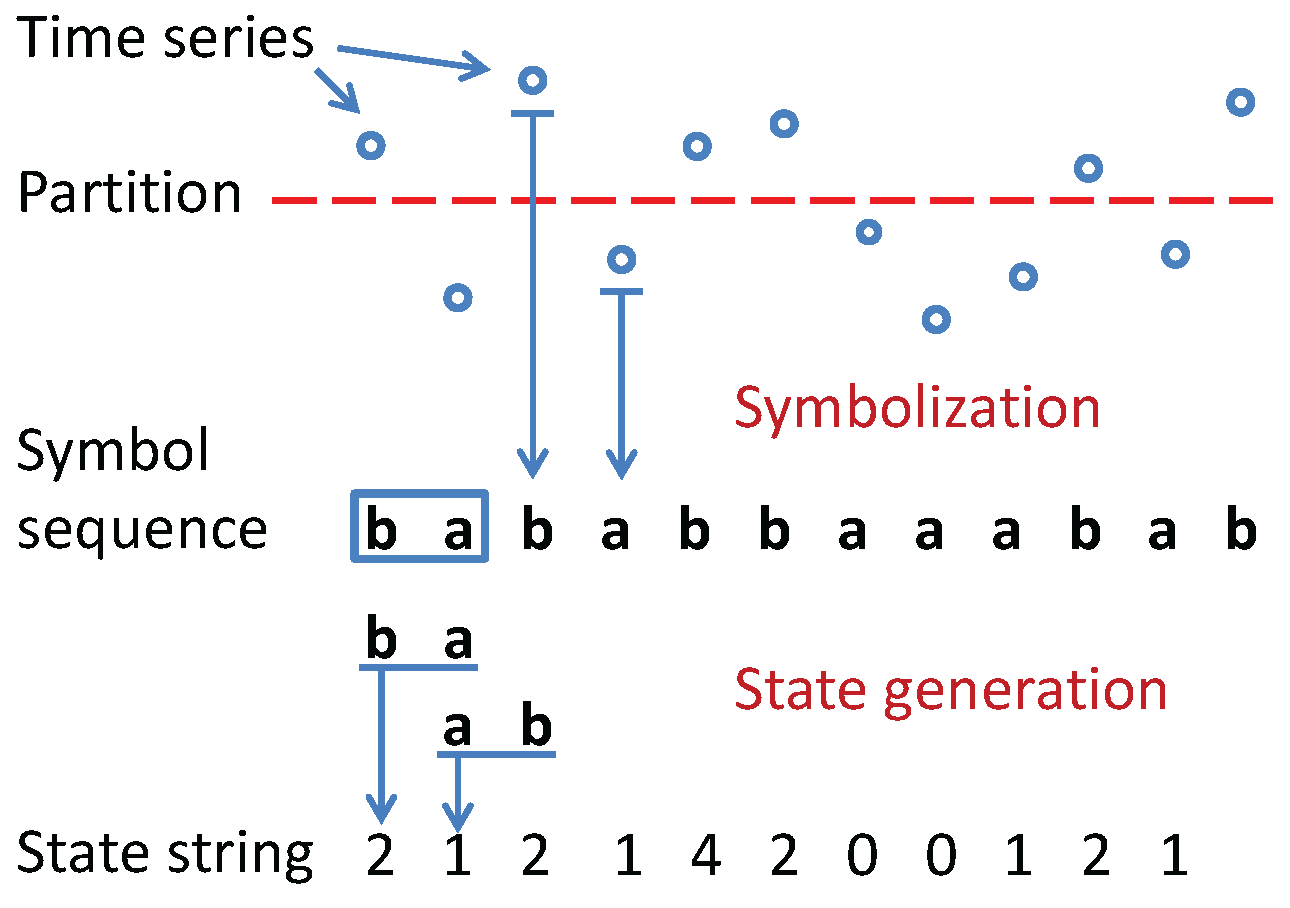
- Coarse-graining of time series to convert the scalar or vector-valued data into symbol strings, where the symbols are drawn from a (finite) alphabet [8].
- Unsupervised symbolization of time series: Simultaneous selection of symbols and words based on information-theoretic measures.
- Word selection for a given symbolic series: Adaptive variable embedding based on the mutual information between symbols and potential words.
- Determination of symbol alphabet size: Prevention of excessive symbolization for information extraction.
- Validation on both simulation and experimental data: Demonstration of performance robustness with presence of added zero-mean Gaussian noise and background noise of varying environment.
2. Mathematical Preliminaries
2.1. Probabilistic Deterministic Finite Automata
- 1.
- Σ is a non-empty finite set, called the symbol alphabet;
- 2.
- is a non-empty finite set, called the set of states;
- 3.
- is the state transition map;
- 4.
- is a set of initial states ();
- 5.
- is a set of final states ().
- 1.
- Σ is a non-empty finite set, called the symbol alphabet, with cardinality ;
- 2.
- is a non-empty finite set, called the set of states, with cardinality ;
- 3.
- is the state transition map;
- 4.
- is the symbol generation matrix (also called probability morph matrix) that satisfies the condition , and is the probability of emission of the symbol when the state is observed.
- 1.
- is the state set corresponding to a symbol string , where is the (finite) cardinality of the state set.
- 2.
- is the alphabet set of symbol string , where is the (finite) cardinality of the alphabet Σ of symbols.
- 3.
- is the state transition mapping. It is noted that the PFSA structure is built on and thus, the transition map explains the same symbol string;
- 4.
- is the morph matrix of size ; the -th element of Π denotes the probability of finding the symbol at next time step while making a transition from the state .
2.2. Information Theory
2.3. Distance Measurement for Symbol Sequences
3. Problem Statement
- Problem#1: Determination of the alphabet size , which is the number of symbols in the alphabet , for representation of the time series as a string of symbols.
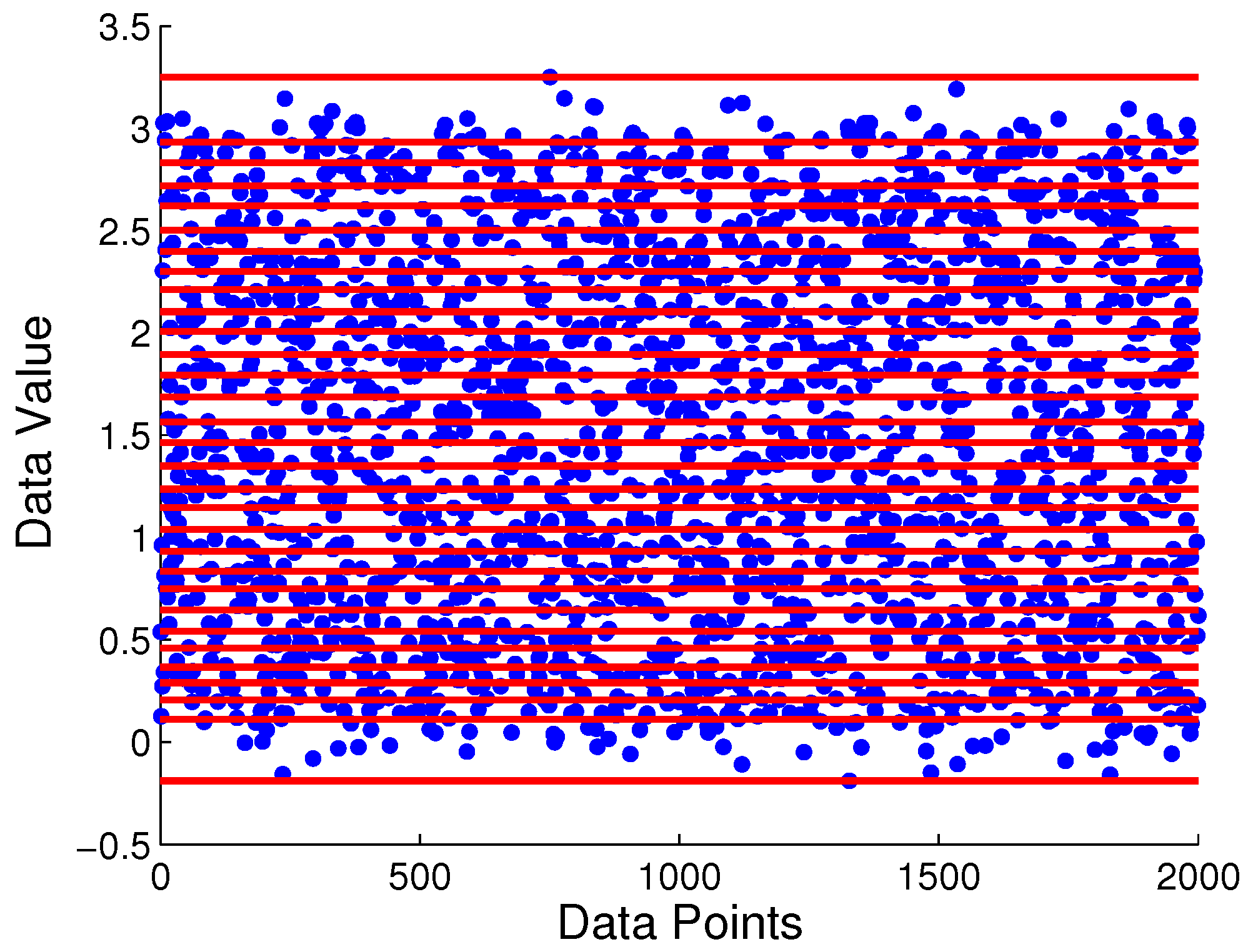
- Problem#2: Identification of the partitioning boundary locations, , which quantizes the signal space into a finite number of mutually exclusive and exhaustive regions. Each region is associated with a unique symbol, to which the time series signal in that region is mapped.
- Problem#3: Identification of the state set , which consists of meaningful (i.e., relevant) symbol patterns that could reduce the uncertainty of the temporal transition in the symbol sequence [10].
- Crterion#1: The frequency of the symbol block occurring in the symbol sequence.
- Crterion#2: Influence of the symbol block on the next observed symbol in temporal order.
| Algorithm 1 Maximum Entropy Partitioning |
| Require: Finite-length time series |
| and alphabet size . |
| Ensure: Partition position vector |
| 1: Sort the time series in the ascending order; |
| 2: Let K=length(), which is the length of the time series; |
| 3: Assign = , i.e., the minimum element of |
| 4: for i=2 to do |
| 5: = |
| 6: end for |
| 7: Assign = , i.e., the maximum element of |
4. Technical Approach
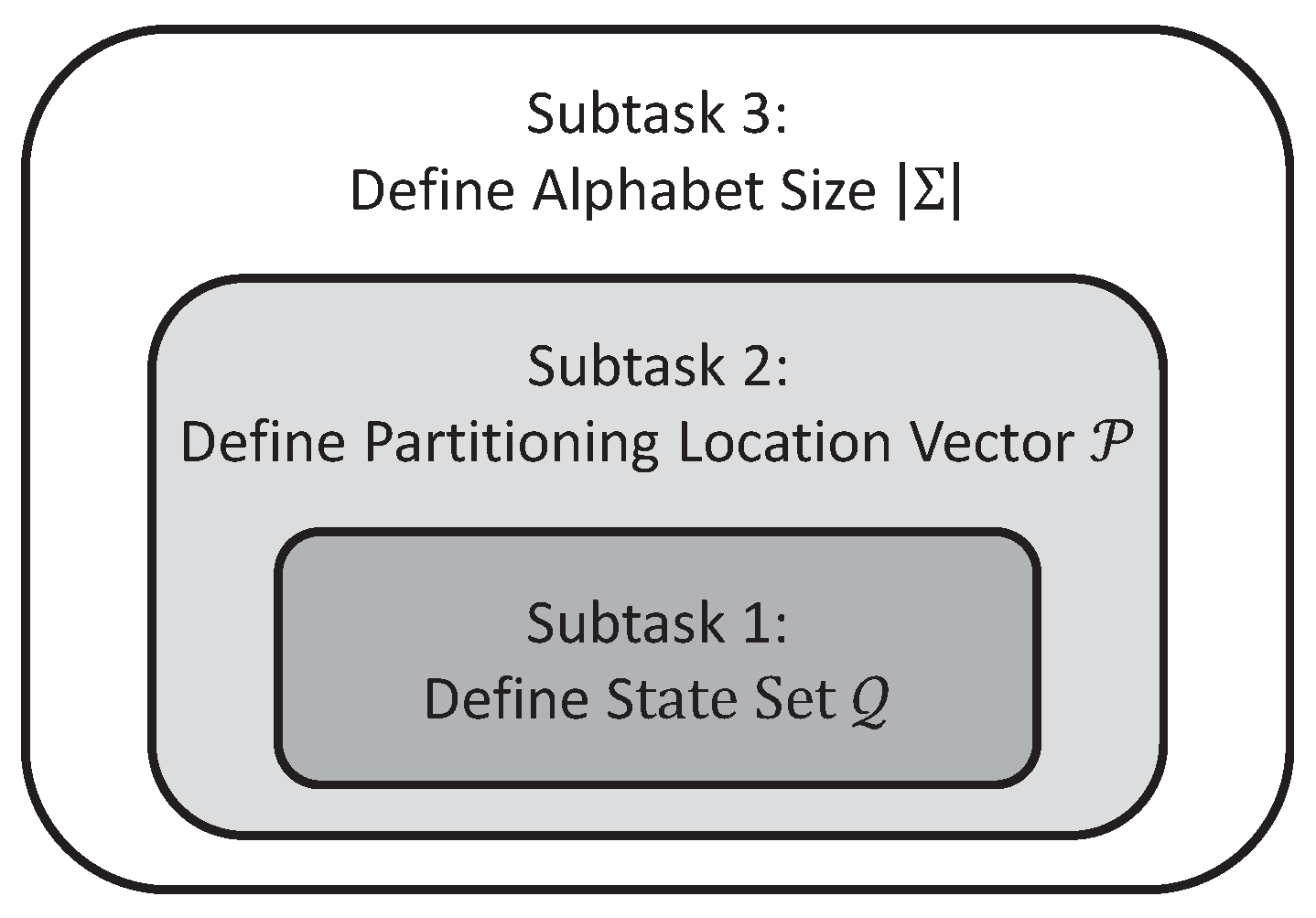
- Subtask 1: Identification of the state set that maximizes the mutual information via variable Markov Modeling for any given alphabet size and partitioning location vector .
- Subtask 2: Identification of the partitioning location vector among a pre-defined candidate set, which maximizes the mutual information for any given alphabet size , while the state set is obtained from Subtask 1 for each individual candidate.
- Subtask 3: Identification of the alphabet size , which maximizes the mutual information , while the state set and the partitioning location vector are obtained from Subtask 1 and Subtask 2, respectively, for each choice of alphabet size .
| Algorithm 2 State Splitting for Variable-Depth D-Markov Machine |
| Require: Symbol sequences |
| threshold for state splitting and |
| Ensure: State set |
| 1: Initialize: Create a 1-Markov machine |
| 2: repeat |
| 3: |
| 4: for i=1 to do |
| 5: if and then |
| 6: |
| 7: end if |
| 8: end for |
| 9: until |
| Algorithm 3 Partitioning by Sequential Selection Based on an Information-Theoretic Measure |
| Require: Time series , Alphabet size , and number, m, of candidate partitioning locations. |
| Ensure: Partitioning location vector and the maximum mutual information for alphabet size . |
| 1: Create the set of candidate partitioning locations via MEP in Algorithm 1. |
| 2: Assign the partitioning location vector and . |
| 3: for n=2 to do |
4: Obtain locally optimal partitioning
|
| 5: The specific partitioning location , corresponding to the the maximum mutual information , is removed from C and is included in the set of selected partitioning locations to construct the locally optimal . |
| 6: end for |
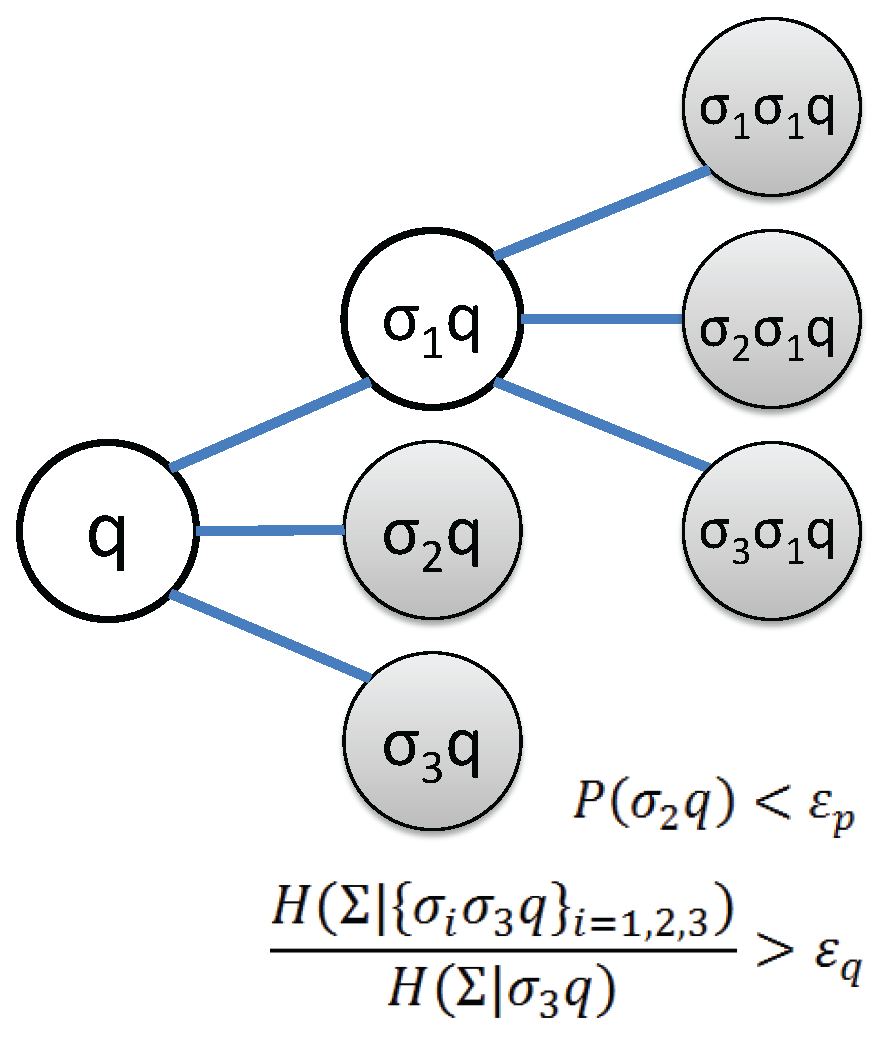
4.1. Subtask 1: Determine the State Set
- Threshold for occurrence probability , indicating whether a state has relevant statistical information or not.
- Threshold for conditional entropy reduction that determines whether states of longer memory is necessary or not.
4.2. Subtask 2: Identification of Partitioning Locations
4.3. Subtask 3: Determine the Alphabet Size
5. Performance Validation
- Numerical simulation of a PFSA model.
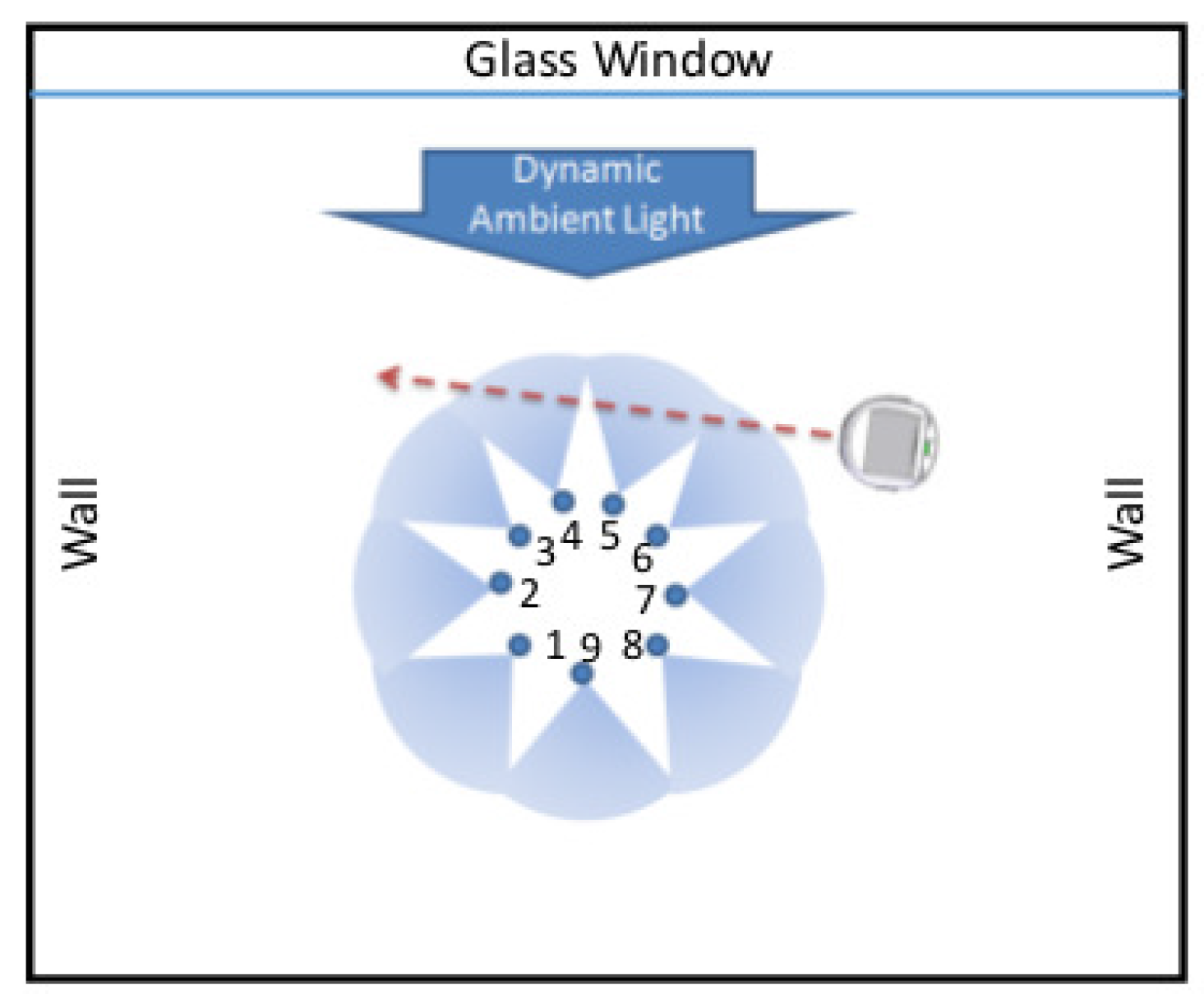
- Laboratory-scale experiments on a local passive infrared sensor network for target detection under dynamic environment.
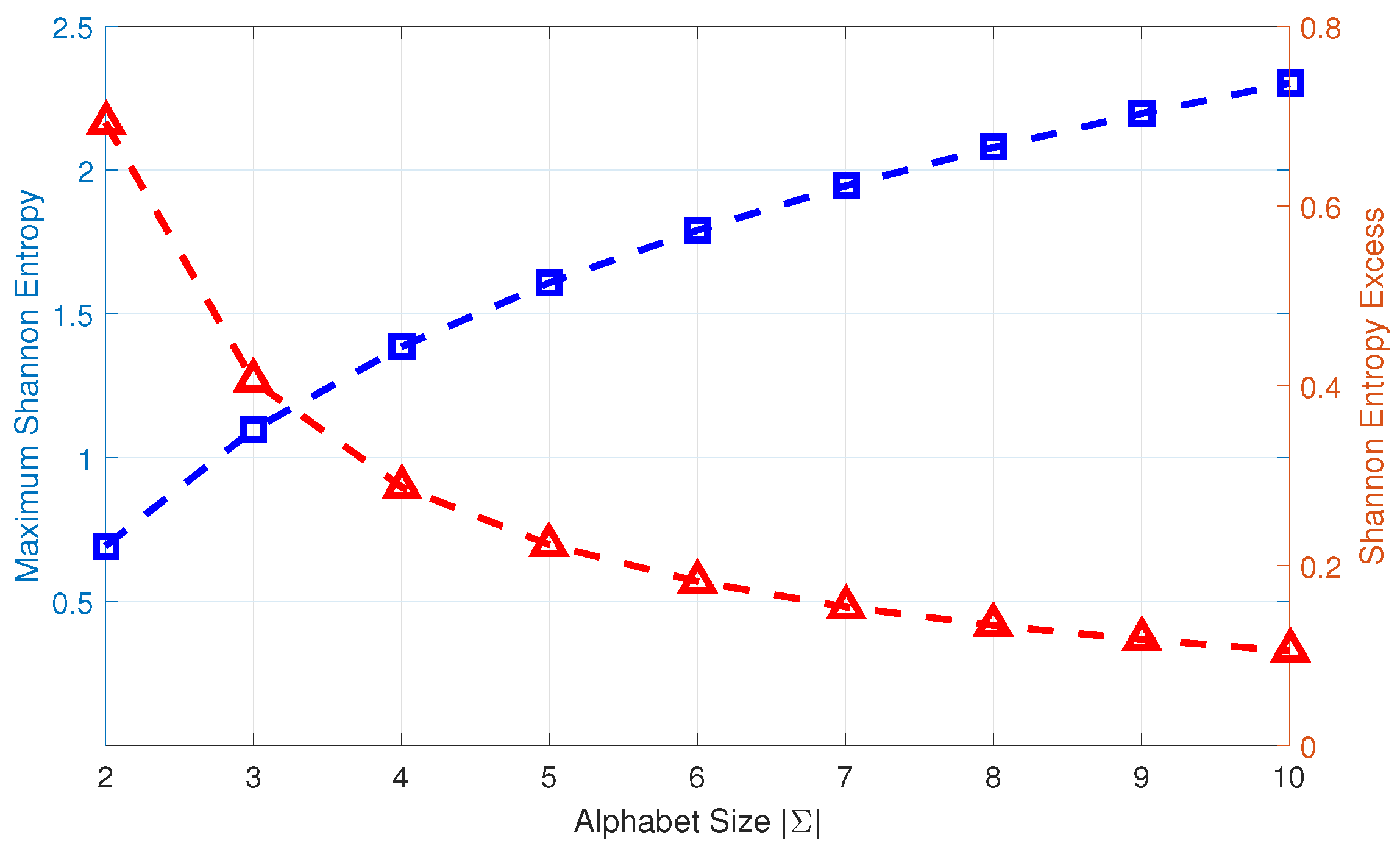
- The threshold for alphabet size selection in Equation (16).
- The threshold of occurrence probability for state splitting in Algorithm 2.
- The threshold of conditional entropy reduction for state splitting in Algorithm 2.
5.1. Numerical Simulation
5.2. Experimental Validation in a Laboratory Environment
5.2.1. Data Collection
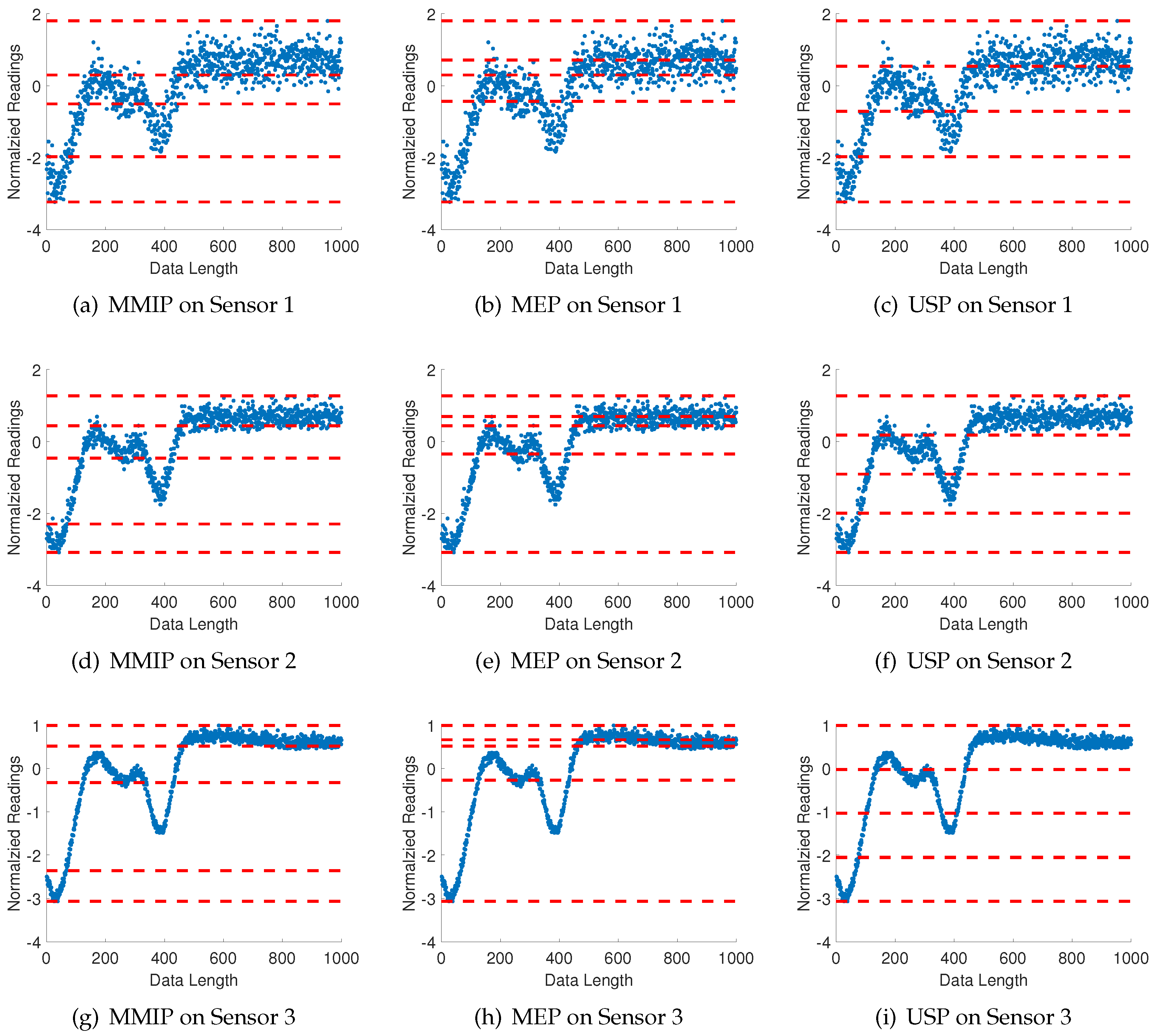
5.2.2. Consensus Partitioning among Multiple Time Series
| Algorithm 4 Consensus Partition Position Selection for Multiple Time Series |
| Require: Multiple time series , Alphabet size , and number m of candidates for a partitioning position. |
| Ensure: Partition position vector and the average maximum mutual information among all time series for the given alphabet size . |
| 1: Create a set of candidate partitioning locations via MEP (Algorithm 1) for k-th time series. |
| 2: for n=2 to do |
3:
|
| 4: The specific partitioning locations , corresponding to the the maximum mutual information , are removed from for each time series and is included in the set of selected partitioning locations to construct the optimal . |
| 5: end for |
5.2.3. Results
6. Conclusions and Future Work
- Determination of the symbol alphabet size .
- Identification of the boundary locations for partitioning, , of the time series.
- Identification of the state set in the PFSA model.
- Vector time series: Generalization of the proposed symbolization algorithm from scalar-valued (i.e., one dimensional) time series to vector-valued (i.e., multi-dimensional) time series.
- Extension of the proposed symbolization method for information extraction from time series: One such potential approach is the usage of ordinal patterns [34] in the symbolized time series, which defines symbols into characteristic zones, instead of partitioning the full data range.
- Investigation of the effects of the sampling rate on partitioning of the time series: The choice of symbols and states is influenced by the sampling rate of data acquisition. It is necessary to establish an adaptive algorithm that will allow autonomous downsampling or upsampling of time series before symbolization.
- Threshold parameters, and : Quantitative evaluation of these parameters as inputs to Equation (16) and Algorithm 2.
- Suboptimality of greedy search: Quantification of estimated losses in the proposed greedy search algorithm with respect to an optimal or near-optimal algorithm.
- Comparative evaluation: Extensive investigation to further evaluate the proposed method for comparison with other reported work on symbolization of time series (e.g., Symbolic Aggregate approXimation (SAX) [35]).
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hadamard, J. Les surfaces à courbures opposées et leurs lignes géodésique. J. Math. Pures Appl. 1898, 4, 27–73. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Lin, J.; Keogh, E.; Lonardi, S.; Chiu, B. A symbolic representation of time series, with implications for streaming algorithms. In Proceedings of the 8th ACM SIGMOD wOrkshop on Research Issues in Data Mining and Knowledge Discovery, San Diego, CA, USA, 13 June 2003; pp. 2–11. [Google Scholar]
- Daw, C.S.; Finney, C.E.A.; Tracy, E.R. A review of symbolic analysis of experimental data. Rev. Sci. Instrum. 2003, 74, 915–930. [Google Scholar] [CrossRef]
- Ray, A. Symbolic dynamic analysis of complex systems for anomaly detection. Signal Process. 2004, 84, 1115–1130. [Google Scholar] [CrossRef]
- Mukherjee, K.; Ray, A. State splitting and merging in probabilistic finite state automata for signal representation and analysis. Signal Process. 2014, 104, 105–119. [Google Scholar] [CrossRef]
- Martin, L.; Puterman, M.L. Markov Decision Processes: Discrete Stochastic Dynamic Programming; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Lind, D.; Marcus, B. An Introduction to Symbolic Dynamics and Coding; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Rajagopalan, V.; Ray, A. Symbolic time series analysis via wavelet-based partitioning. Signal Process. 2006, 86, 3309–3320. [Google Scholar] [CrossRef]
- Graben, P.B. Estimating and improving the signal-to-noise ratio of time series by symbolic dynamics. Phys. Rev. E 2001, 64, 051104. [Google Scholar] [CrossRef] [PubMed]
- Piccardi, C. On the control of chaotic systems via symbolic time series analysis. Chaos 2004, 14, 1026–1034. [Google Scholar] [CrossRef] [PubMed]
- Alamdari, M.M.; Samali, B.; Li, J. Damage localization based on symbolic time series analysis. Struct. Control Health Monit. 2015, 22, 374–393. [Google Scholar] [CrossRef]
- Sarkar, S.; Chattopadhyay, P.; Ray, A. Symbolization of dynamic data-driven systems for signal representation. Signal Image Video Process. 2016. [Google Scholar] [CrossRef]
- Kennel, M.B.; Mees, A.I. Context-tree modeling of observed symbolic dynamics. Phys. Rev. E 2002, 66, 056209. [Google Scholar] [CrossRef] [PubMed]
- Takens, F. Detecting Strange Attractors in Turbulence; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Rissanen, J. A universal data compression system. IEEE Trans. Inf. Theory 1983, 29, 656–664. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Bakar, A.A.; Hamdan, A.R. Dynamic data discretization technique based on frequency and k-nearest neighbour algorithm. In Proceedings of the 2nd Conference on Data Mining and Optimization, DMO’09, Pekan Bangi, Malaysia, 27–28 October 2009; pp. 10–14. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer: New York, NY, USA; Secaucus, NJ, USA, 2006. [Google Scholar]
- Lehrman, M.; Rechester, A.B.; White, R.B. Symbolic analysis of chaotic signals and turbulent fluctuations. Phys. Rev. Lett. 1997, 78, 54. [Google Scholar] [CrossRef]
- Mörchen, F.; Ultsch, A. Optimizing time series discretization for knowledge discovery. In Proceedings of the Eleventh ACM SIGKDD International Conference on Knowledge Discovery in Data Mining, Chicago, IL, USA, 21–24 August 2005; pp. 660–665. [Google Scholar]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Barron, A.; Rissanen, J.; Yu, B. The minimum description length principle in coding and modeling. IEEE Trans. Inf. Theory 1998, 44, 2743–2760. [Google Scholar] [CrossRef]
- Willems, F.M.J.; Shtarkov, Y.M.; Tjalkens, T.J. The context-tree weighting method: basic properties. IEEE Trans. Inf. Theory 1995, 41, 653–664. [Google Scholar] [CrossRef]
- Darema, F. Dynamic data driven applications systems: New capabilities for application simulations and measurements. In Proceedings of the 5th International Conference on Computational Science—ICCS 2005, Atlanta, GA, USA, 22–25 May 2005. [Google Scholar]
- Crochemore, M.; Hancart, C. Automata for matching patterns. In Handbook of Formal Languages; Springer: Berlin/Heidelberg, Germany, 1997; Volume 2, Chapter 9; pp. 399–462. [Google Scholar]
- Béal, M.P.; Perrin, D. Symbolic dynamics and finite automata. In Handbook of Formal Languages; Springer: Berlin/Heidelberg, Germany, 1997; Volume 2, Chapter 10; pp. 463–506. [Google Scholar]
- Sipser, M. Introduction to the Theory of Computation; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Palmer, N.; Goldberg, P.W. Pac-learnability of probabilistic deterministic finite state automata in terms of variation distance. Theor. Comput. Sci. 2007, 387, 18–31. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Feldman, D.P. A Brief Introduction to: Information Theory, Excess Entropy and Computational Mechanics; College of the Atlantic: Bar Harbor, ME, USA, 2002; Volume 105, pp. 381–386. [Google Scholar]
- Dupont, P.; Denis, F.; Esposito, Y. Links between probabilistic automata and hidden markov models, probability distributions, learning models and induction algorithms. Pattern Recognit. 2005, 38, 1349–1371. [Google Scholar] [CrossRef]
- Li, Y.; Jha, D.K.; Ray, A.; Wettergren, T.A. Information fusion of passive sensors for detection of moving targets in dynamic environments. IEEE Trans. Cybern. 2017, 47, 93–104. [Google Scholar] [CrossRef] [PubMed]
- Robot, K., III. User Manual, version 2.1. Available online: https://www.k-team.com/mobile-robotics-products/khepera-iii (accessed on 30 March 2017).
- Kulp, C.W.; Chobot, J.M.; Freitas, H.R.; Sprechini, G.D. Using ordinal partition transition networks to analyze ecg data. Chaos 2016, 26, 073114. [Google Scholar] [CrossRef] [PubMed]
- Malinowski, S.; Guyet, T.; Quiniou, R.; Tavenard, R. 1d-sax: A novel symbolic representation for time series. In Proceedings of the International Symposium on Intelligent Data Analysis, IDA2013: Advances in Intelligent Data Analysis XII, London, UK, 17–19 October 2013; pp. 273–284. [Google Scholar]
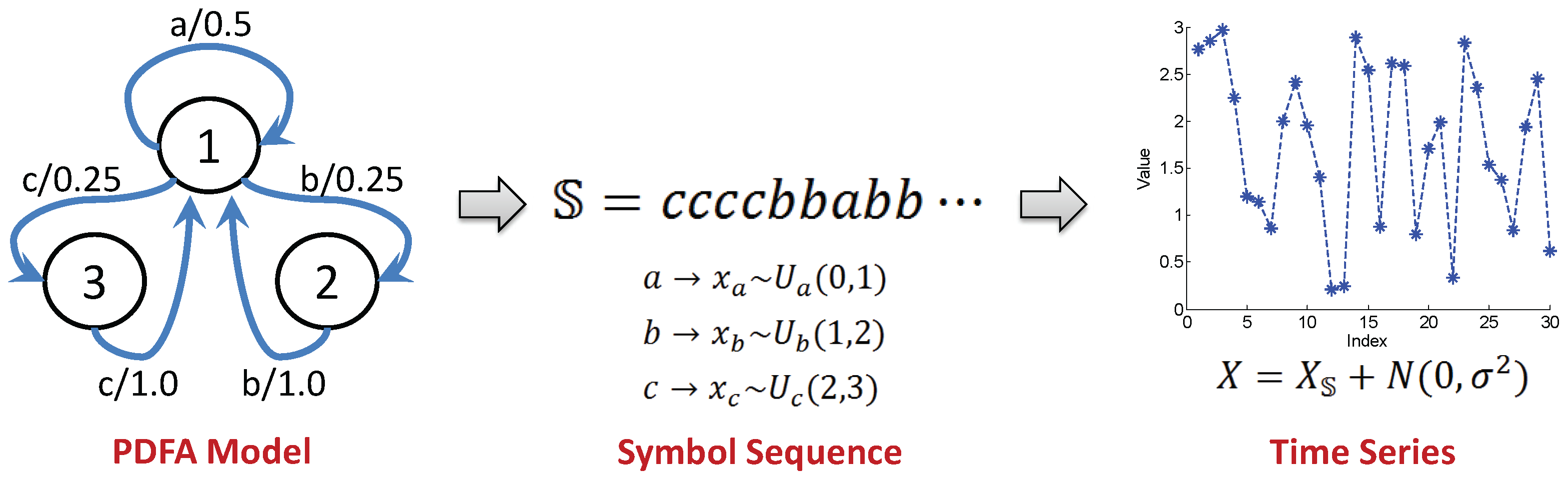


| Alphabet | a | b | c | ||
|---|---|---|---|---|---|
| a | |||||
| State | |||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Ray, A. Unsupervised Symbolization of Signal Time Series for Extraction of the Embedded Information. Entropy 2017, 19, 148. https://doi.org/10.3390/e19040148
Li Y, Ray A. Unsupervised Symbolization of Signal Time Series for Extraction of the Embedded Information. Entropy. 2017; 19(4):148. https://doi.org/10.3390/e19040148
Chicago/Turabian StyleLi, Yue, and Asok Ray. 2017. "Unsupervised Symbolization of Signal Time Series for Extraction of the Embedded Information" Entropy 19, no. 4: 148. https://doi.org/10.3390/e19040148






