Paradigms of Cognition ^†

Abstract

An abstract, quantitative theory which connects elements of information—key ingredients in the cognitive proces—is developed. Seemingly unrelated results are thereby unified. As an indication of this, consider results in classical probabilistic information theory involving information projections and so-called Pythagorean inequalities. This has a certain resemblance to classical results in geometry bearing Pythagoras’ name. By appealing to the abstract theory presented here, you have a common point of reference for these results. In fact, the new theory provides a general framework for the treatment of a multitude of global optimization problems across a range of disciplines such as geometry, statistics and statistical physics. Several applications are given, among them an “explanation” of Tsallis entropy is suggested. For this, as well as for the general development of the abstract underlying theory, emphasis is placed on interpretations and associated philosophical considerations. Technically, game theory is the key tool.

Contents

1	Introduction		2
2	Information without Probability		5
	2.1	The World and You . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	5
	2.2	Truth and Belief . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	5
	2.3	A Tendency to Act, a Wish to Control . . . . . . . . . . . . . . . . . . . . . . .	6
	2.4	Atomic Situations, Controllability and Visibility . . . . . . . . . . . . . . .	7
	2.5	Knowledge, Perception and Deformation . . . . . . . . . . . . . . . . . . . .	8
	2.6	Effort and Description . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	9
	2.7	Information Triples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	11
	2.8	Relativization, Updating . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	15
	2.9	Feasible Preparations, Core and Robustness . . . . . . . . . . . . . . . . . .	16
	2.10	Inference via Games, Some Basic Concepts . . . . . . . . . . . . . . . . . .	18
	2.11	Refined Notions of Properness . . . . . . . . . . . . . . . . . . . . . . . . . . . .	21
	2.12	Inference via Games, Some Basic Results . . . . . . . . . . . . . . . . . . . .	22
	2.13	Games Based on Utility, Updating . . . . . . . . . . . . . . . . . . . . . . . . . .	28
	2.14	Formulating Results with a Geometric Flavour . . . . . . . . . . . . . . . .	29
	2.15	Adding Convexity . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	32
	2.16	Jensen-Shannon Divergence at Work . . . . . . . . . . . . . . . . . . . . . . . .	36
3	Examples, towards Applications		42
	3.1	Primitive Triples and Generation by Integration . . . . . . . . . . . . . . .	42
	3.2	A Geometric Model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	48
	3.3	Universal Coding and Prediction . . . . . . . . . . . . . . . . . . . . . . . . . . .	50
	3.4	Sylvester’s Problem from Location Theory . . . . . . . . . . . . . . . . . . .	52
	3.5	Capacity Problems, an Indication . . . . . . . . . . . . . . . . . . . . . . . . . .	53
	3.6	Tsallis Worlds . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	54
	3.7	Maximum Entropy Problems of Classical Shannon Theory . . . . . .	58
	3.8	Determining D-Projections . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	60
4	Conclusions		61
A	Notions of Properness		62
B	Protection against Misinformation		65
C	Cause and Effect		66
D	Negative Definite Kernels and Squared Metrics		66

1. Introduction

Originally, the driving force behind this study was to extend the clear and convincing operational interpretations associated with classical information theory as developed by Shannon [1] and followers, to the theory promoted by Tsallis for statistical physics and thermodynamics, cf., [2,3]. That there are difficulties is witnessed by the fact that, despite its apparent success, some well known physicists still find grounds for criticism. Evidence of this attitude may be found in Gross [4].

A possible solution to the problem is presented towards the end of our study, in Theorem 18. It is based on the idea that, possibly, what the physicist perceives as the essence in a particular situation could be a result of both the true state of the situation and the physicists preconceptions as expressed by his beliefs. In case there is no deformation from truth and belief to perception, i.e., if “what you see is what is true”, you regain the classical notions of Boltzmann, Gibbs and Shannon.

The approach indicated in Theorem 18 rests on philosophical considerations and associated interpretations. As it turns out, this approach is applicable in a far more abstract setting than needed for the discussion of the particular problem. As a result, a general abstract, quantitative theory is developed. This theory, presented in Section 2, with its many subsections is the main contribution of our research. A number of possible applications, including Theorem 18, are listed in Section 3, which has a number of sub-sections covering applications from different areas. They serve as justification for the work which has gone into the development of the general abstract theory. The conclusions are collected in Section 4.

The theory may be seen as an extension of classical Shannon theory. One does not achieve the same degree of clarity as in the classical theory, where coding provides a solid reference. However, the results developed in Section 2 and Section 3 demonstrate that the extension to a more abstract framework is meaningful and opens up for new areas of research. In addition, previous results are consolidated and unified.

The theory of Section 2 is an abstract theory of information without probability. Inspiration from Shannon Theory and from the theory of inference within statistics and statistical physics is apparent. However, the ideas are presented here as an independent theory.

Previous endeavours in the direction taken include research by Ingarden and Urbanik [5] who wrote “... information seems intuitively a much simpler and more elementary notion than that of probability ... [it] represents a more primary step of knowledge than that of cognition of probability ...”. We also point to Kolmogorov, cf., [6,7] who in the latter reference (but going back to 1970, it seems) stated “Information theory must precede probability theory and not be based on it”. The ideas by Ingarden and Urbanik were taken up by Kampé de Fériet, see the survey in [8]. The work of Kampé de Fériet is rooted in logic. Logic is also a key ingredient in comprehensive studies over some 40 years by Jaynes, collected posthumously in [9]. Although many philosophically-oriented discussions are contained in the work of Jaynes, the situations he deals with are limited to probabilistic models and intended mainly for a study of statistical physics.

The work by Amari and Nagaoka in information geometry, cf., [10], may also be viewed as a broad attempt to free oneself from a tie to probability. There are many followers of the theory developed by Amari and Nagaoka. Here we only mention the recent thesis by Anthonis [11] which has a base in physics.

In complexity theory as developed by Solomonoff, Kolmogorov and others, cf., the recent survey [12] by Rathmanner and Hutter, we have a highly theoretical discipline which aims at inference not necessarily tied to probabilistic modeling. The Minimum Description Length Principle may be considered an important spin-off of this theory. It is mainly directed at problems of statistical inference and was developed, primarily, by Rissanen and by Barron and Yu, cf., [13]. We also point to the treatise [14] by Grünwald. In this work you find discussions of many of the issues dealt with here, including a discussion of the work of Jaynes.

Still other areas of research have a bearing on “information without probability”, e.g., semiotics, philosophy of information, pragmatism, symbolic linguistics, placebo research, social information and learning theory. Many areas within psychology are also of relevance. Some specific works of interest include Jumarie [15], Shafer and Vovk [16], Gernert [17], Bundesen and Habekost [18], Benedetti [19] and Brier [20]. The handbook [21] edited by Adriaans and Bentham and the encyclopaedia article [22] by Adriaans collect views on the very concept of “information”. Over the years, an overwhelming amount of thought has been devoted to that concept in one form or another. Most of this bulk of material is entirely philosophical and not open to quantitative analysis. Part of it is impractical and presently mainly of theoretical interest. Moreover, some is far from Shannon’s theory which we hold as a cornerstone of quantitative information theory. In fact, we consider it a requirement of any quantitative theory of information to be downward compatible with basic parts of Shannon theory. This requirement is largely respected in the present work, but not entirely. For example, we do not know if one can meaningfully lift the concept of coding as known from Shannon theory to a more abstract level.

In many respects, our endeavours go “beyond Shannon”. So does, e.g., Brier in his development of cybersemiotics, cf., [20,23]. Brier goes deeper into some of the philosophical aspects than we do and also attempts a broad coverage by incorporating not only the exact natural sciences but also life science, the humanities and the social sciences. Though not foreign to such a wider scope, our study aims at more concrete results by basing the study more directly on quantitative elements. Both studies emphasize the role of the individual in the cognitive process.

A special feature of our development is the appeal to game theoretical considerations, cf., especially Section 2.10, Section 2.12 and Section 2.13. To illuminate the importance we attach to this aspect we quote from Jaynes’ preface to [9] where he comments on the maximum entropy principle, the central principle of inference promoted by Jaynes:

“... it [maximum entropy] predicts only observable facts (functions of future or past observations) rather than values of parameters which may exist only in our imagination ... it protects us against drawing conclusions not warranted by the data. But when the information is extremely vague, it may be difficult to define any appropriate sample space, and one may wonder whether still more primitive principles than maximum entropy can be found. There is room for much new creative thought here.”

This is one central place where game theory comes in. It represents a main addition, so we claim, to Jaynes’ work In passing, it is noted that at the conference “Maximum Entropy and Bayesian Methods”, Paris 1992, the author had much hoped to discuss the impact of game theoretical reasoning with professor Jaynes. Unfortunately, Jaynes, who died in 1998, was too ill at the time to participate. He never incorporated arguments such as those in [24] which can be conceived as supportive of his own theory.

The merits of game theory in relation to information theoretical inference were first indicated in the probabilistic, Shannon-like setting, independently of each other, by Pfaffelhuber [25] and by the author [26]. More recent references include Harremoës and Topsøe [27], Grünwald and Dawid [28], Friedman et al. [29] (a utility-based work) and Dayi [30]. As sources of background material [31,32,33] may be helpful.

The quantitative elements we work with are brought into play via a focus on description effort—or just effort. From this concept, general notions of entropy and redundancy (and the close to equivalent notion of divergence) are derived. The information triples we shall take as the key object of study are expressions of the concepts effort/entropy/redundancy (or effort/entropy/divergence). By a “change of sign”, the triples may, just as well, concern utility/max-utility/divergence.

Apart from introducing game theory into the picture, a main feature of the present work lies in its abstract nature with a focus on interpretations rather than on axiomatics which was the emphasis of many previous authors, including Jaynes.

The set of interpretations we shall emphasize in Section 2 is not be the only one possible. Different sets of interpretations are briefly indicated in Appendix B and Appendix C. Though some of this played a role in the development, in statistics, of the notion of properness, we have relegated the material to the appendices, not to disturb the flow of presentation and also as we consider this material to be of lesser significance when comparing it with the main line of thought.

Section 3 may be viewed as a justification of the partly speculative deliberations of Section 2.1, Section 2.2, Section 2.3, Section 2.4, Section 2.5, Section 2.6, Section 2.7, Section 2.8, Section 2.9, Section 2.10, Section 2.11, Section 2.12, Section 2.13, Section 2.14, Section 2.15 and Section 2.16. Also, in view of the rather elaborate theory of Section 2 with many new concepts and unusual notation, it may well be that occasional reference to the material in Section 3 will ease the absorption of the theoretical material.

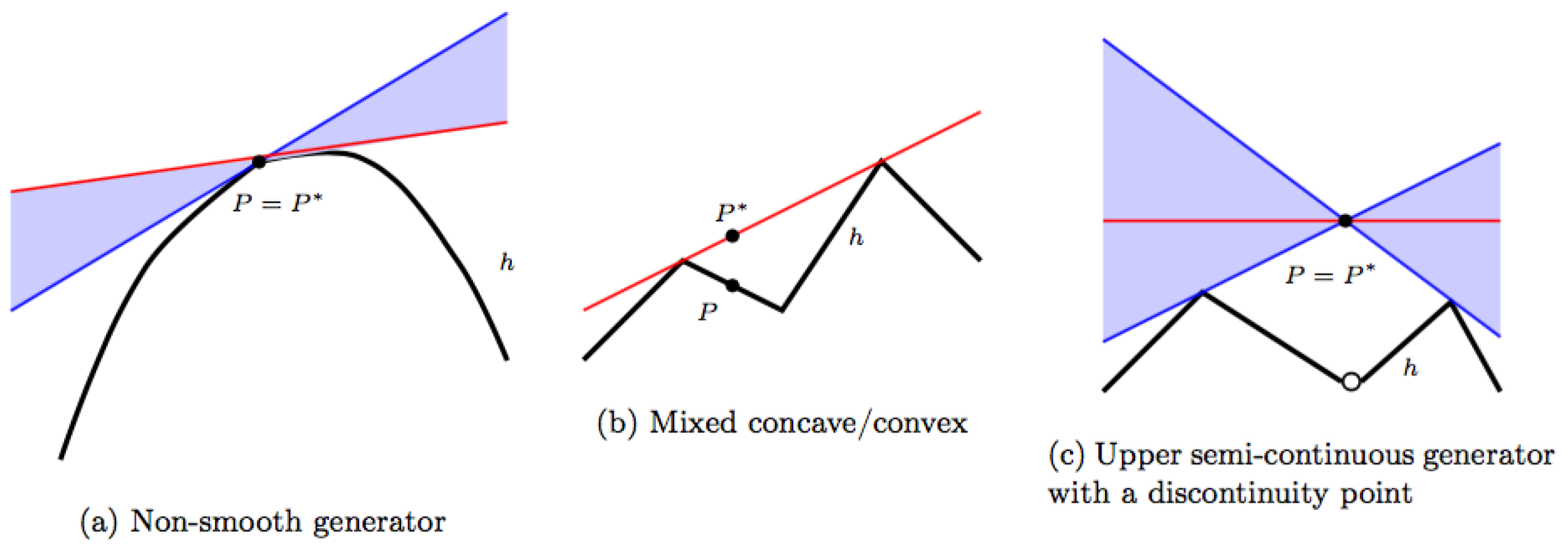
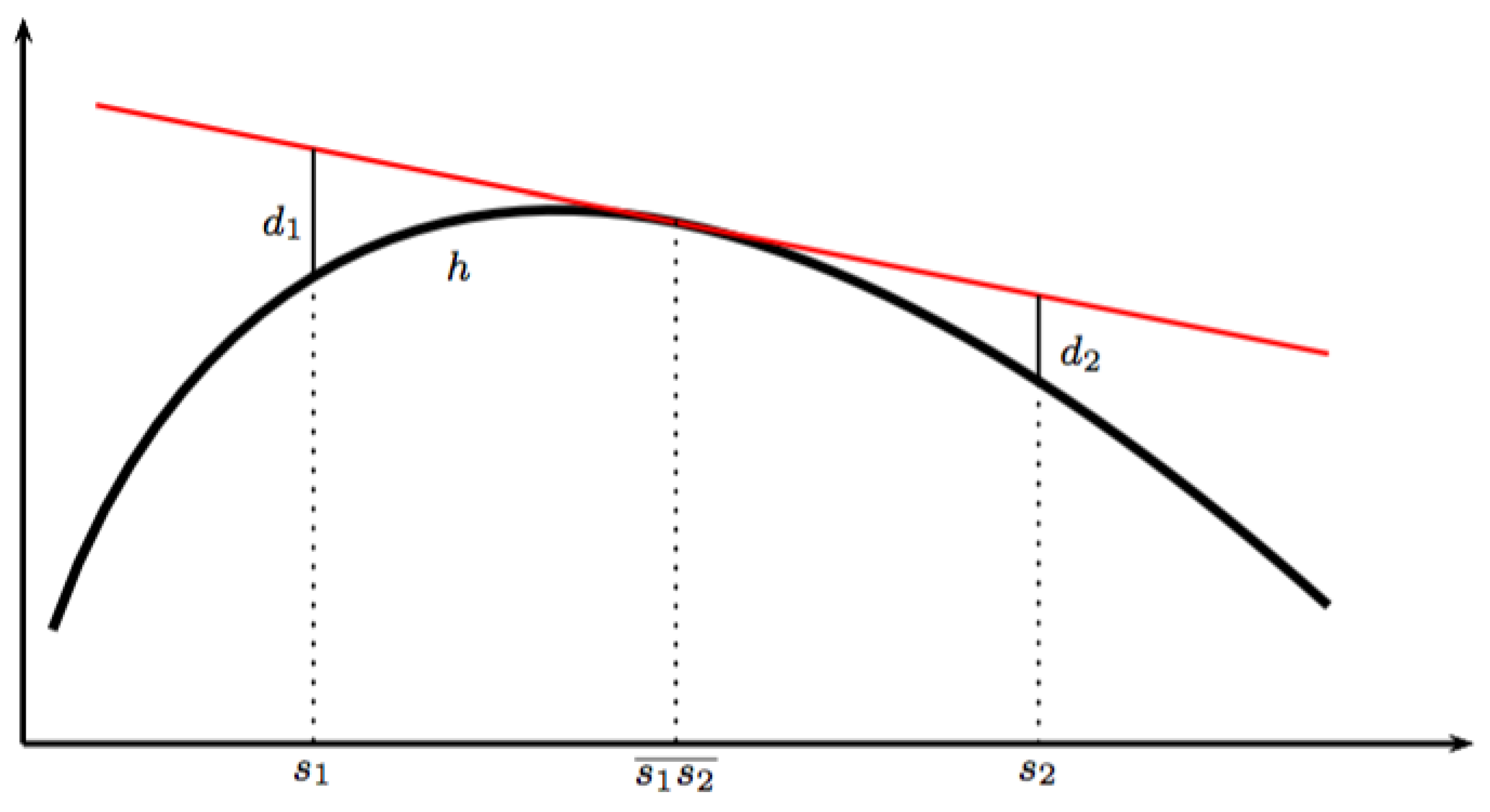
In Section 3.1, the natural building stones behind the information triples is presented. This is closely related to the well-known construction associated with Bregman’s name. The construction may be expanded by allowing non-smooth functions as “generators”. Pursuing this leads to situations where the standard notion of properness breaks down and needs a replacement by weaker notions. Such notions are introduced at the end of Section 2.10 but may only be appreciated after acquaintance with the less abstract material in Appendix A.

The applications presented—or indications of potential applications—come from combinatorial geometry, probabilistic information theory, statistics and statistical physics. For most of them, we focus on providing the key notions needed for the theory to work, thus largely leaving concrete applications aside. The aim is to provide enough details in order to demonstrate that our modeling can be applied in quite different contexts. For the case of discrete probabilistic models we do, however, embark on a more thorough analysis. The reason for this is, firstly, that this is what triggered the research reported on and, secondly, with a thorough discussion of modeling in this context, virtually all elements introduced in the many sub-sections of Section 2 have a clear and natural interpretation. In fact, full appreciation of the abstract theory may only be achieved after reading the material in Section 3.6 and Section 3.7.

Our treatment is formally developed independently of previous research. However, unconsciously or not, it depends on earlier studies as referred to above and on the tradition developed over time. More specifically, we mention that our focus on description effort, especially the notion of properness, cf., Section 2.6, is closely related to ideas first developed for areas touching on meteorology, statistics and information theory.

Previous relevant writings of the author include [34,35,36,37,38]. The present study is here published as a substantial expansion of the latter. For instance, elements related to control—modeling an observer’s active response to belief—and a detailed discussion of Jensen-Shannon divergence as well as more cumbersome technical details were left out in [38]. Thus, [38] may best serve as an easy-to-read appetizer to the present more heavy and comprehensive theory.

2. Information without Probability

2.1. The World and You

By $\mathrm{\Omega }$ we denote the actual world, perhaps one among several possible worlds. Two fictitious persons play a major role in our modeling, “Nature” and “Observer”. These “persons” behave quite differently and, though stereotypical, the reader may associate opposing sexes to them, say female for Nature, male for Observer. The interplay between the two takes place in relation to studies of situations from the world. Observer’s aim is to gain insight about situations studied. It may be helpful to think of Observer as “you”, say a physicist, psychologist, statistician, information theoretician or what the case may be. Nature is seen as an expression of the world itself and reflects the rules of the world. Mostly, such rules may be identified with laws of nature. However, we shall consider models where the rules express an interplay between Nature and Observer and as such may not be absolutes, independent of observer’s interference.

The insight or knowledge sought by Observer will be focused on inference concerning particular situations under study. A different form of inference not focused on any particular situation may also be of relevance if Observer does not know which world he is placed in. Of course, the actual world is a possible world or it could not exist. So Observer may, based on experience gained from situations encountered, attempt to ascertain which one out of a multitude of possible worlds is actualized.

The notions introduced are left as loose indications. They will take more shape as the modeling progresses. The terminology chosen here and later on is intended to provoke associations to common day experiences of the cognitive process. In addition, the terminology is largely consistent with usage in philosophy.

2.2. Truth and Belief

Nature is the holder of truth. Observer seeks the truth but is relegated to belief. However, Observer possesses a conscious and creative mind which can be exploited in order to obtain knowledge as effortlessly as possible. In contrast, Nature does not have a mind—and still, the reader may find it helpful to think of Nature as a kind of “person”!

We introduce a set X, the state space, and a set Y, the belief reservoir. Elements of X, generically denoted by x, are truth instances or states of truth or just states, whereas elements of Y, generically denoted by y, are belief instances. We assume that $Y\supseteq X$. Therefore, in any situation, it is conceivable that Observer actually believes what is true. Mostly, $Y=X$ will hold. Then, whatever Observer believes, could be true.

Typically, in any situation, we imagine that Nature chooses a state and that Observer chooses a belief instance. This leads to the introduction of certain games which will be studied systematically later on, starting with Section 2.10.

Though there may be no such thing as absolute truth, it is tempting to imagine that there is and to think of Natures choice as an expression of just that. This then helps to maintain a distinction between Nature and Observer. However, a closer analysis reveals that what goes on at Natures side is most correctly thought of as another manifestation of Observer. Thus the two sides cannot be separated. Rather, a key to our modeling is the interplay between the two.

For some models it may be appropriate to introduce a set $X_0\subseteq X$ of realistic states. States not in $X_0$ are considered unrealistic, out of reach for Observer, typically because they would involve availability of unlimited resources. Moreover, some models involve a set $Y_{\det }\subseteq Y$ of certain beliefs. Beliefs from $Y_{\det }$ are chosen by Observer if he is quite determined on what is going on—but of course, he could be wrong. If nothing is said to the contrary, you can take $X_0=X$ and $Y_{\det }=\mathrm{\varnothing }$.

In a specific situation, Nature’s choice may not be free within all of X. Rather, it may be restricted to a non-empty subset $𝒫$ of X, the preparation. The idea is that Observer, perhaps a physicist, can “prepare” a situation, thereby forcing Nature to restrict the choice of state accordingly. For instance, by placing a gas in a heat bath, Nature is restricted to states which have a mean energy consistent with the prescribed temperature.

A situation is normally characterized by specifying a preparation $\mathcal{P}$. A state x is consistent—viz., consistent with the preparation $\mathcal{P}$ of the situation—if $x\in \mathcal{P}$. Later on, we shall consider preparation families which are sets, generically denoted by $\mathbb{P}$, whose members are preparations.

Faced with a specific situation with preparation $\mathcal{P}$, Observer speculates about the state of truth chosen by Nature. Observer may express his opinion by assigning a belief instance to the situation. If this is always chosen from the preparation $\mathcal{P}$, Observer will only believe what could be true. Sometimes, Observer may prefer to assign a belief instance in Y\P to the situation. Then this instance cannot possibly be one chosen by Nature. Nevertheless, it may be an adequate choice if an instance inside $\mathcal{P}$ would contradict Observer’s subjective beliefs. Therefore, the chosen instance may be the “closest” to the actual truth instance in a subjective sense. Anyhow, Observer’s choice of belief instance is considered a subjective choice which takes available information into account such as general insight and any prior information. Qualitatively, these thoughts agree with Bayesian thinking, and as such enjoy the merits, but are also subject to the standard criticism, which applies to this line of thought, cf., [12,39].

2.3. A Tendency to Act, a Wish to Control

Two considerations will lead us to new and important structural elements.

First, we point to the mantra that belief is a tendency to act. This is a rewording taken from Good [40] who suggested this point of view as a possible interpretation of the notion of belief. In daily life, action appears more often than not to be a spontaneous reaction in situations man is faced with, rather than a result of rational considerations. Or reaction depends on psychological factors or brain activity largely outside conscious control. In contrast, we shall rely on rational thinking based on quantitative considerations. As a preparation we introduce a set $\widehat{Y}$, the action space, and a map from Y into $\widehat{Y}$, referred to as response. Elements of $\widehat{Y}$ are called actions. We use the notation $\widehat{y}$ to indicate the action which is Observer’s response in situations where Observer’s belief is represented by the belief instance y. Note that as we have assumed that $X\subseteq Y$, $\widehat{x}$ is well defined for every state x.

Response need not be injective, thus it is in general not possible to infer Observer’s belief from Observer’s action. Response need not either be surjective, though for most applications it will be so. Actions not in the range are idle for the actual model under discussion but may become relevant if the setting is later expanded.

Belief instances, say $y_1$ and $y_2$, with the same response are response-equivalent, notationally written $y_1\widehat{\sim }{y}_2$.

If the model contains certain beliefs, i.e., if $Y_{\det }\ne \mathrm{\varnothing }$, we assume that $\widehat{Y}$ contains a special element, the empty action, and that this action is chosen by Observer in response to any certain belief instance. In such cases, Observer sees no reason to take any action. If Observer finds several actions equally attractive, one could allow response to be a set-valued map. However, for the present study we insist that response is an ordinary map defined on all of Y. This will actually be quite important.

For a preparation $\mathcal{P}$, $\widehat{\mathcal{P}}$ denotes the set of $\widehat{x}$ with $x\in \mathcal{P}$.

Let us turn to another tendency of man, the wish to control. This makes us introduce a set W, the control space. The elements of W are referred to as controls. For the present modeling, this will not, formally, lead to further complications as we shall take W and $\widehat{Y}$ to be identical: $W=\widehat{Y}$. This simplification may be defended by taking the point of view that in order to exercise control, you have to act, typically by setting up appropriate experiments. Moreover, you may consider it the purpose of Observer’s action to exercise control. Thus, in an idealized and simplified model as here presented, we simply identify the two aspects, action and control. Later elaborations of the modeling may lead to a clear distinction between action and the more passive concept of control. As $\widehat{Y}$ and W are identified, we shall often use w as a generic element of $\widehat{Y}=W$ and we shall denote the empty action—the same as the empty control—by $w_{\mathrm{\varnothing }}$.

The simplest models are obtained when response is an injection or even a bijection. Moreover, simplest among these models are the cases when $Y=\widehat{Y}=W$ and response is the identity map. This corresponds to a further identification of belief with action or control. Even then it makes a difference if you think about an element as an expression of belief, as an expression of action or as an expression of control.

Although many models do not need the introduction of $\widehat{Y}$ (or W), the further development will to a large extent refer first and foremost to $\widehat{Y}$-related concepts. Technically, this results in greater generality, as response need not be injective. Belief-type concepts, often indicated by referring to the “Y-domain”, will then be derived from action- or control-based concepts, often indicated by pointing to the “$\widehat{Y}$-domain”. The qualifying indication may be omitted if it is clear from the context whether we work in the one domain or the other.

2.4. Atomic Situations, Controllability and Visibility

Two relations will be introduced. Controllability is the primary one from which the other one, visibility, will be derived. These relations constitute refinements which may be disregarded at a first reading. This can be done by taking the relations to be the diffuse relations , in notation below, $X\otimes \widehat{Y}=X\times \widehat{Y}$ and $X\otimes Y=X\times Y$. The reader may recall that in general mathematical jargon, a diffuse relation is one without restrictions, i.e., one for which any element is in relation to any other element.

Pairs of states and belief instances or pairs of states and controls are key ingredients in situations from the world. However, not all such pairs will be allowed. Instead, we imagine that offhand, Observer has some limited insight into Natures behaviour and therefore, Observer takes care not to choose “completely stupid” belief instances or controls, as the case may be.

We express these ideas in the $\widehat{Y}$-domain by introducing a relation from X to $\widehat{Y}$, called controllability and denoted $X\otimes \widehat{Y}$. Thus $X\otimes \widehat{Y}$ is a subset of the product set $X\times \widehat{Y}$. Elements of $X\otimes \widehat{Y}$ are atomic situations (in the $\widehat{Y}$-domain). If a preparation $\mathcal{P}$ is given, it may suffice to consider the restriction $\mathcal{P}\otimes \widehat{Y}$ which consists of all atomic situations $(x,w)$ with $x\in \mathcal{P}$.

For an atomic situation $(x,w)$, we write $w\succ x$ and say that w controls x or that x can be controlled by w. An atomic situation $(x,w)$ is an adapted pair if w is adapted to x in the sense that $w=\widehat{x}$.

For a preparation $\mathcal{P}$ we write $w\succ \mathcal{P}$, and call w a control of $\mathcal{P}$, if w controls every state in $\mathcal{P}$ ($\forall x\in \mathcal{P}:w\succ x$). We also express this by saying that w controls $\mathcal{P}$. By $^\left[\mathcal{P}\right]$ we denote the set of all controls of $\mathcal{P}$. We write $^\left[x\right]$ if $\mathcal{P}$ is the singleton set $\left\{x\right\}$. In case $X\otimes \widehat{Y}$ is the diffuse relation, $^\left[\mathcal{P}\right]=\widehat{Y}$ for any preparation $\mathcal{P}$.

For $\mathcal{Q}\subseteq \widehat{Y}$, $\left]\mathcal{Q}\right[$ denotes the control region of $\mathcal{Q}$, the set of $x\in X$ for which $w\succ x$ for some $w\in \mathcal{Q}$. We write $\left]w\right[$ if $\mathcal{Q}$ is the singleton set $\left\{w\right\}$. Clearly, the statements $w\in ^\left[\mathcal{P}\right]$, $w\succ \mathcal{P}$ and $\mathcal{P}\subseteq \left[w\right]$ are equivalent.

We assume that the following conditions hold:

$$\begin{array}{c}\forall x\in X:\widehat{x}\succ x,\hfill \end{array}$$

(1)

$$\begin{array}{c}\forall w\in \widehat{Y}:\left]w\right[\ne \mathrm{\varnothing },\hfill \end{array}$$

(2)

and normally also that

$$\exists y\in Y:\widehat{y}\succ X.$$

(3)

The first condition is essential and the second one is rather innocent. The third condition is introduced when we want to ensure that X (or Y) is not “too large”. Models where (3) does not hold are considered unrealistic, beyond what man (Observer) can grasp. If response is surjective, it amounts to the condition $^\left[X\right]\ne \mathrm{\varnothing }$. It is illuminating to have models of classical Shannon theory in mind, cf., Section 3.7.

For a preparation $\mathcal{P}$, we define the centre of $\mathcal{P}$ ($\widehat{Y}$-domain) as the set of controls in $\widehat{\mathcal{P}}$ which control $\mathcal{P}$:

$$\mathrm{ctr}^(\mathcal{P})=\widehat{\mathcal{P}}\cap ^\left[\mathcal{P}\right].$$

(4)

From controllability we derive the relation of visibility for the Y-domain, denoted $X\otimes Y$, and given by

$$X\otimes Y=\{(x,y)\in X\times Y|\widehat{y}\succ x\}.$$

(5)

Restrictions $\mathcal{P}\otimes Y=\{(x,y)\in X\otimes Y|x\in \mathcal{P}\}$ are at times of relevance.

If $(x,y)\in X\otimes Y$, we say that $(x,y)$ is an atomic situation (in the Y-domain) and write $y\succ x$. Such a situation is an adapted pair if $(x,\widehat{y})$ is so in the $\widehat{Y}$-domain, i.e., if $y\widehat{\sim }x$ and $(x,y)$ is a perfect match if $y=x$. The two notions coincide if response is injective. An atomic situation $(x,y)$ is certain if $y\in Y_{\det }$.

Note that we use the same sign, ≻, for visibility and for controllability. The context will have to show if we work in the Y- or in the $\widehat{Y}$-domain. We see that $y\succ x$ if and only if $\widehat{y}\succ x$. If this is so, we also say that y covers x or that x is visible from y.

By (1) and by the defining relation (5), $x\succ x$ for all $x\in X$, thus $X\otimes Y$ contains the diagonal $X\times X$. The outlook (or view) from $y\in Y$ is the set $\left]y\right[=\left\{x\right|y\succ x\}$. Clearly, $]y[=]\widehat{y}[$. By (2) and (5), this set is non-empty and, when (3) holds, for at least one belief instance, the outlook is all of X.

For a preparation $\mathcal{P}$ we write $y\succ \mathcal{P}$, and call y a viewpoint of $\mathcal{P}$, if $y\succ x$ for every $x\in \mathcal{P}$. The set of all viewpoints of $\mathcal{P}$ is denoted $\left[\mathcal{P}\right]$. We write $\left[x\right]$ if $\mathcal{P}$ is the singleton $\mathcal{P}=\left\{x\right\}$. By $\mathrm{ctr}(\mathcal{P})$, the centre of $𝒫$ (Y-domain), we denote the set of viewpoints in the preparation:

$$\mathrm{ctr}(\mathcal{P})=\mathcal{P}\cap \left[\mathcal{P}\right].$$

(6)

Note that $\mathrm{ctr}^(\mathcal{P})=\left\{\widehat{x}\right|x\in \mathrm{ctr}(\mathcal{P})\}$.

In any situation, Observer should ensure that from his chosen belief instance, every state which could conceivably be chosen by Nature is visible. Therefore, in a situation where the preparation $\mathcal{P}$ is known to Observer, Observer should only consider belief instances in $\left[\mathcal{P}\right]$.

In the sequel we shall often consider bivariate functions, generically denoted by either $\widehat{f}$ ($\widehat{Y}$-domain) or by f (Y-domain). The $\widehat{f}$-type functions are defined either on $X\otimes \widehat{Y}$ or on some subset of the form $\mathcal{P}\times ^\left[\mathcal{P}\right]$ for some preparation $\mathcal{P}$. The range of $\widehat{f}$ may be any abstract set but will often be a subset of the extended real line. Given $\widehat{f}$, it is understood that f without the hat denotes the derived function defined by $f(x,y)=\widehat{f}(x,\widehat{y})$ for pairs $(x,y)$ for which $(x,\widehat{y})$ is in the domain of definition of $\widehat{f}$. The domain of definition of the derived function is either $X\otimes Y$ or the set $\mathcal{P}\times \left[\mathcal{P}\right]$ if $\widehat{f}$ is defined on $\mathcal{P}\times ^\left[\mathcal{P}\right]$.

Every derived function depends only on response in the sense that $f(x,y_1)=f(x,y_2)$ if only $y_1\widehat{\sim }{y}_2$. If response is a surjection, there is a natural one-to-one relation between $\widehat{Y}$-type functions and Y-type functions which depend only on response.

Consider an f-type function defined on all of $X\otimes Y$. For $y\in Y$, $f^y$ denotes the marginal function given y, defined on $\left]y\right[$ by $f^y(x)=f(x,y)$. The marginal function given $x\in X$ is the function $f_x$ defined by $f_x(y)=f(x,y)$ for $y\in \left[x\right]$. We write $f^y<\infty$ on $𝒫$ to express, firstly, that $y\succ \mathcal{P}$ so that $f^y$ is well defined on all of $𝒫$ and, secondly, that this marginal function is finite on $𝒫$. We write $f^y<\infty$ if $f^y<\infty$ on X.

2.5. Knowledge, Perception and Deformation

Observer strives for knowledge, conceived as the synthesis of extensive experience. Referring to probabilistic thinking, we could point to situations where accidental experimental data are smoothed out over time as you enter the regime of the law of large numbers. However, Observer’s endeavours may result in less definitive insight, a more immediate reaction which we refer to as perception. It reflects how Observer perceives situations from the world or, with a different focus, how situations from the world are presented to Observer.

In the same way as we have introduced truth- and belief instances, we consider knowledge instances, also referred to as perceptions. Typically, they are denoted by z and taken from a set denoted Z, the knowledge base or perception base.

A simplifying assumption for our modeling is that the rules of the world $\mathrm{\Omega }$ contain a special function, $\widehat{\mathrm{\Pi }}$, which maps $X\otimes \widehat{Y}$ into Z, generically,

$$z=\widehat{\mathrm{\Pi }}(x,w).$$

(7)

The derived function, $\mathrm{\Pi }$, then maps $X\otimes Y$ into Z. Both functions are referred to as the deformation. The context will show which one we have in mind, $\widehat{\mathrm{\Pi }}$ or $\mathrm{\Pi }$.

Thus knowledge can be derived deterministically from truth and belief alone, and as far as belief is concerned, we only have to know the associated response. In terms of perception, Observer’s perception z of an atomic situation $(x,y)$ is given by $z=\mathrm{\Pi }(x,y)=\widehat{\mathrm{\Pi }}(x,\widehat{y})$.

In our modeling, the world is characterized by the deformation. We may thus talk about the world with deformation $\mathrm{\Pi }$, $\mathrm{\Omega }={\mathrm{\Omega }}_{\mathrm{\Pi }}$. The rules of the world may contain other structural elements, but such elements are not specified in the present study. Possibilities which could be considered in future developments include context, noise from the environment, and dynamics. To some extent, such features can be expressed in the present modeling by defining $X,Y$ and Z appropriately and by introducing suitable interpretations.

In case response is a bijection and Z contains X as well as Y we may consider the deformations ${\mathrm{\Pi }}_1$ and ${\mathrm{\Pi }}_0$ defined by ${\mathrm{\Pi }}_1(x,y)=x$, respectively ${\mathrm{\Pi }}_0(x,y)=y$. The associated worlds are ${\mathrm{\Omega }}_1={\mathrm{\Omega }}_{{\mathrm{\Pi }}_1}$ and ${\mathrm{\Omega }}_0={\mathrm{\Omega }}_{{\mathrm{\Pi }}_0}$. In ${\mathrm{\Omega }}_1$, “what you see is what is true”, whereas in ${\mathrm{\Omega }}_0$, “you only see what you believe”—or, in some interpretations, you only see what you want to see. The world ${\mathrm{\Omega }}_1$ is the classical world where, optimistically, truth can be learned, whereas, in ${\mathrm{\Omega }}_0$, you cannot learn anything about truth. We refer to ${\mathrm{\Omega }}_0$ as a black hole. It is a narcissistic world, a world of extreme scepticism, only reflecting Observer’s beliefs and bearing no trace of Nature. If Z is provided with a linear structure, we can consider further deformations ${\mathrm{\Pi }}_q$ depending on a parameter q by putting ${\mathrm{\Pi }}_q(x,y)=qx+(1-q)y$. Worlds associated with deformations of this type are denoted ${\mathrm{\Omega }}_q$. These are the worlds we find of relevance for the discussion of Tsallis entropy, cf., Section 3.6.

The simplest world to grasp is the classical world, but also the worlds ${\mathrm{\Omega }}_q$ and even a black hole contain elements which are familiar to us from daily experience, especially in relation to certain psychological phenomena. In this connection we point to placebo effects, cf., Benedetti [19], and to visual attention, cf., Bundesen and Habekost [18]. Presently, the relevance of our modeling in relation to these phenomena is purely qualitative.

Considering examples as indicated above, it is natural to expect that knowledge is of a nature closely related to the nature of truth and of belief. A key case to look into is that $Z=X=Y$. However, we shall not make any general assumption in this direction. What we shall do is to follow the advice of Shannon, as far as possible avoiding assumptions which depend on concrete semantic interpretations. As a consequence we shall only in Section 3.6 introduce more specific assumptions about the representation of knowledge.

2.6. Effort and Description

We turn to the introduction of the key quantitative tool we shall work with. In so doing, we will be guided by the view that perception requires effort. Expressed differently, knowledge is obtained at a cost. Since, according to the previous section, knowledge can be derived from truth and belief alone, or from truth and action, no explicit reference to knowledge is necessary. Instead, we model effort (in the $\widehat{Y}$-domain) by a certain bivariate function, the effort function, defined on $X\otimes \widehat{Y}$.

The rules of the world $\mathrm{\Omega }$ may not point directly to an effort function which Observer can favorably work with. Or there may be several sensible functions to choose from. The actual selection is considered a task for Observer.

Effort, description, experiment and measurement are related concepts. We put emphasis on the notion of description, which is intended to aid Observer in his encounters with situations from the world. Logically, description comes before effort. Effort arises when specific ideas about description are developed into a method of description, which you may here identify with an experiment. The implementation of such a method or the performance of the associated experiment involves a cost and this is what we conceive as specified quantitatively by the effort function.

Description depends on semantic interpretations and is often thought of in loose qualitative terms. However, in order to develop precise concepts which can be communicated among humans, quantitative elements will inevitably appear, typically through a finite set of certain real-valued functions, descriptors. The descriptors of Section 3.6 give an indication of what could be involved.

Imagine now that somehow Observer has chosen all elements needed—response, actions, experiments—and settled for an effort function, $\widehat{\mathsf{\Phi }}=\widehat{\mathsf{\Phi }}(x,w)$ defined on $X\otimes \widehat{Y}$. Let us agree on what a “good” effort function should mean. Generally speaking, Observer should aim at experiments with low associated effort. Consider a fixed truth instance x and the various possible actions, in principle free to be any action which controls x. It appears desirable that the action adapted to x should be the one preferred by Observer. Thus effort should be minimal in this case, i.e., $\widehat{\mathsf{\Phi }}(x,w)\ge \widehat{\mathsf{\Phi }}(x,\widehat{x})$ should hold. Further, if the inequality is sharp except for the adapted action, this will have a training effect which, over time, will encourage Observer to choose the optimal action, $\widehat{x}$.

Formally, we define an effort function (in the $\widehat{Y}$-domain) as a function $\widehat{\mathsf{\Phi }}$ on $X\otimes \widehat{Y}$ with values in $]-\infty ,+\infty ]$ such that, for all $x\in X$ and all $w\succ x$,

$$\widehat{\mathsf{\Phi }}(x,w)\ge \widehat{\mathsf{\Phi }}(x,\widehat{x}).$$

(8)

Thus, for all $x\in X$, $\widehat{x}\in \arg \min {\widehat{\mathsf{\Phi }}}_x$. The minimal value of ${\widehat{\mathsf{\Phi }}}_x$ is the entropy of x for which we use the notation $\mathrm{H}(x)$:

$$\mathrm{H}(x)=\widehat{\mathsf{\Phi }}(x,\widehat{x}).$$

(9)

This quantity will be discussed more thoroughly in the sequel. If $w_{\mathrm{\varnothing }}\in \widehat{Y}$, it is to be expected that $\widehat{\mathsf{\Phi }}(x,w_{\mathrm{\varnothing }})=0$ when $w_{\mathrm{\varnothing }}\succ x$.

The effort function is proper, if, for any $x\in X$ with $\mathrm{H}(x)<\infty$, the minimum of ${\widehat{\mathsf{\Phi }}}_x$ is only achieved for the control $\widehat{x}$ adapted to x. As opposed to this notion we have the notion of a degenerate effort function which is one which only depends on the first argument x, i.e., for all $x\in X$, ${\widehat{\mathsf{\Phi }}}_x$ is a constant function.

Note that effort may be negative (but not $-\infty$). This flexibility will later be convenient as it will allow us to pass freely from notions of effort to notions of utility by a simple change of sign. However, for more standard applications, effort functions will be non-negative.

The set of effort functions and the set of proper effort functions over $X\otimes \widehat{Y}$ are ordered positive cones in a natural way. You may note that if, in a sum of effort functions, one of the summands is proper, so is the sum. Two effort functions ${\widehat{\mathsf{\Phi }}}_1$ and ${\widehat{\mathsf{\Phi }}}_2$, which only differ from each other by a positive finite factor are scalarly equivalent. If an effort function is proper, so is every scalarly equivalent one. There may be many non-scalarly equivalent effort functions. The choice among scalarly equivalent ones amounts to a choice of unit.

Proper effort functions could have been taken as the key primitive concept on which other concepts, especially response, can be based. To illustrate this, assume that $Y=X$ and consider a function $\widehat{\mathsf{\Phi }}:X\otimes \widehat{Y}\mapsto ]-\infty ,\infty ]$ such that, for every state x for which ${\widehat{\mathsf{\Phi }}}_x$ is not identically $+\infty$, $\arg \min {\widehat{\mathsf{\Phi }}}_x$ is a singleton. The minimal value of ${\widehat{\mathsf{\Phi }}}_x$ is again the entropy $\mathrm{H}(x)$ and we may define the set of realistic states by $X_0=\{\mathrm{H}<\infty \}$ and, more importantly, response $x\mapsto \widehat{x}$ by the requirement that $\widehat{\mathsf{\Phi }}(x,\widehat{x})=\min {\widehat{\mathsf{\Phi }}}_x$. This defines response uniquely on $X_0$ and for $x\notin X_0$, the definition of $\widehat{x}$ is really immaterial and any element in $\widehat{Y}$ which controls x will do.

Turning to the Y-domain, we define an effort function (Y-domain), as a function $\mathsf{\Phi }:X\otimes Y\mapsto ]-\infty ,\infty ]$ such that

$$\mathsf{\Phi }(x,y)\ge \mathsf{\Phi }(x,x)\mathrm{for}\mathrm{all}(x,y)\in X\otimes Y.$$

(10)

Entropy is given by $\mathrm{H}(x)=\mathsf{\Phi }(x,x)$. If there are certain atomic situation, it is natural to expect that effort vanishes for such situations. The effort function is proper if equality in (10) only holds if either $\mathrm{H}(x)=\infty$ or else $y=x$. We also express this by saying that $\mathsf{\Phi }$ satisfies the perfect match principle. An effort function is degenerate if, for every $(x,y)\in X\otimes Y$, $\mathsf{\Phi }(x,y)=\mathrm{H}(x)$.

The notions just introduced were defined directly with reference to the Y-domain. However, it lies nearby also to consider functions which can be derived from $\widehat{Y}$-effort functions $\widehat{\mathsf{\Phi }}$. They are derived effort functions and, in case $\widehat{\mathsf{\Phi }}$ is proper, proper derived effort functions. The two strategies for definitions, intrinsic and via derivation, give slightly different concepts. In case response is injective, the resulting notions are equivalent. In general, derived effort functions depend only on response, i.e., if $y_1\succ x$ and $y_2\succ x$ and if $y_1\widehat{\sim }{y}_2$ then $\mathsf{\Phi }(x,y_1)=\mathsf{\Phi }(x,y_2)$. In the other direction, for a proper derived effort function, you can only conclude response-equivalence, $y\widehat{\sim }x$, if $\mathsf{\Phi }(x,y)=\mathrm{H}(x)$ and $\mathrm{H}(x)<\infty$.

Formally, the definitions related to Y-effort functions may be conceived as a special case of the definitions pertaining to the $\widehat{Y}$-domain (put $\widehat{Y}=Y$ and take the identity map as response).

We shall talk about effort functions without a qualifying prefix, $\widehat{Y}$ or Y, if it is clear from the context what we have in mind. We shall always point out if we have derived functions in mind.

The effort functions introduced determine net effort. However, the implementation of the method of description—which we imagine lies behind—may, in addition to a specific cost, entail a certain overhead and, occasionally, it is appropriate to include this overhead in the effort. We refer to Section 3.6 for instances of this.

We imagine that the choice of effort function involves considerations related to knowledge and to the rules of the world. However, once $\widehat{\mathsf{\Phi }}$, hence also $\mathsf{\Phi }$ are fixed, these other elements are only present indirectly. The ideas of Section 2.5 have thus mainly served as motivation for the further abstract development. The ideas will be taken up again when in Section 3.6 we turn to a study of probabilistic models.

The author was led to consider proper effort functions in order to illuminate certain aspects of statistical physics, cf., [34,37]. However, the ideas have been around for quite some time, especially among statisticians. For them it has been more natural to work with functions taken with the reverse sign by looking at “score” rather than effort. Our notion of proper effort functions, when specialized to a probabilistic setting, matches the notion of proper scoring rules as you find it in the statistical literature. As to the literature, Csiszár [41] comments on the early sources, including Brier [42], a forerunner of research which followed, cf., Good [40], Savage [43] (see e.g., Section 9.4) and Fischer [44]. See also the reference work [45] by Gneiting and Raftery. For research of Dawid and collaborators—partly in line with what you find here—see [28,46,47,48].

2.7. Information Triples

As advocated in the last section, effort is a notion of central importance. However, this notion should not stand alone but be discussed together with other fundamental concepts of information. This point of view will be emphasized by the introduction of a notion of information triples, the main notion of the present study. We start by philosophizing over the very concept of information.

Information in any particular situation concerns truth. If $𝒫$ is a preparation, “$x\in \mathcal{P}$” signifies that the true state is to be found among the states in $𝒫$. If $𝒫$ is a singleton, we talk about full information and use the notation “x” rather than “$x\in \left\{x\right\}$”; otherwise, we talk about partial information.

We shall not be concerned with how information can be obtained—if at all. Perhaps, Observer only speculates about the potential possibility of acquiring information, either through his own activity or otherwise, e.g., via the involvement of an aid or a third party, an informer.

Information will be related to quantitatively defined concepts. As our basis we take a proper effort function $\widehat{\mathsf{\Phi }}$. Following Shannon we disregard semantic content. Instead, we focus on the possibility for Observer to benefit from information by a saving of effort. Accordingly, we view $\widehat{\mathsf{\Phi }}(x,w)$ as the information content of “x” in an atomic situation with x as truth instance and w as action or control—indeed, if you are told that x is the true state, you need not allocate the effort $\widehat{\mathsf{\Phi }}(x,w)$ to the situation which you were otherwise prepared to do. The somewhat intangible and elusive concept of “information” is, therefore, measured by the more concrete and physical notion of effort, hence the unit of information is the same as the unit used for effort.

There is a huge literature elucidating what information really “is”. Suffice it here to refer to [21] and, as an example of a discussion more closely targeted on our main themes, we refer to Caticha [49] who maintains that “Just as a force is defined as that which induces a change in motion, so information is that which induces a change in beliefs”. One may just as well—or even better—focus on action. Then we can claim that “information” is that which induces a change of action.

The central concept of the theory developed by Shannon is that of entropy. This concept was already introduced in the preceding section. Here, we elaborate on possible interpretations. One view is that entropy is guaranteed saving of effort. With effort given by $\widehat{\mathsf{\Phi }}$ we are led to define the entropy $\mathrm{H}(x)$ associated with the information “x” as the minimum over w of $\widehat{\mathsf{\Phi }}(x,w)$. Thus, by (8), (9) holds.

The considerations above make most sense if, one way or another, Observer eventually obtains full information about the true state. However, if, instead, you view entropy as necessary allocation of effort, understood as the effort you have to allocate in order to have a chance to obtain full information, it does not appear important actually to obtain that information. In passing, one may think that a more neutral terminology such as “necessity” could have been chosen in place of “entropy”. That could be less awkward when you turn to other applications of the abstract theory than classical Shannon theory or statistical physics.

As yet a third route to entropy we suggest to view it as a quantitative expression of the complexity of the various states, maintaining that to evaluate complexity, Observer may use minimal accepted effort, the effort he is willing to allocate to the various states in order to obtain the information in question.

Entropy may also be obtained with reference only to the Y-domain. Indeed, with $\mathsf{\Phi }$ the derived effort function, for each state x, $\mathrm{H}(x)=\mathsf{\Phi }(x,x)$.

Whichever route to entropy you take—including the game theoretical route of Section 2.10—it appears that subjective elements are involved, typically through Observer’s choice of description and associated experiments. If, modulo scalar equivalence, the actual world only allows one proper effort function, then entropy and notions related to entropy are of a more objective nature. We shall later see examples of such worlds but also for such worlds subjective elements may enter if Observer is considering which world is the actual one.

Apart from effort itself, and the derived notion of entropy, we turn to the introduction of two other basic concepts which make sense in our abstract setting, viz., redundancy for the $\widehat{Y}$-domain and its counterpart, divergence, for the Y-domain.

To define redundancy, consider an atomic situation $(x,w)\in X\otimes \widehat{Y}$. Then redundancy $\widehat{\mathrm{D}}$ between x and w is measured by the difference between actual and minimal effort, i.e., ideally, as

$$\widehat{\mathrm{D}}(x,w)=\widehat{\mathsf{\Phi }}(x,w)-\mathrm{H}(x).$$

(11)

Assume, for a moment, that entropy is finite-valued. Then redundancy in (11) is well defined. Furthermore, redundancy is non-negative and only vanishes if $(x,w)$ is an adapted pair.

However, we find it important to be able to deal with models for which entropy may be infinite. We do that by simply assuming that appropriate versions of redundancy and divergence exist with desirable properties. The simple device we shall apply in order to reach a sensible definition is to rewrite the defining relation (11), isolating effort on the left hand side.

With the above preparations, we are ready to introduce the key concepts of our study. We start with concepts for the $\widehat{Y}$-domain and follow up after that by parallel concepts for the Y-domain.

We consider certain triples $(\widehat{\mathsf{\Phi }},\mathrm{H},\widehat{\mathrm{D}})$ of functions taking values in $]-\infty ,\infty ]$ with $\widehat{\mathsf{\Phi }}$ and $\widehat{\mathrm{D}}$ defined on $X\otimes \widehat{Y}$ and H defined on X. If need be we may talk about triples over $X\otimes \widehat{Y}$ or we may point to the $\widehat{Y}$-domain. Such triples must satisfy special conditions in order to be of interest. The most important properties to consider are the following four:

$$\begin{array}{cc}\hfill & \widehat{\mathsf{\Phi }}(x,w)=\mathrm{H}(x)+\widehat{\mathrm{D}}(x,w)(\mathit{linking}\mathit{identity},\mathrm{L});\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & \widehat{\mathrm{D}}(x,w)\ge 0(\mathit{fundamental}\mathit{inequality},\mathrm{F});\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & \widehat{\mathrm{D}}(x,\widehat{x})=0(\mathit{soundness},\mathrm{S});\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & w\ne \widehat{x}\Rightarrow \widehat{\mathrm{D}}(x,w)>0(\mathit{properness},\mathrm{P}).\hfill \end{array}$$

(15)

The properties (12), (13) and (15) are considered for all $(x,w)\in X\otimes \widehat{Y}$ and (14) for all $x\in X$. The linking identity (12) may be written shortly as $\widehat{\mathsf{\Phi }}=\mathrm{H}+\widehat{\mathrm{D}}$ or, formally correct with $\widehat{\mathrm{pr}}$ the projection of $X\otimes \widehat{Y}$ onto X, as $\widehat{\mathsf{\Phi }}=\mathrm{H}\circ \widehat{\mathrm{pr}}+\widehat{\mathrm{D}}$.

An information triple is a triple $(\widehat{\mathsf{\Phi }},\mathrm{H},\widehat{\mathrm{D}})$ which satisfies the three first conditions (L, F and S). For such triples the function $\widehat{\mathsf{\Phi }}$ is the associated effort function, H the associated entropy and $\widehat{\mathrm{D}}$ the associated redundancy. This does not conflict with previous terminology. In particular, the associated effort function is indeed an effort function in the sense of Section 2.6.

Information triples with the same redundancy are said to be equivalent. Equivalent triples may have quite different properties and one may search for representatives with good properties.

A proper information triple in the Y-domain is an information triple for which redundancy is proper, i.e., (15) holds. Clearly, the effort function of a proper information triple is proper in the sense of Section 2.6. Moreover, if a triple is proper, so is any equivalent one.

An information triple is degenerate if redundancy vanishes: $\widehat{\mathrm{D}}(x,w)=0$ for all $(x,w)\in X\otimes \widehat{Y}$. The effort function of a degenerate information triple is degenerate.

Among the four defining properties, the last three (FSP) only involve redundancy. Accordingly, a function $\widehat{D}$ defined on $X\otimes \widehat{Y}$ is a general redundancy function if it satisfies the fundamental inequality as well as the requirements of soundness and properness. Note that for such a redundancy function, $(\widehat{\mathrm{D}},0,\widehat{\mathrm{D}})$ is a proper information triple and that any equivalent information triple may be obtained from $(\widehat{\mathrm{D}},0,\widehat{\mathrm{D}})$ by a natural process of addition related to any function on X with values in $]-\infty ,\infty ]$, taking this function as the entropy function. To be precise, what is involved structurally is that you add information triples, one of which is proper and the other degenerate, viz., you add $(\widehat{\mathrm{D}},0,\widehat{\mathrm{D}})$ and $(\mathrm{H},\mathrm{H},0)$. For further details on this theme, see Section 3.1.

Normally, given a proper effort function $\widehat{\mathsf{\Phi }}$, there is a natural way to extend the redundancy function as defined by (11) when $\mathrm{H}(x)<\infty$, so that a proper information triple emerges. For this reason, we may talk about the information triple generated by $\widehat{\mathsf{\Phi }}$. Then, the problem of indeterminacy of redundancy disappears. The slightly strengthened assumption that redundancy can be defined “appropriately” on all of $X\otimes \widehat{Y}$ will, as it turns out, present no limitation in concrete cases of interest.

We turn briefly to Y-type triples. They are triples $(\mathsf{\Phi },\mathrm{H},\mathrm{D})$ with $\mathsf{\Phi }$ and D defined on $X\otimes Y$ and H defined on X. Key properties to consider are quite parallel to what we have discussed for the $\widehat{Y}$-domain:

$$\begin{array}{cc}\hfill & \mathsf{\Phi }(x,y)=\mathrm{H}(x)+\mathrm{D}(x,y)(\mathit{linking}\mathit{identity},\mathrm{L});\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & \mathrm{D}(x,y)\ge 0(\mathit{fundamental}\mathit{inequality},\mathrm{F});\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & \mathrm{D}(x,\widehat{x})=0(\mathit{soundness},\mathrm{S});\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & y\ne x\Rightarrow \mathrm{D}(x,y)>0(\mathit{properness},\mathrm{P}).\hfill \end{array}$$

(19)

An information triple in the Y-domain is a triple which satisfies the conditions L, F and S. For such triples, $\mathsf{\Phi }$ is the associated effort, H the associated entropy and D the associated divergence.

A proper information triple is one for which divergence is proper. Such triples are intrinsically defined in the sense that they do not depend on any action space or response function. If divergence vanishes, the triple is degenerate. The effort function of a proper information triple is proper in the sense of Section 2.6 and the effort function of a degenerate triple is degenerate.

A triple $(\mathsf{\Phi },\mathrm{H},\mathrm{D})$ is a derived information triple, respectively a derived proper information triple, if there exists a triple $(\widehat{\mathsf{\Phi }},\mathrm{H},\widehat{\mathrm{D}})$ satisfying the corresponding properties for the $\widehat{Y}$-domain such that $\mathsf{\Phi }$ is derived from $\widehat{\mathsf{\Phi }}$ and D from $\widehat{\mathrm{D}}$. Note that a derived proper information triple need not be a proper information triple according to the intrinsic definition. Indeed, from $\mathrm{D}(x,y)=0$ you can only conclude that x and y are response equivalent. Of course, if response is injective, the two types of proper information triples for the Y-domain—intrinsically defined or defined via derivation—are equivalent concepts.

A general divergence function D on $X\otimes Y$ is a function on $X\otimes Y$ which satisfies the F, S and P-requirements. Note that we include the property of properness in the definition. A general derived divergence function is one which can be derived from a general redundancy function.

For the Y-domain, notions of equivalence (same divergence!) and of addition of information triples are defined in the obvious manner.

Instead of taking triples as introduced above as the basis, it is quite often more natural to focus on triples of the “opposite nature”. This refers to situations where it is appropriate to focus on a positively oriented quantity such as utility or pay-off rather than on effort. Typically, this is the case for studies of economy, meteorology and statistics where one also meets the notion of “score” as previously indicated. In order to distinguish the two types of triples from each other, we may refer to them as being effort-based, respectively utility-based.

For the $\widehat{Y}$-domain, $(\widehat{\mathrm{U}},\mathrm{M},\widehat{\mathrm{D}})$ is a utility-based information triple if $(-\widehat{\mathrm{U}},-\mathrm{M},\widehat{\mathrm{D}})$ is so as an effort-based triple and, for the Y-domain, $(\mathrm{U},\mathrm{M},\mathrm{D})$ is a utility-based information triple if $(-\mathrm{U},-\mathrm{M},\mathrm{D})$ is so as an effort-based triple. Properness and other concepts introduced for effort-based triples carry over in the obvious way to utility-based triples.

For utility-based triples, $\widehat{\mathrm{U}}$ and U are called utility, M is called max-utility. As for effort-based triples, $\widehat{\mathrm{D}}$ is redundancy and D divergence. The linking identity takes the form $\widehat{\mathrm{U}}=\mathrm{M}-\widehat{\mathrm{D}}$ ($\mathrm{U}=\mathrm{M}-\mathrm{D}$) which can never result in the indeterminate form $\infty -\infty$ since, by definition, $\widehat{\mathrm{U}}$ and U, hence also M, can never assume the value $+\infty$.

In view of the main examples we have in mind, we have found it most illuminating to take effort rather than utility as the basic concept to work with, and hence to develop the main results for effort-based quantities. Anyhow, even if you are primarily interested in considerations based on effort, you are easily led to consider also utility-based quantities as we shall see right away in the next section.

The concept of proper information triples is, except for minor technical details, equivalent to the concept of proper effort functions. Apart from a slight technical advantage, the triples constitute a preferable base for information theoretical investigations as the three truly basic notions of information are all emphasized together with their basic interrelationship—the linking identity. Historically, the notions arose for classical probabilistic information theoretical models, cf., Section 3.7. Effort functions go back to Kerridge [50] who coined the term inaccuracy, entropy goes back to Shannon [1] and divergence to Kullback [51]. The term “redundancy” which we have used for another side of divergence, corresponds to one usage in information theory, though there the term is used in several other ways which are not expressed in our abstract setting.

As an aside, it is tempting for the author to point to the pioneering work of Edgar Rubin going back to the twenties. Unfortunately, this was only published posthumously in 1956, cf., [52,53,54]. Rubin made experiments over human speech and focused on what he called the reserve of understanding. This is a quantitative measure of the amount you can cut out of a persons speech without seriously disrupting a listeners ability to understand what has been said. It can be conceived as a forerunner of the notion of redundancy.

Our way to information triples was through effort and one may ask why we did not go directly to the triples. For one thing, triples lead to a smooth axiomatic theory, as will be demonstrated in the present research, compare also with our previous contribution [55]. However, though axiomatization can be technically attractive, we find that a focus on interpretation as in our more philosophical and speculative approach, is of primary importance and contributes best to an understanding of central concepts of information. Axiomatics only comes in after basic interpretations are in place.

A comment on the choice of terminology in relation to the concept of properness is in place. This concept is at times considered to be unnecessarily strong and we shall later, at the end of Section 2.10 and in Appendix A, develop weaker notions. When only a redundancy function or a divergence function is given and not a full information triple, we have chosen to incorporate the requirement of properness in its usual form in the definition of what we understand by a general redundancy function or a general divergence function.

2.8. Relativization, Updating

In this section we shall work entirely in the Y-domain. We start by considering a proper effort-based information triple $(\mathsf{\Phi },\mathrm{H},\mathrm{D})$ over $X\otimes Y$. Often, it is natural to measure effort relative to some standard performance rather than by $\mathsf{\Phi }$ itself. An especially important instance of this kind of relativization concerns situations where Observer originally fixed a prior, say $y_0\in Y$, but now wants to update his belief by replacing $y_0$ with a posterior y. Perhaps Observer—through his own actions or via an informer—has obtained the information “$x\in \mathcal{P}$” for some preparation $𝒫$. If $y_0\notin \mathcal{P}$, Observer may want to replace $y_0$ by a posterior $y\in \mathcal{P}$. In a first attempt of a reasonable definition, the associated updating gain is given by the quantity ${\mathrm{U}}_{|y_0}$ obtained by comparing performance under the posterior with performance under the prior:

$${\mathrm{U}}_{|y_0}(x,y)=\mathsf{\Phi }(x,y_0)-\mathsf{\Phi }(x,y).$$

(20)

A difficulty with (20) concerns the possible indeterminate form $\infty -\infty$. If we ignore the difficulty and apply the linking identity (16) to both terms in (20), entropy $\mathrm{H}(x)$ cancels out and we find the expression

$${\mathrm{U}}_{|y_0}(x,y)=\mathrm{D}(x,y_0)-\mathrm{D}(x,y).$$

(21)

This is less likely to be indeterminate. When not of the indeterminate form $\infty -\infty$, we therefore agree to use (21) as the formal definition of updating gain, more precisely of relative updating gain with $y_0$ as prior. For the present study, we shall only work with updating gain when the marginal function ${\mathrm{D}}^{y_0}$ (defined in accordance with concepts and notation introduced in Section 2.4) is finite on some preparation $𝒫$ under consideration. Assuming that this is the case, we realize that

$$({\mathrm{U}}_{|y_0},{\mathrm{D}}^{y_0},\mathrm{D})$$

(22)

is a proper utility-based information triple over $\mathcal{P}\otimes Y$. For such triples we put $Y_{\det }=\left\{y_0\right\}$, i.e., we take $y_0$ as the only certain belief instance. Max-utility is identified as the marginal function ${\mathrm{D}}^{y_0}$ on $𝒫$ and divergence is the original divergence function restricted to $\mathcal{P}\otimes Y$.

It is important to note that the triples which occur in this way by varying $y_0$ and $𝒫$ do not require the full effort function $\mathsf{\Phi }$ in order to make sense. It suffices to start out with a general divergence function on $X\otimes Y$. When the construction is based on a general divergence function D, we refer to (22) as the updating triple generated by D and with $y_0$ as prior.

Though rather trivial, the observations regarding updating gain are important as they show that results in that setting may be obtained from results based on effort. To emphasize this, we introduce—based only on a general divergence function D—the effort-based information triple associated with (22) as the triple

$$({\mathsf{\Phi }}_{|y_0},-{\mathrm{D}}^{y_0},\mathrm{D})$$

(23)

with ${\mathsf{\Phi }}_{|y_0}$ given by

$${\mathsf{\Phi }}_{|y_0}(x,y)=\mathrm{D}(x,y)-\mathrm{D}(x,y_0).$$

(24)

This is a perfectly feasible effort-based triple over $\mathcal{P}\otimes Y$ whenever ${\mathrm{D}}^{y_0}$ is finite on $𝒫$. Clearly, it is proper.

In Section 2.13 and Section 2.15 we shall derive results about minimum divergence (information projections) from results about maximum entropy by exploiting the simple facts here uncovered.

As we have seen, natural information triples may be derived from a general divergence function by a simple process of relativization. While we are at it, we note that in case $Y=X$, also reverse divergence $(x,y)\mapsto \mathrm{D}(y,x)$ defines a genuine divergence function on $X\otimes Y$ (in contrast, reverse description effort need not define a genuine effort function). Therefore, if ${\mathrm{D}}_{y_0}<\infty$ and we put ${\mathsf{\Phi }}_{|y_0}^r(x,y)=\mathrm{D}(y,x)-\mathrm{D}(y_0,x)$,

$$({\mathsf{\Phi }}_{|y_0}^r(x,y),-\mathrm{D}(y_0,x),\mathrm{D}(y,x))$$

(25)

defines a genuine proper information triple (when restricting the variables x and y appropriately). However, these triples are not found to be that significant.

2.9. Feasible Preparations, Core and Robustness

We claim that description is a key to obtainable information, to what can be known. Not every possible information “$x\in \mathcal{P}$” for any odd preparation $𝒫$ can be expected to reflect a realistic situation. The question we ask is “what can Observer know?” or “what kind of information can Observer hope to obtain?”. We thus want to investigate “limits to knowledge” and “limits to information”. In order to provide an answer, we shall identify classes of preparations which represent feasible information. These classes will be defined with reference to an effort function $\widehat{\mathsf{\Phi }}$. For this section, $\widehat{\mathsf{\Phi }}$ need not be proper.

Given $w\in \widehat{Y}$ and a level $h<\infty$, we define the level set ${\mathcal{P}}^w(h)$ and the sub level set ${\mathcal{P}}^w(h^{\downarrow })$ by

$${\mathcal{P}}^w(h)=\{{\widehat{\mathsf{\Phi }}}^w=h\};{\mathcal{P}}^w(h^{\downarrow })=\{{\widehat{\mathsf{\Phi }}}^w\le h\},$$

(26)

i.e., as the set of states which are controlled by w, either at the level h or at the maximum level h. These sets are genuine preparations whenever they are non-empty. When w is the response of a state $x\in X$, ${\mathcal{P}}^w(h^{\downarrow })$ is non-empty whenever $h\ge \mathrm{H}(x)$. As level- and sub level sets for other functions will appear later on, cf., Section 2.14, we may for clarity refer to ${\mathcal{P}}^w(h)$ and to ${\mathcal{P}}^w(h^{\downarrow })$ as, respectively, ${\widehat{\mathsf{\Phi }}}^w$-level sets and ${\widehat{\mathsf{\Phi }}}^w$-sub level sets.

The preparations in (26) we call primitive strict, respectively primitive slack preparations. A general strict, respectively a general slack preparation is a finite non-empty intersection of primitive strict, respectively primitive slack preparations. The genus of these preparations is the smallest number of primitive preparations (either strict or slack as the case may be) which can enter into the definition just given. Thus primitive preparations are of genus 1.

If $\mathbf{w}=(w_1,\cdots ,w_n)$ are elements of $\widehat{Y}$ and $\mathbf{h}=(h_1,\cdots ,h_n)$ are real numbers, the sets

$${\mathcal{P}}^{\mathbf{w}}(\mathbf{h})=\bigcap _{i\le n}{\mathcal{P}}^{w_i}(h_i)\mathrm{and}{\mathcal{P}}^{\mathbf{w}}({\mathbf{h}}^{\downarrow })=\bigcap _{i\le n}{\mathcal{P}}^{w_i}(h_i^{\downarrow })$$

(27)

define strict, respectively slack preparations of genus at most n whenever they are non-empty. The set ${\mathcal{P}}^{\mathbf{w}}(\mathbf{h})$ is the corona of ${\mathcal{P}}^{\mathbf{w}}({\mathbf{h}}^{\downarrow })$ whenever it is non-empty.

The preparations introduced above via the representation (27) are those we consider to be feasible and we formally refer to them as the feasible preparations. They provide the answer to the question about what can be known. They are the key ingredients in situations which Observer can be faced with. In any such situation a main problem concerns inference, an issue we shall take up in the next section.

Often, families of feasible preparations are of interest. Given $\mathbf{w}=(w_1,\cdots ,w_n)$, we denote by ${\mathbb{P}}^{\mathbf{w}}$, respectively ${\mathbb{P}}^{\mathbf{w}\downarrow }$, the families which consist of all preparations ${\mathcal{P}}^{\mathbf{w}}(\mathbf{h})$, respectively ${\mathcal{P}}^{\mathbf{w}}({\mathbf{h}}^{\downarrow })$, which can be obtained by varying $\mathbf{h}$.

Clearly, the feasible preparations can also be expressed by reference to the derived effort function $\mathsf{\Phi }$ rather than $\widehat{\mathsf{\Phi }}$. We use the notation ${\mathcal{P}}^y(h)$ and ${\mathcal{P}}^y(h^{\downarrow })$ for, respectively, the ${\mathsf{\Phi }}^y$-level set $\{{\mathsf{\Phi }}^y=h\}$ and the ${\mathsf{\Phi }}^y$-sub level set $\{{\mathsf{\Phi }}^y\le h\}$. If $\widehat{y}=w$, ${\mathcal{P}}^y(h)={\mathcal{P}}^w(h)$ and ${\mathcal{P}}^y(h^{\downarrow })={\mathcal{P}}^w(h^{\downarrow })$ (note that for an expression such as ${\mathcal{P}}^q(h)$, the nature of q determines if this is a $\widehat{\mathsf{\Phi }}$- or a $\mathsf{\Phi }$-level set). For finite sequences $\mathbf{y}=(y_1,\cdots ,y_n)$ of elements of Y and $\mathbf{h}=(h_1,\cdots ,h_n)$ of real numbers, the sets ${\mathcal{P}}^{\mathbf{y}}(\mathbf{h})$ and ${\mathcal{P}}^{\mathbf{y}}({\mathbf{h}}^{\downarrow })$ are defined in the obvious manner as are the families of preparations ${\mathbb{P}}^{\mathbf{y}}$, respectively ${\mathbb{P}}^{\mathbf{y}\downarrow }$.

The level sets may be used to define certain special belief instances or controls which will later, theoretically as well as for applications, play a significant role. Given is a certain preparation $\mathcal{P}$. Then, the core of $\mathcal{P}$ consists of all belief instances y for which the effort $\mathsf{\Phi }(x,y)$ is finite and independent of x as long as x is consistent. This notion, appropriately adjusted, also makes sense for the $\widehat{Y}$-domain. Notation and defining requirements are given as follows:

$$\begin{array}{cc}\hfill \mathrm{core}(\mathcal{P})& =\{y\succ \mathcal{P}|\exists h<\infty :\mathcal{P}\subseteq {\mathcal{P}}^y(h)\},\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill \mathrm{core}^(\mathcal{P})& =\{w\succ \mathcal{P}|\exists h<\infty :\mathcal{P}\subseteq {\mathcal{P}}^w(h)\}.\hfill \end{array}$$

(29)

If $y\in \mathrm{core}(\mathcal{P})$, respectively $w\in \mathrm{core}^(\mathcal{P})$, we also say that y, respectively w, is robust.

We shall refine the notions above in two ways. Firstly, for a family $\mathbb{P}$ of preparations—such as a family of the form ${\mathbb{P}}^{\mathbf{w}}$ defined above—the core is defined as the intersection of the individual cores:

$$\begin{array}{cc}\hfill \mathrm{core}(\mathbb{P})& =\bigcap _{\mathcal{P}\in \mathbb{P}}\mathrm{core}(\mathcal{P}),\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill \mathrm{core}^(\mathbb{P})& =\bigcap _{\mathcal{P}\in \mathbb{P}}\mathrm{core}^(\mathcal{P}).\hfill \end{array}$$

(31)

The second refinement we have in mind depends on on an auxiliary preparation $\mathcal{E}$, assumed to be a subset of the given preparation $\mathcal{P}$. For the $\widehat{Y}$-domain, a control $w^{*}\succ \mathcal{P}$ is a $(\mathcal{E},\mathcal{P})$-robust strategy for Observer if there exists a finite constant h, such that the following two conditions hold:

$$\begin{array}{cc}\hfill & \widehat{\mathsf{\Phi }}(x,w^{*})=h\text{ for all }x\in \mathcal{E},\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill & \widehat{\mathsf{\Phi }}(x,w^{*})\le h\text{ for all }x\in \mathcal{P}\hfill \end{array}$$

(33)

When $\mathcal{E}=\mathcal{P}$ we recover the original notion of robustness. The similar notion for belief instances is defined in the obvious way. Notation and defining relations for the corresponding adjustments of the notion of core are as follows:

$$\begin{array}{cc}\hfill \mathrm{core}(\mathcal{E}|\mathcal{P})& =\{y\succ \mathcal{P}|\exists h<\infty :\mathcal{E}\subseteq {\mathcal{P}}^y(h),\mathcal{P}\subseteq {\mathcal{P}}^y(h^{\downarrow })\},\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill \mathrm{core}^(\mathcal{E}|\mathcal{P})& =\{w\succ \mathcal{P}|\exists h<\infty :\mathcal{E}\subseteq {\mathcal{P}}^w(h),\mathcal{P}\subseteq {\mathcal{P}}^w(h^{\downarrow })\}.\hfill \end{array}$$

(35)

From a formal point of view, it does not matter if we use ${\mathcal{P}}^w$-type sets or ${\mathcal{P}}^y$-type sets as the basis for the definition of feasible preparations. However, entering into more speculative interpretations, the ${\mathcal{P}}^w$-type sets which emphasize control seem preferable. Individual controls $w\in \widehat{Y}$ or a collection of such controls point to experiments which Observer may perform. An experimental setup identifies a certain preparation, and thus determines what is known to Observer. Determining all preparations which can arise in this way, we are led to the class of feasible preparations as defined above.

As to the nature of the various controls, we imagine that they are derived from description. To control a situation, you must be able to describe it, and with a description you have the key to control. We may imagine that, corresponding to a control w, Observer can realize a certain experimental setup consisting of various parts – measuring instruments and the like. In particular, there is a special handle which is used to fix the level of effort. If the level, perhaps best thought of as a kind of temperature, is fixed to be h, the states available to Nature are those in the appropriate feasible preparation. Several experiments can be carried out with the same equipment by adjusting the setting of the handle. If Observer wants to constrain the states by other means, he can add equipment corresponding to another control $w^{\prime }$ and choose a level $h^{\prime }$ for the experimental setup constructed based on $w^{\prime }$. The result is a restriction of the available states to the intersection of the two preparations involved. If the preparation is ${\mathcal{P}}^w(h^{\downarrow })$ and the actual state is not inside this preparation, you may imagine that the result is overheating and breakdown of the experimental setup! Thus you must keep the state inside the preparation and this may well be what requires an effort as specified by $\widehat{\mathsf{\Phi }}$.

2.10. Inference via Games, Some Basic Concepts

For this section, $(\widehat{\mathsf{\Phi }},\mathrm{H},\widehat{D})$ is an effort-based information triple over $X\otimes \widehat{Y}$ and $(\mathsf{\Phi },\mathrm{H},\mathrm{D})$ the derived triple over $X\otimes Y$. Further, a preparation $\mathcal{P}$ is given, conceived as the partial information “$x\in \mathcal{P}$”. In practice, $𝒫$ will be a feasible preparation, but we need not assume so for this section.

The process of inference concerns the identification of “sensible” states in $𝒫$—ideally only one such state, the inferred state. In many cases, this can be achieved by game theoretical methods involving a two-person zero-sum game. As it turns out, this will result in double inference where also either control instances or belief instances will be identified—ideally, only one such instance, the inferred control or the inferred belief instance as the case may be.

An inferred state, say $x^{*}$, brings Observer as close as possible to the truth in a way specified by the method applied. The same may be said about an inferred belief instance—or you may find it more appropriate to view an inferred belief instance as a final representation of Observers subjective views and conviction. Turning to controls, an inferred control is conceived as an invitation to Observer to act, say regarding the setup of experiments and performance of subsequent observations. In this way, actions by Observer as dictated by an inferred control $w^{*}$ is conceived as that which is needed for Observer in order to justify the inference $x^{*}$ about truth. In short, double inference gives Observer information both about what can be inferred about truth and how.

Given $𝒫$, we shall study two closely related two-person zero-sum games, the control game $\widehat{\gamma }(\mathcal{P})$, and the belief game $\gamma (\mathcal{P})$, also referred to as the derived game. If need be, we may write $\widehat{\gamma }(\mathcal{P}|\widehat{\mathsf{\Phi }})$ and $\gamma (\mathcal{P}|\mathsf{\Phi })$. The games have Nature and Observer as players and $\widehat{\mathsf{\Phi }}$, respectively $\mathsf{\Phi }$ as objective function. Nature is understood to be a maximizer, Observer a minimizer. For both games, strategies for Nature involve the choice of a consistent state. Observer strategies for $\widehat{\gamma }(\mathcal{P})$ are controls from which every state in $𝒫$ can be controlled. For $\gamma (\mathcal{P})$, Observer strategies are belief instances from which every state in $\mathcal{P}$ is visible, in other words, they are viewpoints of $\mathcal{P}$. Thus pairs of permissible strategies for the two games are either pairs $(x,w)$ with $x\in \mathcal{P}$ and $w\succ \mathcal{P}$ (with the understanding that $w\in \widehat{Y}$) or pairs $(x,y)$ with $x\in \mathcal{P}$ and $y\succ \mathcal{P}$ (with the understanding that $y\in Y$). In consistency with the discussion in Section 2.4, an observer strategy may be thought of as a strategy which is not “completely stupid” whatever the strategy of Nature, as long as that strategy is consistent. The choice of strategy for Observer may be a real choice, whereas, for Nature, it is often more appropriate to have a fictive choice in mind which reflects Observer’s speculations over what the truth could be.

A remark is in order regarding models where it is unnatural to work with controls and only belief is involved. Then the basis will be an effort-based information triple $(\mathsf{\Phi },\mathrm{H},\mathrm{D})$ over $X\otimes Y$ and only one type of game, $\gamma (\mathcal{P})$ will be involved. Formally, this may be considered a derived game by artificially introducing $\widehat{Y}=Y$, $X\otimes \widehat{Y}=X\otimes Y$, by taking response to be the identity map and by taking $(\widehat{\mathsf{\Phi }},\mathrm{H},\widehat{\mathrm{D}})$ to be identical with $(\mathsf{\Phi },\mathrm{H},\mathrm{D})$ Thus the approach we shall take with a primary focus on the control games, based on objects for the $\widehat{Y}$-domain is, formally, the more general one.

Following standard philosophy of game theory, Observer should always be prepared for a choice by Nature which is least favourable to him. One can argue that in our setting anything else would mean that Observer would not have used all available information. The line of thought goes well with Jaynes thinking as collected in [9], though there you find no reference to game theory.

In order for our exposition to be self-contained and also because our games are slightly at variance with what is normally considered, we shall here give full details regarding definitions and proofs. As references to game theory and applications to the physical sciences, ref. [32,56,57] may be useful.

Let us introduce basic notions for the control game and then comment more briefly on the derived game. The two values of $\widehat{\gamma }(\mathcal{P})$ are, for Nature,

$$\underset{x\in \mathcal{P}}{\sup }\underset{w\succ x}{\inf }\widehat{\mathsf{\Phi }}(x,w)$$

(36)

and, for Observer,

$$\underset{w\succ \mathcal{P}}{\inf }\underset{x\in \mathcal{P}}{\sup }\widehat{\mathsf{\Phi }}(x,w).$$

(37)

Note the slight deviation from usual practice in that w in the infimum in (36) varies over $^\left[x\right]$ and not just over $^\left[\mathcal{P}\right]$ or some other set independent of x. Philosophically, one may argue that Nature does not know of the restriction to $𝒫$—this is something Observer has arranged—and hence cannot know of any restriction besides the natural one $w\succ x$. As the infimum in (36) is nothing but the entropy $\mathrm{H}(x)$, the value for Nature is the maximum entropy value, also referred to as the MaxEnt-value:

$${\mathrm{H}}_{\max }(\mathcal{P})=\underset{x\in \mathcal{P}}{\sup }\mathrm{H}(x).$$

(38)

Problems on the determination of ${\mathrm{H}}_{\max }(\mathcal{P})$ and associated strategies are classical problems known from information theory or statistical physics. If $x^{*}\in \mathcal{P}$ and $\mathrm{H}(x^{*})={\mathrm{H}}_{\max }(\mathcal{P})$, $x^{*}$ is an optimal strategy for Nature, also referred to as a MaxEnt-state or MaxEnt-strategy. The archetypal concrete problems of this nature are discussed in Section 3.7.

As to the value for Observer, we identify the supremum in (37) with the risk associated with the strategy w and denote it by $\widehat{\mathrm{Ri}}(w|\mathcal{P})$:

$$\widehat{\mathrm{Ri}}(w|\mathcal{P})=\underset{x\in \mathcal{P}}{\sup }\widehat{\mathsf{\Phi }}(x,w).$$

(39)

The value for Observer then is the minimal risk of the game, also referred to as the MinRisk-value:

$${\widehat{\mathrm{Ri}}}_{\min }(\mathcal{P})=\underset{w\succ \mathcal{P}}{\inf }\widehat{\mathrm{Ri}}(w|\mathcal{P}).$$

(40)

An optimal strategy for Observer is a control $w^{*}\succ \mathcal{P}$ with $\widehat{\mathrm{Ri}}(w^{*}|\mathcal{P})={\widehat{\mathrm{Ri}}}_{\min }(\mathcal{P})$, also referred to as a MinRisk-control or a MinRisk-strategy. Note the general validity of the minimax inequality:

$${\mathrm{H}}_{\max }(\mathcal{P})\le {\widehat{\mathrm{Ri}}}_{\min }(\mathcal{P}).$$

(41)

Indeed, for arbitrary $x\in \mathcal{P}$ and arbitrary $w\succ \mathcal{P}$,

$$\mathrm{H}(x)=\widehat{\mathsf{\Phi }}(x,\widehat{x})\le \widehat{\mathsf{\Phi }}(x,w)\le \widehat{\mathrm{Ri}}(w|\mathcal{P})$$

and taking supremum over x and infimum over w, (41) follows. If (41) holds with equality and defines a finite quantity, the game is said to be in game theoretical equilibrium, or just in equilibrium, and the common value of ${\mathrm{H}}_{\max }(\mathcal{P})$ and ${\widehat{\mathrm{Ri}}}_{\min }(\mathcal{P})$ is the value of the game.

A further notion of equilibrium is attached to Nash’s name. It should, however, be said that for the relatively simple case here considered (two players, zero sum), the ideas we need originated with von Neumann, see [58,59] and, for a historical study, Kjeldsen [60]. A pair of permissible strategies $(x^{*},w^{*})$ is a Nash equilibrium pair for $\widehat{\gamma }(\mathcal{P})$ if, with these strategies, none of the players have an incentive to change strategy—provided the opponent does not do so either. This means, for Nature, that

$$\forall x\in \mathcal{P}:\widehat{\mathsf{\Phi }}(x,w^{*})\le \widehat{\mathsf{\Phi }}(x^{*},w^{*}),$$

(42)

and, for Observer, that

$$\forall w\succ \mathcal{P}:\widehat{\mathsf{\Phi }}(x^{*},w)\ge \widehat{\mathsf{\Phi }}(x^{*},w^{*}).$$

(43)

The inequalities (42) and (43) constitute a special case of the celebrated saddle-value inequalities of game theory. Note that, in our case, one of these inequalities (43), is automatic if $(x^{*},w^{*})$ is an adapted pair. This implies that $x^{*}\in \mathrm{ctr}(\mathcal{P})$ and that $w^{*}\in \widehat{\mathcal{P}}$ as follows from the following trivial observation:

Proposition 1.

If $x^{*}$ and $w^{*}$ are permissible strategies for the two players in $\widehat{\gamma }(\mathcal{P})$ and if $w^{*}$ is adapted to $x^{*}$, then $x^{*}\in \mathrm{ctr}(\mathcal{P})$ and $w^{*}\in \mathrm{ctr}^(\mathcal{P})$.

Proof. 

By hypothesis, $x^{*}\in \mathcal{P}$, $w^{*}\succ \mathcal{P}$ and $w^{*}=\widehat{x^{*}}$, hence $w^{*}\in \widehat{\mathcal{P}}\cap ^\left[\mathcal{P}\right]=\mathrm{ctr}^(\mathcal{P})$, equivalent to the statement $x^{*}\in \mathrm{ctr}(\mathcal{P})$. ☐

Key notions and definitions for the belief game $\gamma (\mathcal{P})$ are quite parallel to what we have discussed for the control game. Briefly, the values of $\gamma (\mathcal{P})$ are ${\sup }_{x\in \mathcal{P}}{\inf }_{y\succ x}\mathsf{\Phi }(x,y)$ (for Nature) and ${\inf }_{y\succ \mathcal{P}}{\sup }_{x\in \mathcal{P}}\mathsf{\Phi }(x,y)$ (for Observer) and notions of strategies and optimal strategies are defined in an obvious manner. We notice that the value for Nature in $\gamma (\mathcal{P})$ is ${\mathrm{H}}_{\max }(\mathcal{P})$, the same as the value for Nature in $\widehat{\gamma }(\mathcal{P})$ and that the notion of optimal strategies for Nature in the two games are equivalent notions. We use Ri as notation for risk in $\gamma (\mathcal{P})$, i.e., for $y\succ \mathcal{P}$

$$\mathrm{Ri}(y|\mathcal{P})=\underset{x\in \mathcal{P}}{\sup }\mathsf{\Phi }(x,y).$$

(44)

Clearly, for any $y\succ \mathcal{P}$,

$$\mathrm{Ri}(y|\mathcal{P})=\widehat{\mathrm{Ri}}(\widehat{y}|\mathcal{P}).$$

(45)

Therefore, if $y_1\widehat{\sim }{y}_2$ and one of these belief instances is a viewpoint of $\mathcal{P}$, then so is the other and the associated risks are the same. The value for Observer in $\gamma (\mathcal{P})$ is

$${\mathrm{Ri}}_{\min }(\mathcal{P})=\underset{y\succ \mathcal{P}}{\inf }\mathrm{Ri}(y|\mathcal{P}).$$

(46)

The game $\gamma (\mathcal{P})$ is in equilibrium if the two values of the game coincide and are finite. A pair $(x^{*},y^{*})$ of permissible strategies is a Nash equilibrium pair for $\gamma (\mathcal{P})$ if the two saddle-value inequalities hold:

$$\begin{array}{cc}\hfill & \forall x\in \mathcal{P}:\mathsf{\Phi }(x,y^{*})\le \mathsf{\Phi }(x^{*},y^{*}),\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill & \forall y\succ \mathcal{P}:\mathsf{\Phi }(x^{*},y)\ge \mathsf{\Phi }(x^{*},y^{*}).\hfill \end{array}$$

(48)

Basic relationships between the values for the players in the belief game and the control game may be summarized as follows.

Proposition 2.

The values for Nature in $\gamma (\mathcal{P})$ and in $\widehat{\gamma }(\mathcal{P})$ coincide and are equal to the MaxEnt value ${\mathrm{H}}_{\max }(\mathcal{P})$. The corresponding values for Observer in the two games are ${\mathrm{Ri}}_{\min }(\mathcal{P})$, respectively ${\widehat{\mathrm{Ri}}}_{\min }(\mathcal{P})$. In general,

$${\mathrm{Ri}}_{\min }(\mathcal{P})\ge {\widehat{\mathrm{Ri}}}_{\min }(\mathcal{P}).$$

(49)

If response is surjective, equality holds in (49). Equality also holds if $\gamma (\mathcal{P})$ is in equilibrium. In that case also $\widehat{\gamma }(\mathcal{P})$ is in equilibrium and the values for the two games coincide: ${\mathrm{Ri}}_{\min }(\mathcal{P})={\widehat{\mathrm{Ri}}}_{\min }(\mathcal{P})={\mathrm{H}}_{\max }(\mathcal{P})$.

Proof. 

The first statement regarding the values for Nature is trivial and also noted above. The inequality (49) follows by (45), which also implies that equality holds in case response is surjective. If $\gamma (\mathcal{P})$ is in equilibrium, apply the minimax inequality to $\widehat{\gamma }(\mathcal{P})$, exploit equilibrium of $\gamma (\mathcal{P})$ as well as the inequality (49) and you find that

$${\widehat{\mathrm{Ri}}}_{\min }(\mathcal{P})\ge {\mathrm{H}}_{\max }(\mathcal{P})={\mathrm{Ri}}_{\min }(\mathcal{P})\ge {\widehat{\mathrm{Ri}}}_{\min }(\mathcal{P}).$$

It follows that also $\widehat{\gamma }(\mathcal{P})$ is in equilibrium. Clearly, the values for the two games coincide. ☐

As it will turn out, in a great many cases of relevance for the applications, it is possible rather directly to identify optimal strategies for the players and to show that the games considered are in equilibrium. Furthermore, in many cases there is a natural relationship between the $\widehat{\gamma }$- and the $\gamma$-type games with the effect that, typically, there is a unique optimal strategy for Observer in $\widehat{\gamma }(\mathcal{P})$ and this strategy, a certain control, is adapted to any optimal strategy for Nature in the games $\widehat{\gamma }(\mathcal{P})$ and $\gamma (\mathcal{P})$. Even more so, there is a tendency for the unique optimal control to be robust.

Results to support these claims will be taken up in Section 2.12. The results require that somehow you have good candidates for the hoped-for optimal strategies. For this, the indicated tendency towards robustness is a clue to how such candidates can actually be found in concrete cases of interest. In fact, a search for optimal objects via robustness is very efficient and more natural than the usual approach via the differential calculus as we shall also comment on in Section 2.12.

2.11. Refined Notions of Properness

The discussion to follow may appear unnecessary since normally, the standard notion of properness will apply. However, there are interesting cases where this is not so. Therefore, there is a need to look for suitable weaker notions which are still strong enough to have desirable consequences especially regarding properties of optimal strategies. As justification of the good sense in considering also the weaker notions of properness presented below we point to the general results of Section 2.12 and to the extended applicability of a a well-known construction due to Bregman, cf., Section 3.1 and Appendix A.

With assumptions as in Section 2.10, let us assume that $\widehat{\gamma }(\mathcal{P})$ is in equilibrium and, for simplicity, that there is a unique MaxEnt-state $x^{*}$. Let us think of the system which Observer is studying as a physical system subject to the laws of statistical physics. Then Observer will expect that after some lead-in time, the system will stabilize and $x^{*}$ will represent the true state of the system. Observer aims at choosing a control which is optimal and at the same time adapted to Natures choice, $x^{*}$. Unfortunately, Observer does not know which state this is among the consistent states. So Observer cannot just choose the control $w^{*}=\widehat{x^{*}}$ adapted to $x^{*}$, but has to somehow choose some control of $\mathcal{P}$, say w.

At this point we introduce a built-in learning mechanism operating over time which may lead Observer in the right direction. The idea is illuminated by introducing an all-knowing being, Guru. Guru will not reveal the truth to Observer directly but may respond to specific questions. With this option, Observer may eventually end up by a choice of just the right control.

The three questions we shall consider all concern the entropy $\mathrm{H}(x^{*})$ which Observer expects to be the MaxEnt-value. The questions are all related to the inequality

$$\widehat{\mathsf{\Phi }}(x,w)\le \mathrm{H}(x^{*}).$$

(50)

The questions put higher and higher demands on the chosen control w and are as follows:

$Q_1$:

Does (50) hold for $x=x^{*}$?

$Q_2$:

Does (50) hold for all consistent x?

$Q_3$:

Does (50) even hold with equality for all consistent x?

With Question $Q_1$, Observer wants to know if the effort he applies is minimal. Clearly, in view of the linking identity and the fundamental inequality—and as $\mathrm{H}(x^{*})<\infty$ by the assumed equilibrium of $\widehat{\gamma }(\mathcal{P})$—the question is equivalent to asking if $\widehat{\mathrm{D}}(x^{*},w)=0$. If the reply is negative, Observer knows that his choice cannot be optimal and he will then choose another control. But even with an affirmative answer, i.e., when $\widehat{\mathrm{D}}(x^{*},w)=0$, Observer may not be satisfied and may, therefore, continue the questioning. If the information triple is proper, an affirmative answer to $Q_1$ will tell Observer that $w=\widehat{x^{*}}$ and he may be satisfied—even though it could still happen, as examples will show, that w is not optimal. Further questioning may thus only be needed if the information triple is not proper—or not known to be proper.

For the second question, $Q_2$, Observer is worried about his risk in case the state should somehow change. The question is equivalent to asking if $\widehat{\mathrm{Ri}}(w|\mathcal{P})\le \mathrm{H}(x^{*})$. With a negative reply, Observer will dismiss the choice of w, if for no other reason, because w cannot be optimal then. If the reply is positive, w is optimal and one may wonder if Observer will still find any further checking necessary. The suggested third question $Q_3$ reflects the ambition of Observer that he wants the control to be robust at the level $\mathrm{H}(x^{*})$.

Motivated by our considerations, we shall say that the information triple $(\widehat{\mathsf{\Phi }},\mathrm{H},\widehat{\mathrm{D}})$ is $Q_1$, $Q_2$ or $Q_3$-proper over $\mathcal{P}$ if, with $x^{*}\in \mathcal{P}$, we can conclude that w is adapted to $x^{*}$ from affirmative answers to, respectively, question $Q_1$, $Q_2$ or $Q_3$. If we just talk about, say $Q_2$-properness, it is understood that the conditions hold with $\mathcal{P}=X$. If the entropy function is finite-valued, $Q_1$-properness is equivalent to (standard) properness.

Concerning questions being asked to Guru, one may wonder why Observer does not simply ask directly either if the chosen control is optimal or if it is adapted to the truth. In this connection, we remark that questions which can be asked to Guru must depend on the possibilities for Observer’s communication with the system. For a further discussion of this, one should replace Guru with some mathematically defined rules for this communication. Such rules may reflect the kind of experiments and associated measurements which Observer can perform on the system.

2.12. Inference via Games, Some Basic Results

We shall investigate the possibility to identify optimal strategies based on a suggestion of possible candidates. Moreover, when optimal strategies exist, we shall look at the ensuing consequences. This approach will involve problems which are easy to handle technically and yet, it may be argued that from an applied point of view the results obtained are of greater significance than theoretically more sophisticated results, such as those developed in Section 2.16. Several examples illustrating this point of view are listed in Section 3.

As in the previous section, an effort-based information triple $(\widehat{\mathsf{\Phi }},\mathrm{H},\widehat{\mathrm{D}})$ over $X\otimes \widehat{Y}$, the underlying triple, is given together with a preparation $\mathcal{P}$.

When we speak about an optimal state without any further specification it is understood that we have an optimal strategy for Nature in one of the games $\widehat{\gamma }(\mathcal{P})$ or $\gamma (\mathcal{P})$ in mind. As we observed in the previous section it does not matter which game we think of. Moreover, when we speak of an optimal belief instance, respectively an optimal control it is also clear what we have in mind, viz., an optimal strategy for Observer in $\gamma (\mathcal{P})$, respectively in $\widehat{\gamma }(\mathcal{P})$.

In our first result we investigate situations where, in addition to a requirement of equilibrium, there exist optimal strategies for both players.

Theorem 1 (Optimal strategies, basics).

(i): If $\gamma (\mathcal{P})$ is in equilibrium and both players have optimal strategies in this game, then also $\widehat{\gamma }(\mathcal{P})$ is in equilibrium and optimal strategies for both players in that game exist. Further, the values of the two games agree and, if $(x^{*},y^{*})$ are optimal strategies in $\gamma (\mathcal{P})$, then $(x^{*},\widehat{y^{*}})$ are optimal strategies in $\widehat{\gamma }(\mathcal{P})$ (but there may be many other optimal strategies).

(ii): Now assume that $(\widehat{\mathsf{\Phi }},\mathrm{H},\widehat{\mathrm{D}})$ is proper. Then, if $\widehat{\gamma }(\mathcal{P})$ is in equilibrium and both players have optimal strategies, say $x^{*}$ and $w^{*}$, then $x^{*}\in \mathrm{ctr}(\mathcal{P})$, $w^{*}\in \mathrm{ctr}^(\mathcal{P})$ and $w^{*}=\widehat{x^{*}}$. It follows that the optimal control is unique. Furthermore, also $\gamma (\mathcal{P})$ is in equilibrium and both players have optimal strategies. A belief instance is optimal in $\gamma (\mathcal{P})$ if and only if it has $w^{*}$ as response. If response is injective, each of the three optimal strategies associated with $\gamma (\mathcal{P})$ and $\widehat{\gamma }(\mathcal{P})$—the optimal state $x^{*}$, the optimal belief instance $y^{*}$ and the optimal control $w^{*}$—are unique and $x^{*}=y^{*}$.

Proof. 

(i): Assume that $\gamma (\mathcal{P})$ is in equilibrium and that $(x^{*},y^{*})$ are optimal strategies for this game. A bit parallel to the reasoning in the proof of Proposition 2, we find that under the stated conditions

$${\mathrm{H}}_{\max }(\mathcal{P})=\mathrm{H}(x^{*})=\mathrm{Ri}(y^{*}|\mathcal{P})=\widehat{\mathrm{Ri}}(\widehat{y^{*}}|\mathcal{P})$$

and the claimed assertions follow readily.

(ii): Now assume that $\widehat{\gamma }(\mathcal{P})$ is in equilibrium and that $(x^{*},w^{*})$ are optimal strategies for this game. By the defining relations (8) and (9), by the assumed equilibrium, by optimality of $x^{*}$ and of $w^{*}$ and by the definition (39) of risk, we find that

$$\widehat{\mathsf{\Phi }}(x^{*},w^{*})\ge \widehat{\mathsf{\Phi }}(x^{*},\widehat{x^{*}})=\mathrm{H}(x^{*})={\mathrm{H}}_{\max }(\mathcal{P})={\widehat{\mathrm{Ri}}}_{\min }(\mathcal{P})=\widehat{\mathrm{Ri}}(w^{*}|\mathcal{P})\ge \widehat{\mathsf{\Phi }}(x^{*},w^{*}),$$

(51)

hence equality must hold throughout. Further, as $\mathrm{H}(x^{*})<\infty$, we conclude that $\widehat{\mathrm{D}}(x^{*},w^{*})=0$, hence by properness that $w^{*}=\widehat{x^{*}}$. Then, by Proposition 1, $x^{*}\in \mathrm{ctr}(\mathcal{P})$ and $w^{*}\in \mathrm{ctr}^(\mathcal{P})$.

Since $x^{*}$ above was an arbitrary optimal strategy for Nature and $w^{*}$ an arbitrary optimal strategy for Observer, and by the fact $w^{*}=\widehat{x^{*}}$ just established, we conclude that the optimal Observer strategy is unique and further, that all optimal strategies for Nature are response-equivalent, lie in $\mathrm{ctr}(\mathcal{P})$ and have the optimal control as response.

We leave it to the reader to establish the stated results for $\gamma (\mathcal{P})$, say by noting that $y\succ \mathcal{P}$ is equivalent with $\widehat{y}\succ \mathcal{P}$ and that $\mathrm{Ri}(y|\mathcal{P})=\widehat{\mathrm{Ri}}(\widehat{y}|\mathcal{P})$ and by using the first facts established.

In case response is injective, the uniqueness assertions are easily established and the identity of $x^{*}$ and $y^{*}$ follows as these belief instances are response-equivalent. ☐

Some remarks are in order.

Remark 1.

Simple and very concrete “toy examples” over discrete sets—either finite or countably infinite—may be constructed to illuminate various assumptions and to investigate the limits of the conclusions. This involves matrix games which are easy to visualize. In this way one realizes that the games may be in equilibrium and yet there may be no optimal strategy for any of the players or there may be one or several optimal strategies for one of the players and none for the other. Three such examples for games in equilibrium and with an underlying proper information triple are indicated in Figure 1 where the rows are states and the columns controls (or belief instances). In case (a) there is a unique optimal control but no optimal state, in case (b) there is a unique optimal state but no optimal control and in case (c) all controls are optimal but there is no optimal state. It is also easy to construct an example where all states are optimal but no control is so.

Remark 2.

Regarding the necessity of injectivity of response in the last part of the theorem, note that if this condition does not hold, there may be strategies for Nature with the optimal control $w^{*}$ as response which are not optimal. Simple examples, say with “collapse of response”, i.e., with $\widehat{Y}$ a singleton, will demonstrate that.

Remark 3.

Several remarks on the assumption of properness are in place. First note that we did not have to assume that response is surjective in order to prove that the optimal strategy $w^{*}$ in the second part of the theorem is in the range of this map. The assumed properness takes care of that. However, we need not assume that properness in its strongest form holds but may work with the weaker forms introduced in Section 2.11.

To make this more precise, first note that all assertions of the second part of Theorem 1 continue to hold if properness is replaced by $Q_2$-properness. This follows from the discussion in Section 2.11 by noting that from the relations in (51) one can conclude, not only that $\widehat{\mathrm{D}}(x^{*},w)=0$, but also that $\widehat{\mathrm{Ri}}(w|\mathcal{P})\le \mathrm{H}(x^{*})$. In this way some of the concrete models discussed in Appendix A, can be handled—but not all.

We add, without going through the details, that if we assume that the weaker $Q_3$-properness holds in conjunction with an assumption of robustness, viz., that all controls which are adapted to an optimal state are robust, then uniqueness of a robust optimal control is secured. The robustness condition appears to be related to a requirement that response be defined “appropriately”. For the models of Appendix A this requires that special care is taken when defining response at boundary points of the state space.

In the sequel some results are proved under the assumption of $Q_2$-properness. This is, so we claim, a simple, worth while and natural extension over results proved only under an assumption of standard $Q_1$-properness. Even more general results involving also robustness as just indicated may well be possible. However, it seems that before that will make much sense, one should develop results and constructions going beyond what is indicated in Appendix A and in Corollary 6 further on.

Inspired by Theorem 1, a pair $(x^{*},w^{*})$ of permissible strategies is said to be a bi-optimal pair, if $\mathrm{H}(x^{*})=\widehat{\mathrm{Ri}}(w^{*}|\mathcal{P})<\infty$ and if $w^{*}$ is the only optimal control. As follows from the theorem and from Remark 3, the required uniqueness property of $w^{*}$ is automatic under an assumption of $Q_2$-properness of the underlying information triple and further, $w^{*}$ must be adapted to $x^{*}$.

If we have only given a state $x^{*}$, we say that the state is bi-optimal if $(x^{*},w^{*})$ is a bi-optimal pair with $w^{*}$ adapted to $x^{*}$.

Whereas it may be difficult to find optimal strategies, it is often easy to check if given candidates are in fact optimal:

Theorem 2.

[Identification] Under the assumptions of $Q_2$-properness, let $x^{*}$ be a state in $\mathrm{ctr}(\mathcal{P})$ with finite entropy and let $w^{*}$ be a control of $\mathcal{P}$.

Then a necessary and sufficient condition that the pair $(x^{*},w^{*})$ is bi-optimal is that it is a Nash equilibrium pair. If this is so, $w^{*}$ is adapted to $x^{*}$.

Proof. 

First note that (42) is equivalent with the requirement $\widehat{\mathrm{Ri}}(w^{*}|\mathcal{P})\le \widehat{\mathsf{\Phi }}(x^{*},w^{*})$ and that, because $\widehat{x^{*}}\succ \mathcal{P}$ is known to hold (as $x^{*}\succ \mathcal{P}$), (43) is equivalent with the requirement $\mathsf{\Phi }(x^{*},w^{*})\le \mathrm{H}(x^{*})$.

Thus, when (42) and (43) hold, we find, also invoking the minimax inequality, that

$$\widehat{\mathrm{Ri}}(w^{*}|\mathcal{P})\le \widehat{\mathsf{\Phi }}(x^{*},w^{*})\le \mathrm{H}(x^{*})\le \widehat{\mathrm{Ri}}(w^{*}|\mathcal{P})$$

hence, recalling that $\mathrm{H}(x^{*})<\infty$, both $\widehat{\mathrm{D}}(x^{*},w^{*})=0$ and $\widehat{\mathrm{Ri}}(w^{*}|\mathcal{P})=\mathrm{H}(x^{*})$ follow. By $Q_2$-properness, we then realize that $w^{*}$ is adapted to $x^{*}$. Collecting facts established, we conclude that $(x^{*},w^{*})$ is a bi-optimal pair. This proves sufficiency.

The necessity and the last part of the theorem follow from Theorem 1 and the above noticed equivalent forms of the saddle-value inequalities. ☐

Elaborating slightly, we obtain the following corollary:

Corollary 1.

Under the assumption of $Q_2$-properness, if $(x^{*},w^{*})$ are permissible strategies for $\widehat{\gamma }(\mathcal{P})$ with $x^{*}\in \mathrm{ctr}(\mathcal{P})$, $\mathrm{H}(x^{*})<\infty$ and with $w^{*}$ adapted to $x^{*}$, then a necessary and sufficient condition that $\widehat{\gamma }(\mathcal{P})$ and $\gamma (\mathcal{P})$ are in equilibrium with $x^{*}$ as bi-optimal state is that $\widehat{\mathrm{Ri}}(w^{*}|\mathcal{P})\le \mathrm{H}(x^{*})$, i.e., that

$$\forall x\in \mathcal{P}:\widehat{\mathsf{\Phi }}(x,w^{*})\le \mathrm{H}(x^{*}).$$

(52)

Proof. 

Under the conditions stated, (43) is automatic and (52) is a reformulation of (42). Thus (52) implies that $(x^{*},w^{*})$ is a Nash equilibrium pair and the result follows from Theorem 2. ☐

An important and trivial consequence of the existence of a bi-optimal state is the validity of the Pythagorean inequalities. Let $x^{*}$ be a bi-optimal state and $w^{*}$ its response. The direct Pythagorean inequality, or just the Pythagorean inequality, is the inequality $\mathrm{H}(x)+\widehat{\mathrm{D}}(x,w^{*})\le \mathrm{H}(x^{*})$, typically considered for $x\in \mathcal{P}$. This is nothing but a trivial rewriting of (52). When it holds, $\mathrm{H}(x^{*})={\mathrm{H}}_{\max }(\mathcal{P})$ and the inequality for an individual state $x\in \mathcal{P}$ is, therefore, a sharper form of the trivial inequality $\mathrm{H}(x)\le {\mathrm{H}}_{\max }(\mathcal{P})$. The dual Pythagorean inequality is the inequality $\widehat{\mathrm{Ri}}(w^{*}|\mathcal{P})+\widehat{\mathrm{D}}(x^{*},w)\le \widehat{\mathrm{Ri}}(w|\mathcal{P})$, typically considered for $w\succ \mathcal{P}$. When it holds, $\widehat{\mathrm{Ri}}(w^{*}|\mathcal{P})={\widehat{\mathrm{Ri}}}_{\min }(\mathcal{P})$, and the inequality for an individual strategy $w\succ \mathcal{P}$ is, therefore, a sharper form of the trivial inequality ${\widehat{\mathrm{Ri}}}_{\min }(\mathcal{P})\le \widehat{\mathrm{Ri}}(w|\mathcal{P})$.

Theorem 3.

[Pythagorean inequalities] Under the assumption of $Q_2$-properness, if $\gamma (\mathcal{P})$ and $\widehat{\gamma }(\mathcal{P})$ are in equilibrium with $x^{*}$ as bi-optimal state then, with $w^{*}=\widehat{x^{*}}$, the direct as well as the dual Pythagorean inequalities hold:

$$\begin{array}{cc}\hfill \forall x\in \mathcal{P}:& \mathrm{H}(x)+\widehat{\mathrm{D}}(x,w^{*})\le \mathrm{H}(x^{*}),\hfill \end{array}$$

(53)

$$\begin{array}{cc}\hfill \forall w\succ \mathcal{P}:& \widehat{\mathrm{Ri}}(w^{*}|\mathcal{P})+\widehat{\mathrm{D}}(x^{*},w)\le \widehat{\mathrm{Ri}}(w|\mathcal{P}).\hfill \end{array}$$

(54)

Proof. 

As to (53), this follows from Corollary 1. Also (54) must hold since, for $w\succ \mathcal{P}$,

$$\widehat{\mathrm{Ri}}(w^{*}|\mathcal{P})+\widehat{\mathrm{D}}(x^{*},w)=\mathrm{H}(x^{*})+\widehat{\mathrm{D}}(x^{*},w)=\widehat{\mathsf{\Phi }}(x^{*},w)\le \widehat{\mathrm{Ri}}(w|\mathcal{P}).$$

☐

The Pythagorean flavour of (53) is more pronounced when one turns to models of updating, cf., Section 2.13 and Section 3.2.

Let us elaborate on the direct Pythagorean inequality. First, let us agree that a control w of $\mathcal{P}$ is a Pythagorean control for $\widehat{\gamma }(\mathcal{P})$ if, for every $x\in \mathcal{P}$,

$$\mathrm{H}(x)+\widehat{\mathrm{D}}(x,w)\le {\mathrm{H}}_{\max }(\mathcal{P}).$$

(55)

This notion will be used whether or not $\widehat{\gamma }(\mathcal{P})$ is in equilibrium and whether or not this game has optimal strategies. In particular, it applies in cases when no MaxEnt-state exists. Of course, the notion is only of interest if ${\mathrm{H}}_{\max }(\mathcal{P})<\infty$.

Translating to the Y-domain, we say that y is a Pythagorean belief instance for $\gamma (\mathcal{P})$ if $y\succ \mathcal{P}$ and if, for every $x\in \mathcal{P}$,

$$\mathrm{H}(x)+\mathrm{D}(x,y)\le {\mathrm{H}}_{\max }(\mathcal{P}).$$

(56)

Theorem 4.

Under the assumption of $Q_2$-properness, assume that a MaxEnt-state exists for the preparation $\mathcal{P}$ and that ${\mathrm{H}}_{\max }(\mathcal{P})<\infty$. Then the following three conditions are equivalent:

• a Pythagorean control for $\widehat{\gamma }(\mathcal{P})$ exists;
• a Pythagorean belief instance for $\gamma (\mathcal{P})$ exists;
• The games $\widehat{\gamma }(\mathcal{P})$ and $\gamma (\mathcal{P})$ are in equilibrium and a bi-optimal state for these games exist.

If these conditions are fulfilled, the Pythagorean control, $w^{*}$, is unique and identical to the optimal strategy for Observer in $\widehat{\gamma }(\mathcal{P})$. Further, a belief instance, $y^{*}$ with $y^{*}\succ \mathcal{P}$ is a Pythagorean belief instance if and only if it has $w^{*}$ as response.

Proof. 

Assume that w is a Pythagorean control. Then, by (55), $\widehat{\mathrm{Ri}}(w|\mathcal{P})\le {\mathrm{H}}_{\max }(\mathcal{P})$. Choose a MaxEnt-state $x^{*}$. Then ${\mathrm{H}}_{\max }(\mathcal{P})=\mathrm{H}(x^{*})<\infty$ and (55) with $x=x^{*}$ implies that $\widehat{\mathrm{D}}(x^{*},w)=0$. As $\widehat{\mathrm{Ri}}(w|\mathcal{P})\le \mathrm{H}(x^{*})$ also holds, $Q_2$-properness shows that $w=x^{*}$. Then, by Corollary 1, $\widehat{\gamma }(\mathcal{P})$ and $\gamma (\mathcal{P})$ are in equilibrium with $x^{*}$ as bi-optimal state. Appealing also to previous results, all statements of the theorem follow. ☐

The three results to follow are often useful in applications.

Theorem 5.

[Robustness theorem] Under the assumption of $Q_2$-properness, let $(x^{*},w^{*})$ be an adapted pair and assume that $w^{*}$ is robust for $\widehat{\gamma }(\mathcal{P})$, say at the level h of robustness, and that $x^{*}$ is consistent. Then $\widehat{\gamma }(\mathcal{P})$ is in equilibrium with h as value and with $x^{*}$ as bi-optimal state. Furthermore, for any $x\in \mathcal{P}$, the Pythagorean inequality holds with equality:

$$\mathrm{H}(x)+\widehat{\mathrm{D}}(x,w^{*})={\mathrm{H}}_{\max }(\mathcal{P}).$$

(57)

Similarly, if $x^{*}$ and $y^{*}$ are response-equivalent, if $y^{*}$ is robust for $\gamma (\mathcal{P})$ and if $x^{*}$ is consistent, then $\gamma (\mathcal{P})$ is in equilibrium with $x^{*}$ as bi-optimal state and, for $x\in \mathcal{P}$,

$$\mathrm{H}(x)+\mathrm{D}(x,y^{*})={\mathrm{H}}_{\max }(\mathcal{P}).$$

(58)

The equality (57) or (58) for $x\in \mathcal{P}$ is the Pythagorean equality, here in an abstract version. A more compact geometry flavored formulation of the first part of Theorem 5 in the direction of Corollary 1 runs as follows:

Corollary 2.

Under the assumption of $Q_2$-properness, if h is finite and $x^{*}\in \mathcal{P}\subseteq {\mathcal{P}}^{\widehat{x^{*}}}(h)$, then $h=\mathrm{H}(x^{*})$ and $\widehat{\gamma }(\mathcal{P})$ is in equilibrium with $x^{*}$ as bi-optimal state.

In case response is injective, the second part of Theorem 5 really only involves one element, $x^{*}$, as the other element, $y^{*}$, has to be identical to $x^{*}$. The two essential conditions are one on $x^{*}$ as a strategy for Nature, viz., that it is consistent, and one on $x^{*}$ as a strategy for Observer, viz., that it is robust. There can only be one such element. If we drop the condition of consistency, there may be many more such elements. They form the previously defined core of $\gamma (\mathcal{P})$.

For preparation families we find the following result:

Theorem 6.

Under the standard assumption on properness, consider a preparation family ${\mathbb{P}}^{\mathbf{y}}$ with $\mathbf{y}=(y_1,\cdots ,y_n)$. Let $x^{*}$ be a state, put $y^{*}=x^{*}$ and assume that $y^{*}\in \mathrm{core}({\mathbb{P}}^{\mathbf{y}}|\mathsf{\Phi })$. Further, put $\mathbf{h}=(h_1,\cdots ,h_n)$ with $h_i=\mathsf{\Phi }(x^{*},y_i)$ for $i=1,\cdots ,n$ and assume that these constants are finite. Then ${\mathcal{P}}^{\mathbf{y}}(\mathbf{h})\in {\mathbb{P}}^{\mathbf{y}}$ and $\gamma \left({\mathcal{P}}^{\mathbf{y}}(\mathbf{h})\right)$ is in equilibrium and has $x^{*}$ as bi-optimal state. In particular, $x^{*}$ is the MaxEnt strategy for ${\mathcal{P}}^{\mathbf{y}}(\mathbf{h})$.

This follows directly from the involved definitions and from Theorem 5. The reader will easily establish an analogous result for the $\widehat{Y}$-domain.

The notions of robustness and core also make sense for games defined in terms of proper or just $Q_2$-proper utility-based information triples. If $(\mathrm{U},\mathrm{M},\mathrm{D})$ is such a triple, we simply apply the above definitions to the associated effort-based triple $(-\mathrm{U},-\mathrm{M},D)$.

Theorem 2 points to a strategy which is often fruitful in the search for a MaxEnt-strategy, viz., first to determine the core of the given preparation and then to select that element (if any) in the core which is consistent. This route to determine MaxEnt strategies does not involve the infinitesimal calculus, in particular, it does not need the use of Lagrange multipliers. Researchers of statistical physics may claim that you need the Lagrange multipliers as they are of special physical significance, see e.g., Kuic [61]. In that connection, one will find that these quantities turn up anyhow and in a more natural way if you follow the approach via robustness, cf., [62].

The notion of robustness has not received much attention in a game theoretical setting. It is implicit in [26,63] and perhaps first formulated in [24]. Apparently, the existence of suitable robust strategies is a strong assumption. However, for typical models appearing in applications, the assumption is often fulfilled when optimal strategies exist. Results from [27] point in that direction.

Dual versions of the notions and results indicated above could be introduced, depending on (54) rather than on (53). However, it seems that the notions related to the direct Pythagorean inequality are the more useful ones.

For the result to follow we need an abstract version of Jeffrey’s divergence given, for two states $x_1$ and $x_2$, by

$$\mathrm{J}(x_1,x_2)=\mathrm{D}(x_1,x_2)+\mathrm{D}(x_2,x_1).$$

(59)

Corollary 3.

[transitivity inequality] Assume that $(\mathsf{\Phi },\mathrm{H},\mathrm{D})$ is a $Q_2$-proper information triple. If $\gamma (\mathcal{P})$ is in equilibrium with $x^{*}$ as a bi-optimal state, then, for every state $x\in \mathcal{P}$ and every belief instance $y\succ \mathcal{P}$, the inequality

$$\mathrm{H}(x)+\mathrm{D}(x,x^{*})+\mathrm{D}(x^{*},y)\le \mathrm{Ri}(y|\mathcal{P})$$

(60)

holds. In particular, for every $x\in \mathrm{ctr}(\mathcal{P})$,

$$\mathrm{H}(x)+\mathrm{J}(x,x^{*})\le \mathrm{Ri}(x|\mathcal{P}).$$

(61)

Proof. 

First note that also $\widehat{\gamma }(\mathcal{P})$ is in equilibrium with $x^{*}$ as bi-optimal state. Then, putting $w^{*}=\widehat{x^{*}}$, (53) and (54) hold. Therefore, and as $\mathrm{H}(x^{*})=\widehat{\mathrm{Ri}}(w^{*}|\mathcal{P})$, for $x\in \mathcal{P}$ and $w\succ \mathcal{P}$,

$$\mathrm{H}(x)+\widehat{\mathrm{D}}(x,w^{*})+\widehat{\mathrm{D}}(x^{*},w)\le \widehat{\mathrm{Ri}}(w|\mathcal{P}).$$

(62)

To a given belief instance y with $y\succ \mathcal{P}$ we then apply (62) with $w=\widehat{y}$. As $\widehat{\mathrm{D}}(x,w^{*})=\mathrm{D}(x,x^{*})$, $\widehat{\mathrm{D}}(x^{*},w)=\mathrm{D}(x^{*},y)$ and $\widehat{\mathrm{Ri}}(w|\mathcal{P})=\mathrm{Ri}(y|\mathcal{P})$, (60) follows. ☐

We refer to (60) as the transitivity inequality. It is a sharper version of the minimax inequality $\mathrm{H}(x)\le \mathrm{Ri}(y|\mathcal{P})$. It combines both Pythagorean inequalities and these are easily derived from it. If $\mathrm{Ri}(y|\mathcal{P})<\infty$, the inequality holds with equality if and only if both Pythagorean inequalities (53) and (54) hold with equality.

As to the last part of Corollary 3, we note that if you put $r=\mathrm{Ri}(x|\mathcal{P})-\mathrm{H}(x)$, then the bi-optimal state has Jeffrey divergence at most r from x.

For the final result of this section we shall work in the Y-domain based on the derived triple $(\mathsf{\Phi },\mathrm{H},\mathrm{D})$.

First we point to an extra property of bi-optimal states which follows from (53). In order to formulate this in a convenient way we need some definitions. A sequence $(x_n)$ of states converges in divergence to the state x, written $x_n\stackrel{\mathrm{D}}{\to }x$, if ${\lim }_{n\to \infty }\mathrm{D}(x_n,x)=0$. This requires that $(x_n,x)\in X\otimes Y$ for all n (or for all n sufficiently large). If $x_n\in \mathcal{P}$ for all n, we say that $(x_n)$ is asymptotically optimal, more precisely asymptotically optimal for Nature in the game $\gamma (\mathcal{P})$, if $\mathrm{H}(x_n)\to {\mathrm{H}}_{\max }(\mathcal{P})$ as $n\to \infty$. Finally, a state x (not necessarily in $𝒫$) is a maximum entropy-attractor for $𝒫$ with respect to convergence in divergence, more briefly, a ${\mathrm{H}}_{\max }$-attractor for $\mathcal{P}$ wrt D-convergence, if $x_n\stackrel{\mathrm{D}}{\to }x$ for every asymptotically optimal sequence $(x_n)$.

We can now state a trivial corollary to Theorem 3 (transformed to the Y-domain):

Corollary 4.

Any bi-optimal state $x^{*}$ for a game $\gamma (\mathcal{P})$ in equilibrium, is a ${\mathrm{H}}_{\max }$-attractor for $𝒫$ wrt D-convergence.

We shall later demonstrate the existence of attractors in certain cases when the bi-optimal state may not exist. However, that will also involve a variant of the notion of attractor which relates to a different kind of convergence, convergence in Jensen-Shannon divergence, rather than convergence in divergence. The two concepts are identical in key cases as we shall later demonstrate (discussion after the proof of Theorem 11).

2.13. Games Based on Utility, Updating

In the previous section we investigated games related to an effort-based information triple. Similar notions and results apply when we start-out with a utility-based triple. Let us work in the Y-domain and base the first part of our discussion on a proper utility-based information triple $(\mathrm{U},\mathrm{M},\mathrm{D})$ over $X\otimes Y$. Then, given a preparation $𝒫$, the associated game $\gamma (\mathcal{P})=\gamma (\mathcal{P}|\mathrm{U})$ has Observer as maximizer and Nature as minimizer and the two values of the game are, for Nature, the minimax utility ${\mathrm{M}}_{\min }(\mathcal{P})$:

$${\mathrm{M}}_{\min }(\mathcal{P})=\underset{x\in \mathcal{P}}{\inf }\underset{y\succ x}{\sup }\mathrm{U}(x,y)=\underset{x\in \mathcal{P}}{\inf }\mathrm{U}(x,x)=\underset{x\in \mathcal{P}}{\inf }\mathrm{M}(x)$$

(63)

and, for Observer, the corresponding maximin value

$$\underset{y\succ \mathcal{P}}{\sup }\underset{x\in \mathcal{P}}{\inf }\mathrm{U}(x,y).$$

(64)

For $y\succ \mathcal{P}$, the infimum occurring here is the guaranteed utility associated with the strategy y. We denote it $\mathrm{Gtu}(y|\mathcal{P})$. The maximin value (64) is also referred to as the maximal guaranteed utility. We denote it ${\mathrm{Gtu}}_{\max }(\mathcal{P})$:

$${\mathrm{Gtu}}_{\max }(\mathcal{P})=\underset{y\succ \mathcal{P}}{\sup }\mathrm{Gtu}(y|\mathcal{P})=\underset{y\succ \mathcal{P}}{\sup }\underset{x\in \mathcal{P}}{\inf }\mathrm{U}(x,y).$$

(65)

Notions and results, e.g., related to equilibrium, to optimal or bi-optimal states etc. are developed in an obvious manner, either by following Section 2.12 in parallel or by applying the results of Section 2.12 to the effort-based triple $(-\mathrm{U},-\mathrm{M},\mathrm{D})$. The reader who wishes so will also be able to relax the assumption of properness to $Q_2$-properness.

Here, we limit the discussion to an elaboration of the important case of updating, cf., Section 2.8. For updating, according to Section 2.8, we do not need a full information triple. Therefore, for the remainder of the section we take as our basis a general divergence function D on $X\otimes Y$, a preparation $𝒫$ and a prior $y_0$ with ${\mathrm{D}}^{y_0}<\infty$ on $𝒫$. The game associated with the utility-based information triple $({\mathrm{U}}_{|y_0},{\mathrm{D}}^{y_0},\mathrm{D})$ we denote $\gamma (\mathcal{P};y_0)$. According to (63), the value for Nature in this game is ${\inf }_{x\in \mathcal{P}}{\mathrm{D}}^{y_0}(x)$, also denoted ${\mathrm{D}}_{\min }(\mathcal{P};y_0)$ and referred to as the minimum divergence value or the MinDiv-value:

$${\mathrm{D}}_{\min }(\mathcal{P};y_0)=\underset{x\in \mathcal{P}}{\inf }\mathrm{D}(x,y_0).$$

(66)

An optimal strategy for Nature is here called a D-projection of $y_0$ on $𝒫$. Consider an Observer strategy $y\succ \mathcal{P}$, i.e., a possible posterior. We use the same notation as in the general case, “Gtu” , to indicate Observer’s evaluation of the performance of the posterior. Incidentally, the letters can here be taken to stand for “guaranteed updating (gain)”. Thus

$$\mathrm{Gtu}(y|\mathcal{P};y_0)=\underset{x\in \mathcal{P}}{\inf }{\mathrm{U}}_{|y_0}(x,y)=\underset{x\in \mathcal{P}}{\inf }(\mathrm{D}(x,y_0)-\mathrm{D}(x,y))$$

(67)

is the guaranteed updating gain associated with the choice of y as posterior, and

$${\mathrm{Gtu}}_{\max }(\mathcal{P};y_0)=\underset{y\succ \mathcal{P}}{\sup }\mathrm{Gtu}(y|\mathcal{P};y_0)$$

(68)

is Observer’s value of the game, the maximum guaranteed updating gain, or the MaxGtu-value of $\gamma (\mathcal{P};y_0)$.

The basic results for the updating game may be summarized as follows:

Theorem 7.

Let D be a general divergence function on $X\otimes Y$, $𝒫$ a preparation and $y_0$ a belief instance with ${\mathrm{D}}^{y_0}<\infty$ on $𝒫$. Consider the updating game $\gamma =\gamma (\mathcal{P};y_0)$.

If $x^{*}\in \mathrm{ctr}(\mathcal{P})$, then γ is in equilibrium with $x^{*}$ as bi-optimal state if and only if the Pythagorean inequality

$$\mathrm{D}(x,y_0)\ge \mathrm{D}(x,x^{*})+\mathrm{D}(x^{*},y_0)$$

(69)

holds for every $x\in \mathcal{P}$. Moreover, if this condition is satisfied, $x^{*}$ is the D-projection of $y_0$ on $𝒫$. Furthermore, the dual Pythagorean inequality

$$\mathrm{Gtu}(y|\mathcal{P};y_0)+\mathrm{D}(x^{*},y)\le \mathrm{Gtu}(x^{*}|\mathcal{P};y_0)$$

(70)

holds for every $y\succ \mathcal{P}$.

The proof can be carried out by applying Corollary 1 and Theorem 3 to the effort function ${\mathsf{\Phi }}_{|y_0}$ associated with the updating game considered, cf., (24). Details are left to the reader.

The concept of attractors also makes sense for updating games. Then the relevant notion is that of a relative attractor given $y_0$, also referred to as the ${\mathrm{D}}_{\min }^{y_0}$-attractor, which is defined as a state $x^{*}$ such that, for every sequence $(x_n)$ in $𝒫$ with $\mathrm{D}(x_n,y_0)\to {\mathrm{D}}_{\min }(\mathcal{P};y_0)$ it holds that $x_n\stackrel{\mathrm{D}}{\to }{x}^{*}$. In the situation covered by Theorem 7—assuming also that limit states for convergence in divergence are unique—the relative attractor exists and coincides with the bi-optimal state.

The Pythagorean inequality originated with Chentsov [64] and Csiszár [63] where updating in a probabilistic setting was considered. Further versions, still probabilistic in nature can be found in Csiszár [65] and in Csiszár and Matús [66]. In [67] these authors present a general abstract study, adapting a functional analytical approach building technically on meticulous exploitation of tools of convex analysis, partly developed by the authors. This source may also be consulted for information about the historical development and related works. As a work depending on a reversed Pythagorean inequality related to the triple (25), we mention Glonti et al. [68].

The reader should be aware that our notation deviates from what is most commonly found in the literature and promoted by Csiszár, mainly for classical Shannon Theory. Thus a relative attractor is mostly called a generalized I-projection (information projection). We have chosen to stick to the terminology with attractors, partly as their discussion is based on the primary results involving MaxEnt-analysis for which a terminology of projection is less natural.

2.14. Formulating Results with a Geometric Flavour

The results of Section 2.12 are formulated analytically. In this section we make a translation to results which have a certain geometric flavour. We shall work entirely in the Y-domain. No mention of controls or response will occur. This corresponds to a model with $\widehat{Y}=Y=X$ and where response is the identity map. Throughout the section results are based on a proper effort-based information triple $(\mathsf{\Phi },\mathrm{H},\mathrm{D})$.

In the previous sections, we had a fixed preparation in mind. Here, we shall also discuss to which extent you can change a preparation without changing the optimal strategy.

Sub Level sets of the form $\{{\mathsf{\Phi }}^y\le a\}$ play a a key role. These sets appeared before as primitive feasible preparations. Here they have a different role and we prefer to use the bracket notation as above.

Proposition 3.

Let $x^{*}$ be a state with finite entropy $h=\mathrm{H}(x^{*})$. Then, given a preparation $𝒫$, the necessary and sufficient condition that the game $\gamma (\mathcal{P})$ is in equilibrium with $x^{*}$ as bi-optimal state is that $𝒫$ is squeezed in between $\left\{x^{*}\right\}$ and $\{{\mathsf{\Phi }}^{x^{*}}\le h\}$, i.e., that $x^{*}\in \mathcal{P}\subseteq \{{\mathsf{\Phi }}^{x^{*}}\le h\}$. In particular, $\{{\mathsf{\Phi }}^{x^{*}}\le h\}$ is the largest such preparation.

This follows directly from Theorem 2 and Corollary 1.

For a fixed preparation $𝒫$, we can express the two values of $\gamma (\mathcal{P})$, ${\mathrm{H}}_{\max }(\mathcal{P})$ and ${\mathrm{Ri}}_{\min }(\mathcal{P})$, in a geometrically flavoured way. This can be done whether or not the game is in equilibrium and the result can thus be used to check if the game is in fact in equilibrium. It is convenient to introduce some preparatory terminology.

Firstly, a subset of X is an entropy sub level set if it is a (non-empty) set of the form $\{\mathrm{H}\le a\}$. The size of such a set is the smallest number a which can occur in this representation, clearly equal to the MaxEnt-value associated with the preparation $\{\mathrm{H}\le a\}$. Given a preparation $𝒫$, the associated enveloping entropy sub level set is the smallest entropy sub level set containing $𝒫$.

Secondly, and quite analogously in view of (38) and (39), we introduce the size of the ${\mathsf{\Phi }}^y$-sub level set $\{{\mathsf{\Phi }}^y\le a\}$ as the smallest number a which can occur in this representation. And we define the enveloping ${\mathsf{\Phi }}^y$-sub level set associated with $𝒫$ to be the smallest ${\mathsf{\Phi }}^y$-sub level set containing $𝒫$.

Proposition 4.

Consider the game $\gamma (\mathcal{P})$ associated with a preparation $𝒫$. Then:

(i) 

The MaxEnt-value ${\mathrm{H}}_{\max }(\mathcal{P})$ is the size of the enveloping entropy sub level set associated with $𝒫$;

(ii) 

For fixed $y\succ \mathcal{P}$, $\mathrm{Ri}(y|\mathcal{P})$ is the size of the enveloping ${\mathsf{\Phi }}^y$-sub level set associated with $𝒫$.

(iii) 

The MinRisk-value ${\mathrm{Ri}}_{\min }(\mathcal{P})$ is the infimum over $y\succ \mathcal{P}$ of the sizes of the enveloping ${\mathsf{\Phi }}^y$-sub level sets associated with $𝒫$.

In view of (38)–(40), this is obvious. Some comments on the result are in order. In (i) it is understood that the size is infinite if no entropy sub level set exists which contains $𝒫$. A similar convention applies to (ii). Also note that the result gives rise to a simple geometrically flavoured proof of the minimax inequality (41) by noting that for each $y\succ \mathcal{P}$ and each h, $\{{\mathsf{\Phi }}^y\le h\}\subseteq \{\mathrm{H}\le h\}$.

There are two families of sets involved in Proposition 4, the entropy sub level sets and the ${\mathsf{\Phi }}^y$-sub level sets. As the proposition shows, both families give valuable information about the games we are interested in. From the second family alone, one can in fact obtain rather complete information. Indeed, if $\{{\mathsf{\Phi }}^y\le a\}$ contains a given preparation for appropriately chosen y and a, the associated game is well behaved:

Proposition 5.

Given a preparation $𝒫$, a necessary and sufficient condition that $\gamma (\mathcal{P})$ is in equilibrium and has a bi-optimal state is that $\{{\mathsf{\Phi }}^y\le a\}\supseteq \mathcal{P}$ for some $(y,a)$ with $y\in \mathcal{P}$ and $a=\mathrm{H}(y)$. When the condition is fulfilled, a is the value of the game and y the bi-optimal state.

The simple proof is left to the reader. It is the sufficiency which is most useful in practical applications.

The results above translate without difficulty to results about games associated with a utility-based information triple $(\mathrm{U},\mathrm{M},\mathrm{D})$. For this, superlevel sets of the form $\{{\mathrm{U}}^y\ge k\}$ as well as strict sub level sets of the form either $\{\mathrm{M}<a\}$ or $\{{\mathrm{U}}^y<a\}$ play an important role. The notion of size of these latter sets, those defined by strict inequality, is defined as the largest value of a which can occur in the representations given.

We shall consider the largest sets of the form $\{\mathrm{M}<a\}$, respectively $\{{\mathrm{U}}^y<a\}$, which are contained in the complement $\mathsf{\complement }\mathcal{P}$ or, as we shall consistently prefer to say below, which are external to $𝒫$.

Either directly—or as corollaries to Propositions 3–5 applied to the effort-based triple $(-\mathrm{U},-\mathrm{M},\mathrm{D})$—one derives the following results:

Proposition 6.

Let $(\mathrm{U},\mathrm{M},\mathrm{D})$ be a utility-based information triple and consider a state $x^{*}$ with $k=\mathrm{M}(x^{*})>-\infty$. Then, for any preparation $𝒫$, the game $\gamma (\mathcal{P}|\mathrm{U})$ is in equilibrium with $x^{*}$ as bi-optimal state if and only if $x^{*}\in \mathcal{P}\subseteq \{{\mathrm{U}}^{x^{*}}\ge k\}$. In particular, the largest such preparation is the superlevel set $\{{\mathrm{U}}^{x^{*}}\ge k\}$.

Proposition 7.

Let $(\mathrm{U},\mathrm{M},\mathrm{D})$ be a utility-based information triple and consider a preparation $𝒫$ and the associated game $\gamma (\mathcal{P}|\mathrm{U})$. Then:

(i) 

The value ${\mathrm{M}}_{\min }(\mathcal{P})$ is the size of the largest strict sub level set $\{\mathrm{M}<a\}$ which is external to $𝒫$.

(ii) 

For fixed $y\succ \mathcal{P}$, $\mathrm{Gtu}(y|\mathcal{P})$ is the size of the largest strict sub level set $\{{\mathrm{U}}^y<a\}$ which is external to $𝒫$.

(iii) 

The value ${\mathrm{Gtu}}_{\max }(\mathcal{P})$, as the supremum of $\mathrm{Gtu}(y|\mathcal{P})$, is the supremum of all sizes of sets of the form $\{{\mathrm{U}}^y<a\}$ with $y\succ \mathcal{P}$ which are external to $𝒫$.

Proposition 8.

Let $(\mathrm{U},\mathrm{M},\mathrm{D})$ be a utility-based information triple and consider a preparation $𝒫$. Then a necessary and sufficient condition that $\gamma (\mathcal{P}|\mathrm{U})$ is in equilibrium and has a bi-optimal state is that $\{{\mathrm{U}}^y<a\}$ is external to $𝒫$ for some $(y,a)$ with $y\in \mathcal{P}$ and $a=\mathrm{M}(y)$. When the condition is fulfilled, a is the value of the game and y the bi-optimal state.

We also note that the minimax inequality ${\mathrm{Gtu}}_{\max }(\mathcal{P})\le {\mathrm{M}}_{\min }(\mathcal{P})$ follows from Proposition 7 by applying the fact that, generally, $\{\mathrm{M}<a\}\subseteq \{{\mathrm{U}}^y<a\}$.

Let us look specifically at models of updating, cf., Section 2.13.

Given is a general divergence function D on $X\otimes Y$ and we consider preparations $𝒫$ and priors $y_0$ for which ${\mathrm{D}}^{y_0}<\infty$ on $𝒫$. The sets we shall focus on related to the games $\gamma (\mathcal{P};y_0)$ are of two types, which we associate with, respectively “balls” and “half-spaces”. Firstly, for $r>0$, consider the open divergence ball with radius r and centre $y_0$, defined as the ${\mathrm{D}}^{y_0}$-sub level set

$$\mathrm{B}(r|y_0)=\{{\mathrm{D}}^{y_0}<r\}.$$

(71)

In case $r=\mathrm{D}(x^{*},y_0)$ for some state $x^{*}$, we write this set as $\mathrm{B}(x^{*}|y_0)$:

$$\mathrm{B}(x^{*}|y_0)=\mathrm{B}(\mathrm{D}(x^{*},y_0)|y_0)=\left\{x\right|\mathrm{D}(x,y_0)<\mathrm{D}(x^{*},y_0)\}.$$

(72)

And, secondly, we consider sets—all referred to as half-spaces—of one of the following forms

$$\begin{array}{cc}\hfill & {\sigma }^{+}(y,a|y_0)=\left\{x\right|{\mathrm{U}}_{|y_0}<a\}=\left\{x\right|\mathrm{D}(x,y_0)-\mathrm{D}(x,y)<a\}\hfill \end{array}$$

(73)

$$\begin{array}{cc}\hfill & {\sigma }^{-}(y,a|y_0)=\left\{x\right|{\mathrm{U}}_{|y_0}\ge a\}=\left\{x\right|\mathrm{D}(x,y_0)-\mathrm{D}(x,y)\ge a\}\hfill \end{array}$$

(74)

$$\begin{array}{cc}\hfill & {\sigma }^{+}(y|y_0)=\left\{x\right|{\mathrm{U}}_{|y_0}<\mathrm{D}(y,y_0)\}=\left\{x\right|\mathrm{D}(x,y_0)-\mathrm{D}(x,y)<\mathrm{D}(y,y_0)\}\hfill \end{array}$$

(75)

$$\begin{array}{cc}\hfill & {\sigma }^{-}(y|y_0)=\left\{x\right|{\mathrm{U}}_{|y_0}\ge \mathrm{D}(y,y_0\}=\left\{x\right|\mathrm{D}(x,y_0)-\mathrm{D}(x,y)\ge \mathrm{D}(y,y_0)\}\hfill \end{array}$$

(76)

Associated with the sets introduced we define certain “boundary sets” , respectively peripheries and hyper-spaces. Notation and definition for the former type of sets is given by

$$\begin{array}{cc}\hfill \partial \mathrm{B}(r|y_0)& =\left\{x\right|\mathrm{D}(x,y_0)=r\}\mathrm{and}\hfill \\ \hfill \partial \mathrm{B}(x^{*}|y_o)& =\left\{x\right|\mathrm{D}(x,y_0)=\mathrm{D}(x^{*},y_0)\}\hfill \end{array}$$

and for the latter type we use

$$\begin{array}{cc}\hfill \partial \sigma (y,a|y_0)& =\left\{x\right|\mathrm{D}(x,y_0)-\mathrm{D}(x,y)=a\}\mathrm{and}\hfill \\ \hfill \partial \sigma (y|y_0)& =\left\{x\right|\mathrm{D}(x,y_0)-\mathrm{D}(x,y)=\mathrm{D}(y,y_0)\}.\hfill \end{array}$$

When translating basic parts of Propositions 6–8 to the setting we are now considering, we find the following result:

Proposition 9.

Let D be a general divergence function on $X\otimes Y$ and consider a belief instance $y_0\succ X$ such that ${\mathrm{D}}^{y_0}<\infty$. Then the following results hold for the associated updating games with $y_0$ as prior:

(i) 

For any $x^{*}\in X$, the largest preparation $𝒫$ for which $\gamma (\mathcal{P};y_0)$ is in equilibrium with $x^{*}$ as bi-optimal state, hence with $x^{*}$ as the D-projection of $y_0$ on $𝒫$, is the half-space ${\sigma }^{-}(x^{*}|y_o)$.

(ii) 

For a fixed updating game $\gamma (\mathcal{P};y_0)$, the MinDiv-value ${\mathrm{D}}_{\min }(\mathcal{P};y_0)$ is the size of the largest strict divergence ball $\mathrm{B}(r|y_0)$ which is external to $𝒫$, and the maximal guaranteed updating gain ${\mathrm{Gtu}}_{\max }(\mathcal{P};y_0)$ is the supremum of a for which there exists $y\succ \mathcal{P}$ such that the half-space ${\sigma }^{+}(y,a|y_0)$ is external to $𝒫$.

(iii) 

An updating game $\gamma (\mathcal{P};y_0)$ is in equilibrium and has a bi-optimal state if and only if, for some $y\in \mathcal{P}$, the half-space ${\sigma }^{+}(y|y_0)$ is external to $𝒫$. When this condition holds, y is the bi-optimal state, hence the D-projection of $y_0$ on $𝒫$.

For illustrations see cases (a) and (b) shown in the figure in Section 3.2.

2.15. Adding Convexity

It has been recognized since long that notions of convexity play an important role for basic properties of Shannon theory and for optimization theory in general, cf. in particular Boyd and Vandenberghe [54] which also has a bearing on many of the concrete problems treated later on. Deliberately, we have postponed the introduction of this element until this late moment, thereby demonstrating that a large number of concepts and results can be formulated quite abstractly and do not require convexity considerations. Also, it will become more clear exactly where convexity is needed.

We shall study results which can be obtained under added algebraic assumptions related to convexity considerations.

We assume that X is a convex set. The convex hull of a preparation $𝒫$ is denoted $\mathrm{co}(\mathcal{P})$. We assume that controllability is adapted to the convex structure in the sense that a control w controls a convex combination, say $w\succ \overline{x}=\sum {\alpha }_i{x}_i$, if and only if w controls every $x_i$ with ${\alpha }_i>0$. It follows, that all control regions $\left]w\right[$ are convex. Also note that, for every convex combination $\overline{x}=\sum {\alpha }_i{x}_i$, we conclude from $\overline{x}\succ \overline{x}$ that $\widehat{\overline{x}}\succ x_i$ for all i with ${\alpha }_i>0$ and hence, if we switch to the Y-domain, $\overline{x}\succ x_i$ for every i with ${\alpha }_i>0$.

Regarding convex combinations, they are understood to be finite convex combination, often written as above without introducing any special notation for the relevant index set.

Properties of Concavity, convexity and affinity of real-valued functions f defined on X or on a convex subset of X are largely defined in the usual way. Thus, for concavity, the condition is that if $\sum {\alpha }_i{x}_i$ is a convex combination of elements in the domain of definition of f, then $f(\sum {\alpha }_i{x}_i)\ge \sum {\alpha }_{i}f(x_i)$. For convexity the inequality sign is turned around and for affinity it is replaced by equality. The notions make sense and will also be applied to extended real-valued functions provided they do not assume both values $+\infty$ and $-\infty$. One comment has to be made, though. We only require that X is a convex set. However, X could be affine, i.e., combinations $\sum {\alpha }_i{x}_i$ could be defined whenever the coefficients ${\alpha }_i$ are arbitrary real numbers which sum up to 1. This will be the case for some models. We shall then point out if stated results hold for arbitrary affine combinations, not just for convex combinations.

The above definitions and concepts along with associated assumptions will always be understood to apply when, in the sequel, we work with a convex state space.

The basis in this section, except for the last part (Example 1 and Proposition 10), is a proper effort-based information triple $(\widehat{\mathsf{\Phi }},\mathrm{H},\widehat{\mathrm{D}})$ over $X\otimes \widehat{Y}$. The derived information triple over $X\otimes Y$ is denoted $(\mathsf{\Phi },\mathrm{H},\mathrm{D})$. When there is also given a preparation $\mathcal{P}$, the results developed continue to hold under $Q_2$-properness.

Emphasis will be on concavity, convexity or affinity for the w-marginals ${\widehat{\mathsf{\Phi }}}^w$—either all of them or only those with a control in the range of the response function. Note that, say affinity for ${\widehat{\mathsf{\Phi }}}^w$ with w of the form $\widehat{x}$ for some $x\in X$ amounts to the same as affinity of ${\mathsf{\Phi }}^x$.

Basic properties of entropy and redundancy (hence also divergence) under added conditions about the marginals ${\widehat{\mathsf{\Phi }}}^w$ or ${\mathsf{\Phi }}^y$ are contained in the following result:

Theorem 8 (Deviation from affinity).

(i) 

If the marginals ${\mathsf{\Phi }}^x$ with $x\in X$ are concave, then, for every convex combination $\overline{x}=\sum {\alpha }_i{x}_i$ of elements in X,

$$\mathrm{H}\left(\sum {\alpha }_i{x}_i\right)\ge \sum {\alpha }_i\mathrm{H}(x_i)+\sum {\alpha }_i\mathrm{D}(x_i,\overline{x}).$$

(77)

In particular, H is concave and if $\mathrm{H}(\overline{x})=\sum {\alpha }_i\mathrm{H}(x_i)$ and this quantity is finite, then all $x_i$ with ${\alpha }_i>0$ are response equivalent, in fact $x_i\widehat{\sim }\overline{x}$ for these indices. If response is injective, the entropy function is strictly concave.

(ii) 

If the marginals ${\mathsf{\Phi }}^x$ with $x\in X$ are even affine, equality holds in (77):

$$\mathrm{H}\left(\sum {\alpha }_i{x}_i\right)=\sum {\alpha }_i\mathrm{H}(x_i)+\sum {\alpha }_i\mathrm{D}(x_i,\overline{x}).$$

(78)

(iii) 

If the marginals ${\widehat{\mathsf{\Phi }}}^w$ with $w\in \widehat{Y}$ are affine and if $\mathrm{H}(\overline{x})<\infty$ for a convex combination $\overline{x}={\sum }_i{\alpha }_i{x}_i$ then, for every control w with $w\succ \overline{x}$,

$$\sum {\alpha }_i\widehat{\mathrm{D}}(x_i,w)=\widehat{\mathrm{D}}\left(\sum {\alpha }_i{x}_i,w\right)+\sum {\alpha }_i\mathrm{D}(x_i,\overline{x}).$$

(79)

(iv) 

If the marginals ${\widehat{\mathsf{\Phi }}}^w$ with $w\in \widehat{Y}$ are affine, if $\mathcal{P}$ is a convex preparation with ${\mathrm{H}}_{\max }(\mathcal{P})<\infty$ and if $w\in ^\left[\mathcal{P}\right]$, then the restriction of ${\widehat{\mathrm{D}}}^w$ to $\mathcal{P}$ is convex and if $\sum {\alpha }_i\widehat{\mathrm{D}}(x_i,w)=\widehat{\mathrm{D}}(\overline{x},w)$ for a convex combination $\overline{x}=\sum {\alpha }_i{x}_i$ of states in $\mathcal{P}$, then all $x_i$ with ${\alpha }_i>0$ are response equivalent, in fact $x_i\widehat{\sim }\overline{x}$ for these indices. If response is injective, the restriction of ${\widehat{\mathrm{D}}}^w$ to $\mathcal{P}$ is strictly convex.

Proof. 

The result is a natural extension of (the main parts of) Theorem 1 of [55] and the proof is similar: For (i), apply linking to rewrite the right hand side, then upper bound the expression you get by the assumed concavity and you end with the upper bound $\mathsf{\Phi }(\overline{x},\overline{x})=\mathrm{H}(\overline{x})$. The results about concavity of H are easy consequences and property (ii) is proved similarly. For the basic assertion of (iii), add $\sum {\alpha }_i\widehat{\mathrm{D}}(x_i,w)$ to both sides of (78), and use linking to rewrite the right hand side. Then apply the assumed affinity and the term $\widehat{\mathsf{\Phi }}(\overline{x},w)$ appears to which you once more apply linking. Finally subtract $\mathrm{H}(\overline{x})$ from both sides. The assertions of (iv) are easy consequences. ☐

Several comments are in place. First, as a simple corollary to (i) of Theorem 8 we note the following:

Corollary 5.

Assume that the marginals ${\widehat{\mathsf{\Phi }}}^x$ with $x\in X$ are concave and consider the game $\widehat{\gamma }(\mathcal{P})$ for a convex preparation $\mathcal{P}$. Then the set of optimal strategies for Nature in this game is convex and, in case response is injective and ${\mathrm{H}}_{\max }(\mathcal{P})<\infty$, there can be at most one optimal strategy for Nature.

Conditions of affinity will play a main role for many results to follow. Notions of affine equivalence applies in various contexts ($\widehat{Y}$-domain, Y-domain, effort-based or utility-based). Some examples will suffice: The effort functions ${\widehat{\mathsf{\Phi }}}_1$ and ${\widehat{\mathsf{\Phi }}}_2$ over $X\otimes \widehat{Y}$ are affinely equivalent if there exists a finite-valued affine function f on X such that, for $(x,w)\in X\otimes \widehat{Y}$, ${\widehat{\mathsf{\Phi }}}_2(x,w)={\widehat{\mathsf{\Phi }}}_1(x,w)+f(x)$. If so, ${\widehat{\mathsf{\Phi }}}_1$ and ${\widehat{\mathsf{\Phi }}}_2$ are equivalent (${\mathrm{D}}_1={\mathrm{D}}_2$). Moreover, two effort-based information triples $({\mathsf{\Phi }}_1,{\mathrm{H}}_1,{\mathrm{D}}_1)$ and $({\mathsf{\Phi }}_2,{\mathrm{H}}_2,{\mathrm{D}}_2)$ are affinely equivalent if they are equivalent and there exists a finite-valued affine function f on X such that, for $(x,y)\in X\otimes Y$, ${\mathrm{H}}_2(x)={\mathrm{H}}_1(x)+f(x)$. Then of course, also ${\mathsf{\Phi }}_2(x,y)={\mathsf{\Phi }}_1(x,y)+f(x)$.

A simple and practically important result which follows readily from affinity conditions exploits the notion of robustness in its weakened form introduced in Section 2.9, cf., (32) and (33). The result is an extension of Theorem 5.

Theorem 9.

Let X be a convex state space and let $(\widehat{\mathsf{\Phi }},\mathrm{H},\widehat{\mathrm{D}})$ be a proper information triple over $X\otimes \widehat{Y}$ for which the marginals ${\widehat{\mathsf{\Phi }}}^w$ with $w\in \widehat{Y}$ are all affine. Let $(x^{*},w^{*})$ be a pair of permissible strategies for $\widehat{\gamma }(\mathcal{P})$ with $w^{*}$ adapted to $x^{*}$. Assume that $x^{*}\in \mathrm{co}(\mathcal{E})$ and that $w^{*}$ is $(\mathcal{E},\mathcal{P})$-robust. Then $\widehat{\gamma }(\mathcal{P})$ is in equilibrium with $x^{*}$ as bi-optimal strategy.

Proof. 

Let $h<\infty$ be the constant for which (32) and (33) hold. By affinity, (32) extends to states in $\mathrm{co}(\mathcal{E})$, hence $\mathrm{H}(x^{*})=\widehat{\mathsf{\Phi }}(x^{*},w^{*})=h$. The result now follows from Theorem 2. ☐

Then some comments on (79). In the terminology of [69], this is the compensation identity with the last term as compensation term. This term appears as a measure of deviation from affinity, both in relation to entropy, cf., (78), and in relation to redundancy (hence also to divergence), cf., (79). The significance of such terms is being more widely recognized. This applies in particular to the case of an even mixture $\overline{x}=\frac{1}{2}{x}_1+\frac{1}{2}{x}_2$, for which the term is called Jensen-Shannon divergence, briefly just JSD-divergence, between $x_1$ and $x_2$. We shall use the notation

$$\mathrm{JSD}(x_1,x_2)=\frac{1}{2}\mathrm{D}(x_1,\overline{x_1{x}_2})+\frac{1}{2}\mathrm{D}(x_2,\overline{x_1{x}_2}),$$

(80)

where a “bar” signals “midpoint of”, a notation to be used often in the sequel:

$$\overline{xy}=\frac{1}{2}x+\frac{1}{2}y.$$

(81)

For even mixtures of two states, the compensation identity states that

$$\frac{1}{2}\left(\mathrm{D}(x_1,y)+\mathrm{D}(x_2,y)\right)=\mathrm{D}(\overline{x_1{x}_2},y)+\mathrm{JSD}(x_1,x_2).$$

(82)

which, for classical Shannon theory, is sometimes called the parallelogram identity. The identity makes sense for an arbitrary general divergence function but one should note the requirement of finiteness in (79), expressed somewhat indirectly via the entropy function. That some restriction is important will be seen from Example 1 below. When (82) holds, you may apply it with $y=x_1$ and with $y=x_2$, and derive the identity

$$\mathrm{D}(\overline{x_1{x}_2},x_1)-\mathrm{D}(\overline{x_1{x}_2},x_2)=\frac{1}{2}\left(\mathrm{D}(x_2,x_1)-\mathrm{D}(x_1,x_2)\right).$$

(83)

Previously, JSD-divergence has mainly been studied in the context of classical Shannon theory. For our more abstract theory, we have chosen to put emphasis on it, especially in the formulation of technical assumptions which are needed for the proofs of some basic results to follow. Note that JSD-divergence is everywhere defined on $X\times X$ which D-divergence need not be. In the next section we take up a closer study of Jensen-Shannon divergence.

The purpose of the next result is to indicate that it is conceivable that for many concrete situations, a bi-optimal state will be robust, i.e., lie in the core of the preparation concerned. This result, in a more concrete set-up goes back to Csiszár, cf., [63]. It depends on the following notion: A state x is an algebraic inner point of $\mathcal{P}$ (typically assumed convex) if, for every $x_1\in \mathcal{P}$ distinct from x, there exists $x_2\in \mathcal{P}$ such that x is a genuine convex combination of $x_1$ and $x_2$.

Corollary 6.

Assume that ${\mathsf{\Phi }}^x$ is affine for all $x\in X$ and let $\mathcal{P}$ be a convex preparation. If $\gamma (\mathcal{P})$ is in equilibrium and has a bi-optimal state $x^{*}$ and if this state is algebraic inner in $\mathcal{P}$, then $x^{*}$ is robust for $\gamma (\mathcal{P})$ at the robustness level ${\mathrm{H}}_{\max }(\mathcal{P})$. In particular, $x^{*}\in \mathrm{core}(\mathcal{P})$.

Proof. 

With assumptions as stated, consider any $x\in \mathcal{P}$ distinct from $x^{*}$ and determine $x^{\prime }\in \mathcal{P}$ such that $x^{*}$ is a genuine convex combination of x and $x^{\prime }$, say $x^{*}=\alpha x+\beta x^{\prime }$. We find that $\mathsf{\Phi }(x,x^{*})\le \mathrm{Ri}(x^{*}|\mathcal{P})={\mathrm{H}}_{\max }(\mathcal{P})$. Similarly, $\mathsf{\Phi }(x^{\prime },x^{*})\le {\mathrm{H}}_{\max }(\mathcal{P})$. As the convex combination $\alpha \mathsf{\Phi }(x,x^{*})+\beta \mathsf{\Phi }(x^{\prime },x^{*})$ equals $\mathsf{\Phi }(\alpha x+\beta x^{\prime },x^{*})=\mathsf{\Phi }(x^{*},x^{*})=\mathrm{H}(x^{*})={\mathrm{H}}_{\max }(\mathcal{P})$, we conclude that $\mathsf{\Phi }(x,x^{*})={\mathrm{H}}_{\max }(\mathcal{P})$. As this holds for every $x\in \mathcal{P}$, the result follows. ☐

An example is in place to illuminate the importance of the finiteness condition in relation to the compensation identity. We shall work in the Y-domain, for which the identity takes the following form:

$$\sum {\alpha }_i\mathrm{D}(x_i,y)=\mathrm{D}\left(\sum {\alpha }_i{x}_i,y\right)+\sum {\alpha }_i\mathrm{D}(x_i,\overline{x}).$$

(84)

The identity can be considered for more or less any bivariate function D on $X\otimes Y$. As before let X be convex and assume that $Y=X$. We further assume that D is a general divergence function on $X\otimes Y$. It may be that D is derived from an information triple over $X\otimes \widehat{Y}$, but we do not assume so. In particular, no response function is involved.

In order to check if the compensation identity holds for D, you may check if the difference $\sum {\alpha }_i\mathrm{D}(x_i,y)-\mathrm{D}(\sum {\alpha }_i{x}_i,y)$ is well defined and independent of y. Or you may inspect more closely the expression for D. If this expression, apart from pure x-only dependent terms, only contains terms which, for fixed y, are linear terms in x, a suitable entropy can be identified and the compensation identity (84) will hold (when $\mathrm{H}(\overline{x})<\infty$). The procedure is demonstrated in the following example which, at the same time, also illustrates the role of the two assumptions made in part (iii) of Theorem 8 in order for (79) or (84) to hold.

Example 1.

Let $X=Y=\widehat{Y}$ be copies of the real line $]-\infty ,\infty [$ provided with the standard structure, let response be the identity map and let visibility be the diffuse relation. Further, let α be a positive parameter and consider the bivariate function D given by

$$\mathrm{D}(x,y)={|x-y|}^{\alpha }.$$

(85)

Clearly, this is a genuine general divergence function.

If $\alpha \ne 2$, (84) does not hold. Indeed, if you consider the mixture $\overline{x}=\frac{1}{2}0+\frac{1}{2}1$ and as y take $y=1$, then the left hand side of (84) equals $\frac{1}{2}$ whereas the right hand side equals $2^{1-\alpha }$. Thus, when $\alpha \ne 2$, there is no information triple $(\mathsf{\Phi },\mathrm{H},\mathrm{D})$ equivalent to $(\mathrm{D},0,\mathrm{D})$ for which (84) holds generally. So you cannot add a finite entropy function to $(\mathrm{D},0,\mathrm{D})$ and obtain an effort function with affine marginals.

If $\alpha =2$, the matter is quite different. Then $\mathrm{D}(x,y)=x^2+y^2-2xy$ and you can subtract $x^2$ to obtain a function with linear dependency on x for a given value of y. In other words, if you consider the triple equivalent to $(\mathrm{D},0,\mathrm{D})$ for which entropy is given by $\mathrm{H}(x)=-x^2$, all conditions of Theorem 8, (iii) are fulfilled, thus (84) must hold. Further material on this and similar examples can be found in Section 3.1.

For our last observation of this section we return to an updating triple $({\mathrm{U}}_{|y_0},{\mathrm{D}}^{y_0},\mathrm{D})$ as introduced in Section 2.8, cf. (22). Here, D is a general divergence and $y_0$ a prior. A certain preparation $\mathcal{P}$ is also given and it is assumed that ${\mathrm{D}}^{y_0}<\infty$ on $\mathcal{P}$. The triple $({\mathrm{U}}_{|y_0},{\mathrm{D}}^{y_0},\mathrm{D})$ is a genuine proper utility-based information triple over $\mathcal{P}\otimes Y$. It is still assumed that X is convex and that $Y=X$. The observation we want to point out is the following:

Lemma 1.

If, in addition to assumptions above, the compensation identity (84) holds for all convex combinations of states in $\mathcal{P}$ and all $y\in Y$, then all marginal functions of the utility function ${\mathrm{U}}_{|y_0}$ obtained by fixing an element $y\in Y$ are affine.

Proof. 

Consider any $y\in Y$ and any convex combination $\overline{x}=\sum {\alpha }_i{x}_i$ of states in $𝒫$. As ${\mathrm{D}}^{y_0}<\infty$ on $𝒫$, the sum $\sum {\alpha }_i\mathrm{D}(x_i,y_0)$ is finite. By the compensation identity, so is the sum $\sum {\alpha }_i\mathrm{D}(x_i,\overline{x})$. For $y\in Y$, we find that

$$\begin{array}{cc}\hfill {\mathrm{U}}_{|y_0}(\overline{x},y)& =\mathrm{D}(\overline{x},y_0)-\mathrm{D}(\overline{x},y)\hfill \\ & =\left(\sum {\alpha }_i\mathrm{D}(x_i,y_0)-\sum {\alpha }_i\mathrm{D}(x_i,\overline{x})\right)\hfill \\ & -\left(\sum {\alpha }_i\mathrm{D}(x_i,y)-\sum {\alpha }_i\mathrm{D}(x_i,\overline{x})\right)\hfill \\ & =\sum {\alpha }_i\mathrm{D}(x_i,y_0)-\sum {\alpha }_i\mathrm{D}(x_i,y)\hfill \\ & =\sum {\alpha }_i{\mathrm{U}}_{|y_0}(x_i,y).\hfill \end{array}$$

This is the affinity relation sought. ☐

The significance of this result is that it will later allow us to apply results for the updating games under convexity assumptions, cf., Theorem 15.

2.16. Jensen-Shannon Divergence at Work

As in the previous section, X is a convex set. We assume now that $Y=X$. For the first part of the section we take as base a general divergence function D over $X\otimes Y$. No preparation, effort function or entropy function will appear until later in the section. We work entirely in the Y-domain.

As is no surprise, not all results of information theory are constructive and in order to be able to handle situations where constructive methods are not available, we shall introduce topologically flavored notions and methods. Previously, as in [55], we introduced topology into the picture by referring to a “reference topology” which could be a topology with no very direct relation to the theory developed. Now we apply a different approach and insist that everything topological can be expressed in terms of quantities of direct interest for the theory dealt with. In fact, the previously defined Jensen-Shannon divergence (JSD), cf., (80), will now be the central quantity to work with. This notion of divergence is an everywhere defined, smoothed and symmetrized version of standard divergence. It may take the value $+\infty$. The following properties are obvious in view of the definition:

$$\begin{array}{cc}\hfill \mathrm{JSD}(x,y)& \ge 0(\text{JSD is }\mathit{non}-\mathit{negative}),\hfill \end{array}$$

(86)

$$\begin{array}{cc}\hfill \mathrm{JSD}(y,x)& =\mathrm{JSD}(x,y)(\text{JSD is }\mathit{symmetric}),\hfill \end{array}$$

(87)

$$\begin{array}{cc}\hfill \mathrm{JSD}(x,x)& =0(\text{JSD is }\mathit{sound}),\hfill \end{array}$$

(88)

$$\begin{array}{cc}\hfill \mathrm{JSD}(x,y)& >0\mathrm{if}y\ne x(\text{JSD is }\mathit{proper}).\hfill \end{array}$$

(89)

These properties hold for all $x,y\in X$. The same properties hold for any bivariate function on $X\otimes Y$ which is a function of some metric with a function defined on $[0,\infty [$ which vanishes at 0 and nowhere else. In several concrete cases, Jensen-Shannon divergence is of this type, in some central cases even in a very simple way as JSD will be a squared metric in the cases we have in mind. For research in this direction, we refer to Endres and Schindelin [70], Fuglede and Topsøe [71] and Briët and Harremoës [72]. The present study is a further indication of the significance of Jensen-Shannon divergence.

Jensen-Shannon divergence defines a natural sequential notion of convergence in X. To be precise, a sequence $(x_n)={(x_n)}_{n\ge 1}$ converges in Jensen-Shannon divergence to x and we write $x_n\stackrel{\mathrm{JSD}}{⟶}x$, if $\mathrm{JSD}(x_n,x)\to 0$ as $n\to \infty$. We shall only pay attention to convergence of ordinary sequences. Convergence in Jensen-Shannon divergence is also referred to as JSD-convergence.

A sequence ${(x_n)}_{n\in \mathbb{N}}$ is a JSD-Cauchy sequence if

$$\underset{n,m\to \infty }{\lim }\mathrm{JSD}(x_n,x_m)=0.$$

(90)

We shall consider the following five properties:

$$\begin{array}{cc}\hfill \mathrm{C}1& (\mathit{soundness}):x_n\equiv x\Rightarrow x_n\stackrel{\mathrm{JSD}}{⟶}x;\hfill \end{array}$$

(91)

$$\begin{array}{c}\mathrm{C}2(\mathit{subsequence}\mathit{consistency}):\hfill \\ x_n\stackrel{\mathrm{JSD}}{⟶}x\Rightarrow x_{n_k}\stackrel{\mathrm{JSD}}{⟶}x\text{for any subsequence};\hfill \end{array}$$

(92)

$$\begin{array}{cc}\hfill \mathrm{C}3& (\mathit{unique}\mathit{limits}):x_n\stackrel{\mathrm{JSD}}{⟶}x\wedge x_n\stackrel{\mathrm{JSD}}{⟶}y\Rightarrow y=x;\hfill \end{array}$$

(93)

$$\begin{array}{c}\mathrm{C}4(\mathit{subsubsequence}\mathit{principle}):\hfill \\ \mathrm{If}\forall (x_{n_k})\exists (x_{n_{k_l}}):x_{n_{k_l}}\stackrel{\mathrm{JSD}}{⟶}x\mathrm{then}{x}_n\stackrel{\mathrm{JSD}}{⟶}x;\hfill \end{array}$$

(94)

$$\begin{array}{cc}\hfill \mathrm{C}5& (\mathit{completeness}):\text{any JSD-Cauchy sequence is JSD-convergent}.\hfill \end{array}$$

(95)

We may use terminology such as JSD-convergence has unique limits or JSD convergence is complete, for example. Clearly C1, C2 and C4 hold generally. Completeness (C5) will be taken as an independent axiom. Adding two relatively innocent technical axioms, we shall also establish C3.

The axiom ASC of algebraic sequential continuity wrt JSD-convergence is the requirement that, for convex combinations $z_n={\alpha }_n{x}_n+{\beta }_n{y}_n$ and for a convex combination $z=\alpha x+\beta y$ such that $x_n\stackrel{\mathrm{JSD}}{⟶}x$, $y_n\stackrel{\mathrm{JSD}}{⟶}y$ and ${\alpha }_n\to \alpha$ (hence also ${\beta }_n\to \beta$) it holds that $z_n\stackrel{\mathrm{JSD}}{⟶}z$.

The axiom JSC of joint sequential lower semi-continuity of divergence is the requirement that, for $x_n\stackrel{\mathrm{JSD}}{⟶}x$ and $y_n\stackrel{\mathrm{JSD}}{⟶}y$, it holds that, properly interpreted,

$$\mathrm{D}(x,y)\le \underset{n\to \infty }{\text{lim inf}}\mathrm{D}(x_n,y_n).$$

(96)

Regarding the proper interpretation of (96), we shall agree to define $\mathrm{D}(x,y)=\infty$ whenever $y\nsucc x$. Thus the axiom implies that if the right hand side of (96) is finite, then $y\succ x$ must hold.

The significance of the properties C1-4 lies in a general result dueto Kisynski [73], see also Dudley [74], according to which these conditions ensure that the notion of convergence studied is topological, i.e., that there exists a topology on X for which sequential convergence coincides with the given notion of convergence. When this is so, there exists a unique strongest such topology, which we refer to as the associated topology. For this topology, a set is open if and only if any sequence which converges in the notion of convergence to a point in the set, eventually lies in the set. Note that, typically, there are many topologies for which sequential convergence coincides with a given notion of convergence. As a concrete example consider $X=\mathbb{N}$ and note that the convergent sequences for the discrete topology (the eventually constant sequences) coincides with the class of convergent sequences for the strictly weaker topology specified by taking $G\subseteq \mathbb{N}$ to be open if either $1\notin G$ or else $\lim {\mu }_n([1,n])=1$ with ${\mu }_n$ the uniform probability measure over $[1,n]$ (this is, essentially, “Appert space” of [75]).

We are now ready to prove the following result:

Theorem 10.

Under the added axioms ASC and JSC, the convergence properties C1-4 hold, hence JSD-convergence is topological and the associated topology is well defined. Further, JSD is a sequentially lower semi-continuous notion, i.e., for $x_n\stackrel{\mathrm{JSD}}{⟶}x$ and $y_n\stackrel{\mathrm{JSD}}{⟶}y$, the following inequality holds:

$$\mathrm{JSD}(x,y)\le \underset{n\to \infty }{\text{lim inf}}\mathrm{JSD}(x_n,x_m).$$

(97)

Proof. 

To establish (97), note that by axiom ASC the convergence $\overline{x_n{y}_n}\stackrel{\mathrm{JSD}}{⟶}\overline{xy}$ is ensured. Then, by axiom JSC,

$$\mathrm{D}(x,\overline{xy})\le \text{lim inf }\mathrm{D}(x_n,\overline{x_n{y}_n}).$$

(98)

Similarly,

$$\mathrm{D}(y,\overline{xy})\le \text{lim inf }\mathrm{D}(y_n,\overline{x_n{y}_n}).$$

(99)

As the left hand side in (97) is the sum of the left hand sides of (98) and (99), and as the sum of the two right hand sides is dominated by the right hand side in (97), (97) must hold.

As to property C3, assume that $x_n\stackrel{\mathrm{JSD}}{⟶}x$ and that $x_n\stackrel{\mathrm{JSD}}{⟶}y$. Then, by (97), $\mathrm{JSD}(x,y)\le \text{lim inf }\mathrm{JSD}(x_n,x_n)=0$ and hence $\mathrm{D}(x,\overline{xy})=0$ follows. By properness, $x=\overline{xy}$ and then $x=y$ follows. ☐

Under the discussion of properties (86)–(89) we indicated that often JSD is directly related to a metric in that a relation of the form

$$\mathrm{JSD}(x,y)=f\left(\rho (x,y)\right)$$

(100)

holds for some metric $\rho$. In such cases it is mostly easy to identify the associated topology (without relying on any extra axioms). We leave it to the reader to prove the following simple result.

Proposition 10.

Assume that, for some metric ρ on X and some continuous and strictly increasing function f on $[0,\infty [$ with $f(0)=0$, Equation (100) holds for all $(x,y)\in X\times X$. Then the associated topology for JSD-convergence exists and can be identified as the metric topology defined by ρ. Further, JSD is jointly lower semi-continuous. If the metric ρ is complete, so is JSD.

Under suitable conditions we now aim at establishing existence of optimal strategies for the players in the games $\gamma (\mathcal{P})$. However, in certain important cases Nature does not have an optimal strategy. Instead, we aim at showing that rather generally replacements in the form of ${\mathrm{H}}_{\max }$-attractors exist. We shall aim at attractors for JSD-convergence but, as it will turn out, under conditions stated, that will amount to the same thing as attractors for D-convergence. The result below, stated in rather full detail for reference purposes, is a main technical result of the present contribution.

Theorem 11.

Consider a convex state space X, let $Y=X$ and let $(\mathsf{\Phi },\mathrm{H},\mathrm{D})$ be a proper information triple over $X\otimes Y$ with affine marginals ${\mathsf{\Phi }}^y$ for all $y\in Y$. Assume that the axioms ASC, JSC and the axiom of JSD-completeness which all relate to the divergence function D hold.

Then, for every convex preparation $\mathcal{P}$ with ${\mathrm{H}}_{\max }(\mathcal{P})<\infty$, $\gamma (\mathcal{P})$ is in equilibrium and there exists a unique optimal strategy $y^{*}$ for Observer and a unique ${\mathrm{H}}_{\max }$-attractor $x^{*}$ wrt JSD-convergence. Furthermore, $y^{*}=x^{*}$ and the direct as well as the dual Pythagorean inequalities hold, i.e., for $x\in \mathcal{P}$ and $y\succ \mathcal{P}$,

$$\begin{array}{cc}\hfill \mathrm{H}(x)+\mathrm{D}(x,y^{*})& \le {\mathrm{H}}_{\max }(\mathcal{P});\hfill \\ \hfill {\mathrm{Ri}}_{\min }(\mathcal{P})+\mathrm{D}(x^{*},y)& \le \mathrm{Ri}(y|\mathcal{P}).\hfill \end{array}$$

Proof. 

First we prove an auxiliary result, viz that if, for a sequence $(x_n)$ of states in $\mathcal{P}$ and for a state $x\in X$, $x_n\stackrel{\mathrm{D}}{\to }x$ holds, then also $x_n\stackrel{\mathrm{JSD}}{⟶}x$ must hold.

To see this, note that by assumptions made, we conclude from (iii) of Theorem 8 that, for all n, m and all $y\in Y$,

$$\frac{1}{2}\mathrm{D}(x_n,y)+\frac{1}{2}\mathrm{D}(x_m,y)=\mathrm{D}(\overline{x_n{x}_m},y)+\mathrm{JSD}(x_n,x_m).$$

(101)

Applying this with $y=x$, we see that $(x_n)$ is a JSD-Cauchy sequence. By completeness, there exists $x^{\prime }\in X$ such that $x_n\stackrel{\mathrm{JSD}}{⟶}{x}^{\prime }$. By axiom JSD, $\mathrm{D}(x^{\prime },x)\le {\text{lim inf}}_{n\to \infty }\mathrm{D}(x_n,x)=0$, hence $x^{\prime }=x$ and $x_n\stackrel{\mathrm{JSD}}{⟶}x$ follows.

Now, let $(x_n)$ be an asymptotically optimal sequence for $\gamma (\mathcal{P})$. Then (i) of Theorem 8 applied to $\overline{x_n{x}_m}$ shows that

$${\mathrm{H}}_{\max }(\mathcal{P})\ge \mathrm{H}(\overline{x_n{x}_m})=\frac{1}{2}\mathrm{H}(x_n)+\frac{1}{2}\mathrm{H}(x_m)+\mathrm{JSD}(x_n,x_m)$$

and we realize that $(x_n)$ is a JSD-Cauchy sequence. Therefore the sequence is JSD-convergent, say $x_n\stackrel{\mathrm{JSD}}{⟶}x$. If also $(z_n)$ is an asymptotically optimal sequence, there must, likewise, exist $z\in X$ such that $z_n\stackrel{\mathrm{JSD}}{⟶}z$. As the alternating sequence $x_1,z_1,x_2,z_2,\cdots$ is also asymptotically optimal, that sequence too JSD-converges, say with $a\in X$ as limit state. By properties C2 and C3 we find that $x=a=z$. This shows that there exists a unique ${\mathrm{H}}_{\max }$-attractor wrt JSD-convergence. Let $x^{*}$ be this unique attractor.

Then we remark that if there exists an optimal strategy $y^{*}$ for Observer in $\gamma (\mathcal{P})$, there can only be one such strategy and it must coincide with $x^{*}$. To see this, note that if $y^{*}$ is optimal, $\mathrm{Ri}(y^{*}|\mathcal{P})\le {\mathrm{H}}_{\max }(\mathcal{P})$, hence, for every $x\in \mathcal{P}$, $\mathrm{H}(x)+\mathrm{D}(x,y^{*})\le {\mathrm{H}}_{\max }(\mathcal{P})$ and hence $y^{*}$ is also an ${\mathrm{H}}_{\max }$-attractor wrt convergence in D (cf., also Corollary 4). By the auxiliary fact established in the beginning of the proof, $y^{*}$ is also an ${\mathrm{H}}_{\max }$-attractor wrt JSD-convergence, hence must coincide with $x^{*}$ as claimed.

Now fix an asymptotically optimal sequence, say $(x_n)$. Then, for $x\in \mathcal{P}$ consider “suitable” convex combinations ${\xi }_n={\alpha }_n{x}_n+{\beta }_{n}x$ with ${\beta }_n\to 0$ and all ${\beta }_n$ positive (in fact, ${\beta }_n=\frac{1}{n}$ if the difference ${\delta }_n={\mathrm{H}}_{\max }(\mathcal{P})-\mathrm{H}(x_n)$ either vanishes or is larger than 1 and otherwise ${\beta }_n=\sqrt{{\delta }_n}$ will do). Then

$$\begin{array}{cc}\hfill {\mathrm{H}}_{\max }(\mathcal{P})& \ge \mathrm{H}({\xi }_n)={\alpha }_n\mathrm{H}(x_n)+{\beta }_n\mathrm{H}(x)+{\alpha }_n\mathrm{D}(x_n,{\xi }_n)+{\beta }_n\mathrm{D}(x,{\xi }_n)\hfill \\ & \ge {\alpha }_n\mathrm{H}(x_n)+{\beta }_n\left(\mathrm{H}(x)+\mathrm{D}(x,{\xi }_n)\right),\hfill \end{array}$$

hence

$$\mathrm{H}(x)+\mathrm{D}(x,{\xi }_n)\le \frac{1}{{\beta }_n}\left({\mathrm{H}}_{\max }(\mathcal{P})-\mathrm{H}(x_n)\right)+\mathrm{H}(x_n).$$

Clearly, we can select the ${\beta }_n$’s such that this quantity converges to ${\mathrm{H}}_{\max }(\mathcal{P})$ as $n\to \infty$. By axiom ASC, ${\xi }_n$ converges in JSD-divergence to $x^{*}$ and then, by axiom JSC, we conclude that $\mathrm{H}(x)+\mathrm{D}(x,x^{*})\le {\mathrm{H}}_{\max }(\mathcal{P})$. Since this holds for every consistent state x, $\mathrm{Ri}(x^{*}|\mathcal{P})\le {\mathrm{H}}_{\max }(\mathcal{P})$, from which we conclude that $\gamma (\mathcal{P})$ is in equilibrium, that the direct Pythagorean inequality holds and that $x^{*}$ is an optimal strategy for Observer. As we have seen before, this strategy is unique.

As, for any $y\in X$,

$$\begin{array}{c}{\mathrm{Ri}}_{\min }(\mathcal{P})+\mathrm{D}(x^{*},y)=\underset{n\to \infty }{\lim }\mathrm{H}(x_n)+\mathrm{D}(x^{*},y)\hfill \\ \le \underset{n\to \infty }{\lim }\mathrm{H}(x_n)+\underset{n\to \infty }{\text{lim inf}}\mathrm{D}(x_n,y)\hfill \\ =\underset{n\to \infty }{\text{lim inf}}\mathsf{\Phi }(x_n,y)\le \mathrm{Ri}(y|\mathcal{P}),\hfill \end{array}$$

also the dual Pythagorean inequality holds. ☐

Several remarks concerning this theorem are in order.

Firstly, note that for the auxiliary result we started out to prove, we had to appeal (implicitly) to the finiteness condition ${\mathrm{H}}_{\max }(\mathcal{P})<\infty$ in view of the condition $\mathrm{H}(\overline{x})<\infty$ in (iii) of Theorem 8. Alternatively, we could instead demand that the compensation identity holds unconditionally.

Then, in general, the D-notion and the JSD-notion of convergence may differ from each other (with D-convergence the stronger of the two). However, it follows from the theorem that under the conditions stated, it does not matter whether we define ${\mathrm{H}}_{\max }$-attractors wrt D-convergence or wrt JSD-convergence. We may, therefore, simply talk about an ${\mathrm{H}}_{\max }$-attractor, or even just an attractor, without specifying the mode of convergence we have in mind.

Further, it lies nearby to ask if also the inequality $\mathrm{H}(x^{*})\le {\mathrm{H}}_{max}(\mathcal{P})$ can be added to the conclusions in Theorem 11. If H is sequentially lower semi-continuous wrt D-convergence (or wrt JSD-convergence)—as will normally (always?) be the case—the inequality obviously holds. Assume now that this is the case. Then there are two possibilities why an attractor $x^{*}$ may fail to be an optimal strategy for Nature, either because $x^{*}\notin \mathcal{P}$ or, more interestingly, because there is an entropy loss in that $\mathrm{H}(x^{*})<{\mathrm{H}}_{\max }(\mathcal{P})$. In Harremoës and Topsøe [76], the authors speculate that the phenomena of entropy loss could be important in computational linguistics and provide a partial explanation behind Zipf’s law.

Following up on the remark above, we may investigate what can be accomplished if we work with a state $x^{*}$ which is known to be consistent and apply the same technique of proof as for Theorem 11. What we find is that in the presence of convexity (and with technical axioms added), the essential inequality $\mathrm{Ri}(y^{*}|\mathcal{P})\le \mathrm{H}(x^{*})$ is not needed in full strength. It suffices to assume one of the facts which flow from that inequality, viz., that $\mathrm{H}(x^{*})={\mathrm{H}}_{\max }(\mathcal{P})$. To be precise:

Theorem 12.

With assumptions as in Theorem 11, let $𝒫$ be a convex preparation and $x^{*}$ a consistent state with finite entropy which is also a possible strategy for Observer, i.e., $x^{*}\succ \mathcal{P}$. Then the condition $\mathrm{H}(x^{*})={\mathrm{H}}_{\max }(\mathcal{P})$ is not only necessary, but also sufficient for $\mathrm{Ri}(x^{*}|\mathcal{P})\le \mathrm{H}(x^{*})$ to hold, hence for $\gamma (\mathcal{P})$ to be in equilibrium with $x^{*}$ as bi-optimal state.

Proof. 

Consider a state $x\in \mathcal{P}$ and apply (77) to a convex combination of the form $y_n=(1-\frac{1}{n})x^{*}+\frac{1}{n}x$. We find that $\mathrm{H}(x^{*})\ge \mathrm{H}(y_n)\ge (1-\frac{1}{n})\mathrm{H}(x^{*})+\frac{1}{n}\mathrm{H}(x)+\frac{1}{n}\mathrm{D}(x,y_n)$ from which we conclude that $\mathrm{H}(x)+\mathrm{D}(x,y_n)\le \mathrm{H}(x^{*})$. By axiom JSD, $x^{*}\succ x$ and $\mathrm{H}(x)+\mathrm{D}(x,x^{*})\le \mathrm{H}(x^{*})$ follows. As $x\in \mathcal{P}$ was arbitrary, the desired inequality follows. Apply Corollary 1 and the result follows. ☐

After these remarks let us turn to another key result:

Theorem 13.

Let $\mathcal{P}$ be any preparation—convex or not—such that ${\mathrm{H}}_{\max }(\mathcal{P})<\infty$. Keeping the other assumptions of Theorem 11 as they are, the game $\gamma (\mathcal{P})$ is in equilibrium if and only if entropy is not increased by taking convex mixtures in the sense that

$${\mathrm{H}}_{\max }(\mathrm{co}(\mathcal{P}))={\mathrm{H}}_{\max }(\mathcal{P}).$$

(102)

When (102) holds, $\gamma (\mathcal{P})$ and $\gamma (\mathrm{co}(\mathcal{P}))$ have the same unique optimal strategy $y^{*}$ for Observer and the same ${\mathrm{H}}_{\max }$-attractor, $x^{*}$ for Nature and the two agree: $x^{*}=y^{*}$.

Proof. 

First remark that if (102) holds, ${\mathrm{H}}_{\max }(\mathrm{co}(\mathcal{P}))<\infty$ and Theorem 11 applies. All claimed properties then follow easily from that result.

To prove necessity, note that quite generally,

$${\mathrm{Ri}}_{\min }(\mathrm{co}(\mathcal{P}))={\mathrm{Ri}}_{\min }(\mathcal{P}).$$

(103)

In more detail, the condition $y\succ \mathrm{co}(\mathcal{P})$ is equivalent with $y\succ \mathcal{P}$, and, for each belief instance $y\in Y$,

$$\mathrm{Ri}(y|\mathrm{co}(\mathcal{P}))=\mathrm{Ri}(y|\mathcal{P}).$$

(104)

This follows by standard assumptions made in the beginning of Section 2.15 according to which visibility is adapted to the convex structure and by affinity of the marginals ${\mathsf{\Phi }}^y$ (convexity would do). Then, if $\gamma (\mathcal{P})$ is in equilibrium, we can argue that

$${\mathrm{H}}_{\max }(\mathrm{co}(\mathcal{P}))\le {\mathrm{Ri}}_{\min }(\mathrm{co}(\mathcal{P}))={\mathrm{Ri}}_{\min }(\mathcal{P})={\mathrm{H}}_{max}(\mathcal{P})$$

and (102) follows. ☐

As we saw, the result is essentially a corollary to Theorem 11. The proof above is modeled after the proof of a less abstract result in [55].

We have formulated results for the Y-domain which appear less involved. We leave it to the reader to formulate and prove versions of the two key theorems above for the $\widehat{Y}$-domain.

Translating Theorems 11 and 12 to a setting based on utility—this requires an obvious dual notion of attractors aiming at minimax utility rather than at maximin effort (i.e., maximal entropy)—one finds the following result:

Theorem 14.

Again with X a convex state space, let $(\mathrm{U},\mathrm{M},\mathrm{D})$ be a proper utility-based information triple with affine marginals ${\mathrm{U}}^y$ for $y\in X$. Assume that the technical axioms ASC and JSC hold. Further assume that JSD-divergence is complete. Let $𝒫$ be a convex preparation for which ${\mathrm{M}}_{\min }(\mathcal{P})>-\infty$. Then:

(i) 

Without further assumptions, the utility game $\gamma (\mathcal{P}|\mathrm{U})$ is in equilibrium and there exists a unique optimal strategy $y^{*}$ for Observer and a unique ${\mathrm{M}}_{\min }$-attractor $x^{*}$. Furthermore, $y^{*}=x^{*}$ and the direct as well as the dual Pythagorean inequalities hold, i.e., for $x\in \mathcal{P}$ and $y\in Y$,

$$\begin{array}{cc}\hfill {\mathrm{M}}_{\min }(\mathcal{P})+\mathrm{D}(x,y^{*})& \le \mathrm{M}(x);\hfill \end{array}$$

(105)

$$\begin{array}{cc}\hfill \mathrm{Gtu}(y|\mathcal{P})+\mathrm{D}(x^{*},y)& \le {\mathrm{Gtu}}_{\max }(\mathcal{P}).\hfill \end{array}$$

(106)

(ii) 

In case $x^{*}$ is a consistent state with finite max-utility, i.e., $\mathrm{M}(x^{*})>-\infty$ for which $\mathrm{M}(x^{*})={\mathrm{M}}_{\min }(\mathcal{P})$, $x^{*}\in \mathrm{ctr}(\mathcal{P})$ and the game $\gamma (\mathcal{P}|\mathrm{U})$ is in equilibrium and has $x^{*}$ as bi-optimal state. In particular, the Pythagorean inequality

$$\mathrm{M}(x^{*})+\mathrm{D}(x,y^{*})\le \mathrm{M}(x)$$

(107)

holds for every $x\in \mathcal{P}$.

Let us collect the key results about updating games in one theorem:

Theorem 15.

Let X be convex, let $\mathcal{P}$ be any preparation and let D be a general divergence on $X\otimes Y$ with $Y=X$ for which the compensation identity holds. Assume that the technical axioms ASC and JSC hold and that JSD-divergence is complete. Consider a prior $y_0\in Y$ and assume that ${\mathrm{D}}^{y_0}<\infty$ on $\mathcal{P}$ and that ${\mathrm{M}}_{\min }(\mathcal{P};y_0)>-\infty$. Then:

(i) 

Without adding extra conditions, Observer has a unique optimal strategy, $y^{*}$, in the game $\gamma (\mathcal{P};y_0)$.

(ii) 

Observer strategies for $\gamma (\mathrm{co}(\mathcal{P});y_0)$ and for $\gamma (\mathcal{P};y_0)$ coincide, i.e., $[\mathrm{co}(\mathcal{P})]=\left[\mathcal{P}\right]$ and, for every such strategy y, $\mathrm{Gtu}(y|\mathrm{co}(\mathcal{P});y_0)=\mathrm{Gtu}(y|\mathcal{P};y_0)$, hence

$${\mathrm{Gtu}}_{\max }(\mathrm{co}(\mathcal{P});y_0)={\mathrm{Gtu}}_{\max }(\mathcal{P};y_0).$$

(108)

(iii) 

If $𝒫$ is convex, the game $\gamma (\mathcal{P};y_0)$ is in equilibrium and the ${\mathrm{D}}_{\min }^{y_0}$-attractor exists. This attractor, say $x^{*}$, is identical to the optimal Observer strategy $y^{*}$ from (i); it is the D-projection of $y_0$ on $𝒫$ if and only if $x^{*}\in \mathcal{P}$.

(iv) 

The game $\gamma (\mathcal{P};y_0)$ is in equilibrium if and only if

$${\mathrm{D}}_{\min }(\mathrm{co}(\mathcal{P});y_0)={\mathrm{D}}_{\min }(\mathcal{P};y_0).$$

(109)

Proof. 

This may be proved by applying the key results of this section, also recalling Lemma 1. Details are left to the reader. ☐

Further properties of Jensen-Shannon divergence are worth investigating. This concerns in particular the notion of negative definiteness, cf., [71,72]. Some indications are in place. When the property holds, JSD is the square of a Hilbert metric in a natural sense (loc. cit.). Investigating this property, one will quickly realize that, modulo finiteness conditions on the entropy function (say ${\mathrm{H}}_{\max }(X)<\infty$), JSD is negative definite if and only if the entropy function is midpoint-negative definite, i.e., for any finite sequence of states ${(x_i)}_{i\le n}$ and any associated sequence of real numbers ${(c_i)}_{i\le n}$ with ${\sum }_i{c}_i=0$, it holds that ${\sum }_{i,j}{c}_i{c}_j\mathrm{H}(\overline{x_i{x}_j})\le 0$. If this property holds with a restriction on n we express the property by saying that H is $MP(n)$-negative definite. Clearly, MP(2)-negative definiteness is equivalent to midpoint concavity of H. In the same way as we introduced the notion of $MP(n)$-negative definiteness for H, we may introduce a notion of n-negative definiteness of JSD.

Whereas the results about embeddability in a Hilbert space are rather deep, if we just ask for the property to be a squared metric, the matter is much simpler:

Proposition 11.

Assume that JSD is everywhere finite. Then the following conditions are equivalent:

• JSD is the square of a metric;
• JSD is 3-negative definite;
• H is $MP(3)$-negative definite

This result depends on the properties (86)–(89). The key argument is not specific to JSD. For the sake of good order, we provide a proof of the basic general result in Appendix D.

3. Examples, towards Applications

3.1. Primitive Triples and Generation by Integration

Natural building blocks for information triples will be defined. We shall here concentrate on a simple, important and easy-to-apply approach.

A possible expansion of the considerations in the present section is dealt with in the Appendix A. This is related to our introduction of weaker concepts of properness and will allow you to work more generally with non-smooth “generators” (see below). Desirable is also an introduction of an action space and of the notion of response. How this can be done is indicated in Appendix A. We have chosen not to deal with the possible refinements in the main text, partly to keep the exposition simple, partly as a few technical issues may still need a closer investigation.

Let I be a subinterval of $[-\infty ,\infty [$ with endpoints a and b ($-\infty \le a<b\le \infty$). Either none, one or both endpoints belong to I but neither $+\infty$ nor $-\infty$ are members of I. Provide I with its usual algebraic and topological structure. We take I as state space as well as belief reservoir. Thus $X=Y=I$. Visibility is normally taken to be the diffuse relation so that any state $s\in I$ is visible from any belief instance. However, at times a more restricted notion of visibility is relevant, especially for $I=[0,1]$ or $I=[0,\infty [$. Then

$$I\otimes I=I^2\setminus \left\{(s,u)\right|s>0,u=0\}$$

(110)

is a better choice.

We agree that in this section, visibility $I\otimes I$ is either the discrete relation $I\times I$ or else given by (110) in certain cases when $0\in I$ is a left endpoint of I.

An effort-based information triple over $I\otimes I$ is said to be primitive. The “primitivity” lies in the fact that the state space and belief reservoir appear to be as simple as one can think of—if you do not want to enter into discrete structures with a finite or countably infinite state space. We use lower case letters as in $(\varphi ,\mathrm{h},\mathrm{d})$ for such triples. Upper case letters will then occur for constructions via a process of summation or integration, starting with primitive triples.

We are especially interested in proper primitive triples. The conditions they must satisfy are as follows (linking, fundamental inequality, soundness and properness):

$$\begin{array}{cc}\hfill \varphi (s,u)& =\mathrm{h}(s)+\mathrm{d}(s,u),\hfill \end{array}$$

(111)

$$\begin{array}{cc}\hfill \mathrm{d}(s,u)& \ge 0,\hfill \end{array}$$

(112)

$$\begin{array}{cc}\hfill \mathrm{d}(s,s)& =0,\hfill \end{array}$$

(113)

$$\begin{array}{cc}\hfill \mathrm{d}(s,u)& =0\Rightarrow u=s.\hfill \end{array}$$

(114)

It is understood here and later on that such requirements are to hold for all $s\in I$ (for (113)) or for all $(s,u)\in I\otimes I$ (for (111), (112) and (114)). From Section 2.15 we know that it is desirable for the effort function to have affine marginals ${\varphi }^u$. For this to be the case, there must exist functions on I, $\eta$ and $\xi$ say, such that

$$\varphi (s,u)=s\eta (u)+\xi (u)$$

(115)

for $(s,u)\in I\otimes I$. There is a simple way to generate a multitude of such information triples. The method is inspired by Bregman, [77], who used the construction for other purposes. Given is a Bregman generator h which is here understood to be a continuous, real-valued, strictly concave function on I which is sufficiently smooth on the interior of the interval, say continuously differentiable. We take this function as the entropy function, h. Defining effort and divergence by

$$\begin{array}{cc}\hfill \varphi (s,u)& =\mathrm{h}(u)+(s-u){\mathrm{h}}^{\prime }(u),\hfill \end{array}$$

(116)

$$\begin{array}{cc}\hfill \mathrm{d}(s,u)& =\mathrm{h}(u)-\mathrm{h}(s)+(s-u){\mathrm{h}}^{\prime }(u),\hfill \end{array}$$

(117)

the triple $(\varphi ,\mathrm{h},\mathrm{d})$ is indeed a proper primitive information triple with affine marginals, ${\varphi }^u$. Figure 2 illustrates what is involved.

It is also easy to illustrate geometrically what Jensen-Shannon divergence amounts to. Referring to Figure 3, we find that the Jensen-Shannon divergence between $s_1$ and $s_2$, for primitive triples denoted by jsd is given by

$$\mathrm{jsd}(s_1,s_2)=\frac{1}{2}{d}_1+\frac{1}{2}{d}_2.$$

(118)

It follows geometrically that

$$\mathrm{jsd}(s_1,s_2)\le \frac{1}{2}\mathrm{d}(s_1,s_2)+\frac{1}{2}\mathrm{d}(s_2,s_1).$$

(119)

We also find that for a bounded interval I, JSD-convergence and D-divergence are equivalent concepts and that the associated topology is the standard topology on I.

The utility-based analogues of notions introduced are defined in an obvious manner (see also examples below). We shall use $(\mathrm{u},\mathrm{m},\mathrm{d})$ as generic notation for primitive utility-based triples.

As two examples of effort-based Bregman generated primitive triples, we point to the standard algebraic triple given by

$$\begin{array}{cc}\hfill \varphi (s,u)& =u^2-2su,\hfill \end{array}$$

(120)

$$\begin{array}{cc}\hfill \mathrm{h}(s)& =-s^2,\hfill \end{array}$$

(121)

$$\begin{array}{cc}\hfill \mathrm{d}(s,u)& ={(s-u)}^2\hfill \end{array}$$

(122)

over $]-\infty ,+\infty [$ and to the standard logarithmic triple

$$\begin{array}{cc}\hfill \varphi (s,u)& =u-s+s\ln \frac{1}{u},\hfill \end{array}$$

(123)

$$\begin{array}{cc}\hfill \mathrm{h}(s)& =s\ln \frac{1}{s},\hfill \end{array}$$

(124)

$$\begin{array}{cc}\hfill \mathrm{d}(s,u)& =u-s+s\ln \frac{s}{u}.\hfill \end{array}$$

(125)

over $[0,\infty ]$. Both triples are given in their effort-based versions. If need be, we refer to these triples as standard primitive effort-based triples.

The first triple is equivalent to a triple we met in Example 1. It leads to basic concepts of real Hilbert space theory by a natural process of summation or, more generally, integration. By a similar process, the second triple leads to basic concepts of Shannon information theory. Before elaborating on that, we shall generalize both examples by the introduction of a parameter q. In fact, we shall see that, modulo affine equivalence, both examples can be conceived as belonging to the same family of triples.

In order to modify the standard algebraic triple, it lies nearby to consider generators of the form

$${\mathrm{h}}_q(s)=\alpha (q)s^q+\beta (q)s+\gamma (q)$$

(126)

with $\alpha ,\beta$ and $\gamma$ functions depending on a real parameter q. Let us agree to work mainly with $I=[0,\infty ]$ as state space. Then q could in principle be any real parameter. For each fixed q, ${\mathrm{h}}_q$ is either strictly concave—an effort-based Bregman generator—strictly convex—a utility-based Bregman generator—(or degenerate). Applications of (116) and (117) give the formulas

$$\begin{array}{cc}\hfill {\varphi }_q(s,u)& =\alpha (q)(1-q)u^q+\alpha (q)qs{u}^{q-1}+\beta (q)s+\gamma (q)\hfill \end{array}$$

(127)

$$\begin{array}{cc}\hfill {\mathrm{d}}_q(s,u)& =\alpha (q)(1-q)u^q+\alpha (q)qs{u}^{q-1}-\alpha (q)s^q.\hfill \end{array}$$

(128)

When $\alpha (q)q(q-1)$ is negative, ${\mathrm{h}}_q$ is a genuine effort-based Bregman generator and the triple $({\varphi }_q,{\mathrm{h}}_q,{\mathrm{d}}_q)$ is a proper primitive effort-based information triple. When $\alpha (q)q(q-1)$ is positive, ${\mathrm{h}}_q$ is strictly convex and the triple $({\varphi }_q,{\mathrm{h}}_q,-{\mathrm{d}}_q)$ is a proper primitive utility-based information triple (which should then rather be denoted $({\mathrm{u}}_q,{\mathrm{m}}_q,{\mathrm{d}}_q)$). Thus, if you consider the triple $({\varphi }_q,{\mathrm{h}}_q,|{\mathrm{d}}_q|)$ you are certain to obtain a primitive triple, either effort-based or utility-based (or degenerate). It also follows from (126)–(128) that modulo affine equivalence, the triples you obtain from different choices of $\alpha$, $\beta$ and $\gamma$ are scalarly equivalent. For some choices you may prefer to restrict the parameter so that only effort-based triples emerge, for others you may find it interesting to focus on triples where there is a smooth variation from effort-based to utility-based triples. In applications—purely speculative at the moment—this could reflect situations in economic or physical or chemical systems where e.g., a change from positive to negative rent or from exothermic to endothermic reaction can take place.

If you choose $\alpha =1$ and $\beta =\gamma =0$, then $({\varphi }_q,{\mathrm{h}}_q,|{\mathrm{d}}_q|)$ equals

$$\left((1-q)u^q+qs{u}^{q-1},s^q,|(1-q)u^q+qs{u}^{q-1}-s^q|\right).$$

(129)

As you go from large to small values of q this primitive triple starts out as utility-based, then, for $q=1$, becomes degenerate, after which it switches to the effort-based mode until, for $q=0$, it again becomes degenerate, after which it switches back to the utility-based mode. For $q=2$, the triple is the utility-based standard algebraic triple, the utility-based version of the triple given in (120)–(122). That triple is most naturally considered over $I\otimes I$ with $I=]-\infty ,\infty [$.

We can remove the “singularity” of the system at $q=1$ by blowing up the generator near $q=1$. Let us choose $\alpha ,\beta$ and $\gamma$ as follows:

$$\alpha (q)=\frac{1}{1-q},\beta (q)=\frac{-1}{1-q},\gamma (q)={\gamma }_0.$$

(130)

Here, the constant ${\gamma }_0$ represents an eventual overhead With choices as specified, we obtain the triples $({\varphi }_q,{\mathrm{h}}_q,{\mathrm{d}}_q)$ with

$$\begin{array}{cc}\hfill {\varphi }_q(s,u)& =u^q+\frac{1}{1-q}\left(q{u}^{q-1}-1\right)s+{\gamma }_0,\hfill \end{array}$$

(131)

$$\begin{array}{cc}\hfill {\mathrm{h}}_q(s)& =s\frac{s^{q-1}-1}{1-q}+{\gamma }_0,\hfill \end{array}$$

(132)

$$\begin{array}{cc}\hfill {\mathrm{d}}_q(s,u)& =u^q+\frac{q}{1-q}{u}^{q-1}s-\frac{1}{1-q}{s}^q.\hfill \end{array}$$

(133)

The Equation (131) gives you gross effort with net effort obtained by putting ${\gamma }_0=0$. Similarly, (132) is gross entropy and the same formula with ${\gamma }_0=0$ gives you net entropy.

The family of triples (131)–(133) is well defined for all $q\ge 0$ if we allow for an interpretation by continuity for $q=1$. For $q=0$ the triple is degenerate, for $q>0$ it determines a proper primitive effort-based information triples. For $q=1$ continuity considerations show that $({\varphi }_1,{\mathrm{h}}_1,{\mathrm{d}}_1)$ is identical to the standard logarithmic triple given in (123)–(125) (assuming that the overhead is neglected, ${\gamma }_0=0$).

The triples we have identified may all be conceived to be of the same structure as the standard logarithmic triple. What is meant by this, is that if we, following Tsallis [78], introduce the deformed logarithms, ${\ln }_q$, defined by the formula

$${\ln }_{q}t=\left\{\begin{array}{c}\ln t\mathrm{if}q=1\hfill \\ \frac{1}{1-q}\left(t^{1-q}-1\right)\mathrm{otherwise},\hfill \end{array}\right.$$

(134)

then the Formulas (131)–(133) may be expressed as follows in terms of the deformed logarithms:

$$\begin{array}{cc}\hfill {\varphi }_q(s,u)& =u^q-s+qs{\ln }_q(\frac{1}{u})+{\gamma }_0,\hfill \end{array}$$

(135)

$$\begin{array}{cc}\hfill {\mathrm{h}}_q(s)& =s{\ln }_q(\frac{1}{s})+{\gamma }_0,\hfill \end{array}$$

(136)

$$\begin{array}{cc}\hfill {\mathrm{d}}_q(s,u)& =u^q-s+qs{\ln }_q(\frac{1}{u})-s{\ln }_q(\frac{1}{s}).\hfill \end{array}$$

(137)

These formulas are used for $s,u\ge 0$ and $q\ge 0$ (for negative q you do not obtain effort-based quantities). Note that if $q\le 1$, then ${\ln }_q\frac{1}{t}=\infty$ for $t=0$. The formulas indicate that it is not so much the logarithmic function $t\mapsto {\ln }_{q}t$ which is of importance but more so the function $t\mapsto {\ln }_q\frac{1}{t}$. This is no surprise to information theorists as the latter expression has a well known interpretation in terms of coding when $q=1$, provided t represents a probability. No convincing interpretation of ${\ln }_q\frac{1}{t}$ appears to be known for other values of q. For $q=1$, (135)–(137) reduce to (123)–(125) pertaining to the standard logarithmic triple.

The family of triples (135)–(137), $q\ge 0$, is referred to as the family of deformed primitive triples—adding a qualifying “effort-based” if need be. The analogous utility-based primitive is the family of triples $({\mathrm{u}}_q,{\mathrm{m}}_q,{\mathrm{d}}_q)=(-{\varphi }_q,-{\mathrm{h}}_q,{\mathrm{d}}_q)$, i.e., for $q\ge 0$,

$$\begin{array}{cc}\hfill {\mathrm{u}}_q(s,u)& =-u^q+s-qs{\ln }_q(\frac{1}{u})-{\gamma }_0,\hfill \end{array}$$

(138)

$$\begin{array}{cc}\hfill {\mathrm{m}}_q(s)& =-s{\ln }_q(\frac{1}{s})-{\gamma }_0,\hfill \end{array}$$

(139)

$$\begin{array}{cc}\hfill {\mathrm{d}}_q(s,u)& =u^q-s+qs{\ln }_q(\frac{1}{u})-s{\ln }_q(\frac{1}{s}).\hfill \end{array}$$

(140)

Let us return to the process of integration hinted at in the beginning of the section. A substantial amount of concrete triples which illustrate the theory developed can be constructed by combining the Bregman construction with a process of integration.

Integration may be applied to any family of information triples and gives us new triples to work with. Note that by linearity of integration, the important property of affinity of marginals is preserved.

We comment mainly on integration of effort-based triples with a view towards applications in information theory and in statistical physics. Consider integration of one and the same primitive triple $(\varphi ,\mathrm{h},\mathrm{d})$ over $I\otimes I$ with Bregman generator h. Partly for technical convenience we assume that h is non-negative. Then effort, entropy and divergence, will all be non-negative, also in the integrated version. Considering the intended applications, this is only natural.

Let T be a set provided with a Borel structure and with an associated measure $\mu$. Let $X=Y$ be the function space consisting of all measurable functions $x:T\mapsto I$. Functions in X are identified if they agree $\mu$-almost everywhere. Note that X is a convex cone. Consider the integrated triple

$$(\mathsf{\Phi },\mathrm{H},\mathrm{D})={\int }_T(\varphi ,\mathrm{h},\mathrm{d})d\mu (t)$$

(141)

by which we express that the following equations hold:

$$\begin{array}{cc}\hfill \mathsf{\Phi }(x,y)& ={\int }_T\varphi \left(x(t),y(t)\right)d\mu (t),\hfill \end{array}$$

(142)

$$\begin{array}{cc}\hfill \mathrm{H}(x)& ={\int }_T\mathrm{h}\left(x(t)\right)d\mu (t),\hfill \end{array}$$

(143)

$$\begin{array}{cc}\hfill \mathrm{D}(x,y)& ={\int }_T\mathrm{d}\left(x(t),y(t)\right)d\mu (t).\hfill \end{array}$$

(144)

As $\mathrm{h}\ge 0$, H is well defined and $0\le \mathrm{H}(x)\le \infty$ for all $x\in X$ and as $t\mapsto (x(t),y(t))$ is measurable and $(s,u)\mapsto \mathrm{d}(s,u)$ non-negative and measurable, cf., (117), D is well-defined by (144). By linking, also $\mathsf{\Phi }$ is well defined. Thus, $(\mathsf{\Phi },\mathrm{H},\mathrm{D})$ is a well defined triple over $X\times Y$. We leave it to the reader to verify that $(\mathsf{\Phi },\mathrm{H},\mathrm{D})$ is a proper information triple. Moreover, if $\varphi$ has affine marginals ${\varphi }^u$ for all $u\in I$, then $\mathsf{\Phi }$ has affine marginals ${\mathsf{\Phi }}^y$ for all $y\in Y$. The divergence functions which can be obtained in this way are Bregman divergences. Note that with this construction, the essential fundamental inequality $\mathrm{D}\ge 0$ even holds pointwise as $\mathrm{d}\ge 0$. For this reason, when we discuss the integrated triple, we refer to (112) as the pointwise fundamental inequality.

Bregman divergence may be used to modify visibility by taking $X\otimes Y$ to consist of all pairs $(x,y)\in X\times Y$ with $\mathrm{D}(x,y)<\infty$.

For the standard logarithmic triple (123)–(125), one may construct discrete models, say over a finite or countably infinite alphabet T, by a process of summation related to the interval $I=[0,\infty ]$ rather than the traditional choice $I=[0,1]$. States will then be certain sequences ${(x_i)}_{i\in T}$, which may be conceived as intensity sequences consisting of point intensities rather than the usual probability sequences of point probabilities. As regularity conditions one could take sequences with bounded intensities or sequences for which the primitive entropy function h of (124) satisfies the requirement ${\sum }_{i\in T}h(x_i)>-\infty$. For this to work technically, we realize the importance of the pointwise fundamental inequality for d of (125) and note that this requires the inclusion of the term $u-s$ in d. Thus one may suggest to replace classicalprobability spaces with certain intensity spaces.

Returning to the classical choice with discrete probability distributions over a discrete alphabet T, $\mathsf{\Phi }$ becomes discrete Kerridge inaccuracy, H classical Shannon entropy and D discrete Kullback-Leibler divergence. If we generalize to cover non-discrete settings, entropy can only be finite for distributions with countable support, whereas the generalization of divergence makes sense more generally. For instance, we may consider the generator $s\mapsto s\ln \frac{1}{s}$ on the entire half-line $I=[0,\infty [$ and for $(T,\mu )$ take an arbitrary measure space, provided with some measure $\mu$. As state space we can then, as one possibility, take the set of measures absolutely continuous with respect to $\mu$ and with finite-valued Radon-Nikodym derivatives with respect to $\mu$. For two such measures, say $P=pd\mu$ and $Q=qd\mu$ we find that

$$\mathrm{D}(P,Q)=\int \left(p(t)\ln \frac{p(t)}{q(t)}+q(t)-p(t)\right)d\mu (t).$$

(145)

This may be called generalized Kullback-Leibler divergence. It is the more natural divergence to consider. For one thing, the integrand is non-negative by the pointwise fundamental inequality. If we restrict attention to finite measures P and Q with the same total mass, this reduces to the standard expression $\int p\ln \frac{p}{q}d\mu$. The standard expression also gives a divergence measure if the two measures are finite and $Q(T)\le P(T)$ and, moreover, the important compensation identity also holds in this case since the additional terms (stemming from $u-s$ in (125)) are integrable and affine.

Now consider extensions to cover also integration of the family $({\varphi }_q,{\mathrm{h}}_q,{\mathrm{d}}_q)$. It is natural to consider these triples over $I\otimes I$ with $I=[0,1]$ in order to ensure that ${\mathrm{h}}_q\ge 0$. By integration we obtain the triples

$$({\mathsf{\Phi }}_q,{\mathrm{H}}_q,{\mathrm{D}}_q)$$

(146)

defined over appropriate function spaces, typically representing probability distributions. For $q>0$ these triples are proper effort-based information triples. For $q=0$ you obtain degenerate triples. The quantity ${\mathrm{H}}_q$, is meaningful in discrete cases with T finite or countably infinite, and defines Tsallis entropy. For the continuous case, Tsallis entropy does not make much sense, but the divergence function ${\mathrm{D}}_q$ does.

So far, we have discussed integration of primitive triples. This concerns a process where the original state space (the interval I) is changed to a new state space and then, an information triple over the new state space is constructed. A similar process applies if we start out with a family ${\left(({\mathsf{\Phi }}_t,{\mathrm{H}}_t,{\mathrm{D}}_t)\right)}_{t\in T}$ of proper information triples over the same state space X (formally, over $X\times Y$ or $X\otimes Y$ with structures as usual and, typically, $Y=X$). Then we may consider the integrated triple

$$(\mathsf{\Phi },\mathrm{H},\mathrm{D})={\int }_T({\mathsf{\Phi }}_t,{\mathrm{H}}_t,{\mathrm{D}}_t)d\mu (t)$$

(147)

defined by

$$\begin{array}{cc}\hfill \mathsf{\Phi }(x,y)& ={\int }_T{\mathsf{\Phi }}_t(x,y)d\mu (t),\hfill \end{array}$$

(148)

$$\begin{array}{cc}\hfill \mathrm{H}(x)& ={\int }_T{\mathrm{H}}_t(x,y)d\mu (t),\hfill \end{array}$$

(149)

$$\begin{array}{cc}\hfill \mathrm{D}(x,y)& ={\int }_T{\mathrm{D}}_t(x,y)d\mu (t).\hfill \end{array}$$

(150)

With suitable measurability conditions, $(\mathsf{\Phi },\mathrm{H},\mathrm{D})$ is a well-defined proper information triple. Also, the standard restriction of affinity is preserved by this process. As a useful but trivial remark, we note that properness of the integrated triple only needs properness of $({\mathsf{\Phi }}_t,{\mathrm{H}}_t,{\mathrm{D}}_t)$ for a set of positive $\mu$-measure. An instance of this feature with T a two-element set was already discussed in Section 2.7.

The most obvious application of the process of integration probably is to integrate the utility-based standard algebraic triple $(\mathrm{u},\mathrm{m},\mathrm{d})=(-u^2+2su,s^2,{(s-u)}^2)$, cf., (129). This triple is considered over $I\otimes I$ with $I=]-\infty ,\infty [$. Integrating over a measure space $(T,\mu )$, you are led to take as state space the ${\mathrm{L}}^2$-space over $(T,\mu )$. In standard notation, the integrated triple $(\mathrm{U},\mathrm{M},\mathrm{D})$ is given by

$$\begin{array}{cc}\hfill \mathrm{U}(x,y)& =-{\parallel y\parallel }^2+2\langle x,y\rangle ,\hfill \end{array}$$

(151)

$$\begin{array}{cc}\hfill \mathrm{M}(x)& ={\parallel x\parallel }^2\hfill \end{array}$$

(152)

$$\begin{array}{cc}\hfill \mathrm{D}(x,y)& ={\parallel x-y\parallel }^2.\hfill \end{array}$$

(153)

We collect in Section 3.2 comments on these classical concepts, seen in the light of the theory here developed.

Some comments on the generation of information triples by the method inspired by Bregman [77] are in order. The focus of Bregman’s method has often been on the divergence measures it generates. Before Bregman’s work one mainly studied f-divergences, introduced independently by Csiszár [79], Morimoto [80] and by Ali and Silvey [81]. We find that often, Bregman divergences occur more naturally and have more convincing interpretations.

As we have seen, the widely studied entropies bearing Tsallis’ name can be derived via a Bregman-type construction. In Section 3.6 we shall have a closer look at these entropies. They have received a good deal of attention, especially within statistical physics. Some comments on the origin of these measures of entropy are in place. Tsallis’ trend-setting paper [2] is from 1988 but, originally, the entropies go back to Havrda and Charvát [82], to Daróczy [83] and to Lindhard and Nielsen [84,85] who all, independently of each other, found the notion of interest. Characterizations via functional equations were derived in Aczél and Daróczy [86], see also the reference work [87] as well as [41]. Regarding the physical literature, there is a casual reference to Lindhard’s work in one of Jaynes’ papers [88]. However, only after the publication of Tsallis 1988-paper mathematicians and, especially, physicists took an interest in the “new” entropy measures. We refer to the database maintained by Tsallis with more than 2000 references. From the recent literature we only point to Naudts, ref. [89] who also emphasized the convenient approach via Bregman generators.

3.2. A Geometric Model

Let us return to the model $(\mathrm{U},\mathrm{M},\mathrm{D})$ given by (151)–(153) of Section 3.1. This is the utility-based information triple $(-{\parallel y\parallel }^2+{2\langle x,y\rangle ,\parallel x\parallel }^2,{\parallel x-y\parallel }^2)$ pertaining to the Hilbert space $X=Y={\mathrm{L}}^2(T,\mu )$. The triple is proper and has affine marginals ${\mathrm{U}}^y$ given y.

In this case, the linking identity (after rearrangement of terms) is identical to the cosine relation. Other well-known basic facts of inner-product spaces can be derived by combining the linear structure of such spaces with the basic properties of information triples. Thus, the identity you obtain from the compensation identity (79) applied to D is of central importance for classical least squares analysis (apparently, the identity has no special name in this setting—it goes back at least to Gauss).

Games directly associated with the information triple $(\mathrm{U},\mathrm{M},\mathrm{D})$ involve minimization of M over various preparations, in other terms, the search for elements closest to the origin subject to certain restrictions. Let us, instead comment on relative games, which are games depending on the specification of a preparation and a prior $y_0\in Y$, cf., Section 2.8. If the preparation $𝒫$ is convex and closed, the D-projection $x^{*}$ of $y_0$ on $𝒫$ exists; it is the unique point in $𝒫$ which is closest in norm to $y_0$ (though classical, the reader may appreciate to note that this existence result is derived with ease from the compensation identity and completeness of Hilbert space). As standard convexity- and continuity assumptions are also in place, Theorem 15 applies. It follows that the game $\gamma (\mathcal{P};y_0)$ is in equilibrium with the D-projection $x^{*}$ as bi-optimal state. The updating gain for this game is given by (21), i.e.,

$${\mathrm{U}}_{|y_0}(x,y)=\parallel x-y_0{\parallel }^2-{\parallel x-y\parallel }^2.$$

(154)

In this case the Pythagorean inequality reduces to the classical inequality

$$\parallel x-y_0{\parallel }^2\ge \parallel x-x^{*}{\parallel }^2+{\parallel x^{*}-y_0\parallel }^2,$$

(155)

valid for every $x\in \mathcal{P}$.

Combining Proposition 9 and Theorem 15 we obtain rather complete information about the updating games, also for preparations which are not necessarily convex. For instance, Figure 4, case (a) illustrates a case with unique optimal strategies for both players and yet, the game is not in equilibrium. Case (b) illustrates a typical case with a game in equilibrium. For both figures, $x^{*}$ denotes the optimal strategy for Nature and $y^{*}$ the optimal strategy for Observer. Indicated on the figures you also find the largest strict divergence ball $\mathrm{B}(x^{*}|y_0)$ and the largest half-space ${\sigma }^{+}(y^{*}|y_0)$ which is external to $𝒫$. The two values of the game can then be determined from the figures, $\parallel x^{*}-y_0{\parallel }^2$ for Nature, respectively $\parallel y^{*}-y_0{\parallel }^2$ for Observer.

Lastly some words on the typical preparations you meet in practice. In consistency with the philosophy expressed in Section 2.9 these are the feasible preparations. The strict ones are affine subspaces and the slack ones are convex polyhedral subsets. We shall determine the core of families of strict preparations:

Proposition 12.

Consider a family $\mathbb{P}={\mathbb{P}}^{\mathbf{y}}$ of strict feasible preparations determined by finitely many points $\mathbf{y}=(y_1,\cdots ,y_n)$ in X. The core of this family consists of all points in the affine subspace through $y_0$ generated by the vectors $y_i-y_0;i=1,\cdots ,n$, i.e.,

$$\mathrm{core}(\mathbb{P})=\{y_0+\sum {\alpha }_i(y_i-y_0)|({\alpha }_1,\cdots ,{\alpha }_n)\in {\mathbb{R}}^n\}.$$

(156)

Proof. 

An individual member $𝒫$ of $\mathbb{P}$ is determined by considering all $x\in X$ for which the values of ${\mathrm{U}}_{|y_0}(x,y_i);i=1,\cdots ,n$ have been fixed. Note that fixing these values is the same as fixing the inner products $\langle x-y_0,y_i-y_0\rangle$ or, equivalently, the inner products $\langle x,y_i-y_0\rangle$. If $y^{*}$ is of the form given by (156), $y^{*}=y_0+\sum {\alpha }_i(y_i-y_0)$, then $\langle x,y^{*}-y_0\rangle =\sum {\alpha }_i\langle x,y_i-y_0\rangle$ and we realize that this is independent of x if x is restricted to run over some preparation in $\mathbb{P}$. Then also ${\mathrm{U}}_{|y_0}(x,y^{*})$ is independent of x when x is so restricted. We conclude that $y^{*}\in \mathrm{core}(\mathbb{P})$. This proves the inclusion “⊇” of (156).

To prove the other inclusion, assume, as we may, that $y_0=0$ and that the $y_i$ forms an orthonormal system. Consider a point $y^{*}\in \mathrm{core}(\mathbb{P})$. Determine $\mathcal{P}\in \mathbb{P}$ such that $y^{*}\in \mathcal{P}$. By Theorem 5, $y^{*}$ is the bi-optimal state of $\gamma (\mathcal{P};y_0)$. Let $c_i;i=1,\cdots ,n$ denote the common values of $\langle x,y_i\rangle$ for $x\in \mathcal{P}$. Then $x^{*}=\sum c_i{y}_i$ is the orthogonal projection of $y_0=0$ on $𝒫$, hence $y^{*}=x^{*}$. This argument shows that the core is contained in the subspace generated by the $y_i$. This is the result we want as we assumed that $y_0=0$. ☐

In order to determine the projection of $y_0$ on a specific preparation $\mathcal{P}={\mathcal{P}}^{\mathbf{y}}(\mathbf{h})\in \mathbb{P}$, we simply intersect $\mathrm{core}(\mathbb{P})$ with $𝒫$. If you do this analytically, one may avoid trivial cases and assume that $y_i-y_0;i=1,\cdots ,n$ are linearly independent. In Figure 4, case (c) we have illustrated the situation in the simple case when $n=1$.

3.3. Universal Coding and Prediction

In this and in the next two sections we present problems where randomization plays a role. It will be realized that apart from this, the discussion of the three problems treated, though different in nature, relies on the same type of considerations (Kuhn-Tucker type results).

We start by discussing a problem of universal coding and prediction.

Let $\mathbb{A}$ be a discrete finite set, the common alphabet and consider languages whose written representation use letters from $\mathbb{A}$. Let $\mathcal{P}$ be a finite set of such languages, referred to as the selection, e.g., the selection could be English, German and French. Assume that for each individual language from $\mathcal{P}$ we know the distribution of single letters in a typical text from that language, and let us identify a language with the corresponding distribution over $\mathbb{A}$. In this way, the selection is identified with a certain finite subset $\mathcal{P}\subseteq$ of $M_{+}^1(\mathbb{A})$, the set of all distributions over $\mathbb{A}$.

When we observe letters from $\mathbb{A}$ generated by a typical text from just one of the languages, say with associated single-letter distribution $P\in M_{+}^1(\mathbb{A})$, information theory tells us how to encode letters from $\mathbb{A}$ in strings of letters from a reference alphabet, say the binary alphabet consisting of the two elements 0 and 1, so as to minimize the expected length of the encoded binary strings. The encoded string corresponding to the letter $x\in \mathbb{A}$, will then have a length $\kappa (x)$ which is given roughly as

$$\kappa (x)\approx \log \frac{1}{P(x)}$$

(157)

with log denoting binary logarithms. This choice ensures that the average code length

$$\langle \kappa ,P\rangle =\sum _{x\in \mathbb{A}}P(x)\kappa (x)$$

(158)

is minimal.

The precise sense in which (157)—even with exact equality—is the undisputed right choice will not be discussed here. It is a cornerstone of information theory for which you may consult standard text books on information theory such as [90] or an introductory text such as Topsøe [91]. Note that (157) with equality implies that ${\sum }_{x\in \mathbb{A}}{2}^{-\kappa (x)}=1$ (Kraft’s equality).

Let us change to a more theoretical concept of encoding by idealization, forgetting that the length of a binary sequence is a natural number and by a change to natural units rather than binary units. This leads us to redefine a code over $\mathbb{A}$ to be a map $\kappa :\mathbb{A}\mapsto [0,\infty ]$ such that

$$\sum _{x\in \mathbb{A}}\exp (-\kappa (x))=1,$$

(159)

i.e., such that Kraft’s equality with natural units holds. Denote by $\mathrm{K}(\mathbb{A})$ the set of all such codes. The requirement (159) amounts to the requirement that the correspondence $\kappa \leftrightarrow P$ given by

$$\kappa (x)=\ln \frac{1}{P(x)};x\in \mathbb{A}$$

(160)

is a one-to-one correspondence between $M_{+}^1(\mathbb{A})$ and $\mathrm{K}(\mathbb{A})$. We also express (160) by saying that $\kappa$ is adapted to P and we write $\kappa =\widehat{P}$. As is easily seen, either directly or referring to previous material from Section 3.1, $\kappa =\widehat{P}$ is the unique code for which the average code length $\langle \kappa ,P\rangle$ is minimal.

With this property in mind, we define the redundancy of a pair $(P,\kappa )\in M_{+}^1(\mathbb{A})\times \mathrm{K}(\mathbb{A})$ as the quantity

$$\widehat{\mathrm{D}}(P,\kappa )=\sum _{x\in \mathbb{A}}P(x)\left(\kappa (x)-\ln \frac{1}{P(x)}\right).$$

(161)

From our discussion we know—in a theoretical idealized way at least—how to encode letters from $\mathbb{A}$ if we want to process letters from a text source generated by a single language in an optimal manner. We shall investigate what can be done if we receive text from an unknown language, except that we know that the language is one from the given selection.

We agree to call a code $\kappa \in \mathrm{K}(\mathbb{A})$ universal for the language selection $\mathcal{P}$ if the risk, here defined as

$${\widehat{\mathrm{Ri}}}_0(\kappa |\mathcal{P})=\underset{P\in \mathcal{P}}{\max }\widehat{\mathrm{D}}(P,\kappa )$$

(162)

is minimal. The associated distribution under the correspondence $\kappa \leftrightarrow P$ is then said to be a universal predictor. Note that the risk ${\widehat{\mathrm{Ri}}}_0$ is associated with the information triple $(\widehat{\mathrm{D}},0,\widehat{D})$ and that a universal code is the same as an optimal strategy for Observer in the game associated with this triple. Clearly, the game in question is not in equilibrium, hence equilibrium type results as developed previously are not of much use. Instead it turns out that a very direct approach will lead to an identification of universal objects.

Theorem 16.

Let $(P^{*},{\kappa }^{*})\in M_{+}^1(\mathbb{A})\times \mathrm{K}(\mathbb{A})$ with ${\kappa }^{*}$ adapted to $P^{*}$. Assume further that for some finite constant R,

$$\widehat{\mathrm{D}}(P,{\kappa }^{*})\le RforallP\in \mathcal{P}$$

(163)

and that $P^{*}$ can be written as a convex combination of a set of distributions in $\mathcal{P}$ for which equality holds in (163). Then ${\kappa }^{*}$ is the unique universal code and $P^{*}$ the unique universal predictor.

Proof. 

Clearly, ${\widehat{\mathrm{Ri}}}_0({\kappa }^{*}|\mathcal{P})=R$.

Then consider any code $\kappa$ different from ${\kappa }^{*}$. Write $P^{*}$ as a convex combination $P^{*}={\sum }_i{\alpha }_i{P}_i$ of distributions in $\mathcal{P}$ all of which satisfy the relation $\widehat{\mathrm{D}}(P_i,{\kappa }^{*})=R$. Then the compensation identity tells us that

$$\begin{array}{cc}\hfill {\widehat{\mathrm{Ri}}}_0(\kappa |\mathcal{P})& =\sum _i{\alpha }_i{\widehat{\mathrm{Ri}}}_0(\kappa |\mathcal{P})\ge \sum _i{\alpha }_i\widehat{\mathrm{D}}(P_i,\kappa )\hfill \\ & =\widehat{\mathrm{D}}(P^{*},\kappa )+\sum _i{\alpha }_i\widehat{\mathrm{D}}(P_i,{\kappa }^{*})=\widehat{\mathrm{D}}(P^{*},\kappa )+R.\hfill \end{array}$$

Thus, as $\widehat{\mathrm{D}}$ is proper, ${\widehat{\mathrm{Ri}}}_0(\kappa |\mathcal{P})>R$. As this holds for all $\kappa \ne {\kappa }^{*}$, the result follows. ☐

Note the essential point that $\widehat{\mathrm{D}}$ satisfies the compensation identity. That this is so follows either by direct calculation or, more systematically, by applying (iii) of Theorem 8 to the triple you obtain by adding entropy to $(\widehat{\mathrm{D}},0,\widehat{\mathrm{D}})$. For the derived domain you then work with the typical Shannon triple, listed explicitly in (185)–(187). So, after all, the information triples are also useful for the above problem.

It can be shown that the result always applies in the sense that the unique optimal code and the unique optimal predictor exist and that they satisfy the conditions stated in the theorem. Note that the representation of the optimal predictor as given in the theorem may not be unique.

3.4. Sylvester’s Problem from Location Theory

As starting point we take a simple Y-domain model with $Y=X$, a convex set. For visibility we take the diffuse relation $X\times Y$. Given is a finite-valued general divergence function over $X\times Y$ for which the compensation identity (79) holds.

As a concrete example, one may have in mind, take that of a Euclidean space X provided with norm-squared distance, $\mathrm{D}(x,y)={\parallel x-y\parallel }^2$. Moreover, as the motivating problem, consider Sylvester’s problem, to determine the point with the least maximal distance to a given finite set $\mathcal{P}$ of points in X, cf., [92] or the monograph [93]. For the original problem, X was the Euclidean plane. However, the problem makes good sense in the general setting with X any convex set provided with a suitable replacement for classical squared distance.

The problem is a minimax problem and may formally be conceived as related to the special proper information triple $(\mathrm{D},0,\mathrm{D})$. Indeed, the problem is to find optimal Observer strategies for the associated game $\gamma (\mathcal{P})$ and to calculate Observer’s value of the game, the MinRisk-value ${\mathrm{Ri}}_{\min }(\mathcal{P})$. However, this game is rather trivial as Natures value in the game is 0. Thus no equilibrium-type results are available.

To find a remedy, we apply a process of randomization. For that, we no longer consider X as the state space but take the convex space $\tilde{X}=\mathrm{MOL}(X)$ of molecular probability measures as a new state space. An element $\alpha \in \tilde{X}$ is represented as a family $\alpha ={({\alpha }_x)}_{x\in X}$ of non-negative numbers such that ${\sum }_{x\in X}{\alpha }_x=1$ and such that the support of $\alpha$, i.e., the set $\mathrm{supp}(\alpha )=\left\{x\right|{\alpha }_x>0\}$, is finite.

The new model we shall construct is conceived as a $\widehat{Y}$-type model. As state space we take $\tilde{X}$. Just as X, this is a convex set. For formal reasons—so that the modeling fits the general abstract theory—we may also take $\tilde{X}$ as belief reservoir, though we will have no need really to consider belief instances. Instead, control will be in the focus, and for the set of control instances we shall take $Y=X$. Once more for formal reasons, we consider the barycentric map which maps an (artificial) belief instance into its barycenter as response. This map will play an important role for the modeling. Let the map be $\alpha \mapsto \mathrm{b}(\alpha )$ with $\alpha \in \tilde{X}$ and barycenter of $\alpha$ given by

$$\mathrm{b}(\alpha )=\sum _{x\in X}{\alpha }_{x}x.$$

(164)

The good sense in considering elements of X as controls is the idea from location theory, that from a point in X, conceived as a location, you should try to control the given points in the set $\mathcal{P}$ as best you can.

With these preparations, we may consider the triple $(\tilde{\mathsf{\Phi }},\tilde{\mathrm{H}},\tilde{\mathrm{D}})$ over $\tilde{X}\times Y$ given by

$$\begin{array}{cc}\hfill & \tilde{\mathsf{\Phi }}(\alpha ,y)=\sum _{x\in X}{\alpha }_x\mathrm{D}(x,y),\hfill \end{array}$$

(165)

$$\begin{array}{cc}\hfill & \tilde{\mathrm{H}}(\alpha )=\sum _{x\in X}{\alpha }_x\mathrm{D}(x,\mathrm{b}(\alpha )),\hfill \end{array}$$

(166)

$$\begin{array}{cc}\hfill & \tilde{\mathrm{D}}(\alpha ,y)=\mathrm{D}(\mathrm{b}(\alpha ),y).\hfill \end{array}$$

(167)

For $\mathcal{P}\subseteq X$, denote by $\tilde{\mathcal{P}}$ the set of $\alpha \in \tilde{X}$ which are supported by $\mathcal{P}$, i.e., ${\sum }_{x\in \mathcal{P}}{\alpha }_x=1$. By $\tilde{\gamma }(\tilde{\mathcal{P}})$ we denote the game corresponding to the triple $(\tilde{\mathsf{\Phi }},\tilde{\mathrm{H}},\tilde{\mathrm{D}})$ with $\tilde{P}$ as preparation. A basic fact which contributes to the significance of games of this type is that, as easily seen, risk does not increase when you replace the game $\gamma (\mathcal{P})$ with $\tilde{\gamma }(\tilde{\mathcal{P}})$, in particular, with self-explanatory notation,

$${\widetilde{\mathrm{Ri}}}_{\min }(\tilde{\mathcal{P}})={\mathrm{Ri}}_{\min }(\mathcal{P}).$$

(168)

This fact relies on the affinity of the marginals of $\tilde{\mathsf{\Phi }}$ for fixed y.

Theorem 17.

The triple $(\tilde{\mathsf{\Phi }},\tilde{\mathrm{H}},\tilde{\mathrm{D}})$ over $\tilde{X}\times Y$ is a proper information triple over $\tilde{X}\times Y$ and the triple has affine marginals.

Let $\mathcal{P}$ be a subset of X and consider the game $\tilde{\gamma }(\tilde{\mathcal{P}})$. Consider a pair $({\alpha }^{*},y^{*})\in \tilde{\mathcal{P}}\times Y$ of strategies in the game $\tilde{\gamma }(\tilde{\mathcal{P}})$ with $y^{*}$ adapted to ${\alpha }^{*}$, i.e., $y^{*}=\mathrm{b}({\alpha }^{*})$. Then if, for some constant R,

$$\begin{array}{cc}\hfill \forall x\in X:& \mathrm{D}(x,y^{*})\le R,\hfill \end{array}$$

(169)

$$\begin{array}{cc}\hfill \forall x\in \mathrm{supp}({\alpha }^{*}):& \mathrm{D}(x,y^{*})=R,\hfill \end{array}$$

(170)

$y^{*}$ is the unique optimal strategy for Observer in $\tilde{\gamma }(\tilde{\mathcal{P}})$ as well as in $\gamma (\mathcal{P})$. Further, ${\mathrm{Ri}}_{\min }(\mathcal{P})=R$ and $x^{*}$ is a bi-optimal strategy for $\tilde{\gamma }(\tilde{\mathcal{P}})$.

Proof. 

With preparations done, the first part is trivial, and the second is also so, obtainable as an application of Corollary 1. ☐

Note that the linking identity is just another way of formulating the compensation identity and that the entropy function is the compensation term in that identity.

With Theorem 17 we have a solution to Sylvester’s problem for an abstract model provided you can somehow point to a possible solution. It can be shown, modulo technical assumptions to ensure existence of optimal strategies, that the sought optimal Observer strategy must be of the form as stated in the theorem.

3.5. Capacity Problems, an Indication

Problems concerning capacity are among the most well known problems from information theory. They concern the determination of capacity defined as maximal information transmission rate under various conditions and on the associated optimal ways of coding. We shall only define one of the basic concepts and derive a key relation and leave it to the reader to consult the literature for more concrete results.

We first elaborate on the information triple given in the previous section by (165)–(167). The entropy function of that triple we may think of as related to information transmission rate of information theory (then also related to the notion of mutual information which is, however, not investigated further in the present study). This refers to the map $x\mapsto y$ as a map from an input letter to an output letter. Then an element $\alpha \in \tilde{X}$ represents a distribution over the input letters, a source, and response tells you what is happening on the output side. It is important to study how the rate behaves under mixtures. Thus we have a need to study elements in $\tilde{\tilde{X}}=\mathrm{MOL}(\tilde{X})$. The result one needs exploits the flexibility of the modeling, especially related to Theorem 8.

First, define information transmission rate related to $\alpha \in \tilde{X}$ simply as

$$\mathrm{I}(\alpha )=\tilde{\mathrm{H}}(\alpha ).$$

(171)

We wish to emphasize the following result:

Lemma 2.

With the setting as above, consider any $w={(w_{\alpha })}_{\alpha \in \tilde{X}}\in \tilde{\tilde{X}}$ and put ${\alpha }_0={\sum }_{\alpha \in \tilde{X}}{w}_{\alpha }\alpha$. Then, for every $w\in \tilde{\tilde{X}}$,

$$\mathrm{I}(\sum _{\alpha \in \tilde{X}}{w}_{\alpha }\alpha )=\sum _{\alpha \in \tilde{X}}{w}_{\alpha }\mathrm{I}(\alpha )+\sum _{\alpha \in \tilde{X}}{w}_{\alpha }\mathrm{D}\left(\mathrm{b}(\alpha ),\mathrm{b}({\alpha }_0)\right).$$

(172)

Proof. 

If you write $\tilde{\mathrm{H}}$ in place of I, this follows from the identity (77) of Theorem 8 with $\tilde{\mathrm{H}}$ in place of H. ☐

With the technical lemma in place, a study of abstract models of information transmission systems runs smoothly and you can derive operational necessary and sufficient conditions for the requirements of optimal strategies. On Natures side, an optimal strategy is an input distribution for which the transmission rate reaches the maximum, the capacity of the system. The result is a Kuhn-Tucker type result, well known from general convexity theory and from Information theory, and much resembles the results of the previous two sections. We refer to Topsøe [94] for an exposition of a result which exploits the lemma just proved.

3.6. Tsallis Worlds

Recall the introduction in Section 3.1 of the family of Tsallis entropies. In this section we present arguments which may help to appreciate the significance of these measures of entropy.

The main result, Theorem 18 was presented in a different form in [36] and, less formally, in [35]. Here we present detailed proofs which were not provided in these sources.

The introduction in Section 3.1 of the Bregman generators ${\mathrm{h}}_q$ and thereby, via a process of integration, of Tsallis entropy, cf., (146), does not in itself constitute an acceptable interpretation. Via coding considerations, the significance of the Bregman generator ${\mathrm{h}}_1$, leading to the notion of Shannon entropy is well understood. Despite some attempts to extend this to more general entropy measures, cf., [95,96,97], a general approach via coding has not yet been fully convincing. In [98] you find a previous attempt of the author centred on a certain property of factorization.

The results presented here indicate that possibly, a convincing and generally acceptable physical justification of Tsallis entropy can be provided by involving deformation between the physical system studied and the physicist. Previous endeavours to find physical justification for Tsallis entropy are discussed in detail in Tsallis, [99]. We share the view that though the “Tsallis-q” can be viewed just as a parameter introduced simply to fit data, this is not satisfactory and operational justification is needed. Deformation as here emphasized in combination with a notion of description may offer a common ground on the way to more insight.

To set the scene for our study, introduce the alphabet $\mathbb{A}$, a discrete set of basic events which are identified by an index, typically denoted by i. Sensible indexing is often of importance and depends on the concrete physical application. The semiotic assignment of indices shall facilitate technical handling and catalyze semantic awareness. As we have no concrete application in mind, no extra structure is introduced which could justify a specific choice of indices.

The state space X is taken to be identical to the belief reservoir Y and, for simplicity, equal to $M_{+}^1(\mathbb{A})$, the set of probability distributions over $\mathbb{A}$ (you could have worked, instead and more generally, with sets involving intensity as suggested in Section 3.1). Generically, $x={(x_i)}_{i\in \mathbb{A}}$ will denote a state and $y={(y_i)}_{i\in \mathbb{A}}$ a belief instance. Thus x and y are characterized by their point probabilities. As $Y_{\det }$, the set of certain belief instances, we take the set of deterministic distributions over $\mathbb{A}$. Visibility $y\succ x$ shall mean that x is absolutely continuous wrt y. Thus $X\otimes Y$ consists of all pairs $(x,y)\in M_{+}^1(\mathbb{A})\times M_{+}^1(\mathbb{A})$ with $\mathrm{supp}(x)\subseteq \mathrm{supp}(y)$, with @supp@ denoting support. We shall not need a control space or a response function.

A knowledge instance will be a family $z={(z_i)}_{i\in \mathbb{A}}$ over $\mathbb{A}$ of real numbers, not necessarily a probability distribution. The interpretation of $z_i$ is as the intensity with which the basic event indexed by i is presented to Observer. For this reason, z is referred to as the intensity function. The individual elements $z_i$ are the local intensities.

The deformation between x, y and z is given by a deformation $\mathrm{\Pi }$, cf., Section 2.5. We assume that $\mathrm{\Pi }$ acts locally, i.e., that there exists a real-valued function $\pi$, the local deformation, defined on ${[0,1]}^2=[0,1]\times [0,1]$ such that, when $z=\mathrm{\Pi }(x,y)$, then $z_i=\pi (x_i,y_i)$ for all $i\in \mathbb{A}$. The world defined in this way by a local deformation is denoted ${\mathrm{\Omega }}_{\pi }$ or, if need be, ${\mathrm{\Omega }}_{\pi }(\mathbb{A})$. From now on, when we talk about a “deformation”, we have a local deformation in mind.

Regarding regularity conditions, we assume that $\pi$ is finite on $[0,1]\times ]0,1]$, continuous on ${[0,1]}^2\setminus \left\{(0,0)\right\}$ and continuously differentiable on $]0,1[\times ]0,1[$. The deformation is weakly consistent if ${\sum }_{i\in \mathbb{A}}{z}_i=1$ whenever $(x,y)\in X\otimes Y$ and ${(z_i)}_{i\in \mathbb{A}}=\mathrm{\Pi }(x,y)$. If you can even conclude that $z={(z_i)}_{i\in \mathbb{A}}$ is a probability distribution, $\pi$ is strongly consistent. The deformation $\pi$ is sound if $\pi (s,s)=s$ for every $s\in [0,1]$.

For $q\in \mathbb{R}$, the algebraic deformation ${\pi }_q$ is given on ${[0,1]}^2$ by

$${\pi }_q(s,t)=qs+(1-q)t.$$

(173)

These deformations are all sound and weakly consistent and, for $0\le q\le 1$, even strongly consistent. The corresponding worlds are denoted ${\mathrm{\Omega }}_q={\mathrm{\Omega }}_q(\mathbb{A})$. The notation is consistent with the notation introduced in Section 2.5. The significance of the algebraic deformations is derived from the following result.

Lemma 3.

Assume that the alphabet $\mathbb{A}$ is countably infinite. Then only the algebraic deformations are weakly consistent.

Proof. 

Let $\pi$ be weakly consistent and put $q=\pi (1,0)$. Consider a deterministic distribution $\delta$ over $\mathbb{A}$ and apply weak consistency with $x=y=\delta$ to find that $\pi (0,0)=0$. Thus, if x and y both have support in a subset ${\mathbb{A}}_0\subseteq \mathbb{A}$, you can neglect contributions stemming from $(x_i,y_i)$ with $i\notin {\mathbb{A}}_0$ and conclude consistency over ${\mathbb{A}}_0$, i.e., that ${\sum }_{i\in {\mathbb{A}}_0}\pi (x_i,y_i)=1$. By weak consistency (in the extended form just established), $\pi (s,t)+\pi (1-s,1-t)=1$ for all $(s,t)\in [0,1]\times [0,1]$, in particular, $\pi (0,1)=1-q$. Consider $(x_0,y_0)=(0,1)$ and $(x_i,y_i)=(\frac{1}{n},0)$ for $i=1,\cdots ,n$, apply weak consistency and conclude that $\pi (\frac{1}{n},0)=\frac{1}{n}q$. Then, for $p\in \mathbb{N}$, consider vectors $(x_i,y_i)$ of the form $(0,1),(\frac{1}{n},0),\cdots ,(\frac{1}{n},0),(\frac{p}{n},0)$. By weak consistency and previous findings, conclude that $\pi (s,0)=sq$ for all rational $s\in [0,1]$. By continuity, this formula holds for all $s\in [0,1]$. Quite analogously, $\pi (0,t)=t(1-q)$ for all $t\in [0,1]$. Finally, $\pi ={\pi }_q$ follows by weak consistency applied to $(s,t),(1-s,0),(0,1-t)$.  ☐

In particular, if $\mathbb{A}$ is infinite then, automatically, a weakly consistent deformation is sound. In fact, all concrete deformations we shall deal with will be sound.

Instead of searching only for a suitable entropy function for the world ${\mathrm{\Omega }}_{\pi }$, we find it more rewarding to search for a suitable full information triple for this world. Let us analyze what such a triple, say $(\mathsf{\Phi },\mathrm{H},\mathrm{D})$, could be. A natural demand is that $\mathsf{\Phi },\mathrm{H}$ and D should all act locally. Therefore, according to Section 3.1 what we are really searching for is a primitive information triple $(\varphi ,\mathrm{h},\mathrm{d})$ over $[0,1]\times [0,1]\setminus \{(s,u)|s>0,u=0\}$, cf., (110), such that $(\mathsf{\Phi },\mathrm{H},\mathrm{D})$ is obtained from this triple by integration over $\mathbb{A}$ equipped with counting measure. In particular, the requirements (111)–(114) must be satisfied. Obvious names for the sought functions $\varphi ,\mathrm{h}$ and d are, respectively, local effort, local entropy and local divergence.

Let us suggest a suitable form of local effort. It will depend on the notion of a descriptor, defined as any continuous, strictly decreasing function on $[0,1]$ which is finite-valued and continuously differentiable on $[0,1]$, vanishes at $t=1$ and satisfies the condition that

$${\kappa }^{\prime }(1)=-1.$$

(174)

The value $\kappa (u)$ is conceived as the effort you have to allocate to any basic event in which you have a belief expressed by u. The condition $\kappa (1)=0$ reflects the fact that if you feel certain that a basic event will occur, there is no reason why you should allocate any effort at all to that event. Also, it is to be expected that events you do not have much belief in are more difficult to describe than those you believe in with a higher degree of confidence. Therefore, we may just as well assume from the outset that $\kappa$ is decreasing. The norming requirement (174) will enable comparisons of effort, entropy and divergence across different descriptors or even different worlds. The unit defined implicitly by (174) is the natural information unit, the “nat”.

An important class of descriptors is the class ${({\kappa }_q)}_{q\ge 0}$ given on $[0,1]$ by

$${\kappa }_q(s)={\ln }_q\frac{1}{s}.$$

(175)

With access to a descriptor you may suggest to assign the effort $\kappa (u)$ to an event with belief instance u, but you should multiply this effort with the intensity with which the event is presented to you. This gives the suggestion $\varphi (s,u)=\pi (s,u)\kappa (u)$ for local effort. Then local divergence should be the function $\mathrm{d}(s,u)=\pi (s,u)\kappa (u)-\pi (s,s)\kappa (s)$. However, this is not going to work as the fundamental inequality (112) is bound to fail (consider $(s,u)$ with u close to 1). Fortunately, insight gained in Section 3.1 indicates how one may modify the suggestion in order to have a chance that the fundamental inequality could hold, viz., by adding an overhead term. Therefore, given a descriptor, we now suggest to define the local functions as follows:

$$\begin{array}{cc}\hfill {\varphi }_{\pi }(s,u|\kappa )& =\pi (s,u)\kappa (u)+u\hfill \end{array}$$

(176)

$$\begin{array}{cc}\hfill {\mathrm{h}}_{\pi }(s|\kappa )& =\pi (s,s)\kappa (s)+s\hfill \end{array}$$

(177)

$$\begin{array}{cc}\hfill {\mathrm{d}}_{\pi }(s,u)|\kappa )& =\left(\pi (s,u)\kappa (u)+u\right)-\left(\pi (s,s)\kappa (s)+s\right).\hfill \end{array}$$

(178)

One may study modifications with more general overhead terms, but we shall not do so. The important thing is to realize that something has to be done. Moreover, inspired by the fact that for the important cases with descriptors of the form ${\kappa }_q$, adding a simple linear overhead as suggested above works. This is stated explicitly in Corollary 7 below.

Lemma 4.

Let π be a deformation and κ a descriptor. Assume that ${\mathrm{d}}_{\pi }(·,·|\kappa )$ given by (178) is a genuine primitive divergence function, i.e., that (112) (the pointwise fundamental inequality) and (114) (pointwise properness) hold. Then $\left({\mathsf{\Phi }}_{\pi }(·,·|\kappa ),{\mathrm{H}}_{\pi }(·|\kappa ),{\mathrm{D}}_{\pi }(·,·|\kappa )\right)$ obtained by integration of the local quantities given in (176)–(178) over $\mathbb{A}$ is a proper information triple over $X\otimes Y$.

The proof follows directly from the discussion in Section 3.1.

Note that for sound deformations, the measures of entropy constructed this way only depend on the descriptor, not on the deformation.

Also note that the quantities defined really give gross effort and gross entropy. In particular, minimal entropy is not 0 as usual, but 1. This may appear odd but, on the other hand, the way to these quantities was very natural and one may ask if it is not advantageous in many situations to incorporate an overhead. Moreover, why not use the overhead to fix the unit of effort?

We also remark that if we allow incomplete probability measures Q as belief instances, then this change of the space $X\otimes Y$ will not change the conclusion above. However, sticking to probability measures also for belief instances, we may subtract the number 1 from gross effort and from gross entropy and obtain the more familiar net-quantities.

Corollary 7.

For $0<q\le \infty$ the deformation ${\pi }_q$ and the descriptor ${\kappa }_q$ satisfy the conditions of Lemma 4. Accordingly, the information triple generated by integration over $\mathbb{A}$ is a proper information triple. Furthermore, the effort function has affine marginals.

The obtained effort- and entropy functions are gross-quantities. The corresponding net-quantities give the information triple $({\mathsf{\Phi }}_q,{\mathrm{H}}_q,{\mathrm{D}}_q)$ in (146) of Section 3.1. In particular, ${\mathrm{H}}_q$ is standard Tsallis entropy with q as parameter.

The simple checking is left to the reader.

We turn to problems of another nature, viz., if, given a deformation, one can find an appropriate descriptor such that the generated global description effort is proper.

Lemma 5.

Assume that the alphabet $\mathbb{A}$ has at least three elements. Let π be a sound deformation and denote by χ the function on $]0,1[$ defined by

$$\chi (t)=\frac{\partial \pi }{\partial t}(t,t).$$

(179)

Under the assumption that χ is bounded in the vicinity of $t=1$, there can only exist one descriptor κ such that the net-effort function generated by π and κ, i.e., the function Φ given by

$$\mathsf{\Phi }(x,y)=\sum _{i\in \mathbb{A}}\pi (x_i,y_i)\kappa (y_i)$$

(180)

is a proper effort function over $X\otimes Y$. Indeed, κ must be the unique solution in $[0,1]$ to the differential equation

$$\chi (t)\kappa (t)+t{\kappa }^{\prime }(t)=-1$$

(181)

for which $\kappa (1)={\lim }_{t\to 1}\kappa (t)=0$.

Proof. 

Assume that $\kappa$ exists with ${\mathsf{\Phi }}_{\pi }(·,·|\kappa )$ proper. For $0<t<1$ put

$$f(t)=\chi (t)\kappa (t)+t{\kappa }^{\prime }(t).$$

Consider a, for the time, fixed probability vector $x=(x_1,x_2,x_3)$ with positive point probabilities. Then the function F given by

$$F(y)=F(y_1,y_2,y_3)=\sum _1^3\pi (x_i,y_i)\kappa (y_i)$$

on $]0,1[\times ]0,1[\times ]0,1[$ assumes its minimal value at the interior point $y=x$ when restricted to probability distributions. As standard regularity conditions are fulfilled, there exists a Lagrange multiplier $\lambda$ such that, for $i=1,2,3$,

$$\frac{\partial }{\partial y_i}(F(y)-\lambda \sum _1^3{y}_i)=0$$

when $y=x$. This shows that $f(x_1)=f(x_2)=f(x_3)$.

Using this with $(x_1,x_2,x_3)=(\frac{1}{2},x,\frac{1}{2}-x)$ for a value of x in $]0,\frac{1}{2}[$, we conclude that f is constant on $]0,\frac{1}{2}[$. Then consider a value $x\in [\frac{1}{2},1]$ and the probability vector $\left(x,\frac{1}{2}(1-x),\frac{1}{2}(1-x)\right)$ and conclude from the first part of the proof that $f(x)=f\left(\frac{1}{2}(1-x)\right)$. As $0<\frac{1}{2}(1-x)<\frac{1}{2}$, we conclude that $f(x)=f(\frac{1}{2})$. Thus f is constant on $[0,1]$. By letting $t\to 1$ in (181) and appealing to the technical boundedness assumption, we conclude that the value of the constant is $-1$.  ☐

Note the use in the above proof of Lagrange multipliers in the study of properties that hold under the realization of an extremum. This is quite different from the usage we have opted against where the technique is used as a tool to verify that an extremum has been found. In the latter case, we claim that, typically, more adequate intrinsic methods apply.

We can now formulate one of the main results:

Theorem 18.

Assume that the alphabet has at least three elements.

(i) 

If $q\le 0$, there is no descriptor which, together with ${\pi }_q$, generates a proper effort function.

(ii) 

If $q>0$ there exists a unique descriptor, ${\kappa }_q$ defined by (175) which, together with ${\pi }_q$ generates a proper effort function. The generated information triple $({\mathsf{\Phi }}_q,{\mathrm{H}}_q,{\mathrm{D}}_q)$ is proper.

Proof. 

By Lemma 5 we see that ${\kappa }_q$ given by (175) is the only descriptor which, together with ${\pi }_q$, could possibly generate a proper effort function. That it does so for $q>0$, follows by Lemma 4. For $q\le 0$, this is not the case as the reader can verify by considering atomic situations with $x=(1-\epsilon ,\epsilon )$ and $y=(\frac{1}{2},\frac{1}{2})$ and letting $\epsilon$ tend to 0.  ☐

We may add that for the case of a black hole, $q=0$, the descriptor is given by ${\kappa }_0(s)=\frac{1}{s}-1$ and, using $|·|$ for “number of elements in ⋯” , the generated information triple $({\mathsf{\Phi }}_0,{\mathrm{H}}_0,{\mathrm{D}}_0)$ is given by

$$\begin{array}{cc}\hfill {\mathsf{\Phi }}_0(x,y)& =|\mathrm{supp}(y)|,\hfill \end{array}$$

(182)

$$\begin{array}{cc}\hfill {\mathrm{H}}_0(x)& =|\mathrm{supp}(x)|,\hfill \end{array}$$

(183)

$$\begin{array}{cc}\hfill {\mathrm{D}}_0(x,y)& =|\mathrm{supp}(y)\setminus \mathrm{supp}(x)|\hfill \end{array}$$

(184)

for all $y\succ x$. Note that if terms of the form $\pi (x_i,y_i)\kappa (y_i)$ were to be interpreted by continuity, the resulting triple would be discrete.

We have noted that the descriptor is uniquely determined from the deformation. Therefore, in principle, only the deformation needs to be known. Examples will show that different deformations may well determine the same descriptor. For instance, deformation defined as a geometric average rather than an arithmetic average as in the definition of ${\pi }_q$ will lead to the same descriptor. Thus, knowing only the descriptor, you cannot know which world you operate in, in particular, you cannot determine divergence or description effort. But you can determine the entropy function. This emphasizes again the general thesis, that entropy should never be considered alone.

Finally a comment on the descriptors ${\kappa }_q$. A focus on their inverses is also in order. They may be interpreted as probability checkers: Indeed, if, in a Tsallis world with parameter q, you have access to a nats and ask how complex an event this will allow you to describe, the appropriate answer is “you can describe any event with a probability as low as ${\kappa }^{-1}(a)$”. Thus, when $q\le 1$, however large your resources to nats are, there are events so complex that you cannot describe them, whereas, if $q>1$ you can describe any event if you have access to K nats if only K is sufficiently large ($K\ge \frac{1}{q-1}$).

3.7. Maximum Entropy Problems of Classical Shannon Theory

Terminology and results as developed in Section 2 are evidently inspired by maximum entropy problems of classical information theory. The classical problems concern inference of probability distributions over some finite or countably infinite alphabet $\mathbb{A}$, typically with preparations given in terms of certain constraints, often interpreted as “moment constraints” related to random variables of interest. Such preparations will, modulo technical conditions, be feasible in the sense as defined in Section 2.9. Examples are numerous, from information theory proper, from statistics, from statistical physics or elsewhere. The variety of possibilities may be grasped from the collection of examples in Kapur’s monograph [100]. The abstract results developed in Section 2 can favorably be applied to all such examples. This then has a unifying effect. However, for many concrete examples, it may involve a considerable amount of effort actually to verify the requirements needed for the abstract results to apply. This may involve the verification of Nash’s inequality (52) or the determination of the core of models under study, cf., Theorems 5 and 6. No detailed calculations for specific examples will be carried out here.

A very large number of researchers have worked with these problems. The related publications of the present author comprises [26,101]. We shall focus on applications of the general theory from Section 2.

The basic model we shall discuss is the same as in Section 3.6 based on a finite or countably infinite alphabet $\mathbb{A}$. Note that, in principle, discrete alphabets with more than enumerably many elements could be allowed. However, that would contradict the sensible requirement (3).

The relevant information triple is the proper information triple composed of Kerridge inaccuracy, Shannon entropy and Kullback-Leibler divergence:

$$\begin{array}{cc}\hfill \mathsf{\Phi }(P,Q)& =\sum _{a\in \mathbb{A}}P(a)\ln \frac{1}{Q(a)};\hfill \end{array}$$

(185)

$$\begin{array}{cc}\hfill \mathrm{H}(P)& =\sum _{a\in \mathbb{A}}P(a)\ln \frac{1}{P(a)};\hfill \end{array}$$

(186)

$$\begin{array}{cc}\hfill \mathrm{D}(P,Q)& =\sum _{a\in \mathbb{A}}P(a)\ln \frac{P(a)}{Q(a)}.\hfill \end{array}$$

(187)

We shall also work with the action space $\widehat{Y}=\mathrm{K}(\mathbb{A})$ introduced in Section 3.3 and as response we take the bijection $Q\mapsto \widehat{Q}$ from Y to $\widehat{Y}$ given, for $a\in \mathbb{A}$, by

$$\widehat{Q}(a)=\ln \frac{1}{Q(a)}.$$

(188)

Controllability is the relation for which control $\kappa \succ P$ means that $P(a)=0$ whenever $\kappa (a)=\infty$. The information triple to work with in the $\widehat{Y}$-domain is $(\widehat{\mathsf{\Phi }},\mathrm{H},\widehat{\mathrm{D}})$ with entropy as above and with

$$\begin{array}{cc}\hfill \widehat{\mathsf{\Phi }}(P,\kappa )& =\sum _{a\in \mathbb{A}}P(a)\kappa (a),\hfill \end{array}$$

(189)

$$\begin{array}{cc}\hfill \widehat{\mathrm{D}}(P,\kappa )& =\sum _{a\in \mathbb{A}}P(a)(\kappa (a)-\widehat{P}(a)).\hfill \end{array}$$

(190)

The triples $(\mathsf{\Phi },\mathrm{H},\mathrm{D})$ and $(\widehat{\mathsf{\Phi }},\mathrm{H},\widehat{\mathrm{D}})$ are genuine proper information triples with affine marginals. Thus all parts of the abstract results developed are available and ready to apply. However, we limit the discussion by focusing only on the role of the feasible preparations, leaving elaborations in concrete examples to those interested.

Thinking of states P as determining the distribution of a random element $\xi$ over $\mathbb{A}$, it is often desirable to consider preparations corresponding to the prescription of one or more mean values of $\xi$. A typical preparation consists of all $P\in X$ such that

$$\sum _{a\in \mathbb{A}}P(a)\lambda (a)=c$$

(191)

with c a given constant and $\lambda ={(\lambda (a))}_{a\in \mathbb{A}}$ a given function on $\mathbb{A}$. This is a strict feasible preparation if and only if the partition function (a special Dirichlet series),

$$Z(\beta )=\sum _{a\in \mathbb{A}}\exp \left(-\beta \lambda (a)\right)$$

(192)

has a finite abscissa of convergence, i.e., converges for some finite constant $\beta$, cf., [26] (or monographs on Dirichlet series). However, for the most important part, having concrete applications in mind, viz., the “if”-part, this is clear. Indeed, if the condition is fulfilled, there exist constants ${\alpha }_0$ and ${\beta }_0$ such that the function ${\kappa }_0$ given for $a\in \mathbb{A}$ by

$${\kappa }_0(a)={\alpha }_0+{\beta }_0\lambda (a)$$

(193)

defines a code. Then $\mathcal{P}={\mathcal{P}}^{{\kappa }_0}(k)$ for some constant k, hence it is a strict feasible preparation of genus 1. It is a member of the preparation family $\mathbb{P}={\mathbb{P}}^{{\kappa }_0}$. Consider, for any $\beta$ with $Z(\beta )<\infty$, the code ${\kappa }_{\beta }$ given for $a\in \mathbb{A}$ by

$${\kappa }_{\beta }(a)=\ln Z(\beta )+\beta \lambda (a).$$

(194)

Then this code is a member of $\mathrm{core}^({\mathbb{P}}^{{\kappa }_0})$ as is easily seen. In fact all members of the core are of this form (this fact can be proved as a kind of exercise in linear algebra, but more elegant proofs using the structure of the problem should be possible). If we can adjust the parameter $\beta$ such that the corresponding distribution $P_{\beta }$ given by

$$P_{\beta }(a)=\frac{\exp \left(-\beta \lambda (a)\right)}{Z(\beta )}\mathrm{for}a\in \mathbb{A}$$

(195)

is a member of the original preparation $\mathcal{P}$, this must be the maximum entropy distribution of $\mathcal{P}$, as follows from Theorem 6, translated to the $\widehat{Y}$-domain.

Schematically then: In searching for the MaxEnt distribution of a given preparation, first identify the preparation as a feasible preparation (of genus 1 or higher), then calculate if possible the appropriate partition function and finally adjust parameters to fit the original constraint(s). This gives you the MaxEnt distribution searched for. If calculations are prohibitive, you may resort to numerical, algorithmic or graphical methods instead.

As already mentioned, the literature very often solves MaxEnt-problems by the introduction of Lagrange multipliers. As shown, this is not necessary. An intrinsic approach building on the abstract theory of Section 2 appears preferable. For one thing, the fact that you obtain a maximum for the entropy function (and not just a stationary point) is automatic—it is all hidden in the fundamental inequality. For another, the quantities you work with when appealing to the abstract theory, have natural interpretations.

3.8. Determining D-Projections

The setting is basically the same as in the previous section, especially we again consider a preparation $\mathcal{P}$ given by (191). The problem we shall consider is how to update a given prior $Q_0\in M_{+}^1(\mathbb{A})$. Then, the triple $(\mathsf{\Phi },\mathrm{H},\mathrm{D})$ given by (185) is no longer relevant but should be replaced by the triple $({\mathrm{U}}_{|Q_0},{\mathrm{D}}^{Q_0},\mathrm{D})$ as defined in Section 2.8, cf., (21). This makes good sense if ${\mathrm{D}}^{Q_0}$ is finite on $\mathcal{P}$. The update we seek is the D-projection of $Q_0$ on $\mathcal{P}$ as defined in Section 2.13 in connection with (66).

We shall apply much the same strategy as in the previous section. However, we choose not to introduce response and an action space in this setting (this can be done with controls consisting of code improvements which are code length functions measured relative to the code ${\kappa }_0$ associated with $Q_0$). Instead, we work directly in the Y-domain and seek a representation of $\mathcal{P}$ as a strict feasible preparation of genus 1, now to be understood with respect to ${\mathrm{U}}_{|Q_0}$. Analyzing what this amounts to, we find that if the partition function, now defined by

$$Z(\beta )=\sum _{a\in \mathbb{A}}{Q}_0(a)\exp (-\beta \lambda (a)),$$

(196)

converges for some $\beta <\infty$, a representation as required is indeed possible. Assuming that this is the case we realize that for each $\beta$ with $Z(\beta )<\infty$, the distribution $Q_{\beta }$ defined by

$$Q_{\beta }(a)=\frac{Q_0(a)\exp (-\beta \lambda (a))}{Z(\beta )}\mathrm{for}a\in \mathbb{A}$$

(197)

is a member of the core of $\mathcal{P}$. Then it is a matter of adjusting $\beta$ such that $Q_{\beta }$ is consistent, and we have found the sought update.

The cancellation that takes place from (20) to (21) allows an extension of the discussion of updating from the discrete setting to a setting based on a general measurable space. For instance, one may consider a measurable space provided with a $\sigma$-finite reference measure $\mu$ and then work with distributions that have densities with respect to $\mu$. As is well known, cf., also Section 3.1, the definition of Kullback-Leibler divergence makes good sense in the more general setting. Thus updating problems can be formulated quite generally. If the prior has density $q_0$, the partition function one should work with is given by $Z(\beta )=\int \exp (-\beta \lambda )q_{0}d\mu$. Strategies for updating may be formulated much in analogy with the strategies of Section 3.7. Further details and consideration of concrete examples are left to the interested reader.

4. Conclusions

The theory presented provides a general abstract framework for the treatment of a wide range of optimization problems within geometry, statistics, statistical physics and other disciplines. Looking back, considering the methods applied and the demonstrated wide applicability, two factors seem to be essential, the type of modeling and affinity. Regarding the modeling, the key focus was on our information triples involving three interrelated quantities, effort, entropy and divergence—dually, utility, max-utility and divergence—each one being in itself of great significance and seen together playing distinct well-defined roles.

Regarding the focus on affinity, it is true that for the basic theoretical results this is not necessary. However, for almost every successful concrete application, affinity seems to pop up and appears both as a necessity and as a guarantee of success. There is something fundamental about this—possibly rooted in deep facts concerning the essential nature of observation, description and measuring.

On the theoretical side, one should note the emphasis placed on Jensen-Shannon divergence.

The game theoretical approach expressing the “man/system” or, as here, the “Observer/Nature” interface has played a major role. It has led to minimax and maximin problems. Adding convexity, it is an empirical fact that interesting and tractable optimization problems of this nature either concerns a minimax or a maximin problem for which the first optimization is easy to solve. This aspect is also present in our modeling through the linking identity and the fundamental inequality. Thus, for fixed second argument, minimal effort in our basic models is a quantity given by assumptions made and called entropy.

The extensive appeal to loose, sometimes speculative philosophical considerations is another pronounced feature of the exposition. This is intended as a guide to sensible model building and may also catalyze the consideration of meaningful applications to look into.

Other attempts to build quite general theories in this area of science include Jaynes [9], Csiszár and Matús [67], Amari and Nagaoka [10] and then the recent work of Pavon and Ferrante [102]. In the latter we find a focus on the same kind of issues as we have promoted, simplicity of modeling and affinity. With simplicity also, as here, pointing to the unnecessary appeal to techniques involving Lagrange multipliers. The base for the modeling of Pavon and Ferrante is geometry via a lemma of geometric orthogonality. So, as “models of the world” these authors, as well as Amari and Nagaoka and their followers take geometry, whereas we take a more “social” approach via game theory, emphasizing man’s role in the world.

We believe that the approach presented here is technically the more elementary one.

Along the way, our approach gave rise to a few points worth emphasizing. A modeling of what can be known (Section 2.9) appears to be a useful concept. The suggested weak notions of properness in Section 2.11 is new whereas the material in Appendix A, which serves as a partial justification, may well be common knowledge. The notion of deformation introduced in Section 2.5 and its role in the discussion of Tsallis entropy in Section 3.6 has been announced before but is here given a more full treatment, also incorporating a Bregman construction in Section 3.1. Regarding the discussion of Tsallis entropy also note the emphasis on the descriptors ${\kappa }_q$.

Many issues are left for further discussion and consolidation of the theory. Some of the possibilities are indicated in the text. Others involve a look at sufficiency, duality, mutual information, learning theory and more. Much of this appears feasible. However, there is an important area where we do not see that our approach and results provide any clue, viz., quantum information theory. Let this challenge to the reader be the last word for now.