Oscillations in Multiparticle Production Processes ^†

Abstract

We discuss two examples of oscillations apparently hidden in some experimental results for high-energy multiparticle production processes: (i) the log-periodic oscillatory pattern decorating the power-like Tsallis distributions of transverse momenta; (ii) the oscillations of the modified combinants obtained from the measured multiplicity distributions. Our calculations are confronted with $pp$ data from the Large Hadron Collider (LHC). We show that in both cases, these phenomena can provide new insight into the dynamics of these processes.

1. Introduction

In this work, we argue that closer scrutiny of the available experimental results from Large Hadron Collider (LHC) experiments can result in some new, so-far unnoticed (or underrated) features, which can provide new insight into the dynamics of the processes under consideration. More specifically, we shall concentrate on multiparticle production processes at high energies and on two examples of hidden oscillations apparently visible there: (i) the log-periodic oscillations in data on the large transverse momenta spectra, $f \left(p_T\right)$ (presented in Section 2); (ii) the oscillations of some coefficients in the recurrence relation defining the multiplicity distributions, $P(N)$ (presented in Section 3).

As will be seen, the first phenomenon is connected with the fact that large $p_T$ distributions follow a quasi power-like pattern, which is best described by the Tsallis distribution [1,2,3]:

$$f \left(p_T\right)=C {\left(1+\frac{p_T}{nT}\right)}^{-n},n=\frac{1}{q-1}$$

(1)

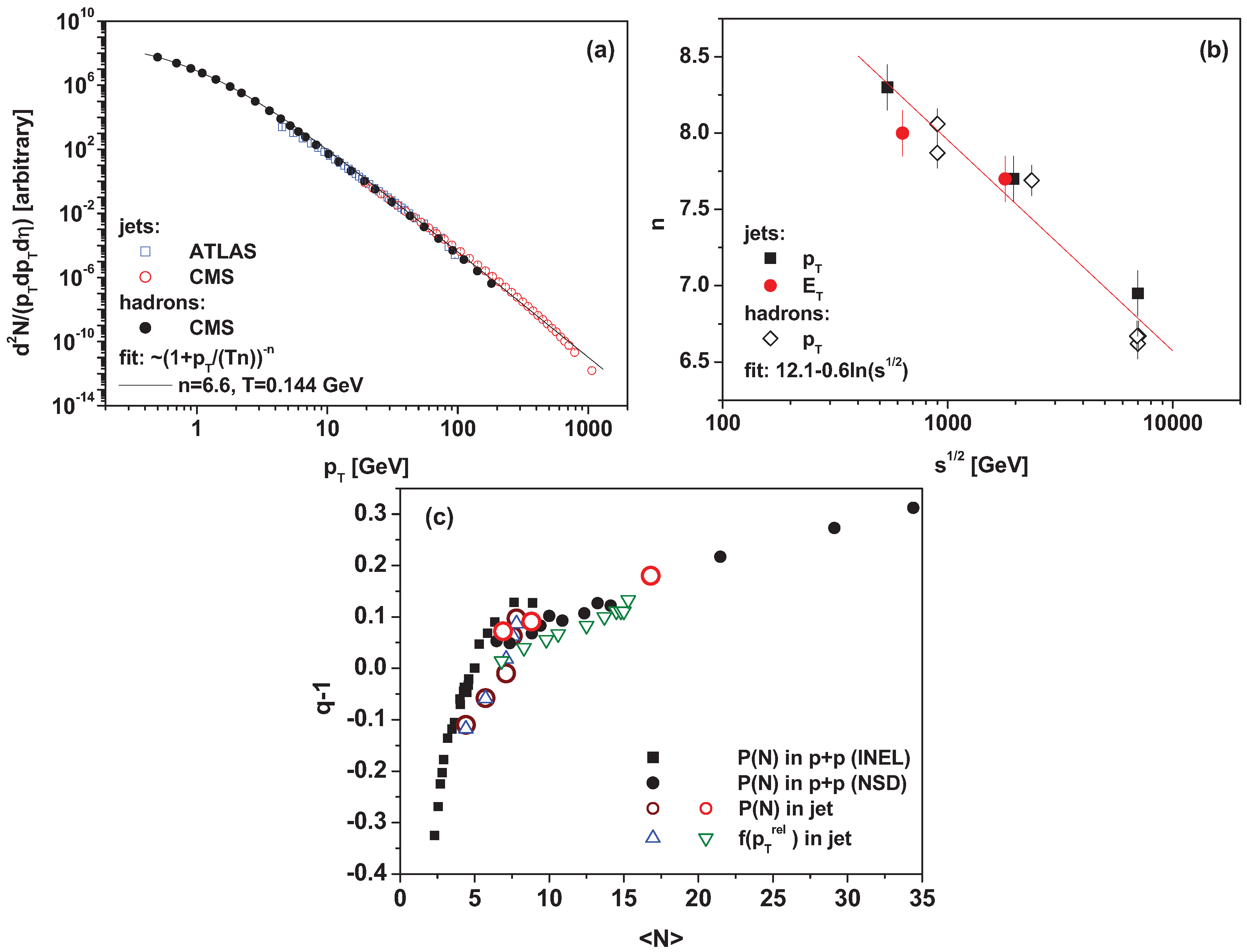
This is a quasi power-law distribution with two parameters: power index n (connected with the nonextensivity parameter q) and scale parameter T (in many applications identified with temperature) [3]. In Figure 1, we present examples of applications of the nonextensive approach to multiparticle distributions represented by Equation (1). Figure 1a,b show the high-quality Tsallis fit as well as a kind of self-similarity of $p_T$ distributions of jets and hadrons [4]. Figure 1c demonstrates that the values of the nonextensivity parameters q for particles in jets correspond rather closely to values of q obtained from the inclusive distributions measured in $pp$ collisions [4,5]. (This observation should be connected with the fact that multiplicity distributions, $P(N)$, are closely connected with the nonextensive approach, and that $q-1=Var(N)/{<N>}^2-1/<N>$ for negative binomial distributions (NBDs), Poisson distributions (PDs) and binomial distributions (BDs) [5]). In general, one observes the self-similar characteristics of the production process, in both cases originating from their cascading characteristic, which always results in a Tsallis distribution. (In fact, this is a very old idea, introduced by Hagedorn in [6,7], that the production of hadrons proceeds through the formation of fireballs, which produces a statistical equilibrium of an undetermined number of all kinds of fireballs, each of which in turn is considered to be a fireball. This idea returned recently in the form of thermofractals introduced in [8]. We note that the NBD discussed below also has a self-similar character [9]. We note also that the self-similarity and fractality features of the multiparticle production process were exhaustively discussed in [10,11].). In the pure dynamical QCD approach to hadronization, one could think of partons fragmenting into final-state hadrons through multiple sub-jet production [11].

2. Log-Periodic Oscillations in Data on Large $p_T$ Momenta Distributions

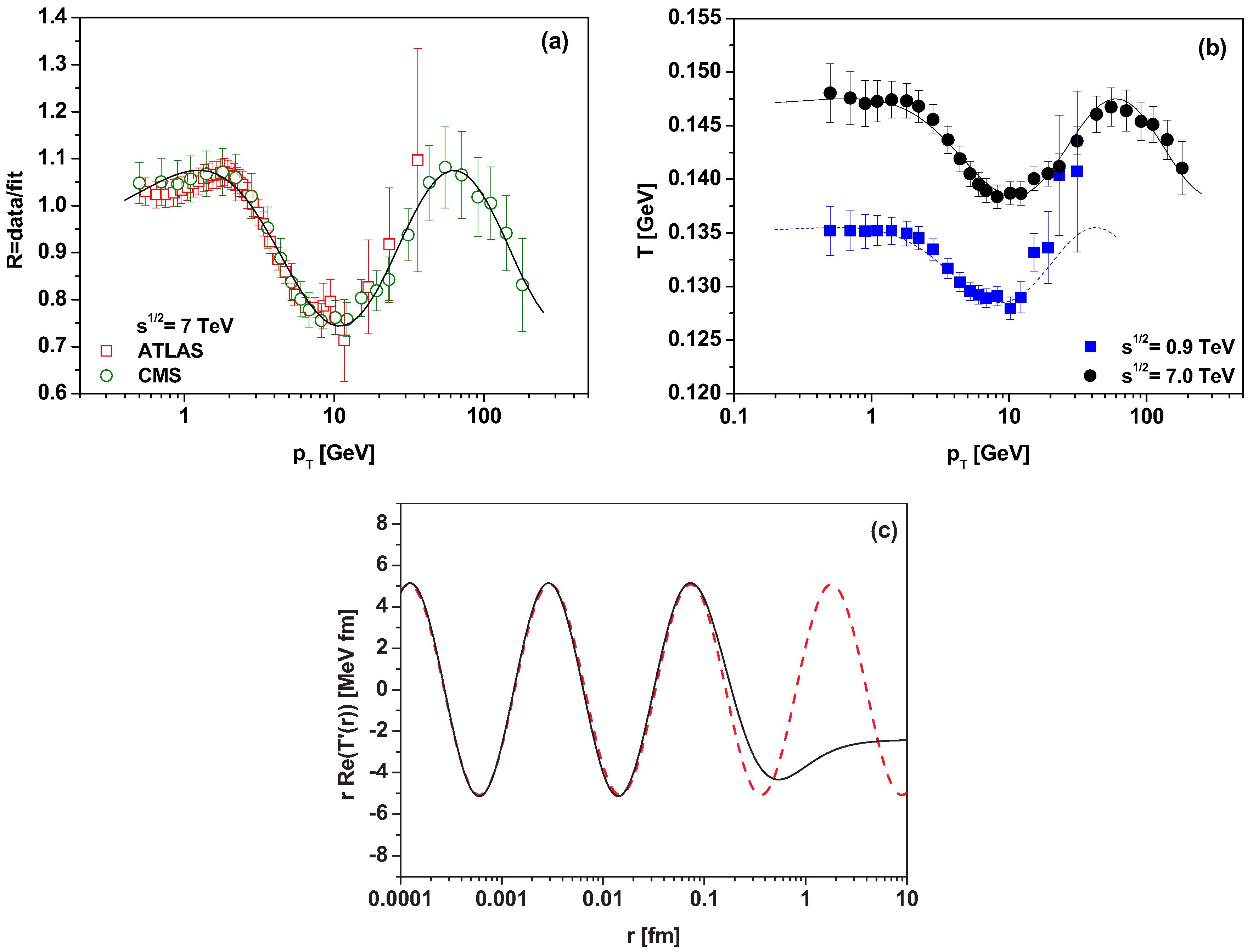
To start with the first example, we note that, despite the exceptional quality of the Tsallis fit presented in Figure 1a (in fact, only such a two-parameter quasi-power-like formula can fit the data over the whole range of $p_T$), the ratio $R=data/fit$ (which is expected to be a flat function of $p_T$, $R\left(p_T\right)\sim 1$) presented in Figure 2a shows clear log-periodic oscillatory behaviour as a function of the transverse momentum $p_T$. In fact, it turns out that such behaviour occurs (at the same strength) in data from all LHC experiments, at all energies (provided that the range of the measured $p_T$ is large enough), and that its amplitude increases substantially for the nuclear collisions [21]. These observations strongly suggest that closer scrutiny should be undertaken to understand its possible physical origin.

We note that we have two parameters in the Tsallis formula (Equation (1)), n and T, and each of them (or both, but we do not consider such a situation) could be a priori responsible for the observed effect. We start with the power index n. In this case, the observed oscillations may be related to some scale invariance present in the system and are an immanent feature of any power-like distribution [23]. In [24], we showed that they also appear in quasi-power-like distributions of the Tsallis type. In general, they are attributed to a discrete scale invariance (connected with a possible fractal structure of the process under consideration) and are described by introducing a complex power index n (or q). This, in turn, has a number of interesting consequences [25,26,27], such as a complex heat capacity of the system or complex probability and complex multiplicative noise, all of these known already from other branches of physics. In short, one relies on the fact that power-like distributions, say $O(x)=C{x}^{-m}$, exhibit scale invariant behaviour, $Q(\lambda x)=\mu O(x)$, where parameters $\lambda$ and $\mu$ are, in general, related by the condition that $\mu {\lambda }^m=1=\exp (2\pi ik),k=0,1,2,\cdots$, which means that the power index m can take complex values: $m=-\frac{\ln \mu }{\ln \lambda }+i\frac{2\pi k}{\ln \lambda }$. In the case of a Tsallis distribution, this means that Equation (1) is decorated by some oscillating factor $R\left(p_T\right)$, the form of which (when keeping only the $k=0$ and $k=1$ terms) is

$$R\left(p_T\right)=a+b\left[\cos \left(p_T+d\right)+f\right]$$

(2)

As one can see in Figure 2, this perfectly fits the observed log-oscillatory pattern.

The second possibility is to keep n constant but allow the scale parameter T to vary with $p_T$ in such a way as to allow a fit to the data on $R\left(p_T\right)$ [27]. The result is shown in Figure 2b. The resulting $T\left(p_T\right)$ has the form of log-periodic oscillations in $p_T$, which can be parameterized by

$$T\left(p_T\right)=\tilde{a}+\tilde{b}\left[\sin \left(p_T+\tilde{d}\right)+\tilde{f}\right]$$

(3)

Such behaviour of $T\left(p_T\right)$ can originate from the well-known stochastic equation for the temperature evolution, which in the Langevin formulation has the following form:

$$\frac{dT}{dt}+\frac{1}{\tau }T+\xi (t)=\Phi$$

(4)

where $\tau$ is the relaxation time and $\xi (t)$ is time-dependent white noise. Assuming additionally that we have time-dependent transverse momentum $p_T=p_T(t)$ increasing in a way following the scenario of the preferential growth of networks [28],

$$\frac{d{p}_T}{dt}=\frac{1}{{\tau }_0}\left(\frac{p_T}{n}\pm T\right)$$

(5)

where n is the power index and ${\tau }_0$ is some characteristic time-step, one may write

$$\frac{1}{{\tau }_0}\left(\frac{p_T}{n}\pm T\right)\frac{dT}{d{p}_T}+\frac{1}{\tau }T+\xi (t)=\Phi$$

(6)

Equation (3) is obtained in two cases: (i) The noise term increases logarithmically with $p_T$ while the relaxation time $\tau$ remains constant:

$$\xi \left(t,p_T\right)={\xi }_0(t)+\frac{{\omega }^2}{n}\ln \left(p_T\right)$$

(7)

(ii) The white noise is constant, $\xi \left(t,p_T\right)={\xi }_0(t)$, but the relaxation time becomes $p_T$-dependent, for example,

$$\tau =\tau \left(p_T\right)=\frac{n{\tau }_0}{n+{\omega }^2\ln \left(p_T\right)}$$

(8)

In both cases $\omega$ is some new parameter [3,27]. (To fit data, one needs only a rather small admixture of the stochastic processes with noise depending on $p_T$. The main contribution comes from the usual energy-independent Gaussian white noise. We note that whereas each of the proposed approaches is based on a different dynamical picture, they are numerically equivalent.).

However, we can use Equation (3) in a way that allows us to look deeper into our dynamical process. To this end, we calculate the Fourier transform of $T\left(p_T\right)$ presented there:

$$T(r)=\sqrt{\frac{2}{\pi }}{\int }_0^{\infty }T\left(p_T\right)e^{i{p}_{T}r}d{p}_T=T_0+T^{\prime }(r)$$

(9)

One can see now how the temperature T (more exactly, its part that varies with r, $T^{\prime }(r)$) changes with distance r from the collision axis (defined in the plane perpendicular to the collision axis and located at the collision point). The result of this operation is seen in Figure 2c as specific log-periodic oscillations in $p_T$. Such behaviour can be studied by considering the flow of a compressible fluid in a cylindrical source. Assuming oscillations with small amplitude and velocity $\mathit{v}$, and introducing the velocity potential f such that $\mathit{v}=\mathit{grad}f$, one finds that f must satisfy the following cylindrical wave equation:

$$\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial f}{\partial r}\right)-\frac{1}{c^2}\frac{{\partial }^{2}f}{\partial t^2}=0$$

(10)

It can be shown that this represents a travelling sound wave with velocity $\mathit{v}$ in the direction of propagation. Because the oscillating part of the temperature, $T^{\prime }$, is related to the velocity v, then

$$T^{\prime }=\frac{c\kappa T}{c_P}v$$

(11)

where $\kappa =\frac{1}{V}{\left(\frac{\partial V}{\partial T}\right)}_P$ is the coefficient of thermal expansion and $c_P$ denotes the specific heat at constant pressure [29]; in the case of a monochromatic wave where $f(r,t)=f(r)\exp (-i\omega t)$, we have that

$$\frac{{\partial }^{2}f(r)}{\partial r^2}+\frac{1}{r}\frac{\partial f(r)}{\partial r}+K^{2}f(r)=0,K=K(r)=\frac{\omega }{c(r)}$$

(12)

with K being the wave number depending in general on r. For

$$K(r)=\frac{\alpha }{r}$$

(13)

the solution of Equation (12) takes the form of some log-periodic oscillation:

$$f(r)\propto \sin [\alpha \ln (r)]$$

(14)

Because in our case $f(r)\propto vr$, using Equation (11), we can write that

$$r{T}^{\prime }(r)\propto \frac{c\kappa T_0}{c_P}f(r)=\frac{c\kappa T_0}{c_P}\sin [\alpha \ln (r)]$$

(15)

which is what we have used in describing the $T^{\prime }(r)$ presented in panel (c) of Figure 2. The space picture of the collision (in the plane perpendicular to the collision axis and located at the collision point) that emerges is some regular logarithmic structure for small distances, which disappears when r reaches the dimension of the nucleon, that is, for r ∼ 1 fm. Whether it is connected with the parton structure of the nucleon remains for the moment an open question.

To end this section, we note that Equation (12) with $K(r)$ given by Equation (13) is scale invariant and that $f(\lambda r)=f(r)$. We note also that in the variable $\xi =\ln r$, Equation (12) is also self-similar because in this variable, it takes the form of the traveling wave equation:

$$\frac{{\partial }^{2}F(\xi )}{\partial {\xi }^2}+{\alpha }^{2}F(\xi )=0$$

(16)

which has the self-similar solution

$$F(\xi )\propto \cos [\alpha \xi ]$$

(17)

for which $F(\xi +\ln \lambda )=F(\xi )$ (with $\alpha =\frac{2\pi k}{\ln \lambda }$ or $\lambda =\exp \left(\frac{2\pi k}{\alpha }\right)$, where $k=1,2,3,\dots$). This is the self-similar solution of the second kind, usually encountered in the description of the intermediate asymptotic. Such asymptotics are observed in phenomena that do not depend on the initial conditions because sufficient time has already passed; nevertheless the system considered is still out of equilibrium [30].

3. Oscillations Hidden in the Multiplicity Distributions Data

Whereas the previous section is concerned with oscillations hidden in the distributions of produced particles in transverse momenta $f\left(p_T\right)$ (which by using the Fourier transformation allows us to gain some insight into the space picture of the interaction process), in this section, we concentrate on another important characteristic of the multiparticle production process, namely, on the question of how many particles are produced and with what probability, that is, on the multiplicity distribution function $P(N)$, where N is the observed number of particles. This is usually one of the first observables measured in any multiparticle production experiment [11].

At first we note that any $P(N)$ can be defined in terms of some recurrence relation, the most popular takes the following form:

$$(N+1)P(N+1)=g(N)P(N)\mathrm{where}g(N)=\alpha +\beta N$$

(18)

Such a linear form of $g(N)$ leads to a NBD, BD or PD:

$$\begin{array}{cc}\hfill NBD:& P(N)=\frac{\Gamma (N+k)}{\Gamma (N+1)\Gamma (k)}{p}^N{(1-p)}^k\mathrm{with}\alpha =kp,\beta =\frac{\alpha }{k}\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill BD:& P(N)=\frac{K!}{N!(K-N)!}{p}^N{(1-p)}^{K-N}\mathrm{with}\alpha =\frac{Kp}{1-p},\beta =-\frac{\alpha }{K}\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill PD:& P(N)=\frac{{\lambda }^N}{N!}\exp (-\lambda )\mathrm{with}\alpha =\lambda ,\beta =0\hfill \end{array}$$

(21)

Suitable modifications of $g(N)$ result in more involved distributions $P(N)$ (cf. [31] for references).

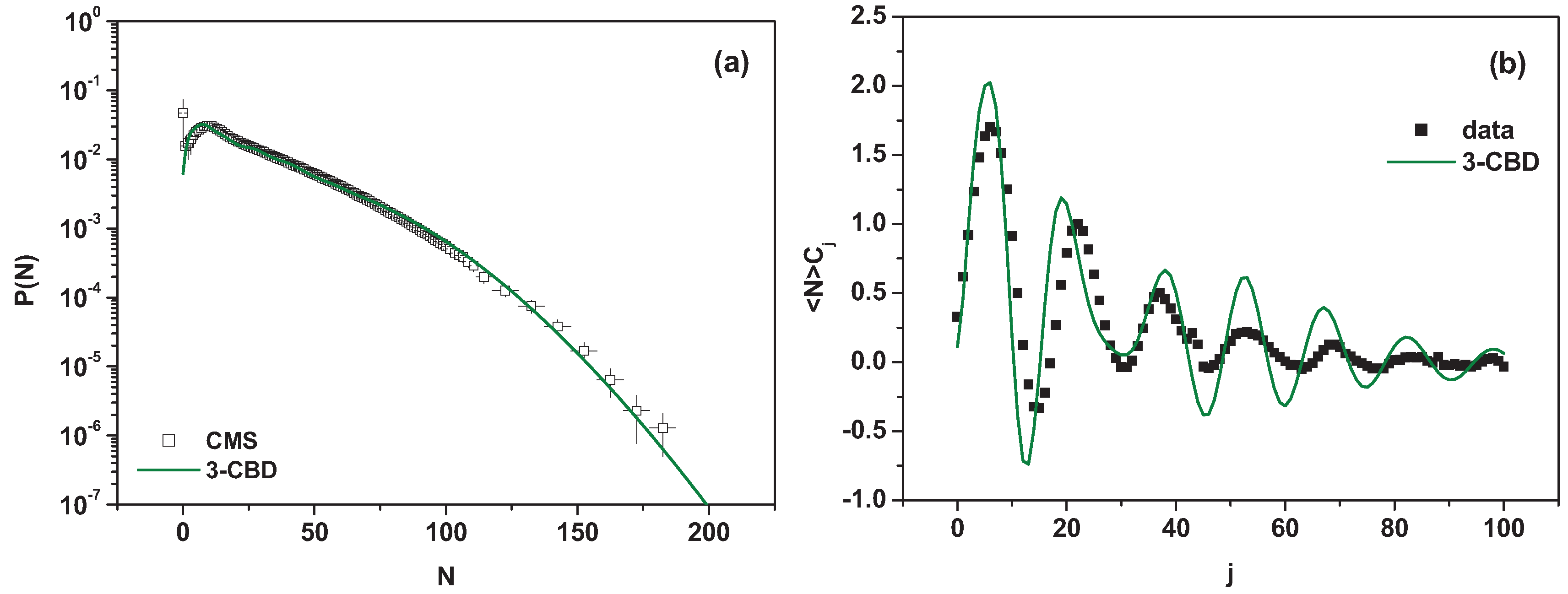
The most popular form of $P(N)$ is the NBD type of distribution, Equation (19). However, with a growing energy and number of produced secondaries, the NBD starts to deviate from data for large N, and one has to use combinations of NBDs (two [32], three [33] and multicomponent NBDs [34] were proposed) or try to use some other form of $P(N)$ [11,35,36]. For example, in Figure 3a, a single NBD is compared with a two-NBD. However, as shown there, the improvement, although substantial, is not completely adequate. It is best seen when looking at the ratio $R=P_{CMS}(N)/P_{fit}(N)$, which still shows some wiggly structure (albeit substantially weaker than in the case of using only a single NBD to fit the data). Taken seriously, this observation suggests that there is some additional information hidden in the $P(N)$. The question of how to retrieve this information was addressed in [31] by resorting to a more general form of Equation (18) usually used in counting statistics when dealing with cascade stochastic processes [37] in which all multiplicities are connected. In this case, one has coefficients $C_j$ defining the corresponding $P(N)$ in the following way:

$$(N+1)P(N+1)=\langle N\rangle {\displaystyle \sum _{j=0}^N}{C}_{j}P(N-j)$$

(22)

These coefficients contain the memory of particle $N+1$ about all $N-j$ previously produced particles. Assuming now that all $P(N)$ are given by experiment, one can reverse Equation (22) and obtain a recurrence formula for the coefficients $C_j$:

$$\langle N\rangle C_j=(j+1)\left[\frac{P(j+1)}{P(0)}\right]-\langle N\rangle {\displaystyle \sum _{i=0}^{j-1}}\left[\frac{P(j-i)}{P(0)}\right]$$

(23)

As can be seen in Figure 3c, the coefficients $C_j$ obtained from the data presented in Figure 3a show oscillatory behaviour (with period roughly equal to 16) gradually disappearing with N. They can be fitted by the following formula:

$$\langle N\rangle C_j={\left(a^2+b^2\right)}^{j/2}\sin \left[c+j \arctan (b/a)\right]+d^j$$

(24)

with parameters $a=0.89$, $b=0.37$, $c=5.36$, and $d=0.95$. Such oscillations do not appear in the single NBD fit presented in Figure 3a, and there is only a small trace of oscillations for the two-NBD fit presented in Figure 3a. This is because for a single NBD, one has a smooth exponential dependence of the corresponding $C_j$ on the rank j:

$$C_j=\frac{k}{\langle N\rangle }{p}^{j+1}=\frac{k}{k+m}\exp (j \ln p)$$

(25)

and one can expect any structure only for the multi-NBD cases [31].

Before proceeding further we note that the coefficients $C_j$ are closely related to the combinants $C_j^{\star }$, which were introduced in [40] (see also [11,41,42]) and are defined in terms of the generating function $G(z)$ as

$$C_j^{\star }=\frac{1}{j!}\frac{d^j\ln G(z)}{d{z}^j}{|}_{z=0},\mathrm{where}G(z)={\displaystyle \sum _{N=0}^{\infty }}P(N)z^N$$

(26)

or by the following relation [31]:

$$\ln G(z)=\ln P(0)+{\displaystyle \sum _{j=1}^{\infty }}{C}_j^{\star }{z}^j$$

(27)

From the above, one can deduce the following [31]:

$$C_j=\frac{j+1}{\langle N\rangle }{C}_{j+1}^{\star }$$

(28)

This means that one can rewrite the recurrence relation, Equation (22), in terms of the combinants $C_j^{\star }$:

$$(N+1)P(N+1)={\displaystyle \sum _{j=0}^N}(j+1)C_j^{\star }P(N-j)$$

(29)

When compared with Equation (22), this allows us to express our coefficients $C_j$, which henceforth we shall call modified combinants, by the generating function $G(z)$ of $P(N)$:

$$\langle N\rangle C_j=\frac{1}{j!}\frac{d^{j+1}\ln G(z)}{d{z}^{j+1}}{|}_{z=0}$$

(30)

This is the relation we use in the following when calculating the $C_j$ from distributions defined by some $G(z)$.

To continue our reasoning, we note first that whereas a single NBD does not lead to oscillatory behaviour of the modified combinants $C_j$, there is a distribution for which the corresponding $C_j$ oscillate in a maximum way. This is the BD for which the modified combinants are given by the following formula:

$$C_j={(-1)}^j\frac{K}{\langle N\rangle }{\left(\frac{\langle N\rangle }{K-\langle N\rangle }\right)}^{(j+1)}=\frac{{(-1)}^j}{1-p}{\left(\frac{p}{1-p}\right)}^j$$

(31)

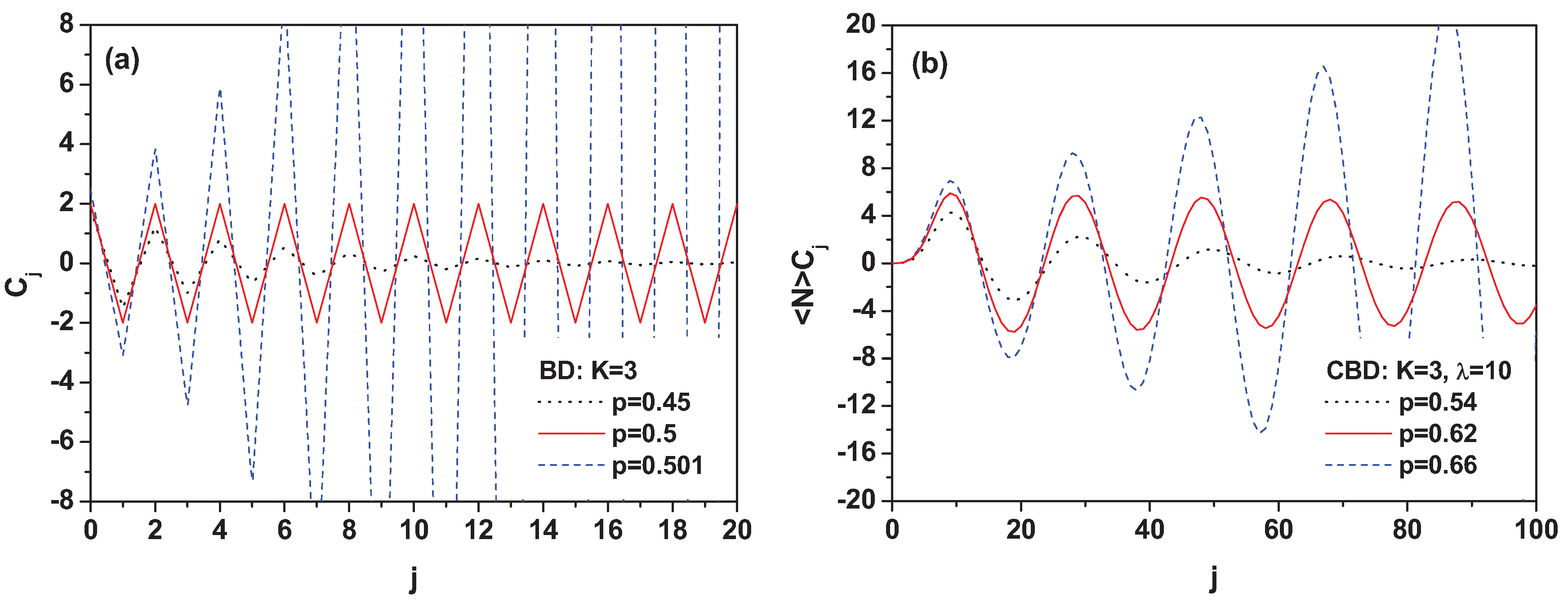
which oscillates rapidly with a period equal to 2. In Figure 4a, one can see that the amplitude of these oscillations depends on p; generally the $C_j$ increase with rank j for $p>0.5$ and decrease for $p<0.5$. However, their general shape lacks the fading-down feature of the $C_j$ observed experimentally. This suggests that the BD alone is not enough to explain the data but must be somehow combined with some other distribution. (In fact, in [43], we have already used a combination of elementary emitting cells (EECs) producing particles following a geometrical distribution (our aim at that time was to explain the phenomenon of Bose–Einstein correlations). For a constant number k of EECs, one obtains the NBD as the resultant $P(N)$, whereas for k distributed according to the BD, the resulting $P(N)$ is a modified NBD. However, we could not find a set of parameters providing both the observed $P(N)$ and oscillating $C_j$. We note that originally, the NBD was seen as a compound PD, with the number of clusters given by a PD and the particle inside the clusters distributed according to a logarithmic distribution [44].).

We resort therefore to the idea of compound distributions (CDs) [45], which, from the point of view of the physics involved in our case, could for example describe a production process in which a number M of some objects (clusters, fireballs, etc.) are produced following, in general, some distribution $f(M)$ (with generating function $F(z)$), and subsequently decay independently into a number of secondaries, $n_{i=1,\cdots ,M}$, always following some other (the same for all) distribution $g(n)$ (with a generating function $G(z)$). The distribution $h(N)$, where

$$N={\displaystyle \sum _{i=0}^M}{n}_i$$

(32)

is a CD of f and g: $h=f\otimes g$. For CDs, we have that

$$\langle N\rangle =\langle M\rangle \langle n\rangle \mathrm{and}Var(N)=\langle M\rangle Var(n)+Var(M){\langle n\rangle }^2$$

(33)

and its generating function $H(z)$ is equal to

$$H(z)=F[G(z)]$$

(34)

It should be mentioned that for the class of distributions of M that satisfy our recursion relation, Equation (18), the CD $h=f\otimes g$ is given by Panjer’s recursion relation [46]:

$$Nh(N)={\displaystyle \sum _{j=1}^N}[\beta N+(\alpha -\beta )j]g(j)h(N-j)={\displaystyle \sum _{j=1}^N}{C}_j^{(P)}(N)h(N-j)$$

(35)

with the initial value $h(0)=f(0)$. However, the coefficients $C_j^{(P)}$ occurring here depend on N, contrary to our recursion given by Equation (22), for which the modified combinants, $C_j$, are independent of N. Moreover, Equation (22) is not limited to the class of distributions satisfying Equation (18) but is valid for any distribution $P(N)$. For this reason, the recursion relation, Equation (35), is not suitable for us.

To visualize the CD in action, we take for f a BD with generating function $F(z)={(pz+1-p)}^K$, and for g we take a PD with generating function $G(z)=\exp [\lambda (z-1)]$. The generating function of the resultant distribution is now equal to

$$H(z)={\left\{p\exp [\lambda (z-1)]+1-p\right\}}^K$$

(36)

and the corresponding modified combinants are

$$\begin{array}{cc}\hfill \langle N\rangle C_j& =\frac{K{\lambda }^{j+2}\exp (-\lambda )}{j!}{\displaystyle \sum _{i=1}^{j+2}}{\left[\frac{p}{1-p+p\exp (-\lambda )}\right]}^i\frac{1}{i}{\displaystyle \sum _{k=0}^i}{(-1)}^{k+1}\left(\genfrac{}{}{0pt}{}{i}{k}\right)k^{j+1}=\hfill \\ & =\frac{K{\lambda }^{j+2}\exp (-\lambda )}{j!}{\displaystyle \sum _{i=1}^{j+2}}{\left[\frac{p}{1-p+p\exp (-\lambda )}\right]}^{i}S(j+1,i)\hfill \end{array}$$

(37)

where

$$S(n,k)=\left\{\begin{array}{c}n\\ k\end{array}\right\}=\frac{1}{k!}{\displaystyle \sum _{i=0}^k}{(-1)}^{k-i}\left(\genfrac{}{}{0pt}{}{k}{i}\right)i^n$$

(38)

is the Stirling number of the second kind. Figure 4b shows the above modified combinants for the compound binomial distribution (CBD; a combination of a BD with a PD) with $K=3$ and $\lambda =10$ calculated for three different values of p in the BD: $p=0.54,0.62,0.66$. We note that in general, the period of the oscillations is equal to $2\lambda$, that is, in Figure 4b, where $\lambda =10$ it is equal 20. The multiplicity distribution in this case is

$$\begin{array}{ccc}\hfill P(0)& =& {\left(1-p+p{e}^{-\lambda }\right)}^K\hfill \end{array}$$

(39)

$$\begin{array}{ccc}\hfill P(N)& =& \frac{1}{N!}\frac{d^{N}H(z)}{d{z}^N}{|}_{z=0}=\frac{1}{N!}{\displaystyle \sum _{i=1}^K}i!\left(\genfrac{}{}{0pt}{}{K}{i}\right){\left(\lambda p{e}^{-\lambda }\right)}^i{\left(1-p+p{e}^{-\lambda }\right)}^{K-i}S(N,i)\hfill \end{array}$$

(40)

The proper normalization comes from the fact that $H(1)=1$. This shows that the choice of a BD as the basis of the CDs to be used seems to be crucial to obtain oscillatory $C_j$ (e.g., a CD formed from a NBD and some other NBD provides smooth $C_j$).

Unfortunately, such a single component CBD (depending on three parameters: p, K and $\lambda$; $P(N)=h(N;p,K,\lambda )$ does not describe the experimental $P(N)$. We return therefore to the idea of using a multicomponent version of the CBD, for example, a three-component CBD defined as follows (with $w_i$ being weights):

$$P(N)={\displaystyle \sum _{i=1,2,3}}{w}_{i}h\left(N;p_i,K_i,{\lambda }_i\right);{\displaystyle \sum _{i=1,2,3}}{w}_i=1$$

(41)

As can be seen in Figure 5, in this case, the fit to $P(N)$ is quite good, and the modified combinants $C_j$ follow an oscillatory pattern as far as the period of the oscillations is concerned, albeit their amplitudes still decaying too slowly.

4. Summary

To summarize, we would like to mention that power law and quasi-power-law distributions are ubiquitous in many different, apparently very disparate, branches of science (such as, e.g., earthquakes, escape probabilities in chaotic maps close to crisis, biased diffusion of tracers in random systems, kinetic and dynamic processes in random quenched and fractal media, diffusion limited aggregates, growth models, or stock markets near financial crashes, to name only a few). Also ubiquitous is the fact that, in most cases, they are decorated with log-periodic oscillations of different kinds [23,24,26,27]. It is then natural to expect that oscillations of certain variables constitute a universal phenomenon, which should occur in a large class of stochastic processes, independently of the microscopic details. In this paper, we have concentrated on some specific oscillation phenomena seen at LHC energies in transverse momentum distributions. Their log-periodic characteristics suggest that either the exponent of the power-like behavior of these distributions is complex, or that there is a scale parameter that exhibits specific log-periodic oscillations. Whereas the most natural thing seems to be attributing the observed oscillations to some discrete scale invariance present in the system considered [23,24], it turns out that such scale-invariant functions also satisfy some specific wave equations showing a self-similarity property [21]. In both cases, these functions exhibit log-periodic behavior.

Concerning the second topic considered here, the presence of oscillations in counting statistics, one should realize that it is also a well-established phenomenon. The known examples include oscillations of the high-order cumulants of the probability distributions describing the transport through a double quantum dot, oscillations in quantum optics (in the photon distribution function in slightly squeezed states; see [47] for more information and references). In elementary particle physics, oscillations of the $H_q$ moments, which represent ratios of the cumulants to factorial moments, also have a long history [11,35,36].

Our expectation that the oscillations discussed here could also be observed (and successfully measured) in multiparticle production processes is new. To see these, one must first deduce from the experimental data on the multiplicity distribution $P(N)$ the modified combinants $C_j$ (which are defined by the recurrence relation presented in Equation (22); we note that, contrary to the $H_q$ moments, the $C_j$ are independent of the multiplicity distribution $P(N)$ for $N>j$). In the case for which these modified combinants show oscillatory behavior, they can be used to search for some underlying dynamical mechanism that could be responsible for it. The present situation is such that the measured multiplicity distributions $P(N)$ (for which, as we claim in [31], the corresponding modified combinants $C_j$ oscillate), are most frequently described by NBDs (the modified combinants of which do not oscillate). Furthermore, with increasing collision energy and increasing multiplicity of produced secondaries, some systematic discrepancies between the data and the NBD form of the $P(N)$ used to fit them become more and more apparent. We propose therefore to use a novel phenomenological approach to the observed multiplicity distributions on the basis of the modified combinants $C_j$ obtained from the measured multiplicity distributions. Together with the fitted multiplicity distributions $P(N)$, these would allow for a more detailed quantitative description of the complex structure of the multiparticle production process. We argue that the observed strong oscillations of the coefficients $C_j$ in the $pp$ data at LHC energies indicate the compound characteristics of the measured distributions $P(N)$ with a central role played by the BD, which provides the oscillatory characteristics of the $C_j$. This must be supplemented by some other distribution in such a way that the CD fits both the observed $P(N)$ and the $C_j$ deduced from it. However, at the moment, we are not able to obtain fits to both $P(N)$ and $C_j$ of acceptable quality. Therefore, these oscillations still await their physical justification, that is, the identification of some physical process (or combination of such processes) that would result in such phenomena.

We close by noting that both phenomena discussed here describe, in fact, different dynamical aspects of the multiparticle production process at high energies. The quasi-power-like distributions and the related log-periodic oscillations are related with events with rather small multiplicities of secondaries with large and very large momenta; these are called hard collisions, and they essentially probe the collision dynamics towards the edge of the phase space. The multiparticle distributions collect instead all produced particles, the majority of which come from the soft collisions concentrated in the middle of the phase space. In this sense, both the phenomena discussed provide us with complementary new information on these processes and, because of this, they should be considered, as much as possible, jointly. (Because of some similarities observed between hadronic, nuclear and $e^{+}{e}^{-}$ collisions [11,48,49] (see also Chapter 20 of [50]), one might expect that the phenomena discussed above will also appear in these reactions. However, this is a separate problem, too extensive and not yet sufficiently discussed to be presented here).