Construction of New Fractional Repetition Codes from Relative Difference Sets with λ=1
Abstract
:1. Introduction
2. Preliminaries
2.1. Regenerating Codes and Fractional Repetition Codes
- 1.
- The cardinality of each is α.
- 2.
- Each element of Ω is contained in exactly ρ sets in N.
- 3.
- Let denote any -sized subset of N and . Each is β-recoverable from some d-sized subset of . Let be the maximum value of τ such that this property holds.
2.2. Relative Difference Sets and q-Ary m-Sequences
3. The Proposed FR Codes
3.1. Construction of FR Codes from RDSs
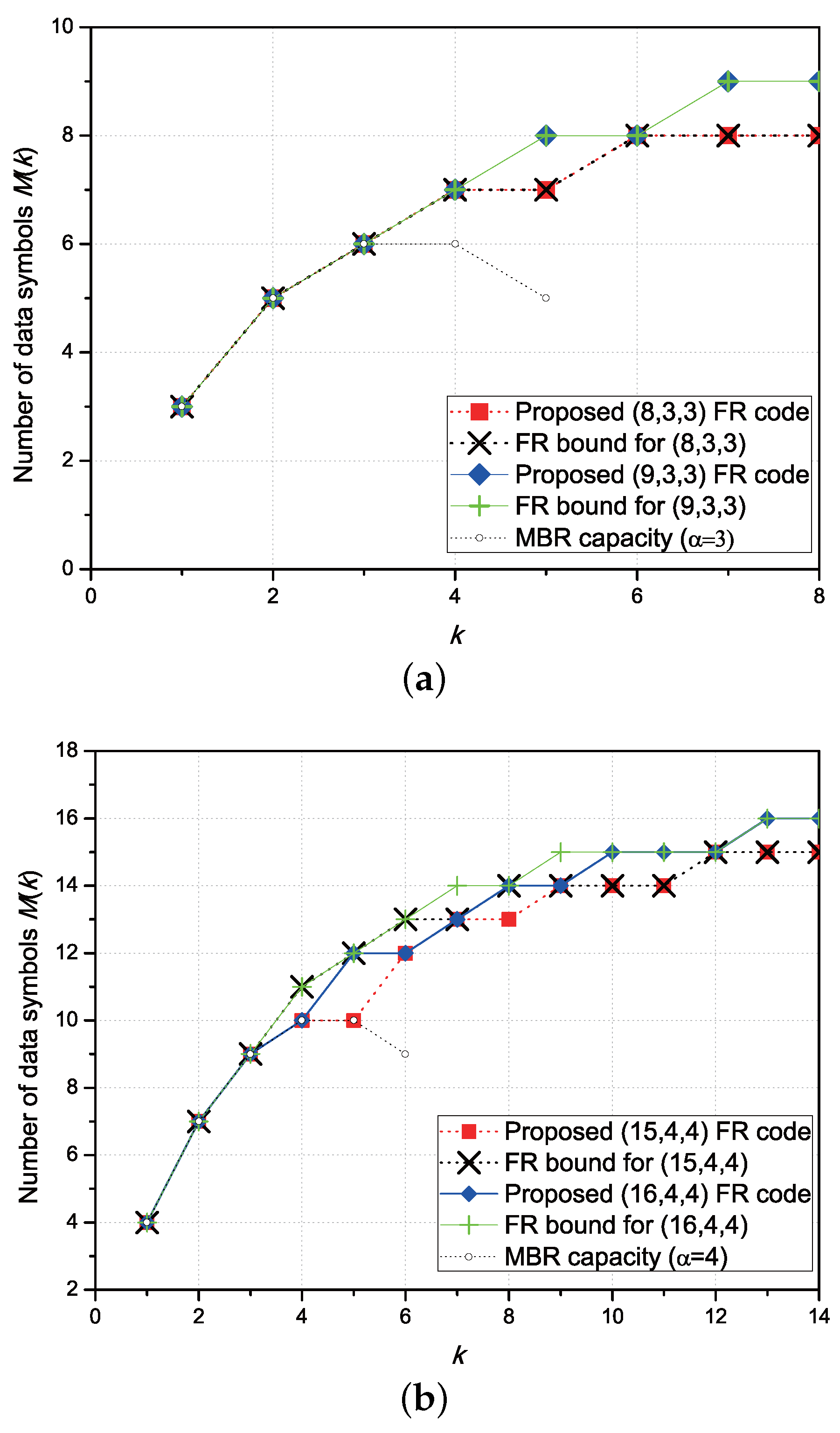
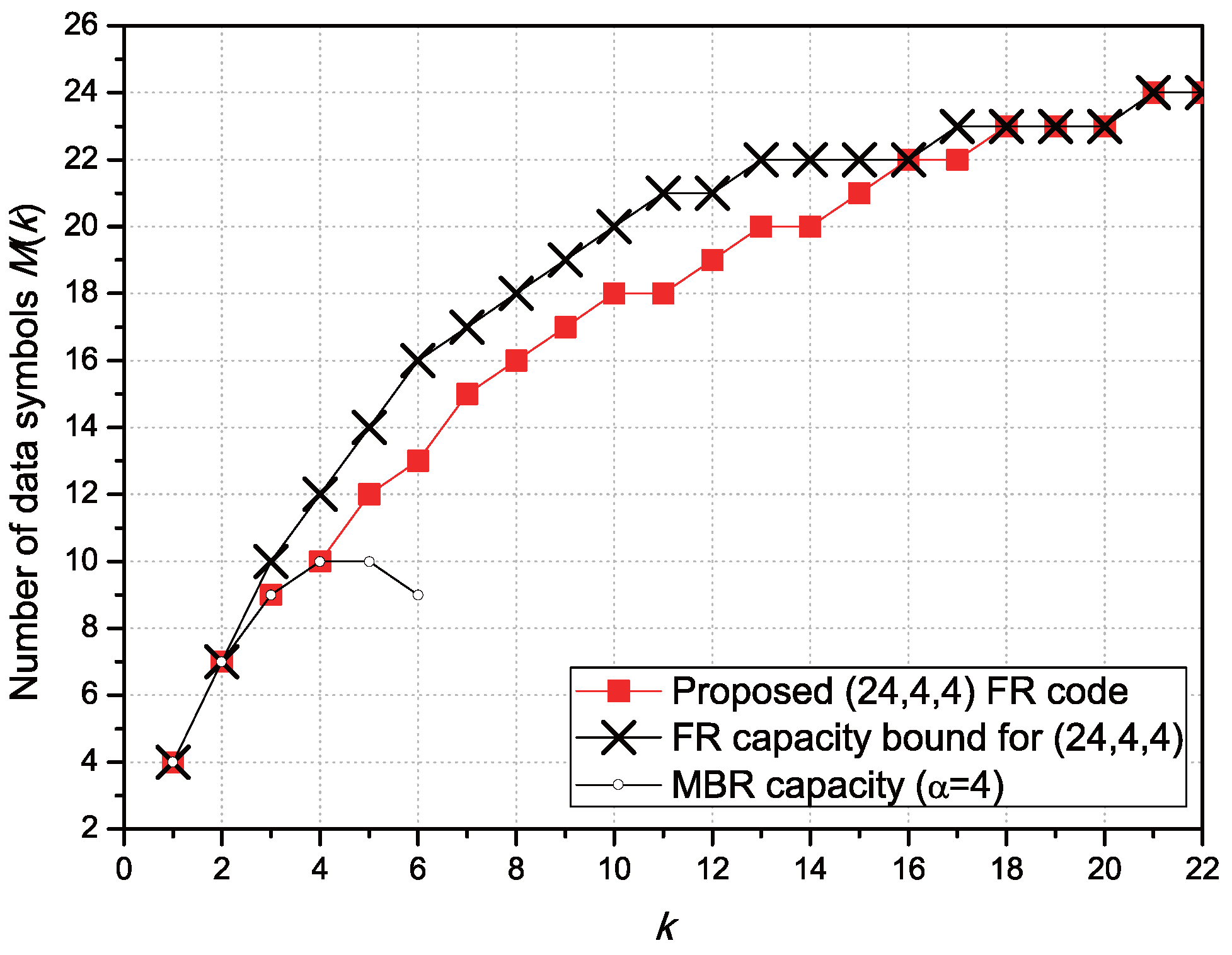
3.2. Properties of the Proposed FR Codes
4. Modification of the Proposed FR Codes
5. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kim, S.-H.; Lee, I.-Y. Block access token renewal scheme based on secret sharing in Apache Hadoop. Entropy 2014, 16, 4185–4198. [Google Scholar] [CrossRef]
- Tamura, Y.; Yamada, S. Reliability analysis based on a jump diffusion model with two Wiener processes for cloud computing with big data. Entropy 2015, 17, 4533–4546. [Google Scholar] [CrossRef]
- Gopalan, P.; Huang, C.; Simitci, H.; Yekhanin, S. On the locality of codeword symbols. IEEE Trans. Inf. Theory 2012, 58, 6925–6934. [Google Scholar] [CrossRef]
- Papailiopoulos, D.S.; Dimakis, A.G. Locally repairable codes. IEEE Trans. Inf. Theory 2014, 60, 5843–5855. [Google Scholar] [CrossRef]
- Song, W.; Dau, S.H.; Yuen, C.; Li, J. Optimal locally repairable linear codes. IEEE J. Sel. Areas Commun. 2014, 32, 1019–1036. [Google Scholar] [CrossRef]
- Song, W.; Dau, S.H.; Yuen, C. Erasure codes with symbol locality and group decodability for distributed storage. In Proceedings of the IEEE Information Theory Workshop, Jeju, Korea, 11–15 October 2015; pp. 74–78. [Google Scholar]
- Dau, S.H.; Kiah, H.M.; Song, W.; Yuen, C. Locally encodable and decodable codes for distributed storage systems. In Proceedings of the IEEE Global Communications Conference, San Diego, CA, USA, 6–10 December 2015; pp. 1–7. [Google Scholar]
- Dimakis, A.G.; Godfrey, P.B.; Wainwright, M.J.; Ramchandran, K. Network coding for distributed storage systems. In Proceedings of the IEEE International Conference on Computer Communications, Anchorage, AK, USA, 6–12 May 2007; pp. 2000–2008. [Google Scholar]
- Wu, Y.; Dimakis, A.G.; Ramchandran, K. Deterministic regenerating codes for distributed storage. In Proceedings of the Annual Allerton Conference on Communication, Control, and Computing, Urbana-Champaign, IL, USA, 18 September 2007. [Google Scholar]
- Shah, N.B.; Rashmi, K.V.; Kumar, P.V.; Ramchandran, K. Distributed storage codes with repair-by-transfer and nonachievability of interior points on the storage-bandwidth tradeoff. IEEE Trans. Inf. Theory 2012, 58, 1837–1852. [Google Scholar] [CrossRef]
- Rashmi, K.V.; Shah, N.B.; Kumar, P.V. Optimal exact-regenerating codes for distributed storage at the MSR and MBR points via a product-matrix construction. IEEE Trans. Inf. Theory 2011, 57, 5227–5239. [Google Scholar] [CrossRef]
- Tian, C. Characterizing the rate region of the (4, 3, 3) exact-repair regenerating codes. IEEE J. Sel. Areas Commun. 2014, 32, 967–975. [Google Scholar] [CrossRef]
- Ernvall, T. Codes between MBR and MSR points with exact repair property. IEEE Trans. Inf. Theory 2014, 60, 6993–7005. [Google Scholar] [CrossRef]
- Tian, C.; Sasidharan, B.; Aggarwal, V.; Vaishampayan, V.A.; Kumar, P.V. Layered exact-repair regenerating codes via embedded error correction and block designs. IEEE Trans. Inf. Theory 2015, 61, 1933–1947. [Google Scholar] [CrossRef]
- Rouayheb, S.E.; Ramchandran, K. Fractional repetition codes for repair in distributed storage systems. In Proceedings of the Annual Allerton Conference on Communication, Control, and Computing, Urbana-Champaign, IL, USA, 29 September–1 October 2010; pp. 1510–1517. [Google Scholar]
- Anil, S.; Gupta, M.K.; Gulliver, T.A. Enumerating Some Fractional Repetition Codes. arxiv 2013, arXiv:1303.6801. [Google Scholar]
- Koo, J.C.; Gill, J.T., III. Scalable constructions of fractional repetition codes in distributed storage systems. In Proceedings of the Annual Allerton Conference on Communication, Control, and Computing, Urbana-Champaign, IL, USA, 28–30 September 2011; pp. 1366–1373. [Google Scholar]
- Olmez, O.; Ramamoorthy, A. Fractional repetition codes with flexible repair from combinatorial designs. IEEE Trans. Inf. Theory 2016, 62, 1565–1591. [Google Scholar] [CrossRef]
- Zhu, B.; Shum, K.W.; Li, H.; Hou, H. General fractional repetition codes for distributed storage systems. IEEE Commun. Lett. 2014, 18, 660–663. [Google Scholar] [CrossRef]
- Zhu, B.; Shum, K.W.; Li, H. Heterogeneity-aware codes with uncoded repair for distributed storage systems. IEEE Commun. Lett. 2015, 19, 901–904. [Google Scholar] [CrossRef]
- Silberstein, N.; Etzion, T. Optimal fractional repetition codes based on graphs and designs. IEEE Trans. Inf. Theory 2015, 61, 4164–4180. [Google Scholar] [CrossRef]
- Park, H.; Kim, Y.-S. Construction of fractional repetition codes with variable parameters for distributed storage systems. Entropy 2016, 18, 441. [Google Scholar] [CrossRef]
- Pawar, S.; Noorshams, N.; Rouayheb, S.E.; Ramchandran, K. DRESS codes for the storage cloud: Simple randomized constructions. In Proceedings of the IEEE International Symposium on Information Theory, St. Petersburg, Russia, 31 July–5 August 2011; pp. 2338–2342. [Google Scholar]
- Butson, A.T. Relations among generalized Hadamard matrices, relative difference sets, and maximal length linear recurring sequences. Canad. J. Math. 1963, 15, 42–48. [Google Scholar] [CrossRef]
- Elliott, J.E.H.; Butson, A.T. Relative difference sets. Ill. J. Math. 1966, 10, 517–531. [Google Scholar]
- Klapper, A. d-Form sequence: Families of sequences with low correlation values and large linear span. IEEE Trans. Inf. Theory 1995, 41, 423–431. [Google Scholar] [CrossRef]
- Kim, S.-H.; No, J.-S.; Chung, H.; Helleseth, T. New cyclic relative difference sets constructed from homogeneous functions with difference-balanced property. IEEE Trans. Inf. Theory 2005, 51, 1155–1163. [Google Scholar] [CrossRef]
- Colbourn, C.J.; Dinitz, J.H. Handbook of Combinatorial Designs, 2nd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Pott, A.; Schmidt, K.-U.; Zhou, Y. Semifields, relative difference sets, and bent functions. Radon Ser. Comput. Appl. Math. 2014, 16, 161–178. [Google Scholar]
- Hou, X.-D.; Sehgal, S.K. Two generalized constructions of relative difference sets. J. Algebraic Comb. 2000, 12, 145–153. [Google Scholar] [CrossRef]


| q or l | Original | Decimated | Construction |
|---|---|---|---|
| 3 | |||
| 1 | |||
| - | 2 | ||
| − | 1 | ||
| - | 2 | ||
| 3 | |||
| , , | 1 | ||
| - | 2 | ||
| , , | 1 | ||
| - | 2 | ||
| 3 | |||
| 1 | |||
| , , | 1 | ||
| , , , , | 1 | ||
| - | 2 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.-S.; Park, H.; No, J.-S. Construction of New Fractional Repetition Codes from Relative Difference Sets with λ=1. Entropy 2017, 19, 563. https://doi.org/10.3390/e19100563
Kim Y-S, Park H, No J-S. Construction of New Fractional Repetition Codes from Relative Difference Sets with λ=1. Entropy. 2017; 19(10):563. https://doi.org/10.3390/e19100563
Chicago/Turabian StyleKim, Young-Sik, Hosung Park, and Jong-Seon No. 2017. "Construction of New Fractional Repetition Codes from Relative Difference Sets with λ=1" Entropy 19, no. 10: 563. https://doi.org/10.3390/e19100563





