Enhanced Energy Distribution for Quantum Information Heat Engines
Abstract
:1. Introduction
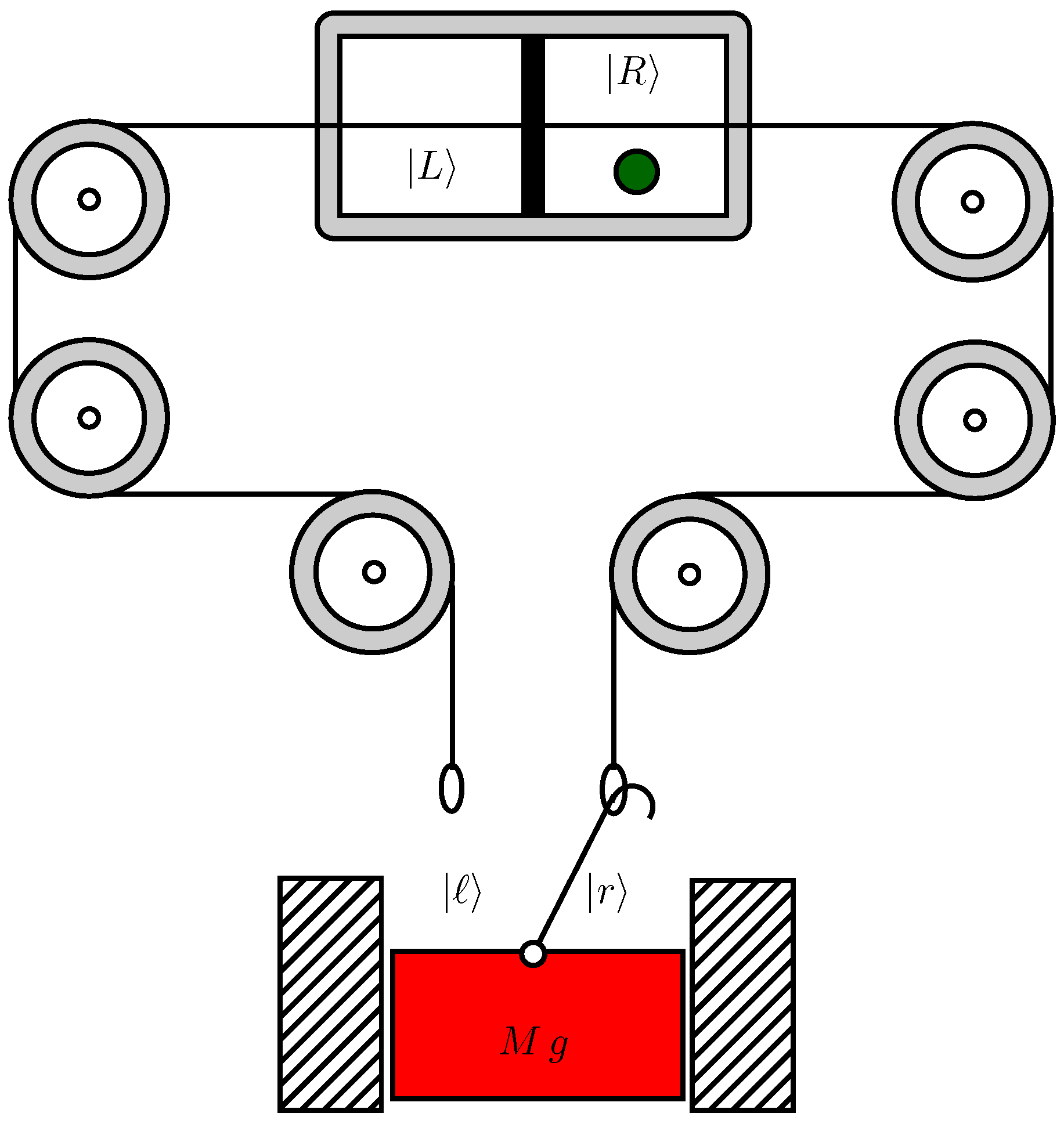
2. Short Description of a Quantum Information Heat Engine
3. Scenario for Energy Distribution through Quantum Information in Multipartite Systems
- (i)
- any user can independently make that the other ones () access the energy of one bit in their part of . This possibility can be implemented by using generalized Greenberger–Horne–Zeilinger (GHZ) states, also known as cat states. An n-partite GHZ state is a pure state:with two remarkable properties: (1) any local measurement destroys the entanglement and (2) the partial states are completely unpolarized (useless for energy conversion). User can measure its qubit and then classically broadcast the result to all other users who can subsequently convert their bits into work.
- (ii)
- only if all users agree, one of them can convert the energy. For this purpose, we may use a classically correlated mixed state:where may be 0 or 1 and, for notational simplicity, we defineAccording to Equation (8), is a mixture of all even parity pure states. It can only furnish one bit of information upon knowing all but one bits measured on the standard basis. We will now prove this. For that purpose, we will show that any operation on qubits, say , gives no information about qubit 1. Let be the Krauss operators; then, ignoring a possible normalization factor, the state of the system after it is:where , what accounts for the fact that the operation is on the last qubits. Expanding we haveNext, we separate the (set of even parity -tuples of bits) and (set of odd parity -tuples of bits) contributions so thatSubsequently, we trace over all but the first and second qubits to obtain ; let the constants be defined by:so that the partial trace resultsand, finally, tracing over the second qubit, we obtain:which shows that no information is gained about qubit 1, as it had been previously anticipated.
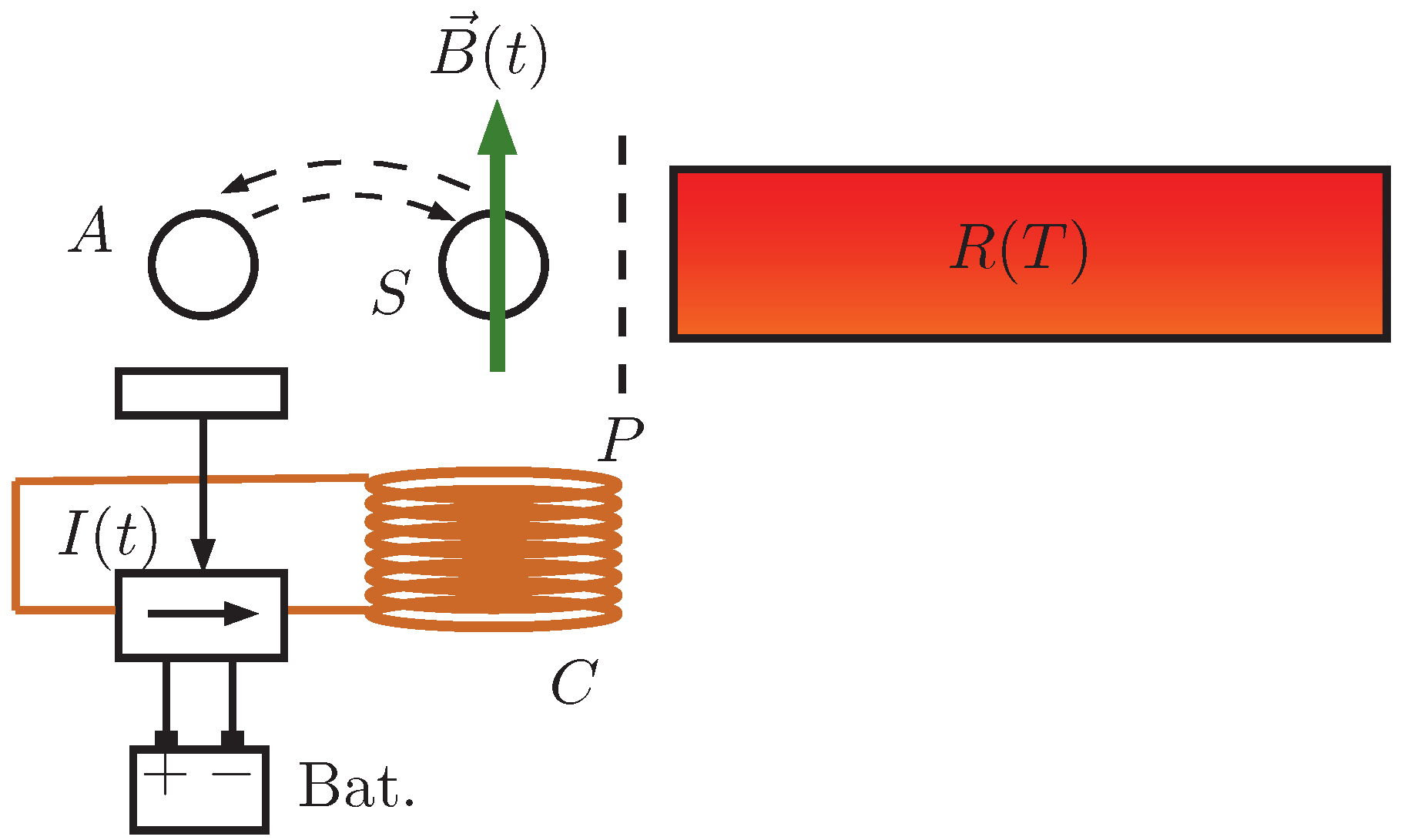
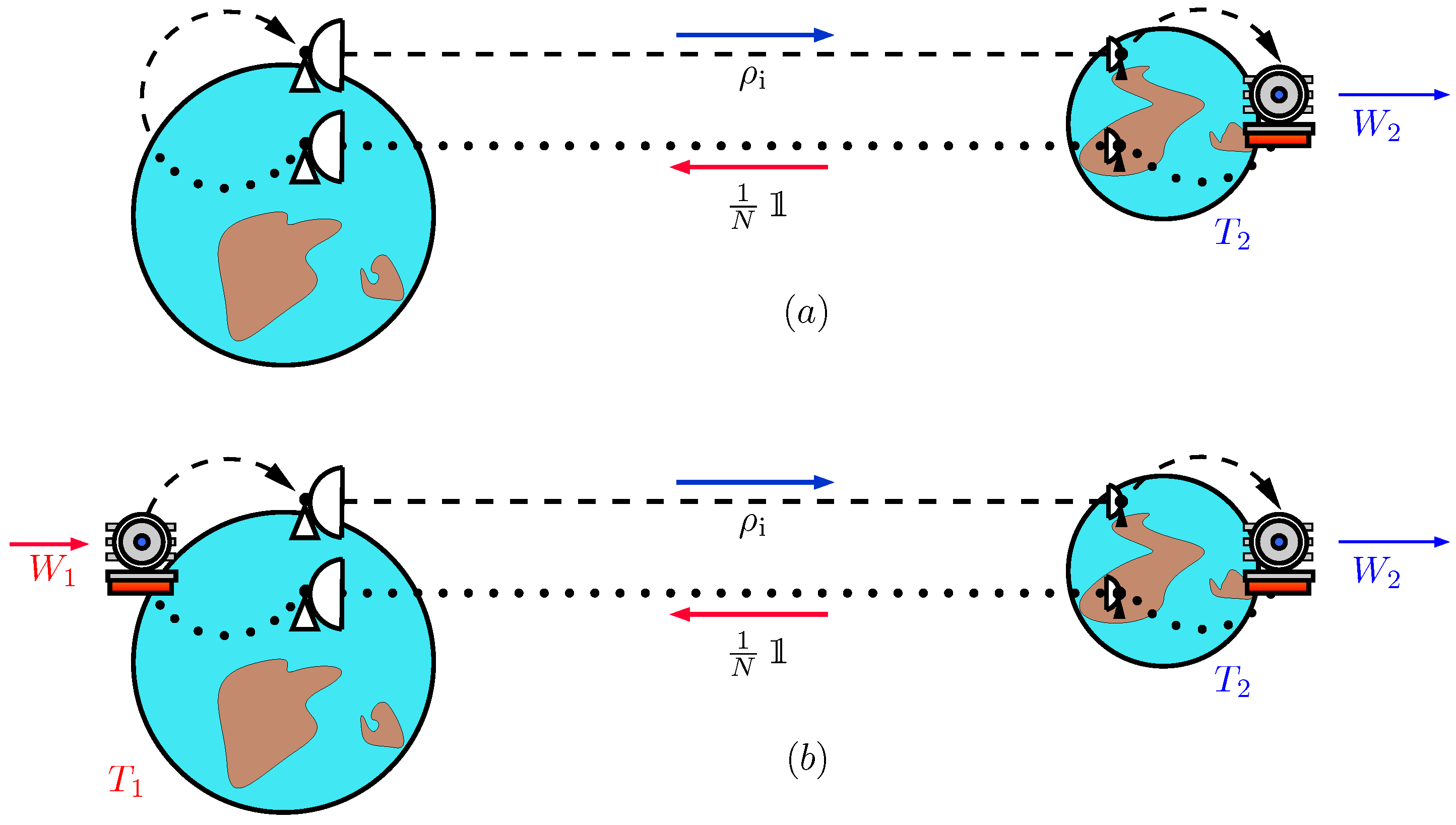
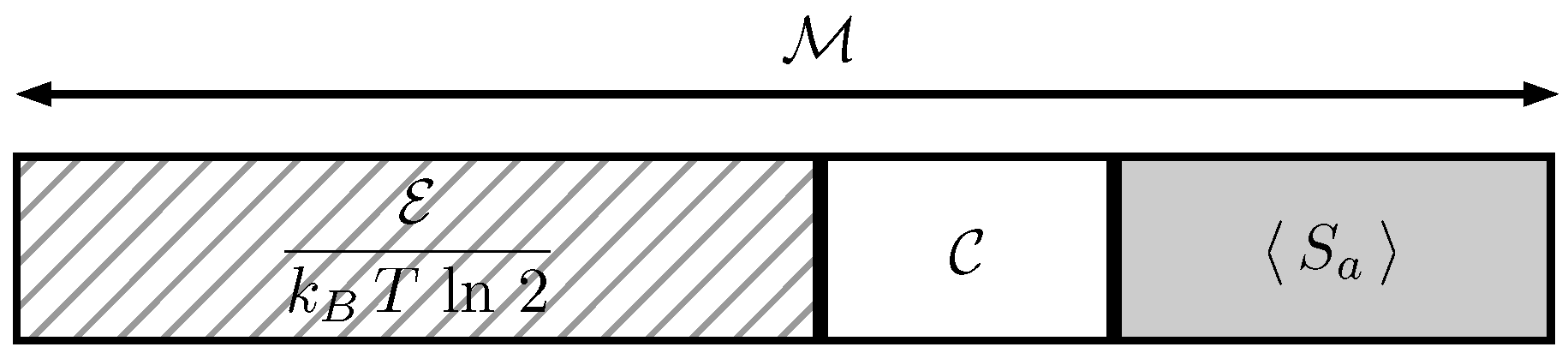
4. Mutual Limitation between Communication and Energy Extraction
5. Simultaneous Supply of Information and Work Extraction Capability
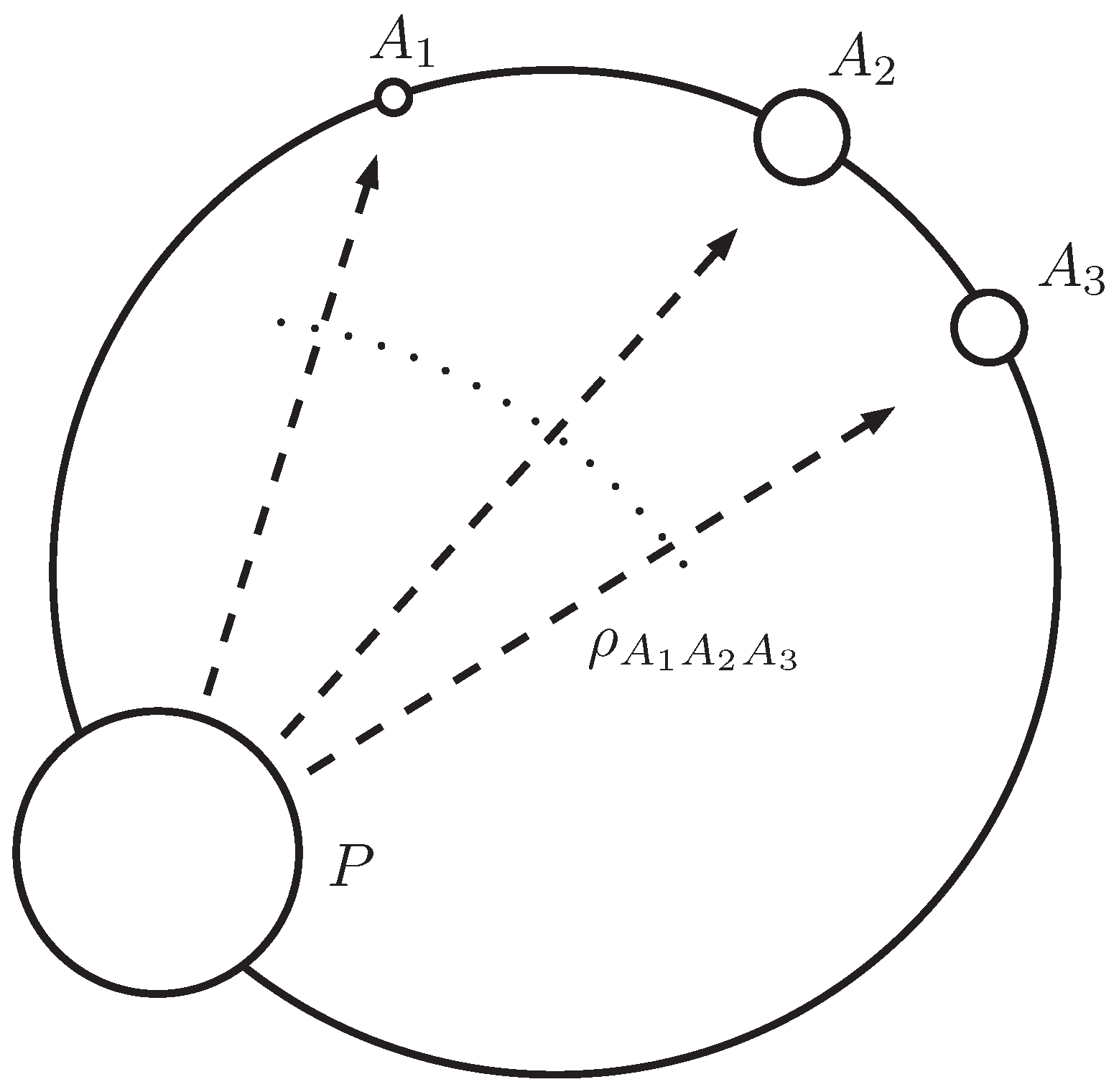
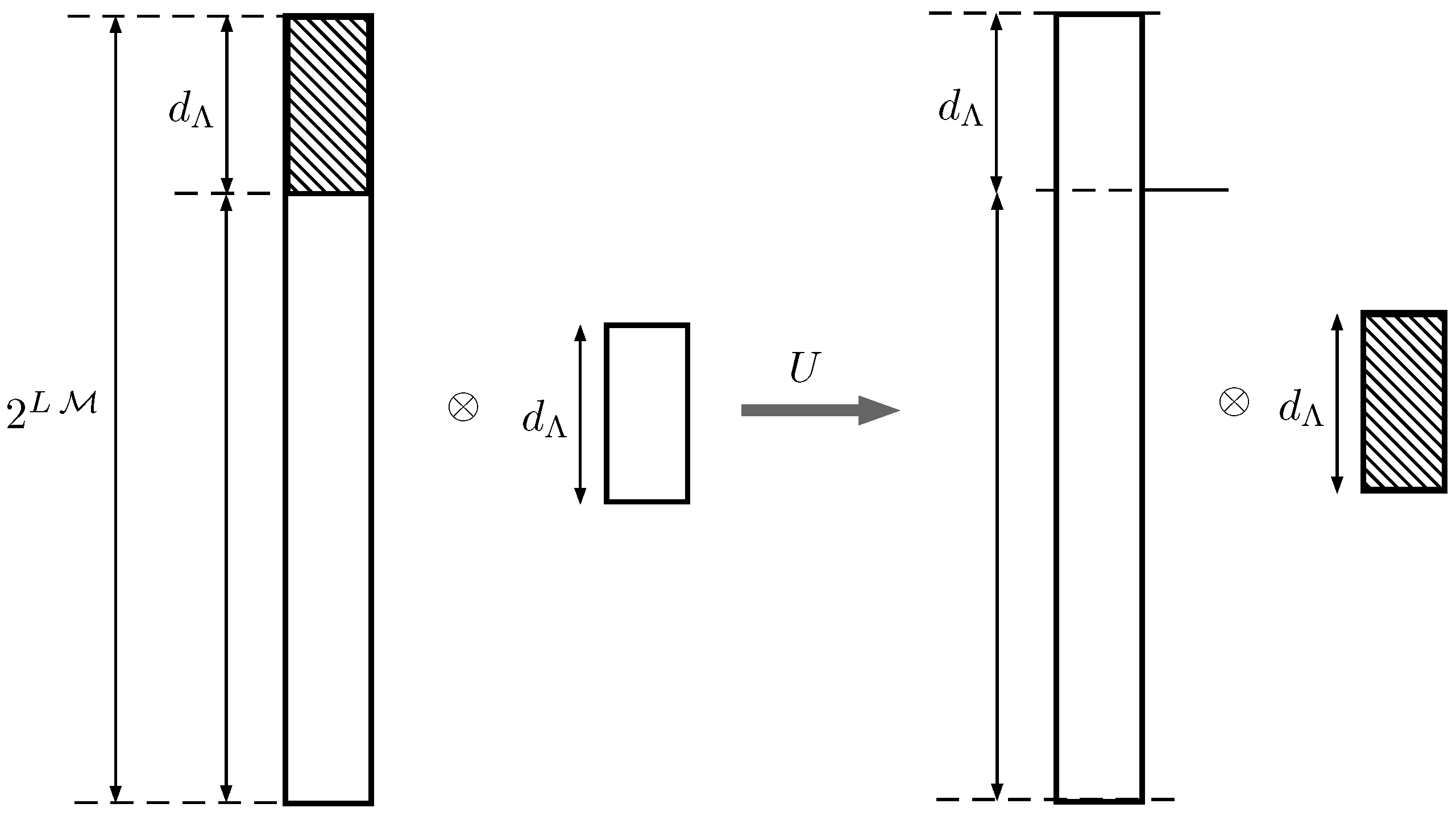
- there is a typical subspace , whose orthogonal projector is that verifieswhere , andin the following, we drop the subscripts and simply write Λ to denote the subspace ;
- the dimension of Λ is bounded by
- there is a communication protocol between Alice and Bob, whose information is coded (in [59], the codes are constructed by choosing a number of codewords independently, according to the a priori string probability for each codeword. The choice is supposed to be random and the results concerning the probability of error are averaged over the different possibilities) in the order in which Alice arranges the letters before sending them to Bob, where the frequency of letter is , that achieves bits per letter with a probability of error . When Bob receives the codewords sent by Alice, he performs a positive-operator valued measure (POVM) (positive-operator measure (POM) in the reference article [59]), defined by a collection of effects , where all of the kets belong to the typical subspace Λ. All the ensuing process of decoding relays only on the result of this POVM.
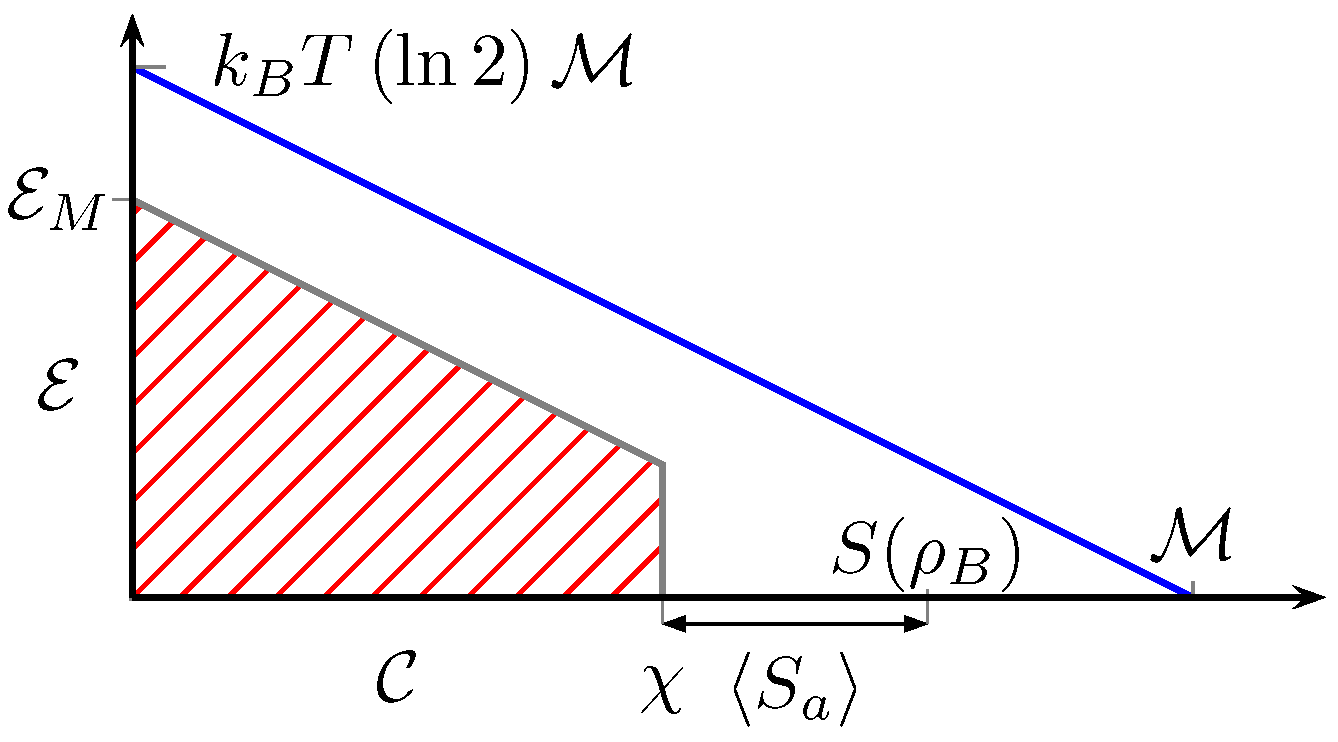
6. Results and Conclusions
- Simple transmission of messenger systems whose state is not completely depolarized for the receiver. He can extract a work equal to .
- Encrypted transmission of messenger systems though the use of previously entangled bipartite systems. This technique makes the transmitted system useless for illegitimate users that might intercept them. Quantum systems prove to be able to supply twice as much work as classical ones because of the same physics that is behind the feature of superdense coding in quantum communication protocols.
- In a multi-user scenario, where users initially share generalized GHZ states, any users can enable all the other ones to extract work.
- Also in a multi-user environment, if some correlated classical states are shared among all users, all but one can enable the other to extract work.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Bérut, A.; Arakelyan, A.; Petrosyan, A.; Ciliberto, S.; Dillenschneider, R.; Lutz, E. Experimental verification of Landauer’s principle linking information and thermodynamics. Nature 2012, 483, 187–189. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H. Logical reversibility of computation. IBM J. Res. Dev. 1973, 17, 525–532. [Google Scholar] [CrossRef]
- Feynman, R.; Shor, P.W. Simulating Physics with Computers. SIAM J. Comput. 1982, 26, 1484–1509. [Google Scholar] [CrossRef]
- Benioff, P. Quantum mechanical Hamiltonian models of turing machines. J. Stat. Phys. 1982, 29, 515–546. [Google Scholar] [CrossRef]
- Deutsch, D. Quantum theory, the church-turing principle and the universal quantum computer. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1985, 400, 97–117. [Google Scholar] [CrossRef]
- Galindo, A.; Martin-Delgado, M.A. Information and computation: Classical and quantum aspects. Rev. Mod. Phys. 2002, 74, 347–423. [Google Scholar] [CrossRef]
- Nielsen, M.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Maxwell, J.C. Theory of Heat; Longmans: London, UK, 1871. [Google Scholar]
- Szilard, L. On the decrease of entropy in a thermodynamic system by the intervention of intelligent beings. Behav. Sci. 1964, 9, 301–310. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H. Demons, engines and the second law. Sci. Am. 1987, 257, 108–116. [Google Scholar] [CrossRef]
- Zurek, W.H. Maxwell’s Demon, Szilard’s Engine and Quantum Measurements. In Frontiers of Nonequilibrium Statistical Physics; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Kim, S.; Sagawa, T.; Liberato, S.D.; Ueda, M. Quantum szilard engine. Phys. Rev. Lett. 2011, 106, 070401. [Google Scholar] [CrossRef] [PubMed]
- Kish, L.B.; Granqvist, C.G. Energy requirement of control: Comments on Szilard’s engine and Maxwell’s demon. Europhys. Lett. 2012, 98. [Google Scholar] [CrossRef]
- Horowitz, J.M.; Parrondo, J.M.R. Designing optimal discrete-feedback thermodynamic engines. New J. Phys. 2011, 13, 123019. [Google Scholar] [CrossRef]
- Diaz de la Cruz, J.M.D.; Martin-Delgado, M.A. Quantum-information engines with many-body states attaining optimal extractable work with quantum control. Phys. Rev. A 2014, 89, 032327. [Google Scholar] [CrossRef]
- Uzdin, R.; Kosloff, R. The multilevel four-stroke swap engine and its environment. New J. Phys. 2014, 16, 095003. [Google Scholar] [CrossRef]
- Toyabe, S.; Sagawa, T.; Ueda, M.; Muneyuki, E.; Sano, M. Information heat engine: Converting information to energy by feedback control. Nat. Phys. 2010, 6, 988–992. [Google Scholar] [CrossRef]
- Scully, M.O. Extracting work from a single thermal bath via quantum negentropy. Phys. Rev. Lett. 2001, 87, 220601. [Google Scholar] [CrossRef] [PubMed]
- Scully, M.O.; Rostovtsev, Y.; Sariyanni, Z.E.; Zubairy, M.S. Using quantum erasure to exorcize Maxwell’s demon: I. Concepts and context. Phys. E Low-Dimens. Syst. Nanostruct. 2005, 29, 29–39. [Google Scholar] [CrossRef]
- Rostovtsev, Y.; Sariyanni, Z.E.; Zubairy, M.S.; Scully, M.O. Using quantum erasure to exorcise Maxwell’s demon: II. Analysis. Phys. E Low-Dimens. Syst. Nanostruct. 2005, 29, 40–46. [Google Scholar] [CrossRef]
- Sariyanni, Z.E.; Rostovtsev, Y.; Zubairy, M.S.; Scully, M.O. Using quantum erasure to exorcize Maxwell’s demon: III. Implementation. Phys. E Low-Dimens. Syst. Nanostruct. 2005, 29, 47–52. [Google Scholar] [CrossRef]
- Quan, H.T.; Wang, Y.D.; Liu, Y.X.; Sun, C.P.; Nori, F. Maxwell’s demon assisted thermodynamic cycle in superconducting quantum circuits. Phys. Rev. Lett. 2006, 97, 180402. [Google Scholar] [CrossRef] [PubMed]
- Del Rio, L.; Aberg, J.; Renner, R.; Dahlsten, O.; Vedral, V. The Thermodynamic Meaning of Negative Entropy. Nature 2011, 474, 61–63. [Google Scholar] [PubMed]
- Plesch, M.; Dahlsten, O.; Goold, J.; Vedral, V. Comment on “Quantum Szilard Engine”. Phys. Rev. Lett. 2013, 111, 188901. [Google Scholar] [CrossRef] [PubMed]
- Funo, K.; Watanabe, Y.; Ueda, M. Thermodynamic work gain from entanglement. Phys. Rev. A 2013, 88, 052319. [Google Scholar] [CrossRef]
- Piechocinska, B. Information erasure. Phys. Rev. A 2000, 61, 062314. [Google Scholar] [CrossRef]
- Zhou, Y.; Segal, D. Minimal model of a heat engine: Information theory approach. Phys. Rev. E 2010, 82, 011120. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, S. Quantum-mechanical Maxwell’s demon. Phys. Rev. A 1997, 56, 3374–3382. [Google Scholar] [CrossRef]
- Vidrighin, M.D.; Dahlsten, O.; Barbieri, M.; Kim, M.S.; Vedral, V.; Walmsley, I.A. Photonic Maxwell’s Demon. Phys. Rev. Lett. 2016, 116, 050401. [Google Scholar] [CrossRef] [PubMed]
- Oppenheim, J.; Horodecki, M.; Horodecki, P.; Horodecki, R. Thermodynamical approach to quantifying quantum correlations. Phys. Rev. Lett. 2002, 89, 180402. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Kim, K.; Sagawa, T.; Kim, S. Heat Engine Driven by Purely Quantum Information. Phys. Rev. Lett. 2013. [Google Scholar] [CrossRef] [PubMed]
- Ollivier, H.; Zurek, W. Quantum discord: A measure of the quantumness of correlations. Phys. Rev. Lett. 2002, 88, 017901. [Google Scholar] [CrossRef] [PubMed]
- Zurek, W.H. Quantum discord and Maxwell’s demons. Phys. Rev. A 2003, 67, 012320. [Google Scholar] [CrossRef]
- Hasegawa, H.; Ishikawa, J.; Takara, K.; Driebe, D. Generalization of the second law for a nonequilibrium initial state. Phys. Lett. A 2010, 374. [Google Scholar] [CrossRef]
- Vedral, V. The role of relative entropy in quantum information theory. Rev. Mod. Phys. 2002, 74, 197–234. [Google Scholar] [CrossRef]
- Sagawa, T. Second Law-Like Inequalities with Quantum Relative Entropy: An Introduction. Stat. Mech. 2012. [Google Scholar]
- Brandao, F.; Horodecki, M.; Ng, N.; Oppenheim, J.; Wehner, S. The second laws of quantum thermodynamics. Proc. Natl. Acad. Sci. USA 2015, 112, 3275–3279. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Poletti, D. Quantum statistics and the performance of engine cycles. Phys. Rev. E 2015, 92, 012110. [Google Scholar] [CrossRef] [PubMed]
- Jaramillo, J.; Beau, M.; del Campo, A. Quantum supremacy of many-particle thermal machines. New J. Phys. 2016, 18, 075019. [Google Scholar] [CrossRef]
- Beau, M.; Jaramillo, J.; del Campo, A. Scaling-up quantum heat engines efficiently via shortcuts to adiabaticity. Entropy 2016, 18, 168. [Google Scholar] [CrossRef]
- Jeon, H.J.; Kim, S.W. Optimal work of the quantum Szilard engine under isothermal processes with inevitable irreversibility. New J. Phys. 2016, 18, 043002. [Google Scholar] [CrossRef]
- Kosloff, R.; Feldmann, T. Optimal performance of reciprocating demagnetization quantum refrigerators. Phys. Rev. E 2010, 82, 011134. [Google Scholar] [CrossRef] [PubMed]
- Beretta, G.P. Quantum thermodynamic Carnot and Otto-like cycles for a two-level system. Europhys. Lett. 2012, 99. [Google Scholar] [CrossRef]
- Gordon, G.; Bensky, G.; Gelbwaser-Klimovsky, D.; Rao, D.D.B.; Erez, N.; Kurizki, G. Cooling down quantum bits on ultrashort time scales. New J. Phys. 2009, 11, 123025. [Google Scholar] [CrossRef]
- Dahlsten, O.C.O.; Renner, R.; Rieper, E.; Vedral, V. Inadequacy of von Neumann entropy for characterizing extractable work. New J. Phys. 2011, 13, 053015. [Google Scholar] [CrossRef]
- Horodecki, M.; Oppenheim, J. Fundamental Limitations for Quantum and Nano Thermodynamics. Nat. Commum. 2011. [Google Scholar]
- Egloff, D.; Dahlsten, O.C.; Renner, R.; Vedral, V. Laws of Thermodynamics beyond the von Neumann Regime. 2013. [Google Scholar]
- Hotta, M. A protocol for quantum energy distribution. Phys. Lett. A 2008, 372, 5671–5676. [Google Scholar] [CrossRef]
- Hotta, M. Quantum energy teleportation with trapped ions. Phys. Rev. A 2009, 80, 042323. [Google Scholar] [CrossRef]
- Trevison, J.; Hotta, M. Quantum energy teleportation across a three-spin Ising chain in a Gibbs state. J. Phys. A Math. Theor. 2015, 48, 175302. [Google Scholar] [CrossRef]
- Ma, X.; Herbst, T.; Scheidl, T.; Wang, D.; Kropatschek, S.; Naylor, W.; Wittmann, B.; Mech, A.; Kofler, J.; Anisimova, E.; et al. Quantum teleportation over 143 kilometres using active feed-forward. Nature 2012, 489, 269–273. [Google Scholar] [CrossRef] [PubMed]
- Herbst, T.; Scheidl, T.; Fink, M.; Handsteiner, J.; Wittmann, B.; Ursin, R.; Zeilinger, A. Teleportation of entanglement over 143 km. Proc. Natl. Acad. Sci. USA 2015, 112, 14202–14205. [Google Scholar] [CrossRef] [PubMed]
- Brandão, F.G.S.L.; Horodecki, M.; Oppenheim, J.; Renes, J.M.; Spekkens, R.W. Resource theory of quantum states out of thermal equilibrium. Phys. Rev. Lett. 2013, 111, 250404. [Google Scholar] [CrossRef] [PubMed]
- Horodecki, M.; Oppenheim, J. Fundamental limitations for quantum and nanoscale thermodynamics. Nat. Commun. 2013, 4. [Google Scholar] [CrossRef] [PubMed]
- Sagawa, T.; Ueda, M. Minimal energy cost for thermodynamic information processing: Measurement and information erasure. Phys. Rev. Lett. 2009, 102, 250602. [Google Scholar] [CrossRef] [PubMed]
- De Liberato, S.; Ueda, M. Carnot’s theorem for nonthermal stationary reservoirs. Phys. Rev. E 2011, 84, 051122. [Google Scholar] [CrossRef] [PubMed]
- Holevo, A.S. The capacity of quantum channel with general signal states. IEEE Trans. Inf. Theory 1998, 44, 269–273. [Google Scholar] [CrossRef]
- Schumacher, B.; Westmoreland, M.D. Sending classical information via noisy quantum channels. Phys. Rev. A 1997, 56, 131–138. [Google Scholar] [CrossRef]
- Wilde, M.M. Quantum Information Theory; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diaz de la Cruz, J.M.; Martin-Delgado, M.A. Enhanced Energy Distribution for Quantum Information Heat Engines. Entropy 2016, 18, 335. https://doi.org/10.3390/e18090335
Diaz de la Cruz JM, Martin-Delgado MA. Enhanced Energy Distribution for Quantum Information Heat Engines. Entropy. 2016; 18(9):335. https://doi.org/10.3390/e18090335
Chicago/Turabian StyleDiaz de la Cruz, Jose M., and Miguel Angel Martin-Delgado. 2016. "Enhanced Energy Distribution for Quantum Information Heat Engines" Entropy 18, no. 9: 335. https://doi.org/10.3390/e18090335





