Network Entropies of the Chinese Financial Market
Abstract
:1. Introduction
2. Methodology
2.1. Network Construction
2.2. Network Entropy
3. Results
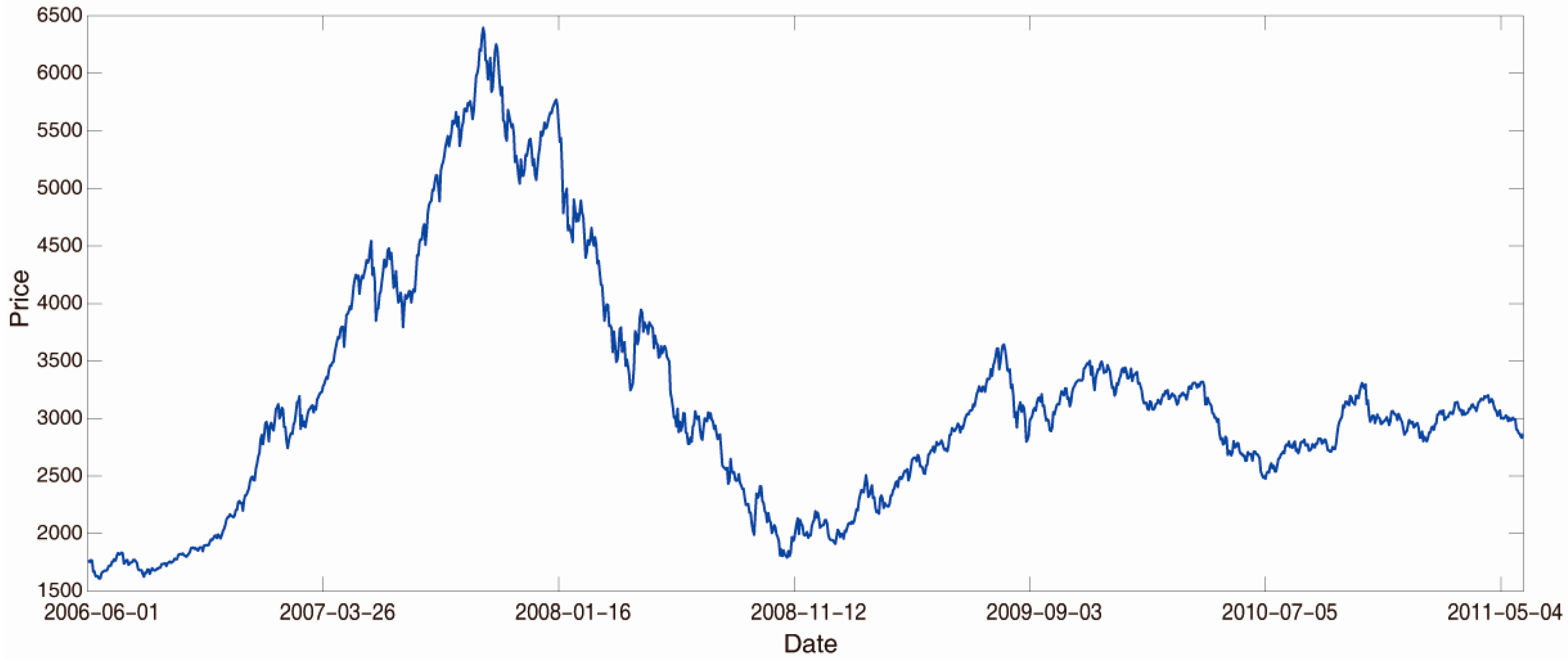
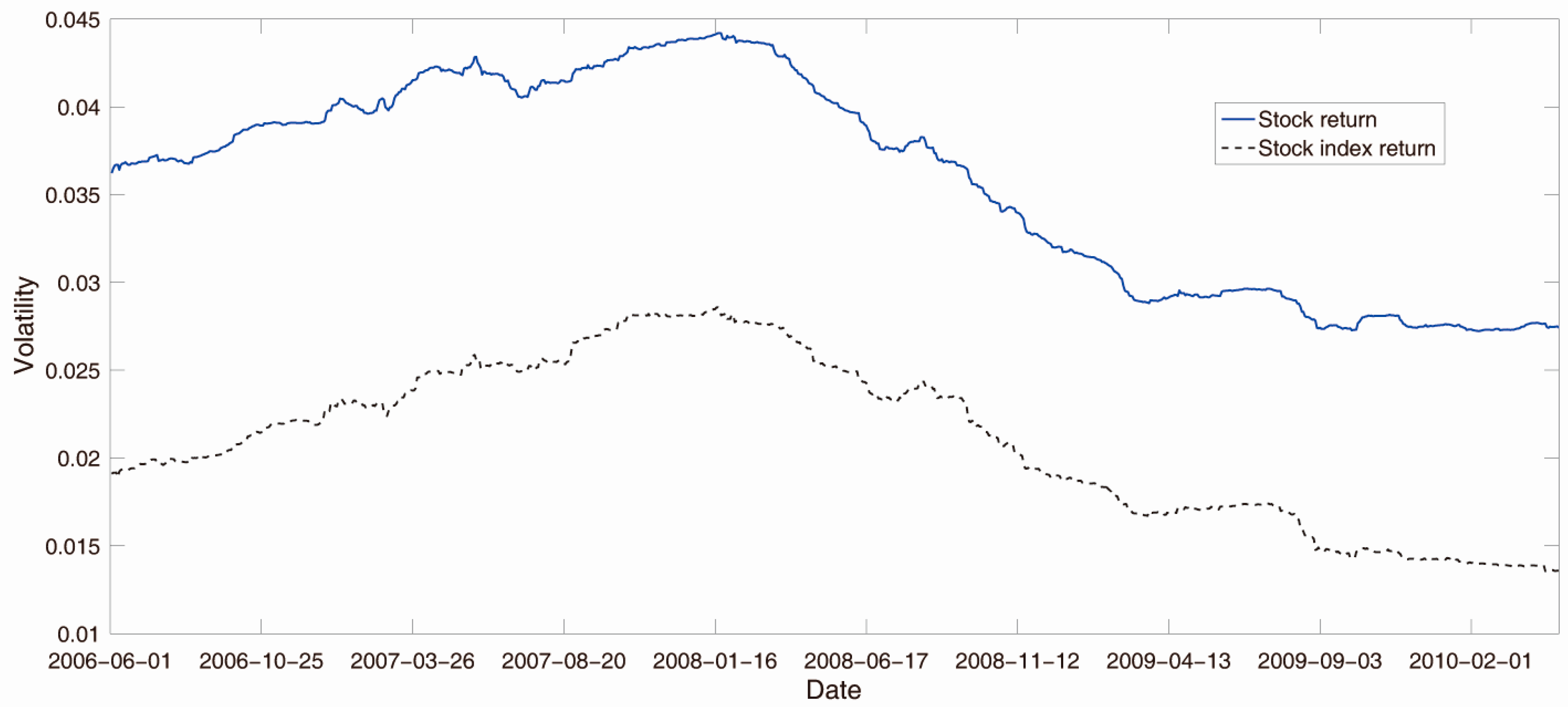
3.1. Data
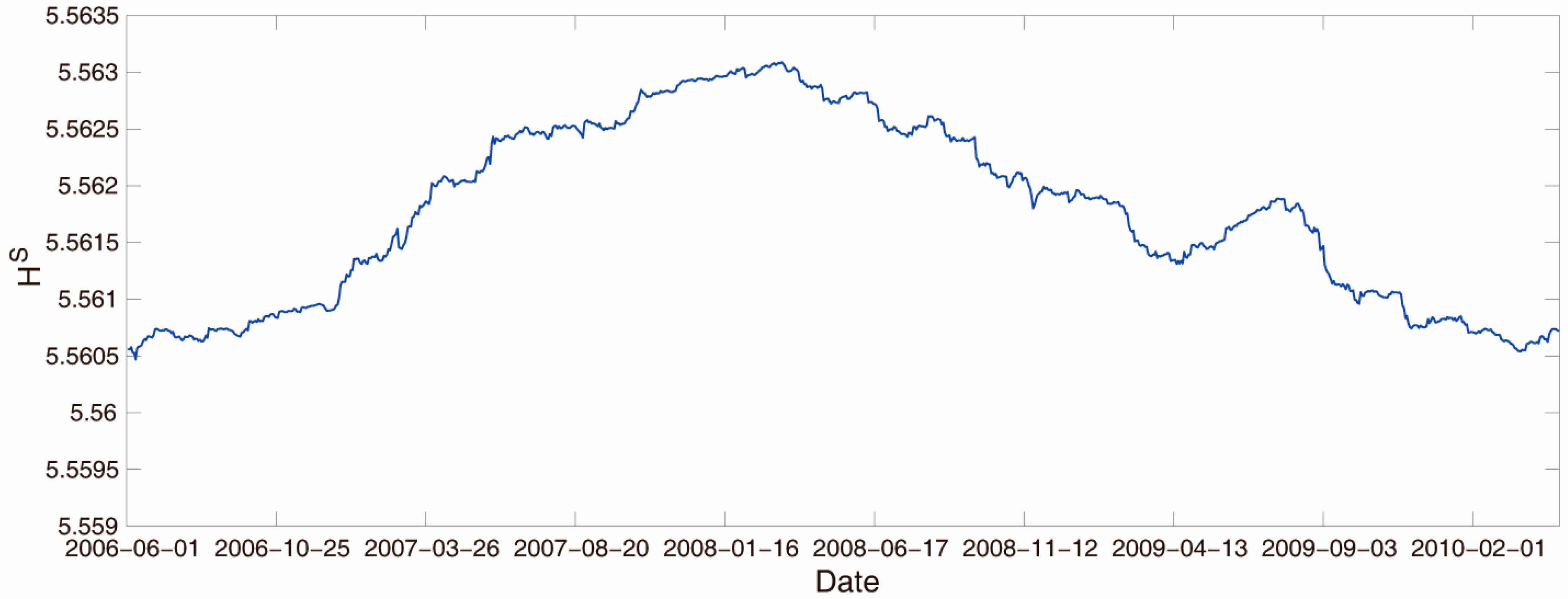
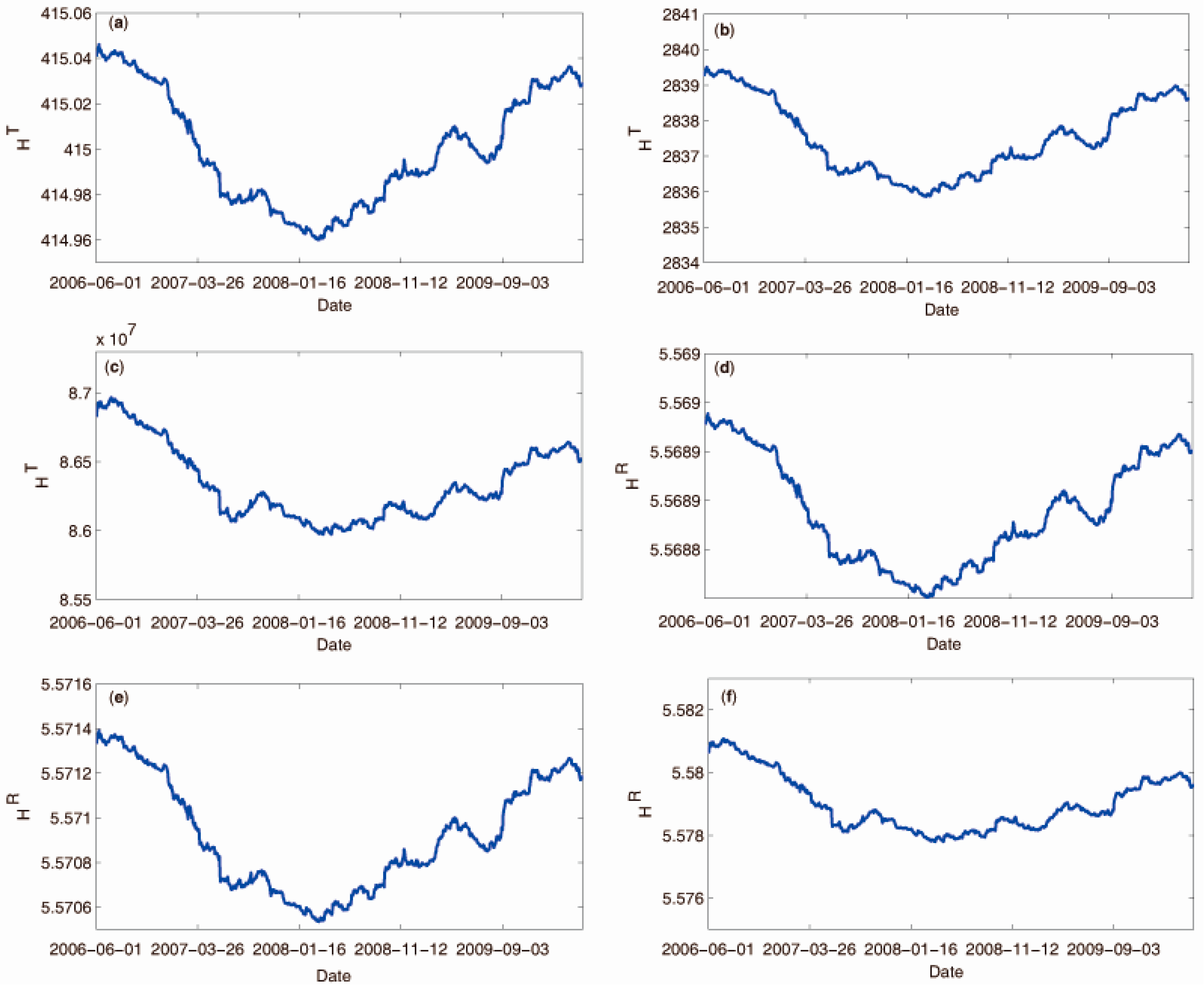
3.2. Empirical Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tirole, J. Illiquidity and all its friends. J. Econ. Lit. 2011, 49, 287–325. [Google Scholar] [CrossRef]
- Yellen, J. Interconnectedness and Systemic Risk: Lessons from the Financial Crisis and Policy Implications. In Proceedings of the American Economic Association/American Finance Association Joint Luncheon, San Diego, CA, USA, 4 January 2013.
- Gençay, R.; Signori, D.; Xue, Y.; Yu, C.; Zhang, K. Economic links and credit spreads. J. Bank. Financ. 2015, 55, 157–169. [Google Scholar] [CrossRef]
- Mantegna, R.N. Hierarchical structure in financial markets. Eur. Phys. J. B 1999, 11, 193–197. [Google Scholar] [CrossRef]
- Vandewalle, N.; Brisbois, F.; Tordoir, X. Non-random topology of stock markets. Quant. Financ. 2001, 1, 372–374. [Google Scholar] [CrossRef]
- Jung, W.S.; Chae, S.; Yang, J.S.; Hie-Tae, M. Characteristics of the Korean stock market correlations. Physica A 2006, 361, 263–271. [Google Scholar] [CrossRef]
- Eom, C.; Oh, G.; Kim, S. Deterministic factors of stock networks based on cross-correlation in financial market. Physica A 2007, 383, 139–146. [Google Scholar] [CrossRef]
- Chi, K.T.; Liu, J.; Lau, F.C.M. A network perspective of the stock market. J. Empir. Financ. 2010, 17, 659–667. [Google Scholar]
- Dal’Maso Peron, T.K.; Rodrigues, F.A. Collective behavior in financial markets. Europhys. Lett. 2011, 96. [Google Scholar] [CrossRef]
- Dal’Maso Peron, T.K.; da Fontoura Costa, L.; Rodrigues, F.A. The structure and resilience of financial market networks. Chaos 2012, 22, 013117. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.F.; Tse, C.K. A complex network perspective of world stock markets: Synchronization and volatility. Int. J. Bifurc. Chaos 2012, 22, 1250142. [Google Scholar] [CrossRef]
- Nobi, A.; Maeng, S.E.; Ha, G.G.; Lee, J.W. Structural changes in the minimal spanning tree and the hierarchical network in the Korean stock market around the global financial crisis. J. Korean Phys. Soc. 2015, 66, 1153–1159. [Google Scholar] [CrossRef]
- Majapa, M.; Gossel, S.J. Topology of the South African stock market network across the 2008 financial crisis. Physica A 2016, 445, 35–47. [Google Scholar] [CrossRef]
- Bian, Y.; Xu, L.; Li, J. Evolving dynamics of trading behavior based on coordination game in complex networks. Physica A 2016, 449, 281–290. [Google Scholar] [CrossRef]
- Gfeller, D.; Chappelier, J.C.; de Los Rios, P. Finding instabilities in the community structure of complex networks. Phys. Rev. E 2005, 72, 056135. [Google Scholar] [CrossRef] [PubMed]
- Bogacz, L.; Burda, Z.; Wacław, B. Homogeneous complex networks. Physica A 2006, 366, 587–607. [Google Scholar] [CrossRef]
- Bianconi, G. The entropy of randomized network ensembles. Europhys. Lett. 2007, 81, 28005. [Google Scholar] [CrossRef]
- Bianconi, G.; Coolen, A.C.C.; Vicente, C.J.P. Entropies of complex networks with hierarchically constrained topologies. Phys. Rev. E 2008, 78, 016114. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Gardeñes, J.; Latora, V. Entropy rate of diffusion processes on complex networks. Phys. Rev. E 2008, 78, 065102. [Google Scholar] [CrossRef] [PubMed]
- Anand, K.; Bianconi, G. Entropy measures for networks: Toward an information theory of complex topologies. Phys. Rev. E 2009, 80, 045102. [Google Scholar]
- Rovelli, C.; Vidotto, F. Single particle in quantum gravity and Braunstein-Ghosh-Severini entropy of a spin network. Phys. Rev. D 2010, 81, 044038. [Google Scholar] [CrossRef]
- Zhang, Q.; Luo, C.; Li, M.; Mahadevan, S. Tsallis information dimension of complex networks. Physica A 2015, 419, 707–717. [Google Scholar] [CrossRef]
- Nie, T.; Guo, Z.; Zhao, K.; Lu, Z.M. Using mapping entropy to identify node centrality in complex networks. Physica A 2016, 453, 290–297. [Google Scholar] [CrossRef]
- Gençay, R.; Gradojevic, N. Overnight interest rates and aggregate market expectations. Econ. Lett. 2008, 100, 27–30. [Google Scholar]
- Gençay, R.; Gradojevic, N. Crash of ′87—Was it expected?: Aggregate market fears and long range dependence. J. Empir. Financ. 2010, 17, 270–282. [Google Scholar] [CrossRef]
- Bentes, S.R.; Menezes, R. Entropy: A new measure of stock market volatility? J. Phys. 2012, 394, 012033. [Google Scholar] [CrossRef]
- Zhou, R.; Cai, R.; Tong, G. Applications of entropy in finance: A review. Entropy 2013, 15, 4909–4931. [Google Scholar] [CrossRef]
- Lee, D. Entropy of Global Financial Linkages. Available online: http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2580650 (accessed on 6 September 2016).
- Demetrius, L.; Manke, T. Robustness and network evolution—An entropic principle. Physica A 2005, 346, 682–696. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Renyi, A. Probability Theory; Dover: New York, NY, USA, 1970. [Google Scholar]
- Tsallis, C.; Mendes, R.S.; Plastino, A.R. The role of constraints within generalized nonextensive statistics. Physica A 1998, 261, 534–554. [Google Scholar] [CrossRef]
- Hsieh, C.S.; Chou, J.H.; Liao, T.L. Monthly Effect in Shanghai Stock Exchange. Available online: http://www.kyu.edu.tw/teacpage/teacpage97/97%E8%AB%96%E6%96%87%E6%88%90%E6%9E%9C%E5%BD%99%E7%B7%A8/207.pdf (accessed on 6 September 2016).
- Jiang, X.F.; Zheng, B. Anti-correlation and subsector structure in financial systems. Europhys. Lett. 2012, 97. [Google Scholar] [CrossRef]
- Shen, J.; Zheng, B. Cross-correlation in financial dynamics. Europhys. Lett. 2009, 86. [Google Scholar] [CrossRef]
- Laloux, L.; Cizeau, P.; Bouchaud, J.P.; Potters, M. Noise dressing of financial correlation matrices. Phys. Rev. Lett. 1999, 83. [Google Scholar] [CrossRef]
- Ingber, L. Trading in Risk Dimensions (TRD). Available online: http://papers.ssrn.com/sol3/papers.cfm?abstract_id=1075430 (accessed on 6 September 2016).
- Borysov, S.S.; Roudi, Y.; Balatsky, A.V. US stock market interaction network as learned by the Boltzmann machine. Eur. Phys. J. B 2015, 88. [Google Scholar] [CrossRef]
- Date of Daily Closing Prices of the A-Share Index of the Shanghai Stock Exchange. Available online: http://2016.sse.com.cn/aboutus/publication/yearly (accessed on 7 September 2016).
- Beck, C. Generalised information and entropy measures in physics. Contermp. Phys. 2009, 50, 495–510. [Google Scholar] [CrossRef]
- Pratt, K.B.; Fink, E. Search for patterns in compressed time series. Int. J. Image Graph. 2002, 2, 89–106. [Google Scholar] [CrossRef]

| RD | α = 0.1 | α = 0.5 | α = 2.5 | α = −0.1 | α = −0.5 | α = −2.5 |
|---|---|---|---|---|---|---|
| 0.0205 | 0.0113 | 0.0275 | 0.9038 | 0.8948 | 0.8234 | |
| 0.0205 | 0.0112 | 0.0289 | 0.9038 | 0.8947 | 0.8222 | |
| 0.0000 | 0.0000 | 0.0015 | 0.0000 | 0.0000 | 0.0012 |
| α = 0.1 | α = 0.5 | α = 2.5 | α = −0.1 | α = −0.5 | α = −2.5 | |
|---|---|---|---|---|---|---|
| 0.9409 | ||||||
| 0.8978 | 0.9193 | 0.9750 | −0.8857 | −0.8591 | −0.7009 | |
| 0.8978 | 0.9193 | 0.9745 | −0.8857 | −0.8591 | −0.7012 | |
| 0.9478 | ||||||
| 0.9060 | 0.9269 | 0.9804 | −0.8941 | −0.8681 | −0.7120 | |
| 0.9060 | 0.9269 | 0.9800 | −0.8941 | −0.8681 | −0.7124 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; He, J.; Song, K. Network Entropies of the Chinese Financial Market. Entropy 2016, 18, 331. https://doi.org/10.3390/e18090331
Li S, He J, Song K. Network Entropies of the Chinese Financial Market. Entropy. 2016; 18(9):331. https://doi.org/10.3390/e18090331
Chicago/Turabian StyleLi, Shouwei, Jianmin He, and Kai Song. 2016. "Network Entropies of the Chinese Financial Market" Entropy 18, no. 9: 331. https://doi.org/10.3390/e18090331






