Generalized Robustness of Contextuality

Abstract

Motivated by the importance of contextuality and a work on the robustness of the entanglement of mixed quantum states, the robustness of contextuality (RoC) $R_C\left(e\right)$ of an empirical model e against non-contextual noises was introduced and discussed in Science China Physics, Mechanics and Astronomy (59(4) and 59(9), 2016). Because noises are not always non-contextual, this paper introduces and discusses the generalized robustness of contextuality (GRoC) $R_g\left(e\right)$ of an empirical model e against general noises. It is proven that $R_g\left(e\right)=0$ if and only if e is non-contextual. This means that the quantity $R_g$ can be used to distinguish contextual empirical models from non-contextual ones. It is also shown that the function $R_g$ is convex on the set of all empirical models and continuous on the set of all no-signaling empirical models. For any two empirical models e and f such that the generalized relative robustness of e with respect to f is finite, a fascinating relationship between the GRoCs of e and f is proven, which reads $R_g\left(e\right)R_g\left(f\right)\le 1$. Lastly, for any n-cycle contextual box e, a relationship between the GRoC $R_g\left(e\right)$ and the extent ${\Delta }_e$ of violating the non-contextual inequalities is established.

1. Introduction

Contextuality is one of the most interesting manifestations of the quantumness of physical systems and manifests itself in the famous Kochen–Specker theorem [1], which states that for every quantum system belonging to a Hilbert space of dimension greater than two, irrespective of its actual state, there exists a finite set of measurements whose results cannot be assigned in a context-independent manner. It exhibits the strength of correlations that comes out of a quantum state when measured by compatible measurements and plays a central role in quantum communication and quantum computation. For example, quantum contextuality is related to quantum error correction [2], random access codes [3], quantum key distribution [4] and one-location quantum games [5]. The work in [6] proved that contextuality can supply the “magic” for quantum computation by establishing a remarkable equivalence between the onset of contextuality and the possibility of universal quantum computation via magic state distillation. An important and interesting question is how to quantify quantum contextuality. A huge effort is being put into quantifying quantum contextuality by the mutual information of contextuality, the relative entropy of contextuality and the cost of contextuality [7].

Contextuality is a basic and amazing quantum property, as well as entanglement [8,9]. Moreover, contextuality has been formulated in terms of “empirical models”, i.e., families of probability distributions [10]. Due to the importance of contextuality and motivated by a work on the robustness of entanglement of mixed quantum states against noise and jamming [11], we proposed and discussed recently in [12,13] the robustness of contextuality (RoC) $R_C\left(e\right)$ and the contextuality cost $C\left(e\right)$ of an empirical model e, where $R_C\left(e\right)$ denotes the minimal amount of contextuality-free mixing needed to wipe out all contextuality of e and $C\left(e\right)$ denotes the minimal amount of contextuality mixing needed to prepare e. The following conclusions have been proven: (i) an empirical model e is contextual if and only if $R_C\left(e\right)>0$; (ii) the robustness of contextuality (RoC) is convex and un-increasing under a non-contextuality-preserving affine mapping; (iii) RoC is bounded and continuous on the set of all no-signaling empirical models; (iv) e is non-contextual if and only if $C\left(e\right)=0$; and (v) e is strongly contextual if and only if $C\left(e\right)=1$. Furthermore, a relationship between $R_C\left(e\right)$ and $C\left(e\right)$ has been obtained. Lastly, we have computed and compared the RoCs of three empirical models. This means that the quantities $R_C\left(e\right)$ and $C\left(e\right)$ are measures for the contextuality of an empirical model e. However, noises are not always non-contextual. Motivated by a work on the generalized robustness of the entanglement of mixed quantum states against noise and jamming [14], in this paper, we consider the generalized robustness of contextuality (GRoC) $R_g\left(e\right)$, which characterizes the minimal amount of mixing with general noises (i.e., both non-contextual empirical models and contextual empirical models), which washes out all contextuality of e.

For any measurement scenarios, the problem of separating non-contextual from contextual correlations has been solved in [10,15]. In particular, Reference [16] provided the complete characterization of the non-contextual correlations for the case of $n\ge 4$ dichotomic observables $X_0,\dots ,X_{n-1}$, where each consecutive pair $C_i=\{X_i,X_{i+1}\}$, sum mod n, is jointly measurable. This generalizes both the Clauser–Horne–Shimony–Holt and the Klyachko–Can–Binicioglu–Shumovsky scenarios [17,18,19,20,21], which are the simplest ones for locality and non-contextuality, respectively. Such correlations can be formulated by an n-cycle box e [16], which is a family of probability distributions ${\left\{e_{C_i}\right\}}_{i=0}^{n-1}$, where $e_{C_i}$ is a probability distribution on all possible outcomes of measurement $C_i$. The contextuality of e can be completely characterized by the extent of violating the non-contextual inequalities in [16]. The work in [13] established the relationship between RoC and the violating of non-contextual inequalities for n-cycle boxes. Does there exist a relationship between the quantities $R_g\left(e\right)$ and the extent of violating the non-contextual inequalities in [16]? In this paper, we will establish such a relationship.

This paper is organized as follows. In Section 2, we recall definitions and relevant results with respect to the contextuality of empirical models and the robustness of contextuality of empirical models and then introduce and observe the generalized robustness of contextuality (GRoC) $R_g\left(e\right)$, which characterizes the minimal amount of mixing with general noises (i.e., both non-contextual empirical models and contextual empirical models), which washes out all contextuality of e. Many properties of GRoC are proven, such as faithfulness, boundedness and continuity. It is worth noting that, for any two empirical models e and f, $R_g\left(e\right)R_g\left(f\right)\le 1$ provided that the generalized relative robustness of e with respect to f is finite, i.e., there exists a finite non-negative number x, such that $\frac{1}{1+x}e+\frac{x}{1+x}f$ is non-contextual. In Section 3, by introducing a quantity ${\Delta }_e$ representing the extent of violating the non-contextual inequalities in [16], we obtain the GRoC of any n-cycle boxes $(n\ge 4)$ and can compare the robustness of contextuality against any noise for any n-cycle box and m-cycle one with $m,n\ge 4$.

2. Generalized Robustness of the Contextuality of Empirical Models

In [10], a measurement cover $\mathcal{M}$ over a nonempty finite set X is defined as a family of nonempty subsets of X, such that ${\bigcup }_{C\in \mathcal{M}}C=X$ and $C,C^{\prime }\in \mathcal{M},C\subseteq C^{\prime }\Rightarrow C=C^{\prime }.$ If in addition, O is a nonempty finite set, then the triple $(X,\mathcal{M},O)$ is said to be a measurement scenario (MS). In this case, the elements of X are called measurements; the ones of $\mathcal{M}$ are called measurement contexts; and ones of O are called the outcomes of the measurements in X. The elements of the set $\mathcal{E}\left(C\right)$ consisting of all mappings $s:C\to O$ are referred to as the events. Furthermore, we use $\mathcal{D}\left(\mathcal{E}\right(C\left)\right)$ to denote the set of all probability distributions over $\mathcal{E}\left(C\right).$

Definition 1 

([10]). Let $(X,\mathcal{M},O)$ be an MS. If $e_C\in \mathcal{D}\left(\mathcal{E}\left(C\right)\right)$ for all $C\in \mathcal{M}$, then the family $e:={\left\{e_C\right\}}_{C\in \mathcal{M}}$ is said to be an empirical model on $(X,\mathcal{M},O)$.

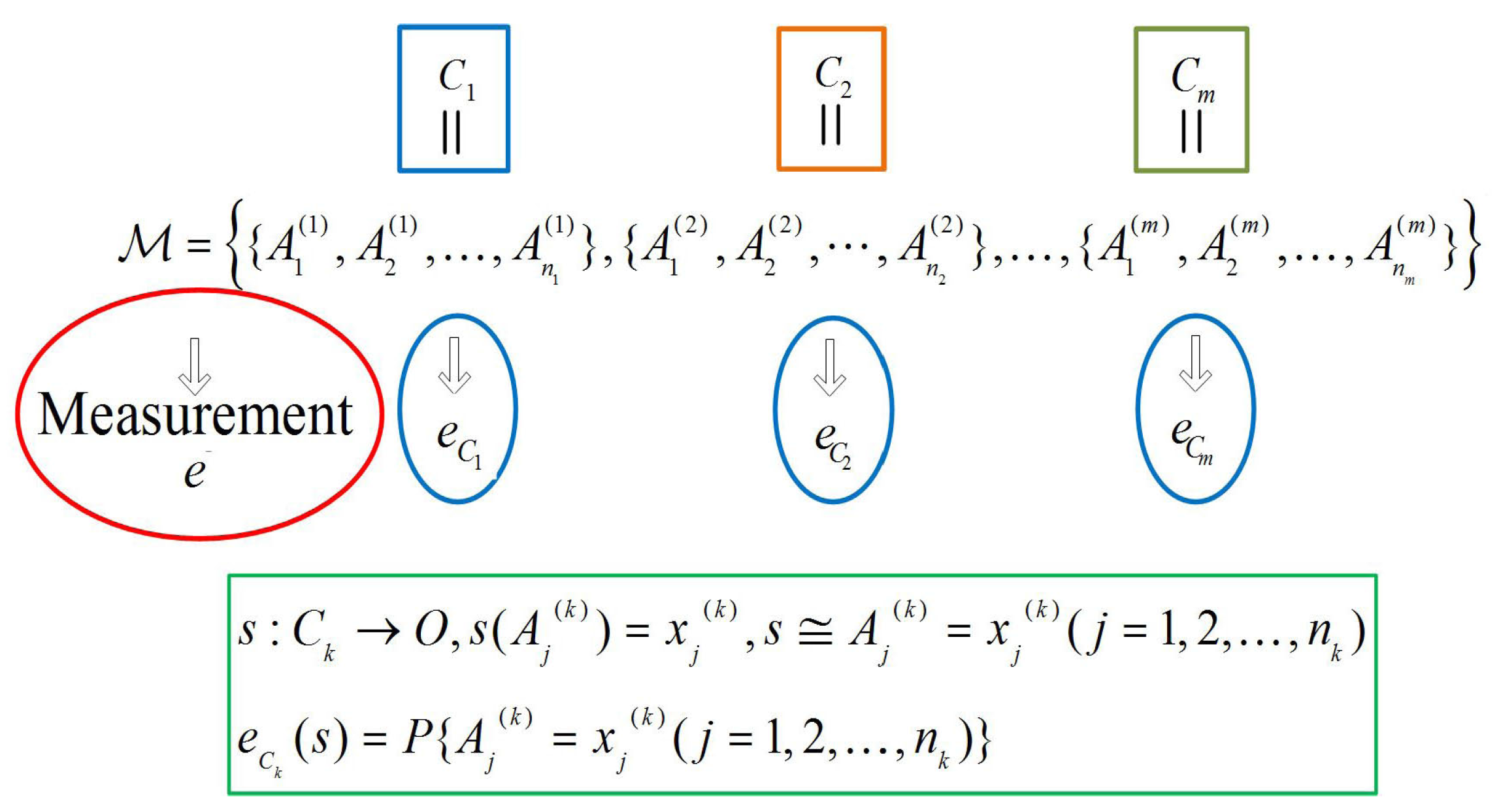
Figure 1 is used to illustrate an empirical model: each context $C_k$ has a joint probability distribution $e_{C_k}$ under a measurement, such that $e_{C_k}\left(s\right)$ is the probability that the event s with $s(A_j^{\left(k\right)})=x_j^{\left(k\right)}(1\le j\le n_k)$ occurs.

Definition 2 

([10]). An empirical model $e={\left\{e_C\right\}}_{C\in \mathcal{M}}$ on an MS $(X,\mathcal{M},O)$ is said to be a no-signaling empirical model if $e_C|C\cap C^{\prime }\left(t\right)=e_{C^{\prime }}|C\cap C^{\prime }\left(t\right)$ for all $t\in \mathcal{E}(C\cap C^{\prime })$ whenever $C,C^{\prime }\in \mathcal{M}$ with $C\cap C^{\prime }\ne \varnothing ,$ where:

$$e_C|C\cap C^{\prime }\left(t\right)=\sum \{e_C\left(s\right):s\in \mathcal{E}\left(C\right),s{|}_{C\cap C^{\prime }}=t\},$$

$$e_{C^{\prime }}|C\cap C^{\prime }\left(t\right)=\sum \left\{e_{C^{\prime }}\left(s^{\prime }\right):s^{\prime }\in \mathcal{E}\left(C^{\prime }\right),s^{\prime }{|}_{C\cap C^{\prime }}=t\right\}.$$

For each event $t:C\cap C^{\prime }\to O$, the value of $e_C|C\cap C^{\prime }$ at t is defined as the sum of all values $e_C\left(s\right)$ with $s\in \mathcal{E}\left(C\right)$, such that ${s|}_{C\cap C^{\prime }}=t$. Similarly, the value of $e_C|C\cap C^{\prime }$ at t is defined as the sum of all values $e_{C^{\prime }}\left(s^{\prime }\right)$ with $s^{\prime }\in \mathcal{E}\left(C^{\prime }\right)$, such that $s^{\prime }{|}_{C\cap C^{\prime }}=t$. See Figure 2.

Let $(X,\mathcal{M},O)$ be an MS. Put:

$$\mathcal{E}\left(X\right)=\{s:s:X\to O\text{is}\text{a}\text{mapping}\},$$

$$\mathcal{D}\left(\mathcal{E}\right(X\left)\right)=\{p:p\text{is}\mathrm{a}\text{probability}\text{distribution}\text{over}\mathcal{E}(X\left)\right\}.$$

For any $p\in \mathcal{D}\left(\mathcal{E}\right(X\left)\right)$ and $C\in \mathcal{M}$, we define:

$$p|C\left(s\right)=\sum \{p\left(s^{\prime }\right):s^{\prime }\in \mathcal{E}\left(X\right),s^{\prime }{|}_C=s\},\forall s\in \mathcal{E}\left(C\right),$$

and obtain $p|C\in \mathcal{D}(\mathcal{E}\left(C\right))$, i.e., $p|C$ is a probability distribution for the measurements in context C.

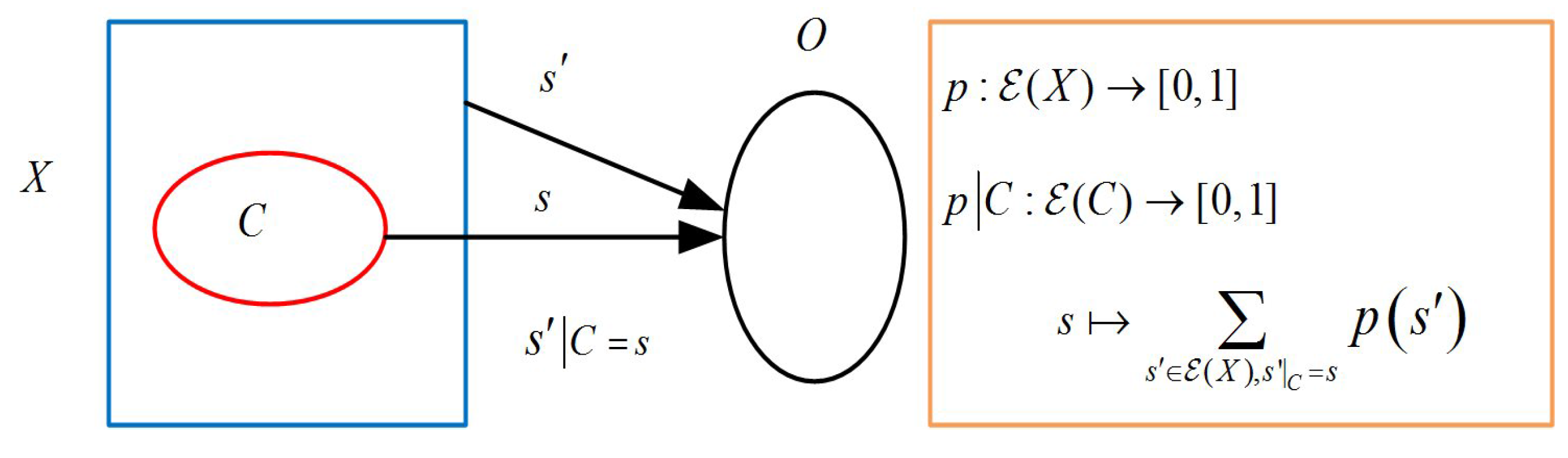
Figure 3 illustrates the value of $p|C$ at $s\in \mathcal{E}\left(C\right)$, i.e., it is defined as the sum of all values $p\left(s^{\prime }\right)$ with $s^{\prime }\in \mathcal{E}\left(X\right)$ such that the restriction of $s^{\prime }$ on C is equal to s: $s^{\prime }{|}_C=s$.

Definition 3 

([10]). An empirical model $e={\left\{e_C\right\}}_{C\in \mathcal{M}}$ on an MS $(X,\mathcal{M},O)$ is said to be non-contextual if there exists $p\in \mathcal{D}\left(\mathcal{E}\right(X\left)\right)$ such that $p|C=e_C$ for all $C\in \mathcal{M}.$ Otherwise, it is said to be contextual.

Remark 1. 

It is easy to check that every non-contextual empirical model is no-signaling.

In the following, we use $EM,NSEM,NCEM$ and $CEM$ to denote the sets of all empirical models, no-signaling empirical models, non-contextual empirical models and contextual empirical models on an MS $(X,\mathcal{M},O)$, respectively.

For any MS $(X,\mathcal{M},O)$, put $m=\left|\mathcal{M}\right|$ (the cardinality of the set $\mathcal{M}$), $\ell ={\sum }_{j=1}^m\left|\mathcal{E}\left(C_i\right)\right|$ and ${\ell }^{\prime }=\left|\mathcal{E}\left(X\right)\right|$. Without loss of generality, we can write:

$$\mathcal{M}=\{C_1,C_2,\dots ,C_m\},\bigcup _{i=1}^m\mathcal{E}\left(C_i\right)=\{s_1,s_2,\dots ,s_{\ell }\},\mathcal{E}\left(X\right)=\{t_1,t_2,\dots ,t_{{\ell }^{\prime }}\}.$$

(1)

Definition 4 

([10]). The incidence matrix associated with an MS $(X,\mathcal{M},O)$ given by (1) is defined as the ℓ by the ${\ell }^{\prime }$ matrix $\mathbf{M}=\left[M_{i,j}\right],$ where $M_{i,j}=1$ if $s_i\in \mathcal{E}\left(C_k\right)$ and $t_j|C_k=s_i$; and $M_{i,j}=0$ otherwise.

Definition 5 

([10]). The incidence vector ${\mathbf{V}}_e$ associated with empirical model $e={\left\{e_{C_k}\right\}}_{C_k\in \mathcal{M}}$ on an MS $(X,\mathcal{M},O)$ given by Equation (1) is defined as the ℓ-dimensional column vector:

$${\mathbf{V}}_e={(V_e\left[1\right],V_e\left[2\right],\dots ,V_e\left[\ell \right])}^T,$$

(2)

where ${\mathbf{V}}_e\left[i\right]=e_{C_k}\left(s_i\right)$ if $s_i\in \mathcal{E}\left(C_k\right)$.

With these notations, the following theorems were proven in [10] (Proposition 4.1 and Theorem 5.5).

Theorem 1 

([10]). $e\in EM$ is non-contextual if and only if the equation $\mathbf{MX}={\mathbf{V}}_e$ has a non-negative real solution $\mathbf{X}={(\mathbf{X}\left[1\right],\mathbf{X}\left[2\right],\dots ,\mathbf{X}\left[{\ell }^{\prime }\right])}^T$ such that ${\sum }_j\mathbf{X}\left[j\right]=1.$

Theorem 2 

([10]). For each $e\in NSEM$, the linear system $\mathbf{MX}={\mathbf{V}}_e$ has a real solution $\mathbf{X}={(\mathbf{X}\left[1\right],\mathbf{X}\left[2\right],\dots ,\mathbf{X}\left[{\ell }^{\prime }\right])}^T$ such that ${\sum }_j\mathbf{X}\left[j\right]=1.$

By looking carefully at the incidence matrix, we obtain the following theorem, which improves Theorem 1.

Theorem 3. 

$e\in EM$ is non-contextual if and only if the equation $\mathbf{MX}={\mathbf{V}}_e$ has a non-negative real solution.

Proof. 

Let $e\in EM$ be non-contextual. Then, we see from Theorem 1 that the equation $\mathbf{MX}={\mathbf{V}}_e$ has a non-negative real solution.

Let $e\in EM$ and the equation $\mathbf{MX}={\mathbf{V}}_e$ have a nonnegative real solution $\mathbf{X}$. Then:

$$\sum _{i=1}^{\ell }\left(\mathbf{MX}\right)\left[i\right]=\sum _{i=1}^{\ell }{\mathbf{V}}_e\left[i\right]=\sum _{i=1}^m\sum _{s\in C_i}{e}_{C_i}\left(s\right)=m.$$

(3)

By directly computing, we obtain that:

$$\sum _{i=1}^{\ell }\left(\mathbf{MX}\right)\left[i\right]=\sum _{i=1}^{\ell }\sum _{j=1}^{{\ell }^{\prime }}\mathbf{M}[i,j]\mathbf{X}\left[j\right]=\sum _{j=1}^{{\ell }^{\prime }}\left(\sum _{i=1}^{\ell }\mathbf{M}[i,j]\right)\mathbf{X}\left[j\right]=\sum _{j=1}^{{\ell }^{\prime }}m\mathbf{X}\left[j\right],$$

where the last equality holds since any entry of $\mathbf{M}$ is either one or zero and the number of ones in every column of $\mathbf{M}$ is m. Combining with Equation (3), we have ${\sum }_{j=1}^{{\ell }^{\prime }}\mathbf{X}\left[j\right]=1$. Therefore, the non-negative real solution $\mathbf{X}$ to $\mathbf{MX}={\mathbf{V}}_e$ satisfies that ${\sum }_{j=1}^{{\ell }^{\prime }}\mathbf{X}\left[j\right]=1$. By Theorem 1, we obtain that e is non-contextual.   □

By Theorem 3, only if the equation $\mathbf{MX}={\mathbf{V}}_e$ has a non-negative real solution, then e is non-contextual.

For given $e,e^{\prime }\in EM$, put:

$${\gamma }_{e,e^{\prime }}\left(x\right)=\frac{1}{1+x}e+\frac{x}{1+x}{e}^{\prime },\forall x\in [0,+\infty ),{\gamma }_{e,e^{\prime }}(+\infty )=e^{\prime }.$$

(4)

Due to the importance of contextuality and motivated by a work on the robustness of entanglement of mixed quantum states against noise and jamming [11], we have proposed and discussed the robustness of contextuality (RoC) $R_C\left(e\right)$ of an empirical model e in [12,13] to quantify the amount of contextuality with respect to non-contextual mixing by asking about the minimal amount of contextuality-free mixing needed to wipe out all contextuality of e. The mathematical definition is as follows.

Definition 6 

([12]). Let $e\in EM$ and $e^{\prime }\in NCEM$. The relative robustness of contextuality of e with respect to $e^{\prime }$ is defined as:

$$R_C\left(e\left|\right|e^{\prime }\right)=min\left\{x\in [0,+\infty ]:{\gamma }_{e,e^{\prime }}\left(x\right)\in NCEM\right\},$$

(5)

and the robustness of contextuality (RoC) of e is defined as:

$$R_C\left(e\right)=min\left\{R_C\left(e\left|\right|e^{\prime }\right):e^{\prime }\in NCEM\right\}.$$

(6)

Contextual empirical model e is the object in which we are interested, and it is contextuality that supplies the “magic” for quantum computation. Although e is contextual, when it is mixed with a non-contextual empirical model $e^{\prime }$, the mixture ${\gamma }_{e,e^{\prime }}\left(x\right)=\frac{1}{1+x}e+\frac{x}{1+x}{e}^{\prime }$ with $x\in [0,+\infty )$ may be non-contextual, and so, the contextuality of e is wiped out by $e^{\prime }$. In this sense, we say that $e^{\prime }$ is noise or jamming. However, noises are not always non-contextual. Motivated by the generalized robustness [14] of entanglement, we investigate the generalized robustness of contextuality $R_g\left(e\right)$, which characterizes the minimal amount of mixing with general noises (i.e., both non-contextual empirical models and contextual ones), which washes out all contextuality of e.

Definition 7. 

$e,e^{\prime }\in EM$. The generalized relative robustness of contextuality of e with respect to $e^{\prime }$ is defined as:

$$R_g\left(e\left|\right|e^{\prime }\right)=\left\{\begin{array}{cc}min\left\{x\in [0,+\infty ]:{\gamma }_{e,e^{\prime }}\left(x\right)\in NCEM\right\},\hfill & {\gamma }_{e,e^{\prime }}\left(x\right)\in NCEM\text{for}\text{some}x\in [0,+\infty )\hfill \\ +\infty ,\hfill & \text{otherwise}\hfill \end{array},\right.$$

(7)

and the generalized robustness of contextuality (GRoC) of e is defined as:

$$R_g\left(e\right)=min\left\{R_g\left(e\left|\right|e^{\prime }\right):e^{\prime }\in EM\right\}.$$

(8)

Considering that the minimums above are taken over compact sets and the functions to be optimized are continuous, we have that Equations (7) and (8) are well defined.

Figure 4 and Figure 5 are given for more intuition about $R_g\left(e\left|\right|e^{\prime }\right)$ and $R_g\left(e\right)$.

Figure 4 shows that $0<R_g\left(e\left|\right|e^{\prime }\right)<+\infty$ implies that ${\gamma }_{e,e^{\prime }}\left(x\right)$ is contextual for all $x\in [0,R_g\left(e\left|\right|e^{\prime }\right))$, and ${\gamma }_{e,e^{\prime }}\left(R_g\left(e\left|\right|e^{\prime }\right)\right)$ is non-contextual. In the case where $e^{\prime }\in NCEM$, ${\gamma }_{e,e^{\prime }}\left(x\right)$ is non-contextual if and only if $x\in [R_g\left(e\left|\right|e^{\prime }\right),+\infty ]$. Figure 5 shows that $R_g\left(e\right)$ is finite, and the smallest radius of the circles containing non-contextual empirical models is $R_g\left(e\right)$. Moreover, the circle with radius $r\in (R_g\left(e\right),+\infty ]$ contains non-contextual empirical models, and the circle with radius $r\in [0,R_g\left(e\right))$ contains only contextual empirical models.

Remark 2. 

By the definitions of RoC and GRoC of an empirical model e, we see that $R_g\left(e\right)\le R_C\left(e\right)$. For any $e\in NSEM$, if $R_g\left(e\right)=R_g\left(e\left|\right|e^{\prime }\right)=x\in (0,\infty )$, then ${\gamma }_{e,e^{\prime }}\left(x\right)$ is non-contextual, and so, ${\gamma }_{e,e^{\prime }}\left(x\right)\in NSEM$ by Remark 1. Thus, $e^{\prime }$ is the no-signaling since $e\in NSEM$ and ${\gamma }_{e,e^{\prime }}\left(x\right)=\frac{1}{1+x}e+\frac{x}{1+x}{e}^{\prime }\in NSEM.$

Using the norm-distance of $EM$ in [12], a sequence ${\left\{e^n\right\}}_{n=1}^{\infty }$ in $EM$ is convergent to e if and only if $e_{C_i}^n\left(s\right)\to e_{C_i}\left(s\right)$ as $n\to \infty$ for all $C_i\in \mathcal{M},s\in \mathcal{E}\left(C_i\right)$. We see from [22] (Section 0.4.6) that there exist invertible matrices $\mathbf{A}$ and $\mathbf{B}$ and identity matrix $\mathbf{I}$ such that:

$$\mathbf{M}=\mathbf{A}\left[\begin{array}{cc}\mathbf{I}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right]\mathbf{B}.$$

(9)

For any positive integer n and $\mathbf{X}\in {\mathbb{R}}^n$, we denote:

$$\left\{\begin{array}{c}{\parallel \mathbf{X}\parallel }_1=\sum _{j=1}^n\left|\mathbf{X}\left[j\right]\right|,\hfill \\ \parallel {\mathbf{A}}^{-1}\parallel =sup\{\parallel {\mathbf{A}}^{-1}{\mathbf{X}\parallel }_1:\mathbf{X}\in {\mathbb{R}}^{\ell }{,\parallel \mathbf{X}\parallel }_1\le 1\}\hfill \\ \parallel {\mathbf{B}}^{-1}\parallel =sup\{\parallel {\mathbf{B}}^{-1}{\mathbf{X}\parallel }_1:\mathbf{X}\in {\mathbb{R}}^{{\ell }^{\prime }}{,\parallel \mathbf{X}\parallel }_1\le 1\}.\hfill \end{array}\right.$$

(10)

Based on the above notations, the boundedness and continuity of GRoC on the set $NSEM$ are proven in the following theorem. Moreover, the following theorem says that GRoC can be used to distinguish non-contextual empirical models from contextual ones.

Theorem 4. 

(i) Let ${\mathbf{X}}_0=\frac{1}{{\ell }^{\prime }}{(1,1,\dots ,1)}^T\in \mathcal{D}\left(\mathcal{E}\left(X\right)\right)$ and ${\mathbf{X}}_0^{♯}$ be the empirical model ${\left\{{\mathbf{X}}_0\right|C_i\}}_{C_i\in \mathcal{M}}$, i.e., the totally mixed non-contextual empirical model. For any $e\in NSEM$, it holds that:

$$0\le R_g\left(e\right)\le m{\ell }^{\prime }\parallel {\mathbf{A}}^{-1}\parallel ·\parallel {\mathbf{B}}^{-1}\parallel <+\infty .$$

(11)

(ii) $R_g\left(e\right)$ is finite for any empirical model e; $R_g\left(e\right)=0$ if and only if e is non-contextual.

(iii) For any $e\in CEM$, it holds that:

$$R_g\left(e\right)=\sup \left\{x\in [0,+\infty ):{\gamma }_{e,e^{\prime }}\left(x\right)\in CEM,\forall e^{\prime }\in EM\right\}.$$

(12)

(iv) The GRoC function $R_g$ is convex on $EM$, i.e., if $e_1,e_2\in EM$, then:

$$R_g(\lambda e_1+(1-\lambda )e_2)\le \lambda R_g\left(e_1\right)+(1-\lambda )R_g\left(e_2\right),\forall \lambda \in (0,1).$$

(13)

(v) $R_g\left(e\right)R_g\left(f\right)\le 1$ for all $e,f\in EM$ with $R_g(e\parallel f)<+\infty$; moreover, for any $e\in EM$, there exists an empirical model f such that $R_g\left(e\right)R_g\left(f\right)\le 1.$

(vi) $R_g$ as a function on $NSEM$ is continuous, that is $\underset{n\to \infty }{lim}{R}_g\left(e^n\right)=R_g\left(e\right)$ provided that $e^n\in NSEM(n=1,2,\dots )$ such that $\underset{n\to \infty }{lim}{e}^n=e$.

Proof. 

(i) Let $e\in NSEM$. Theorem 2 implies that $\mathbf{MX}={\mathbf{V}}_e$ has a real solution $\mathbf{X}={\mathbf{X}}^{\prime }$. Put:

$${\mathbf{Z}}_e=\left(\begin{array}{c}{\mathbf{Z}}_e^1\\ {\mathbf{Z}}_e^2\end{array}\right)={\mathbf{A}}^{-1}{\mathbf{V}}_e,\left(\begin{array}{c}{\mathbf{Y}}_1^{\prime }\\ {\mathbf{Y}}_2^{\prime }\end{array}\right)={\mathbf{BX}}^{\prime },$$

then:

$$\left[\begin{array}{cc}\mathbf{I}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right]\left(\begin{array}{c}{\mathbf{Y}}_1^{\prime }\\ {\mathbf{Y}}_2^{\prime }\end{array}\right)=\left(\begin{array}{c}{\mathbf{Z}}_e^1\\ {\mathbf{Z}}_e^2\end{array}\right).$$

Therefore, ${\mathbf{Z}}_e^2=0$. Put ${\mathbf{X}}_1:={\mathbf{B}}^{-1}\left(\begin{array}{c}{\mathbf{Z}}_e^1\\ \mathbf{0}\end{array}\right),$ then ${\mathbf{MX}}_1={\mathbf{V}}_e$ and so $\mathbf{X}={\mathbf{X}}_1$ is a solution to $\mathbf{MX}={\mathbf{V}}_e$ with:

$$\parallel {\mathbf{X}}_1{\parallel }_1\le \parallel {\mathbf{B}}^{-1}\parallel ·\parallel {\mathbf{Z}}_e^1{\parallel }_1=\parallel {\mathbf{B}}^{-1}\parallel ·\parallel {\mathbf{Z}}_e{\parallel }_1\le \parallel {\mathbf{B}}^{-1}\parallel ·\parallel {\mathbf{A}}^{-1}\parallel ·\parallel {\mathbf{V}}_e{\parallel }_1=m\parallel {\mathbf{B}}^{-1}\parallel ·\parallel {\mathbf{A}}^{-1}\parallel :=B.$$

(14)

Let ${\mathbf{X}}_0=\frac{1}{{\ell }^{\prime }}{(1,1,\dots ,1)}^T\in \mathcal{D}\left(\mathcal{E}\left(X\right)\right)$ and ${\mathbf{X}}_0^{♯}$ be the empirical model ${\left\{{\mathbf{X}}_0\right|C_i\}}_{i=1}^m$. By directly computing, we obtain that $\mathbf{M}{\mathbf{X}}_0={\mathbf{V}}_{{\mathbf{X}}_0^{♯}}$. By Equation (14), we see that $\parallel {\mathbf{X}}_1{\parallel }_1\le B$, and then:

$$({\mathbf{X}}_1+B{\ell }^{\prime }{\mathbf{X}}_0)\left[j\right]={\mathbf{X}}_1\left[j\right]+B{\ell }^{\prime }{\mathbf{X}}_0\left[j\right]\ge -B+B=0,\forall 1\le j\le {\ell }^{\prime }.$$

Hence, $\mathbf{X}=\frac{1}{1+B{\ell }^{\prime }}({\mathbf{X}}_1+B{\ell }^{\prime }{\mathbf{X}}_0)$ is a non-negative solution to $\mathbf{MX}=\frac{1}{1+B{\ell }^{\prime }}\left({\mathbf{V}}_e+B{\ell }^{\prime }{\mathbf{V}}_{{\mathbf{X}}_0^{♯}}\right)$. Using Theorem 3, we obtain that $\frac{1}{1+B{\ell }^{\prime }}(e+B{\ell }^{\prime }{\mathbf{X}}_0^{♯})$ is non-contextual. By Equation (7), we get that $R_g(e\parallel {\mathbf{X}}_0^{♯})\le B{\ell }^{\prime }$. Thus, we obtain by Equations (8) and (14) that Equation (11) holds.

(ii) First, let us prove that $R_g\left(e\right)$ is finite for any empirical model e. To do this, we take an empirical model e and let $f={\mathbf{X}}_0^{♯}$ given in (i). Note that $f_{C_i}={\mathbf{X}}_0|C_i>0$ for all $i=1,2,\dots ,m$, we can choose a small $\epsilon >0$ such that $g:=(1+\epsilon )f+(-\epsilon )e$ is an empirical model. Then, $f={\gamma }_{g,e}\left(\epsilon \right)$, and so, ${\gamma }_{e,g}(1/\epsilon )=f\in NCEM$. This shows that $R_g\left(e\right)\le R_g\left(e\right|\left|g\right)\le 1/\epsilon <+\infty .$ Thus, $R_g\left(e\right)$ is finite, even though it may be very large.

By the definitions of $R_g$ and $R_C$, it is easy to know that $0\le R_g\left(e\right)\le R_C\left(e\right)$ for any $e\in EM$. Since e is non-contextual if and only if $R_C\left(e\right)=0$, we obtain that $R_g\left(e\right)=0$ for non-contextual $e\in EM$. If $R_g\left(e\right)=0$, then there exists $e^{\prime }\in EM$ such that $\frac{1}{1+0}e+\frac{0}{1+0}{e}^{\prime }\in NCEM$ by Equations (7) and (8). Thus, $e\in NCEM$.

(iii) Since e is contextual, we can assume that $R_g\left(e\right)\in (0,+\infty )$ in the following. Put:

$$Y\left(e\right)=\left\{x\in [0,+\infty ):{\gamma }_{e,e^{\prime }}\left(x\right)\in CEM,\forall e^{\prime }\in EM\right\}.$$

Then, $0\in Y\left(e\right)$, and so, $Y\left(e\right)$ is not empty.

At first, we shall show that $R_g\left(e\right)$ is an upper bound of the set $Y\left(e\right).$ Suppose that there exists an $x_0\in Y\left(e\right)$ such that $x_0>R_g\left(e\right).$ Let $R_g\left(e\right)=R_g(e\parallel e^{\prime })$ for some $e^{\prime }\in EM$ such that ${\gamma }_{e,e^{\prime }}\left(y\right)\in NCEM$ where $y=R_g(e\parallel e^{\prime })$. For any $f\in NCEM$, we see from the convexity of $NCEM$ [12] that:

$$g:=\frac{1+y}{1+x_0}{\gamma }_{e,e^{\prime }}\left(y\right)+\frac{x_0-y}{1+x_0}f\in NCEM.$$

Set $e^{\prime \prime }=\frac{y}{x_0}{e}^{\prime }+\frac{x_0-y}{x_0}f\in EM$. Then:

$${\gamma }_{e,e^{\prime \prime }}\left(x_0\right)=\frac{1}{1+x_0}e+\frac{x_0}{1+x_0}\left(\frac{y}{x_0}{e}^{\prime }+\frac{x_0-y}{x_0}f\right)=g\in NCEM,$$

which contradicts the property of $x_0$. This shows that $R_g\left(e\right)$ is an upper bound of the set $Y\left(e\right).$

Then, we shall prove that $R_g\left(e\right)$ is the supremum of the set $Y\left(e\right).$ Since e is contextual, we obtain from (ii) that $R_g\left(e\right)>0$. For any $\epsilon \in (0,R_g\left(e\right))$, take $x=R_g\left(e\right)-\frac{\epsilon }{2}$. Then, $x\in (0,+\infty )$ and $R_g\left(e\right)-\epsilon$ $<x<R_g\left(e\right)$. If there exists an $e^{\prime }\in EM$ such that ${\gamma }_{e,e^{\prime }}\left(x\right)\in NCEM$, then $R_g\left(e\right)\le R_g(e\parallel e^{\prime })\le x<R_g\left(e\right)$, a contradiction. Hence, ${\gamma }_{e,e^{\prime }}\left(x\right)\in CEM$ for all $e^{\prime }\in EM$, and so, $x\in Y\left(e\right)$ with $R_g\left(e\right)-\epsilon <x$. Therefore, $R_g\left(e\right)=supY\left(e\right)$, i.e., (12) holds.

(iv) Let:

$$e_1,e_2\in EM,R_g\left(e_1\right)=x_1,R_g\left(e_2\right)=x_2$$

and $e=\lambda e_1+(1-\lambda )e_2(\lambda \in (0,1))$. Then by (ii) we see that both $x_1$ and $x_2$ are finite. Put $x=\lambda x_1+(1-\lambda )x_2.$ Thus, there exist $e_1^{\prime },e_2^{\prime }\in EM$ such that ${\gamma }_{e_1,e_1^{\prime }}\left(x_1\right),{\gamma }_{e_2,e_2^{\prime }}\left(x_2\right)\in NCEM$ and:

$$R_g\left(e_1\right)=R_g(e_1\left|\right|e_1^{\prime }),R_g\left(e_2\right)=R_g(e_2\left|\right|e_2^{\prime }).$$

Since $\frac{\lambda x_1}{x},\frac{(1-\lambda )x_2}{x}\ge 0$ and $\frac{\lambda x_1}{x}+\frac{(1-\lambda )x_2}{x}=1$, we get $e^{\prime }:=\frac{\lambda x_1}{x}{e}_1^{\prime }+\frac{(1-\lambda )x_2}{x}{e}_2^{\prime }\in EM,$ and:

$$\begin{array}{ccc}\hfill {\gamma }_{e,e^{\prime }}\left(x\right)& =& \frac{1}{1+x}e+\frac{x}{1+x}{e}^{\prime }\hfill \\ & =& \frac{1}{1+x}(\lambda e_1+(1-\lambda )e_2)+\frac{x}{1+x}\left(\frac{\lambda x_1}{x}{e}_1^{\prime }+\frac{(1-\lambda )x_2}{x}{e}_2^{\prime }\right)\hfill \\ & =& \frac{\lambda (1+x_1)}{1+x}\left[\frac{1}{1+x_1}{e}_1+\frac{x_1}{1+x_1}{e}_1^{\prime }\right]+\frac{(1-\lambda )(1+x_2)}{1+x}\left[\frac{1}{1+x_2}{e}_2+\frac{x_2}{1+x_2}{e}_2^{\prime }\right]\hfill \\ & =& \frac{\lambda (1+x_1)}{1+x}{\gamma }_{e_1,e_1^{\prime }}\left(x_1\right)+\frac{(1-\lambda )(1+x_2)}{1+x}{\gamma }_{e_2,e_2^{\prime }}\left(x_2\right).\hfill \end{array}$$

Observing that:

$$\frac{\lambda (1+x_1)}{1+x},\frac{(1-\lambda )(1+x_2)}{1+x}\ge 0,\frac{\lambda (1+x_1)}{1+x}+\frac{(1-\lambda )(1+x_2)}{1+x}=1,$$

we see that ${\gamma }_{e,e^{\prime }}\left(x\right)\in NCEM$. Consequently,

$$R_g(\lambda e_1+(1-\lambda )e_2)=R_g\left(e\right)\le R_g\left(e\right||e^{\prime })\le x=\lambda R_g\left(e_1\right)+(1-\lambda )R_g\left(e_2\right).$$

(v) Assume that $x=R_g(e\parallel f)<+\infty$. Clearly, if $x=0$, then $R_g\left(e\right)=0$ by Equation (8). We see from (ii) that $R_g\left(f\right)<+\infty$, and so, $R_g\left(e\right)R_g\left(f\right)=0<1$. Next, we assume that $x>0$. Then, ${\gamma }_{e,f}\left(x\right)=\frac{e+xf}{1+x}\in NCEM$. Since:

$${\gamma }_{f,e}(\frac{1}{x})=\frac{f+\frac{1}{x}e}{1+\frac{1}{x}}={\gamma }_{e,f}\left(x\right)\in NCEM,$$

we obtain that $R_g(f\parallel e)\le \frac{1}{x}$ and then:

$$R_g\left(e\right)R_g\left(f\right)\le R_g(e\parallel f)R_g(f\parallel e)\le x\times \frac{1}{x}=1.$$

For any $e\in EM$, we see from Equation (8) that there exists an empirical model f such that $R_g(e\parallel f)=R_g\left(e\right)$. The first conclusion of (ii) yields that $R_g(e\parallel f)<\infty$, and then, the first conclusion implies that $R_g\left(e\right)R_g\left(f\right)\le 1$.

(vi) Assume that $e^n\in NSEM(n=1,2,\dots )$ such that $\underset{n\to \infty }{lim}{e}^n=e$. By the closedness of $NSEM$ ([12], Theorem 2.2), we obtain that $e\in NSEM$.

Claim 1. 

$R_g\left(e\right)\le {\displaystyle \underset{n\to \infty }{{\displaystyle \underline{lim}}}}{R}_g\left(e^n\right).$

Put $x={\displaystyle \underset{n\to \infty }{{\displaystyle \underline{lim}}}}{R}_g\left(e^n\right).$ Then, $x=\underset{k\to \infty }{lim}{R}_g\left(e^{n_k}\right)$ for some subsequence ${\left\{e^{n_k}\right\}}_{k=1}^{\infty }$. For each $k=1,2,\dots ,$ there exists $f^k\in NSEM$ such that $R_g\left(e^{n_k}\right)=R_g(e^{n_k}\left|\right|f^k):=x_k\in [0,\infty )$. The compactness of $NSEM$ ([12], Theorem 2.2) yields that there exists a subsequence ${\left\{f^{k_j}\right\}}_{k=1}^{+\infty }$ satisfying $f^{k_j}\to f\in NSEM$ as $j\to \infty$. Since

$$\frac{1}{1+x_{k_j}}{e}^{n_{k_j}}+\frac{x_{k_j}}{1+x_{k_j}}{f}^{k_j}\in NCEM$$

and $NCEM$ is closed, we have:

$$\frac{1}{1+x_{k_j}}{e}^{n_{k_j}}+\frac{x_{k_j}}{1+x_{k_j}}{f}^{k_j}\to \frac{1}{1+x}e+\frac{x}{1+x}f\in NCEM.$$

By Equation (7) and (8), we know that $R_g\left(e\right)\le R_g\left(e\right|\left|f\right)\le x={\displaystyle \underset{n\to \infty }{{\displaystyle \underline{lim}}}}{R}_g\left(e^n\right).$

Claim 2. 

${\displaystyle \underset{n\to \infty }{{\displaystyle \overline{lim}}}}{R}_g\left(e^n\right)\le R_g\left(e\right).$

Assume that ${\displaystyle \underset{n\to \infty }{{\displaystyle \overline{lim}}}}{R}_g\left(e^n\right)=\underset{k\to \infty }{lim}{R}_g\left(e^{n_k}\right)$.

When the set $\{k:e^{n_k}\ne e\}$ is finite, then we obtain that ${\displaystyle \underset{n\to \infty }{{\displaystyle \overline{lim}}}}{R}_g\left(e^n\right)=\underset{k\to \infty }{lim}{R}_g\left(e^{n_k}\right)=R_g\left(e\right)$.

When the set $\{k:e^{n_k}\ne e\}$ is infinite, there exists subsequence ${\left\{e^{n_{k_j}}\right\}}_{j=1}^{\infty }$ of ${\left\{e^{n_k}\right\}}_{k=1}^{\infty }$ such that $e^{n_{k_j}}\ne e$ for any j. For any $C_i\in \mathcal{M}$, take:

$${\mathcal{F}}_{C_i}=\{s\in \mathcal{E}\left(C_i\right):e_{C_i}\left(s\right)=0\},{\mathcal{G}}_{C_i}=\{s\in \mathcal{E}\left(C_i\right):e_{C_i}\left(s\right)\ne 0\}.$$

Then:

$${\mathcal{F}}_{C_i}\bigcap {\mathcal{G}}_{C_i}=\varnothing \text{and}{\mathcal{F}}_{C_i}\bigcup {\mathcal{G}}_{C_i}=\mathcal{E}\left(C_i\right).$$

Since ${\sum }_{s\in \mathcal{E}\left(C_i\right)}{e}_{C_i}\left(s\right)=1$ and $e_{C_i}\left(s\right)\ge 0$ for any $s\in \mathcal{E}\left(C_i\right)$, we get that ${\mathcal{G}}_{C_i}\ne \varnothing$. For any $s\in {\mathcal{G}}_{C_i}$, since $e_{C_i}\left(s\right)>0$ and $e_{C_i}^{n_{k_j}}\left(s\right)\to e_{C_i}\left(s\right)$ as j goes to infinity, we obtain that there exists positive integer $J_{C_i,s}$ such that:

$$e_{C_i}^{n_{k_j}}\left(s\right)>\frac{1}{2}{e}_{C_i}\left(s\right)>0,\forall j>J_{C_i,s}.$$

Take:

$$J=max\{J_{C_i,s}:C_i\in \mathcal{M},s\in {\mathcal{G}}_{C_i}\}.$$

Then, we have that $e_{C_i}^{n_{k_j}}\left(s\right)>0$ for any $j>J$, $C_i\in \mathcal{M}$ and $s\in {\mathcal{G}}_{C_i}$. For any $j>J$, take:

$${\epsilon }_j=\underset{C_i\in \mathcal{M},s\in {\mathcal{G}}_{C_i}}{max}max\left\{0,\frac{e_{C_i}\left(s\right)}{e_{C_i}^{n_{k_j}}\left(s\right)}-1\right\}\le \underset{C_i\in \mathcal{M},s\in {\mathcal{G}}_{C_i}}{max}\left|\frac{e_{C_i}\left(s\right)}{e_{C_i}^{n_{k_j}}\left(s\right)}-1\right|.$$

Thus, ${\epsilon }_j$ is convergent to zero since $e^{n_{k_j}}$ converges to e and ${\epsilon }_j>0$ for any j. Otherwise, when ${\epsilon }_j=0$ for some j, we have $e_{C_i}\left(s\right)\le e_{C_i}^{n_{k_j}}\left(s\right)$ for any $C_i\in \mathcal{M}$ and $s\in \mathcal{E}\left(C_i\right)$. Since:

$$1=\sum _{s\in \mathcal{E}\left(C_i\right)}{e}_{C_i}\left(s\right)=\sum _{s\in {\mathcal{G}}_{C_i}}{e}_{C_i}\left(s\right)\le \sum _{s\in {\mathcal{G}}_{C_i}}{e}_{C_i}^{n_{k_j}}\left(s\right)\le \sum _{s\in \mathcal{E}\left(C_i\right)}{e}_{C_i}^{n_{k_j}}\left(s\right)=1,$$

we obtain that $e_{C_i}^{n_{k_j}}\left(s\right)=e_{C_i}\left(s\right)$ for any $C_i\in \mathcal{M},s\in \mathcal{E}\left(C_i\right)$, and then, $e^{n_{k_j}}=e$, which contradicts the fact that $e^{n_{k_j}}\ne e$ for all j. Thus, we obtain a sequence of positive numbers ${\epsilon }_j$ with limit zero. Take:

$$f_{C_i}^j\left(s\right)=\left\{\begin{array}{cc}\frac{1}{1-\frac{1}{1+{\epsilon }_j}}{e}_{C_i}^{n_{k_j}}\left(s\right),\hfill & s\in {\mathcal{F}}_{C_i}\hfill \\ \frac{e_{C_i}^{n_{k_j}}\left(s\right)-\frac{1}{1+{\epsilon }_j}{e}_{C_i}\left(s\right)}{1-\frac{1}{1+{\epsilon }_j}},\hfill & s\in {\mathcal{G}}_{C_i}\hfill \end{array},\right.$$

for any $C_i\in \mathcal{M},s\in \mathcal{E}\left(C_i\right)$. Since ${\epsilon }_j\ge \frac{e_{C_i}\left(s\right)}{e_{C_i}^{n_{k_j}}\left(s\right)}-1$ for any $C_i\in \mathcal{M}$ and $s\in {\mathcal{G}}_{C_i}$, we have:

$$1+{\epsilon }_j\ge \frac{e_{C_i}\left(s\right)}{e_{C_i}^{n_{k_j}}\left(s\right)}>0,\text{for}\text{any}{C}_i\in \mathcal{M},s\in {\mathcal{G}}_{C_i}.$$

Hence,

$$e_{C_i}^{n_{k_j}}\left(s\right)-\frac{1}{1+{\epsilon }_j}{e}_{C_i}\left(s\right)\ge e_{C_i}^{n_{k_j}}\left(s\right)-\frac{e_{C_i}^{n_{k_j}}\left(s\right)}{e_{C_i}\left(s\right)}{e}_{C_i}\left(s\right)=0,\forall C_i\in \mathcal{M},s\in {\mathcal{G}}_{C_i}$$

and so, for any $C_i\in \mathcal{M}$, we have that $f_{C_i}^j\left(s\right)\ge 0$ for all $s\in \mathcal{E}\left(C_i\right)$. By directly computing, we obtain that ${\sum }_{s\in \mathcal{E}\left(C_i\right)}{f}_{C_i}^j\left(s\right)=1$ for any $C_i\in \mathcal{M}$ and then $f^j\in EM$. Since:

$$e^{n_{k_j}}=\left(1-\frac{1}{1+{\epsilon }_j}\right)f^j+\frac{1}{1+{\epsilon }_j}e,$$

$R_g$ is convex (by (iv)) and $R_g\left(f^j\right)\le m{\ell }^{\prime }\parallel {\mathbf{A}}^{-1}\parallel ·\parallel {\mathbf{B}}^{-1}\parallel$ for any j (by (i)), we obtain that for any j,

$$\begin{array}{ccc}\hfill R_g\left(e^{n_{k_j}}\right)& =& R_g\left(\left(1-\frac{1}{1+{\epsilon }_j}\right)f^j+\frac{1}{1+{\epsilon }_j}e\right)\hfill \\ & \le & \left(1-\frac{1}{1+{\epsilon }_j}\right)R_g\left(f^j\right)+\frac{1}{1+{\epsilon }_j}{R}_g\left(e\right)\hfill \\ & \le & \left(1-\frac{1}{1+{\epsilon }_j}\right)m{\ell }^{\prime }\parallel {\mathbf{A}}^{-1}\parallel ·\parallel {\mathbf{B}}^{-1}\parallel +\frac{1}{1+{\epsilon }_j}{R}_g\left(e\right)\hfill \\ & \to & R_g\left(e\right).\hfill \end{array}$$

Therefore,

$$\underset{n\to \infty }{\overline{lim}}{R}_g\left(e^n\right)=\underset{j\to \infty }{lim}{R}_g\left(e^{n_{k_j}}\right)\le R_g\left(e\right).$$

Combining Claim 1 with Claim 2, we see that:

$$R_g\left(e\right)\le \underset{n\to \infty }{\underline{lim}}{R}_g\left(e^n\right)\le \underset{n\to \infty }{\overline{lim}}{R}_g\left(e^n\right)\le R_g\left(e\right)$$

and then $\underset{n\to \infty }{lim}{R}_g\left(e^n\right)=R_g\left(e\right)$.   □

By Equation (13), we observe that:

$$R_g(\lambda e_1+(1-\lambda )e_2)\le max\{R_g\left(e_1\right),R_g\left(e_2\right)\},\lambda \in (0,1).$$

This means that there does not exist a parameter $\lambda \in (0,1)$ such that:

$$R_g(\lambda e_1+(1-\lambda )e_2)>R_g\left(e_1\right)\text{and}{R}_g(\lambda e_1+(1-\lambda )e_2)>R_g\left(e_2\right).$$

In other words, mixing of two empirical models does not increase simultaneously the GRoC of the mixed empirical models. Theorem 4. (v) says that $R_g\left(e\right)$ and $R_g\left(f\right)$ cannot be large simultaneously whenever $e,f\in EM$ and $R_g(e\parallel f)<+\infty$. By the compactness of $EM$ ([12], Theorem 2.2), we obtain that Claim 1 also holds for $e^n\in EM(n=1,2,\dots )$ such that $\underset{n\to \infty }{lim}{e}^n=e$, i.e. for any $e_0\in EM$ and any $\epsilon >0$, there exists $\delta >0$ such that $R_g\left(e_0\right)-\epsilon <R_g\left(e\right)$ provided that $e\in EM$ with $\parallel e-e_0\parallel <\delta .$

Definition 8 

([10]). An empirical model $e={\left\{e_{C_i}\right\}}_{C_i\in \mathcal{M}}$ is said to be strongly contextual if for any $s\in \mathcal{E}\left(X\right)$ there exists $C_i\in \mathcal{M}$ such that $e_{C_i}\left(s{|}_{C_i}\right)=0.$

Definition 9 

([12]). The quantity:

$$C\left(e\right)=\inf \left\{p\in [0,1]:e=p{e}^{\prime }+(1-p)e^{\prime \prime },e^{\prime }\in EM,e^{\prime \prime }\in NCEM\right\}$$

is called the contextuality cost of $e\in EM$.

Corollary 1. 

There exists a strongly contextual $e_0\in NSEM$ such that:

$$R_g\left(e_0\right)=max\{R_g\left(e\right):e\in NSEM\}.$$

Proof. 

Since $R_g$ is continuous on $NSEM$ and $NSEM$ is a compact set, we obtain that $R_g$ has a maximal value on $NSEM$. For any $e\in CEM\bigcap NSEM$, if e is not strongly contextual, then the cost of contextuality $C\left(e\right)$ of e is strictly less than one ([12], Theorem 4.1), and there exist strongly contextual $f\in NSEM$ and non-contextual $h\in EM$ such that $e=C\left(e\right)f+(1-C(e\left)\right)h$ ([12], Corollary 4.1). Since h is non-contextual, we see from Theorem 4 that $R_g\left(h\right)=0$. It follows from the convexity of $R_g$ (Theorem 4) that:

$$R_g\left(e\right)\le C\left(e\right)R_g\left(f\right)+(1-C\left(e\right))R_g\left(h\right)=C\left(e\right)R_g\left(f\right)<R_g\left(f\right).$$

This shows that the maximal value of $R_g$ over $NSEM$ must be attained at some strongly contextual and no-signaling empirical model.   □

3. The GRoC of $\mathit{n}$-Cycle Boxes

In this section, we consider n dichotomic observables $X_0,\dots ,X_{n-1}$, where each consecutive pair $\{X_i,X_{i+1}\}$, sum mod n, is jointly measurable and take:

$$X={\left\{X_i\right\}}_{i=0}^{n-1},O=\{0,1\},\text{and}\mathcal{M}={\left\{C_i\right\}}_{i=0}^{n-1}\text{with}{C}_i=\{X_i,X_{i+1}\}.$$

Then, $(X,\mathcal{M},O)$ is an MS. The no-signaling empirical models on MS $(X,\mathcal{M},O)$ are said to be n-cycle boxes. To compute the GRoC of n-cycle boxes, the following notations and lemmas are needed. Denote events on measurement context $C_i$ as:

$$s_{00}^i:C_i\to O\text{with}{s}_{00}^i\left(X_i\right)=s_{00}^i\left(X_{i+1}\right)=0;s_{01}^i:C_i\to O\text{with}{s}_{01}^i\left(X_i\right)=0,s_{01}^i\left(X_{i+1}\right)=1;$$

$$s_{10}^i:C_i\to O\text{with}{s}_{10}^i\left(X_i\right)=1,s_{10}^i\left(X_{i+1}\right)=0;s_{11}^i:C_i\to O\text{with}{s}_{11}^i\left(X_i\right)=s_{11}^i\left(X_{i+1}\right)=1,$$

where the sum is mod n. Thus, $\mathcal{E}\left(C_i\right)=\{s_{00}^i,s_{01}^i,s_{10}^i,s_{11}^i\}$ for any $C_i$. For any n-cycle box $e={\left\{e_{C_i}\right\}}_{C_i\in \mathcal{M}}$, take:

$$E_i^e=e_{C_i}\left(s_{00}^i\right)+e_{C_i}\left(s_{11}^i\right)-e_{C_i}\left(s_{01}^i\right)-e_{C_i}\left(s_{10}^i\right).$$

(15)

Put:

$$\mathrm{\Gamma }=\{{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}:{\gamma }_i\in \{-1,1\},|\{i:{\gamma }_i=-1\}\left|\text{is}\text{odd}\right\}.$$

(16)

In the following, we assume that $n\ge 4$ unless otherwise stated and compute $R_g\left(e\right)$.

Lemma 1 

([16]). An n-cycle box e is non-contextual if and only if all $2^{n-1}$ tight non-contextuality inequalities hold, i.e.,

$${\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}=\sum _{i=0}^{n-1}{\gamma }_i{E}_i^e\le n-2,\forall {\left\{{\gamma }_i\right\}}_{i=0}^{n-1}\in \mathrm{\Gamma }.$$

For an n-cycle box e, take:

$${△}_e=\max \left\{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}:{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}\in \mathrm{\Gamma }\right\}-(n-2).$$

(17)

Then, ${△}_e$ quantifies the extent of violating the non-contextual inequalities in Lemma 1. By Lemma 1 and Equation (17), we see that e is non-contextual if and only if ${△}_e\le 0$.

Lemma 2. 

For every contextual n-cycle box e, there exists one and only one non-contextuality inequality of all $2^{n-1}$ tight non-contextuality inequalities that is violated. That is, for an n-cycle box e, if there exists ${\left\{{\gamma }_i\right\}}_{i=0}^{n-1}\in \mathrm{\Gamma }$ such that ${\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}>n-2$, then:

$${\Omega }_{e,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}<n-2,\forall {\left\{{\beta }_i\right\}}_{i=0}^{n-1}\in \mathrm{\Gamma }\backslash \{{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}\}.$$

Proof. 

Assume that ${\left\{{\gamma }_i\right\}}_{i=0}^{n-1}\in \mathrm{\Gamma }$ such that ${\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}>n-2$. Let ${\left\{{\beta }_i\right\}}_{i=0}^{n-1}\in \mathrm{\Gamma }\backslash \{{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}\}$. Then, we obtain by Equation (16) that ${\gamma }_i,{\beta }_i\in \{-1,1\}$; both $\left|\right\{i:{\gamma }_i=-1\left\}\right|$ and $\left|\right\{i:{\beta }_i=-1\left\}\right|$ are odd numbers and ${\left\{{\beta }_i\right\}}_{i=0}^{n-1}\ne {\left\{{\gamma }_i\right\}}_{i=0}^{n-1}$. Therefore, there exist $0\le j\ne k\le n-1$ such that ${\beta }_j=-{\gamma }_j$ and ${\beta }_k=-{\gamma }_k$. Since $e_{C_i}\in \mathcal{D}\left(\mathcal{E}\left(C_i\right)\right),$ we obtain that $|E_i^e|\le 1$ by Equation (15). Moreover, $(n-2)-{\sum }_{i\ne j,k}{\gamma }_i{E}_i^e<{\gamma }_j{E}_j^e+{\gamma }_k{E}_k^e$ since ${\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}>n-2$. Thus,

$$\begin{array}{ccc}\hfill {\Omega }_{e,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}& =& \sum _{i=0}^{n-1}{\beta }_i{E}_i^e\hfill \\ & =& \sum _{i\ne j,k}{\beta }_i{E}_i^e-{\gamma }_j{E}_j^e-{\gamma }_k{E}_k^e\hfill \\ & <& \sum _{i\ne j,k}{\beta }_i{E}_i^e-\left((n-2)-\sum _{i\ne j,k}{\gamma }_i{E}_i^e\right)\hfill \\ & \le & 2\sum _{i\ne j,k}\left|E_i^e\right|-(n-2)\hfill \\ & \le & 2(n-2)-(n-2)\hfill \\ & =& n-2.\hfill \end{array}$$

   □

With these lemmas, we can prove the following theorem.

Theorem 5. 

For any n-cycle box e, it holds that:

$$R_g\left(e\right)=\frac{\max \{{△}_e,0\}}{2n-2}.$$

(18)

Proof. 

• Case (i): If e is non-contextual, then we have that $R_g\left(e\right)=0$ by Theorem 4 (ii) and ${\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}\le n-2$ for any ${\left\{{\gamma }_i\right\}}_{i=0}^{n-1}\in \mathrm{\Gamma }$ by Lemma 1. By Equation (17), we see that ${△}_e\le 0$, and so, (18) holds.
• Case (ii): If e is contextual, then there exists one and only one ${\left\{{\gamma }_i\right\}}_{i=0}^{n-1}\in \mathrm{\Gamma }$ such that ${\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}>n-2$, and so:

  $${\Omega }_{e,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}=\sum _{i=0}^{n-1}{\beta }_i{E}_i^e<n-2,\forall {\left\{{\beta }_i\right\}}_{i=0}^{n-1}\in \mathrm{\Gamma }\backslash \left\{{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}\right\}.$$

  (19)
  Take

  $$x_0=\frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}-(n-2)}{2n-2}.$$
  Then, $x_0=\frac{{△}_e}{2n-2}=\frac{\max \{{△}_e,0\}}{2n-2}$. Clearly, there exists n-cycle box f such that:

  $$E_i^f=\left\{\begin{array}{cc}1,\hfill & \text{if}{\gamma }_i=-1;\hfill \\ -1,\hfill & \text{if}{\gamma }_i=1.\hfill \end{array}\right.$$
• Case (ii${}_a$): If n is an even number, then we obtain that ${\{-{\gamma }_i\}}_{i=0}^{n-1}\in \mathrm{\Gamma }$ and ${\Omega }_{f,{\{-{\gamma }_i\}}_{i=0}^{n-1}}=n$. By Lemma 2, we have that:

  $${\Omega }_{f,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}=\sum _{i=0}^{n-1}{\beta }_i{E}_i^f<n-2,\forall {\left\{{\beta }_i\right\}}_{i=0}^{n-1}\in \mathrm{\Gamma }\backslash \left\{{\{-{\gamma }_i\}}_{i=0}^{n-1}\right\}.$$

  (20)

Claim 3. 

$R_g\left(e\right|\left|f\right)=x_0$.

By Lemma 1 and Inequalities (19) and (20), we obtain that $\frac{1}{1+x}e+\frac{x}{1+x}f$ is non-contextual if and only if:

$$\frac{1}{1+x}{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}+\frac{x}{1+x}{\Omega }_{f,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}=\frac{1}{1+x}{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}-\frac{nx}{1+x}\le n-2$$

and:

$$\frac{1}{1+x}{\Omega }_{e,{\{-{\gamma }_i\}}_{i=0}^{n-1}}+\frac{x}{1+x}{\Omega }_{f,{\{-{\gamma }_i\}}_{i=0}^{n-1}}=-\frac{1}{1+x}{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}+\frac{nx}{1+x}\le n-2,$$

i.e.,

$$x_0=\frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}-(n-2)}{2n-2}\le x\le \frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}+(n-2)}{2}.$$

By Equation (7), we obtain that $R_g\left(e\right|\left|f\right)=x_0$.

Claim 4. 

$R_g\left(e\right)=x_0$.

By Claim 3 and Equation (8), we have $R_g\left(e\right)\le x_0$. Take:

$$E{M}_1=\{h\in EM:{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}>n-2\},$$

$$E{M}_2=\{h\in EM:-n\le {\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}<-(n-2)\}$$

and:

$$E{M}_3=\{h\in EM:-(n-2)\le {\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}\le n-2\}.$$

Then, $E{M}_1\cup E{M}_2\cup E{M}_3=EM$.

For $h\in E{M}_1$, we have:

$$\frac{1}{1+x}{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}+\frac{x}{1+x}{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}>n-2,\forall x\in [0,+\infty ].$$

Hence, we have from Lemma 1 that $\frac{1}{1+x}e+\frac{x}{1+x}h$ is contextual for any $x\in [0,+\infty ]$, and so, $R_g\left(e\right|\left|h\right)=+\infty >x_0$ by Equation (7).

For $h\in E{M}_2$, we have that ${\Omega }_{h,{\{-{\gamma }_i\}}_{i=0}^{n-1}}>n-2$, and so:

$${\Omega }_{h,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}=\sum _{i=0}^{n-1}{\beta }_i{E}_i^h<n-2,\forall {\left\{{\beta }_i\right\}}_{i=0}^{n-1}\in \mathrm{\Gamma }\backslash \left\{{\{-{\gamma }_i\}}_{i=0}^{n-1}\right\}.$$

(21)

By Lemma 1 and Inequalities (19) and (21), we obtain that $\frac{1}{1+x}e+\frac{x}{1+x}h$ is non-contextual if and only if:

$$\frac{1}{1+x}{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}+\frac{x}{1+x}{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}\le n-2$$

and:

$$\frac{1}{1+x}{\Omega }_{e,{\{-{\gamma }_i\}}_{i=0}^{n-1}}+\frac{x}{1+x}{\Omega }_{h,{\{-{\gamma }_i\}}_{i=0}^{n-1}}\le n-2,$$

i.e.,

$$\frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}-(n-2)}{n-2-{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}}\le x\text{and}x\le \frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}+(n-2)}{{\Omega }_{h,{\{-{\gamma }_i\}}_{i=0}^{n-1}}-(n-2)}.$$

Since:

$$\frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}-(n-2)}{n-2-{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}}\le \frac{2}{n-2}\le 1\le \frac{n-2}{2}\le \frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}+(n-2)}{{\Omega }_{h,{\{-{\gamma }_i\}}_{i=0}^{n-1}}-(n-2)}$$

for $n\ge 4$, we obtain that $\frac{1}{1+x}e+\frac{x}{1+x}h$ is non-contextual if and only if:

$$\frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}-(n-2)}{n-2-{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}}\le x\le \frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}+(n-2)}{{\Omega }_{h,{\{-{\gamma }_i\}}_{i=0}^{n-1}}-(n-2)}.$$

(22)

By Equation (7), we get that $R_g\left(e\right|\left|h\right)=\frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}-(n-2)}{n-2-{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}}$. Since ${\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}\ge -n$, we see that $R_g\left(e\right|\left|h\right)\ge x_0$.

When $h\in E{M}_3\bigcap NCEM$, we know that:

$${\Omega }_{h,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}=\sum _{i=0}^{n-1}{\beta }_i{E}_i^h\le n-2,\forall {\left\{{\beta }_i\right\}}_{i=0}^{n-1}\in \mathrm{\Gamma }.$$

(23)

Combining Lemma 1 and Inequalities (19) and (23), we get that $\frac{1}{1+x}e+\frac{x}{1+x}h$ is non-contextual if and only if:

$$\frac{1}{1+x}{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}+\frac{x}{1+x}{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}\le n-2.$$

(24)

If ${\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}=n-2$, then for any $x\in [0,+\infty )$, Inequality (24) is always violated, and so, $\frac{1}{1+x}e+\frac{x}{1+x}h$ is contextual. By Equation (7), we obtain from inequality (24) that $R_g\left(e\right|\left|h\right)=+\infty \ge x_0$. If ${\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}<n-2$, we obtain that $\frac{1}{1+x}e+\frac{x}{1+x}h$ is non-contextual if and only if:

$$\frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}-(n-2)}{n-2-{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}}\le x.$$

By Equation (7), we see that:

$$R_g\left(e\right|\left|h\right)=\frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}-(n-2)}{n-2-{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}}.$$

Since ${\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}>-n$, we obtain that $R_g\left(e\right|\left|h\right)>x_0$.

When $h\in E{M}_3\bigcap CEM$, there exists ${\left\{{\beta }_i\right\}}_{i=0}^{n-1}\in \mathrm{\Gamma }\backslash \{{\left\{{\gamma }_i\right\}}_{i=0}^{n-1},{\{-{\gamma }_i\}}_{i=0}^{n-1}\}$ such that ${\Omega }_{h,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}>n-2$, and then:

$${\Omega }_{h,{\left\{{\alpha }_i\right\}}_{i=0}^{n-1}}<n-2,\forall {\left\{{\alpha }_i\right\}}_{i=0}^{n-1}\in \mathrm{\Gamma }\backslash \{{\left\{{\beta }_i\right\}}_{i=0}^{n-1}\}.$$

(25)

By Lemma 1 and Inequalities (19) and (25), we have that $\frac{1}{1+x}e+\frac{x}{1+x}h$ is non-contextual if and only if:

$$\frac{1}{1+x}{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}+\frac{x}{1+x}{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}\le n-2$$

and:

$$\frac{1}{1+x}{\Omega }_{e,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}+\frac{x}{1+x}{\Omega }_{h,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}\le n-2,$$

i.e.,

$$\frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}-(n-2)}{n-2-{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}}\le x\text{and}x\le \frac{{\Omega }_{e,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}+(n-2)}{{\Omega }_{h,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}-(n-2)}.$$

Hence,

$$R_g\left(e\right|\left|h\right)=\left\{\begin{array}{cc}\frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}-(n-2)}{n-2-{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}},\hfill & \text{if}\frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}-(n-2)}{n-2-{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}}\le \frac{{\Omega }_{e,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}+(n-2)}{{\Omega }_{h,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}-(n-2)};\hfill \\ +\infty ,\hfill & \text{otherwise.}\hfill \end{array}\right.$$

Thus,

$$R_g\left(e\right|\left|h\right)\ge \frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}-(n-2)}{n-2-{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}}.$$

Since ${\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}>-n$, we obtain that $R_g\left(e\right|\left|h\right)>x_0$.

In a word, we obtain that $R_g\left(e\right|\left|h\right)\ge x_0$ for any $h\in EM$ and $R_g\left(e\right|\left|f\right)=x_0$. Therefore, we have from Equation (8) that $R_g\left(e\right)=x_0.$

• Case (ii${}_b$): If n is an odd number, then it is easy to find that:

  $${\Omega }_{f,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}=\sum _{i=0}^{n-1}{\beta }_i{E}_i^f=\sum _{i=0}^{n-1}(-{\beta }_i{\gamma }_i)\le n-2,\forall {\left\{{\beta }_i\right\}}_{i=0}^{n-1}\in \mathrm{\Gamma }.$$

  (26)

Claim 5. 

$R_g\left(e\right|\left|f\right)=x_0$.

From Lemma 1 and Inequalities (19) and (26), we get that $\frac{1}{1+x}e+\frac{x}{1+x}f$ is non-contextual if and only if

$$\frac{1}{1+x}{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}+\frac{x}{1+x}{\Omega }_{f,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}\le n-2$$

i.e.,

$$x_0=\frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}-(n-2)}{2n-2}\le x.$$

Therefore, $R_g\left(e\right|\left|f\right)=x_0$.

Claim 6. 

$R_g\left(e\right)=x_0$.

By Claim 5 and Equation (8), we have $R_g\left(e\right)\le x_0$. Take:

$$E{M}^1=\{h\in EM:{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}\ge n-2\},E{M}^2=\{h\in EM:{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}<(n-2)\}.$$

For $h\in E{M}^1$, it is easy to check that $R_g\left(e\right|\left|h\right)=+\infty \ge x_0.$

For $h\in E{M}^2\bigcap NCEM$, we see from Lemma 1 and Inequality (18) that $\frac{1}{1+x}e+\frac{x}{1+x}h$ is non-contextual if and only if:

$$\frac{1}{1+x}{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}+\frac{x}{1+x}{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}\le n-2,$$

i.e.,

$$\frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}-(n-2)}{n-2-{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}}\le x$$

Hence,

$$R_g\left(e\right|\left|h\right)=\frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}-(n-2)}{n-2-{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}}\ge x_0.$$

For $h\in E{M}^2\bigcap CEM$, there exists ${\left\{{\beta }_i\right\}}_{i=0}^{n-1}\in \mathrm{\Gamma }\backslash \left\{{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}\right\}$ such that ${\Omega }_{h,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}>n-2$, and so:

$${\Omega }_{h,{\left\{{\alpha }_i\right\}}_{i=0}^{n-1}}<n-2,\forall {\left\{{\alpha }_i\right\}}_{i=0}^{n-1}\in \mathrm{\Gamma }\backslash \left\{{\left\{{\beta }_i\right\}}_{i=0}^{n-1}\right\}.$$

(27)

By Lemma 1 and Inequalities (19) and (27), we obtain that $\frac{1}{1+x}e+\frac{x}{1+x}h$ is non-contextual if and only if:

$$\frac{1}{1+x}{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}+\frac{x}{1+x}{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}\le n-2$$

and:

$$\frac{1}{1+x}{\Omega }_{e,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}+\frac{s}{1+x}{\Omega }_{h,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}\le n-2,$$

i.e.,

$$\frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}-(n-2)}{n-2-{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}}\le x\text{and}x\le \frac{n-2-{\Omega }_{e,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}}{{\Omega }_{h,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}-(n-2)}.$$

Hence,

$$R_g\left(e\right|\left|h\right)=\left\{\begin{array}{cc}\frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}-(n-2)}{n-2-{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}},\hfill & \text{if}\frac{n-2-{\Omega }_{e,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}}{{\Omega }_{h,{\left\{{\beta }_i\right\}}_{i=0}^{n-1}}-(n-2)}\ge \frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}-(n-2)}{n-2-{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}};\hfill \\ +\infty ,\hfill & \text{otherwise.}\hfill \end{array}\right.$$

Therefore,

$$R_g\left(e\right|\left|h\right)\ge \frac{{\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}-(n-2)}{n-2-{\Omega }_{h,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}}\ge x_0.$$

Now, we have shown that $R_g\left(e\right|\left|h\right)\ge x_0=R_g\left(e\right|\left|f\right)$ for any $h\in EM$. Therefore, $R_g\left(e\right)=x_0$. This shows that Equation (18) holds.   □

Remark 3. 

In [13], we have computed the robustness of contextuality of an n-cycle box e and obtained that:

$$R_C\left(e\right)=\left\{\begin{array}{cc}\frac{\max \{{△}_e,0\}}{2n-4},\hfill & n\text{is}\text{even;}\hfill \\ \frac{\max \{{△}_e,0\}}{2n-2},\hfill & n\text{is}\text{odd.}\hfill \end{array}\right.$$

Hence, $R_g\left(e\right)=R_C\left(e\right)$ for even n and $R_g\left(e\right)<R_C\left(e\right)$ for odd n.

Example 1. 

For any n-cycle box f, we have $E_i^f\le 1$ for any i, and so, ${\Omega }_{f,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}\le n$ for any ${\left\{{\gamma }_i\right\}}_{i=0}^{n-1}\in \mathrm{\Gamma }$. Hence, ${\Delta }_f\le 2$ by Equation (17), and then, Equation (18) implies that $R_g\left(f\right)\le \frac{1}{n-1}$.

Let us consider the n-chain box $e=C{H}_n$ in [7], which is given by:

$$e_{C_i}\left(s_{00}^i\right)=e_{C_i}\left(s_{11}^i\right)=\frac{1}{2},e_{C_i}\left(s_{01}^i\right)=e_{C_i}\left(s_{10}^i\right)=0(i=0,1,\dots ,n-2),$$

$$e_{C_{n-1}}\left(s_{00}^{n-1}\right)=e_{C_{n-1}}\left(s_{11}^{n-1}\right)=0,e_{C_{n-1}}\left(s_{01}^{n-1}\right)=e_{C_{n-1}}\left(s_{10}^{n-1}\right)=\frac{1}{2}.$$

By taking ${\gamma }_0={\gamma }_1=\cdots ={\gamma }_{n-2}=1$ and ${\gamma }_{n-1}=-1$, we obtain that ${\left\{{\gamma }_i\right\}}_{i=0}^{n-1}\in \mathrm{\Gamma }$ and ${\Omega }_{e,{\left\{{\gamma }_i\right\}}_{i=0}^{n-1}}=n$. Thus, ${\Delta }_e=2$ by Equation (17), and then, Equation (18) implies that $R_g\left(e\right)=\frac{1}{n-1}$. This shows that:

$$max\{R_g\left(e\right):e\mathrm{is} \mathrm{an}n-\mathrm{cycle\; box}\}=R_g\left(C{H}_n\right)=\frac{1}{n-1}.$$

4. Conclusions

Because noises are not always non-contextual, we have introduced and discussed the generalized robustness of contextuality (GRoC) $R_g\left(e\right)$ of an empirical model e against general noises. We also have proven that $R_g\left(e\right)=0$ if and only if e is non-contextual. This means that the quantity $R_g$ can be used to distinguish non-contextual empirical models from contextual ones. For any two empirical models e and f with $R_g(e\parallel f)<\infty$, it has been proven $R_g\left(e\right)R_g\left(f\right)\le 1$, which reveals a fascinating relationship between the GRoCs of e and f. A relationship between GRoC and the extent of violating the non-contextual inequalities for n-cycle$(n\ge 4)$ boxes has also been established, which reads $R_g\left(e\right)=\frac{max\{{\Delta }_e,0\}}{2n-2}$. Thus, for any n-cycle boxes e and f, when ${\Delta }_e\le {\Delta }_f$, we have $R_g\left(e\right)\le R_g\left(f\right)$; when e and f are contextual, we have ${\Delta }_e\le {\Delta }_f$ if and only if $R_g\left(e\right)\le R_g\left(f\right)$. This means that $R_g\left(e\right)$ can be used to quantify the contextuality of n-cycle boxes. Moreover, we have proven that the maximal value of $R_g$ over $NSEM$ must be attained at some strongly contextual model. This shows that to some extent, $R_g\left(e\right)$ contains the quantity of contextuality of e.