Second Law Analysis of Adiabatic and Non-Adiabatic Pipeline Flows of Unstable and Surfactant-Stabilized Emulsions
Abstract
:1. Introduction
2. Theoretical Background
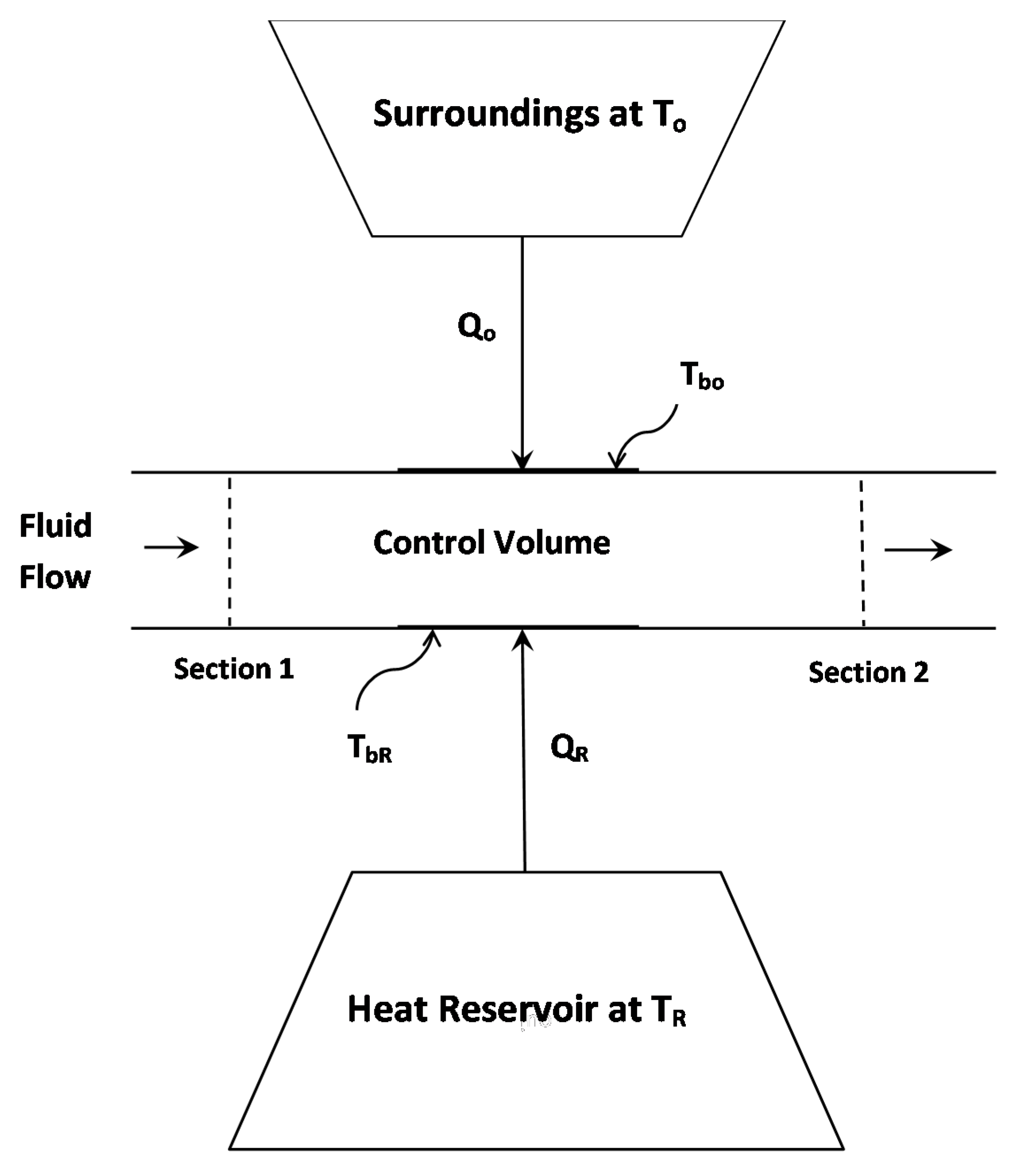
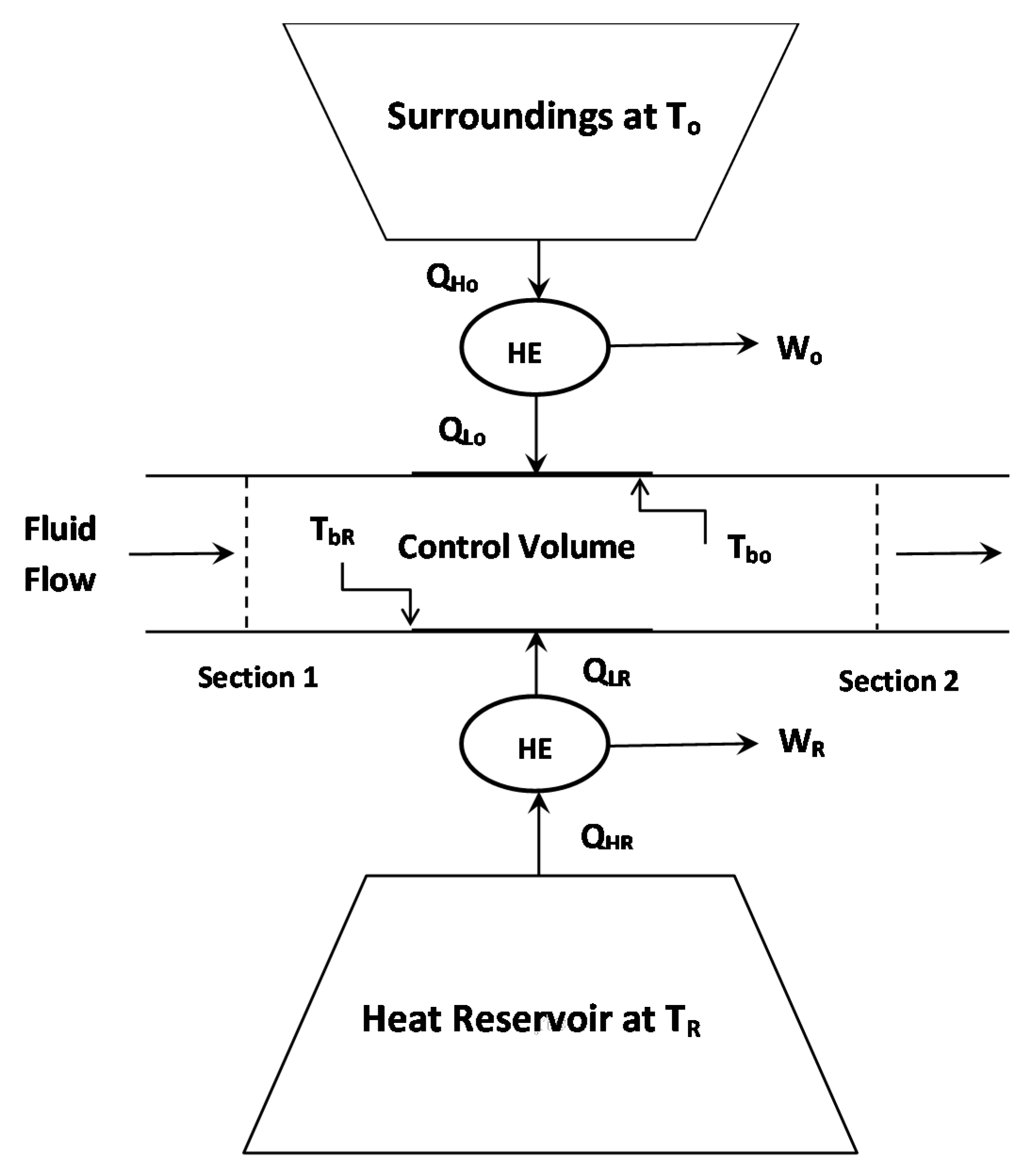
2.1. Non-Adiabatic Flow
2.2. Adiabatic Flow
Entropy Production in Adiabatic Pipeline Flow
3. Experimental Work: Adiabatic Pipeline Flow of Emulsions
Measurement Uncertainties
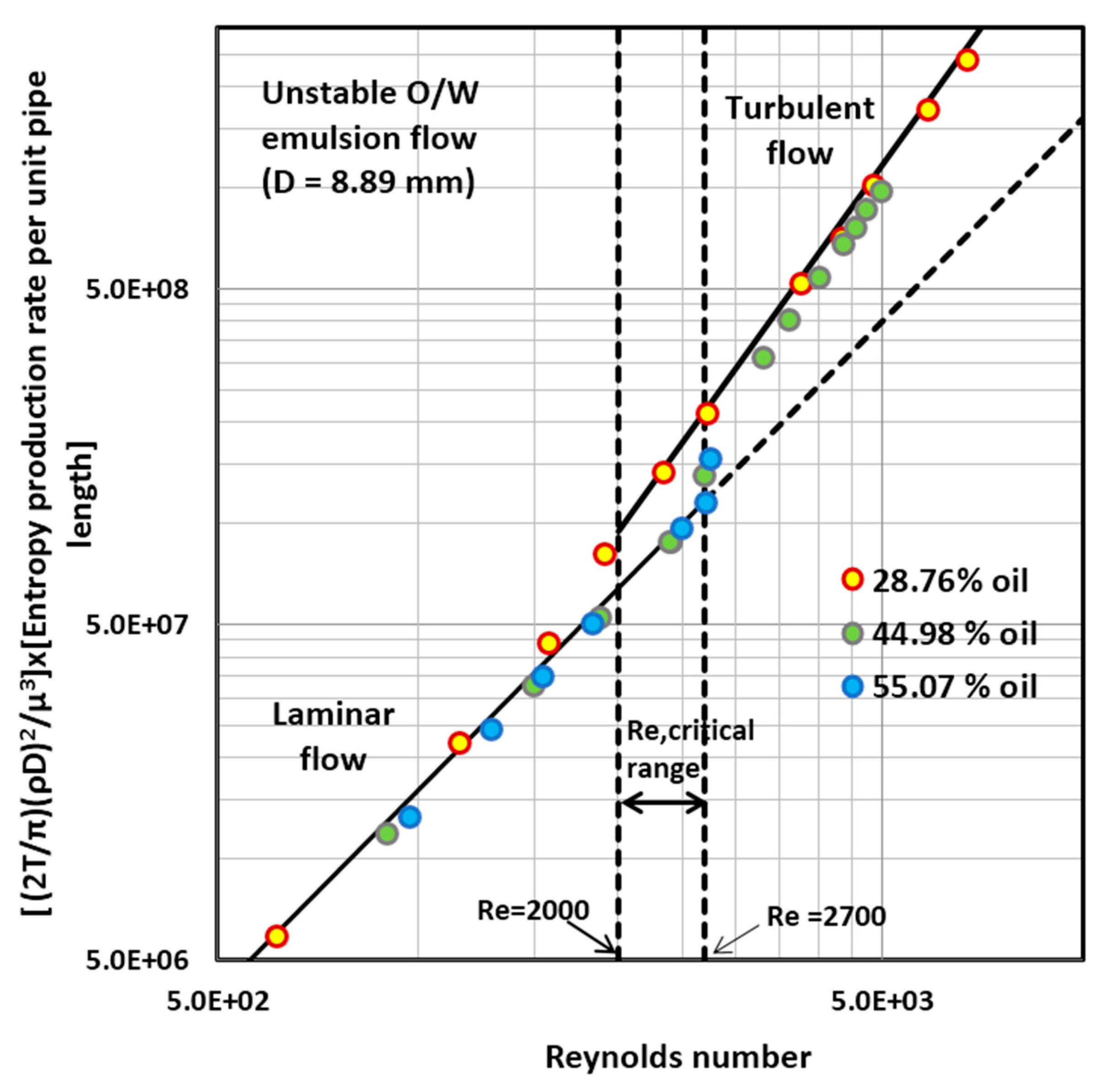
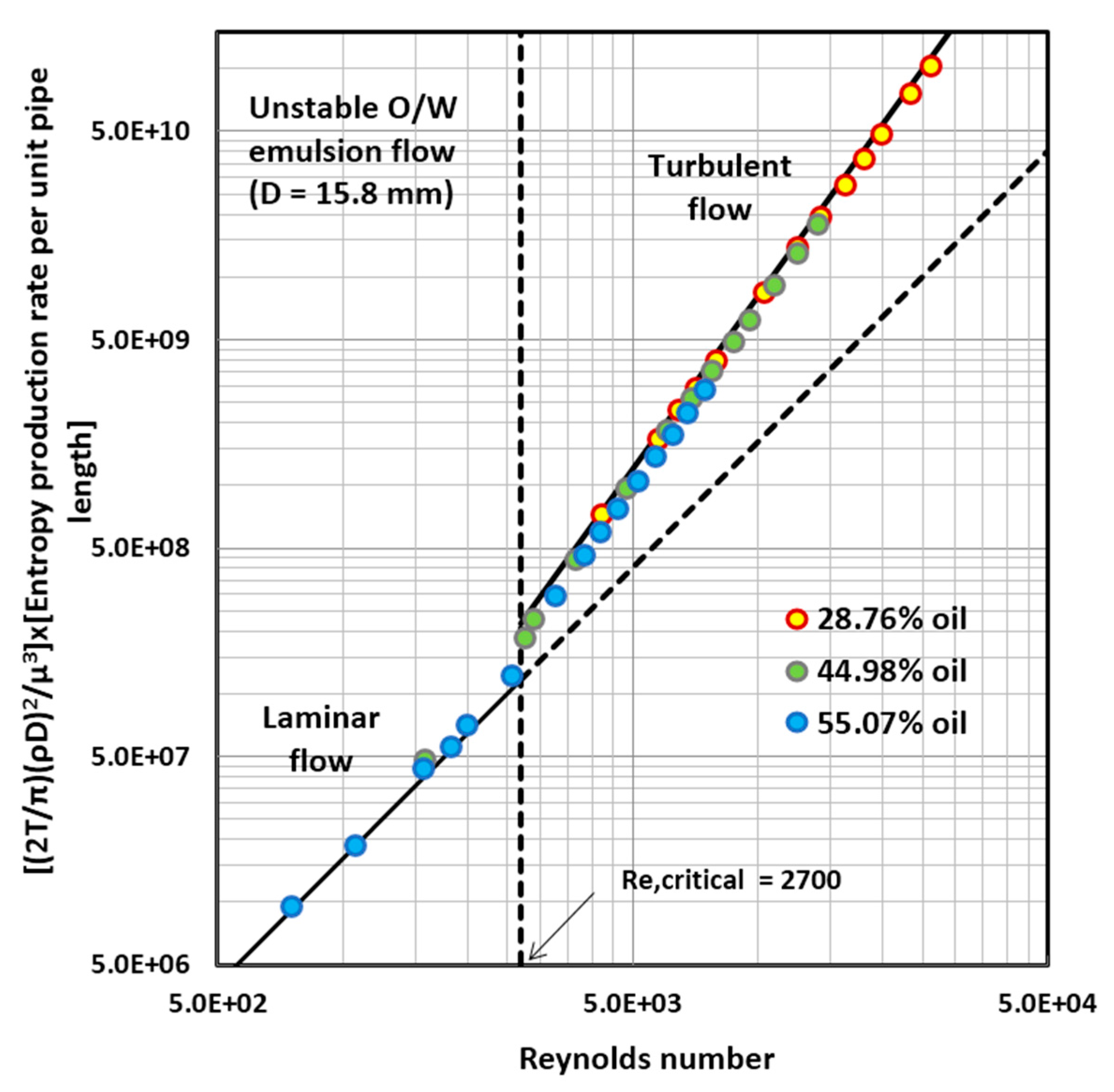
4. Results and Discussion: Adiabatic Pipeline Flow of Emulsions
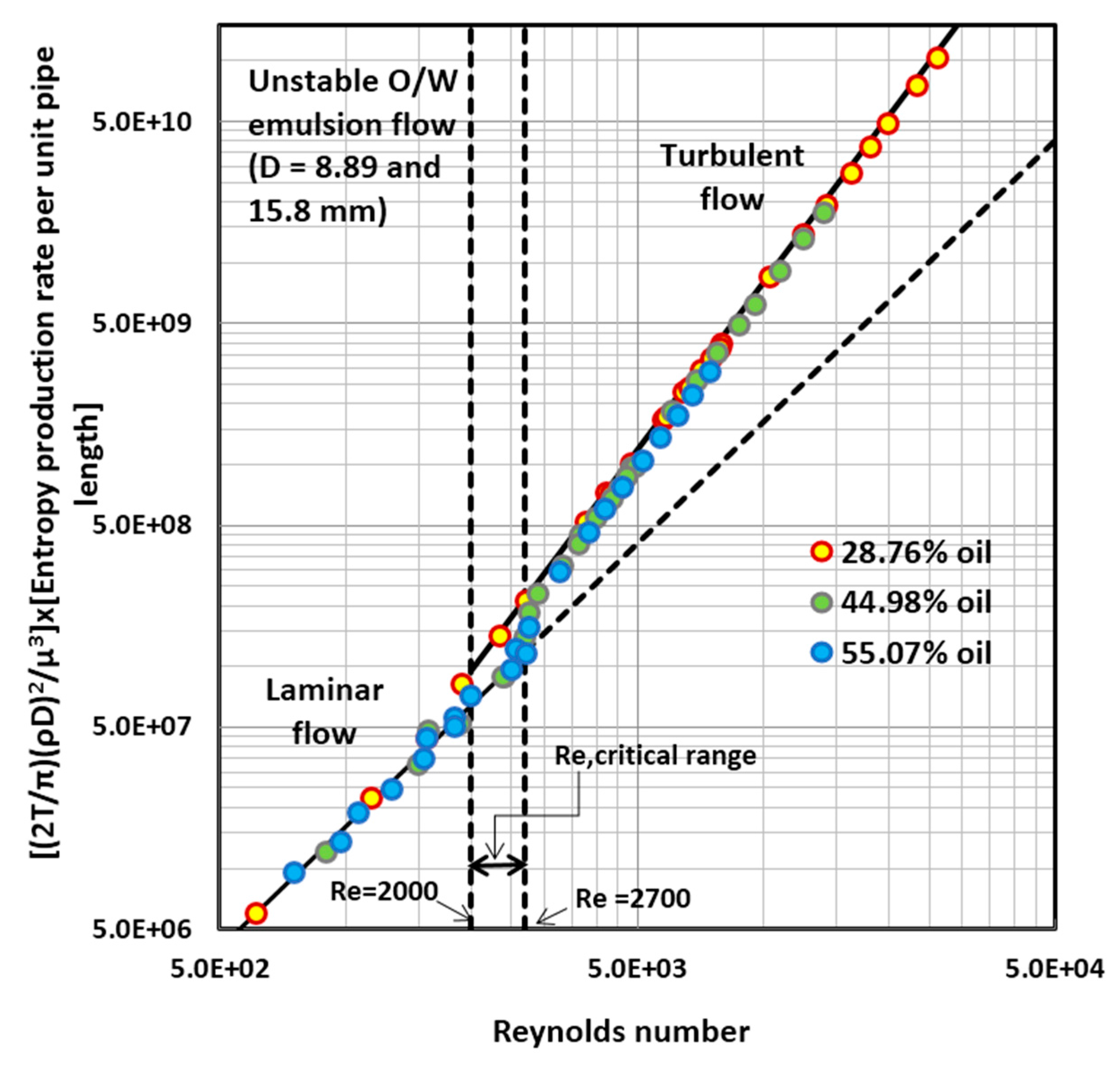
4.1. Entropy Generation in Adiabatic Pipeline Flow of Unstable Oil-in-Water (O/W) Emulsions
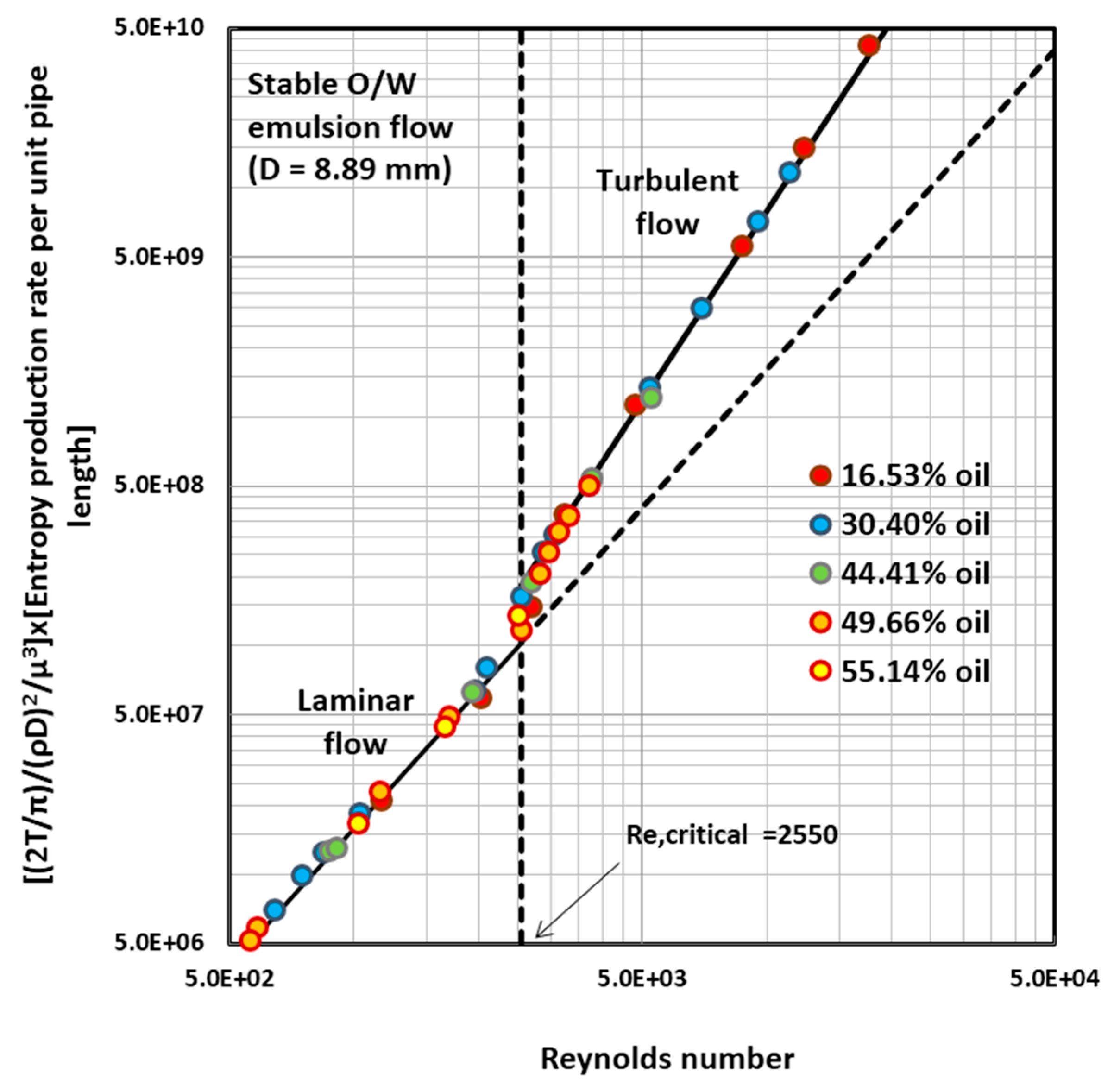
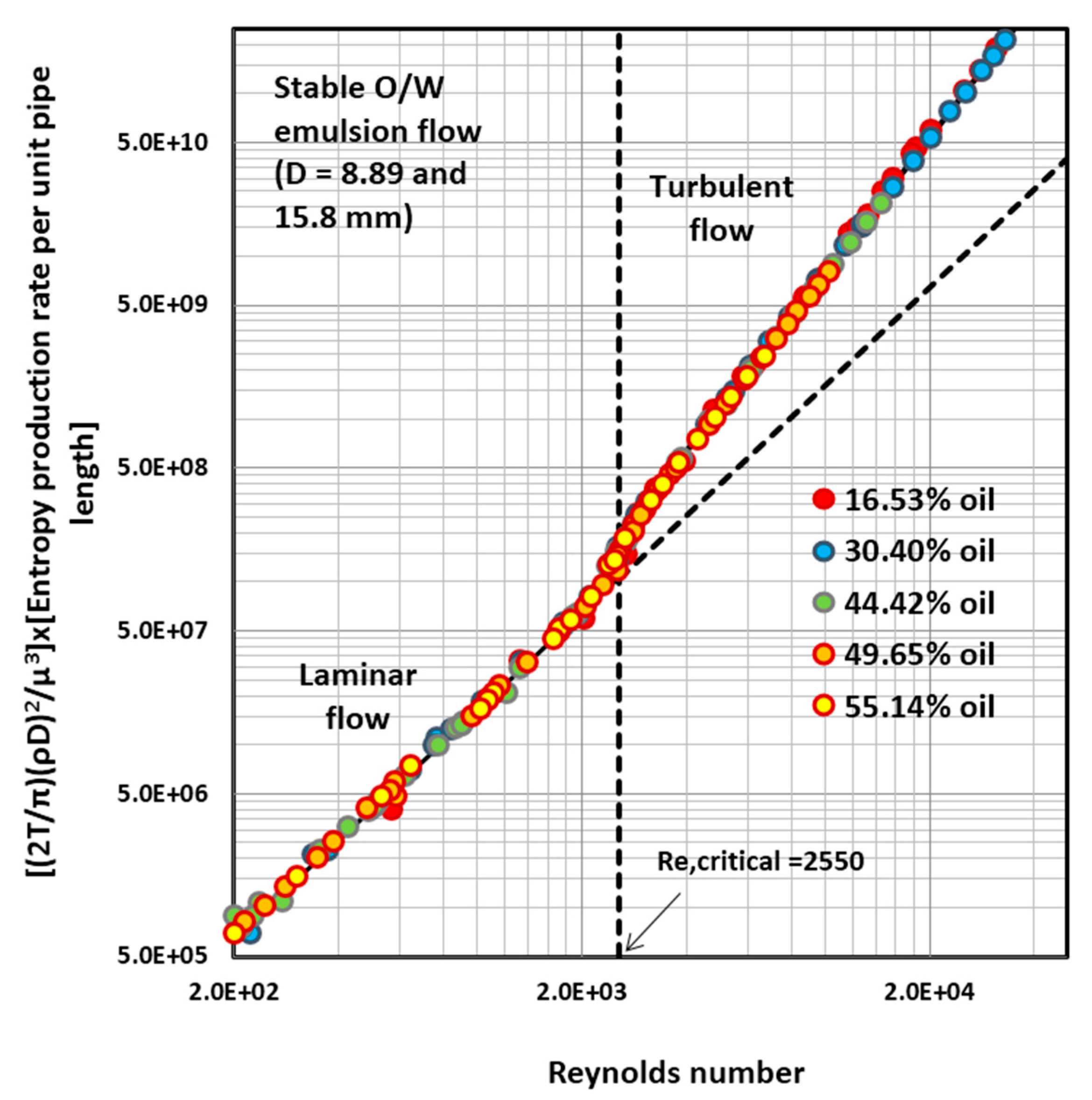
4.2. Entropy Generation in Adiabatic Pipeline Flow of Surfactant-Stabilized Oil-in-Water (O/W) Emulsions
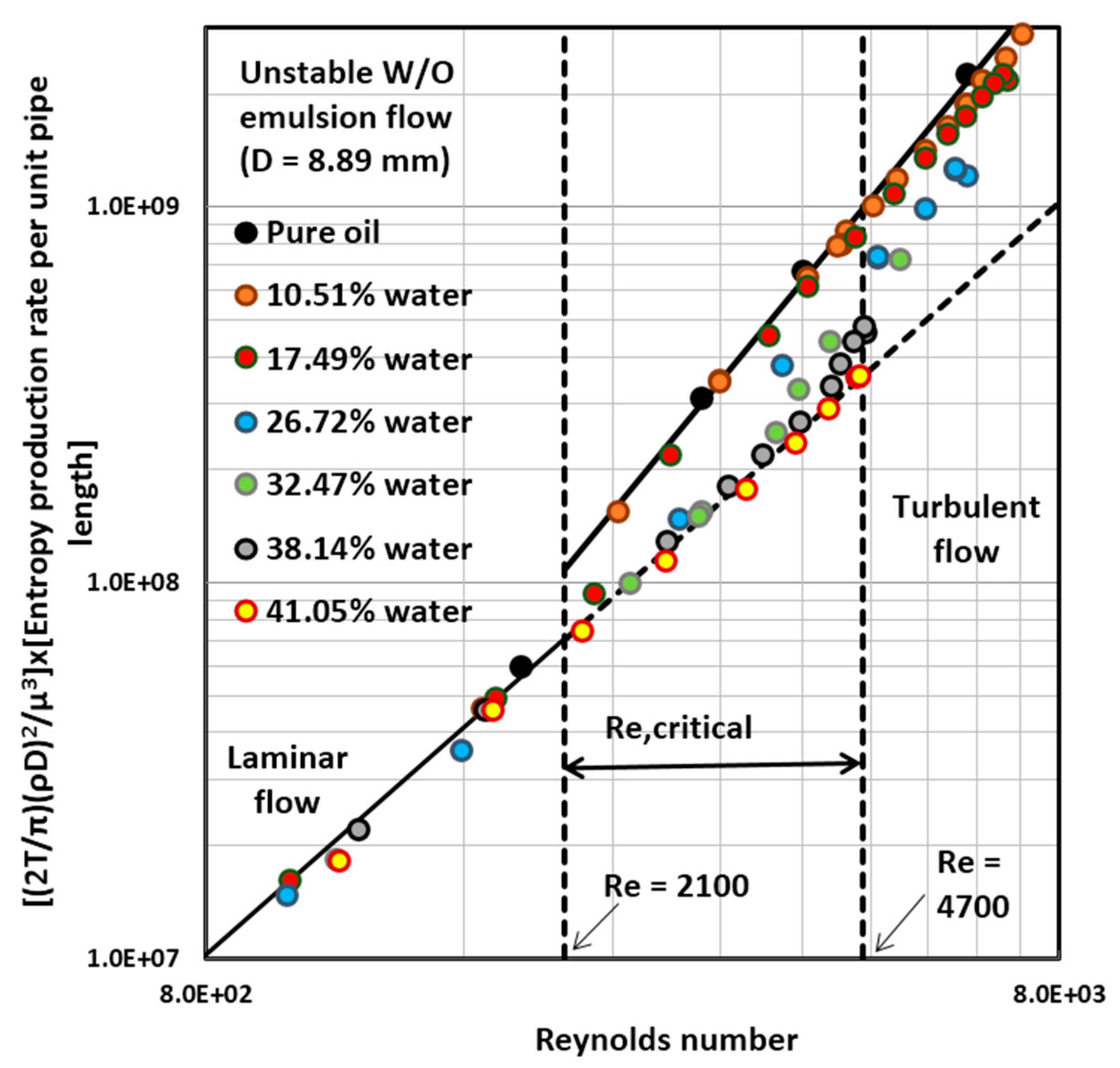
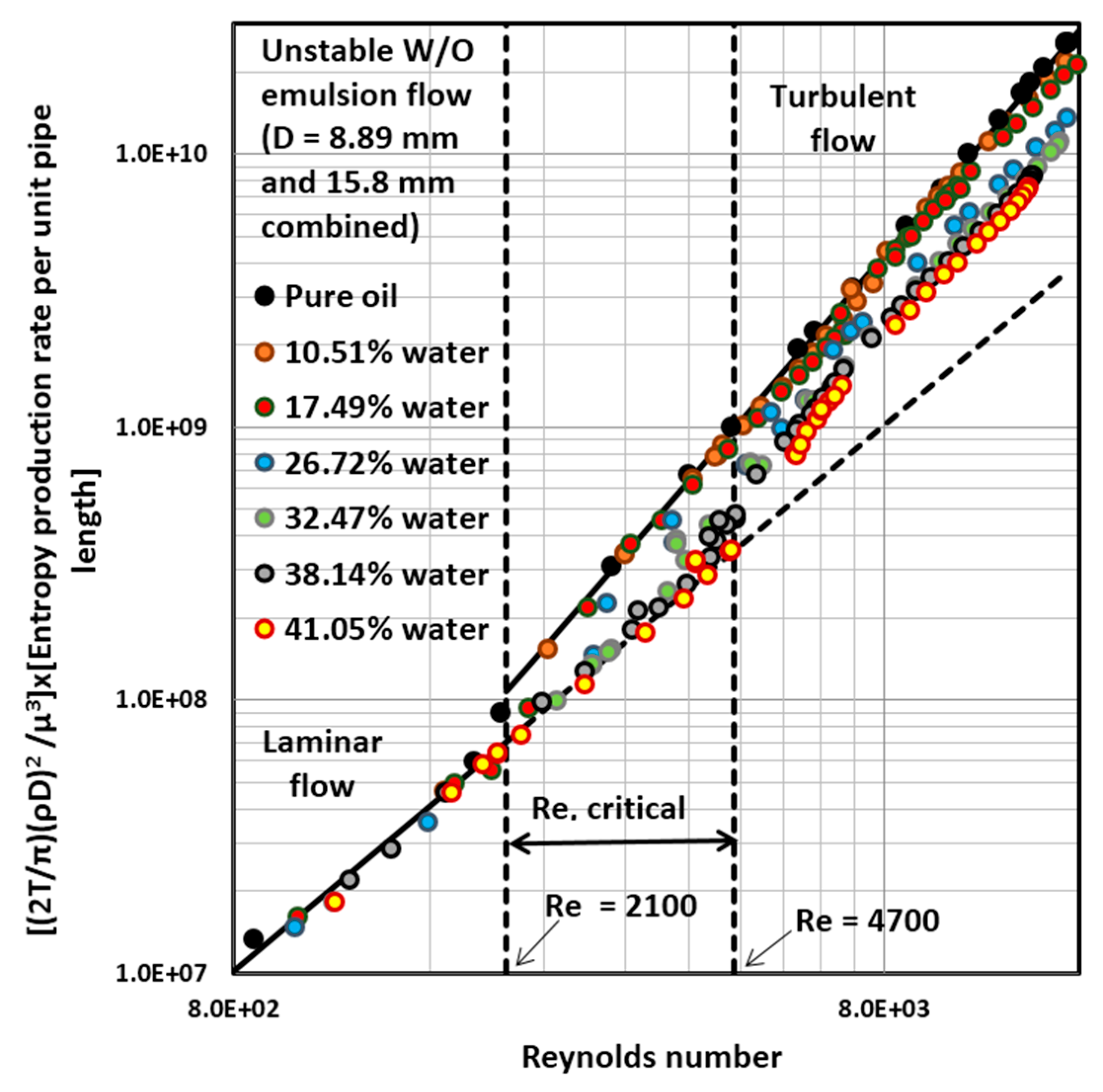
4.3. Entropy Generation in Adiabatic Pipeline Flow of Unstable Water-in-Oil (W/O) Emulsions
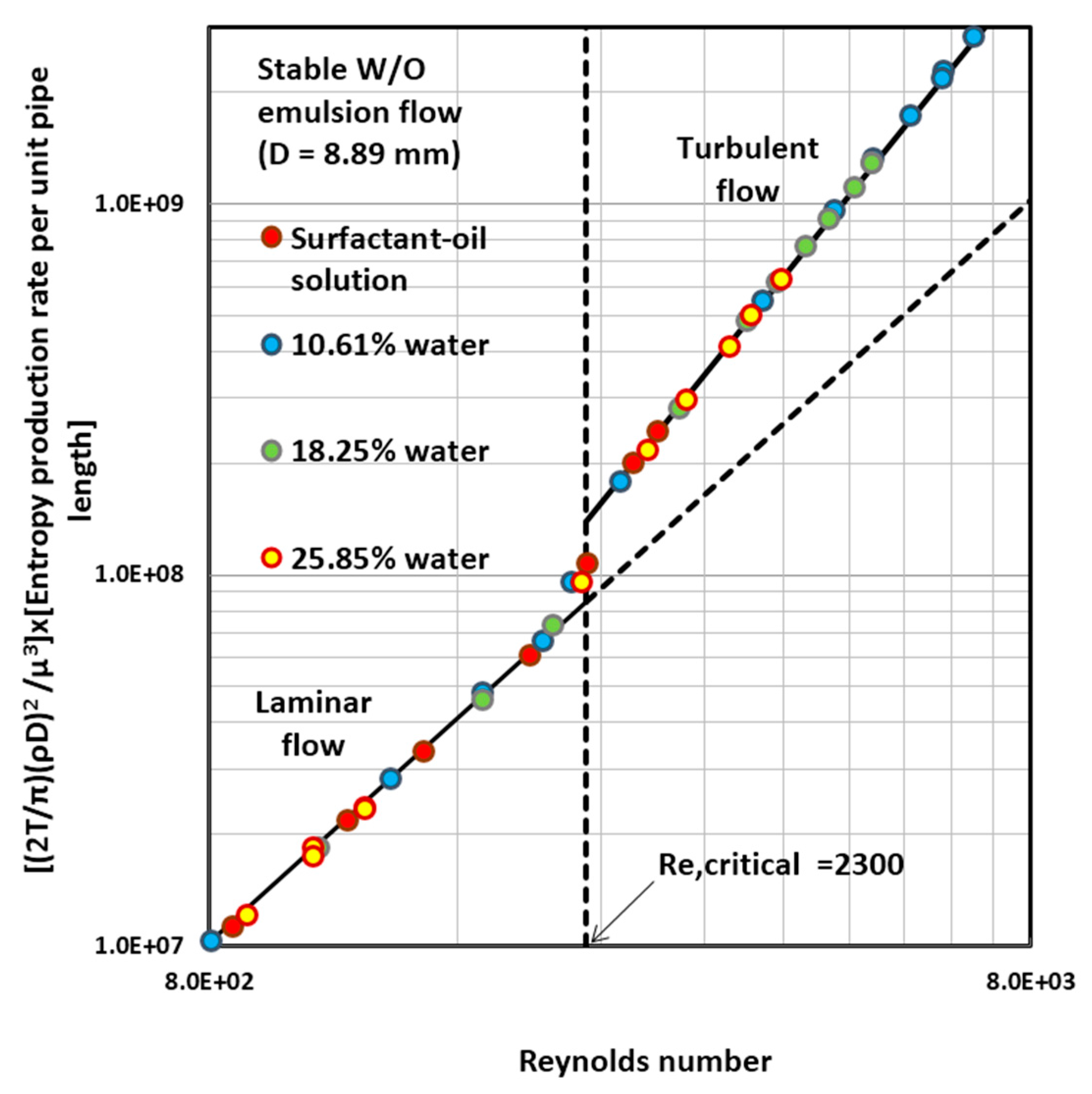
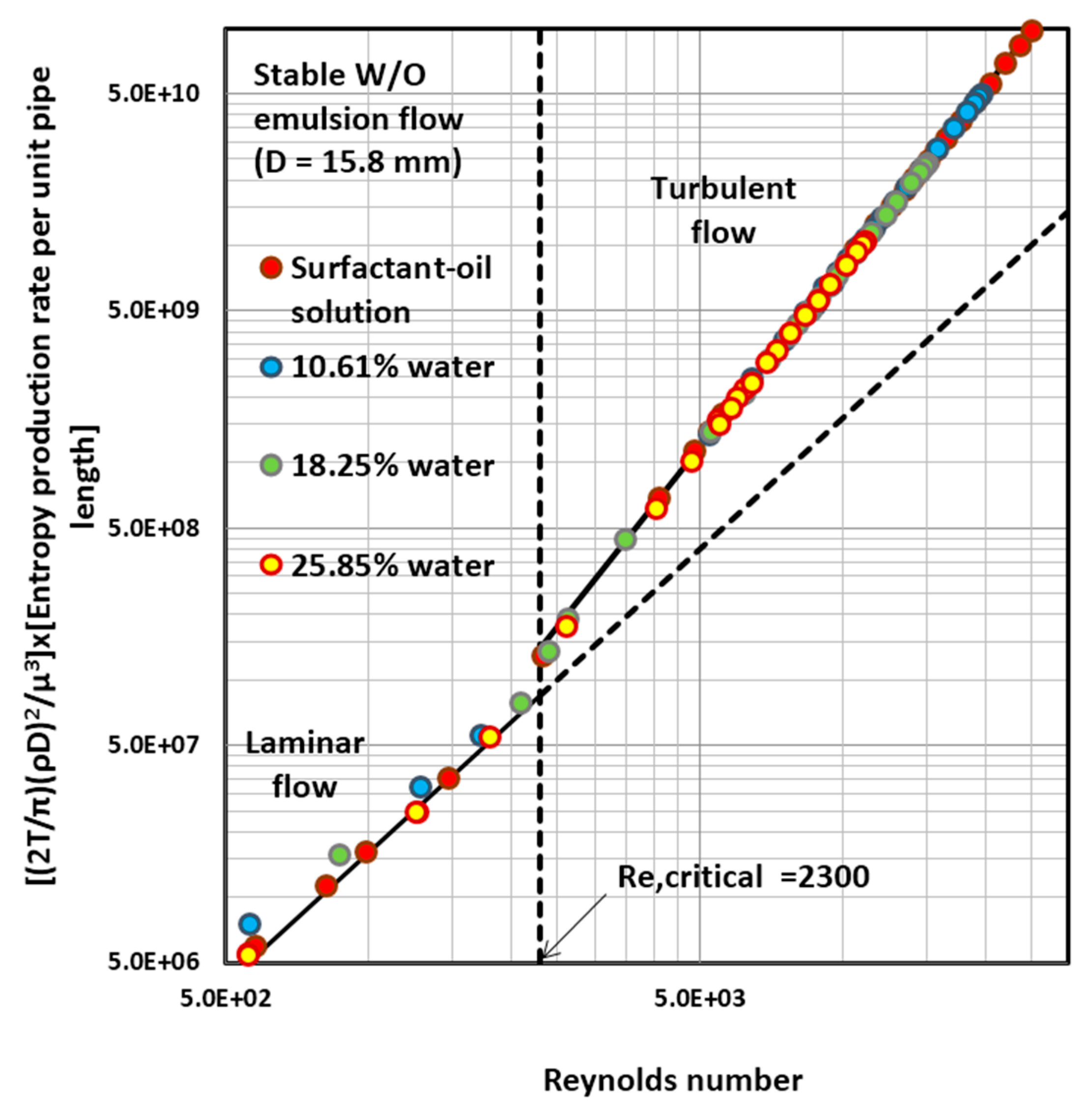
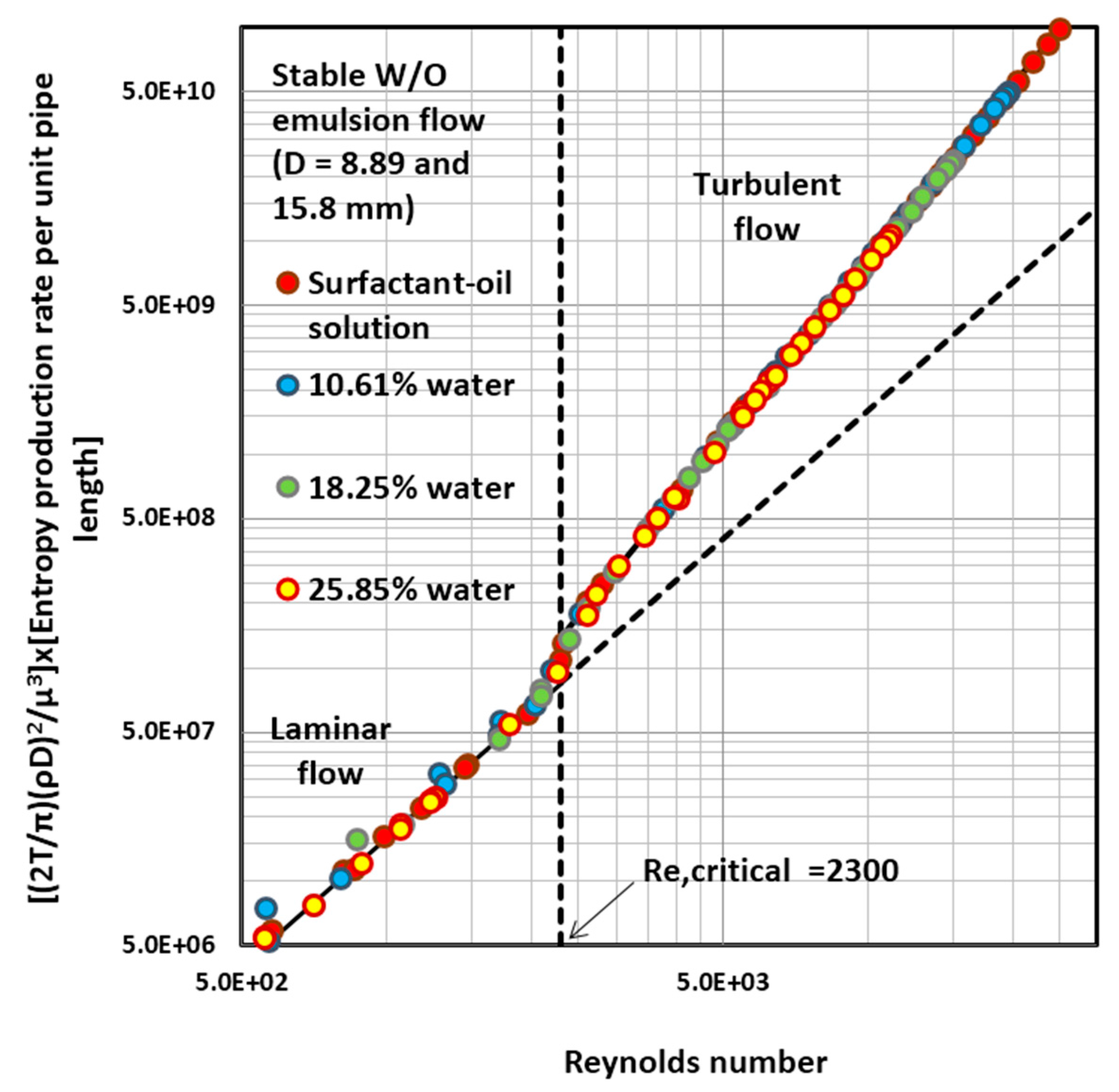
4.4. Entropy Generation in Adiabatic Pipeline Flow of Surfactant-Stabilized Water-in-Oil (W/O) Emulsions
4.5. Discussion
5. Simulation Work: Non-Adiabatic Pipeline Flow of Emulsions
5.1. Estimation of Friction Factor, Heat Transfer Coefficient, and Outlet Temperature
5.2. Estimation of Thermophysical Properties of Emulsions
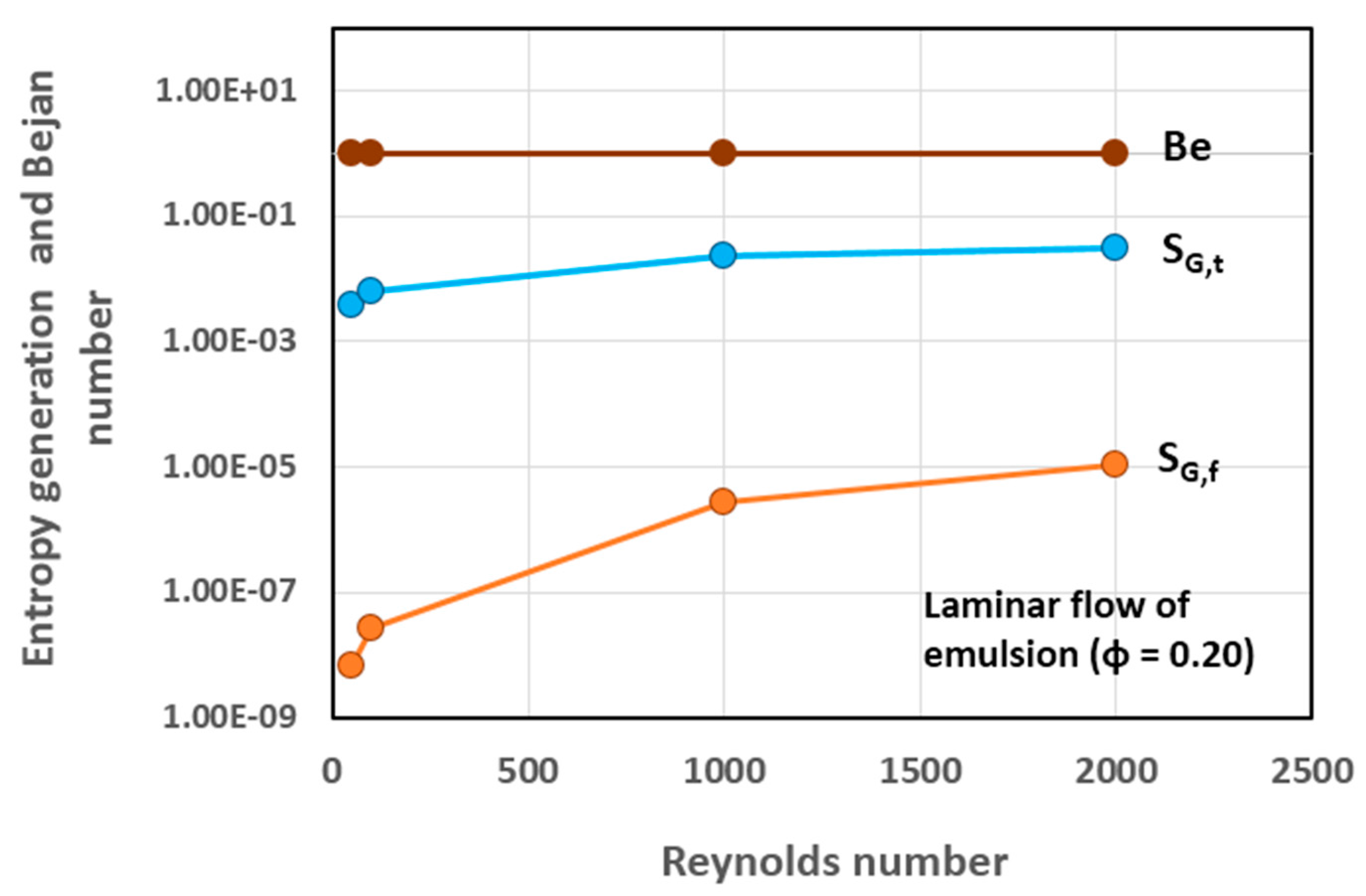
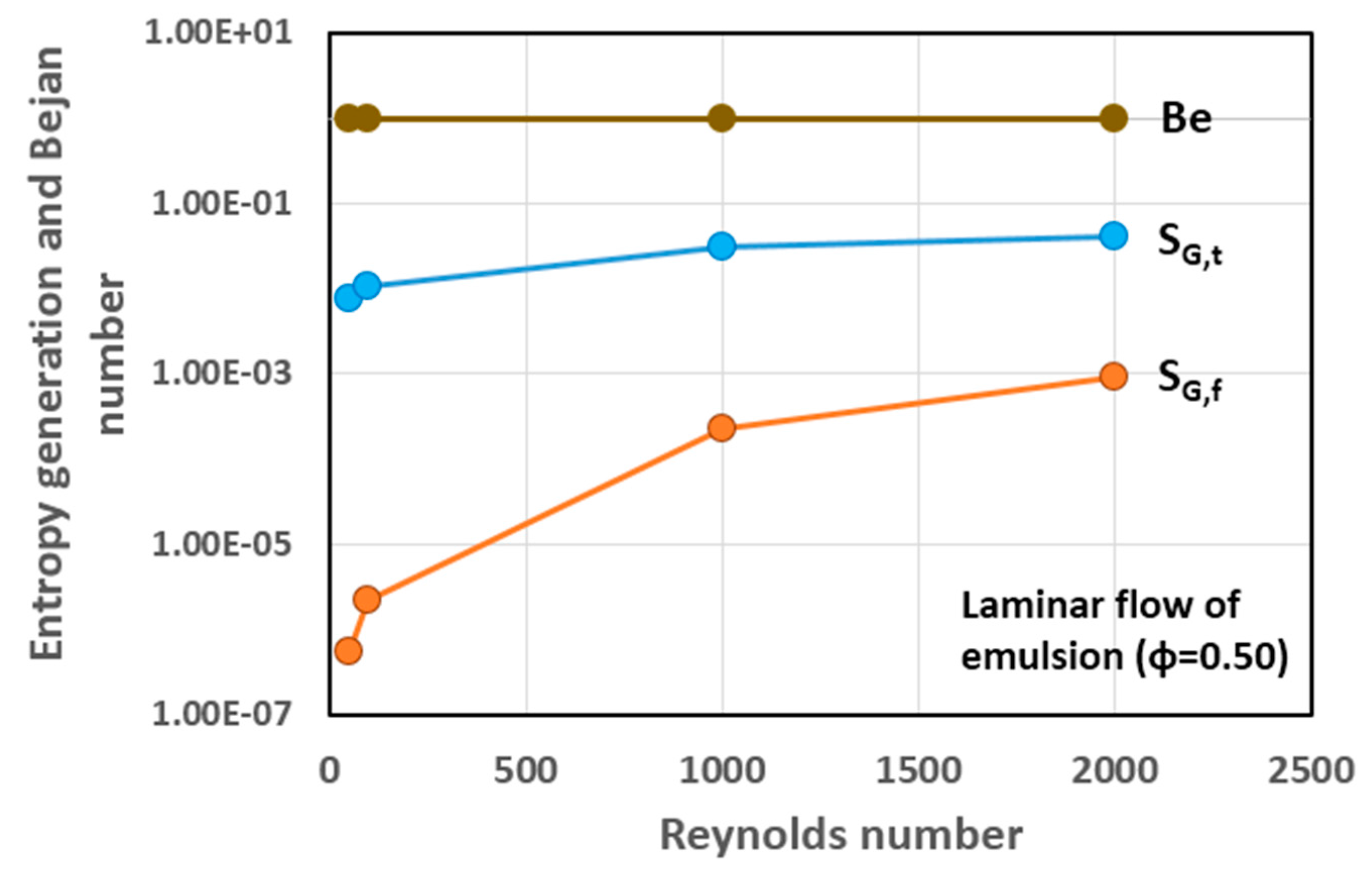
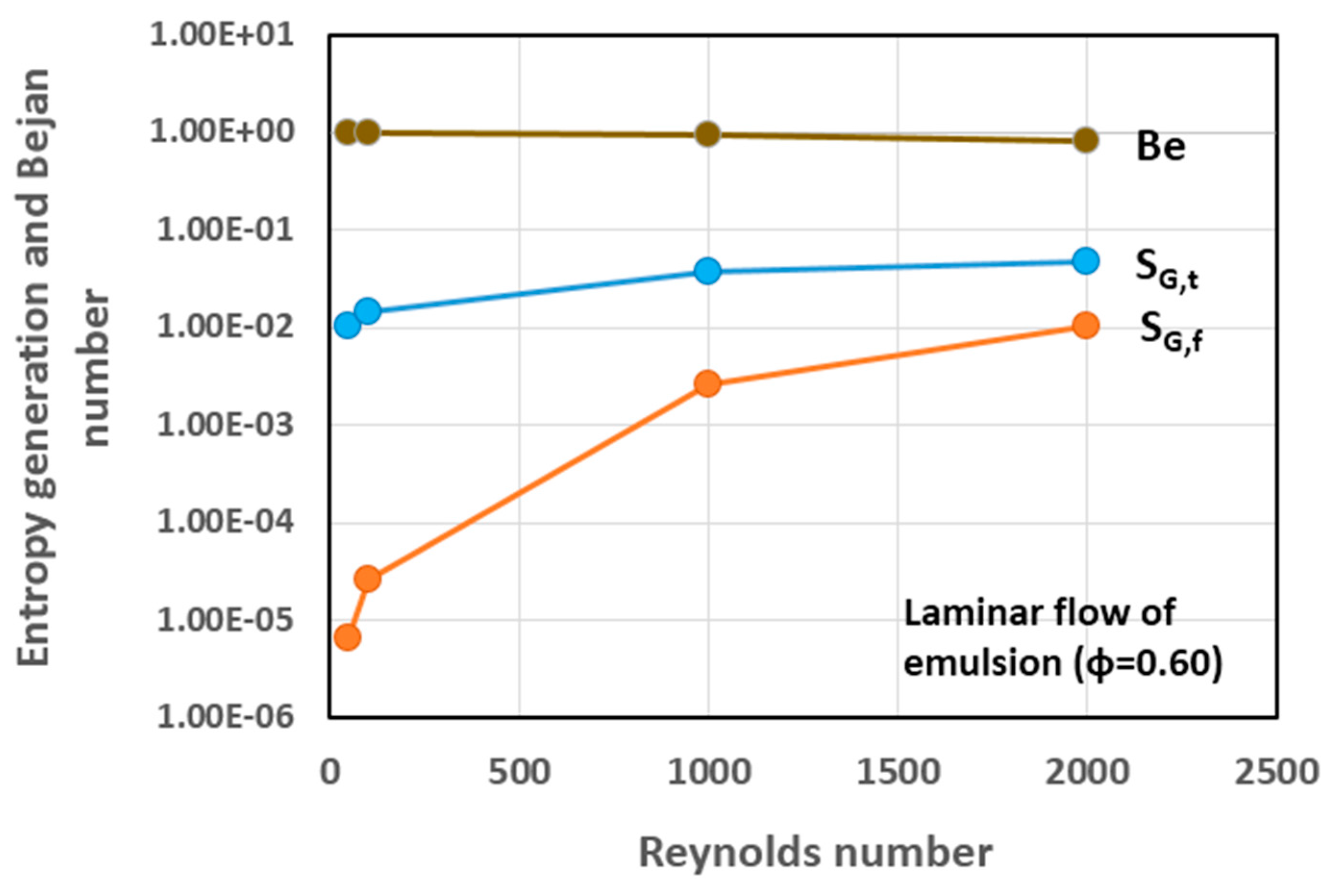
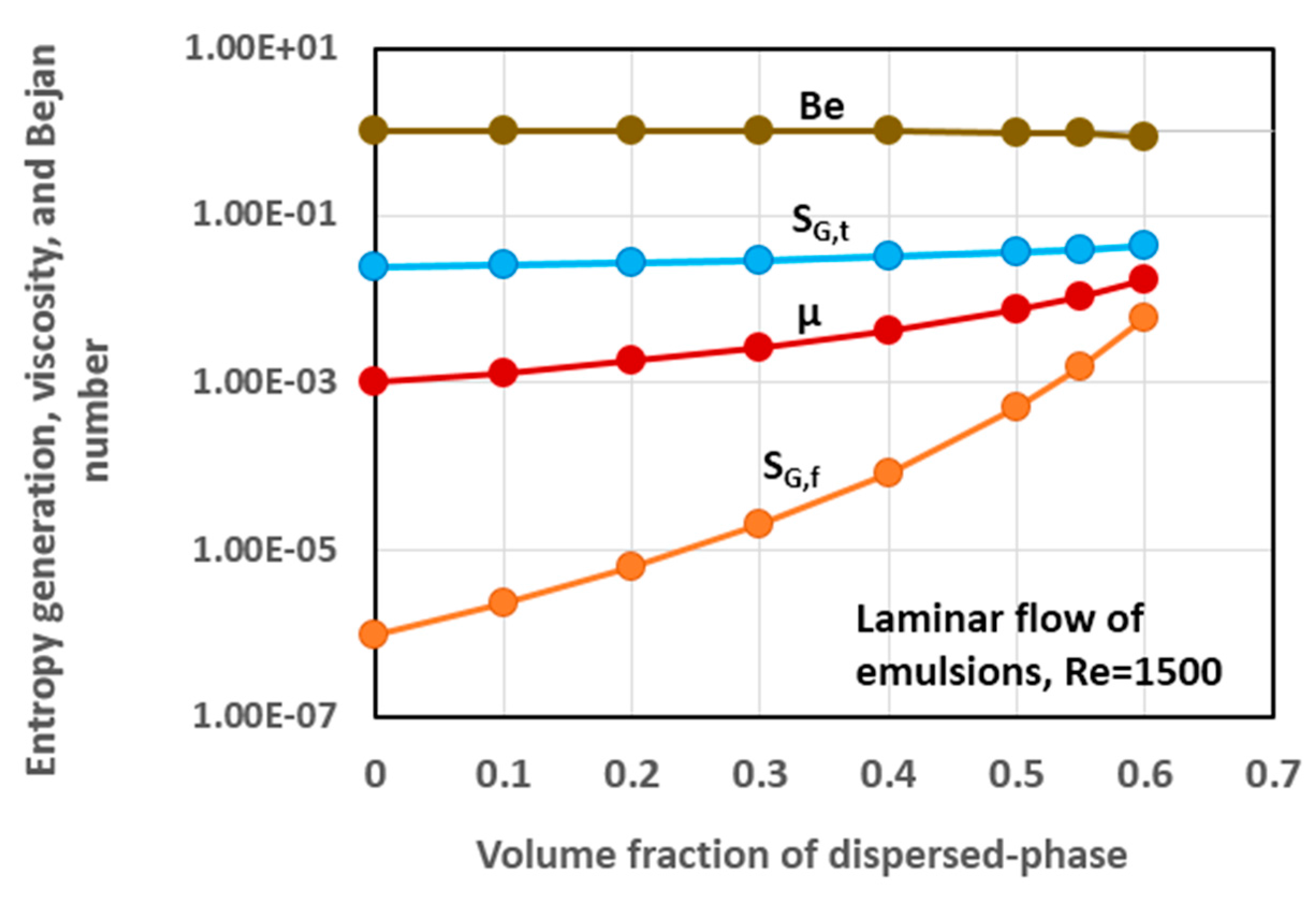
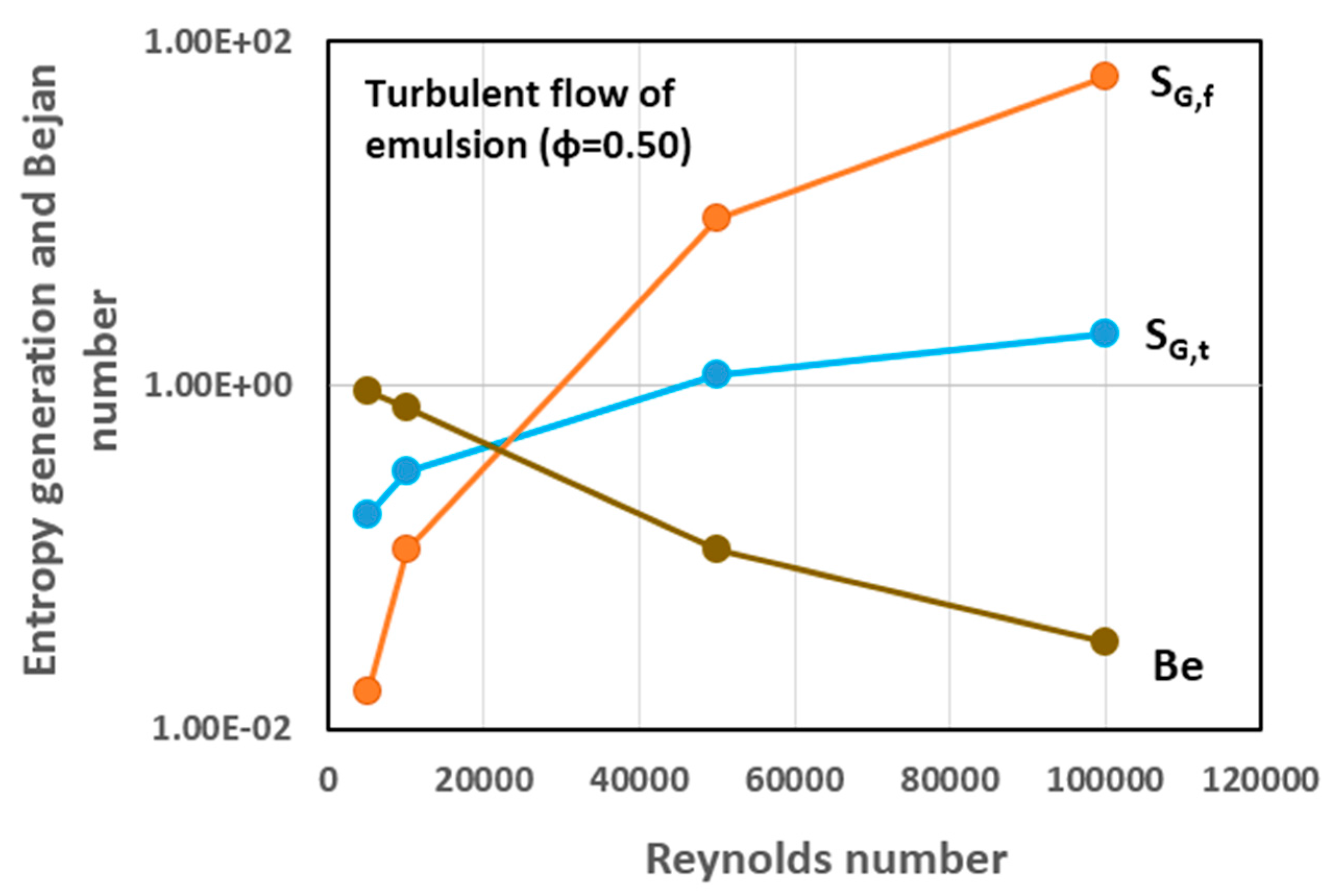
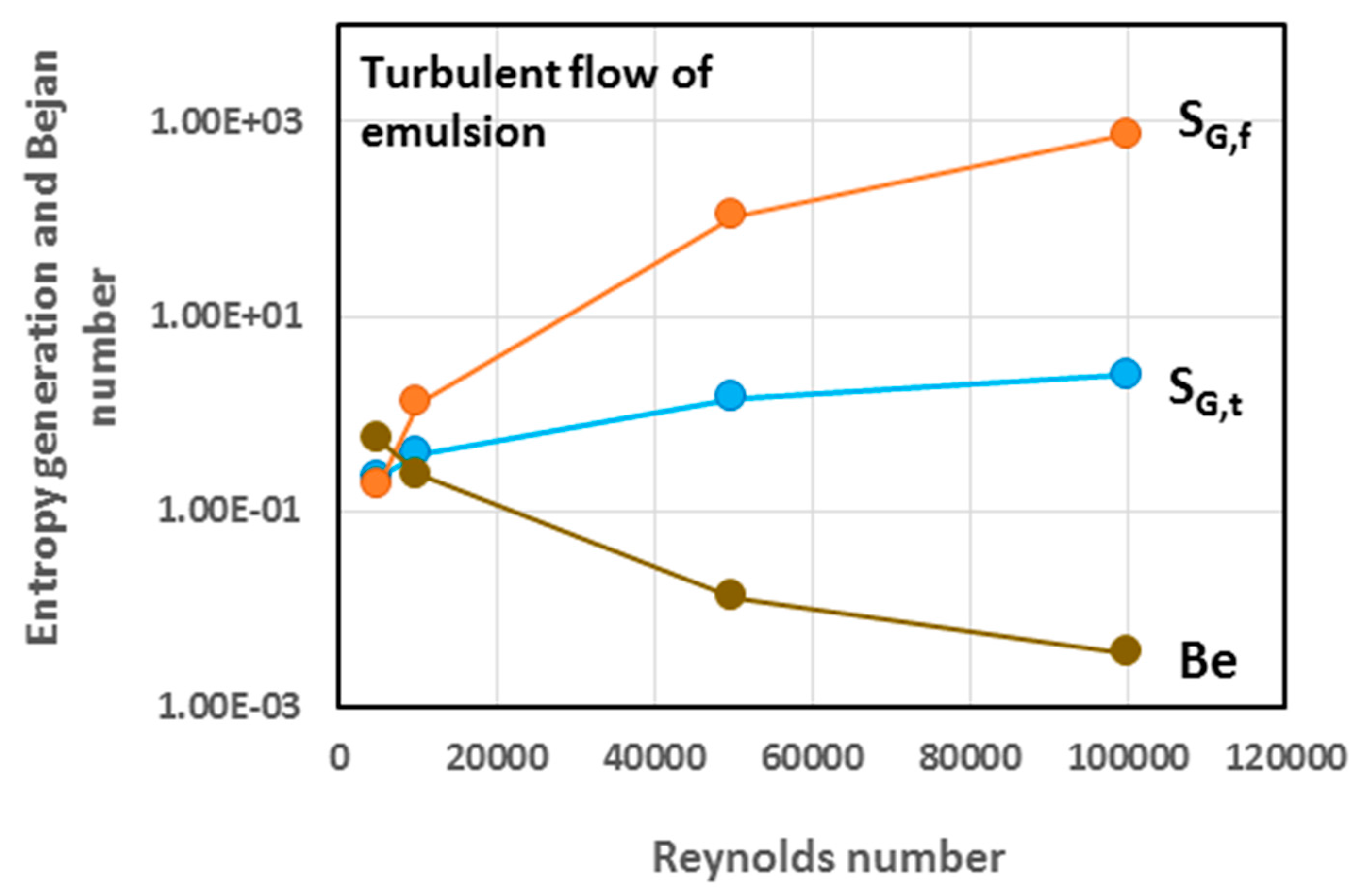
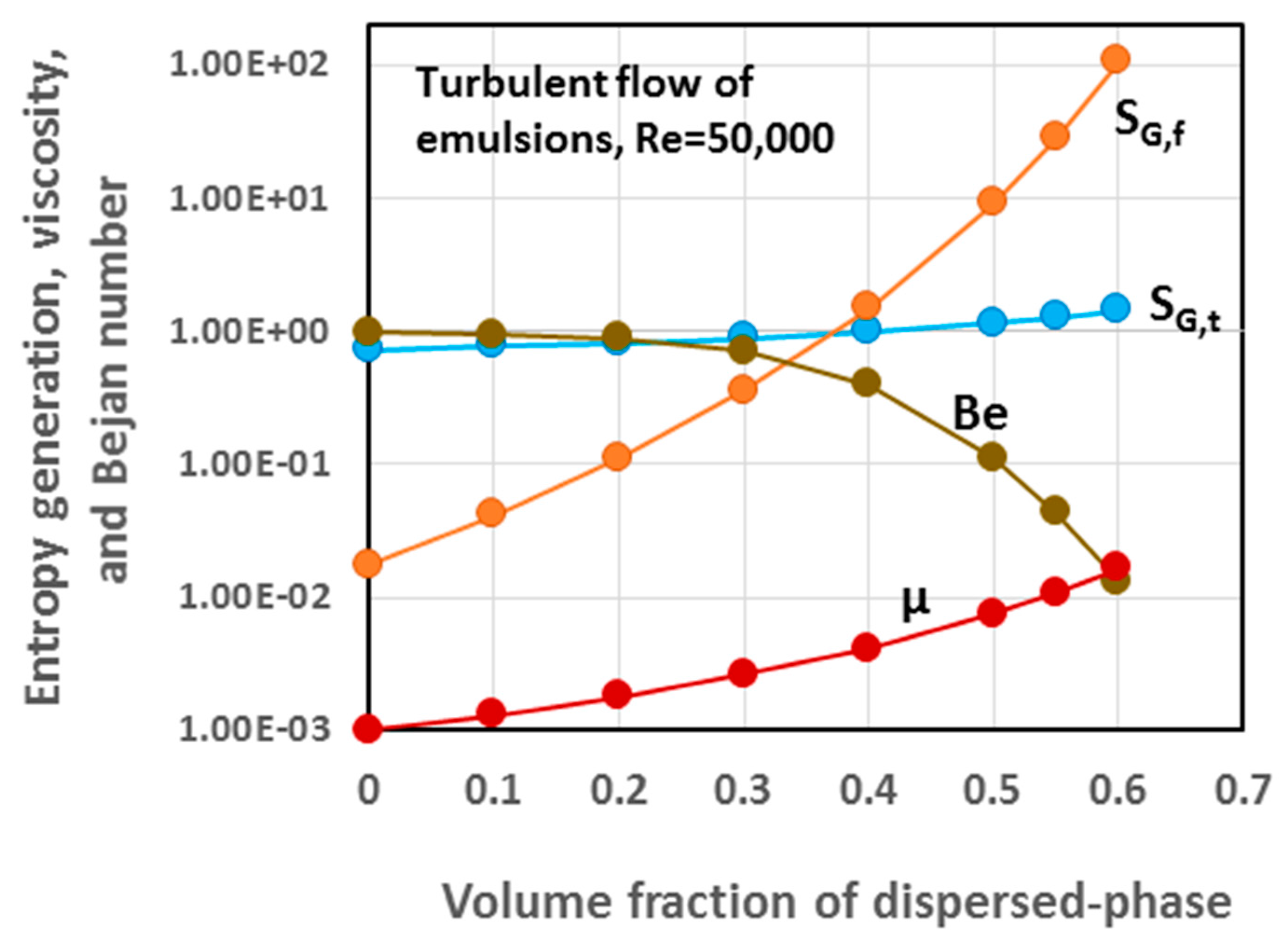
5.3. Simulation Results and Discussion
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Energy Efficiency Guide for Industry in Asia, Energy Equipment: Pump and Pumping Systems, United Nations Environment Programme 2006. Available online: http: //www.energyefficiencyasia.org (accessed on 17 December 2015).
- Smith, J.M.; van Ness, H.C.; Abbott, M.M. Introduction to Chemical Engineering Thermodynamics, 7th ed.; McGraw-Hill: New York, NY, USA, 2005; pp. 635–636. [Google Scholar]
- Abbott, M.M.; van Ness, H.C. Theory and Problems of Thermodynamics, Schaum’s Outline Series, 2nd ed.; McGraw-Hill: New York, NY, USA, 1989; pp. 302–307. [Google Scholar]
- Cengel, Y.; Boles, M. Thermodynamics: An Engineering Approach, 7th ed.; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Bejan, A. Entropy Generation through Heat and Fluid Flow; Wiley & Sons: New York, NY, USA, 1982; pp. 105–107. [Google Scholar]
- Pal, R. Rheology of Particulate Dispersions and Composites; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Pal, R. Effect of droplet size on the rheology of emulsions. AIChE J. 1996, 42, 3181–3190. [Google Scholar] [CrossRef]
- Pal, R. Pipeline flow of unstable and surfactant-stabilized emulsions. AIChE J. 1993, 39, 1754–1764. [Google Scholar] [CrossRef]
- Pal, R.; Rhodes, E. Emulsion flow in pipelines. Int. J. Multiph. Flow 1989, 15, 1011–1017. [Google Scholar] [CrossRef]
- Pal, R. On the flow characteristics of highly concentrated oil-in-water emulsions. Chem. Eng. J. 1990, 43, 53–57. [Google Scholar] [CrossRef]
- Pal, R. Rheology of simple and multiple emulsions. Curr. Opin. Colloid Interface Sci. 2011, 16, 41–60. [Google Scholar] [CrossRef]
- Pal, R. Techniques for measuring the composition (oil and water content) of emulsions—A state of the art review. Colloids Surfaces A 1994, 84, 141–193. [Google Scholar] [CrossRef]
- Pal, R. Entropy production in pipeline flow of dispersions of water in oil. Entropy 2014, 16, 4648–4661. [Google Scholar] [CrossRef]
- Pal, R. Exergy destruction in pipeline flow of surfactant-stabilized oil-in-water emulsions. Energies 2014, 7, 7602–7619. [Google Scholar] [CrossRef]
- Pal, R. Entropy generation in flow of highly concentrated non-Newtonian emulsions in smooth tubes. Entropy 2014, 16, 5178–5197. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization: The Method of Thermodynamic Optimization of Finite-Size Systems and Finite-Time Processes; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; Dewitt, D.P. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Pal, R. New models for the viscosity of nanofluids. J. Nanofluids 2014, 3, 260–266. [Google Scholar] [CrossRef]
- Pal, R. Electromagnetic, Mechanical, and Transport Properties of Composite Materials; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]




| Pipe Inside Diameter (mm) | Entrance Length (m) | Length of Test Section (m) | Exit Length (m) |
|---|---|---|---|
| 8.89 | 0.89 | 3.35 | 0.48 |
| 15.8 | 1.65 | 2.59 | 0.56 |
| Emulsion-Type | Oil-Phase | Aqueous-Phase | Dispersed-Phase Concentrations (% Vol.) |
|---|---|---|---|
| Unstable O/W (Set 1) | Refined mineral oil (Bayol-35) | Tap water | 28.76; 44.98; 55.07 |
| Surfactant-stabilized O/W (Set 2) | Refined mineral oil (Bayol-35) | 1% by wt. surfactant solution in tap water; the surfactant used was Triton X-100 (isooctylphenoxypolyethoxy ethanol) | 16.53; 30.4; 44.41; 49.65; 55.14 |
| Unstable W/O (Set 3) | Refined mineral oil (Bayol-35) | Tap water | 0; 10.51; 17.49; 26.72; 32.47; 38.14; 41.05 |
| Surfactant-stabilized W/O (Set 4) | 1.5% by wt. surfactant solution in mineral oil (Bayol-35); the surfactant used was SPAN-80 (sorbitan monooleate) | Tap water | 0; 10.61; 18.25; 25.85 |
| Property | Matrix (Water) | Dispersed-Phase (Oil) | Emulsion | Emulsion | Emulsion | Emulsion | Emulsion |
|---|---|---|---|---|---|---|---|
| 1000 | 780 | 956 | 934 | 912 | 890 | 868 | |
| Cp(J/(kg·K)) | 4180 | 1470 | 3738 | 3501 | 3253 | 2992 | 2719 |
| 0.60 | 0.15 | 0.488 | 0.436 | 0.388 | 0.343 | 0.30 | |
| 1 | 2.5 | 1.79 | 2.61 | 4.13 | 7.44 | 16.57 | |
| Pr | 7 | 25 | 14 | 21 | 35 | 65 | 150 |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pal, R. Second Law Analysis of Adiabatic and Non-Adiabatic Pipeline Flows of Unstable and Surfactant-Stabilized Emulsions. Entropy 2016, 18, 113. https://doi.org/10.3390/e18040113
Pal R. Second Law Analysis of Adiabatic and Non-Adiabatic Pipeline Flows of Unstable and Surfactant-Stabilized Emulsions. Entropy. 2016; 18(4):113. https://doi.org/10.3390/e18040113
Chicago/Turabian StylePal, Rajinder. 2016. "Second Law Analysis of Adiabatic and Non-Adiabatic Pipeline Flows of Unstable and Surfactant-Stabilized Emulsions" Entropy 18, no. 4: 113. https://doi.org/10.3390/e18040113





