Entropy for the Quantized Field in the Atom-Field Interaction: Initial Thermal Distribution
Abstract
:1. Introduction
2. Initial Mixed State
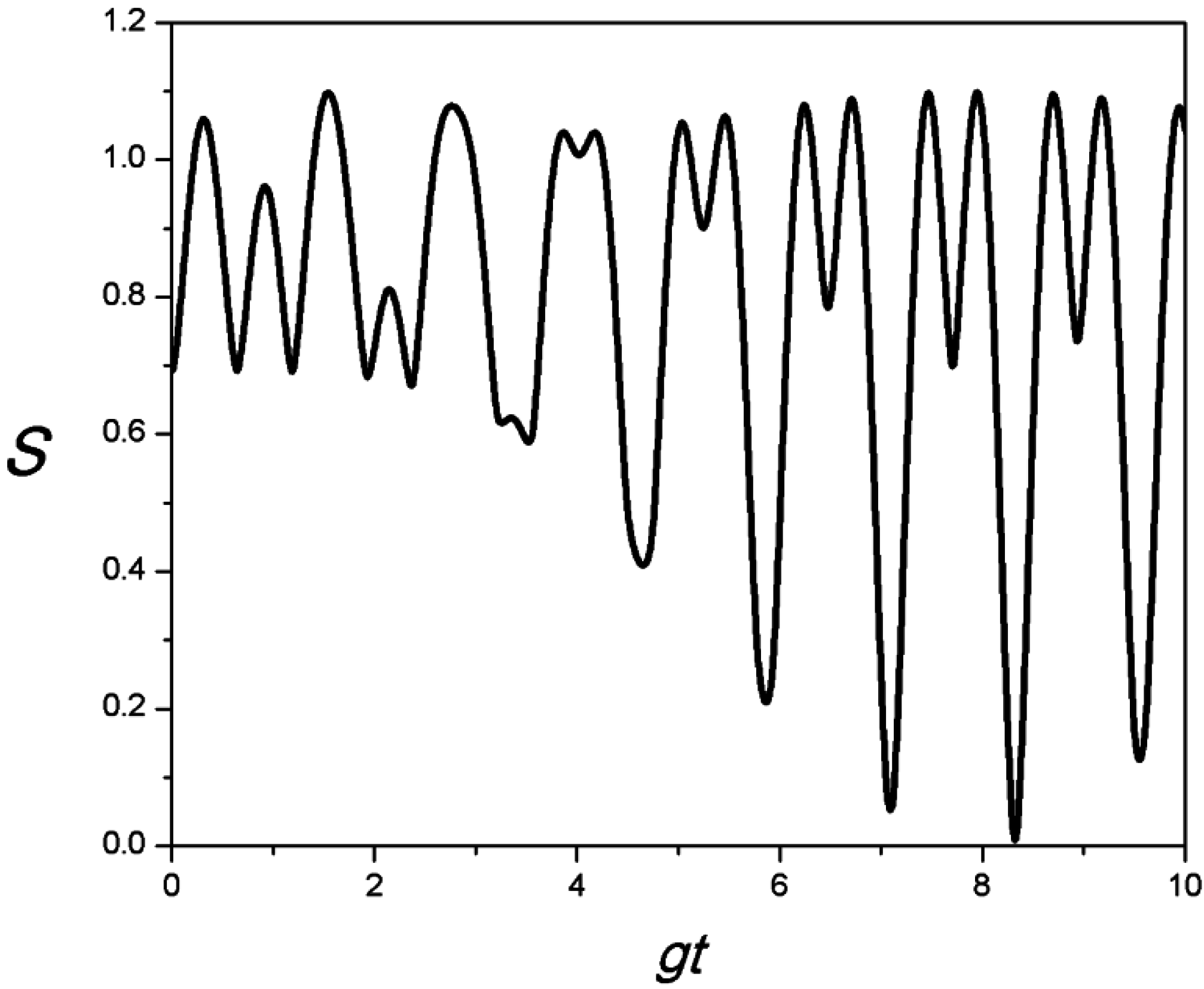
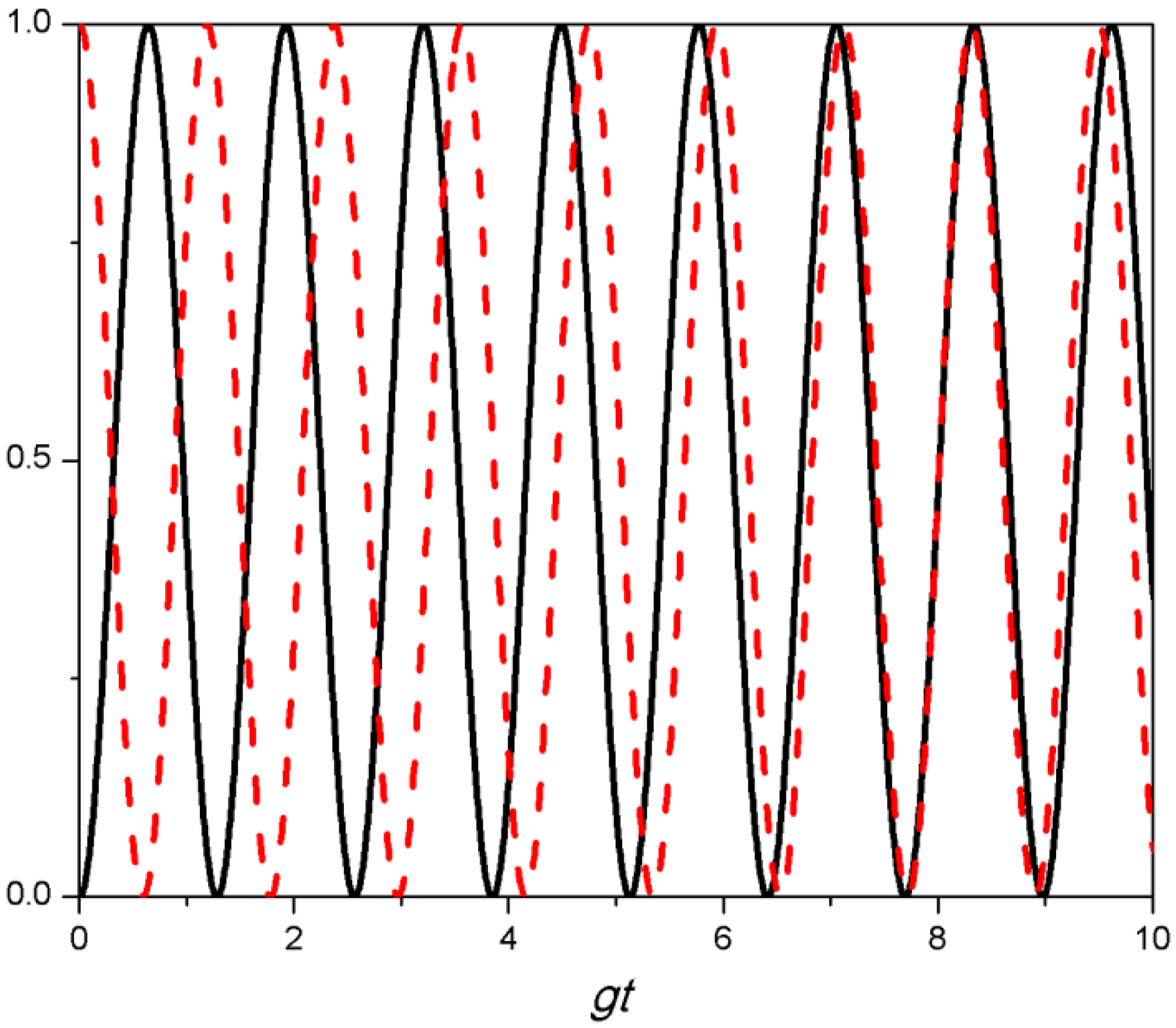
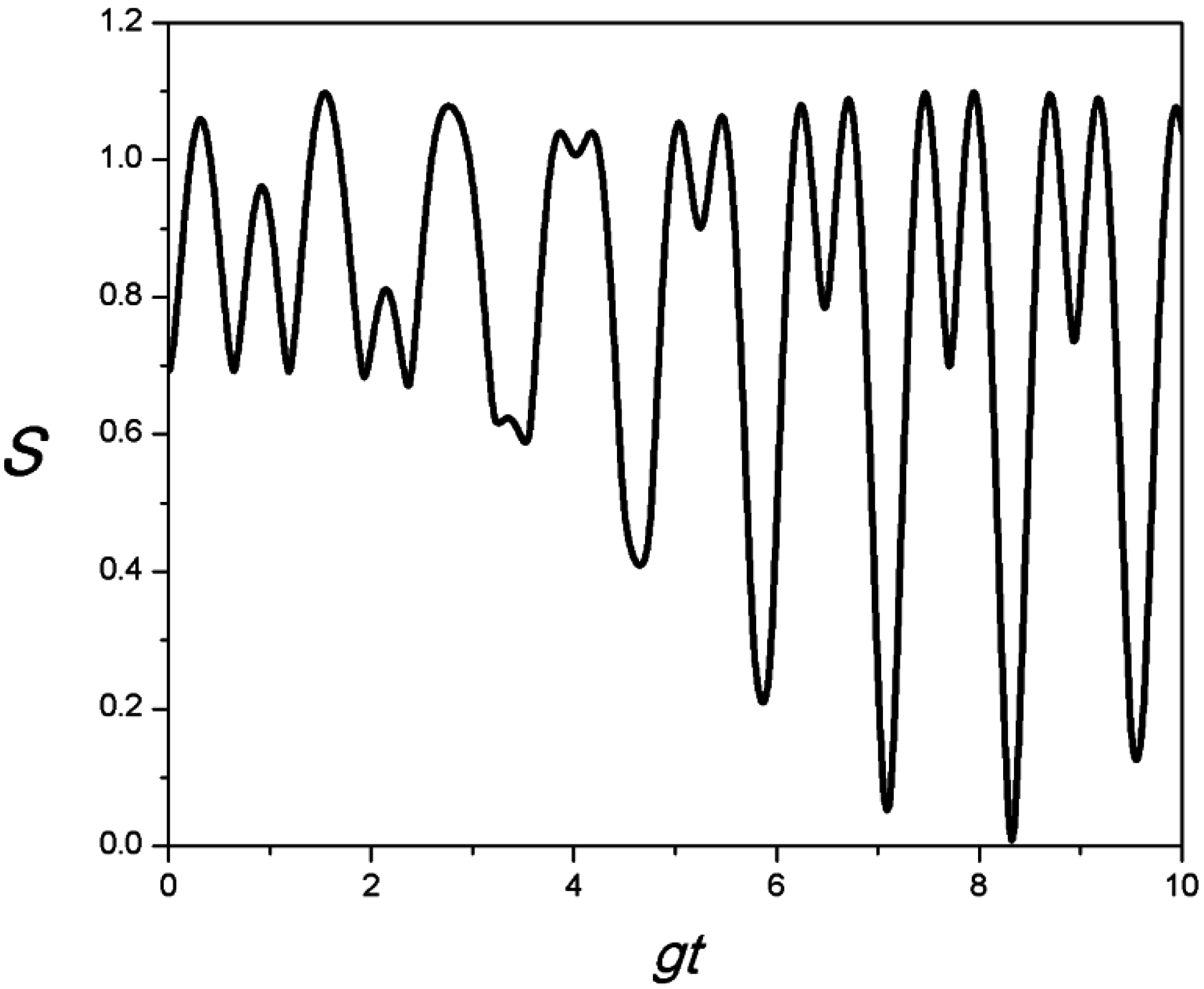
3. Thermal Distribution as Initial Field State
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Moya-Cessa, H. Entropy operator and associated Wigner function. Int. J. Quant. Inf. 2007, 5, 149–155. [Google Scholar] [CrossRef]
- Berrada, K.; Ei Bas, M.; Eleuch, H.; Hassouni, Y. A comparative study of negativity and concurrence based on spin coherent states. Int. J. Mod. Phys. C 2010, 21, 291–305. [Google Scholar] [CrossRef]
- Araki, H.; Lieb, E. Entropy inequalities. Commun. Math. Phys. 1970, 18, 160–170. [Google Scholar] [CrossRef]
- Vidiella-Barranco, A.; Moya-Cessa, H.; Buzek, V. Interaction of superpositions of coherent states of light with two-level atoms. J. Mod. Opt. 1992, 39, 1441–1459. [Google Scholar] [CrossRef]
- Moya-Cessa, H.; Vidiella-Barranco, A. Interaction of squeezed states of light with two-level atoms. J. Mod. Opt. 1992, 39, 2481–2499. [Google Scholar] [CrossRef]
- Jaynes, E.T.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Shore, B.W.; Knight, P.L. The Jaynes-Cummings model. J. Mod. Opt. 1993, 40, 1195–1238. [Google Scholar] [CrossRef]
- Moya-Cessa, H.; Tombesi, P. Filtering number states of the vibrational motion of an ion. Phys. Rev. A 2000, 61. [Google Scholar] [CrossRef]
- Moya-Cessa, H.; Soto-Eguibar, F.; Vargas-Martinez, J.M.; Juarez-Amaro, R.; Zuñiga-Segundo, A. Ion-laser interactions: The most complete solution. Phys. Rep. 2012, 513, 229–261. [Google Scholar] [CrossRef]
- Eleuch, H.; Rostovtsev, Y.V.; Scully, M.O. New analytic solution of Schrödinger’s equation. Europhys. Lett. 2010, 89. [Google Scholar] [CrossRef]
- London, F. Winkelvariable und kanonische Transformationen in der Undulationsmechanik. Z. Phys. 1927, 40, 193–210. [Google Scholar] [CrossRef]
- Susskind, L.; Glogower, J. Quantum mechanical phase and time operator. Physics 1964, 1, 49–61. [Google Scholar]
- Moya-Cessa, H.; Knight, P.L.; Rosenhouse-Dantsker, A. Photon amplification in a two-photon lossless micromaser. Phys. Rev. A 1994, 50, 1814–1821. [Google Scholar] [CrossRef] [PubMed]
- Eleuch, H.; Guérin, S.; Jauslin, H.R. Effects of an environment on a cavity-quantum-electrodynamics system controlled by bichromatic adiabatic passage. Phys. Rev. A 2012, 85. [Google Scholar] [CrossRef]
- Giacobino, E.; Karr, J.-P.; Messin, G.; Eleuch, H.; Baas, A. Quantum optical effects in semiconductor microcavities. C. R. Phys. 2002, 3, 41–52. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrade-Morales, L.A.; Villegas-Martínez, B.M.; Moya-Cessa, H.M. Entropy for the Quantized Field in the Atom-Field Interaction: Initial Thermal Distribution. Entropy 2016, 18, 346. https://doi.org/10.3390/e18100346
Andrade-Morales LA, Villegas-Martínez BM, Moya-Cessa HM. Entropy for the Quantized Field in the Atom-Field Interaction: Initial Thermal Distribution. Entropy. 2016; 18(10):346. https://doi.org/10.3390/e18100346
Chicago/Turabian StyleAndrade-Morales, Luis Amilca, Braulio M. Villegas-Martínez, and Hector M. Moya-Cessa. 2016. "Entropy for the Quantized Field in the Atom-Field Interaction: Initial Thermal Distribution" Entropy 18, no. 10: 346. https://doi.org/10.3390/e18100346




