Proportionate Minimum Error Entropy Algorithm for Sparse System Identification
Abstract
:1. Introduction
2. Proportionate Minimum Error Entropy Algorithm
2.1. Minimum Error Entropy Criterion
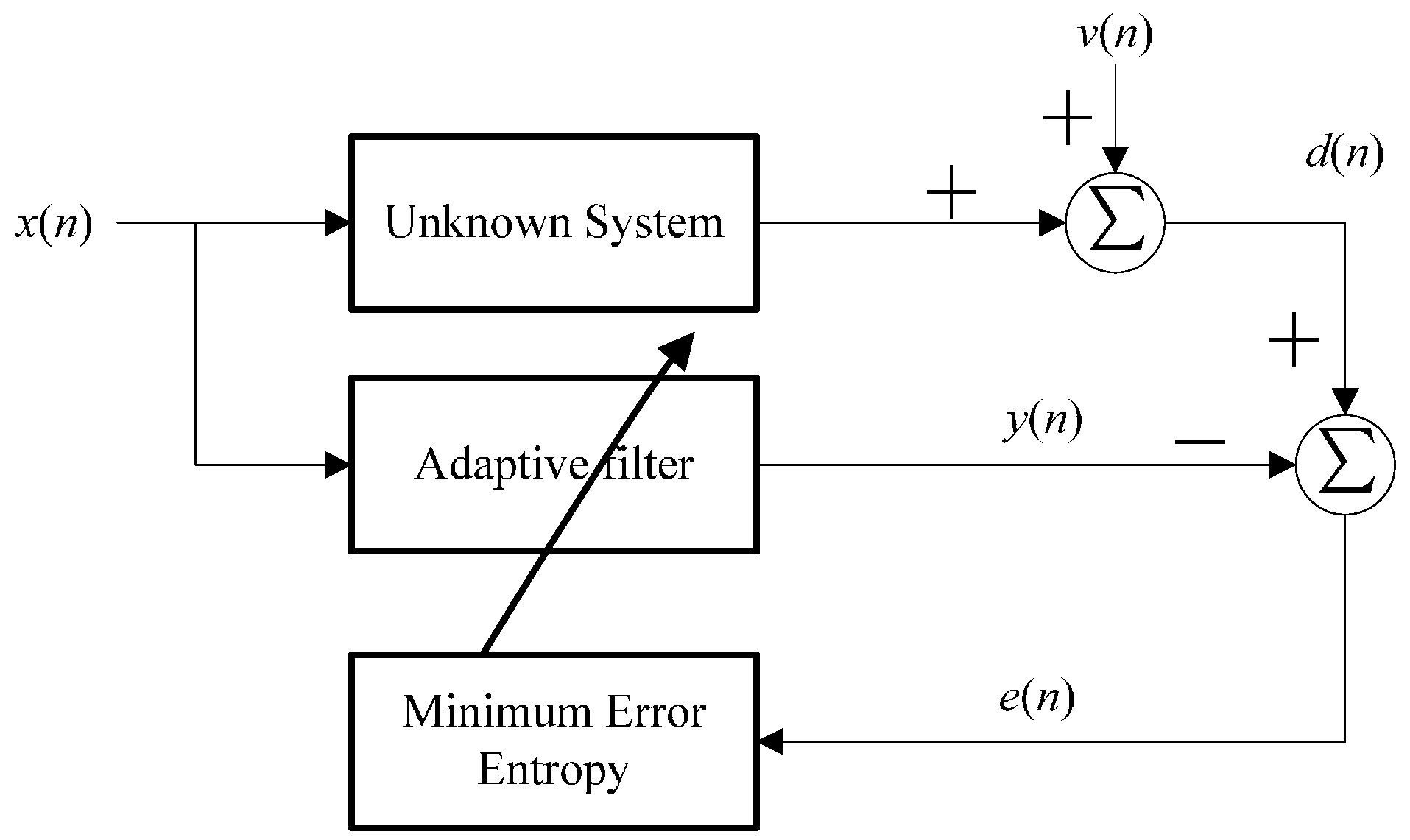
2.2. Proportionate Minimum Error Entropy
3. Mean Square Convergence Analysis
3.1. Energy Conservation Relation
3.2. Sufficient Condition for Mean Square Convergence
4. Simulation Results
- (a)
- Channel 1:
- (b)
- Channel 2:
- (c)
- Channel 3:
- (d)
- Channel 4:
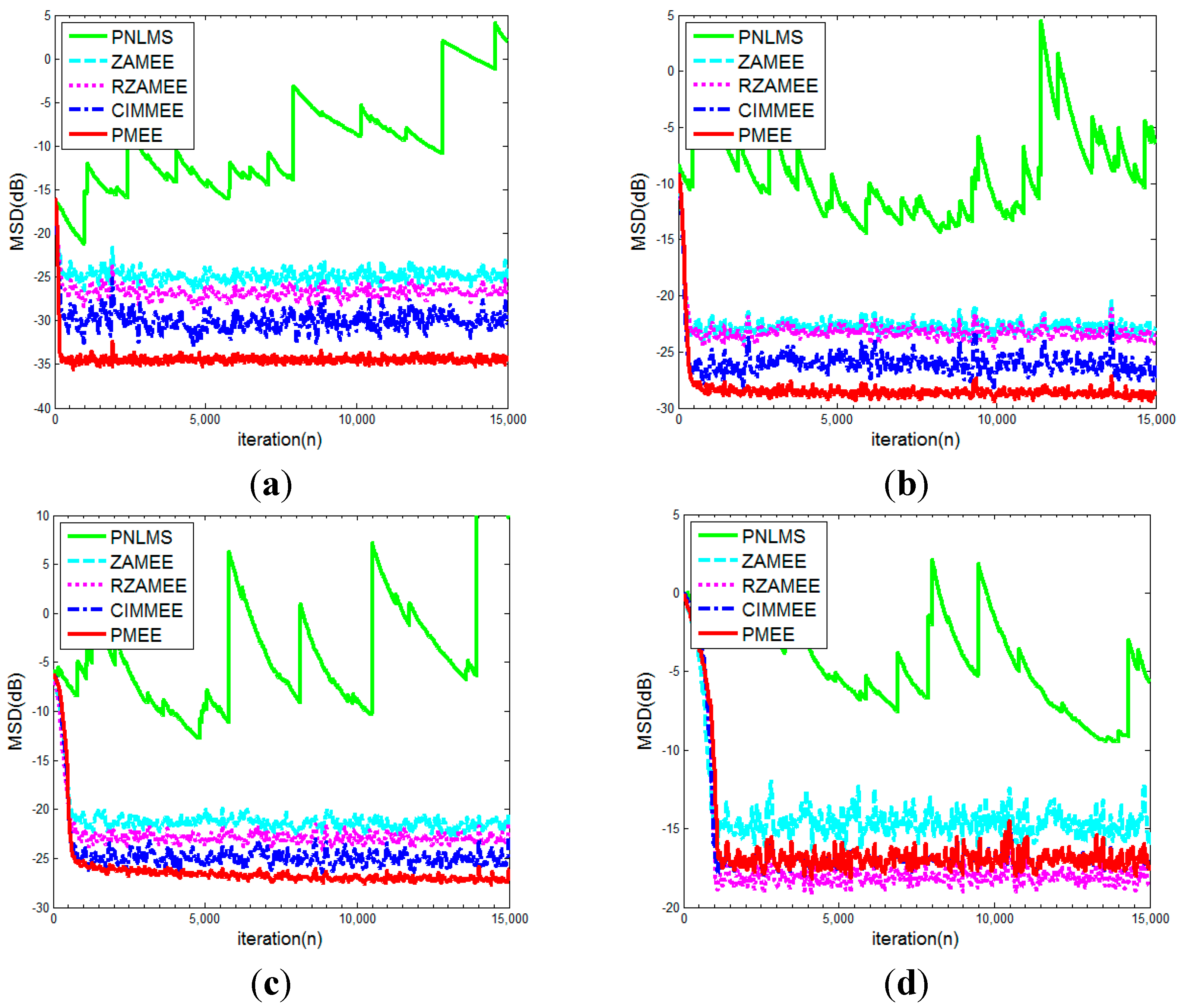
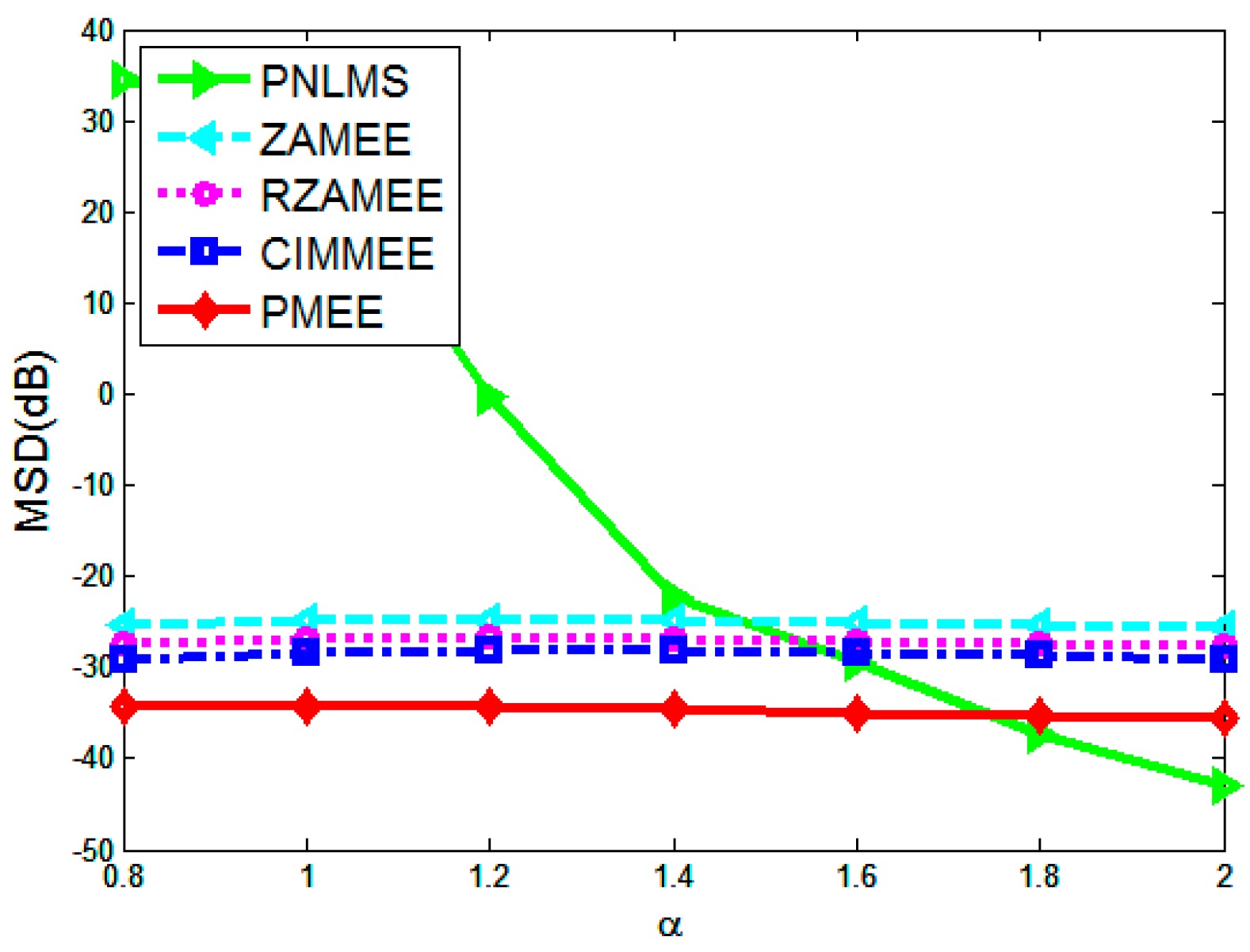
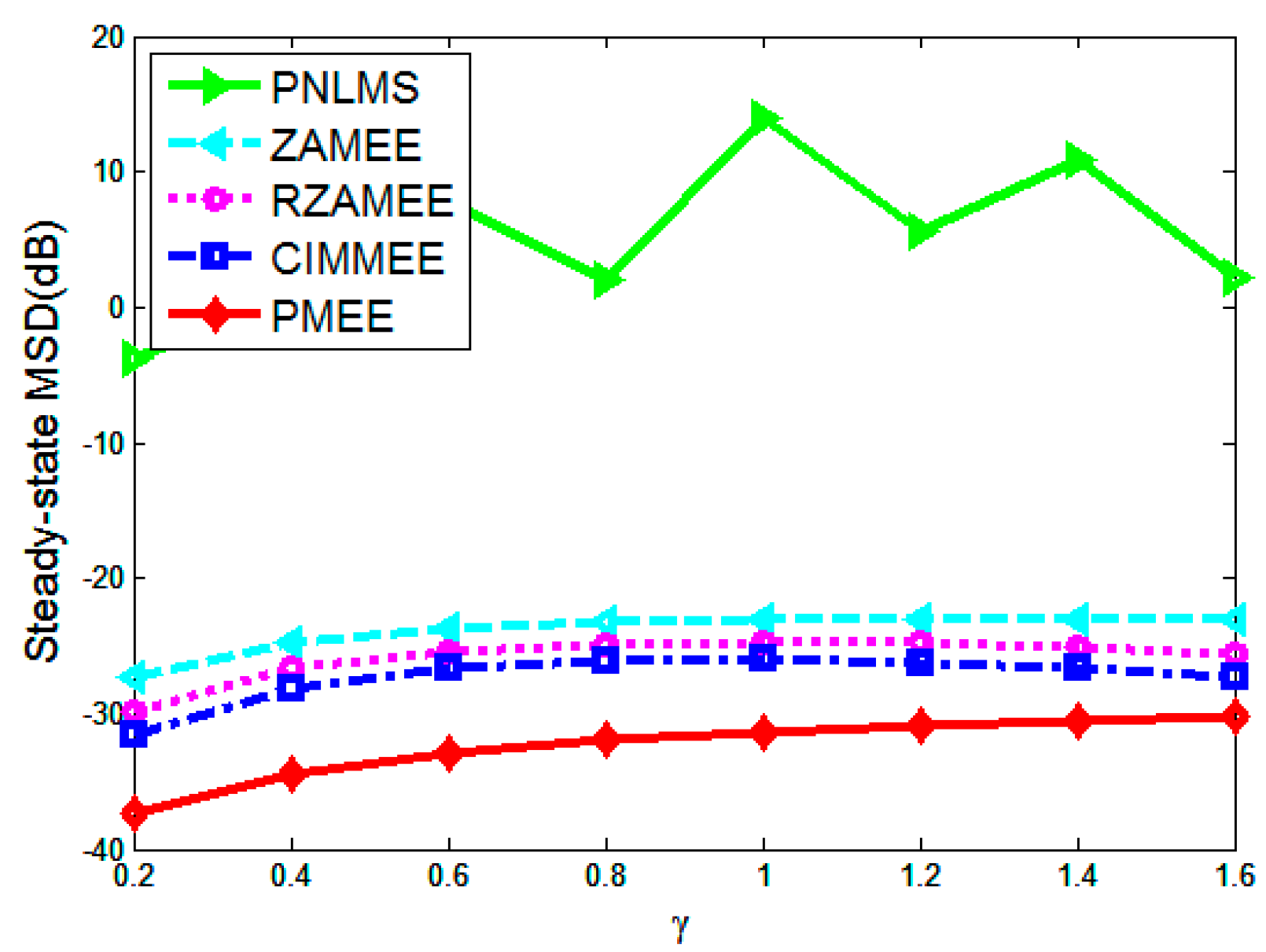
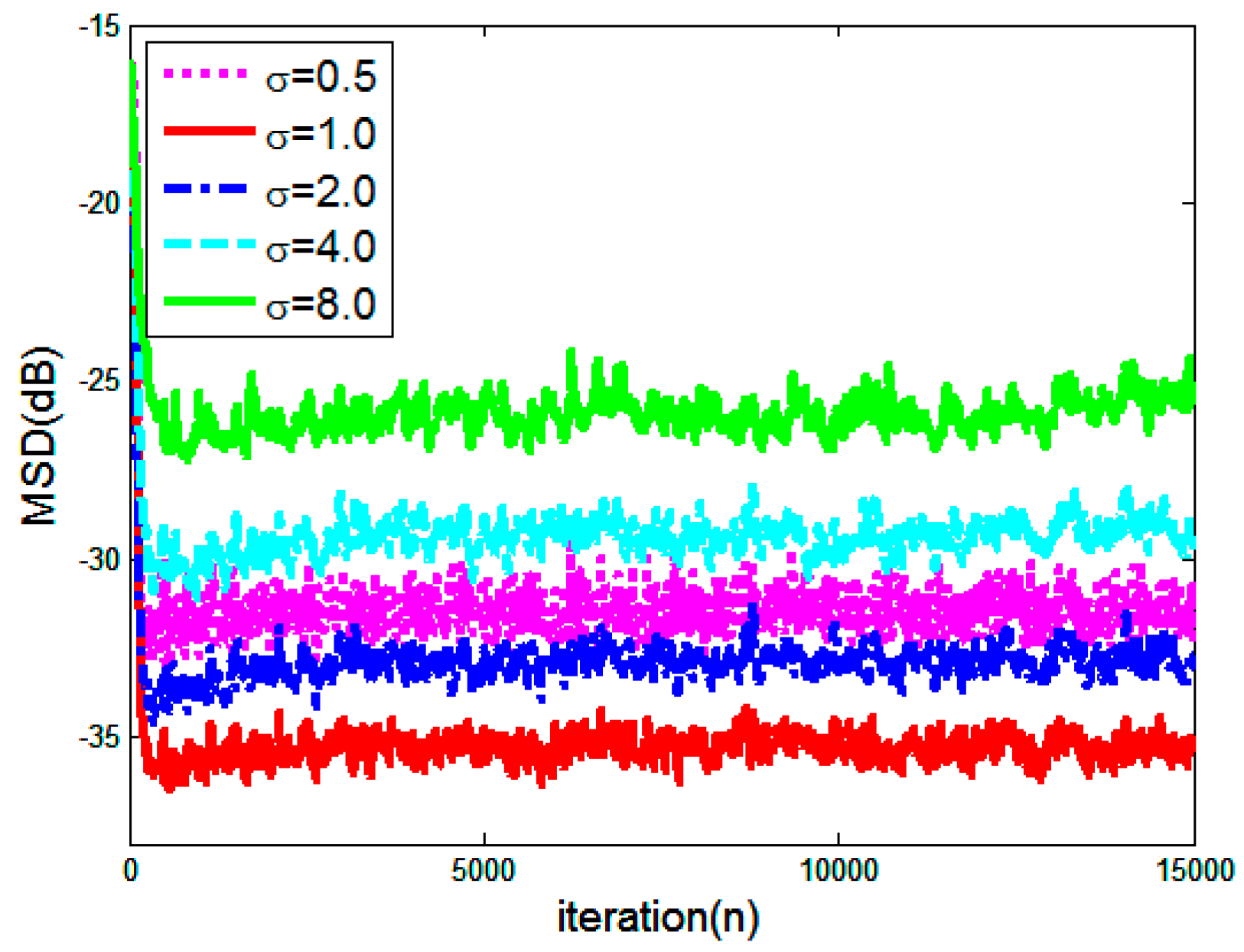
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Huang, Y.; Benesty, J.; Chen, J. Acoustic MIMO Signal Processing; Springer: New York, NY, USA, 2006. [Google Scholar]
- Paleologu, C.; Benesty, J.; Ciochina, S. Sparse Adaptive Filters for Echo Cancellation; Morgan and Claypool: San Rafael, CA, USA, 2010. [Google Scholar]
- Sayed, A.H. Fundamentals of Adaptive Filtering; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Duttweiler, D. Proportionate normalized least-mean-squares adaptation in echo cancellers. IEEE Trans. Speech Audio Process. 2000, 8, 508–518. [Google Scholar] [CrossRef]
- Deng, H.; Doroslovacki, M. Improving convergence of the PNLMS algorithm for sparse impulse response identification. IEEE Signal Process. Lett. 2005, 12, 181–184. [Google Scholar] [CrossRef]
- Laska, B.N.M.; Goubran, R.A.; Bolic, M. Improved proportionate subband NLMS for acoustic echo cancellation in changing environments. IEEE Signal Process. Lett. 2008, 15, 337–340. [Google Scholar] [CrossRef]
- Das Chagas de Souza, F.; Seara, R.; Morgan, D.R. An enhanced IAF-PNLMS adaptive algorithm for sparse impulse response identification. IEEE Trans. Signal Process. 2012, 60, 3301–3307. [Google Scholar] [CrossRef]
- Deng, H.; Doroslovacki, M. Proportionate adaptive algorithms for network echo cancellation. IEEE Trans. Signal Process. 2006, 54, 1794–1803. [Google Scholar] [CrossRef]
- Paleologu, C.; Ciochină, S.; Benesty, J. An efficient proportionate affine projection algorithm for echo cancellation. IEEE Signal Process. Lett. 2010, 17, 165–168. [Google Scholar] [CrossRef]
- Yang, J.; Sobelman, G.E. Efficient μ-law improved proportionate affine projection algorithm for echo cancellation. Electron. Lett. 2010, 47, 73–74. [Google Scholar] [CrossRef]
- Yang, Z.; Zheng, Y.R.; Grant, S.L. Proportionate affine projection sign algorithms for network echo cancellation. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 2273–2284. [Google Scholar] [CrossRef]
- Zhao, H.; Yu, Y.; Gao, S.; Zeng, X.; He, Z. Memory proportionate APA with individual activation factors for acoustic echo cancellation. IEEE Trans. Audio Speech Lang. Process. 2014, 22, 1047–1055. [Google Scholar] [CrossRef]
- Plataniotis, K.N.; Androutsos, D.; Venetsanopoulos, A.N. Nonlinear filtering of non-Gaussian noise. J. Intell. Robot. Syst. 1997, 19, 207–231. [Google Scholar] [CrossRef]
- Weng, B.; Barner, K.E. Nonlinear system identification in impulsive environments. IEEE Trans. Signal Process. 2005, 53, 2588–2594. [Google Scholar] [CrossRef]
- Principe, J.C. Information Theoretic Learning: Renyi’s Entropy and Kernel Perspectives; Springer: New York, NY, USA, 2010. [Google Scholar]
- Chen, B.; Zhu, Y.; Hu, J.C.; Jose Principe, J.C. System Parameter Identification: Information Criteria and Algorithms; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Erdogmus, D.; Principe, J.C. An error-entropy minimization for supervised training of nonlinear adaptive systems. IEEE Trans. Signal Process. 2002, 50, 1780–1786. [Google Scholar] [CrossRef]
- Erdogmus, D.; Principe, J.C. Convergence properties and data efficiency of the minimum error entropy criterion in adaline training. IEEE Trans. Signal Process. 2003, 51, 1966–1978. [Google Scholar] [CrossRef]
- Chen, B.; Zhu, Y.; Hu, J. Mean-square convergence analysis of ADALINE training with minimum error entropy criterion. IEEE Trans. Neural Netw. 2010, 21, 1168–1179. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Hu, J.; Pu, L.; Sun, Z. Stochastic gradient algorithm under (h, phi)-entropy criterion. Circuit Syst. Signal Process. 2007, 26, 941–960. [Google Scholar] [CrossRef]
- Li, C.; Shen, P.; Liu, Y.; Zhang, Z. Diffusion information theoretic learning for distributed estimation over network. IEEE Trans. Signal Process. 2013, 61, 4011–4024. [Google Scholar] [CrossRef]
- Wolsztynski, E.; Thierry, E.; Pronzato, L. Minimum-entropy estimation in semi-parametric models. Signal Process. 2005, 85, 937–949. [Google Scholar] [CrossRef]
- Al-Naffouri, T.Y.; Sayed, A.H. Adaptive filters with error nonlinearities: Mean-square analysis and optimum design. EURASIP J. Appl. Signal Process. 2001, 4, 192–205. [Google Scholar] [CrossRef]
- Chen, B.; Principe, J.C. Some further results on the minimum error entropy estimation. Entropy 2012, 14, 966–977. [Google Scholar] [CrossRef]
- Chen, B.; Principe, J.C. On the Smoothed Minimum Error Entropy Criterion. Entropy 2012, 14, 2311–2323. [Google Scholar] [CrossRef]
- Wu, Z.; Peng, S.; Ma, W.; Chen, B.; Principe, J.C. Minimum Error Entropy Algorithm with Sparsity Penalty Constraints. Entropy 2015, 17, 3419–3437. [Google Scholar] [CrossRef]
- Weng, B.; Barner, K.E. Nonlinear system identification in impulsive environments. IEEE Trans. Signal Process. 2005, 53, 2588–2594. [Google Scholar] [CrossRef]
- Wang, J.; Kuruoglu, E.E.; Zhou, T. Alpha-stable channel capacity. IEEE Commun. Lett. 2011, 15, 1107–1109. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Peng, S.; Chen, B.; Zhao, H.; Principe, J.C. Proportionate Minimum Error Entropy Algorithm for Sparse System Identification. Entropy 2015, 17, 5995-6006. https://doi.org/10.3390/e17095995
Wu Z, Peng S, Chen B, Zhao H, Principe JC. Proportionate Minimum Error Entropy Algorithm for Sparse System Identification. Entropy. 2015; 17(9):5995-6006. https://doi.org/10.3390/e17095995
Chicago/Turabian StyleWu, Zongze, Siyuan Peng, Badong Chen, Haiquan Zhao, and Jose C. Principe. 2015. "Proportionate Minimum Error Entropy Algorithm for Sparse System Identification" Entropy 17, no. 9: 5995-6006. https://doi.org/10.3390/e17095995






