Information Geometry on Complexity and Stochastic Interaction

Abstract

Interdependencies of stochastically interacting units are usually quantified by the Kullback-Leibler divergence of a stationary joint probability distribution on the set of all configurations from the corresponding factorized distribution. This is a spatial approach which does not describe the intrinsically temporal aspects of interaction. In the present paper, the setting is extended to a dynamical version where temporal interdependencies are also captured by using information geometry of Markov chain manifolds.

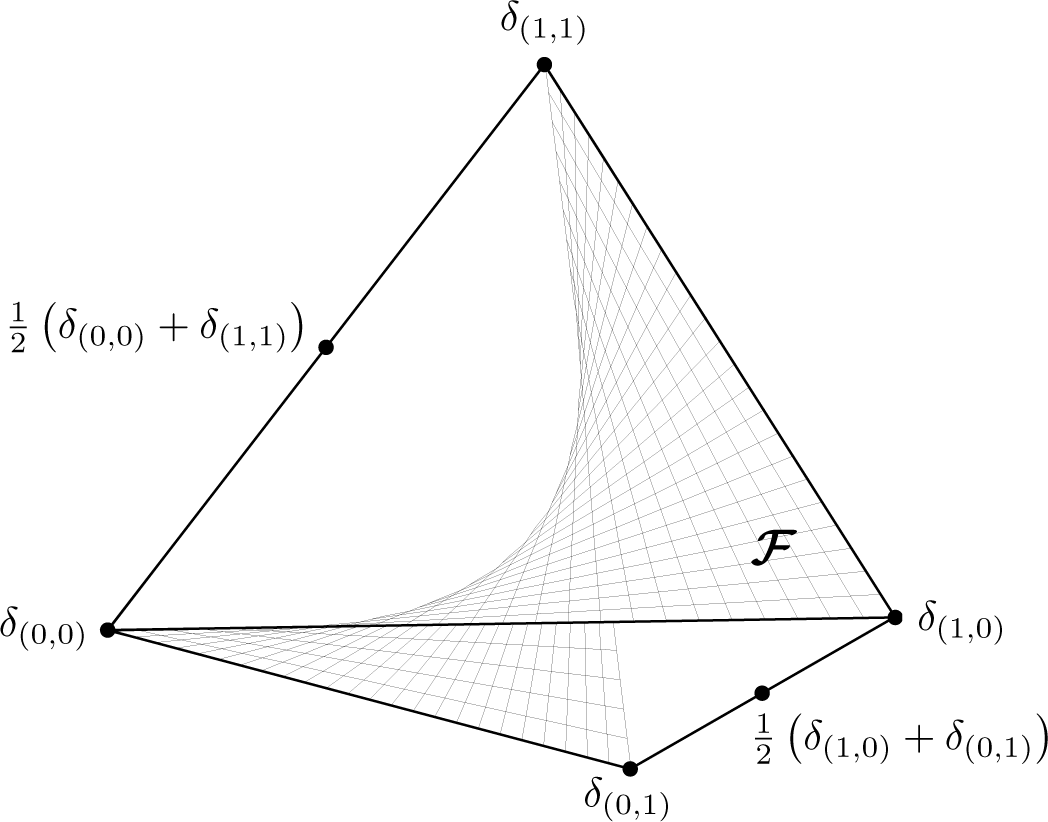
1. Preface: Information Integration and Complexity

Since the publication of Shannon’s pioneering work in 1948 [1], it has been hypothesized that his information theory provides means for understanding information processing and learning in the brain. Already in the 1950s, the principle of redundancy reduction has been proposed independently by Attneave [2] and Barlow [3]. In 1981, Laughlin has provided some experimental evidence for the redundancy reduction principle in terms of the maximization of the output entropy of large monopolar cells of the fly’s compound eye [4]. As only deterministic response functions have been considered, this principle turns out to be equivalent to the mutual information maximization between the input and the output. Later, Linsker [5] has demonstrated that the maximization of mutual information in a layered feed-forward network leads to feature detectors that are similar to those observed by Hubel and Wiesel in the visual system of the cat and the monkey [6,7]. He coined his information-theoretic principle of learning the infomax principle.

The idea that an information-theoretic principle, such as the infomax principle, governs learning processes of neuronal systems has attracted many researchers. A highly recognized contribution in this regard is the work by Bell and Sejnowski [8] which applies the infomax principle to the source separation problem. An exhaustive review of all relevant contributions to that field is not within the scope of this short discussion. I shall focus on approaches that aim at relating such information based principles to the overall complexity of the system. In particular, I shall concentrate on the theory of information integration and complexity, initially proposed by Tononi, Sporns, and Edelman [9], and further developed and analyzed in a series of papers [10–15]. I shall compare this line of research with my own information-geometric approach to complexity, initially proposed in my manuscript [16], entitled Information Geometry on Complexity and Stochastic Interaction, which led to various lines of research that I am going to outline below. This manuscript constitutes the main body of the present paper, starting with Section 2. It quantifies complexity as the extent to which the whole is more than the sum of its parts using information geometry [17]. Thereby, it extends the notion of multi-information [18,19], also called information integration in [9], to the setting of discrete time stochastic processes, in particular Markov chains. This article was originally accepted for publication in IEEE Transactions on Information Theory, subject to minor revision. However, by the end of the unusually long reviewing process I had come to the conclusion that my geometric approach has to be further improved in order to address important aspects of complexity (I shall be more concrete on that). Recent developments, on the other hand, suggest that this work is of relevance in the context of information integration already in its present form [12–15,20,21]. Therefore, it should be useful to provide it together with a discussion of its strengths and shortcomings, thereby relating it to similar work that has been developed since its first publication.

Let us first consider the so-called multi-information [18,19] of a random vector X = (X_v)_v∊V, taking values in a finite set:

$$I(X):={\displaystyle \sum _{v\in V}H(X_v)-H(X)},$$

(1)

where H denotes the Shannon entropy (we assume V to be a non-empty and finite set). The multi-information vanishes if and only if the variables X_v, v ∊ V, are stochastically independent. In their original paper [9], Tononi, Sporns, and Edelman call this quantity integration. Following their intuition, however, the notion of integration should rather refer to a dynamical process, the process of integration, which is causal in nature. In later works, the dynamical aspects have been more explicitly addressed in terms of a causal version of mutual information, leading to improved notions of effective information and information integration, denoted by Φ [10,11]. In fact, most formulated information-theoretic principles are, in some way or another, based on (conditional) mutual information. This directly fits into Shannon’s classical sender-receiver picture [1], where the mutual information has been used in order to quantify the capacity of a communication channel. At first sight, this picture suggests to treat only feed-forward networks, in which information is transmitted from one layer to the next, as in the context of Linsker’s infomax principle. In order to overcome this apparent restriction, however, we can simply unfold the dynamics in time and consider corresponding temporal information flow measures, which allows us to treat also recurrent networks. In what follows, I am going to explain this idea in more detail, thereby providing a motivation of the quantities that are derived in Section 2 in terms of information geometry.

We consider again a non-empty and finite set V of nodes and assume that each v ∊ V receives signals from a set of nodes which we call parents of v and denote by pa(v). Based on the received signals, the node v updates its state according to a Markov kernel K^(v), the mechanism of v, which quantifies the conditional probability of its new state ${{\omega }^{\prime }}_v$ given the current state ω_pa(v) of its parents. If v ∊ pa(v), this update will involve also ω_v for generating the new state ${{\omega }^{\prime }}_v$. How much information is involved from “outside”, that is from ∂(v) := pa(v) \ v, in addition to the information given by ω_v? We can define the local information flow from this set as

$$IF\left(X_{\partial }{}_{(v)}\to {X^{\prime }}_v\right):=H\left({X^{\prime }}_v|X_v\right)-H\left({X^{\prime }}_v|X_v,X_{\partial }{}_{(v)}\right)=MI\left({X^{\prime }}_v;X_{\partial }{}_{(v)}|X_v\right),$$

(2)

where MI stands for the (conditional) mutual information. Note that this is the uncertainty reduction that the node v gains through the knowledge of its parents’ state, in addition to its own state. Now let us define the total information flow in the network. In order to do so, we have to consider the overall transition kernel. Because the nodes update their states in parallel, the global transition kernel is given as

$$K({\omega }^{\prime }|\omega )={\displaystyle \prod _{v\in V}{K}^{(v)}}({{\omega }^{\prime }}_v|{\omega }_{pa(v)}).$$

(3)

In order to quantify the total information flow in the network, we simply add all the local information flows, defined by Equation (2), and obtain

$$IF\left(X\to X^{\prime }\right):={\displaystyle \sum _{v\in V}IF}\left(X_{\partial }{}_{(v)}\to X_v\right).$$

(4)

It is easy to see that the total information flow vanishes whenever the global transition kernel has the following structure which encodes the dynamics of isolated non-communicating nodes:

$$K({\omega }^{\prime }|\omega )={\displaystyle \prod _{v\in V}{K}^{(v)}}({{\omega }^{\prime }}_v|{\omega }_v).$$

(5)

Referring to these kernels as being split, we are now ready to give our network information flow measure, defined by Equation (4), a geometric interpretation. If K has the structure Equation (3) then

$$IF\left(X\to X^{\prime }\right)={\displaystyle \sum _{v\in V}H}\left({X^{\prime }}_v|X_v\right)-H(X^{\prime }|X)$$

(6)

$$=\underset{K^{\prime }\text{split}}{\min }{D}_p(K\Vert K^{\prime }).$$

(7)

Here, D_p(K || K′) is a measure of “distance”, in terms of the Kullback-Leibler divergence, between K and K′ with respect to the distribution p (see definition by Equation (23)). The expression on the right-hand side of Equation (6) can be considered as an extension of the multi-information (1) to the temporal domain. The second equality, Equation (7), gives the total information flow in the network a geometric interpretation as the distance of the global dynamics K from the set of split dynamics. Stated differently, the total information flow can be seen as the extent to which the whole transition X → X′ is more than the sum of its individual transitions $X_v\to {X^{\prime }}_v$, v ∊ V. Note, however, that Equation (6) follows from the additional structure (3) which implies $H(X^{\prime }|X)={\displaystyle \sum {}_{v\in V}H({X^{\prime }}_v|X)}$. This structure encodes the consistency of the dynamics with the network. Equation (7), on the other hand, holds for any transition kernel K. Therefore, without reference to a particular network, the distance min_{K′ split} D_p(K || K′) can be considered as a complexity measure for any transition X → X′, which we denote by C⁽¹⁾(X → X′). The information-geometric derivation of C⁽¹⁾(X → X′) is given in Section 2.4.1. Restricted to kernels that are consistent with a network, the complexity C⁽¹⁾(X → X′) reduces to the total information flow in the network (see Proposition 2 (iv)).

In order to consider the maximization of the complexity measure C⁽¹⁾(X → X′) as a valid information-theoretic principle of learning in neuronal systems, I analyzed the natural gradient field on the manifold of kernels that have the structure given by Equation (3) (see [17,22] for the natural gradient method within information geometry). In [23] I proved the consistency of this gradient in the sense that it is completely local: If every node v maximizes its own local information flow, defined by Equation (2), in terms of the natural gradient, then this will be the best way, again with respect to the natural gradient, to maximize the complexity of the whole system. This suggests that the infomax principle by Linsker and also Laughlin’s ansatz, applied locally to recurrent networks, will actually lead to the maximization of the overall complexity. We used geometric methods to study the maximizers of this complexity analytically [24,25]. We have shown that they are almost deterministic, which has quite interesting implications, for instance for the design of learning systems that are parametrized in a way that allows them to maximize their complexity [26] (see also [27] for an overview of geometric methods for systems design). Furthermore, evidence has been provided in [25] that the maximization of C⁽¹⁾(X → X′) is achieved in terms of a rule that mimics the spike-timing-dependent plasticity of neurons in the context of discrete time. Together with Wennekers, we have studied complexity maximization as first principle of learning in neural networks also in [28–33].

Even though I implicitly assumed that a natural notion of information flow has to reflect the causal interactions of the nodes, I should point out that the above definition of information flow has a shortcoming in this regard. If X_v and X_∂(v) contain the same information, due to a strong stochastic dependence, then the conditional mutual information in Equation (2) will vanish, even though there might be a strong causal effect of ∂(v) on v. Thus, correlation among various potential causes can hide the actual causal information flow. The information flow measure of Equation (2) is one instance of the so-called transfer entropy [34] which is used within the context of Granger causality and has, as a conditional mutual information, the mentioned shortcoming also in more general settings (see a more detailed discussion in [35]). In order to overcome these limitations of the (conditional) mutual information, in a series of papers [35–39] we have proposed the use of information theory in combination with Pearl’s theory of causation [40]. Our approach has been discussed in [41] where a variant of our notion of node exclusion, introduced in [36], has been utilized for an alternative definition. This definition, however, is restricted to direct causal effects and does not capture, in contrast to [35], mediated causal effects.

Let us now draw a parallel to causality issues of the complexity measure introduced in the original work [9], which we refer to as TSE-complexity. In order to do so, consider the following representation of the original TSE-complexity as weighted sum of mutual informations:

$$C_{TSE}(X):={\displaystyle \sum _{A\subseteq V}{\alpha }_{A}MI(X_A;X_{V\backslash A})},$$

(8)

where ${\alpha }_A=\frac{k}{N\left(\begin{array}{c}N\\ k\end{array}\right)}$. Interpreting the mutual information between A and its complement V\A in this sum as an information flow is clearly misleading. These terms are completely associational and neglect the causal nature of information flow. In [10,11], Tononi and Sporns avoid such inconsistencies by injecting noise (maximum entropy distribution) into A and then measuring the effect in V \ A. They use the corresponding interventional mutual information in order to define effective information. Note that, although their notion of noise injection is conceptually similar to the notion of intervention proposed by Pearl, they formalize it differently. However, the idea of considering a post-interventional mutual information is similar to the one formalized in [35,36] using Pearl’s interventional calculus.

Clearly, the measure C⁽¹⁾(X → X′) does not account for all aspects of the system’s complexity. One obvious reason for that can be seen by comparison with the multi-information, defined by Equation (1), which also captures some aspects of complexity in the sense that it quantifies the extent to which the whole is more than the sum of its elements (parts of size one). On the other hand, it attains its (globally) maximal value, if and only if the nodes are completely correlated. Such systems, in particular completely synchronized systems, are generally not considered to be complex. Furthermore, it turns out that these maximizers are determined by the marginals of size two [42]. Stated differently, the maximization of the extent to which the whole is more than the sum of its parts of size one leads to systems that are not more than the sum of their parts of size two (see for a more detailed discussion [43,44]). Therefore, the multi-information does not capture the complexity of a distribution at all levels. The measure C⁽¹⁾(X → X′) has the same shortcoming as the multi-information. In order to study different levels of complexity, one can consider coarse-grainings of the system at different scales in terms of corresponding partitions Π = {S₁,…, S_n} of V. Given such a partition, we can define the information flows among its atoms S_i as we already did for the individual elements v of V. For each S_i, we denote the set of nodes that provide information to S_i from outside by $\partial \left(S_i\right):={\cup }_{v\in S_i}\left(pa\left(v\right)\backslash S_i\right)$. We quantify the information flow into S_i as in Equation (2):

$$IF\left(X_{\partial }{}_{(S_i)}\to X_{S_i}\right):=H\left(X_{S_i}^{\prime }|X_{S_i}\right)-H\left(X_{S_i^{\prime }}|X_{S_i},X_{\partial }{}_{(S_i)}\right)=MI\left(X_{S_i}^{\prime };X_{\partial }{}_{(S_i)}|X_{S_i}\right).$$

(9)

For a transition that satisfies Equation (3), the total information flow among the parts S_i is then given by

$$IF(X\to X^{\prime }|\mathrm{\Pi }):={\displaystyle \sum _{i=1}^{n}IF(X_{\partial (S_i)}\to X_{S_i})}.$$

(10)

We can now define the Π-complexity of a general transition, as we already did for the complete partition:

$$C(X\to X^{\prime }|\mathrm{\Pi }):={\displaystyle \sum _{i=1}^{n}H(X_{S_i}^{\prime }|X_{S_i})}-H(X^{\prime }|X).$$

(11)

Obviously, the Π-complexity coincides with the information flow IF (X → X′ | Π) in the case where the transition kernel is compatible with the network. The information-geometric derivation of C(X → X′ | Π) is given in Section 2.4.1. In the early work [10,11], a similar approach has been proposed where only bipartitions have been considered. Later, an extension to arbitrary partitions has been proposed by Balduzzi and Tononi [12,13] where the complexity defined by Equation (11) appears as measure of effective information. Note, however, that there are important differences. First, the proposed measure by Tononi and his coworkers is reversed in time, so that their quantity is given by Equation (11) where X and X′ have exchanged roles. This time-reversal of the effective information is motivated by its intended role as a measure relevant to conscious experience. This does not make any difference in the case where a stationary distribution is chosen as input distribution. However, in order to be consistent with causal aspects of conscious experience, the authors choose a uniform input distribution, which models the least informative prior about the input.

Note that there is also a closely related measure, referred to as synergistic information in the works [15,45]:

$$SI(X\to X^{\prime }|\mathrm{\Pi }):=MI(X^{\prime };X)-{\displaystyle \sum _{i=1}^{n}MI(X_{S_i}^{\prime };X_{S_i})}$$

(12)

$$=C\left(X\to X\prime |\mathrm{\Pi }\right)-I\left(X_S{}_{{}_1},\dots ,X_{S_n}\right).$$

(13)

The last equation directly follows from Proposition 1 (iii) (see the derivation of Equation (29)). Interpreting the mutual informations as (one-step) predictive information [46–48], the synergistic information quantifies the extent to which the predictive information of the whole system exceeds the sum of predictive informations of the elements.

Now, having for each partition of the system the corresponding Π-complexity of Equation (11), how should one choose among all these complexities the right one? Following the proposal made in [10–13], one should identify the partition (or bipartition) that has the smallest, appropriately normalized, Π-complexity. Although the overall complexity is not explicitly defined in these works, the notion of information integration, denoted by Φ, seems to directly correspond to it. This is confirmed by the fact that information integration is used for the identification of so-called complexes in the system. Loosely speaking, these are defined to be subsets S of V with maximal information integration Φ(S). This suggests that the authors equate information integration with complexity. In a further refinement [12,13] of the information integration concept, this is made even more explicit. In [13], Tononi writes: “In short, integrated information captures the information generated by causal interactions in the whole, over and above the information generated by the parts.”

Defining the overall complexity simply as the minimal one, with respect to all partitions, will ensure that a complex system has a considerably high complexity at all levels. I refer to this choice as the weakest link approach. This is not the only approch to obtain an overall complexty measure from individual ones defined for various levels. In order to give an instructive example for an alternative approach, let us highlight another representation of the TSE-complexity. Instead of the atoms of a partition, this time we consider the subsets of V with a given size k ∊ {1,…, N} and define the following quantity:

$$C^{(k)}(H):=\frac{N}{k\left(\begin{array}{c}N\\ k\end{array}\right)}{\displaystyle \sum _{\begin{array}{c}A\subseteq V\\ |A|=k\end{array}}H(X_A)-H(X)}.$$

(14)

Let us compare this quantity with the multi-information of Equation (1). For k = 1, they are identical. While the multi-information quantifies the extent to which the whole is more than the sum of its elements (subsets of size one), its generalization C^(k)(X) can be interpreted as the extent to which the whole is more than the sum of its parts of size k. Now, defining the overall complexity as the minimal C^(k)(X) would correspond to the weakest link approach which I discussed above in the context of partitions. A complex system would then have considerably high complexity C^(k)(X) at all levels k. However, the TSE-complexity is not constructed according to the weakest link approach, but can be written as a weighted sum of the terms C^(k)(X):

$$C_{TSE}(X)={\displaystyle \sum _{k=1}^N\alpha (k)C^{(k)}(X)},$$

(15)

where $\alpha \left(k\right)=\frac{k}{N}$. The right choice of the weights is important here. I refer to this approach as the average approach. Clearly, one can interpolate between the weakest link approach and the average approach using the standard interpolation between the L^∞-norm (maximum) and the L¹-norm (average) in terms of the L^p-norms, p ≥ 1. However, L^p-norms appear somewhat unnatural for entropic quantities.

The TSE-complexity has also an information-geometric counterpart which has been developed in a series of papers [43,44,49,50]. It is instructive to consider this geometric reformulation of the TSE-complexity. For a distribution p, let p^(k) be the maximum-entropy estimation of p with fixed marginals of order k. In particular, p^(N) = p, and p⁽¹⁾ is the product of the marginals p_v, v ∊ V, of order one. In some sense, p^(k) encodes the structure of p that is contained only in the parts of size k. The deviation of p from p^(k) therefore corresponds to C^(k)(X), as defined in Equation (14). This correspondence can be made more explicit by writing this deviation in terms of a difference of entropies:

$$D\left(p\Vert p^{(k)}\right)=H_{p^{\left(k\right)}}\left(X\right)-H_p\left(X\right),$$

(16)

where D denotes the Kullback-Leibler divergence. If we compare the Equations (16) and (14), then we see that $\frac{N}{k\left(\begin{array}{c}N\\ k\end{array}\right)}{\displaystyle \sum {}_{\begin{array}{c}A\subseteq V\\ |A|=k\end{array}}}H(X_A)$ corresponds to $H_{p^{\left(k\right)}}\left(X\right)$. Indeed, both terms quantify the entropy that is contained in the marginals of order k. From the information-geometric point of view, however, the second term appears more natural. The first term seems to count marginal entropies multiple times so that we can expect that this mean value is larger than $H_{p^{\left(k\right)}}\left(X\right)$. In [43], we have shown that this is indeed true, which implies

$$D\left(p\Vert p^{(k)}\right)\le C^{(k)}\left(X\right).$$

(17)

If we replace the C^(k)(X) in the definition (15) of the TSE-complexity by D(p || p^(k)), then we obtain with the Pythagorean theorem of information geometry the following quantity:

$$I^{\beta }(X):={\displaystyle \sum _{k=1}^{N-1}\beta (k)}D(p^{(k+1)}\Vert p^{(k)}),$$

(18)

where $\beta \left(k\right)=\frac{k\left(k+1\right)}{2}$. Let us compare this with the multi-information. Following [18], we can decompose the multi-information as

$$I(X)=D(p\Vert p^{(1)})={\displaystyle \sum _{k=1}^{N-1}D(p^{(k+1)}\Vert p^{(k)})}.$$

(19)

I already mentioned that high multi-information is achieved for strongly correlated systems, which implies that the global maximizers can be generated by systems that only have pairwise interactions [42], that is p = p⁽²⁾. It follows that in the above decompsition of Equation (19), only the first term D(p⁽²⁾ || p⁽¹⁾) is positive while all the other terms vanish for maximizers of the multi-information. This suggests that the multi-information does not weight all contributions D(p^(k+1) || p^(k)) to the stochastic dependence in a way that would qualify it as a complexity measure. The measure defined by Equation (18), which I see as an information-geometric counterpart of the TSE-complexity, weights the higher-order contributions D(p^(k+1) || p^(k)), k ≥ 2, more strongly. In this geometric picture, we can interpret the TSE-complexity as a rescaling of the multi-information in such a way that its maximization will emphasize not only pairwise interactions.

Concluding this preface, I compared two lines of research, the one pursued by Tononi and coworkers on information integration, and my own information-geometric research on complexity. The fact that both research lines independently identified closely related core concepts of complexity confirms that these concepts are quite natural. The comparison of the involved ideas suggests the following intuitive definition of complexity: The complexity of a system is the extent to which the whole is more than the sum of its parts at all system levels. I argue that information geometry provides natural methods for casting this intuitive definition into a formal and quantitative theory of complexity. My paper [16], included here as Section 2, exemplifies this way of thinking about complexity. It is presented with only minor changes compared to its initial publication, except that the original reference list is replaced by the largely extended up-to-date list of references. This implies repetitions of a few standard definitions which I already used in this preface.

2. “Information Geometry on Complexity and Stochastic Interaction”, Reference [16]

2.1. Introduction

“The whole is more than the sum of its elementary parts.” This statement characterizes the present approach to complexity. Let us put it in a more formal setting. Assume that we have a system consisting of elementary units v ∊ V. With each non-empty subsystem S ⊂ V we associate a set ${\mathcal{O}}_S$ of objects that can be generated by S. Examples for such objects are (deterministic) dynamical systems, stochastic processes, and probability distributions. Furthermore, we assume that there is a “composition” map $\otimes :{\displaystyle {\prod }_{v\in V}{\mathcal{O}}_{\left\{v\right\}}}\hookrightarrow {\mathcal{O}}_V$ that defines how to put objects of the individual units together in order to describe a global object without any interrelations. The image of ⊗ consists of the split global objects which are completely characterized by the individual ones and therefore represent the absence of complexity. In order to quantify complexity, assume that there is given a function D : (x, y) ↦ D(x || y), that measures the divergence of global objects x, $y\in {\mathcal{O}}_V$. We define the complexity of $x\in {\mathcal{O}}_V$ to be the divergence from being split:

$$Complexity\left(x\right):=\begin{array}{c}\inf \\ ysplit\end{array}D\left(x\Vert y\right).$$

(20)

Of course, this approach is very general, and there are many ways to define complexity following this concept. Is there a canonical way? At least, within the probabilistic setting, information geometry [17,51] provides a very convincing framework for this. In the context of random fields, it leads to a measure for “spatial” interdependencies: Given state sets Ω_v, v ∊ V, we define the set O_S of objects that are generated by a subsystem S ⊂ V to be the probability distributions on the product set ${\displaystyle {\prod }_{v\in S}\Omega v}$. A family of individual probability distributions p^(v) on Ω_v can be considered as a distribution on the whole configuration set ${\displaystyle {\prod }_{v\in S}\Omega v}$ by identifying it with the product ${\otimes }_{v\in V}{p}^{(v)}\in {\mathcal{O}}_V$. In order to define the complexity of a distribution $p\in {\mathcal{O}}_V$ on the whole system, according to Equation (20) we have to choose a divergence function. A canonical choice for D is given by the Kullback-Leibler divergence [52,53]:

$$Complexity\left(p\right):=I\left(p\right):=\underset{p^{(v)}\in {\mathcal{O}}_v,v\in V}{\inf }D(p\Vert {\otimes }_{v\in V}{p}^{(v)}).$$

(21)

The distributions with maximal interdependence (complexity) are given by

$$\begin{array}{ccc}\frac{1}{2}\left({\delta }_{\left(0,0\right)}+{\delta }_{\left(1,1\right)}\right)& \text{and}& \frac{1}{2}\left({\delta }_{\left(1,0\right)}+{\delta }_{\left(0,1\right)}\right)\end{array}.$$

Spatial interdependence has been studied by Amari [18] and Ay [23,55] from the information-geometric point of view, where it is referred to as (stochastic) interaction and discussed in view of neural networks. The aim of the present paper is to use the concept of complexity that is formalized by Equation (20) in order to extend spatial interdependence to a dynamical notion of interaction, where the evolution in time is taken into account. Therefore, the term “stochastic interaction” is mainly used in the context of spatio-temporal interdependence.

The present paper is organized as follows. After a brief introduction into the information-geometric description of finite probability spaces in Section 2.2, the general notion of separability is introduced for Markovian transition kernels, and information geometry is used for quantifying non-separability as divergence from separability (Section 2.3). In Section 2.4, the presented theoretical framework is used to derive a dynamical version of the definition in Equation (21), where spatio-temporal interdependencies are quantified and referred to as stochastic interaction. This is illustrated by some simple but instructive examples.

2.2. Preliminaries on Finite Information Geometry

In the following, Ω denotes a non-empty and finite set. The vector space ℝ^Ω of all functions Ω → ℝ carries the natural topology, and we consider subsets as topological subspaces. The set of all probability distributions on Ω is given by

$$\overline{\mathcal{P}}(\mathrm{\Omega }):=\left\{p={\left(p\left(\omega \right)\right)}_{\omega \in \Omega }\in {ℝ}^{\mathrm{\Omega }}:p\left(\omega \right)\ge 0\text{for all}\omega \in \Omega ,{\displaystyle \sum _{\omega \in \mathrm{\Omega }}p(\omega )=1}\right\}.$$

Following the information-geometric description of finite probability spaces, its interior $\mathcal{P}\left(\Omega \right)$ can be considered as a differentiable submanifold of ℝ^Ω with dimension |Ω|−1 and the basis-point independent tangent space

$$\mathrm{T}(\mathrm{\Omega }):=\left\{x\in {ℝ}^{\mathrm{\Omega }}:{\displaystyle \sum _{\omega \in \mathrm{\Omega }}x(\omega )=0}\right\}.$$

(If one considers $\mathcal{P}\left(\Omega \right)$ as an “abstract” differentiable manifold, there are many ways to represent it as a submanifold of ℝ^Ω. In information geometry, the natural embedding presented here is called (−1)-respectively (m)-representation)

With the Fisher metric 〈·,·〉_p : T(Ω) × T(Ω) → ℝ in p ∊$\mathcal{P}\left(\Omega \right)$ defined by

$$(x,y)\mapsto {\langle x,y\rangle }_p:={\displaystyle \sum _{\omega \in \mathrm{\Omega }}\frac{1}{p(\omega )}x(\omega )y(\omega )},$$

$\mathcal{P}\left(\Omega \right)$ becomes a Riemannian manifold [56] (In mathematical biology this metric is also known as Shahshahani metric [57]). The most important additional structure studied in information geometry is given by a pair of dual affine connections on the manifold. Application of such a dual structure to the present situation leads to the notion of (−1)- and (+1)-geodesics: Each two points p, q$\mathcal{P}\left(\Omega \right)$ can be connected by the geodesics ${\gamma }^{(\alpha }{}^{)}={\left({\gamma }_{\omega }^{(\alpha )}\right)}_{\omega \in \mathrm{\Omega }}:\left[0,1\right]\to \mathcal{P}\left(\Omega \right)$, α ∊ {−1, +1, with

$$\begin{array}{ccc}{\gamma }_{\omega }^{(-1)}\left(t\right):=\left(1-t\right)p\left(\omega \right)+tq\left(\omega \right)& \text{and}& {\gamma }_{\omega }^{(+1)}\left(t\right):=r\left(t\right)p{\left(\omega \right)}^{1-t}q{\left(\omega \right)}^t\end{array}.$$

Here, r(t) denotes the normalization factor.

A submanifold ε of $\mathcal{P}\left(\Omega \right)$ is called an exponential family if there exist a point p₀ ∊$\mathcal{P}\left(\Omega \right)$ and vectors v₁,…, v_d ∊ R^Ω, such that it can be expressed as the image of the map ${ℝ}^d\to \mathcal{P}\left(\Omega \right)$, θ = (θ₁,…, θ_d) ↦ p_θ, with

$$p_{\theta }(\omega ):=\frac{p_0(\omega )\exp \left({\displaystyle {\sum }_{i=1}^d{\theta }_i}{v}_i(\omega )\right)}{{\displaystyle {\sum }_{{\omega }^{\prime }\in \mathrm{\Omega }}{p}_0({\omega }^{\prime })}\exp \left({\displaystyle {\sum }_{i=1}^d{\theta }_i}{v}_i({\omega }^{\prime })\right)}.$$

(22)

Let p be a probability distribution in $\mathcal{P}\left(\Omega \right)$. An element p′∊ ε is called (−1)-projection of p onto ε iff the (−1)-geodesic connecting p and p′ intersects ε orthogonally with respect to the Fisher metric. Such a point p′ is unique ([51], Theorem 3.9, p. 91) and can be characterized by the Kullback-Leibler divergence [52,53] (This is a special case of Csiszár’s f-divergence [54])

$$\begin{array}{cc}D:\mathcal{P}(\mathrm{\Omega })\times \mathcal{P}(\mathrm{\Omega })\to {ℝ}_{+},& (p,q)\end{array}\mapsto D(p\Vert q):={\displaystyle \sum _{\omega \in \mathrm{\Omega }}p(\omega )\ln \frac{p(\omega )}{q(\omega )}}.$$

We define the distance D(· || ε) : $\mathcal{P}\left(\Omega \right)\to {ℝ}_{+}$ from E by

$$p\mapsto D(p\Vert \mathcal{E}):=\underset{q\in \epsilon }{\inf }D(|p|q).$$

It is well known that a point p′ ∊ ε is the (−1)-projection of p onto ε if and only if it satisfies the minimizing property D(p || ε) = D(p || p′) ([51], Theorem 3.8, p. 90; [17], Corollary 3.9, p. 63).

In the present paper, the set of states is given by the Cartesian product of individual state sets Ω_v, v ∊ V, where V denotes the set of units. In the following, the unit set and the corresponding state sets are assumed to be non-empty and finite. For a subsystem S ⊂ V, ${\Omega }_S:={\displaystyle {\prod }_{v\in S}{\Omega }_v}$ denotes the set of all configurations on S. The elements of $\overline{\mathcal{P}}\left({\Omega }_S\right)$ are the random fields on S. One has the natural restriction X_S : Ω_V → Ω_S, ω = (ω_v)_v∊V ↦ ω_S := (ω_v)_v∊S, which induces the projection $\overline{\mathcal{P}}\left({\Omega }_V\right)\to \overline{\mathcal{P}}\left({\Omega }_S\right)$, p ↦p_S, where p_S denotes the image measure of p under the variable X_S. If the subsystem S consists of exactly one unit v, we write p_v instead of p_{v}.

The following example, which allows us to put the definition of Equation (21) into the information-geometric setting, represents the main motivation for the present approach to stochastic interaction. It will be generalized in Section 2.4.

Example 1 (FACTORIZABLE DISTRIBUTIONS AND SPATIAL INTERDEPENDENCE). Let V be a finite set of units and Ω_v, v ∊ V, corresponding state sets. Consider the tensorial map

$$\begin{array}{cc}{\displaystyle \prod _{v\in V}\mathcal{P}({\mathrm{\Omega }}_v)\to \mathcal{P}({\mathrm{\Omega }}_V)},& {(p^{(v)})}_{v\in V}\mapsto {\otimes }_{v\in V}{p}^{(v)}\end{array},$$

with

$$({\otimes }_{v\in V}{p}^{(v)})(\omega ):={\displaystyle \prod _{v\in V}{p}^{(v)}({\omega }_v)}.$$

The image $ℱ:=ℱ\left({\Omega }_V\right):=\{{\otimes }_{v\in V}{p}^{\left(v\right)}:p^{(v)}\in \mathcal{P}\left({\Omega }_v\right),v\in V\}$ of this map, which consists of all factorizable and strictly positive probability distributions, is an exponential family in $\mathcal{P}\left({\Omega }_V\right)$ with dim $\mathcal{F}={\displaystyle {\sum }_{v\in V}\left(|\Omega v|-1\right)}$. For the particular case of binary units, that is |Ω_v| = 2 for all v, the dimension of F is equal to the number |V| of units. The following statement is well known [18]: The (−1)-projection of a distribution $p\in \mathcal{P}\left({\Omega }_V\right)$ on $ℱ$ is given by ⊗_v∊V p_v (the p_v, v ∊ V, are the marginal distributions), and one has the representation

$$I(p)=D(p\Vert ℱ)={\displaystyle \sum _{v\in V}H(p_v)-H(p)},$$

where H denotes the Shannon entropy [1]. As stated in the introduction, I(p) is a measure for the spatial interdependencies of the units. It vanishes exactly when the units are stochastically independent.

Before extending the spatial notion of interaction to a dynamical one, in Section 2.3 we consider the more general concept of separability of transition kernels.

2.3. Quantifying Non-Separability

2.3.1. Manifolds of Separable Transition Kernels

Consider a finite set V of units, corresponding state sets Ω_v, v ∊ V, and two subsets A, B ⊂ V with B 6= ∅. A function

$$\begin{array}{cc}K:{\Omega }_A\times {\Omega }_B\to \left[0,1\right],& \left(\omega ,\omega \prime \right)\mapsto K\left(\omega \prime |\omega \right),\end{array}$$

is called Markovian transition kernel if $K\left(·|\omega \right)\in \overline{\mathcal{P}}\left({\Omega }_B\right)$ for all ω ∊ Ω_A, that is

$$\begin{array}{ccc}{\displaystyle \sum _{{\omega }^{\prime }\in {\mathrm{\Omega }}_B}K({\omega }^{\prime }|\omega )}=1,& \text{for all}& \omega \in {\mathrm{\Omega }}_A\end{array}.$$

The set of all such kernels is denoted by $\overline{\mathcal{K}}\left({\Omega }_B|{\Omega }_A\right)$. We write $\mathcal{K}\left({\Omega }_B|{\Omega }_A\right)$ for its interior and $\overline{\mathcal{K}}\left({\Omega }_A\right)$respectively $\mathcal{K}\left({\Omega }_A\right)$ as abbreviation in the case A = B. If A = ∅, then Ω_A consists of exactly one element, namely the empty configuration ϵ. In that case, $\overline{\mathcal{K}}({\Omega }_B|{\Omega }_{\theta })=\overline{K}({\mathrm{\Omega }}_B|\in )$ can naturally be identified with $\overline{\mathcal{P}}\left({\Omega }_B\right)\text{by}p\left(\omega \right):=K\left(\omega |\in \right)$, ω ∊ Ω_B.

Given a probability distribution $p\in \overline{\mathcal{P}}\left({\Omega }_A\right)$ and a transition kernel $K\in \overline{\mathcal{K}}\left({\Omega }_B|{\Omega }_A\right)$, the conditional entropy for (p, K) is defined as

$$H(p,K):={\displaystyle \sum _{\omega \in {\mathrm{\Omega }}_A}p(\omega )H(K(\cdot |\omega )).}$$

For two random variables X, Y with Prob{X = ω} = p(ω) for all ω ∊ Ω_A, and Prob{Y = ω′ | X = ω} = K(ω′ | ω) for all ω ∊ Ω_A with p(ω) > 0 and all ω′ ∊ Ω_B, we set H(Y | X) := H(p, K).

In the present paper, the set $\overline{\mathcal{K}}\left({\Omega }_V\right)$ is interpreted as a model for the dynamics of interacting units, and the information flow associated with this dynamics is studied in Section 2.4. In the present section, we introduce a general notion of separability of transition kernels in order to capture all examples that are discussed in the paper in a unified way.

Consider a family $\mathcal{S}:=\{\left(A_1,B_1\right),\left(A_2,B_2\right),\dots ,\left(A_n,B_n\right)\}$ where the A_i and B_i are subsets of V. We assume that {B₁,…, B_n} is a partition of V, that is B_i ≠ ∅ for all i, B_i ∩ B_j = ∅ for all i ≠ j, and $V=B_1\uplus \cdots \uplus B_n$. Now consider the corresponding tensorial map

$$\begin{array}{cc}\otimes \mathcal{S}:{\displaystyle \prod _{(A,B)\in \mathcal{S}}\mathcal{K}({\mathrm{\Omega }}_B|{\mathrm{\Omega }}_A)\hookrightarrow \mathcal{K}({\mathrm{\Omega }}_V),}& {(K_B^A)}_{(A,B)\in \mathcal{S}}\end{array}\mapsto {\otimes }_{(A,B)\in \mathcal{S}}{K}_B^A,$$

with

$$\begin{array}{ccc}\left({\otimes }_{(A,B)\in \mathcal{S}}{K}_B^A\right)({\omega }^{\prime }|\omega ):={\displaystyle \prod _{(A,B)\in \mathcal{S}}{K}_B^A({{\omega }^{\prime }}_B|{\omega }_A),}& \text{for all}& \omega ,{\omega }^{\prime }\in {\mathrm{\Omega }}_V\end{array}.$$

The image ${\mathcal{K}}_{\mathcal{S}}\left({\Omega }_V\right)$ of ${\otimes }_{\mathcal{S}}$ is a submanifold of $\mathcal{K}\left({\Omega }_V\right)$ with

$$\dim {\mathcal{K}}_{\mathcal{S}}({\mathrm{\Omega }}_V)={\displaystyle \sum _{(A,B)\in \mathcal{S}}|{\mathrm{\Omega }}_A|(|{\mathrm{\Omega }}_B|-1)}.$$

Its elements are the separable transition kernels with respect to $\mathcal{S}$.

Here are the most important examples:

Examples and Definitions 1.

• If we set $\mathcal{S}:=\left\{\left(V,V\right)\right\}$, the tensorial map is nothing but the identity $\mathcal{K}\left({\Omega }_V\right)\to \mathcal{K}\left({\Omega }_V\right)$, and therefore one has ${\mathcal{K}}_{\mathcal{S}}\left({\Omega }_V\right)=\mathcal{K}\left({\Omega }_V\right)$.
• Consider the case where no temporal information is transmitted but all spatial information: $\mathcal{S}:=ind:=\{(\theta ,V)\}$. In that case the tensorial map ${\otimes }_{\mathcal{S}}$ reduces to the natural embedding

  $$\mathcal{K}({\Omega }_V|{\Omega }_{\theta })=\mathcal{P}\left({\Omega }_V\right)\hookrightarrow \mathcal{K}\left({\Omega }_V\right)$$

  which assigns to each probability distribution p the kernel

  $$\begin{array}{cc}K\left(\omega \prime |\omega \right):=p\left(\omega \prime \right),& \omega ,\omega \prime \in {\Omega }_V\end{array}.$$
  Therefore, we write ${\mathcal{K}}_{ind}\left({\Omega }_V\right)=\mathcal{P}\left({\Omega }_V\right)$.
• In addition to the splitting in time which is described in example (2), consider also a complete splitting in space: $\mathcal{S}:=fac:=\{(\theta ,\left\{v\right\}):v\in V\}$. Then we recover the tensorial map of Example 1. Thus, ${\mathcal{K}}_{fac}\left({\Omega }_V\right)$ can be identified with $ℱ\left({\Omega }_V\right)$.
• To model the important class of parallel information processing, we set $\mathcal{S}:=par:=\{\left(V,\left\{v\right\}\right):v\in V\}$. Here, each unit “computes” its new state on the basis of all current states according to a kernel $K^{\left(v\right)}\in \mathcal{K}\left({\Omega }_v|{\Omega }_V\right)$. The transition from a configuration ω = (ω_v)_v∊V of the whole system to a new configuration $\omega \prime ={\left({{\omega }^{\prime }}_v\right)}_v{}_{\in V}$ is done according to the following composed kernel in $\mathcal{K}\left({\Omega }_V\right)$:

  $$\begin{array}{cc}K({\omega }^{\prime }|\omega )={\displaystyle \prod _{v\in V}{K}^{(v)}({{\omega }^{\prime }}_v|\omega ),}& \omega ,{\omega }^{\prime }\in {\mathrm{\Omega }}_V\end{array}.$$
• In applications, parallel processing is adapted to a graph G = (V, E) – here, E ⊂ V × V denotes the set of edges – in order to model constraints for the information flow in the system. This is represented by $\mathcal{S}:=\mathcal{S}\left(G\right):=\{(pa(v),\left\{v\right\}):v\in V\}$. Each unit v is supposed to process only information from its parents pa(v) = {μ ∊ V: (μ, v) ∊ E}, which is modeled by a transition kernel $K^{\left(v\right)}\in \mathcal{K}\left({\Omega }_v|{\Omega }_{pa}{}_{(v)}\right)$. The parallel transition of the whole system is then described by

  $$\begin{array}{cc}K({\omega }^{\prime }|\omega )={\displaystyle \prod _{v\in V}{K}^{(v)}({{\omega }^{\prime }}_v|{\omega }_{pa(v)}),}& \omega ,{\omega }^{\prime }\in {\mathrm{\Omega }}_V\end{array}.$$
• Now, we introduce the example of parallel processing that plays the most important role in the present paper: Consider non-empty and pairwise distinct subsystems S₁,…, S_n of V with V = S₁⊎· · ·⊎S_n and define $\mathcal{S}:=\mathcal{S}(S_1,\dots ,S_n):=\{(S_i,S_i):i=1,\dots ,n\}$. It describes {S₁,…, S_n}-split information processing, where the subsystems do not interact with each other. Each subsystem S_i only processes information from its own current state according to a kernel $K^{\left(i\right)}\in \mathcal{K}\left({\Omega }_{Si}\right)$. The composed transition of the whole system is then given by

  $$\begin{array}{cc}K({\omega }^{\prime }|\omega )={\displaystyle \prod _{i=1}^n{K}^{(i)}}({{\omega }^{\prime }}_{S_i}|{\omega }_{S_i}),& \omega ,{\omega }^{\prime }\in {\mathrm{\Omega }}_V\end{array}.$$
  For the completely split case, where the subsystems are the elementary units, we define $spl:=\mathcal{S}(\{v\},v\in V)=\{\left(\left\{v\right\},\left\{v\right\}\right):v\in V\}$.

2.3.2. Non-Separability as Divergence from Separability

Consider a Markov chain X_n = (X_v,n)_v V, n = 0, 1, 2,…, that is given by an initial distribution $p\in \overline{\mathcal{P}}({\mathrm{\Omega }}_V)$ and a kernel $K\in \overline{\mathcal{K}}\left({\Omega }_V\right)$. The probabilistic properties of this stochastic process are determined by the following set of finite marginals:

$$\begin{array}{l}\text{Prob}\{X_0={\omega }_0,X_1={\omega }_1,\dots ,X_n={\omega }_n\}\\ =p\left({\omega }_0\right)K\left({\omega }_1|{\omega }_0\right)\cdots K\left({\omega }_n|{\omega }_{n-}{}_1\right),n=0,1,2,\dots \end{array}$$

Thus, the set of Markov chains on Ω_V can be identified with

$$\overline{\mathrm{MC}}({\mathrm{\Omega }}_V):=\overline{\mathcal{P}}({\mathrm{\Omega }}_V)\times \overline{\mathcal{K}}({\mathrm{\Omega }}_V)$$

and we also use the notation {X_n} = {X₀, X₁, X₂,…} instead of (p, K). The interior MC(Ω_V ) of the set of Markov chains carries the natural dualistic structure from $\mathcal{P}\left({\Omega }_V\times {\Omega }_V\right)$, which is induced by the diffeomorphic composition map $\otimes :\mathrm{MC}\left({\Omega }_V\right)\to \mathcal{P}\left({\Omega }_V\times {\Omega }_V\right)$,

$$\left(p,K\right)\mapsto p\otimes K,\text{with}(p\otimes K)\left(\omega ,\omega \prime \right):=p\left(\omega \right)K\left(\omega \prime |\omega \right)$$

(⊗ can be extended to a continuous surjective map $\overline{\mathrm{MC}}\left({\Omega }_V\right)\to \overline{\mathcal{P}}\left({\Omega }_V\times {\Omega }_V\right)$). Thus, we can talk about exponential families and (−1)-projections in MC(Ω_V). The “distance” D((p, K) || (p′, K′)) from a Markov chain (p, K) to another one (p′, K′) is given by

$$D(p\otimes K\Vert p\prime \otimes K\prime )=D\left(p\Vert p\prime \right)+D_p\left(K\Vert K\prime \right),$$

with

$$D_p(K\Vert K^{\prime }):={\displaystyle \sum _{\omega \in \mathrm{\Omega }}p(\omega )D(K(\cdot |\omega )\Vert K^{\prime }(\cdot |\omega ))}.$$

(23)

For a set $\mathcal{S}=\{(A_1,B_1),(A_2,B_2),\dots ,(A_n,B_n)\}$, we introduce the exponential family (see Proposition 3)

$${\mathrm{MC}}_{\mathcal{S}}\left({\Omega }_V\right):=\mathcal{P}\left({\Omega }_V\right)\times {\mathcal{K}}_{\mathcal{S}}\left({\Omega }_V\right)\subset \mathrm{MC}\left({\Omega }_V\right),$$

which has dimension $(|{\mathrm{\Omega }}_V|-1)+{\displaystyle \sum {}_{(A,B)\in \mathcal{S}}|{\mathrm{\Omega }}_A|(|{\mathrm{\Omega }}_B|-1)}$.

The set of all these exponential families is partially ordered by inclusion with MC(Ω_V) as the greatest element and MC_fac(Ω_V ) as the least one. This ordering is connected with the following partial ordering ≼ of the sets $\mathcal{S}$ : Given $\mathcal{S}=\left\{\left(A_1,B_1\right),\dots ,\left(A_m,B_m\right)\right\}$ and $\mathcal{S}\prime =\left\{\left({A^{\prime }}_1,{B^{\prime }}_1\right),\dots ,\left({A^{\prime }}_n,{B^{\prime }}_n\right)\right\}$, we write $\mathcal{S}\underset{¯}{\prec }\mathcal{S}$ ( $\mathcal{S}\prime$coarser than $\mathcal{S}$) iff for all (A, B) ∊$\mathcal{S}$ there exists a pair (A′, B′) ∊$\mathcal{S}$′ with A ⊂ A′ and B ⊂ B′. One has

$$\mathcal{S}\underset{¯}{\prec }\mathcal{S}\prime \Rightarrow {\mathcal{K}}_{\mathcal{S}}\left({\Omega }_V\right)\subseteq {\mathcal{K}}_{\mathcal{S}}\left({\Omega }_V\right)\subseteq {\mathcal{K}}_{{\mathcal{S}}^{\prime }}({\mathrm{\Omega }}_V).$$

(24)

Thus, coarsening enlarges the corresponding manifold (the proof is given in the appendix).

Now, we describe the (−1)-projections on the exponential families ${\mathrm{MC}}_{\mathcal{S}}\left({\Omega }_V\right)$:

Proposition 1. Let (p, K) be a Markov chain in MC(Ω_V ) and S ≼S ′. Then:

• (PROJECTION) The (−1)-projection of (p, K) on${\mathrm{MC}}_{\mathcal{S}}\left({\Omega }_V\right)$ is given by (p, $K_{\mathcal{S}}$) with$K_{\mathcal{S}}:={\otimes }_{(A,B)\in \mathcal{S}}{K}_B^A$. Here, the kernels$K_B^A\in \mathcal{K}\left({\Omega }_B|{\Omega }_A\right)$ denote the corresponding marginals of K:

  $$K_B^A({\omega }^{\prime }|\omega ):=\frac{{\displaystyle \sum {}_{\begin{array}{c}\sigma ,{\sigma }^{\prime }\in {\mathrm{\Omega }}_V\\ \sigma A=\omega ,{{\sigma }^{\prime }}_B={\omega }^{\prime }\end{array}}p(\sigma )K({\sigma }^{\prime }|\sigma )}}{{\displaystyle \sum {}_{\begin{array}{c}\sigma \in {\mathrm{\Omega }}_V\\ \sigma A=\omega \end{array}}p(\sigma )}},\omega \in {\mathrm{\Omega }}_A,{\omega }^{\prime }\in {\mathrm{\Omega }}_B.$$
  $K_{\mathcal{S}}$ is the projection of K on $K_{\mathcal{S}}\left({\Omega }_V\right)$ with respect to p.
• (ENTROPIC REPRESENTATION) The corresponding divergence is given by

  $$\begin{array}{l}D((p,K)\Vert {\mathrm{MC}}_{\mathcal{S}}({\mathrm{\Omega }}_V)=D_p(K\Vert K_{\mathcal{S}})\\ ={\displaystyle \sum _{(A,B)\in \mathcal{S}}H(p_A,K_B^A)-H(p,K).}\end{array}$$
• (PYTHAGORIAN THEOREM) One has

  $$D_p\left(K\Vert K_{\mathcal{S}}\right)=D_p\left(K\Vert K_{{\mathcal{S}}^{\prime }}\right)+D_p\left(K_{{\mathcal{S}}^{\prime }}\Vert K_{\mathcal{S}}\right).$$

If $K\in \mathcal{P}\left({\Omega }_V\right)$, that is K(ω′|ω) = p(ω), ω, ω′ ∊ Ω_V, with a probability distribution $p\in \mathcal{P}\left({\Omega }_V\right)$, then the divergence D_p(K||K_fac) is nothing but the measure I(p) for spatial interdependencies that has been discussed in the introduction and in Example 1. More generally, we interpret the divergence $D_p\left(K\Vert K_{\mathcal{S}}\right)$ as a natural measure for the non-separability of (p, K) with respect to $\mathcal{S}$. The corresponding function $I_{\mathcal{S}}:\left(p,K\right)\mapsto I_{\mathcal{S}}\left(p,K\right):=D_p\left(K\Vert K_{\mathcal{S}}\right)$ has a unique continuous extension to the set $\overline{\mathrm{MC}}\left({\Omega }_V\right)$ of all Markov chains which is also denoted by $I_{\mathcal{S}}$ (see Lemma 4.2 in [55]). Thus, non-separability is defined for not necessarily strictly positive Markov chains.

2.4. Application to Stochastic Interaction

2.4.1. The Definition of Stochastic Interaction

As stated in the introduction we use the concept of complexity that is described by the formal definition in Equation (20) in order to define stochastic interaction.

Let V be a set of units and Ω_v, v ∊ V, corresponding state sets. Furthermore, consider non-empty and pairwise distinct subsystems S₁,…, S_n ⊂ V with V = S₁ ⊎⋯⊎ S_n. The stochastic interaction of S₁,…, S_n with respect to $\left(p,K\right)\in \overline{\mathrm{MC}}\left({\Omega }_V\right)$ is quantified by the divergence of (p, K) from the set of Markov chains that represent {S₁,…, S_n}-split information processing, where the subsystems do not interact with each other (see Examples and Definitions 1 (6)). More precisely, we define the stochastic interaction (of the subsystems S₁,…, S_n) to be the function $I_S{}_{{}_1},\dots ,S_n:\overline{\mathrm{MC}}\left({\Omega }_V\right)\to {ℝ}_{+}$ with

$$I_S{}_{{}_1},\dots {,}_{S_n}\left(p,K\right):=I_{\mathcal{S}}\left({{}_S}_{{}_1},\dots {,}_{S_n}\right)\left(p,K\right)=\underset{K^{\prime }\{S_1,\dots ,S_n\}-\text{split}}{\inf }{D}_p\left(K\Vert K\prime \right).$$

(25)

In the case of complete splitting of V = {v₁,…, v_n} into the elementary units, that is S_i := {v_i}, i = 1,…, n, we simply write I instead of I_{v1},…,{v_n}.

The definition of stochastic interaction given by Equation (25) is consistent with the complexity concept that is discussed in the introduction.

Here are some basic properties of I, which are well known in the spatial setting of Example 1:

Proposition 2. Let V be a set of units, Ω_v, v ∊ V, corresponding state sets, and X_n = (X_v,n)_v∊V, n = 0, 1, 2,…, a Markov chain on Ω_V. For a subsystem S ⊂ V, we write X_S,n := (X_v,n)_v∊S. Assume that the chain is given by$\left(p,K\right)\in \overline{\mathrm{MC}}\left({\Omega }_V\right)$, where p is a stationary distribution with respect to K. Then the following holds:

• $$I\{X_n\}={\displaystyle \sum _{v\in V}H(X_{v,n+1}|X_{v,n})-H(X_{n+1}|X_n)}.$$

  (26)
• A, B ⊂ V, A, B ≠ ∅, A ∩ B = ∅, A ⊎ B = V ⇒

  $$I\{X_n\}=I\{X_{A,}{}_n\}+I\left\{X_{B,}{}_n\right\}+I_{A,B}\left\{X_n\right\}.$$
• If the process is parallel, then

  $$\begin{array}{l}I\{X_n\}={\displaystyle \sum _{v\in V}(H(X_{v,n+1}|X_{v,n})-H(X_{v,n+1}|X_n))}\\ ={\displaystyle \sum _{v\in V}MI(X_{v,n+1};X_{V\backslash v,n}|X_{v,n})}.\end{array}$$

  (27)
• If the process is adapted to a graph (V, E) then

  $$\begin{array}{l}I\{X_n\}={\displaystyle \sum _{v\in V}(H(X_{v,n+1}|X_{v,n})-H(X_{v,n+1}|X_{pa(v),n}))}\\ ={\displaystyle \sum _{v\in V}MI(X_{v,n+1};X_{pa(v)\backslash v,n}|X_{v,n})}.\end{array}$$

  (28)

In the statements (iii) and (iv), the conditional mutual information MI(X; Y | Z) of two random variables X, Y with respect to a third one Z is defined to be the difference H(X | Z) − H(X | Y, Z) (see p. 22 in [58]).

If X_n+1 and X_n are independent for all n, the stochastic interaction I{X_n} reduces to the measure I(p) for spatial interdependencies with respect to the stationary distribution p of {X_n} (see Example 1). Thus, the dynamical notion of stochastic interaction is a generalization of the spatial one. Geometrically, this can be illustrated as follows. In addition to the projection K_spl of the kernel K ∊ MC(Ω_V) with respect to a distribution $p\in \mathcal{P}\left({\Omega }_V\right)$ on the set of split kernels, we consider its projections K_ind and K_fac on the set $\mathcal{P}\left({\Omega }_V\right)$ of independent kernels and on the subset $ℱ\left({\Omega }_V\right)$, respectively. From Proposition 1 we know

$$\begin{array}{c}{D}_p\left(K\Vert K_{\mathrm{ind}}\right)=\underset{\left(\left(\mathrm{global}\right)transinformation\right)}{H\left(X_n{}_{+1}\right)-H\left(X_n{}_{+1}|X_n\right),}\\ I\left(p\right)=D_p\left(K_{ind}\Vert K_{fac}\right)=\underset{\left(spatialinterdependence\right)}{{\displaystyle \sum _{v\in V}H}\left(X_{v,n+1}\right)-H\left(X_n{}_{+1}\right)},\\ D_p\left(K_{spl}\Vert K_{fac}\right)=\underset{\left(sumofindividualtransinformations\right)}{{\displaystyle \sum _{v\in V}\left(H\left(X_{v,n+1}\right)-H\left(X_{v,n+1}|X_{v,n}\right)\right)}.}\end{array}$$

According to the Pythagorian relation (Proposition 1 (iii)), we get the following representation of stochastic interaction:

$$\begin{array}{l}I\left\{X_n\right\}=D_p\left(K\Vert K_{spl}\right)\\ =I\left(p\right)+D_p\left(K\Vert K_{ind}\right)-D_p\left(K_{spl}\Vert K_{fac}\right).\end{array}$$

(29)

In the particular case of an independent process, the divergences D_p(K || K_ind) and D_p(K_spl || K_fac) in Equation (29) vanish, and the stochastic interaction coincides with spatial interdependence.

2.4.2. Examples

Example 2 (SOURCE AND RECEIVER). Consider two units 1 = source and 2 = receiver with the state sets Ω₁ and Ω₂. Assume that the information flow is adapted to the graph G = {{1, 2}, {(1, 2)}}, which only allows a transmission from the first unit to the second. In each transition from time n to n + 1, a state X_1,n+1 of the first unit is chosen independently from X_1,n according to a probability distribution $p\in \mathcal{P}\left({\Omega }_1\right)$. The state X_2,n+1 of the second unit at time n + 1 is “computed” from X_1,n according to a kernel $K\in \mathcal{K}\left({\Omega }_2|{\Omega }_1\right)$. Using formula Equation (28), we have

$$I\left\{X_n\right\}=H\left(X_{2,n+1}\right)-H\left(X_{2,n+1}|X_{1,n}\right).$$

This is the well-known mutual information of the variables X_2,n+1 and X_1,n, which has a temporal interpretation within the present approach. It plays an important role in coding and information theory [58].

Example 3 (TWO BINARY UNITS I). Consider two units with the state sets {0, 1}. Each unit copies the state of the other unit with probability 1 − ε. The transition probabilities for the units are given by the following tables:

K(1)(y′| (x, y))	0	1
(0, 0)	1−ε	ε
(0, 1)	ε	1 −ε
(1, 0)	1 −ε	ε
(1, 1)	ε	1 − ε

K(1)(y′| (x, y))	0	1
(0, 0)	1−ε	ε
(0, 1)	ε	1 −ε
(1, 0)	1 −ε	ε
(1, 1)	ε	1 − ε

K(2)(y′| (x, y))	0	1
(0, 0)	1−ε	ε
(0, 1)	1 − ε	ε
(1, 0)	ε	1 − ε
(1, 1)	ε	1 − ε

K(2)(y′| (x, y))	0	1
(0, 0)	1−ε	ε
(0, 1)	1 − ε	ε
(1, 0)	ε	1 − ε
(1, 1)	ε	1 − ε

The transition kernel $K\in {\overline{\mathcal{K}}}_{par}(\{0,1\}\times \{0,0\})$ for the corresponding parallel dynamics of the whole system is then given by

K((x', y')|(x, y))	(0, 0)	(0, 1)	(1, 0)	(1, 1)
(0, 0)	(1−ε)2	(1−ε)ε	ε(1−ε)	ε2
(0, 1)	ε(1−ε)	ε2	(1−ε)2	(1−ε)ε
(1, 0)	(1−ε)ε	(1−ε)2	ε2	ε(1−ε)
(1, 1)	ε2	ε(1−ε)	(1−ε)ε	(1−ε)2

K((x', y')|(x, y))	(0, 0)	(0, 1)	(1, 0)	(1, 1)
(0, 0)	(1−ε)2	(1−ε)ε	ε(1−ε)	ε2
(0, 1)	ε(1−ε)	ε2	(1−ε)2	(1−ε)ε
(1, 0)	(1−ε)ε	(1−ε)2	ε2	ε(1−ε)
(1, 1)	ε2	ε(1−ε)	(1−ε)ε	(1−ε)2

Note that for ε ∊ {0, 1}, K corresponds to the deterministic transformations

$$\epsilon =0:\left(x,y\right)\mapsto \left(y,x\right)\text{and}\epsilon =1:\left(x,y\right)\mapsto \left(1-y,1-x\right),$$

which in an intuitive sense describe complete information exchange of the units. With the unique stationary probability distribution p = ( $\frac{1}{4}$, $\frac{1}{4}$, $\frac{1}{4}$, $\frac{1}{4}$) one can easily compute the marginal kernels

K1(x′|x)	0	1
0	$\frac{1}{2}$	$\frac{1}{2}$
1	$\frac{1}{2}$	$\frac{1}{2}$

K1(x′|x)	0	1
0	$\frac{1}{2}$	$\frac{1}{2}$
1	$\frac{1}{2}$	$\frac{1}{2}$

K2(y′|y)	0	1
0	$\frac{1}{2}$	$\frac{1}{2}$
1	$\frac{1}{2}$	$\frac{1}{2}$

K2(y′|y)	0	1
0	$\frac{1}{2}$	$\frac{1}{2}$
1	$\frac{1}{2}$	$\frac{1}{2}$

which describe the split dynamics according to K_spl = K₁ ⊗ K₂. With Equation (27) we finally get

$$I\left\{X_n\right\}=2\left(\ln 2+\left(1-\epsilon \right)\ln \left(1-\epsilon \right)+\epsilon \ln \epsilon \right).$$

The shape of this function is shown in Figure 3.

This function is symmetric around $\epsilon =\frac{1}{2}$ where it vanishes. In ε = 0 and ε = 1 it attains its maximal value 2 ln 2. As stated above, this corresponds to the deterministic transformations with complete information exchange.

Example 4 (TWO BINARY UNITS II). Consider again two binary units with the state sets {0, 1} and the transition probabilities

K(1)(x′| (x, y))	0	1
(0, 0)	1	0
(0, 1)	1−ε	ε
(1, 0)	ε	1−ε
(1, 1)	0	1

K(1)(x′| (x, y))	0	1
(0, 0)	1	0
(0, 1)	1−ε	ε
(1, 0)	ε	1−ε
(1, 1)	0	1

K(2)(y′| (x, y))	0	1
(0, 0)	0	1
(0, 1)	1−ε	ε
(1, 0)	ε	1−ε
(1, 1)	1	0

K(2)(y′| (x, y))	0	1
(0, 0)	0	1
(0, 1)	1−ε	ε
(1, 0)	ε	1−ε
(1, 1)	1	0

The transition kernel $K\in \overline{\mathcal{K}}(\{0,1\}\times \{0,1\})$ of the corresponding parallel dynamics is given by

K((x', y')|(x, y))	(0, 0)	(0, 1)	(1, 0)	(1, 1)
(0, 0)	0	1	0	0
(0, 1)	(1−ε)2	(1−ε)ε	ε(1−ε)	ε2
(1, 0)	ε2	ε(1−ε)	(1−ε)ε	(1−ε)2
(1, 1)	0	0	1	0

K((x', y')|(x, y))	(0, 0)	(0, 1)	(1, 0)	(1, 1)
(0, 0)	0	1	0	0
(0, 1)	(1−ε)2	(1−ε)ε	ε(1−ε)	ε2
(1, 0)	ε2	ε(1−ε)	(1−ε)ε	(1−ε)2
(1, 1)	0	0	1	0

Note that for ε ∊ {0, 1}, K corresponds to the deterministic transformations

$$\epsilon =0:\left(x,y\right)\mapsto \left(x,1-y\right)\text{and}\epsilon =1:\left(x,y\right)\mapsto \left(y,1-x\right).$$

Thus in an intuitive sense, for ε = 1 the units completely interact with each other, and for ε = 0 there is no interaction. For ε ∊]0, 1[ we compute the interaction with respect to the unique stationary probability distribution

$$p=\frac{1}{4({\epsilon }^2-\epsilon +1)}(2{\epsilon }^2-2\epsilon +1,1,1,2{\epsilon }^2-2\epsilon +1).$$

With the corresponding marginal kernels

K1(x′|x)	0	1
0	$1-\frac{\epsilon }{2({\epsilon }^2-\epsilon +1)}$	$\frac{\epsilon }{2({\epsilon }^2-\epsilon +1)}$
1	$\frac{\epsilon }{2({\epsilon }^2-\epsilon +1)}$	$1-\frac{\epsilon }{2({\epsilon }^2-\epsilon +1)}$

K1(x′|x)	0	1
0	$1-\frac{\epsilon }{2({\epsilon }^2-\epsilon +1)}$	$\frac{\epsilon }{2({\epsilon }^2-\epsilon +1)}$
1	$\frac{\epsilon }{2({\epsilon }^2-\epsilon +1)}$	$1-\frac{\epsilon }{2({\epsilon }^2-\epsilon +1)}$

K2(y′|y)	0	1
0	$\frac{\epsilon }{2({\epsilon }^2-\epsilon +1)}$	$1-\frac{\epsilon }{2({\epsilon }^2-\epsilon +1)}$
1	$1-\frac{\epsilon }{2({\epsilon }^2-\epsilon +1)}$	$\frac{\epsilon }{2({\epsilon }^2-\epsilon +1)}$

K2(y′|y)	0	1
0	$\frac{\epsilon }{2({\epsilon }^2-\epsilon +1)}$	$1-\frac{\epsilon }{2({\epsilon }^2-\epsilon +1)}$
1	$1-\frac{\epsilon }{2({\epsilon }^2-\epsilon +1)}$	$\frac{\epsilon }{2({\epsilon }^2-\epsilon +1)}$

and Equation (27), we get

$$\begin{array}{l}I\{X_n\}=\frac{\epsilon }{2({\epsilon }^2-\epsilon +1)}(-(2{\epsilon }^2-3\epsilon +2)\ln (2{\epsilon }^2-3\epsilon +2)\\ +2({\epsilon }^2-\epsilon +1)\ln 2({\epsilon }^2-\epsilon +1)+(1-\epsilon )\ln (1-\epsilon )).\end{array}$$

This function is monotonically increasing from the minimal value 0 (no interaction) in ε = 0 to its maximal value 2 ln 2 (complete interaction) in ε = 1.

3. Conclusions

Following the general concept that complexity is characterized by the divergence of a composed system from the superposition of its elementary parts, information geometry has been used to derive a measure for spatio-temporal interdependencies among a finite set of units, which is referred to as stochastic interaction. This generalizes the well-known measure for spatial interdependence that is quantified by the Kullback-Leibler divergence of a probability distribution from its factorization [18,55]. Thereby, previous work by Ay [23] is continued, where the optimization of dependencies among stochastic units has been proposed as a principle for neural organization in feed-forward networks. Of course, the present setting is much more general and provides a way to consider also recurrent networks. The dynamical properties of strongly interacting units in the sense of the present paper are studied by Ay and Wennekers in [24], where the emergence of determinism and structure in such systems is demonstrated.