Entropic-Skins Geometry to Describe Wall Turbulence Intermittency
Abstract
:1. Introduction: Intermittency in Wall and Bounded Turbulence
1.1. Intermittency in Turbulence: Departures to Kolmogorov’s Theory
1.2. Extended Self-Similarity and Intermittency Exponents for Homogenous Isotropic Turbulence
1.3. Intermittency for Wall and Bounded Turbulence
2. Multi-Scale Geometry of Turbulence and Intermittency: Entropic-Skins Model
2.1. Geometrical Features of Intermittency in Turbulence
2.2. Wall Turbulence Intermittency through Structure Functions and Scaling Exponents
2.3. Entropic-Skins Model
3. Entropic-Skins Geometry Applied to the Phenomenon of Intermittency
3.1. General Expression for Intermittency Exponents
3.2. Specific Case: Homogeneous and Isotropic Turbulence at High Reynolds Numbers
3.3. Methods to Measure Intermittency Efficiency, Bulk and Crest Dimensions
4. Experimental Section: Scaling Exponents and Intermittency Efficiency
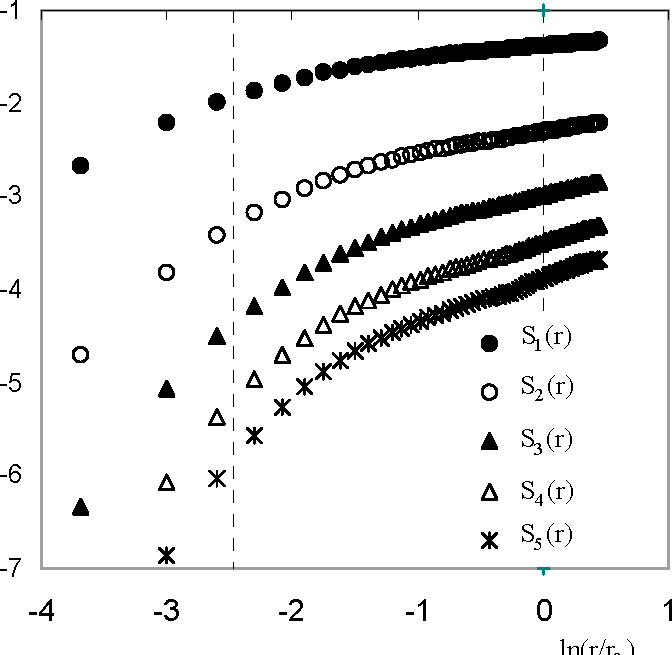
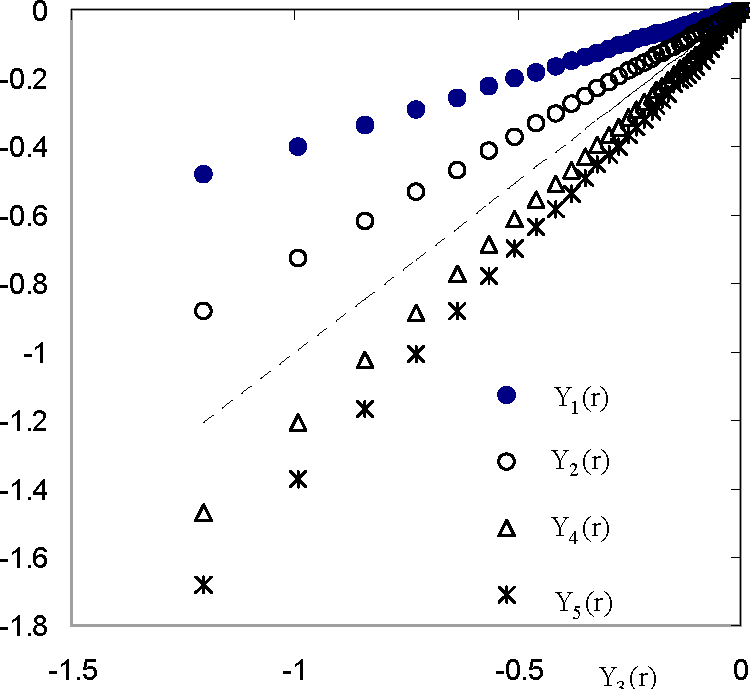
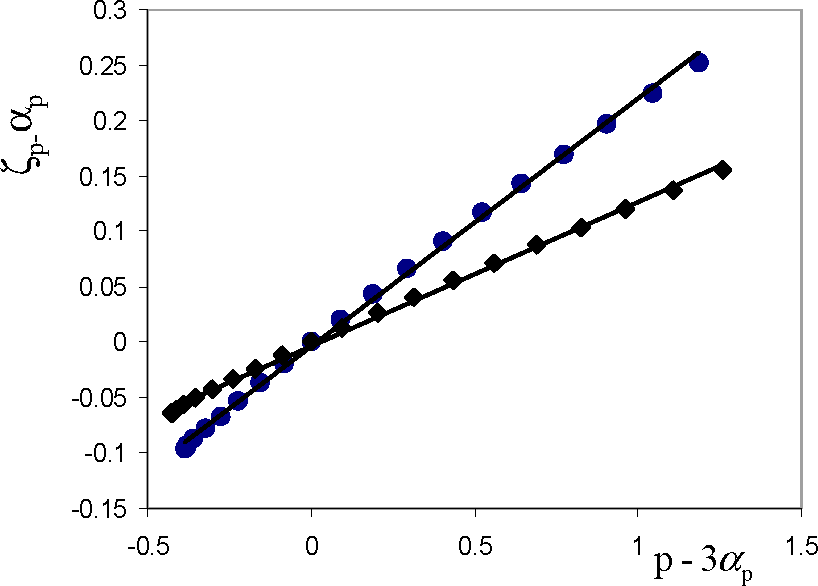
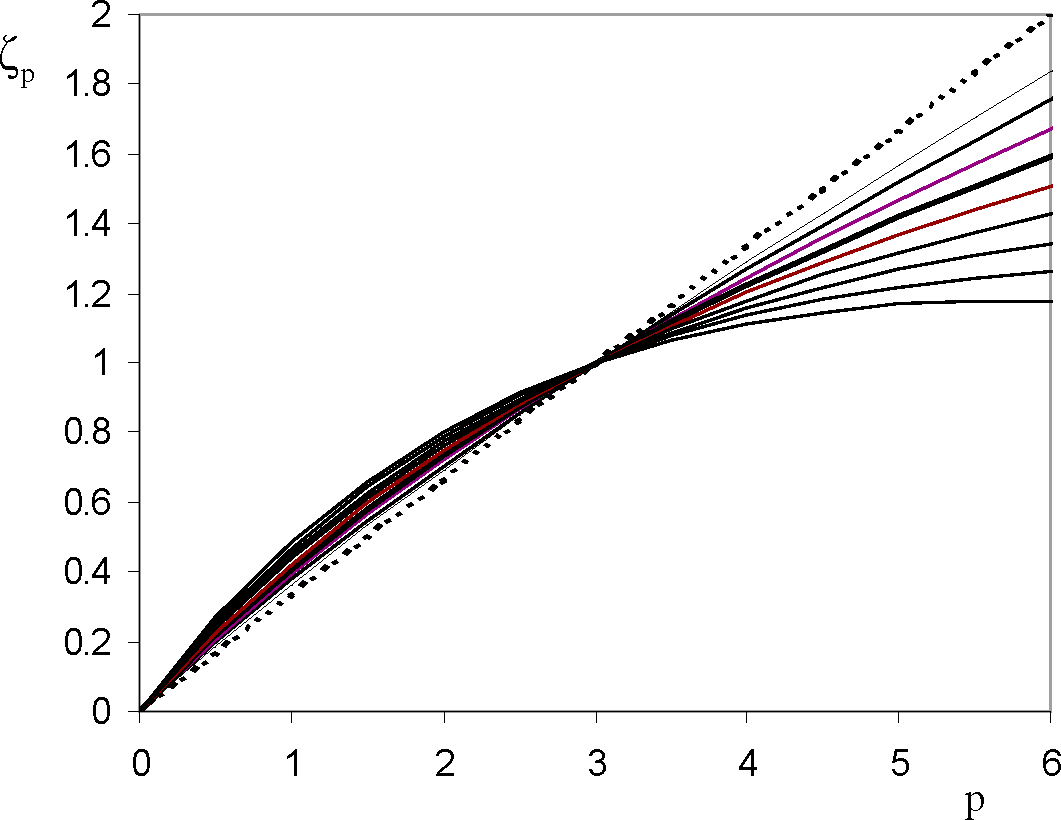
4.1. Scaling Exponents Measured by Extended Self-Similarity
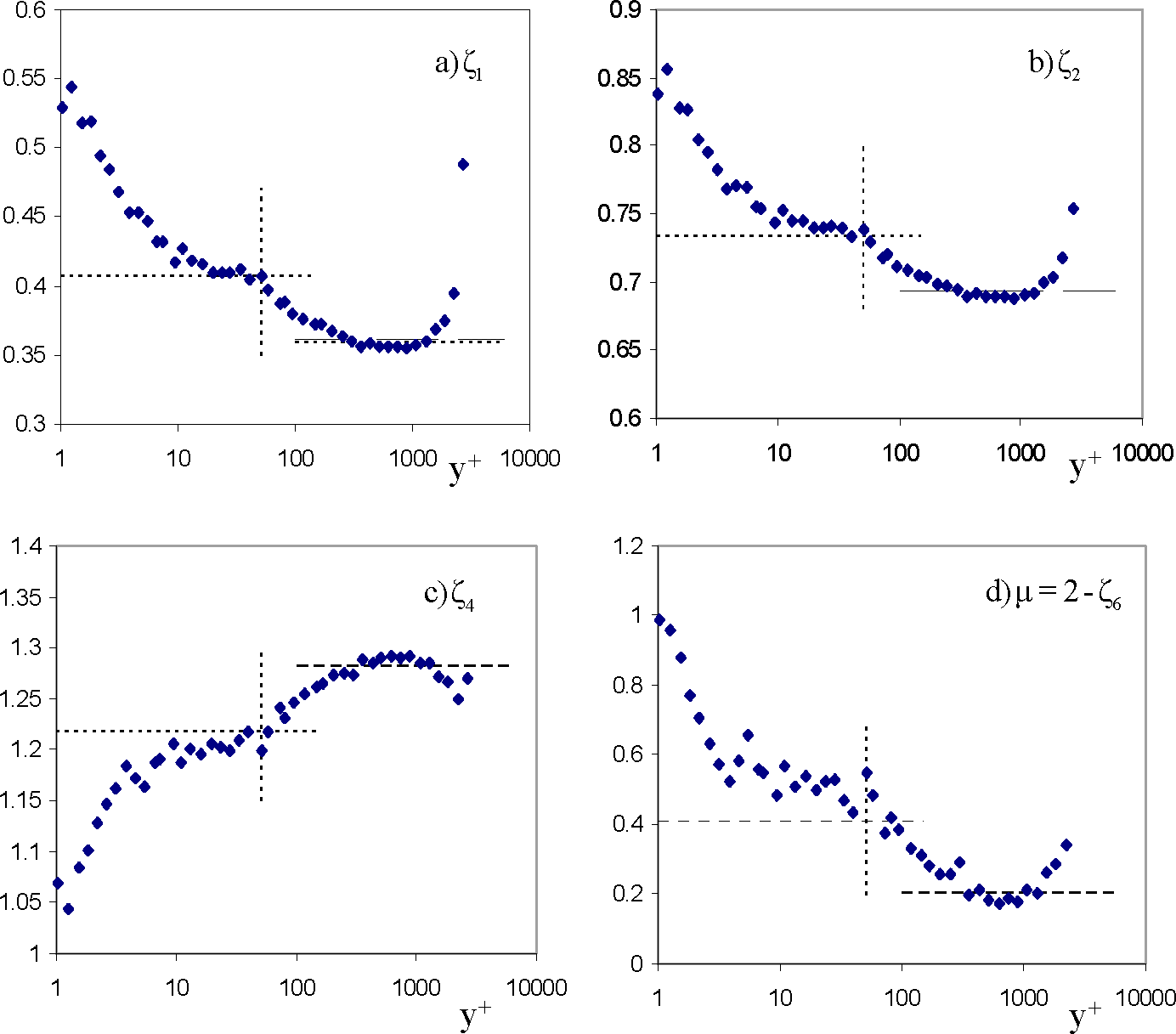
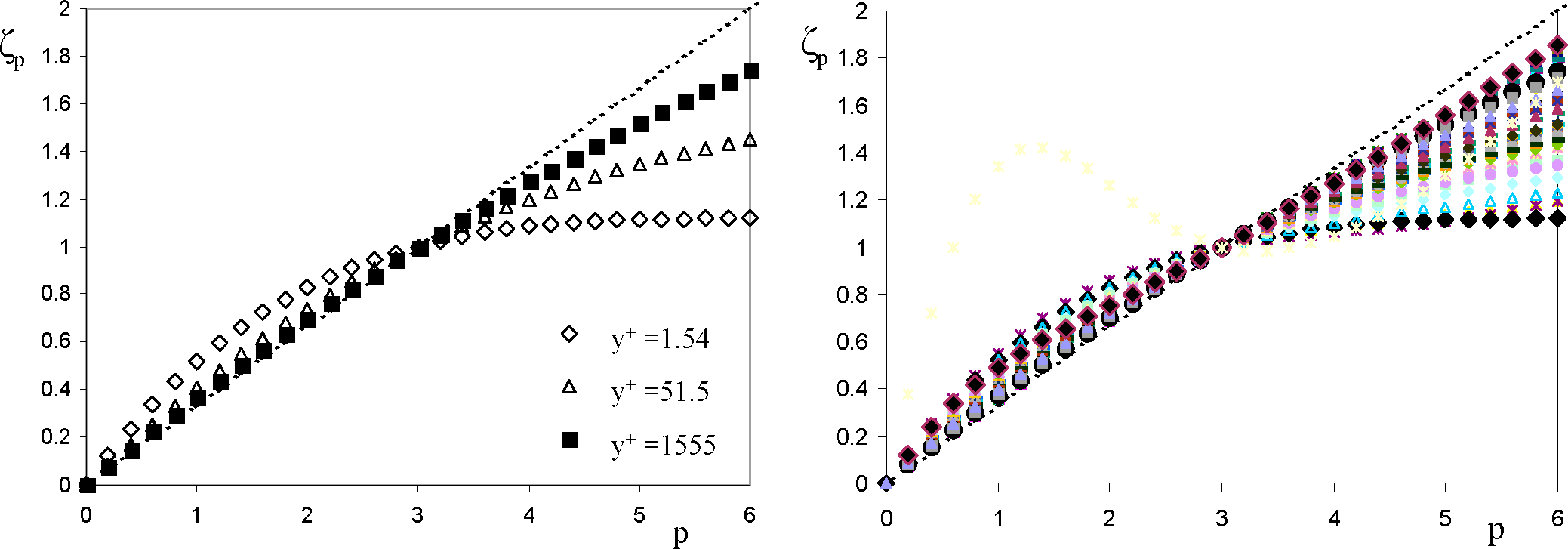
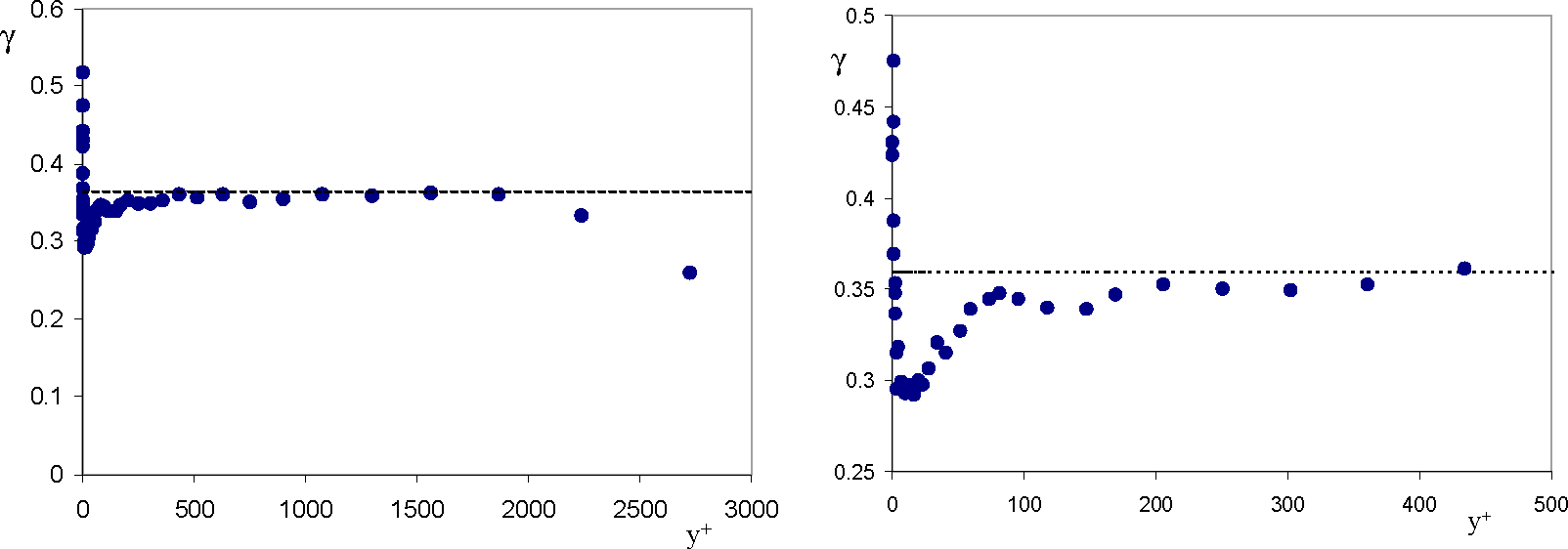
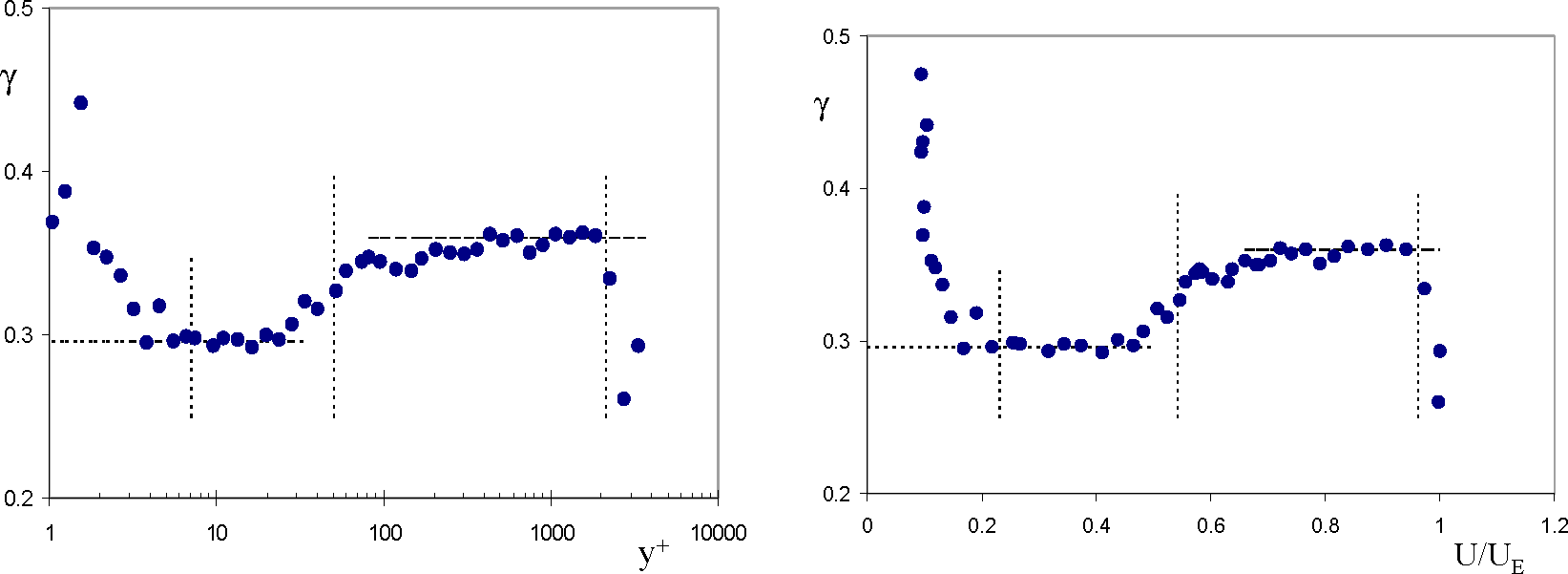
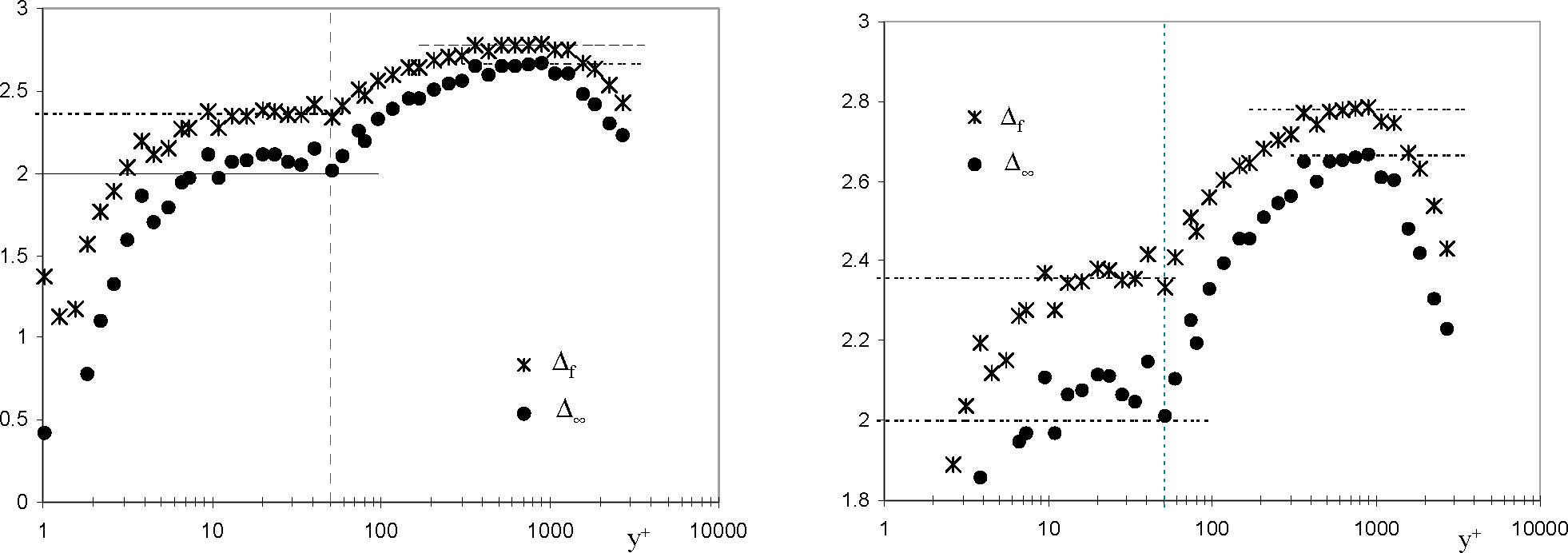
4.2. Intermittent Efficiency, Bulk and Crest Dimensions
5. Conclusions
Acknowledgments
References
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Doklady Akademii Nauk SSSR 1941, 30, 9–13. [Google Scholar]
- Kolmogorov, A.N. On degeneration (decay) of isotropic turbulence in an incompressible flow. Doklady Akademii Nauk SSSR 1941, 32, 538–540. [Google Scholar]
- Anselmet, F.; Gagne, Y.; Hopfinger, E.J.; Antonia, R.A. High-order velocity structure functions in turbulent shear-flows. J. Fluid Mech 1984, 140, 63–89. [Google Scholar]
- Kolmogorov, A.N. A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds numbers. J. Fluid Mech 1962, 13, 82–85. [Google Scholar]
- Frisch, U.; Sulem, P.L.; Nelkin, M. A simple dynamical model of intermittent fully developed turbulence. Fluid Mech 1978, 87, 719–736. [Google Scholar]
- Frisch, U. Turbulence: The Legacy of A.N. Kolmogorov.; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- She, Z.-S.; Lévêque, E. Universal scaling laws in fully developed turbulence. Phys. Rev. Lett. 1994, 72, 336–339. [Google Scholar]
- Benzi, R.; Ciliberto, S.; Tripiccione, R.; Baudet, C.; Massaioli, F.; Succi, S. Extended self-similarity in turbulent flows. Phys. Rev. E 1993, 48, R29–R32. [Google Scholar]
- Dubrulle, B. Intermittency in fully developed turbulence: Log-Poisson statistics and generalized scale covariance. Phys. Rev. Lett. 1994, 73, 959–962. [Google Scholar]
- Protas, B.; Goujon-Durand, S.S.; Wesfreid, J.E. Scaling properties of two-dimensional turbulence in wakes behind bluff bodies. Phys. Rev E 1997, 55, 4165–4169. [Google Scholar]
- Gaudin, E.; Protas, B.; Goujon-Durand, S.; Wojciechowski, J.; Wesfreid, J.E. Spatial properties of velocity structure functions in turbulent wake flows. Phys. Rev. E 1998, 57, R9–R12. [Google Scholar]
- Onorato, M.; Camussi, R.; Iuso, G. Small scale intermittency and bursting in a turbulent channel flow. Phys. Rev. E 2000, 61, 1447–1454. [Google Scholar]
- Toschi, F.; Amati, G.; Succi, S.; Benzi, R.; Piva, R. Intermittency and structure functions in channel flow turbulence. Phys. Rev. Lett. 1999, 83, 5044–5047. [Google Scholar]
- Sreenivasan, K.R. Fractals and multifractals in fluid turbulence. Ann. Rev. Fluid Mech 1991, 23, 539–604. [Google Scholar]
- Sreenivasan, K.R.; Ramshankar, R.; Meneveau, C. Mixing, entrainment and fractal dimensions of surfaces in turbulent flows. Proc. R. Soc. Lond. A 1989, 421, 79–108. [Google Scholar]
- Vassilicos, C.; Hunt, J. Fractal dimensions and spectra of interfaces with application to turbulence. Proc. R. Soc. Lond. A 1991, 435, 505–534. [Google Scholar]
- Catrakis, H.J.; Dimotakis, P.E. Mixing in turbulent jets: scalar measures and isosurface geometry. J. Fluid Mech 1996, 317, 369–406. [Google Scholar]
- Pocheau, A.; Queiros-Conde, D. Scale covariance of the wrinkling law of turbulent propagating interfaces. Phys. Rev. Lett. 1996, 76, 3352–3355. [Google Scholar]
- Queiros-Conde, D. A diffusion equation to describe scale- and time-dependent dimensions of turbulent interfaces. Proc. R. Soc. Lond. A 2003, 459, 3043–3059. [Google Scholar]
- Vincent, A.; Meneguzzi, M. The spatial structure and statistical properties of homogeneous Turbulence. J. Fluid Mech 1991, 225, 1–20. [Google Scholar]
- Douady, S.; Couder, Y.; Brachet, M.E. Direct observation of the intermittency of intense vorticity filaments in turbulence. Phys. Rev. Lett. 1991, 67, 983–988. [Google Scholar]
- Queiros-Conde, D. Geometry of intermittency in fully developed turbulence. C. R. Acad. Sci. IIB 1999, 327, 1385–1390. [Google Scholar]
- Queiros-Conde, D. Entropic-skins model of fully developed turbulence. C. R. Acad. Sci. IIB 2000, 328, 541–546. [Google Scholar]
- Ruiz Chavarria, G.R.; Baudet, C.; Ciliberto, S. Hierarchy of the Energy Dissipation Moments in Fully Developed Turbulence. Phys. Rev. Lett. 1995, 74, 1986–1989. [Google Scholar]
- She, Z-S.; Waymire, E.C. Quantized energy cascade and log-Poisson statistics in fully developed turbulence. Phys. Rev. Lett. 1995, 74, 262–265. [Google Scholar]
- Benzi, R.; Biferale, L.; Trovatore, E. Universal statistics of non-linear energy transfer in turbulent models. Phys. Rev. Lett. 1995, 77, 3114–3117. [Google Scholar]
- Müller, W.-C.; Biskamp, D. Scaling properties of three-dimensional magnetohydrodynamic turbulence. Phys. Rev. Lett. 2000, 84, 475–478. [Google Scholar]
- Liu, L.; She, Z.-S. Hierarchical structure description of intermittent structures of turbulence. Fluid Dyn. Res. 2003, 33, 261–286. [Google Scholar]
- Queiros-Conde, D. Internal symmetry in the multifractal spectrum of fully developed Turbulence. Phys. Rev. E 2001, 64, 015301(R). [Google Scholar]
- Carlier, J.; Stanislas, M. Experimental study of eddy structures in a turbulent boundary layer using particle image velocimetry. J. Fluid Mech 2005, 535, 143–188. [Google Scholar]
- Celani, A.; Lanotte, A.; Mazzino, A.; Vergassola, M. Universality and Saturation of Intermittency in Passive Scalar Turbulence. Phys. Rev. Lett. 2000, 84, 2385–2388. [Google Scholar]
- Moisy, F.; Willaime, H.; Andresen, J.S.; Tabeling, P. Passive Scalar Intermittency in Low Temperature Helium Flows. Phys. Rev. Lett. 2001, 86, 4827–4830. [Google Scholar]

© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Queiros-Conde, D.; Carlier, J.; Grosu, L.; Stanislas, M. Entropic-Skins Geometry to Describe Wall Turbulence Intermittency. Entropy 2015, 17, 2198-2217. https://doi.org/10.3390/e17042198
Queiros-Conde D, Carlier J, Grosu L, Stanislas M. Entropic-Skins Geometry to Describe Wall Turbulence Intermittency. Entropy. 2015; 17(4):2198-2217. https://doi.org/10.3390/e17042198
Chicago/Turabian StyleQueiros-Conde, Diogo, Johan Carlier, Lavinia Grosu, and Michel Stanislas. 2015. "Entropic-Skins Geometry to Describe Wall Turbulence Intermittency" Entropy 17, no. 4: 2198-2217. https://doi.org/10.3390/e17042198




