Wavelet-Tsallis Entropy Detection and Location of Mean Level-Shifts in Long-Memory fGn Signals
Abstract
:1. Introduction
2. Long-Memory fGn Signals
2.1. Wavelet Analysis of Long-Memory Signals
2.2. Estimators of the Long-Memory Parameter
3. Wavelet-Tsallis q-Entropy
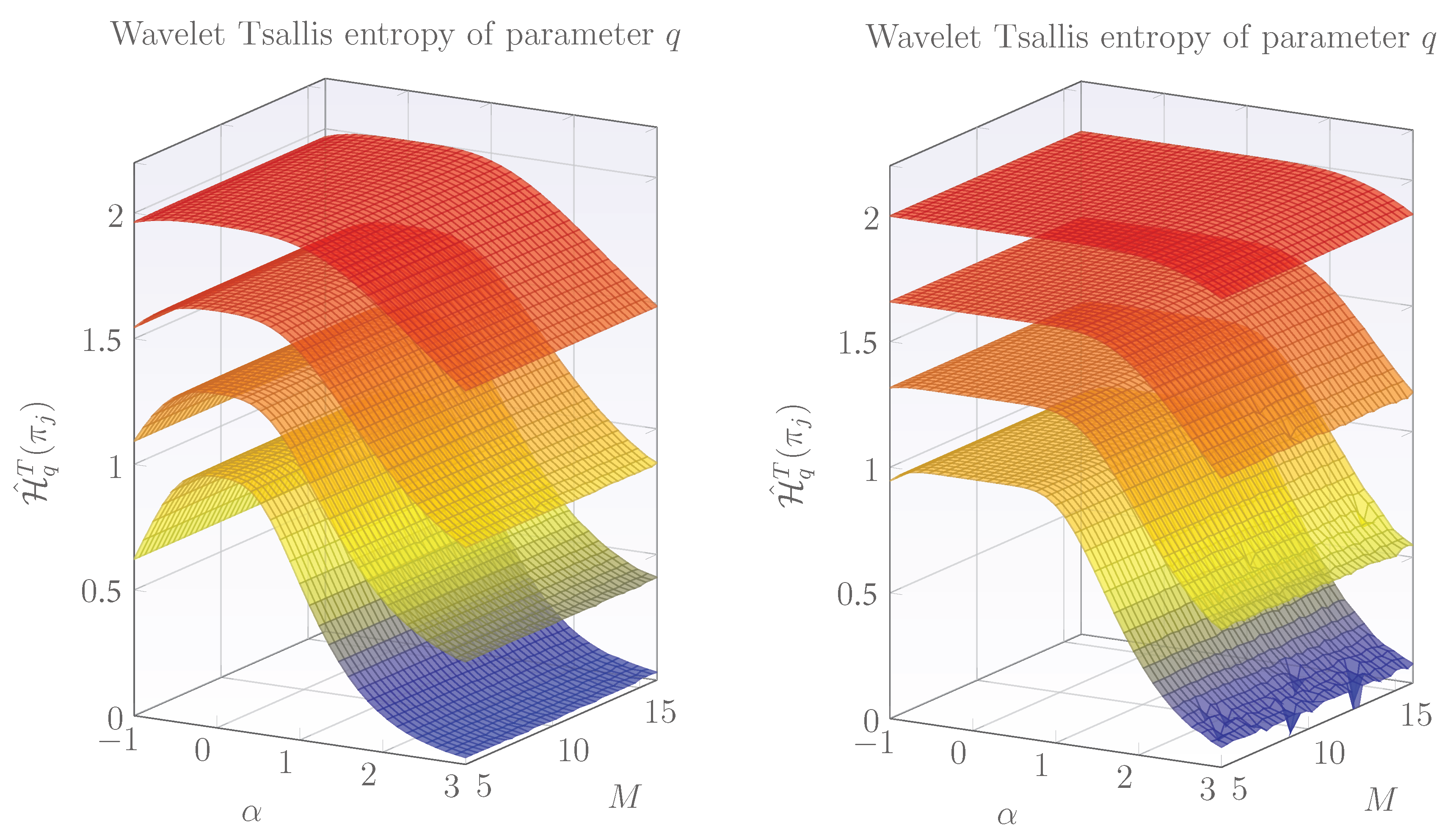
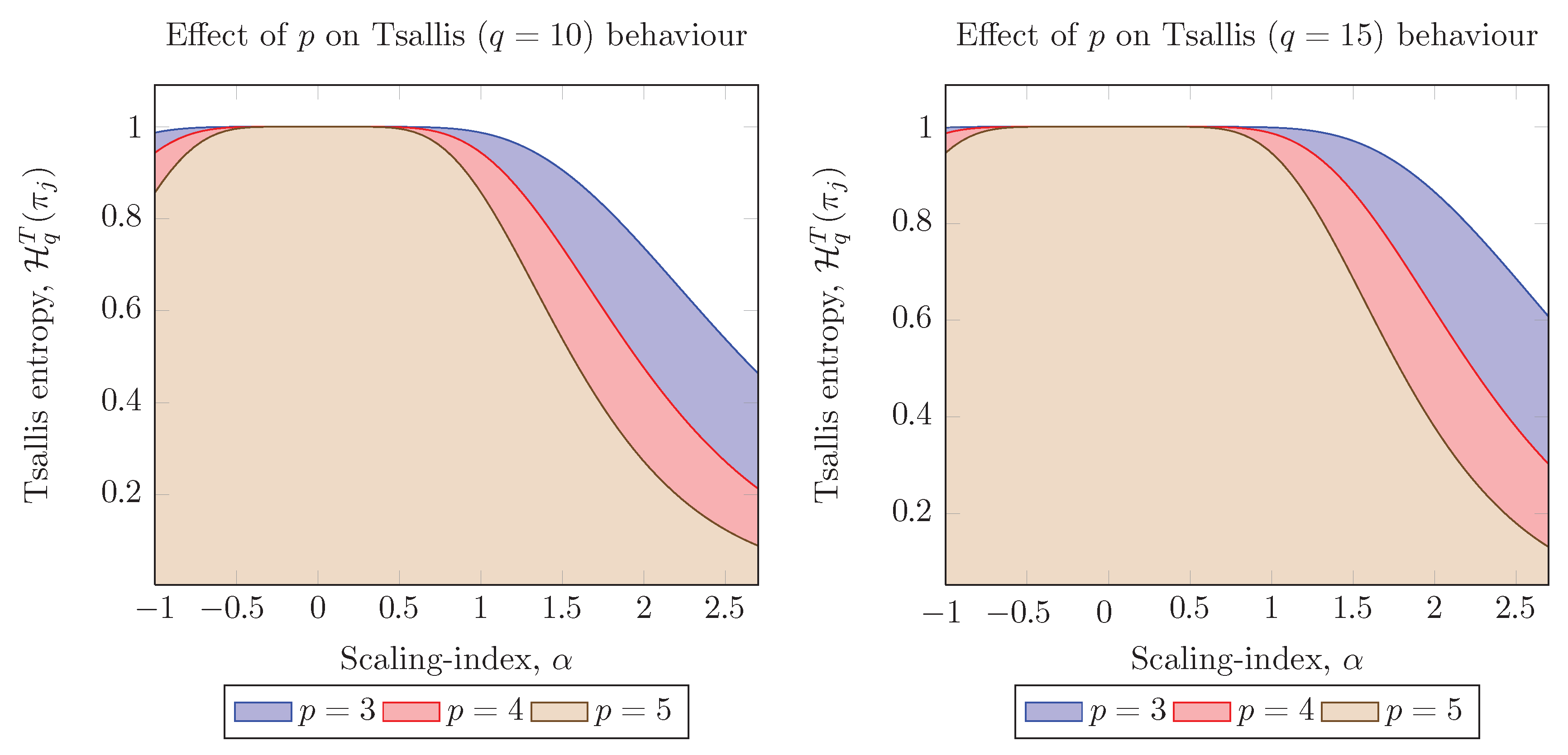
3.1. The Analysis of fGn Signals with Level-Shifts via Wavelet-Tsallis q-Entropy
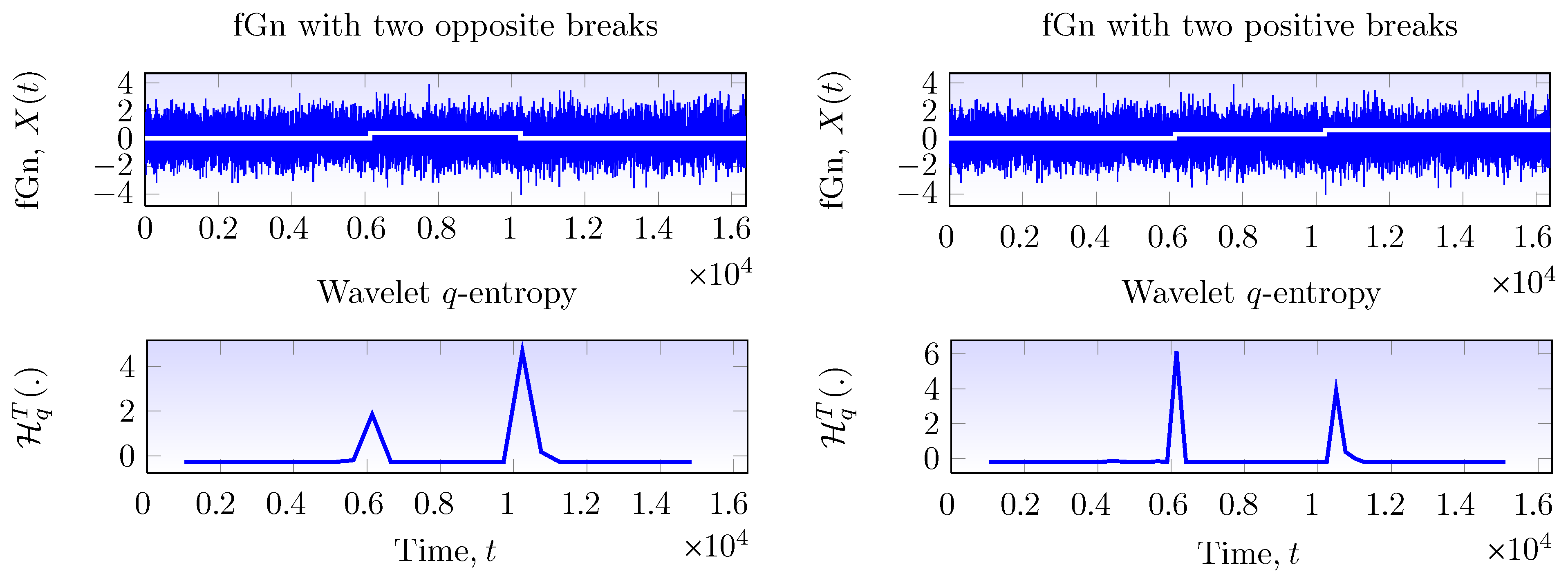

4. A Technique Based on Wavelet-Tsallis q-Entropy for Level-Shift Detection and Location
- (1)
- Compute the wavelet-Tsallis q-entropy as a function of time to signal to obtain .
- (2)
- Perform a transformation and a baseline correction to obtain positive peaks.
- (3)
- Detect and locate peaks in the baseline-corrected wavelet-Tsallis signal using a standard peak detection and location methodology.
5. Results and Discussion
5.1. Detection of Single Level-Shifts in Short-Length fGn Signals
5.2. Detection of Single and Multiple Mean Breaks in Long fGn Signals

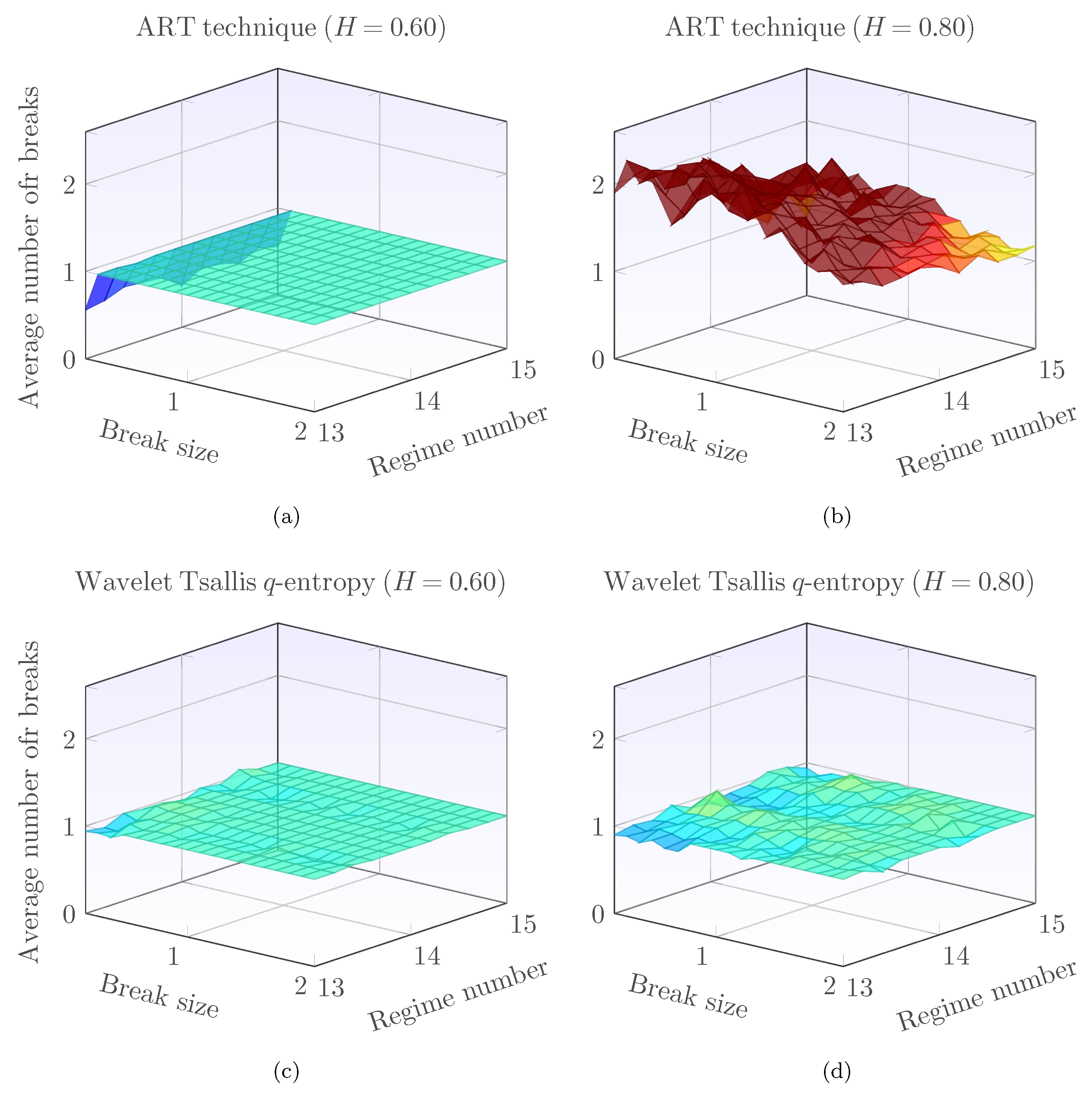

5.3. Detection of Single Level-Shifts in the Presence of Gaussian Noise
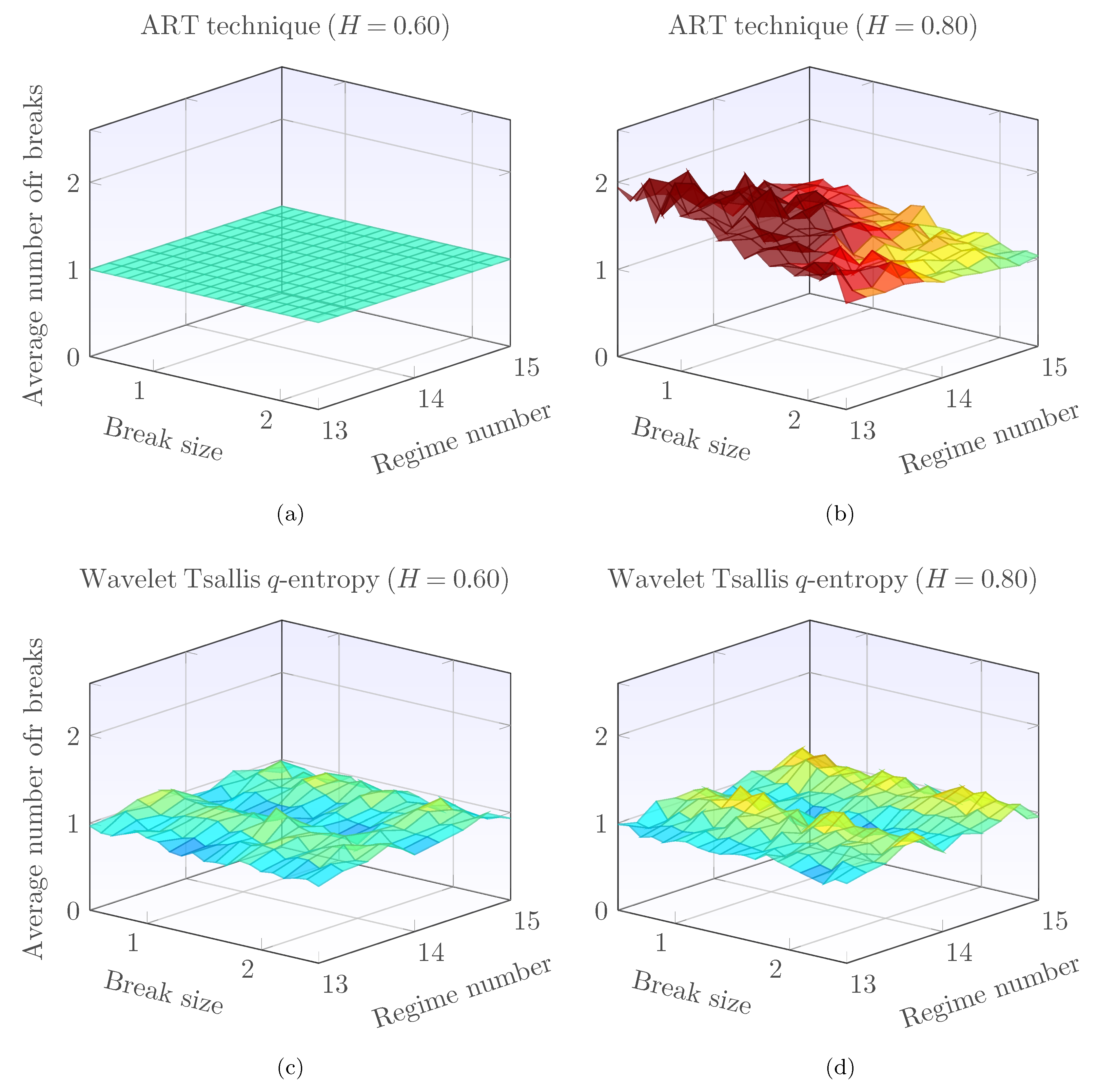
5.4. Location of Single Mean Breaks in fGn Signals
| Atheoretical regression (ART) results | Tsallis q-entropy results | |||||||
| Statistics | Nominal H | Nominal H | ||||||
| 0.6 | 0.7 | 0.8 | 0.9 | 0.6 | 0.7 | 0.8 | 0.9 | |
| Length | ||||||||
| BIAS | 5.00 | 26.00 | -67.00 | 28 | -7.00 | 136 | 30 | -11 |
| σ | 91 | 437 | 584 | 447 | 649 | 935 | 871 | 937 |
| 91 | 436 | 585 | 446 | 646 | 940 | 867 | 932 | |
| μ | 2042 | 2021 | 2114 | 2019 | 2054 | 1911 | 2017 | 2058 |
| Length | ||||||||
| BIAS | 4.000 | 14.00 | 243 | 489 | 0.000 | -114 | 431 | 419 |
| σ | 43.00 | 479 | 1795 | 2141 | 0.000 | 1654 | 3866 | 4075 |
| 43.00 | 477 | 1803 | 2186 | 0.000 | 1649 | 3870 | 4075 | |
| μ | 8187 | 8177 | 7948 | 7702 | 8192 | 8305 | 7760 | 7772 |
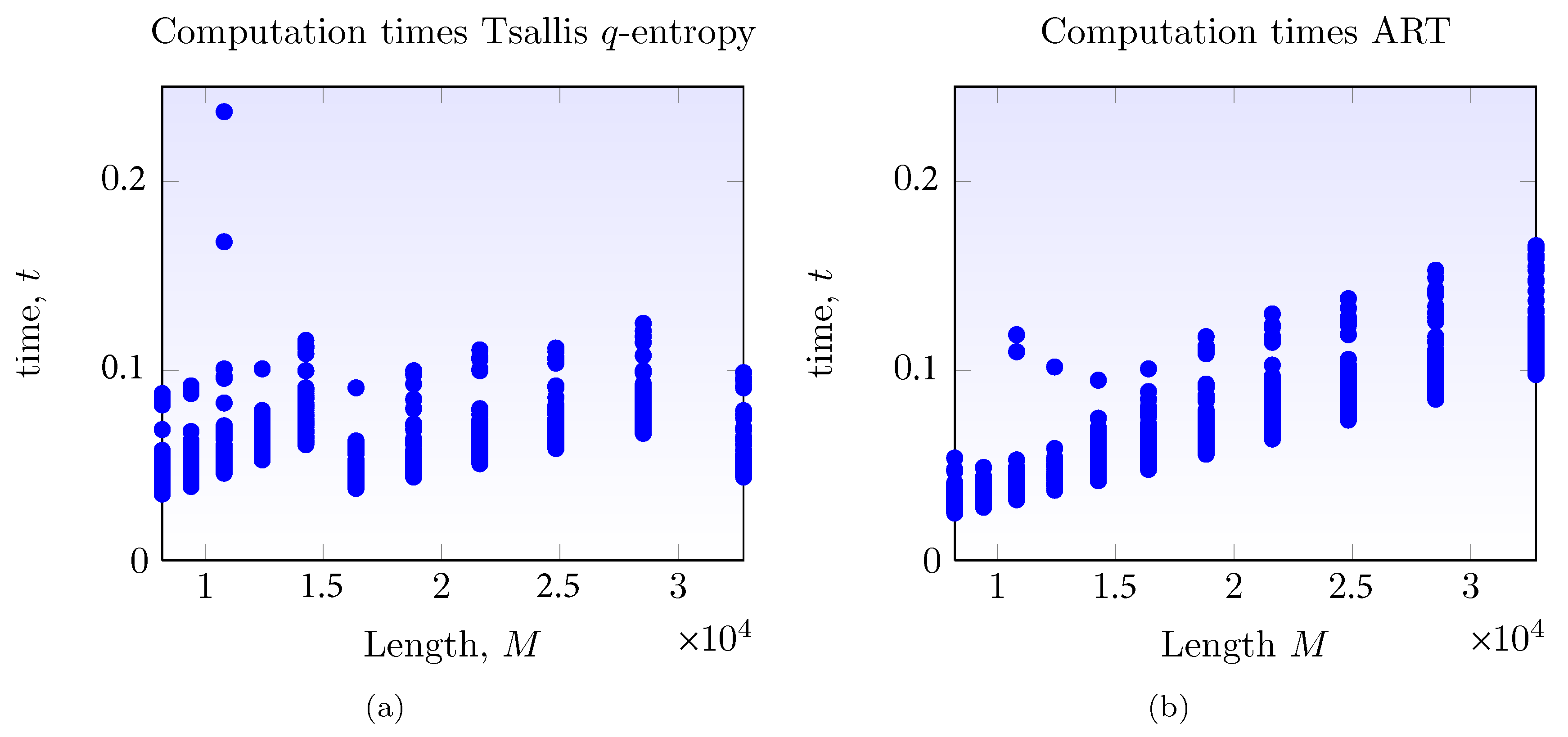
5.5. Computation Times
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Martín-Montoya, L.A.; Aranda-Camacho, N.M.; Quimbary, C.J. Long-range correlations and trends in Colombian seismic time series. Physica A 2015, 421, 124–133. [Google Scholar] [CrossRef]
- Molino-Minero-Re, E.; García-Nocetti, F.; Benítes-Pérez, H. Application of a time-scale local Hurst exponent analysis to time series. Digit. Signal Process. 2015, 37, 92–99. [Google Scholar] [CrossRef]
- Setty, V.A.; Sharma, A.S. Characterizing Detrended Fluctuation Analysis of Multifractional Brownian Motion. Physica A 2015, 419, 698–706. [Google Scholar] [CrossRef]
- Hausdorf, J.M.; Zemany, L.; Peng, C.K.; Goldberger, A. L. Maturation of Gait Dynamics: Stride to stride variability and its temporal organization in children. J. Appl. Physiol. 1999, 86, 1040–1047. [Google Scholar]
- Eke, A.; Herman, P.; Kocsis, L.; Kozak, L.R. Fractal characterization of complexity in temporal physiological signals. Physiol. Meas. 2002, 23, R1–R38. [Google Scholar] [CrossRef] [PubMed]
- Van Orden, G.C.; Holden, J.G.; Turvey, M.T. Human cognition and 1/f scaling. J. Exp. Psychol. Gen. 2005, 134, 117–123. [Google Scholar] [CrossRef] [PubMed]
- Szolgayova, E.; Laaha, G.; Bloschl, G.; Bucher, C. Factors influencing long range dependence in streamflow of European rivers. Hydrol. Process. 2014, 28, 1573–1586. [Google Scholar] [CrossRef]
- Beran, J.; Sherman, R.; Taqqu, M.S.; Willinger, W. Long-Range Dependence in Variable-Bit-Rate Video Traffic. IEEE Trans. Commun. 1995, 43, 1566–1579. [Google Scholar] [CrossRef]
- Shi, Y. Can we distinguish regime switching from long-memory? A simulation evidence. Appl. Econ. 2015, 22, 318–323. [Google Scholar] [CrossRef]
- Eke, A.; Hermán, P.; Bassingthwaighte, J.B.; Raymond, G.; Percival, D.B.; Cannon, M.; Balla, I.; Ikrényi, C. Physiological Time Series: Distinguishing Fractal Noises and Motions. Pflügers Arch. 2000, 439, 403–415. [Google Scholar] [CrossRef] [PubMed]
- Deligneres, D.; Torre, K.; Lemoine, L. Methodological issues in the application of monofractal analyses in psychological and behavioral research. Nonlinear Dyn. Psychol. Life Sci. 2005, 9, 451–477. [Google Scholar]
- Stoev, S.; Taqqu, M.S.; Park, C.; Marron, J.S. On the Wavelet Spectrum Diagnostic for Hurst Parameter Estimation in the Analysis of Internet Traffic. Comput. Netw. 2005, 48, 423–445. [Google Scholar] [CrossRef]
- Abry, P.; Veitch, D. Wavelet Analysis of Long-Range Dependent Traffic. IEEE Trans. Inf. Theory 1998, 44, 2–15. [Google Scholar] [CrossRef]
- Stadnitski, T. Measuring Fractality. Front. Physiol. 2012, 3, 127. [Google Scholar] [CrossRef] [PubMed]
- Rea, W.; Oxley, L.; Reale, M.; Brown, J. Not all estimators are born equal: The empirical properties of some estimators of long-memory. Math. Comput. Simulat. 2013, 93, 29–42. [Google Scholar] [CrossRef]
- Serinaldi, F. Use and misuse of some Hurst parameter estimators applied to stationary and non-stationary financial time series. Physica A 2010, 389, 2770–2781. [Google Scholar] [CrossRef]
- Beran, J. Statistics for Long-Memory Processes; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Malamud, B.D.; Turcotte, D.L. Self-affine time series: Measures of weak and strong persistence. J. Statist. Plann. Inference 1999, 80, 173–196. [Google Scholar] [CrossRef]
- Gallant, J.C.; Moore, I.D.; Hutchinson, M.F.; Gessler, P. Estimating the Fractal Dimension of Profiles: A Comparison of Methods. Math. Geol. 1994, 26, 455–481. [Google Scholar] [CrossRef]
- Fattahi, M.H.; talebbeydokhti, N.; Rakhshandehroo, G.R.; Shamsai, A.; Nikooee, E. The robust fractal analysis of time series: Concerning signal class and length. Fractals 2011, 19, 29–49. [Google Scholar] [CrossRef]
- Ramirez-Pacheco, J.; Torres-Román, D.; Toral-Cruz, H. Distinguishing Stationary/Nonstationary Scaling Processes Using Wavelet Tsallis q-Entropies. Math. Probl. Eng. 2012, 2012, 1–18. [Google Scholar] [CrossRef]
- Holden, J.G.; Riley, M.A.; Gao, J.; Torre, K. Fractal Analyses: Statistical and methodological innovations and best practices. Front. Physiol. 2013, 4, 97. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, B.; van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Samorodnitsky, G.; Taqqu, M. Stable Non-Gaussian Random Processes: Stochastic Models with Infinite Variance; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Percival, D.B. Stochastic Models and Statistical Analysis for Clock Noise. Metrologia 2003, 40, S289–S304. [Google Scholar] [CrossRef]
- Hudgins, L.; Friehe, C.A.; Mayer, M.E. Wavelet Transforms and Atmospheric Turbulence. Phys. Rev. Lett. 1993, 71, 3279–3283. [Google Scholar] [CrossRef] [PubMed]
- Cohen, A.; Kovacevic, J. Wavelets: The Mathematical Background. Proc. IEEE 1996, 84, 514–522. [Google Scholar] [CrossRef]
- Veitch, D.; Abry, P. A Wavelet Based Joint Estimator of the Parameters of Long-Range Dependence. IEEE Trans. Inf. Theory 1999, 45, 878–897. [Google Scholar] [CrossRef]
- Soltani, S.; Simard, P.; Boichu, D. Estimation of the self-similarity parameter using the wavelet transform. Signal Process. 2004, 84, 117–123. [Google Scholar] [CrossRef]
- Shen, H.; Zhu, Z.; Lee, T.C.M. Robust estimation of the self-similarity parameter in network traffic using the wavelet transform. Signal Process. 2007, 87, 2111–2124. [Google Scholar] [CrossRef]
- Flandrin, P. Wavelet Analysis and Synthesis of Fractional Brownian Motion. IEEE Trans. Inf. Theory 1992, 38, 910–917. [Google Scholar] [CrossRef]
- Bardet, J.M. Statistical Study of the Wavelet Analysis of Fractional Brownian Motion. IEEE Trans. Inf. Theory 2002, 48, 991–999. [Google Scholar] [CrossRef]
- Pesquet-Popescu, B. Statistical Properties of the Wavelet Decomposition of certain Non-Gaussian Self-Similar Processes. Signal Process. 1999, 75, 303–322. [Google Scholar] [CrossRef]
- Bryce, R.M.; Sprague, K.B. Revisiting Detrended Fluctuation Analysis. Sci. Rep. 2012, 2, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Deligneres, D.; Ramdani, S.; Lemoine, L.; Torre, K.; Fortes, M.; Ninot, G. Fractal Analyses of short time series: A re-assessment of classical methods. J. of Math. Psychol. 2006, 50, 525–544. [Google Scholar] [CrossRef]
- Esposti, F.; Ferrario, M.; Signorini, M.G. A Blind Method for the estimation of the Hurst exponent in time series: Theory and Methods. Chaos 2008, 18, 033126. [Google Scholar] [CrossRef] [PubMed]
- Schaefer, A.; Brach, J.; Perera, S.; Sejdic, E. A comparative analysis of spectral exponent estimation techniques for 1/fβ processes with applications to the analysis of stride interval time series. J. Neurosci. Methods 2014, 222, 118–130. [Google Scholar] [CrossRef] [PubMed]
- Bonachela, J.; Hinrichsen, H.; Muñoz, M.A. Entropy estimates of small data sets. J. Phys. A Math. Gen. 2008, 41, 202001. [Google Scholar] [CrossRef]
- Kumar, U.; Kumar, V.; Kapur, J.N. Normalized measures of entropy. Int. J. Gen. Syst. 1986, 12, 55–69. [Google Scholar] [CrossRef]
- Martin, M.T.; Plastino, A.R.; Plastino, A. Tsallis-like information measures and the analysis of complex signals. Physica A 2000, 275, 262–271. [Google Scholar] [CrossRef]
- Zunino, L.; Perez, D.G.; Garavaglia, M.; Rosso, O.A. Wavelet Entropy of Stochastic Processes. Physica A 2007, 379, 503–512. [Google Scholar] [CrossRef]
- Quiroga, R.Q.; Rosso, O.A.; Basar, E.; Schumann, M. Wavelet entropy in event-related potentials: A new method shows ordering of EEG oscillations. Biol. Cybern. 2001, 84, 291–299. [Google Scholar] [CrossRef] [PubMed]
- Ren, W.X.; Sun, Z.S. Structural damage identification by using wavelet entropy. Eng. Struct. 2008, 30, 2840–2849. [Google Scholar] [CrossRef]
- Perez, D.G.; Zunino, L.; Martin, M.T.; Garavaglia, M.; Plastino, A.; Rosso, O.A. Model-free stochastic processes studied with q-wavelet-based information tools. Phys. Lett. A 2007, 364, 259–266. [Google Scholar] [CrossRef]
- Zunino, L.; Pérez, D.G.; Martin, M.T.; Plastino, A.; Garavaglia, M.; Rosso, O.A. Characterization of Gaussian Self-similar stochastic processes using wavelet-based information tools. Phys. Rev. E 2007, 75, 021115. [Google Scholar] [CrossRef] [PubMed]
- Rosso, O.A.; Zunino, L.; Pérez, D.G. Extracting features of Gaussian self-similar stochastic processes using wavelet-based information tools. Phys. Rev. E 2007, 76, 061114. [Google Scholar] [CrossRef] [PubMed]
- Ramirez-Pacheco, J.; Torres-Roman, D. Cosh window behavior of wavelet Tsallis q-entropies in 1/fα signals. Electron. Lett. 2011, 47, 186–187. [Google Scholar] [CrossRef]
- Bauwens, L.; Koop, G.; Korobilis, D.; Rombouts, J.V.K. The contribution of structural break models to forecasting Macroeconomic series. J. Appl. Econom. 2014, 30, 596–620. [Google Scholar] [CrossRef]
- Rea, W.; Reale, M.; Capelli, C.; Brown, J.A. Identification of changes in mean with regression trees: An application to market research. Economet. Rev. 2010, 29, 754–777. [Google Scholar] [CrossRef]
- Rea, W.; Reale, M.; Brown, J.; Oxley, L. Long-memory or shifting means in geophysical time series? Math. Comput. Simulat. 2011, 81, 1441–1453. [Google Scholar] [CrossRef]
- Capelli, C.; Penny, R.N.; Rea, W.S.; Reale, M. Detecting multiple mean breaks at unknown points with Atheoretical Regression Trees. Math. Comput. Simulat. 2008, 78, 351–356. [Google Scholar] [CrossRef]
- Yang, C.; He, Z.; Hu, W. Comparison of public peak detection algorithms for MALDI mass spectometry data analysis. BMC Bioinform. 2009, 10, 4. [Google Scholar] [CrossRef] [PubMed]
- Bai, J.; Perron, P. Computation and analysis of multiple structural breaks models. J. Appl. Econom. 2003, 18, 1–22. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramírez-Pacheco, J.C.; Rizo-Domínguez, L.; Cortez-González, J. Wavelet-Tsallis Entropy Detection and Location of Mean Level-Shifts in Long-Memory fGn Signals. Entropy 2015, 17, 7979-7995. https://doi.org/10.3390/e17127856
Ramírez-Pacheco JC, Rizo-Domínguez L, Cortez-González J. Wavelet-Tsallis Entropy Detection and Location of Mean Level-Shifts in Long-Memory fGn Signals. Entropy. 2015; 17(12):7979-7995. https://doi.org/10.3390/e17127856
Chicago/Turabian StyleRamírez-Pacheco, Julio César, Luis Rizo-Domínguez, and Joaquin Cortez-González. 2015. "Wavelet-Tsallis Entropy Detection and Location of Mean Level-Shifts in Long-Memory fGn Signals" Entropy 17, no. 12: 7979-7995. https://doi.org/10.3390/e17127856






