Wiretap Channel with Information Embedding on Actions
Abstract
: Information embedding on actions is a new channel model in which a specific decoder is used to observe the actions taken by the encoder and retrieve part of the message intended for the receiver. We revisit this model and consider a different scenario where a secrecy constraint is imposed. By adding a wiretapper in the model, we aim to send the confidential message to the receiver and keep it secret from the wiretapper as much as possible. We characterize the inner and outer bounds on the capacity-equivocation region of such a channel with noncausal (and causal) channel state information. Furthermore, the lower and upper bounds on the sum secrecy capacity are also obtained. Besides, by eliminating the specific decoder, we get a new outer bound on the capacity-equivocation region of the wiretap channel with action-dependent states and prove it is tighter than the existing outer bound. A binary example is presented to illustrate the tradeoff between the sum secrecy rate and the information embedding rate under the secrecy constraint. We find that the secrecy constraint and the communication requirements of information embedding have a negative impact on improving the secrecy transmission rate of the given communication link.1. Introduction
In wireless communication systems, such as sensor networks, mobile networks and satellite communications, sensitive data is transferred through multiple hops. The nodes in the network usually need to take various type of actions to acquire the state of the network before transferring the packets. The state acquisition in the network often requires the exchange of control information, which uses physical resources within the system. For example, routers measure the network congestion levels via the transmission of probing packets; wireless transceivers evaluate the channel quality through training or feedback; and radio terminals switch among different operating modes, such as transmit, receive or idle. Based on these motivating observations, Weissman introduced channels with action-dependent states where the encoder in a point-to-point channel could take actions to affect the channel state information [1]. The capacity of such a channel where the channel inputs depended noncausally (and causally) on the channel states was determined. After Weissman’s publication, [2] investigated the channel model where both the channel encoder and decoder could probe the channel states and obtained the cost constrained “probing capacity”. Different from this, [1–3] studied the degraded broadcast channel with causal action-dependent states where the transmitter sent two kinds of messages to two different receivers. The capacity region was derived. For the noncausal case, only inner and outer bounds on the capacity region were obtained [4]. Other extensions of the channel with action-dependent states can be seen in [5–10].
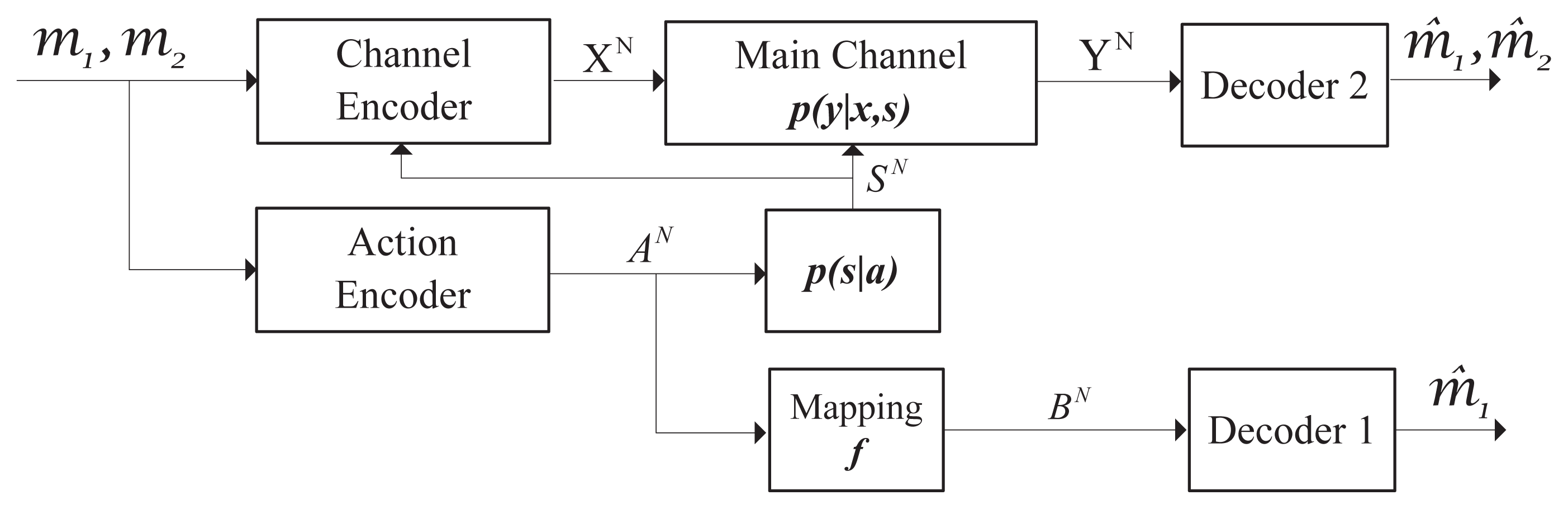
Recently, [11,12] explored information embedding on actions in the channel with noncausal action-dependent states; see Figure 1. In this new setup, an additional decoder was introduced to observe a function of the actions taken by the encoder. It tried to get part of the transmitted message. Actually, the idea of “information embedding” on actions in such a channel is related to the classical topic of information hiding (e.g., [13–17]) and could be explained by the following example. In communication networks, probing the congestion state requires sending training packets to the nearest router. Meanwhile, the router (the “recipient” of the actions) may need to obtain partial information, such as the header of the packet, to find the address of the intended receiver. Since the actions play the role of providing necessary information about the message for the router, it is natural to ask how much information could be embedded in the actions without affecting the system performance. [11] got the capacity-cost region and showed that the communication requirements of the action-cribbing decoder were generally in conflict with the goal of improving the efficiency of the communication link.
However, the above action-dependent channel models [1–12] considered no secrecy constraint, which was extremely important in communications. For instance, the broadcast nature of wireless networks gives rise to the hidden danger of information leakage to malicious receiver when broadcasting the sensitive data and acquiring the state information. Recent works [18,19] studied the secure communication problems in channels with action-dependent states. [18] added a wiretapper to the model in [1] and got the inner and outer bounds on the capacity-equivocation region. The capacity-equivocation region is the set of all the achievable rate pairs (R, Re), where R and Re are the rates of the confidential message and wiretapper’s equivocation about the message. [19] studied the effects of feedback on the secrecy capacity, which is the maximum rate of data transmission at which the message can be communicated in perfect secrecy, of the wiretap channel with action-dependent states.
From the perspective of secure communication, we consider a different communication model in Figure 2, i.e., the wiretap channel with information embedding on actions. In this setup, the transmitter aims to send the confidential message to the receiver and keep it secret from the wiretapper as much as possible. We use equivocation (i.e., the uncertainty about the confidential message) at the wiretapper to measure the level of information leakage. Meanwhile, like [11], a specific decoder is introduced to retrieve a portion of the confidential message (see m1 in Figure 2). The specific decoder observes a function of the message-dependent actions, which affects the formulation of the channel states. Our work is novel in the sense that we consider the secrecy constraint in the information transmission, and we try to characterize how much information could be embedded in the actions without increasing the information leakage.
For the new channel model described above, this paper obtains the inner and outer bounds on the capacity-equivocation region of such a channel with noncausal (and causal) channel state information. Furthermore, the lower and upper bounds on the sum secrecy capacity are also attained. Through a special case where no message needs to be retrieved by the specific decoder, we get a new outer bound on the capacity-equivocation region of the wiretap channel with action-dependent states and prove that it is tighter than the existing outer bound. To illustrate the tradeoff between the sum secrecy rate and the information embedding rate under the secrecy constraint, we provide a binary example. It shows that the sum secrecy rate is reduced when the information embedding rate increases. We find that the secrecy constraint and the communication requirements of the specific decoder have a negative impact on improving the secrecy transmission rate of the given communication link.
The rest of the article is organized as follows. Section 2 describes the wiretap channel with information embedding on actions and outlines the main results. Section 3 discusses the results and presents a binary example. We conclude in Section 4 with a summary of the whole work and some future directions.
2. Channel Model and Main Results
The symbol notations and description of the channel model are presented in Subsection 2.1. Subsection 2.2 characterizes the inner and outer bounds on the capacity-equivocation region of the wiretap channel with information embedding on actions.
2.1. Symbol Notations and Channel Model
Throughout this paper, we use calligraphic letters, e.g.,






The wiretap channel with information embedding on actions is depicted in Figure 2. We aim to send the confidential message (M1, M2) to the legitimate receiver through such a channel and keep it secret from the wiretapper as much as possible. Part of the message embedded in the actions needs to be retrieved by the specific decoder. We use equivocation at the wiretapper to measure the secrecy of the confidential message.
Concretely, the model of wiretap channel with information embedding on actions is specified by {



The main channel is a DMC with discrete input alphabet


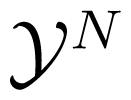
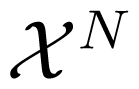
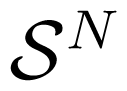
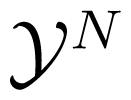

Then, we give the definition of “achievable” and “sum secrecy capacity” as follows.
Definition 1
A rate triple (R1, R2, Re) is said to be achievable for the model in Figure 2 if there exists a channel encoder-decoder, such that:
where ε is an arbitrary small positive real number, (R1, R2) are the rates of the message (M1, M2) and Re is the rate of equivocation. The capacity-equivocation region is defined as the convex closure of all achievable rate triples (R1, R2, Re).
Definition 2
The sum secrecy capacity is the maximum rate at which the confidential message can be sent to the receiver in perfect secrecy. The sum secrecy capacity:
where is the capacity-equivocation region.
Based on the definition in Equation (5), the sum secrecy capacity for the model in Figure 2 with noncausal action-dependent states is , where n is the capacity-equivocation region of the noncausal case. Similarly, we can define the sum secrecy capacity of the causal case, Csc.
2.2. Main Results
In this subsection, four theorems are presented. Theorems 1 and 2 give the inner and outer bounds on the capacity-equivocation region for the channel model in Figure 2 with noncausal action-dependent states. For the causal case, the inner and outer bounds are characterized in Theorems 3 and 4.
Theorem 1
An achievable rate-equivocation region of the wiretap channel with information embedding on actions when the states are noncausally known to the channel encoder is the set:
where the joint distributions p(a, b, u, x, s, y, z) = p(z|y)p(y|x, s)p(x|u, s)p(s|u, a)p(u|a)p(a)1{b=f(a)}, which indicates (A, B, U) → (X, S) → Y → Z form a Markov chain.
Theorem 2
An outer bound on the capacity-equivocation region of the wiretap channel with information embedding on actions when the states are noncausally known to the channel encoder is the set:
where the joint distributions p(a, b, u, x, s, y, z) = p(z|y)p(y|x, s)p(x|u, s)p(q|v)p(v|u)p(a, u, s)1{b=f(a)}, which indicates (B, A, U, V, Q) → (X, S) → Y → Z and Q → V → U → Y → Z form Markov chains.
Comments
Theorems 1 and 2 are proven in Appendix A.
To exhaust in and on, it is enough to restrict
,
and
to satisfy:
This can be easily proven by using the support lemma (see p. 310 in [25]).
Theorem 3
An achievable rate-equivocation of the wiretap channel with information embedding on actions when the states are causally known to the channel encoder is the set:
where the joint distributions p(a, b, u, x, s, y, z) = p(z|y)p(y|x, s)p(x|u, s)p(s|a)p(u|a)p(a)1{b=f(a)}, which indicates (A, B, U) → (X, S) → Y → Z and U → A → S form Markov chains.
Theorem 4
An outer bound on the capacity-equivocation region of the wiretap channel with information embedding on actions when the states are causally known to the channel encoder is the set:
where the joint distributions p(a, b, u, x, s, y, z) = p(z|y)p(y|x, s)p(x|u, s)p(q|v)p(v|u)p(a, u, s)1{b=f(a)}, which indicates (B, A, U, V, Q) → (X, S) → Y → Z and Q → V → U → Y → Z form Markov chains.
Comments
Theorems 3 and 4 are proven in Appendix B.
To exhaust ic and oc, it is enough to restrict
,
and
to satisfy:
This can be easily proven by using the support lemma (see p. 310 in [25]).
Further discussion about the theorems and the comparison with other existing results are given in Section 3.
3. Discussion and Example
In this section, we first calculate the sum secrecy capacities of the noncausal and causal cases. Then, we compare our results with some existing results and present a binary example to illustrate the tradeoff between the sum secrecy rate and the information embedding rate under the secrecy constraint.
3.1. Discussion
Corollary 1
The lower and upper bounds on the sum secrecy capacity of the model in Figure 2 with noncausal action-dependent states are:
and:
respectively.
Proof
According to the definition of Formula (5), in and on, we can easily get Equations (20) and (21).
Similarly, we have the following corollary for the causal case.
Corollary 2
The lower and upper bounds on the sum secrecy capacity of the model in Figure 2 with causal action-dependent states are:
and:
respectively.
Proof
According to the definition of Formula (5), ic and oc, we can easily get Equations (22) and (23).
According to [11], the capacity region of the model in Figure 1 (without the secrecy constraint) is:
Then, the corresponding capacity is:
Compare Formula (26) with (20); we can get Cln ≤ CE. This implies that the secrecy constraint reduces the secrecy transmission rate of the communication link. Therefore, once the problem of information leakage is considered, the system designer has to trade off between the transmission rate and data security. Moreover, without the secrecy constraint, we have the following corollary.
Corollary 3
Without considering the secrecy constraint (i.e., ignoring Re in in), we arrive at the results in [11].
Proof
This corollary is verified by setting Re = 0 in in.
When no message needs to be embedded in the actions, the model in Figure 2 turns to the wiretap channel with action-dependent states [18]; see Figure 3. [18] gave an upper bound on the secrecy capacity of the model with noncausal states as:
Substituting R1 = 0 into on, we get a new upper bound on the secrecy capacity of the model in Figure 3 with noncausal states. This new upper bound is:
where nd is the capacity-equivocation region of the model with noncausal states. Note that the difference between Equations (28) and (27) is the extra term, I(U; S|V ). The cause of the emergence of this term is stated in detail at the end of Appendix A. Then, we give the following corollary.
Corollary 4
For the wiretap channel with noncausal action-dependent states shown in Figure 3, the new upper bound on the secrecy capacity .
Proof
From the two Formulas, (27) and (28), we can get the difference between and Cdain as:
It is easy to see that Λ1 ≥ 0, i.e., our new upper bound . Note that it is always desired to find a smaller upper bound to approach the secrecy capacity.
Similarly, substituting R1 = 0 into oc, we can get an upper bound on the secrecy capacity of the model in Figure 3 with causal states, which is:
where cd is the capacity-equivocation region of the model with causal states. coincides with the upper bound on the secrecy capacity of the model in [18] with causal states.
Then, we study a special channel model where the “action” is removed, i.e., the wiretap channel with noncausal channel state information. In this model, the channel state is generated by nature. This model is a special case of the wiretap channel with information embedding on actions by eliminating the action encoder and the mapping, f. It is also a special case of the model in Figure 3 without action. Setting the random variable, A, in Equation (28) to be a constant, we get a new outer bound of the wiretap channel with noncausal channel state information as:
The outer bound in [20] was derived as . Comparing the two bounds, we see that . This is stated in the following corollary.
Corollary 5
For the wiretap channel with noncausal channel state information [20], the new upper bound on the secrecy capacity .
In addition, in the case of no actions, our model turns into a special case that was also studied in [21]. The comparison between our results and those in [21] for this case is stated as follows.
The achievable rate-equivocation region of the special case obtained from [21] is contained in that obtained from our results.
We also provide an outer bound for this special case.
[21] obtained an achievable rate region for the broadcast wiretap channel with the asymmetric side information, which was:
We first give an equivalent expression of the achievable rate region I as follows.
where Re1 and Re2 are the equivocation rates of the messages, m1 and m2, respectively. We can easily prove that is equivalent to I via replacing Formulas (9), (10) and (11) in [21] accordingly by:
Since information is embedded on the actions, the information embedding rate R1 = 0 when no actions are imposed in our model. At the same time, the specific decoder (Decoder 1) is no longer needed. For this special case, we get its achievable rate-equivocation region from our results (by setting R1 = 0 and A = const in in) as:
As stated in [21], by removing the receiver (

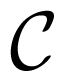
For simplicity, we replace U2, S1, Re2 and Y2 by U, S, Re and Y, respectively. We then show that . For any rate pair , from Equation (43),
From Equations (43) and (44),
Therefore, (R2, Re) ∈ special. This verifies .
Moreover, we get an outer bound for the special case. The outer bound is:
It can be directly gotten from on by setting R1 = 0 and A = const. Note that [21] did not provide an outer bound.
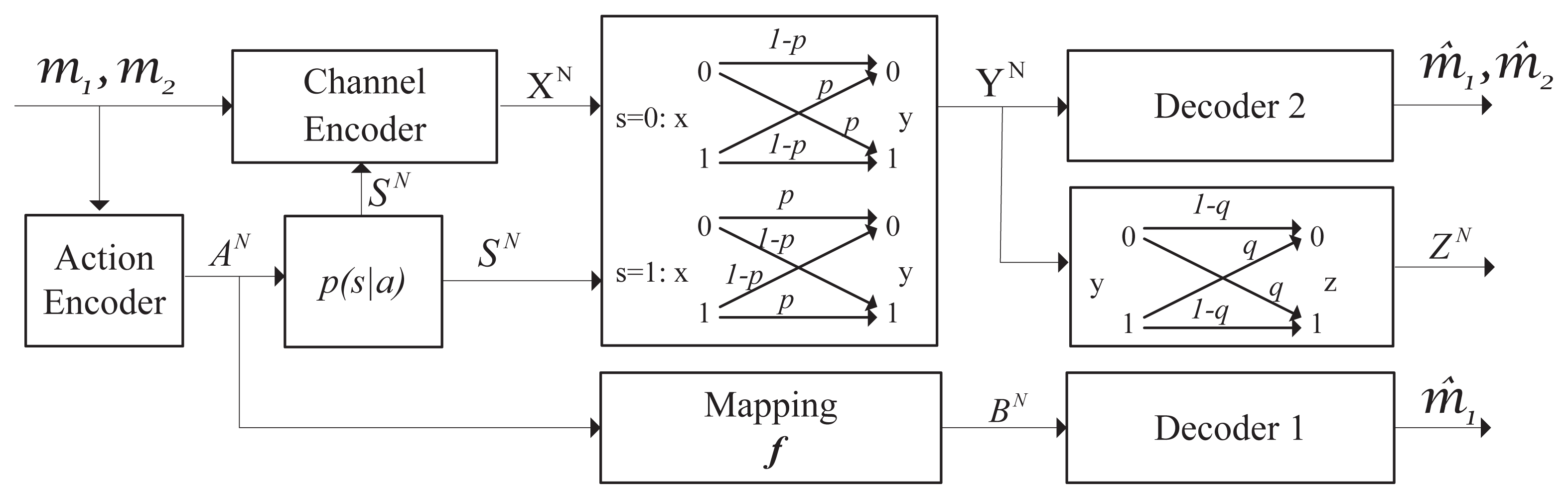
3.2. A Binary Example
We give an example of a binary symmetric channel with causal channel states. The channel model is shown in Figure 4. Let the main channel be a binary symmetric channel (BSC). Its crossover probability is affected by the channel states. The wiretap channel is also assumed to be a BSC with crossover probability q. More precisely, define:
and:
where i ∈ {0, 1}, 0 ≤ p ≤ 1 and 0 ≤ q ≤ 1.
It is assumed that the channel from the action to the channel states is a BSC with crossover probability equal to α, where 0 ≤ α ≤ 1. In this example, the parameter, α, is fixed as 0.2 (the other value of α could also be assumed). Similar to the arguments in [1,18,19], the maximum values of H(A|Z), I(U; Y ) and I(U; Y )−I(U; Z) are achieved when g1:
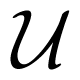

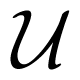
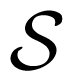

where i, j ∈ {0, 1}. Let B ~ Bernoulli(β), where 0 ≤ β ≤ 1. Let the function, f, be a one-to-one mapping for simplicity. Here, we set:
From the above conditions, we see that the random variables, B, A and U, share the same distribution. Then, the joint distribution p(a, b, s, u, x, y, z) = p(z|y)p(y|x, s)p(x|u, s)p(s|a)p(a|u)p(u)1{b=f(a)} can be calculated. The joint distributions and can also be obtained. By some mathematical calculation and Theorem 3, we can get the maximum sum secrecy rate of the example with causal channel states for given p, q as:
under the constraint H(B) = h(β) ≥ R1 and the secrecy constraint:
where p*q = p+q−2pq and h(p) is the binary entropy function, i.e., h(p) = −p log p−(1−p) log(1−p).
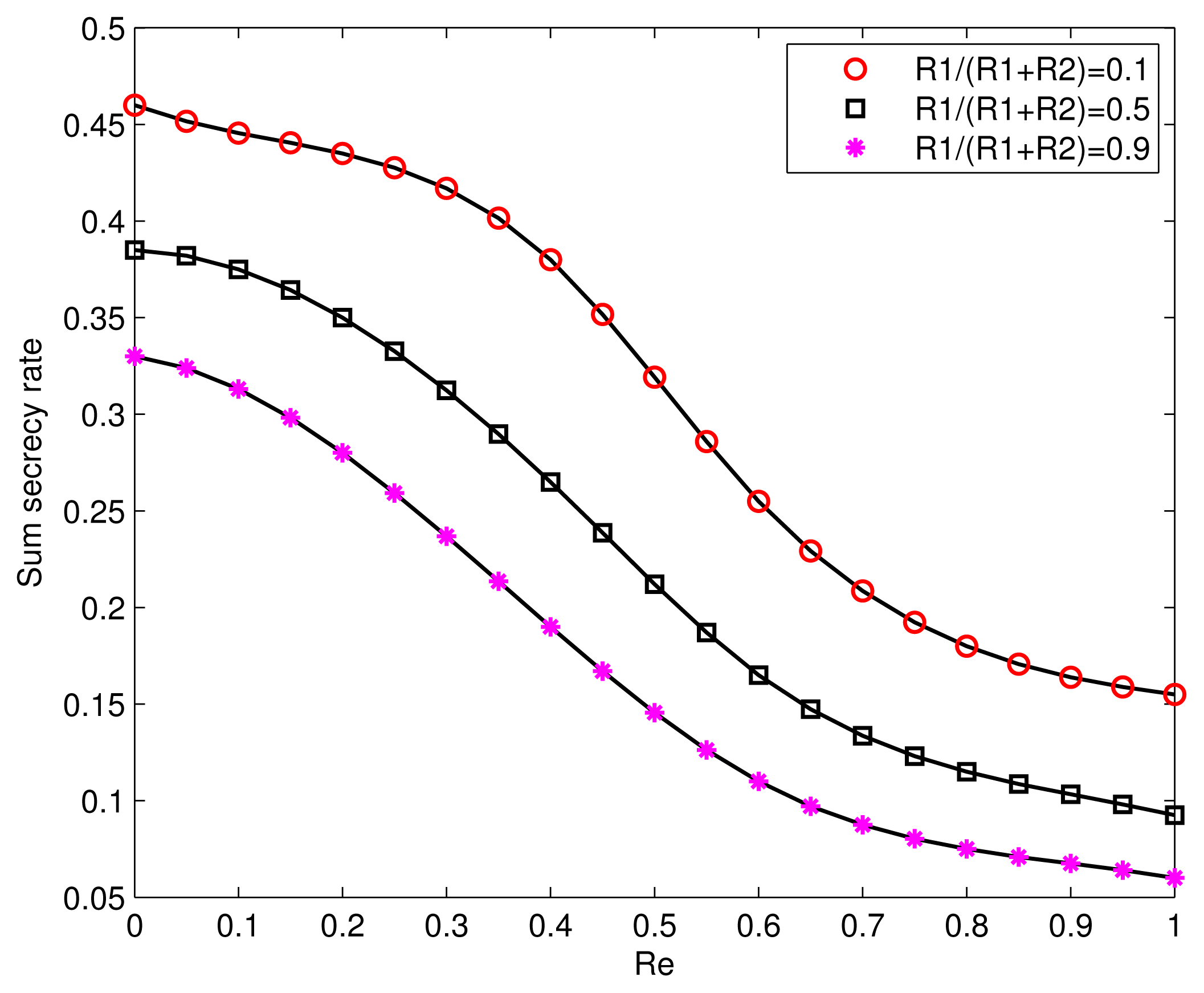
The tradeoff between the sum secrecy rate and the information embedding rate under the secrecy constraint is shown in Figure 5. It can be seen that the sum secrecy rate is reduced when the equivocation rate, Re, increases. In practical communication systems involving security, we always desire a bigger secure transmission rate when the extent of information leakage is at a reasonable level. Moreover, it can be seen that when the information embedding rate, R1, goes up, the sum secrecy rate also decreases. This tells us that the communication requirements of Decoder 1 have a negative impact on improving the secrecy transmission rate of the given communication link.
4. Conclusions
This paper studies the wiretap channel with information embedding on actions. In this extended setup, the confidential message needs to be decoded only by the receiver and kept secret from the wiretapper as much as possible. Meanwhile, a specific decoder is introduced in the model to observe a function of the actions and wishes to decode part of the transmitted message. Our channel model is actually an extension of Ahmadi’s channel with information embedding [11] by considering the secrecy constraint. We get the inner and outer bounds on the capacity-equivocation region of such a channel with noncausal (and causal) channel states. The corresponding lower and upper bounds on the sum secrecy capacity are also obtained. Besides, through a special case, we get a new upper bound on the secrecy capacity of the wiretap channel with action-dependent states and show that it is tighter than the upper bound obtained in [18]. We also discuss the tradeoff between the sum secrecy rate and the information embedding rate under the secrecy constraint.
Some potential directions that are worthy of being explored are listed as follows.
In practical application, the wiretapper may also wish to eavesdrop on the embedded information. In the example of communication networks, the information embedded in the packet for the next router may also be of interest to the eavesdropper. Our current setting does not consider the confidentiality of m1 and m2 separately, so this problem will be further explored.
Only inner and outer bounds on the capacity-equivocation region are obtained at present. We can try to find some special cases where the two bounds match. Moreover, if there exists a channel between AN and BN instead of a function, what will the capacity-equivocation region be?
Adaptive action means that the action sequence is generated by the message and the previous channel states, i.e., ai(m, si−1). Adaptive action is widely used in many applications, such as information hiding, digital watermarking and data storage in the memory. It is valuable to study the adaptive action in our model. From [10], we have already known that adaptive action is not useful in increasing the point-to-point channel capacity. We will study whether it influences the sum secrecy capacity of our channel model under the secrecy constraint.
Acknowledgments
This work was supported in part by the National Natural Science Foundation of China under Grant No. 61171173, 60932003 and 61271220. The authors also would like to thank the anonymous reviewers for helpful comments.
Appendix
A. Proof of Theorems 1 and 2
In this section, Theorems 1 and 2 are proven. To prove Theorem 1, the methods in [18] are utilized, and we present a coding scheme for the model in Figure 2 with noncausal action-dependent states in Subsection A.1. The proof of Theorem 2 is given in Subsection A.2.
A.1. Proof of Theorem 1
We need to prove that any rate-equivocation triple (R1, R2, Re) ∈ in is achievable. Similar to [18], two cases are considered. Since the channel states are noncausally known to the channel encoder, Gel’fand and Pinsker’s coding technique [22] will be used in the encoding process.
A.1.1. H(A|Z) ≥ I(U; Y ) − max{I(U; Z), I(U; S|A)}
In this case, we need to prove that any rate-equivocation triple (R1, R2, Re) satisfying the following constraints are achievable.
It is sufficient to show that the rate triples (R1, R2, Re = I(U; Y ) − max{I(U;Z), I(U; S|A)}) are achievable. The coding scheme includes codebook generation, encoding and decoding. Then we give the equivocation analysis.
Codebook generation and encoding
Let R1 = H(B)−τ1 and R1 + R2 = I(U; Y ) − I(U; S|A) − τ2, where τ1, τ2 are fixed positive numbers. Since Re ≤ R1 + R2, it is easy to get τ2 ≤ max{I(U; S|A), I(U;Z)}−I(U; S|A). For each m1 ∈ {1, 2, …, 2NR1}, an independent and identically distributed (i.i.d) codeword, bN(m1), is generated according to
. Then, 2NR2 action sequences aN(m1, m2) are i.i.d generated for each bN(m1) according to
, where m2 ∈ {1, 2, …, 2NR2}. For each aN(m1, m2), we generate ||
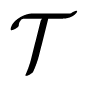
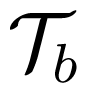
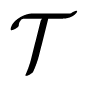
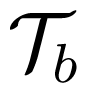
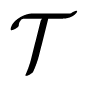
Decoding and error probability analysis
Decoder 1 can decode the message, m1, correctly, since R1 ≤ H(B). For the receiver, he tries to find a unique sequence , such that . It is easy to show the decoding error probabilities Pe1 ≤ ε and Pe2 ≤ ε by similar arguments in [11,12]. We mainly focus on the analysis of equivocation.
Equivocation analysis
where Equation (51) is from the Markov chain (M1, M2) → UN → ZN, and Equation (52) is from that the codewords, uN, are i.i.d and the channels are discrete memoryless.
Next, we bound H(Tb) and H(UN|M1, M2, ZN, Tb). Since ||
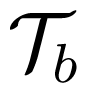
The explanation for bounding is presented as follows. We first show that, given M1, M2 and Tb, the probability of error for ZN to decode UN satisfies Pe ≤ ν. Here, ν is small for sufficiently large N. Given the knowledge of M1, M2 and Tb, the total number of possible codewords of UN is:
where Equation (53) follows from τ2 ≤ max{I(U; S|A), I(U; Z)} − I(U; S|A). Based on Equation (54), we can easily show that a unique codeword uN(m1, m2, tb, tu) exists, such that with high probability. This indicates that the probability of error for ZN to decode UN satisfies Pe ≤ ν. Therefore, by Fano’s inequality, we obtain:
where ν′ is small for sufficiently large N.
Substituting these two results into Equation (52) and utilizing Equation (3), we finish the proof of for the model in Figure 2 with noncausal channel states.
A.1.2. H(A|Z) ≤ I(U; Y ) − max{I(U; Z), I(U; S|A)}
In this case, we need to prove that any rate-equivocation triple (R1, R2, Re) satisfying the following constraints are achievable.
It is sufficient to show that the rate triples (R1, R2, Re = H(A|Z)) are achievable. The coding scheme is as follows.
Codebook generation and encoding
Let
and
, where
are fixed positive numbers. For each m1 ∈ {1, 2, …, 2NR1}, an independent and identically distributed (i.i.d) codeword, bN(m1), is generated according to
. Then, 2NR2 action sequences aN(m1, m2) are i.i.d generated for each bN(m1) according to
, where m2 ∈ {1, 2, …, 2NR2}. For each aN(m1, m2), we generate ||
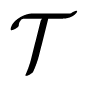
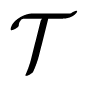
Decoding and error probability analysis
Decoder 1 can decode the message, m1, correctly, since R1 ≤ H(B). For the receiver, he tries to find a unique sequence , such that . It is easy to show the decoding error probabilities Pe1 ≤ ε and Pe2 ≤ ε by similar arguments in [11,12].
Equivocation analysis
We need to prove . The methods in [18] are utilized.
where Equation (56) is from that AN is a function of (M1, M2), and Equation (57) is from that the sequences AN and XN are i.i.d generated and the channels are discrete memoryless.
We complete the proof of Theorem 1.
A.2. Proof of Theorem 2
In this subsection, we prove that all achievable rate triples (R1, R2, Re) for the model in Figure 2 with noncausal channel states are contained in on.
To prove condition in Equation (11), we consider:
where Equation (58) is based on Fano’s inequality.
To prove the condition in Equation (12), we consider:
where Equation (60) is based on Fano’s inequality. Then, the mutual information I(M1, M2; YN) in Equation (60) is calculated as follows.
In the above deduction, Equation (61) is from the Markov chain (M1, M2) → AN → SN. The Equation (62) is from the , which can be derived similarly according to [1] and [18]. The Equation (63) is from the Markov chain . The Equation (64) is from defining .
The condition in Equation (13) is proven as follows.
The condition in Equation (14) is proven as follows.
From Equation (62), we have:
Similarly, we can get:
Substitute Equations (67) and (68) into Equation (66),
where Equation (69) is from the Markov chain and Equation (71) is from defining and Qi = Zi−1.
To serve the single-letter characterization, let us introduce a time-sharing random variable, J, independent of all other random variables and uniformly distributed over {1, 2, …, N}. Set:
Then, substituting the above new random variables into Equations (59), (64) and (71), the conditions in Equations (11), (12) and (14) are verified. From the definition of the auxiliary random variables, the Markov chain Q → V → U → Y → Z is easy to be verified. We complete the proof of Theorem 2.
We note that Dai et al. [18] got an upper bound on Re for the model in Figure 3 as I(U; Y ) − I(V ; Z|Q). Comparing it with our bound on Re, we notice that an extra term, I(U; S|V ), is contained in our bound. The difference between our proof and the proof in [18] about the upper bounds is stated in detail as follows. We both concentrate on zooming H(M1, M2|ZN). In [18], H(M|ZN) was considered, since no embedding information was imposed. From Equation (66),
The two terms in Equation (72) are calculated independently in [18] as:
and:
respectively. Then, the term, I(Ui; Si|Ai), was offset in [18] by subtraction in order to obtain their upper bound. However, the weak aspect of calculating the two terms independently is that the interrelation between the two terms are missed.
In our proof, we focus on calculating I(M1, M2; Y N) − I(M1, M2; ZN). The result is shown in Equation (71). The main difference in the proof steps between our work and [18] is Equations (69) and (70). In the above derivation, we can see that the extra term, I(Ui; Si|Vi), is originated from .
B. Proof of Theorems 3 and 4
In this section, Theorems 3 and 4 are proven. To prove Theorem 3, the methods in [18] are utilized and a coding scheme for the model in Figure 2 with causal action-dependent states is provided in Subsection B.1. Subsection B.2 gives the proof of the outer bound on the capacity-equivocation region.
B.1. Proof of Theorem 3
We need to prove that any achievable rate triple (R1, R2, Re) ∈ ic is achievable. Two cases are considered.
B.1.1. H(A|Z) ≥ I(U; Y ) − I(U; Z)
In this case, we need to prove that any rate-equivocation triple (R1, R2, Re) satisfying the following constraints are achievable.
It is sufficient to show that the rate triples (R1, R2, Re = I(U; Y ) − I(U; Z)) are achievable. The coding scheme includes codebook generation, encoding and decoding. Then, we give the equivocation analysis.
Codebook generation and encoding
Let R1 = H(B) − θ1 and R1 + R2 = I(U; Y ) − θ2, where θ1, θ2 are fixed positive numbers. Since Re ≤ R1 + R2, it is easy to get θ2 ≤ I(U; Z). For each m1 ∈ {1, 2, …, 2NR1}, an independent and identically distributed (i.i.d) codeword, bN(m1), is generated according to
. Then, 2NR2 action sequences aN(m1, m2) are i.i.d generated for each bN(m1) according to
, were m2 ∈ {1, 2, ..., 2NR2}. For each aN(m1, m2), we generate ||
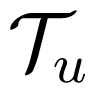
Decoding and error probability analysis
Decoder 1 can decode the message, m1, correctly, since R1 ≤ H(B). For the receiver, he tries to find a unique sequence , such that . It is easy to show the decoding error probabilities Pe1 ≤ ε and Pe2 ≤ ε, and therefore, we omit the proof here. We mainly focus on the analysis of equivocation.
Equivocation analysis
where Equation (73) is from the Markov chain (M1, M2) → UN → ZN, and Equation (74) is from that the codewords, uN, are i.i.d and the channels are discrete memoryless. The conditional entropy, H(UN|M1, M2, ZN), is calculated as follows. Given the message (M1, M2), the number of UN is ||
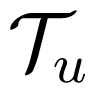
B.1.2. H(A|Z) ≤ I(U; Y ) − I(U; Z)
In this case, we need to prove that any rate-equivocation triple (R1, R2, Re) satisfying the following constraints are achievable.
It is sufficient to show that (R1, R2, Re = H(A|Z)) are achievable. The coding scheme is as follows.
Codebook generation and encoding
Let and , where are fixed positive numbers. For each m1 ∈ {1, 2, …, 2NR1}, an independent and identically distributed (i.i.d) codeword, bN(m1), is generated according to . Then, the 2NR2 action sequences aN(m1, m2) are i.i.d generated for each bN(m1) according to , where m2 ∈ {1, 2, …, 2NR2}. For each aN(m1, m2), a corresponding codeword, uN(m1, m2), is generated according to . To send the message (m1, m2) with the action sequence, aN(m1, m2), and corresponding state sequence sN, the encoder selects the codeword, uN(m1, m2). Then, the input sequence of the channel is generated by .
Decoding and error probability analysis
This step follows similarly from Case A in Section IV.
Equivocation analysis
We need to prove . The methods in [18] are utilized.
where Equation (75) is from that AN is a function of (M1, M2), and Equation (76) is from that the sequences, AN and XN, are i.i.d generated and that the channels are discrete memoryless.
We complete the proof of Theorem 3.
B.2. Proof of Theorem 4
In this subsection, we need to prove that all achievable rate triples (R1, R2, Re) for the model in Figure 2 with causal channel states are contained in on.
The conditions in Equations (16) and (18) follow the same as those of Equations (59) and (65). Therefore, we show Equations (17) and (19) as follows.
To prove the condition in Equation (17), we consider:
where Equation (77) is based on Fano’s inequality and Equation (78) is from defining Ui = (M1, M2, Y i−1, Si−1).
Before proving the condition in Equation (19), we consider:
where Equation (79) is from defining Vi = (M1, M2, Zi−1) and Qi = Zi−1.
Then, utilizing Equations (78) and (79),
where Equation (80) is from Fano’s inequality.
To serve the single-letter characterization, let us introduce a time-sharing random variable, J, independent of all other random variables and uniformly distributed over {1, 2, …, N}. Set:
Then, substituting the above definition into Equations (78) and (81), the conditions in Equations (17) and (19) are verified straightforwardly. From the definition of the auxiliary random variables, the Markov chains Q → V → U → Y → Z and U → A → S are easy to be verified. We complete the proof of Theorem 4.
Conflicts of Interests
The authors declare no conflict of interest.
- Author ContributionXinxing Yin and Zhi Xue did the theoretical work and wrote this paper. All authors have read and approved the final manuscript
References
- Weissman, T. Capacity of channels with action-dependent states. IEEE Trans. Inf. Theory 2010, 56, 5396–5411. [Google Scholar]
- Asnani, H.; Permuter, H.; Weissman, T. Probing capacity. IEEE Trans. Inf. Theory 2011, 57, 7317–7332. [Google Scholar]
- Steinberg, Y.; Weissman, T. The degraded broadcast channel with action-dependent states. Proceedings of the IEEEInternational Symposium on Information Theory (ISIT), Boston, MA, USA, 1–6 July 2012; pp. 596–600.
- Steinberg, Y. The degraded broadcast channel with non-causal action-dependent side information. Proceedings of the IEEE International Symposium on Information Theory (ISIT), Istanbul, Turkey, 7–12 July 2013; pp. 2965–2969.
- Ahmadi, B.; Simeone, O. On channels with action-dependent states. 2012. arXiv:1202.4438 Available online: http://arxiv.org/abs/1202.4438 accessed on 22 July 2012. [Google Scholar]
- Asnani, H.; Permuter, H.; Weissman, T. To observe or not to observe the channel state. Proceedings of the Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 29 September–1 October 2010; pp. 1434–1441.
- Kittichokechai, K.; Oechtering, T.J.; Skoglund, M. Capacity of the channel with action-dependent state and reversible input. Proceedings of IEEE Swedish Communication Technologies Workshop (Swe-CTW), Stockholm, Swedish, 19–21 October2011.
- Kittichokechai, K.; Oechtering, T.J.; Skoglund, M. Coding with action-dependent side information and additional reconstruction requirements. 2012. arXiv:1202.1484 Available online: http://arxiv.org/abs/1202.1484 accessed on 7 February 2012. [Google Scholar]
- Choudhuri, C.; Mitra, U. Action dependent strictly causal state communication. 2012. arXiv:1202.0934. Available online: http://arxiv.org/abs/1202.0934 accessed on 5 February 2012. [Google Scholar]
- Choudhuri, C.; Mitra, U. How useful is adaptive action? Proceedings of the Global Communications Conference, Anaheim, CA, USA, 3–7 December 2012; pp. 2251–2255.
- Ahmadi, B.; Asnani, H.; Simeone, O.; Permuter, H. Information embedding on actions. Proceedings of the IEEE IEEE International Symposium on Information Theory (ISIT), Istanbul, Turkey, 7– 12 July 2013; pp. 186–190.
- Ahmadi, B.; Asnani, H.; Simeone, O.; Permuter, H. Information embedding on actions. 2012. arXiv:1207.6084 Available online: http://arxiv.org/abs/1207.6084 accessed on 25 July 2012. [Google Scholar]
- Petitcolas, F.A.P.; Anderson, R.J.; Kuhn, M.G. Information hiding—A survey. Proc. IEEE 1999, 87, 1062–1078. [Google Scholar]
- Moulin, P.; O’Sullivan, J.A. Information-theoretic analysis of information hiding. IEEE Trans. Inf. Theory 2003, 49, 563–593. [Google Scholar]
- O’Sullivan, J.A.; Moulin, P.; Ettinger, J.M. Information theoretic analysis of steganography. Proceedings of the IEEE International Symposium on Information Theory (ISIT), Cambridge, MA, USA, 16–21 August 1998.
- Zaidi, A.; Vandendorpe, L. Coding schemes for relay-assisted information embedding. IEEE Trans. Inf. Forensics Secur 2009, 4, 70–85. [Google Scholar]
- Zaidi, A.; Piantanida, P.; Duhamel, P. Broadcast- and MAC-aware coding strategies for multiple user information embedding. IEEE Trans. Signal Process 2007, 55, 2974–2992. [Google Scholar]
- Dai, B.; Vinck, A.J.H.; Luo, Y.; Tang, X. Wiretap channel with action-dependent channel state information. Entropy 2013, 15, 445–473. [Google Scholar]
- Dai, B.; Vinck, A.J.H.; Luo, Y. Wiretap channel in the presence of action-dependent states and noiseless feedback. J. Appl. Math 2013, 2013. [Google Scholar] [CrossRef]
- Dai, B.; Luo, Y. Some new results on the wiretap channel with side information. Entropy 2013, 14, 1671–1702. [Google Scholar]
- Le Treust, M.; Zaidi, A.; Lasaulce, S. An achievable rate region for the broadcast wiretap channel with asymmetric side information. Proceedings of the 49th Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 28–30 September 2011; pp. 68–75.
- Gel’fand, S.I.; Pinsker, M.S. Coding for channel with random parameters. Probl. Control Inf. Theory 1980, 9, 19–31. [Google Scholar]
- Cover, T.M. Elements of Information Theory; Wiley: New York, NY, USA, 1991. [Google Scholar]
- El Gamal, A.; Kim, Y. Network Information Theory; Cambridge University Press: New York, NY, USA, 2011. [Google Scholar]
- Csiszár, I.; Köner, J. Information Theory: Coding Theorems for Discrete Memoryless Systems; Academic Press: London, UK, 1981. [Google Scholar]


© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Yin, X.; Xue, Z. Wiretap Channel with Information Embedding on Actions. Entropy 2014, 16, 2105-2130. https://doi.org/10.3390/e16042105
Yin X, Xue Z. Wiretap Channel with Information Embedding on Actions. Entropy. 2014; 16(4):2105-2130. https://doi.org/10.3390/e16042105
Chicago/Turabian StyleYin, Xinxing, and Zhi Xue. 2014. "Wiretap Channel with Information Embedding on Actions" Entropy 16, no. 4: 2105-2130. https://doi.org/10.3390/e16042105