Applied Thermodynamics: Grain Boundary Segregation
Abstract
: Chemical composition of interfaces—free surfaces and grain boundaries—is generally described by the Langmuir–McLean segregation isotherm controlled by Gibbs energy of segregation. Various components of the Gibbs energy of segregation, the standard and the excess ones as well as other thermodynamic state functions—enthalpy, entropy and volume—of interfacial segregation are derived and their physical meaning is elucidated. The importance of the thermodynamic state functions of grain boundary segregation, their dependence on volume solid solubility, mutual solute–solute interaction and pressure effect in ferrous alloys is demonstrated.PACS Codes: 68.35.bd; 68.35.Dv; 68.35.Md; 65.40.gd; 82.65.+r;1. Introduction
The fundamental laws of thermodynamics are applied in many fields of materials science. Their application is particularly important in the field of interfacial segregation, i.e. the accumulation of solute or impurity atoms at an interface. The segregation results in changing bonds at the interface and—in the case of grain boundaries (i.e. interfaces between two differently oriented crystals in a solid)—often in their weakening which results in reduction of material cohesion and consequently, in intergranular brittle fracture leading to irreversible degradation of the material [1]. Although numerous papers published in the last decades provide us with a database of chemical composition of interfaces under specific conditions (for reviews see e.g. [2,3]), it is more desirable to disclose general trends that are capable of predicting materials’ behavior under different thermal and structural conditions using appropriate thermodynamic variables [4,5]. Unfortunately, some thermodynamic data published in literature are of unclear physical meaning and their incorrect interpretation can result in misunderstanding of the fundamentals of interfacial segregation. To avoid this problem, we characterize individual components of the Gibbs energy of grain boundary segregation and consequently, their enthalpy, entropy and volume counterparts, and show the differences among them. Additionally, a reliable application of the basic thermodynamic state functions—the standard enthalpy and entropy of interfacial segregation—as well as of the excess volume is shown.
2. Langmuir–McLean Segregation Isotherm
Of the two different approaches describing interfacial segregation in a general way, i.e. the Gibbs segregation isotherm and the Langmuir–McLean segregation isotherm, the latter is more convenient (and thus applied as well) as it operates with characteristic changes of the Gibbs energy, G (e.g. [1,4,5]). In this approach the segregation of a solute I at an interface Φ in a binary M–I system can be understood as an exchange of the components M and I between Φ and the volume V [6]:
The molar Gibbs energy of “reaction” (1), ΔGr, being the difference of the chemical potentials, (let us note that index j denotes any component in the system throughout the whole paper, i.e. j = I,M here, and ζ = Φ,V), of the right-hand and left-hand terms, is equal to zero in equilibrium [6]:
In Equation (2), , where is the standard chemical potential of pure component j at temperature T and structure of M (for j = M, we use simple notation “M” instead of the notation M(M)), and is the activity of j at ζ. As this definition is applicable to both the crystal volume V and the interface Φ, we obtain:
with the standard molar Gibbs energy of segregation:
The activities in Equation (3) can be replaced by concentrations, , where are the activity coefficients, and are the atomic fractions of components j for ζ = Φ,V. Consequently:
in a binary M–I system, accepting for both, the volume and the interface. In a multicomponent systems with limited amount of segregation sites, i.e. fraction of interface saturation XΦ,sat [2], we may write Equation (5) as:
In Equations (5) and (5a), ΔGI is the Gibbs energy of segregation consisting of two terms, and [1]:
where is the partial molar excess Gibbs energy of segregation [1]:
Equation (5a) with condition (6) represents the general form of the segregation isotherm. It was derived without any non-thermodynamic assumption and, therefore, can be used to describe interfacial segregation independently of the system nature. However, a serious terminological misunderstanding exists as ΔGI in Equations (5) and (5a) is frequently incorrectly called “excess Gibbs energy of segregation”, ΔGxs (e.g. [7]) or ΔGex (e.g. [8]). This ambiguous terminology thus evokes confusion. However, the meaning of excess in the sense of the Lewis theory of non-ideal solutions [9] is the only correct because it represents the deviations between real and ideal behavior (see Equation (6)). In fact, the adjective “interfacial excess” is an unnecessary over-determination because the term interfacial itself already denotes the extra contribution of interfaces with respect to the bulk, and therefore it should not be used in this context [5].
3. Thermodynamic State Functions in Interfacial Segregation and Their Physical Meaning
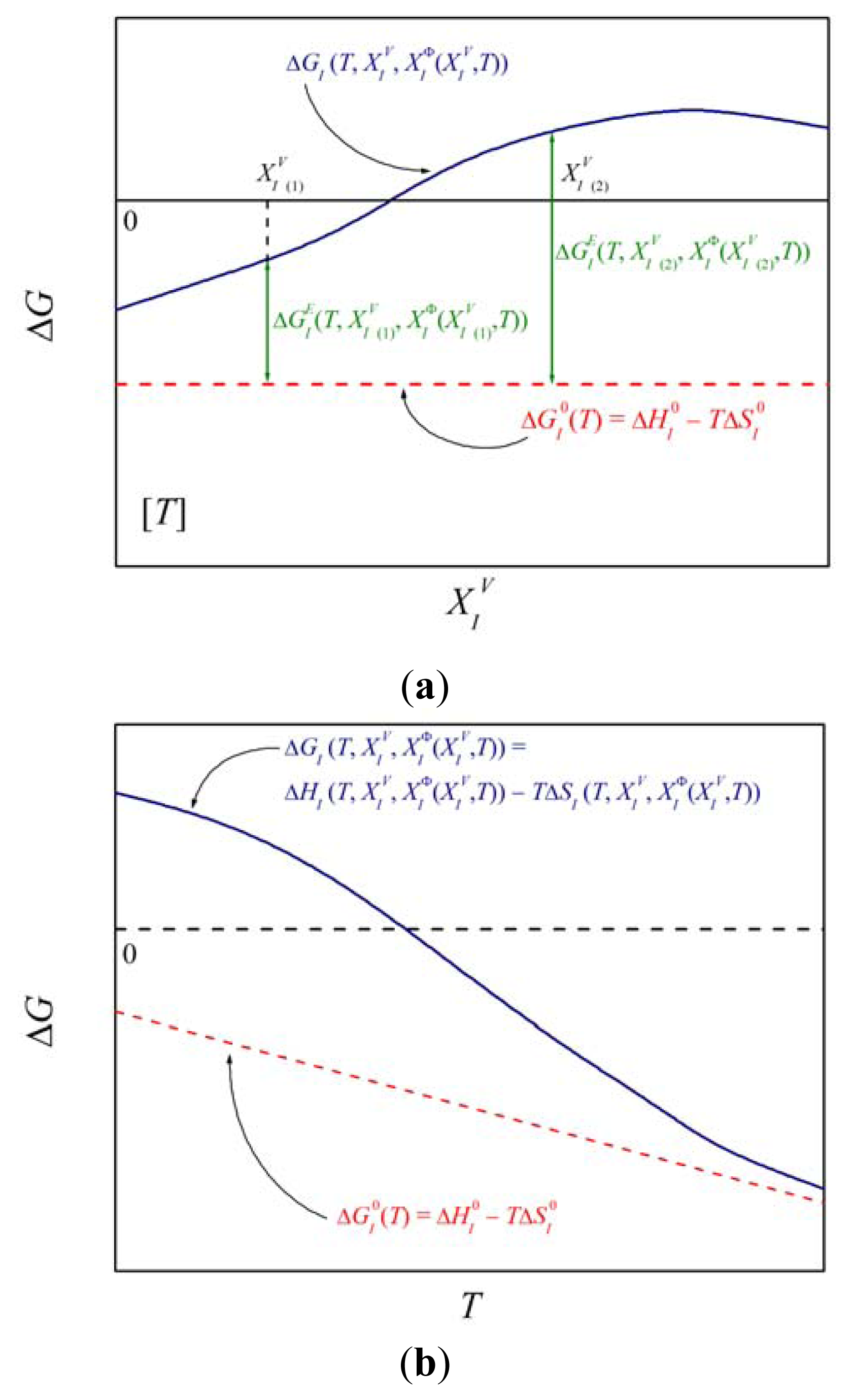
It is evident from the considerations above that there exist three types of thermodynamic state functions of interfacial segregation. In the case of the Gibbs energy, one speaks about the Gibbs energy of segregation, the standard (ideal) Gibbs energy of segregation and the excess Gibbs energy of segregation, the latter characterizing the difference between the Gibbs energy of segregation and the ideal Gibbs energy of segregation. In the following, we will explain the physical meaning of all relevant thermodynamic quantities including the segregation volume which is rarely treated in such a detail.
According to the basic thermodynamic definition:
is composed of the standard molar enthalpy, , and entropy, , of segregation, both of which are defined in the same way as in Equation (4), i.e.:
where and , and and are the respective molar enthalpy and entropy parts of the chemical potentials of solute j at Φ and V. Let us mention that involves all entropy contributions except the configuration entropy [1,5]. As the segregation data are frequently correlated according to the Guttmann model of interfacial segregation in multicomponent systems [10], in which only the summary term (which contains all interaction terms) appears:
where ΔHI and ΔSI are the molar enthalpy and molar entropy of segregation of I at interface Φ.
Application of the fundamental thermodynamic relationship to the grain boundary segregation provides us with [11]:
where σ is the grain boundary energy and A is the grain boundary molar area. According to Equation (11) the molar segregation volume, ΔVI, is defined as:
ΔVI is constructed in the same way as other segregation quantities:
Equation (13) is very close to Equation (1) in Reference [12] for Φ = GB supposing the relaxations terms α and Vr [12] are inherently implemented in the four terms of Equation (13). In the following we will discuss the segregation volume for grain boundaries.
Similarly to ΔGI (Equation (6)), ΔVI also consists of two parts, the standard molar segregation volume, , and the partial molar excess segregation volume, :
As ΔVI is not involved in any model, we will treat this quantity separately later.
Let us note that in some cases the values of the thermodynamic variables are improperly interpreted, resulting in a lack of physical meaning. For example, this is the case when a single value of ΔGI is determined on basis of the measurements of XIΦ at different temperatures (e.g., with Equation (5)) but averaged over the whole temperature range so that it represents an effective value. Similarly, an averaging may be done for systems with different bulk compositions or over numerous interfaces of different crystallography in polycrystals. For details see e.g. References [1,5].
3.1. Thermodynamic State Functions of Interfacial Segregation: ΔGI, ΔHI, ΔSI and ΔVI
Among the state functions of this mode, the Gibbs energy of interfacial segregation, ΔGI, is the most important one as it completely determines interfacial concentration, , at temperature T for bulk atomic fraction, (cf. Equation (5a)). Its importance consists in reflecting the real behavior of the system as indicated by Equation (10). Principally, ΔGI changes not only with changing temperature but also with changing concentrations and due to solute interaction (Figure 1). The corresponding values of ΔHI and ΔSI may also depend on temperature and concentration [1,5]. This means that these values can hardly provide us with any general information, e.g. about the anisotropy of grain boundary segregation, because any orientation dependence of ΔHI and ΔSI varies in a complex way with temperature and composition [1,5].
Besides ΔGI, ΔHI and ΔSI, the segregation volume, ΔVI, may be considered as another variable of equal importance. However, it seems that it has not been included in the description of interfacial segregation till now.
It follows from Equations (5a) and (12), that in case of a binary system M–I [13]:
Integration of Equation (15) results in an expression showing that the segregation volume plays an important role in grain boundary segregation under pressure:
where P0 is the normal pressure. This relationship is principally similar to Equation (4) given by Zhang and Ren [14].
3.2. Standard Molar Thermodynamic Functions of Interfacial Segregation: and
The standard molar thermodynamic state functions possess a special importance in interfacial segregation as they have a very clear physical meaning. According to the definition (Equation (4)), as a combination of standard chemical potentials, is principally independent of concentration (see Figure 1a). only if , i.e. if (Equations (5)–(7)). Certainly this represents a limitation although many systems behave nearly ideally (e.g. phosphorus in dilute Fe–P alloys [15,16]). Moreover, in an infinitesimally diluted solid solution the amount of interfacial solute enrichment is very low. Therefore it is highly probable that the solute atoms segregate at a those sites of the boundary which possess the lowest Gibbs segregation energy. Therefore, characterizes the interfacial segregation of element I at a specific site of interface Φ in the ideal system. and are defined in analogy to with corresponding physical meaning. According to Equations (3) and (8), the standard molar state functions control the relation between the activities at an interface and in the volume in the whole concentration range of a binary M–I system. Similarly to and according to Equations (9a) and (9b), and are concentration independent. Analogously to and , we may define the standard molar specific heat of segregation, , as a combination of molar specific heats of pure substances, and :
The value results from the fact that are insensitive to the presence of structural defects such as dislocations as well as grain boundaries [17], i.e. although an increase of cP was reported in case of nanocrystaline materials [18]. However, the different enhancements of cP of nanocrystalline palladium and copper were ascribed to lower densities of these substances in the nanometer-sized crystalline state [18] representing transition between crystalline and glassy states. In case of a large bicrystal with specified grain boundary we may well accept the relation . Then:
and
It means that and are independent of temperature and is thus a linear function of temperature. As the standard state is defined as pure component j at temperature T and structure of M, and . Consequently, . It means that all non-zero contributions to ΔVI originate from the real behavior of the system ( ). The fact that has a serious consequence for other standard state functions: According to Equation (12) and , both and , and consequently are independent of pressure. The independence of temperature and pressure is a principal property of and which thus change exclusively with the structure (i.e. energy) of the interface (or an interface site) and with the nature of the system. Therefore, and can be used for general purposes, for example, to characterize the anisotropy of interfacial segregation which is directly related to the grain boundary classification [1,5] despite their application is limited to ideal (infinitesimally diluted) systems.
3.3. Excess Thermodynamic Functions of Interfacial Segregation: and
According to Equation (6), the excess molar Gibbs energy of segregation,, represents the difference between real and ideal behavior with respect to interfacial segregation and is exactly defined by the a combination of the activity coefficients (Equation (7)). It is thus evident that depends on composition and non-linearly on temperature (cf. schematic Figure 1b). However, the values of the activity coefficients are unknown and hardly measurable, particularly for interfaces. Therefore, is usually approximated by various models, e.g. by the regular solid solution (Fowler) model for a binary system:
where αIM is the coefficient of binary I–I interaction in M, or by various models for segregation in multicomponent systems, e.g. by the Guttmann model:
with the ternary interaction coefficients, , characterizing the I–J interaction in M, where J represent other solutes in the system [10].
As only the summarizing term is correlated according to the Guttmann model and the quantities and itself do not explicitly appear in the thermodynamic description of interfacial segregation, we will not discuss them.
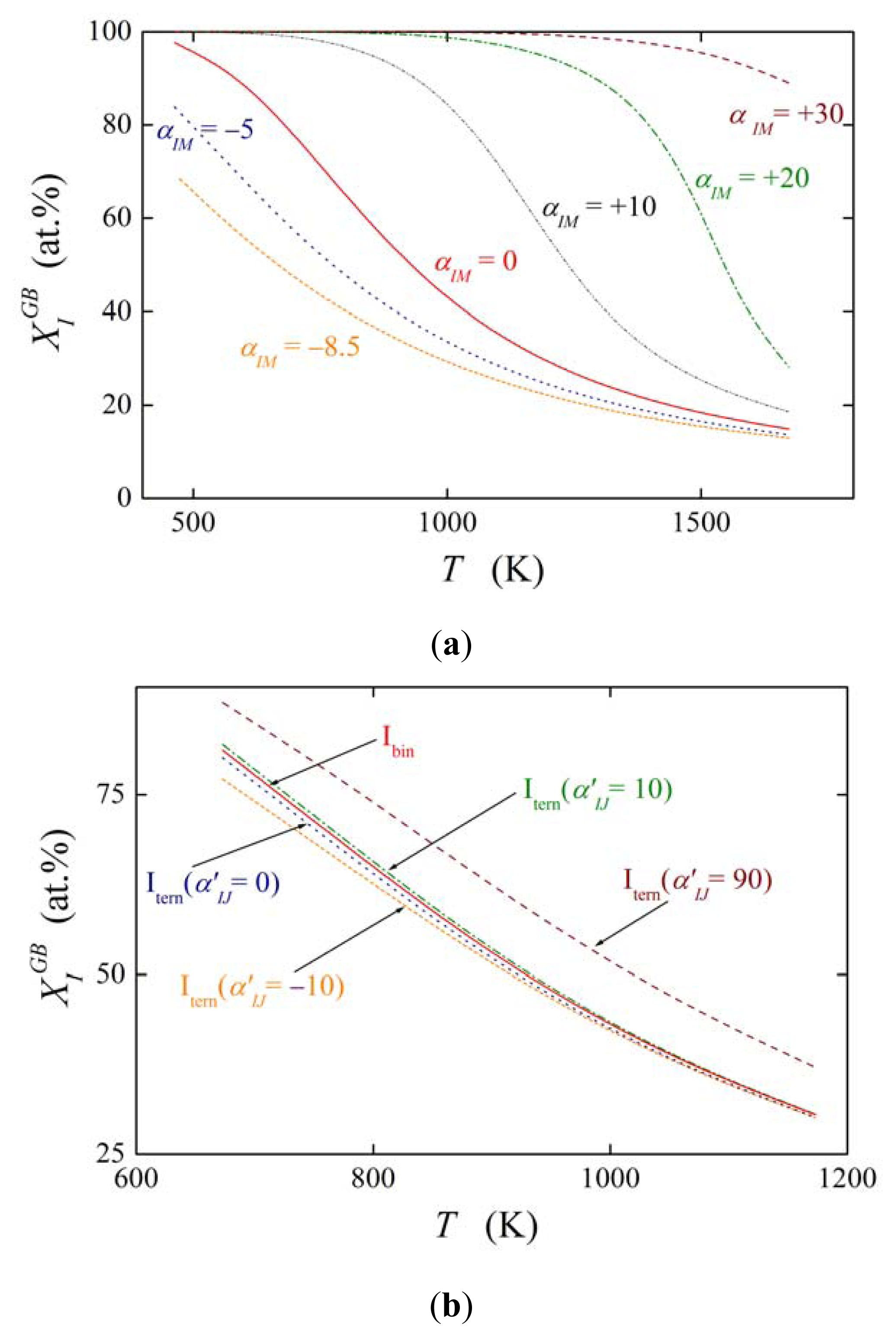
The effect of solute interaction (represented i.e. by ) on grain boundary segregation is displayed in Figure 2. Here, the equilibrium composition is calculated for both the grain boundary of the binary M–I system in the temperature range 473–1673 K according to Equations (5) and (19) assuming a bulk concentration of (i.e. 0.1 at.%), interstitial segregation of I at the grain boundary and the values of and (as for P, Sb and Sn in α-Fe). Figure 2 clearly shows the strong influence of the solute–solute interaction in the binary M–I alloy on the value of . In case of attractive interaction, αIM > 0, the grain boundary concentration of the segregant obviously is increased. Even in case of relatively low values of αIM, e.g. αIM = +10 kJ/mol, the grain boundary enrichment of I is by tens of at.% higher than without interaction (αIM = 0). Repulsive interaction decreases the solute enrichment to a similar extent. This behavior is well understood because repulsive interaction does not allow putting another atom of the same kind in close surrounding of the atom segregated at the interface while attractive interaction exhibits an opposite effect [19]. The effect of ternary interactions ( , Figure 2b) is much less pronounced as that of the binary interactions [20].
Combination of Equations (12), (15) and (19) for a binary alloy with the above condition provides us with:
4. Examples of Application of Thermodynamic State Functions in Interfacial Segregation
4.1. Relationship between and of Grain Boundary Segregation and Volume Solid Solubility
The chemical potential of the solute I at the bulk solid solubility limit, :
is related to the activity at the bulk solid solubility limit, . We can express the Gibbs energy of segregation in an M–I system at the limit of solid solubility, , as:
It follows from the basic thermodynamic relationships that:
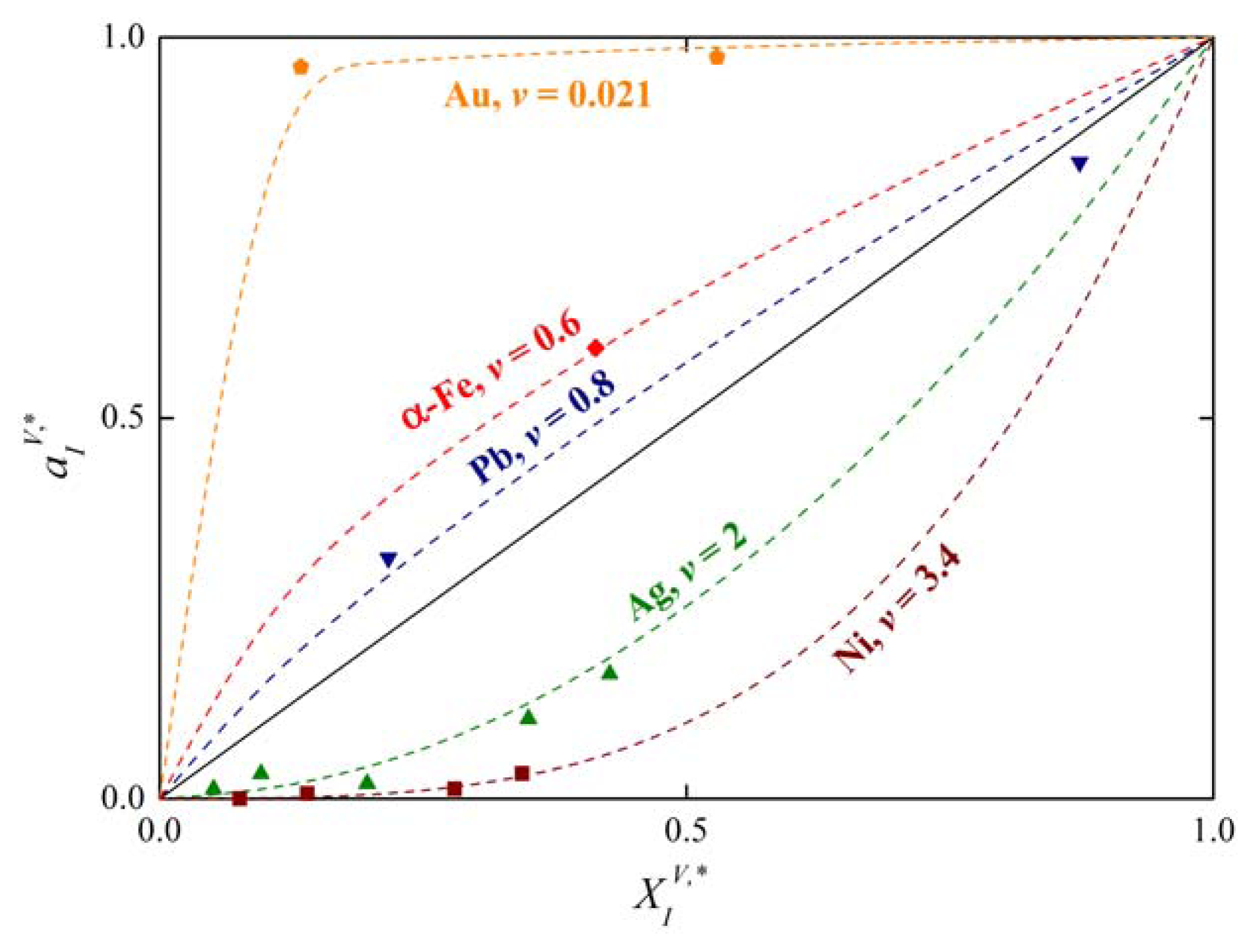
Compilation of numerous literature data [21] shows that the activity of solute I at the solubility limit of numerous elements can be expressed by:
as is apparent in Figure 3. In Equation (25)v is the exponent which is characteristic for the host element. For many binary systems, the product was found to be independent of temperature (Figure 4) [1,22]. It means that if conditions (24) and (25) are fulfilled, and:
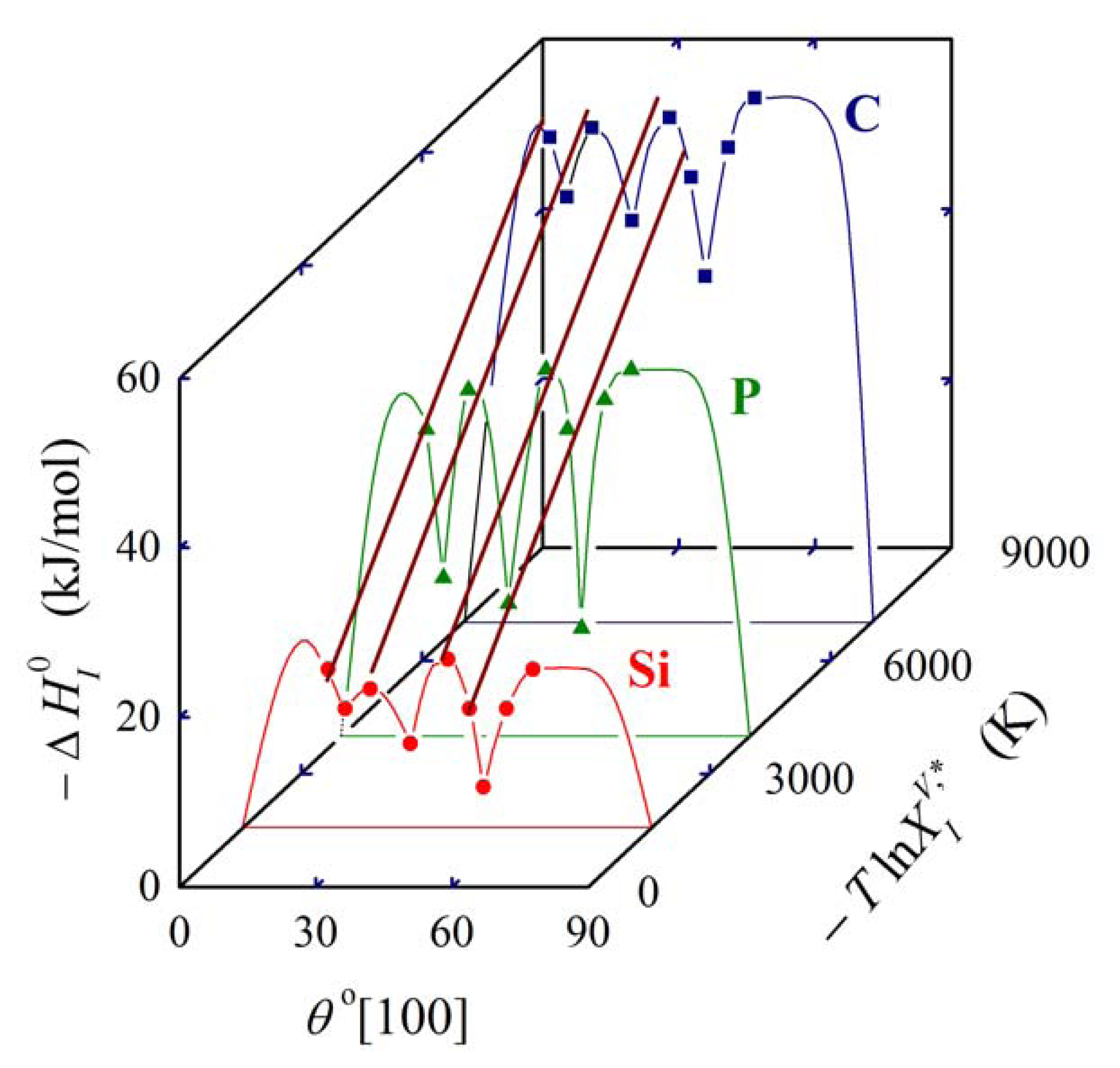
In Equation (27), is the molar enthalpy of segregation of a solute with complete volume solid solubility in solvent M, and the symbol Φ characterizes a specific grain boundary [1,5]. As the product , the above mentioned condition of temperature independence of is preserved. Equation (27) represents an extension and a refinement of the expression , (K = 1.8–10.8) given by Hondros and Seah which relates the grain boundary enrichment ratio to the solid solubility limit [2], and the qualitative idea of Watanabe to extend this simple dependence to account for anisotropy of grain boundary segregation [23] and to construct the so called grain boundary segregation diagram. This idea was later experimentally proved [24]. The grain boundary segregation diagram for solute segregation in α-iron at [100] symmetrical grain boundaries is shown in Figure 5 [1,5].
Analysis of the measured data on segregation of phosphorus, silicon and carbon at individual grain boundaries in α-iron show that the value of the exponent v = 0.77 [1,4,5] which is in good agreement with the value v = 0.6 obtained on basis of Equation (25) from data of Reference [21] (Figure 3). The value of varies from −8 to +8 kJ/mol according to the grain boundary character (the lower value corresponds to highly segregated general grain boundaries while the latter one corresponds to the special grain boundaries characterized by low segregation levels: for a detailed explanation of this characterization see e.g. [1]).
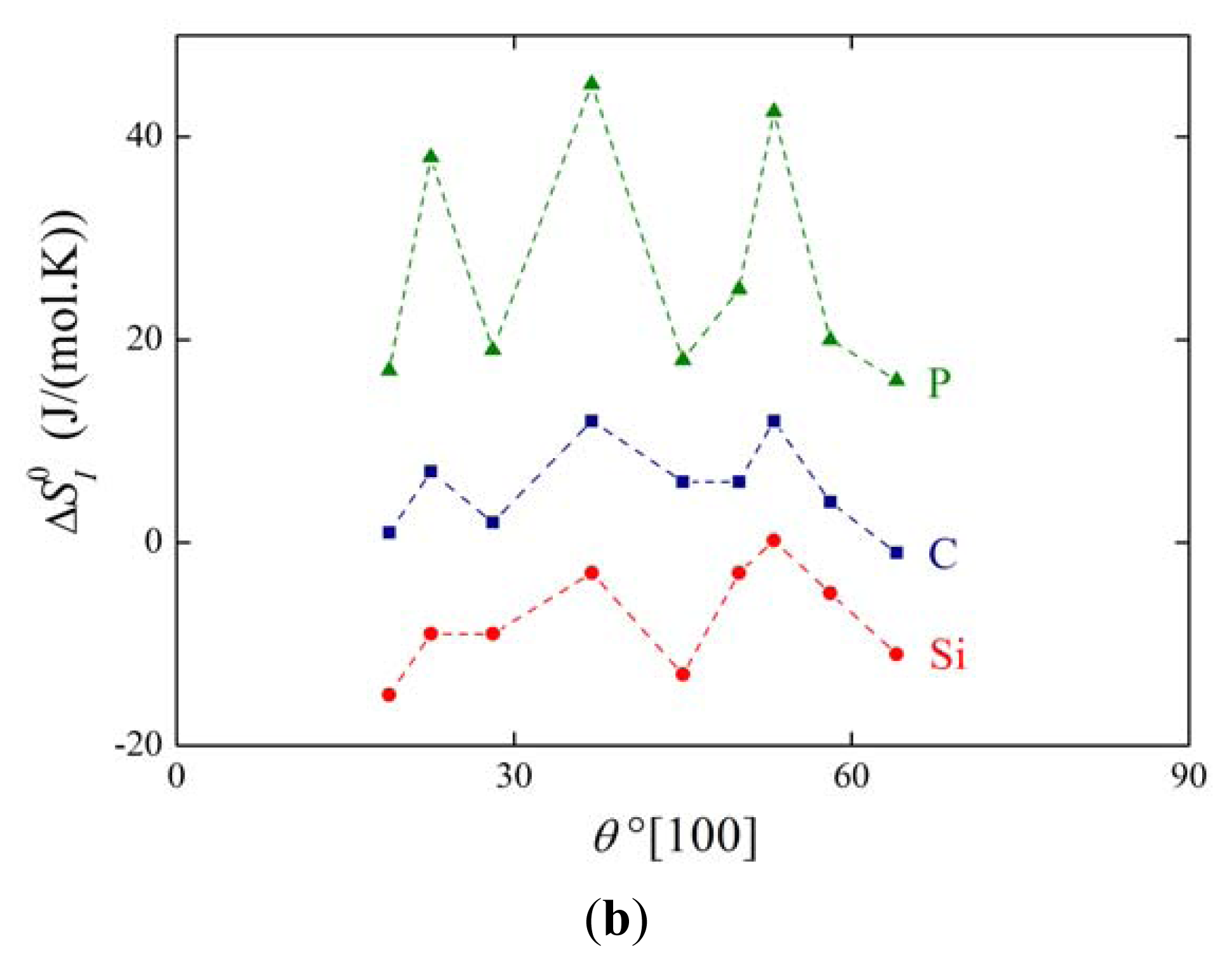
The above mentioned measurements of grain boundary segregation in iron [1,4,5] provided us with the values of both and . As an example, the dependence of and on the misorienation angle for [100] symmetrical grain boundaries is shown in Figure 6. It is obvious that the orientation dependences of and are qualitatively equivalent for all segregating elements.
4.2. Compensation Effect in Grain Boundary Segregation
In principle, we can express the change of the standard molar segregation Gibbs energy of interfacial segregation, , at constant temperature and pressure with a single intensive variable Ψ as [25]:
Analogously, we can express and as:
We may define a temperature TCE as:
at which:
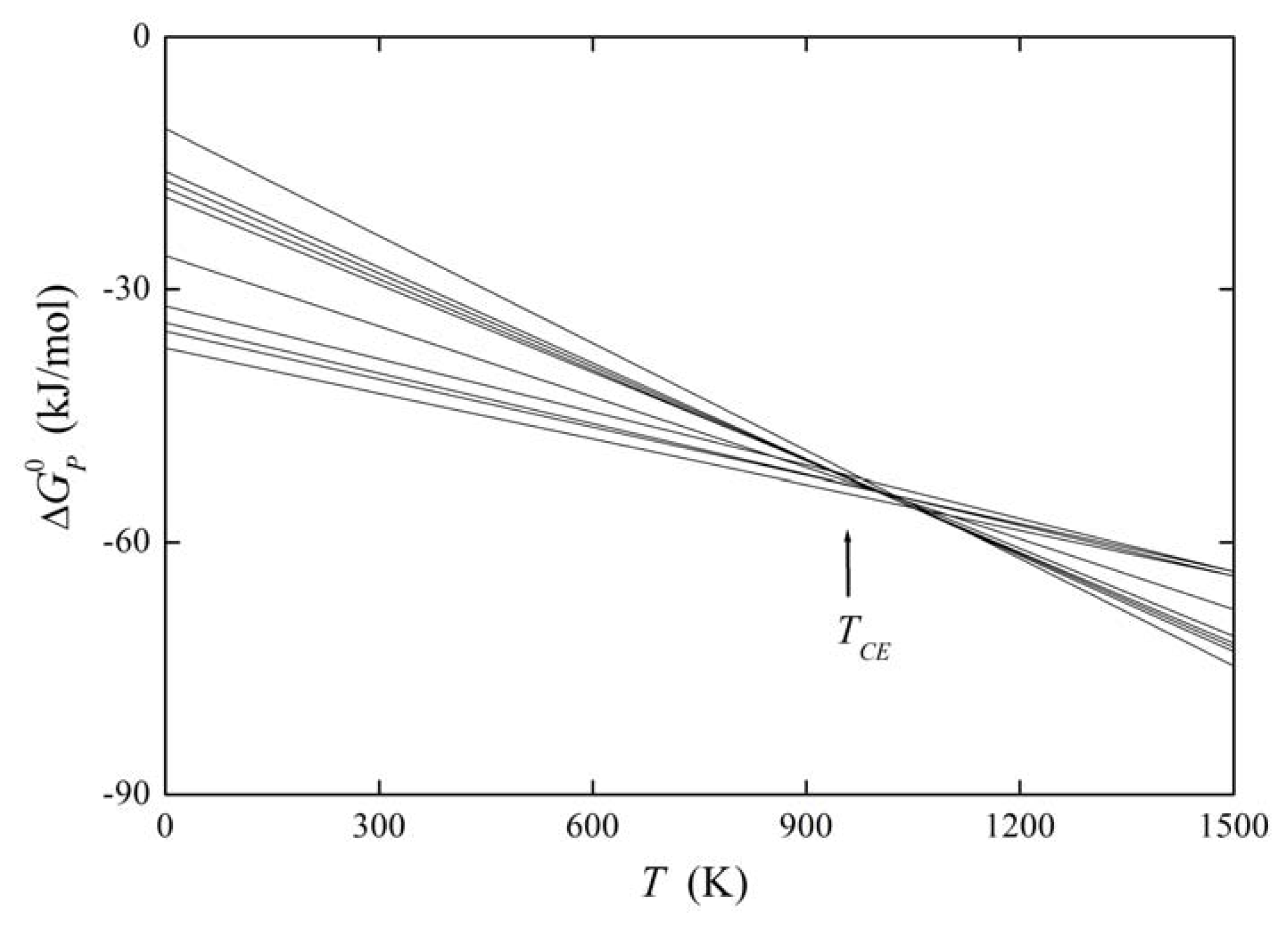
It means that the change of with changing Ψ is compensated by corresponding changes of caused by a change of Ψ. Then TCE is the compensation temperature and the phenomenon is called compensation effect [1,5,26]. If we suppose that Ψ is a variable describing the structure of the grain boundary, we can read Equation (31) as providing us with the constant value of the standard Gibbs energy of a solute at any grain boundary, i.e., all grain boundaries fulfilling the above conditions exhibit the same level of grain boundary segregation. If Ψ represents the nature of the solute, all grain boundaries will exhibit the same value of the grain boundary enrichment ratio, . The former case is documented for example on the basis of experimental data for phosphorus segregation at individual grain boundaries of α-iron in Figure 7. Let us note that condition (31) does not identify a phase transformation characterized by minimum of the Gibbs energy: phase transformation is a sub-category of the compensation effect. At TCE no transformation of the boundaries occurs but they coexist besides each other, despite the temperature changes in the vicinity of TCE [25,27].
Integration of Equation (30) results in [1,5]:
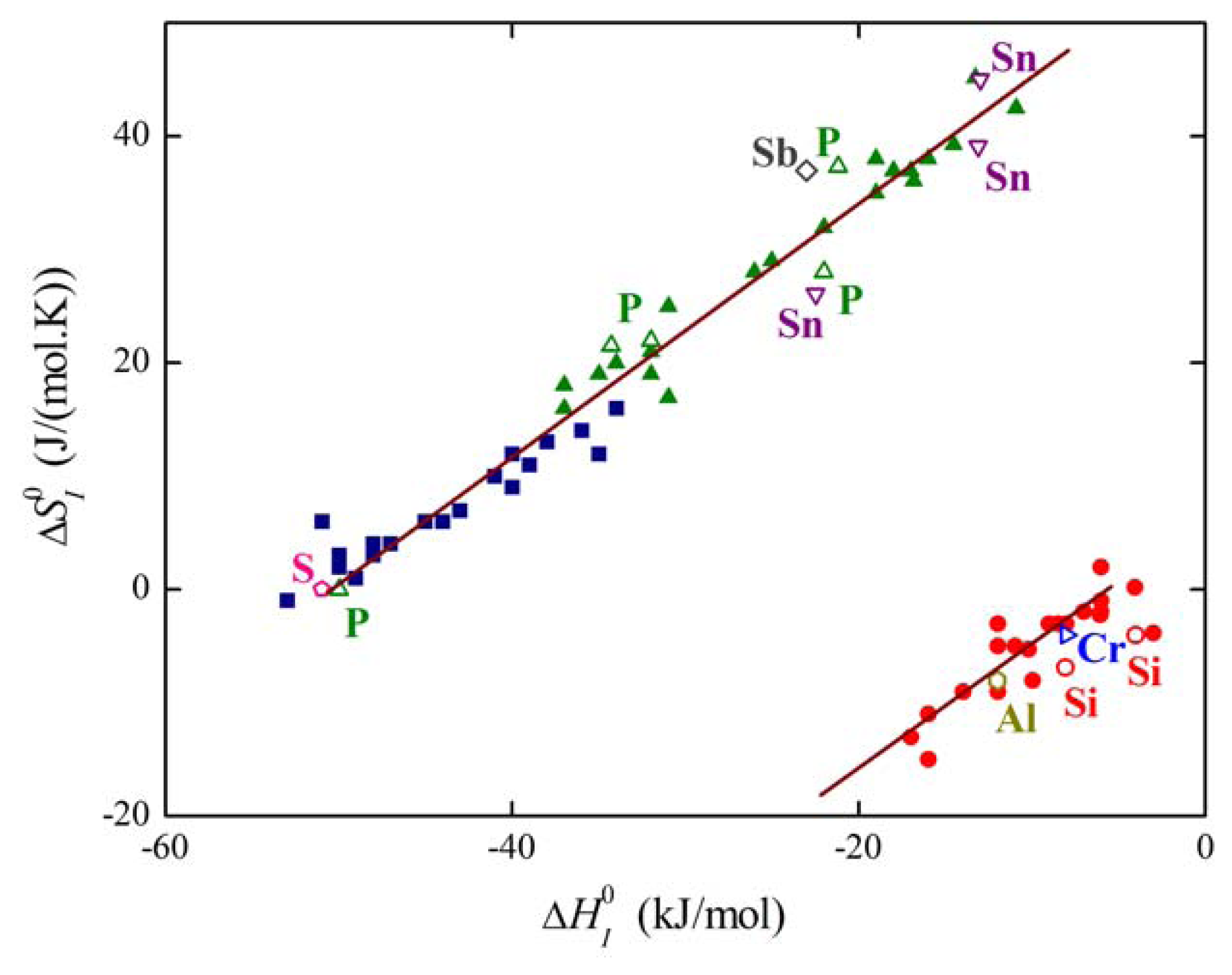
The plot of the relation between and for solute segregation in α-iron is shown in Figure 8. We can distinguish two branches of this dependence: they differ in the type of segregation site: the upper one corresponds to interstitial segregation (ΔS0,CE = 56 J/(mol·K)) while the lower one to substitutional segregation (ΔS0,CE = 5 J/(mol·K)) [1,4,5]. Individual full symbols of the same type correspond to the segregation of a solute at individual grain boundaries in α-iron, empty symbols are data found in literature (for the sources of the data, see [1,5]). Let us note that various solutes segregating at the same type of the site also fit with a single dependence (i.e. with either upper or lower branch in Figure 8). The slope of both dependences corresponds to TCE = 930 K which suggests that the compensation temperature is characteristic for the matrix [1,5,28]. Splitting of the compensation effect into two branches confirms the fact that the compensation effect is only fulfilled if a single mechanism of the phenomenon is active. Therefore, it can be applied to otherwise independent standard quantities and albeit not to ΔHI and ΔSI which additionally change with temperature and composition.
Let us only briefly mention that Equations (27) and (32) with the above mentioned values of and ΔS0,CE can be used to predict the values of and of any element at any grain boundary in α-iron [1,4,5]. It is likely that such prediction may be done for other metallic solvents.
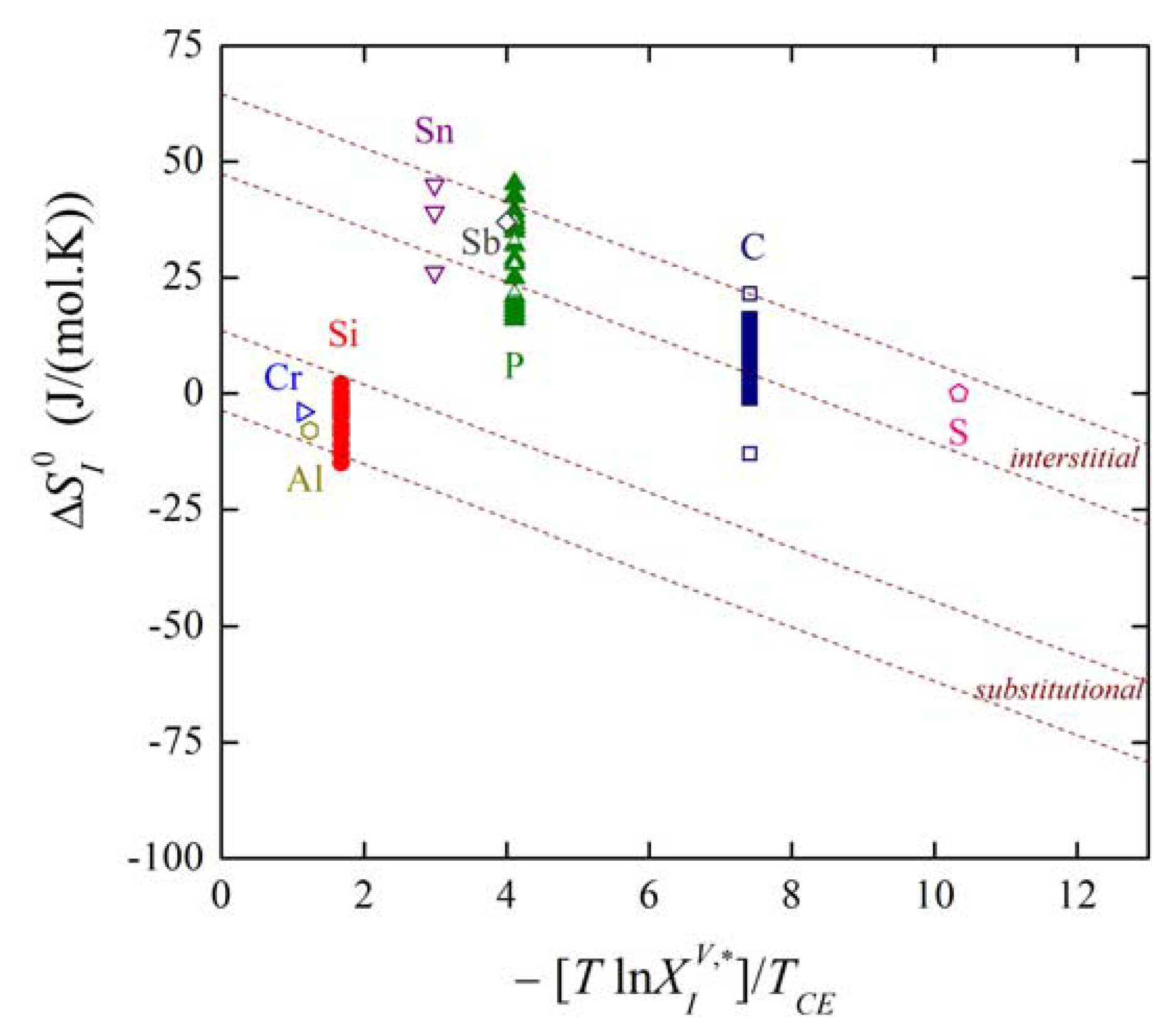
We can also express the dependence of on the volume solid solubility. Combination of Equations (27) and (32) provides us with:
where the notation site refers to the type of segregation, i.e., either interstitial or substitutional. Using the mentioned data, dependence (33) is shown in Figure 9. It is clearly seen that the majority of the experimental data corresponding to both individual grain boundaries (solid symbols) and to grain boundaries in polycrystals found in the literature (empty symbols) fit fairly well to the theoretical lines of individual branches (the upper line of each branch corresponds to special boundaries while the lower one to general boundaries).
The compensation effect was observed not only in case of grain boundary and surface segregation but also for other interfacial properties, such as grain boundary migration and diffusion [5,26,27], and is present in many phenomena of physics, chemistry and biology [25].
4.3. Segregation Volume and Pressure Dependence of Grain Boundary Segregation
During time-dependent experimental studies of non-equilibrium segregation under constant stress, in the beginning a steep change of the grain boundary concentration is observed, followed by the return from an extreme value to a value almost corresponding to that measured without pressure or strain; see e.g. Figure 10 according to Reference [29]).
According to Equation (14) (where we use for simplicity XΦ,sat = XGB,sat = 1, which is often applied in correlation of data on grain boundary segregation [1]), can be obtained from experimental data [29] on pressure/stress dependence of grain boundary segregation of solutes. According to our method [30] the peak-to-peak heights in original Auger spectra were transformed into concentrations supposing simplification of the alloy to a binary Fe–P system. This procedure provides us with the values of XPGB = 0.303 representing the state under normal pressure and XPGB = 0.308 for the state in the stressed sample after equilibration (Figure 10). According to Equation (14) we obtain [13]. Similar value for sulphur was determined from the data of Misra [31] who studied grain boundary segregation of sulphur in a low-alloy steel (doped by 0.01 wt.% S) under plastic stress conditions at 883 K by 343 MPa. However, no changes of XPGB were observed after prolonged annealing of a phosphorus-doped 2.25Cr1Mo steel at 793 K under various loads [32] suggesting and thus, ideal behavior of this system.
The value of can also be estimated in other ways. First, if pure Fe is considered instead of the 2.6NiCrMoV steel [33]. As the average boundary density is of about 50% of the bulk density [33], . Based on the density of FeS (4.82 g/cm3 [34]), if GB is regarded as a Fe-48 at.%S since the atomic fraction of S in 2.6NiCrMoV is 48 at.% after stress-aging for 20 h [35]. Then , and . On the other hand, the values of and were calculated using the density functional theory technique for segregation of S, P and Se, respectively, at {012} grain boundary in Ni [36].
The value of of the order of 10−6–10−5 m3/mol may seem to be low. It suggests that the pressure dependence of ΔGI and consequently of is rather low: Even the value of under pressure/stress of 100 MPa causes a decrease of ΔGI by −1 kJ/mol which represents a change of in the order of several percent. This also explains why the equilibrium segregation under pressure only slightly differs from that under normal pressure [29] (see Figure 10).
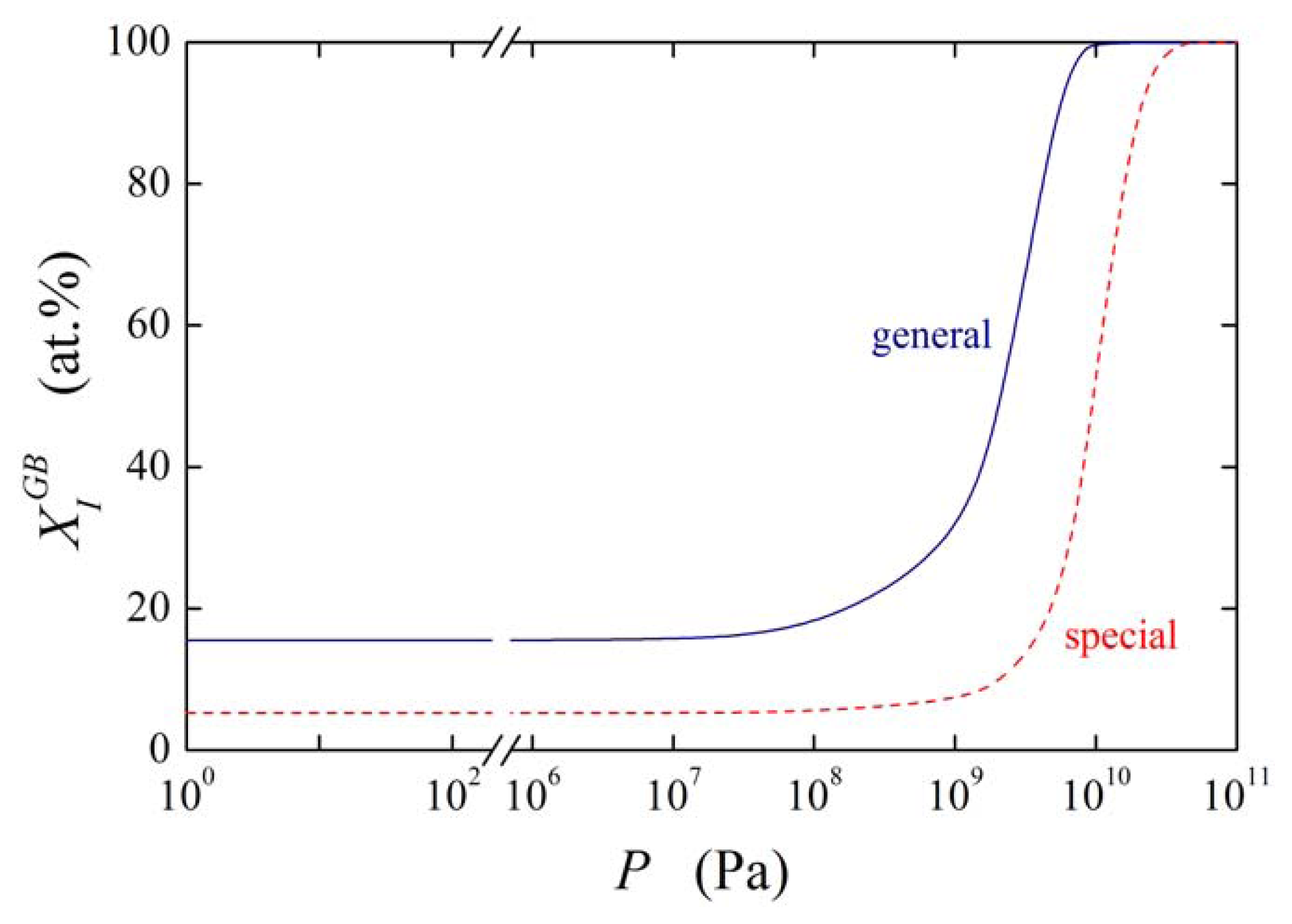
Let us now consider the effect of on in more detail. Supposing the values and (these values may represent e.g. phosphorus segregation in bcc iron [1]) and , the grain boundary concentration of the solute under normal pressure at temperature of 800 K is (i.e. 15.54 at.%). The pressure dependence of the calculated is plotted in Figure 11 for the values of ranging from −8 × 10−6 m3/mol to 0. It is obvious from Figure 11 that starts to change when the pressure is higher than 10 MPa: under these higher pressures the increase of becomes quite steep. We may conclude that although the effect of elastic deformation on grain boundary segregation is small the grain boundary segregation significantly changes with increasing pressure. At high hydrostatic pressures (P > 10 GPa) this effect is rather large: In this case, the equilibrium grain boundary concentration should reach the values up to 100 at.% (cf. Figure 11) [13]. However, during such treatment many other processes occur in the material, e.g. dynamic recrystallization, which will influence the final segregation level; in the present modeling these effects were not taken into account.
Similarly to the basic thermodynamic state variables of segregation ( and ; cf. Figure 6) we may expect that will be anisotropic. Supposing and , and with describe segregation of I at general and special grain boundary, respectively, the pressure dependence of for both types of the grain boundaries at 800 K is shown in Figure 12 for . As expected, the segregation level is lower at the special grain boundary compared to the general one. The concentration change at the special grain boundary requires higher pressure. However, its increase may seem to be surprisingly steeper than in case of the general grain boundary. In both cases a complete saturation of the grain boundary is reached under ultimate pressures.
The segregation volume depends on various intensive variables. We will document it for example of and T. Differentiation of Equation (15) provides us with:
The first term at the right-hand side (in front of the brackets) is positive as well as the first (left) one in the brackets (supposing that less than half of the saturation limit is segregated) as increases with increasing both pressure and . The sign of (i.e. slope of the concentration dependence of the segregation volume) will depend on the value of the term . Intuitively, we may expect the decrease of (i.e. increase of its absolute value) with increasing (and thus with increasing ). For this case, should be positive and prevail over the first term in the brackets on the right hand side of Equation (34). In analogy to Equation (34), the dependence of on temperature is characterized by:
We may expect that (negative) value of increases with increasing temperature and reaches the value at high temperatures (e.g. close to the melting point). To bring this expectation in accordance with Equation (35), the term in the complex brackets should be positive. As is positive and negative (segregation decreases with increasing temperature), the term in the edge brackets on the right-hand side of Equation (35) is negative. Therefore, on the right-hand side of Equation (35) must be negative and of higher absolute value than the other term in the complex brackets. Then .
Based on Equation (21) we may demonstrate the effect of pressure on the Fowler interaction coefficient, αIM (cf. Equation (19)), as:
Supposing XGB,sat = 1 and , we obtain:
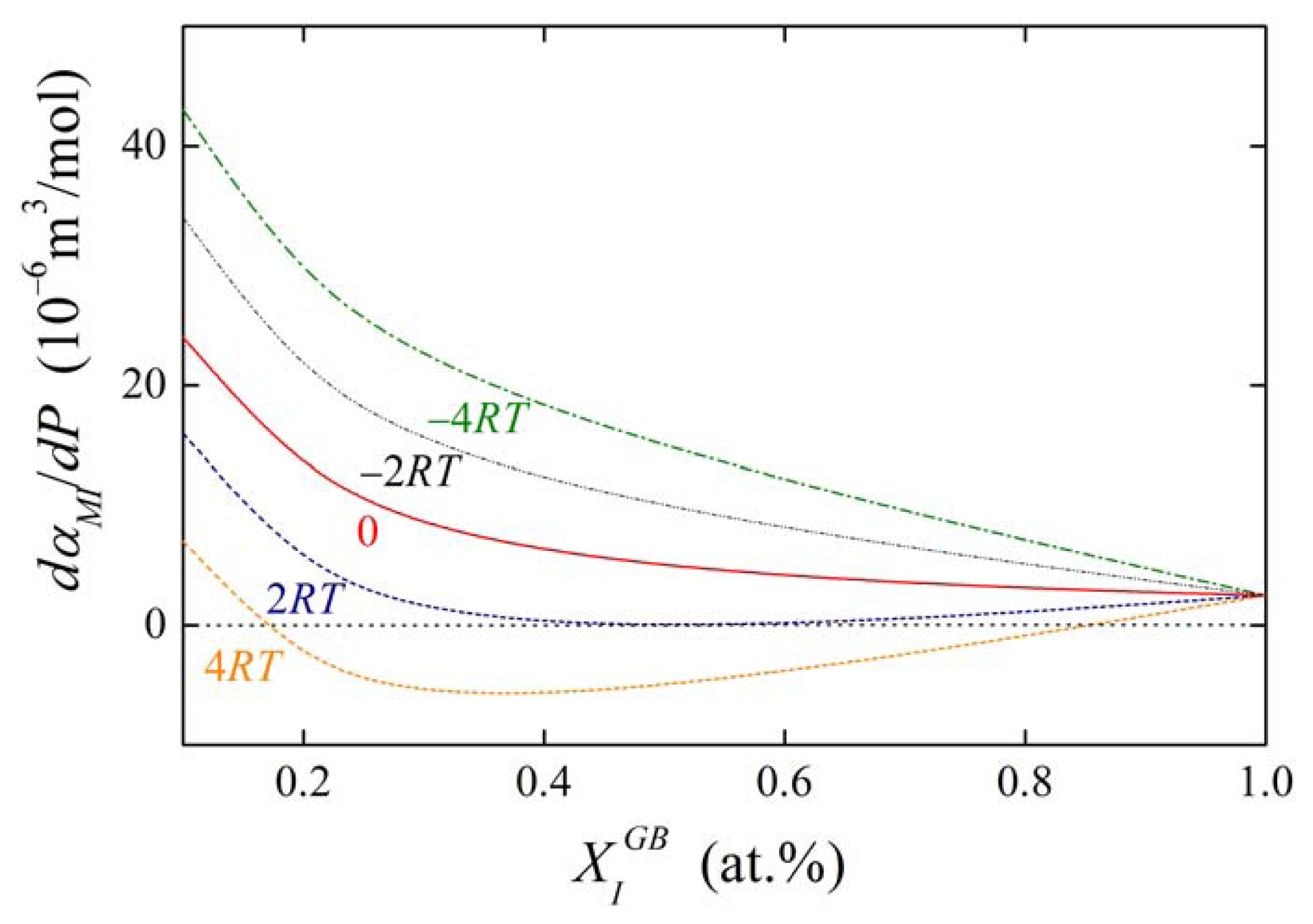
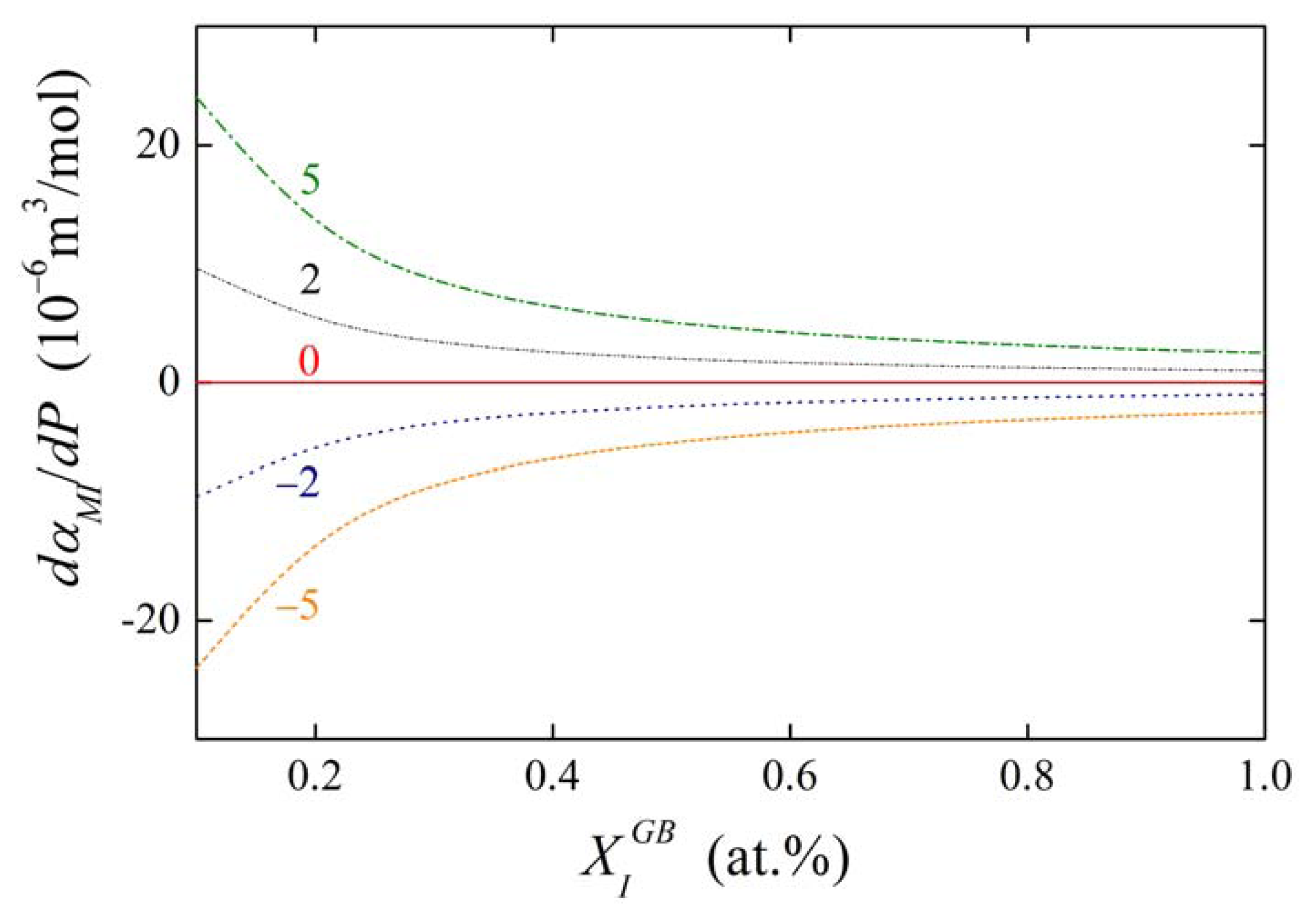
The concentration dependences of the value of dαIM/dP for various values of αIM and are shown in Figures 13 and 14. It is obvious that the value of the fraction on the right-hand side of Equations (36) and (37) is of the order of units in case of high grain boundary concentrations. It means that the value of dαIM/dP is of the same order as , i.e. at the level of 10−6 m3/mol. This suggests that a change of αIM by 1 kJ/mol results in an apparent change of when pressure or stress reaches values of the order of hundreds of MPa. The change of αIM with pressure is more pronounced for low grain boundary concentrations, however, the interaction in case of the dilute alloys can be neglected (cf. Equation (19)). It means that, usually, the pressure change of the interaction coefficient can be neglected.
5. Conclusions
Application of basic thermodynamics to a field of material science with important practical consequences—interfacial segregation—is presented in detail. Based on the Langmuir–McLean segregation isotherm, individual modes of thermodynamic intensive variables—which are used to describe this phenomenon—are discussed from the point of view of their physical meaning together with their potential for application. To the best of our knowledge, the segregation volume is fully defined and discussed for the first time here. It is shown that the standard molar segregation volume is zero at any temperature according to the definition of the standard states while the partial molar excess segregation volume reaches non-zero values in real systems. It is concluded that the grain boundary segregation is not affected by pressure in ideal systems whereas the real systems exhibit apparent pressure dependence. The dependences of the standard molar enthalpy of segregation on the bulk solid solubility and the enthalpy–entropy compensation effect are displayed to enable formulation of a relationship between the standard molar entropy of grain boundary segregation and the volume bulk solid solubility. In addition, a fundamental relationship is derived between the segregation excess volume and pressure changes of the grain boundary concentration of the segregant, and various important consequences of the segregation volume are established.
Acknowledgments
This work was supported by the Czech Science Foundation (Projects No. GAP108/12/0144 (PL) and GAP108/12/0311 (MŠ)), by the Project CEITEC—Central European Institute of Technology (CZ.1.05/1.1.00/02.0068) from the European Regional Development Fund (MŠ), by the Academy of Sciences of the Czech Republic (Institutional Project RVO:68081723 (MŠ)), by the National Natural Science Foundation of China (Project No. 51001011 (LZ)) and by the Fundamental Research Funds for the Central Universities (Project No. FRF-TP-12-042A (LZ)).
Conflicts of Interest
The authors declare no conflict of interest.
- Author ContributionsThis paper was prepared in close cooperation of all four co-authors: Pavel Lejček and Siegfried Hofmann provided the main contribution to the thermodynamics of grain boundary segregation and its anisotropy including the enthalpy–entropy compensation effect. Pavel Lejček and Lei Zheng elaborated the idea of the segregation volume which was later completed by Mojmír Šob for the theoretically calculated data. Pavel Lejček wrote the draft of the article which was critically revised by all other co-authors and finalized in the agreement of all co-authors. All co-authors also approved the final version.
References
- Lejček, P. Grain Boundary Segregation in Metals; Springer: Heidelberg, Germany, 2010. [Google Scholar]
- Hondros, E.D.; Seah, M.P. Segregation to interfaces. Int. Met. Rev 1977, 22, 262–299. [Google Scholar]
- Johnson, W.C., Blakely, J.M., Eds.; Interfacial Segregation; ASM: Metals Park, OH, USA, 1979.
- Lejček, P.; Hofmann, S. Thermodynamics and structural aspects of grain boundary segregation. Crit. Rev. Solid State Mater. Sci 1995, 20, 1–85. [Google Scholar]
- Lejček, P.; Hofmann, S. Thermodynamics of grain boundary segregation and applications to anisotropy, compensation effect and prediction. Crit. Rev. Solid State Mater. Sci 2008, 33, 133–163. [Google Scholar]
- DuPlessis, J. Surface segregation. Solid State Phenom 1990, 11, 1–125. [Google Scholar]
- Wynblatt, P.; Chatain, D. Anisotropy of segregation at grain boundaries and surfaces. Metall. Mater. Trans 2006, 37, 2595–2620. [Google Scholar]
- Polak, M.; Rubinovich, L. The interplay of surface segregation and atomic order in alloys. Surf. Sci. Rep 2000, 38, 127–194. [Google Scholar]
- Lewis, G.N.; Randall, M. Thermodynamics; McGraw–Hill: New York, NY, USA, 1923. [Google Scholar]
- Guttmann, M.; McLean, D. Grain boundary segregation in multicomponent systems. In Interfacial Segregation; Johnson, W.C., Blakely, J.M., Eds.; ASM: Metals Park, OH, USA, 1979; pp. 261–348. [Google Scholar]
- Sutton, A.P.; Balluffi, R.W. Interfaces in Crystalline Solids; Clarendon: Oxford, UK, 1995. [Google Scholar]
- Lojkowski, W. Evidence for pressure effect on impurity segregation in grain boundaries and interstitial grain boundary diffusion mechanism. Defect Diffus. Forum 1996. [Google Scholar]
- Lejček, P.; Zheng, L.; Meng, Y. Excess volume in grain boundary segregation. J. Surf. Anal 2014, 20, 198–201. [Google Scholar]
- Zhang, T.-Y.; Ren, H. Solute concentrations and strains in nanograined materials. Acta Mater 2013, 61, 477–493. [Google Scholar]
- Erhart, H.; Grabke, H.J. Equilibrium segregation of phosphorus at grain boundaries of Fe–P, Fe–C, Fe–Cr–P, and Fe–Cr–C–P alloys. Metal Sci 1981, 15, 401–408. [Google Scholar]
- Janovec, J.; Grman, D.; Perháčová, J.; Lejček, P.; Patscheider, J.; Ševc, P. Thermodynamics of phosphorus grain boundary segregation in polycrystalline low-alloy steels. Surf. Interf. Anal 2000, 30, 354–358. [Google Scholar]
- Cottrell, A.H. Theoretical Physical Metallurgy; Edward Arnold, Publ: London, UK, 1959. [Google Scholar]
- Rupp, J.; Birringer, R. Enhanced specific-heat-capacity (cp) measurements (150–300 K) of nanometer-sized crystalline materials. Phys. Rev. B 1987, 36, 7888–7890. [Google Scholar]
- Lejček, P. Effect of solute interaction on interfacial segregation and grain boundary embrittlement in binary alloys. J. Mater. Sci 2013, 48, 2574–2580. [Google Scholar]
- Lejček, P. Effect of ternary solute interaction on interfacial segregation and grain boundary embrittlement. J. Mater. Sci 2013, 48, 4965–4972. [Google Scholar]
- Hultgren, R., Desai, P., Hawkins, D., Gleiser, M., Kelley, K., Eds.; Selected Values of the Thermodynamic Properties of Binary Alloys; ASM: Metals Park, OH, USA, 1973.
- Kubaschewski, O. Iron—Binary Phase Diagrams; Springer: Berlin, Germany, 1987. [Google Scholar]Massalski, T.B. Binary Alloy Phase Diagrams; ASM: Metals Park, OH, USA, 1987. [Google Scholar]Predel, B. Phase Equilibria of Binary Alloys; Springer: Berlin, Germany, 2003. [Google Scholar]
- Watanabe, T.; Kitamura, S.; Karashima, S. Grain boundary hardening and segregation in α-iron–tin alloy. Acta Metal 1980, 28, 455–463. [Google Scholar]
- Hofmann, S.; Lejček, P. Correlation between segregation enthalpy, solid solubility and interplanar spacing of ∑ = 5 tilt grain boundaries in α-iron. Scripta Metall. Mater 1991, 25, 2259–2262. [Google Scholar]
- Lejček, P. Enthalpy–entropy compensation effect in grain boundary phenomena. Z. Metallkd. Int. J. Mater. Res. Adv. Tech 2005, 96, 1129–1133. [Google Scholar]
- Gottstein, G.; Shvindlerman, L.S. Grain Boundary Migration in Metals; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Lejček, P. Is the compensation effect a phase transition? Solid State Phenom 2008, 138, 339–346. [Google Scholar]
- Lejček, P.; Jäger, A.; Gärtnerová, V. Reversed anisotropy of grain boundary properties and its effect on grain boundary engineering. Acta Mater 2010, 58, 1930–1937. [Google Scholar]
- Shinoda, T.; Nakamura, T. A model for the applied stress effects on the intergranular phosphorus segregation in ferrous materials. Acta Metall 1981, 29, 1637–1644. [Google Scholar]
- Lejček, P. On the determination of surface composition in Auger electron spectroscopy. Surf. Sci 1988, 202, 493–508. [Google Scholar]
- Misra, R.D.K. Issues concerning the effect of applied tensile stress on intergranular segregation in a low alloy steel. Acta Mater 1996, 44, 885–890. [Google Scholar]
- Song, S.-H.; Wu, J.; Weng, L.-Q.; Liu, S.-J. Phosphorus grain boundary segregation under different applied tensile stress levels in a Cr–Mo low alloy steel. Mater. Lett 2010, 64, 849–851. [Google Scholar]
- Jorra, E.; Franz, H.; Peisl, J.; Petry, W.; Wallner, G.; Birringer, R.; Gleiter, H.; Haubold, T. Small-angle neutron scattering from nanocrystalline Pd. Phil. Mag. B 1989, 60, 159–168. [Google Scholar]
- Speight, J.G. Lange’s Handbook of Chemistry; McGraw-Hill: New York, USA, 2005; Table 4–1. [Google Scholar]
- Xu, T.D. Grain-boundary anelastic relaxation and non-equilibrium dilution induced by compressive stress and its kinetic simulation. Phil. Mag 2007, 87, 1581–1599. [Google Scholar]
- Všianská, M.; aŠob, M. Central European Institute of Technology, CEITEC MU, Masaryk University: Brno, Czech Republic, Unpublished data; 2013.

 ) or compressive (
) or compressive (
 ) stress of 30 MPa (according to Reference [29]).
) stress of 30 MPa (according to Reference [29]).
 ) or compressive (
) or compressive (
 ) stress of 30 MPa (according to Reference [29]).
) stress of 30 MPa (according to Reference [29]).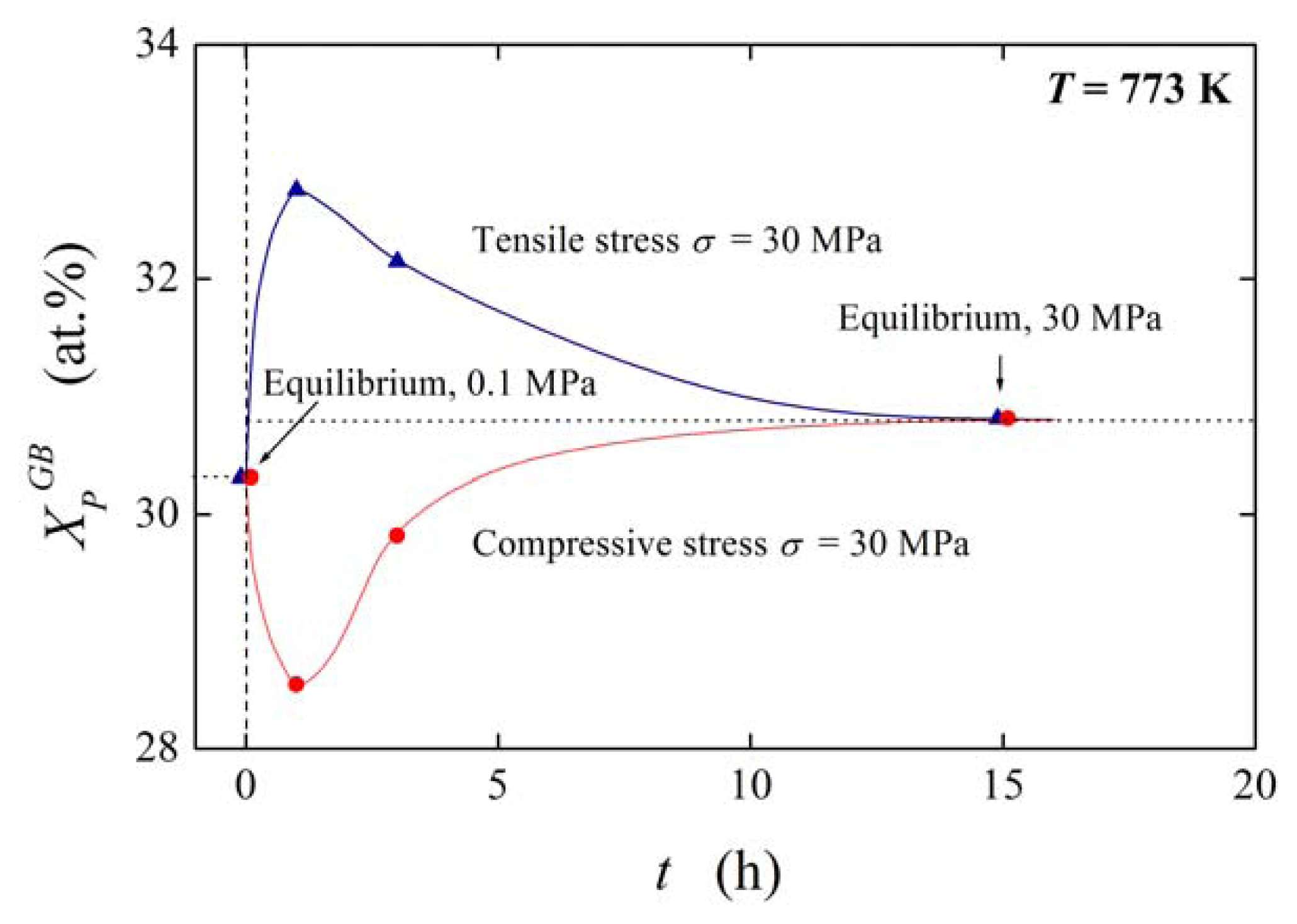

© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lejček, P.; Zheng, L.; Hofmann, S.; Šob, M. Applied Thermodynamics: Grain Boundary Segregation. Entropy 2014, 16, 1462-1483. https://doi.org/10.3390/e16031462
Lejček P, Zheng L, Hofmann S, Šob M. Applied Thermodynamics: Grain Boundary Segregation. Entropy. 2014; 16(3):1462-1483. https://doi.org/10.3390/e16031462
Chicago/Turabian StyleLejček, Pavel, Lei Zheng, Siegfried Hofmann, and Mojmír Šob. 2014. "Applied Thermodynamics: Grain Boundary Segregation" Entropy 16, no. 3: 1462-1483. https://doi.org/10.3390/e16031462




