An Evolutionary Algorithm for the Texture Analysis of Cubic System Materials Derived by the Maximum Entropy Principle
Abstract
:1. Introduction
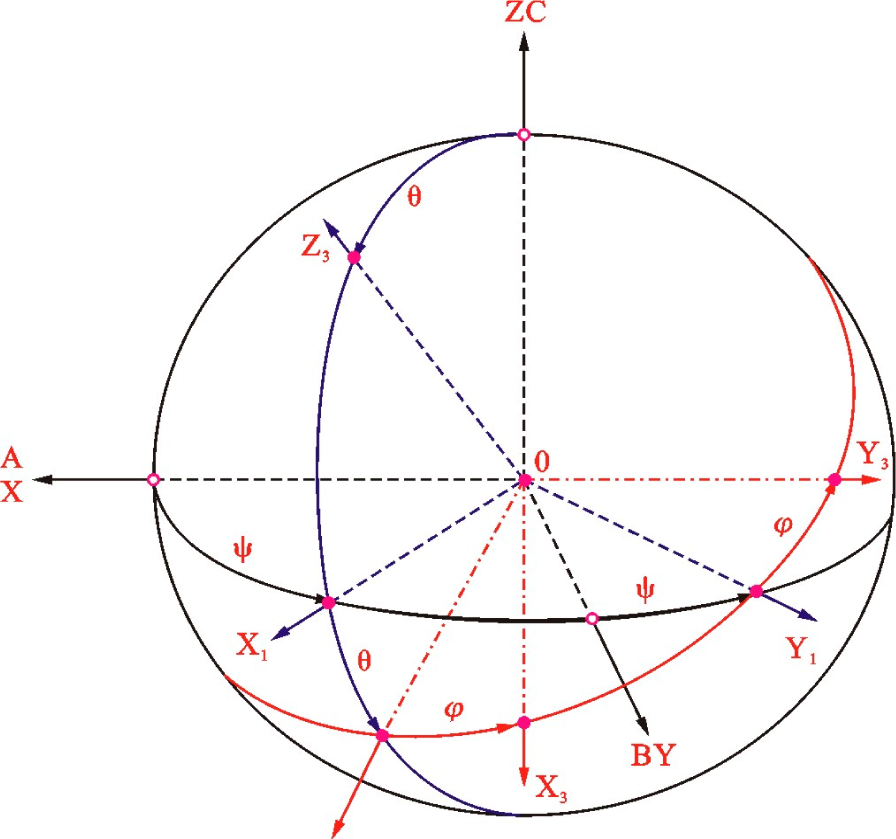
2. General Principle Description
2.1. ODF Representation Derived by MEM
2.2. Differential Evolution Algorithm
2.2.1. Initialization
2.2.2. Mutation
2.2.3. Crossover
2.2.4. Selection
 |
3. Experimental Results and Discussion
3.1. ODF Representation on Aluminum Foils
3.2. ODF Representation on IF-steel Sheets
4. Conclusions
- The complete ODF derived by differential evolution is entirely feasible due to its simple parameterization scheme, whose primary texture component is endowed with the configuration pattern in more details with much less iteration rounds.
- The differential evolution algorithm is suitable for solving the nonlinear equations of quantitative texture analysis, which is proposed in this article for the ODF representation on the cubic textured materials.
- Differential evolution is characterized by global optima to provide better computation results via much less iterations in comparison with those deduced by conventional damped Newton iteration, which shows a universal optimization mechanism for quantitative texture analysis that follows the maximum entropy principle.
Acknowledgments
Appendix
A. Analysis of the Reduced ODF(R-ODF) via Two-step Method
B. Analysis of the Complete ODF(C-ODF) via the Maximum Entropy Method
Author Contributions
Conflicts of Interest
References
- Harris, G.B. Quantitative measurement of preferred orientation in rolled Uranium. Philos. Mag 1952, 43, 113–123. [Google Scholar]
- Bunge, H.J. Mathematische Methoden der Texturanalyse; Akademie-Verlag: Berlin, Germany, 1969; pp. 36–52. [Google Scholar]
- Bunge, H.J. Texture Analysis in Materials Science; Buttleworths: London, UK, 1982; pp. 102–165. [Google Scholar]
- Heizmann, J.J.; Laruelle, C. Simultaneous measurement of several X-ray pole figures. J. Appl. Cryst 1986, 19, 467–472. [Google Scholar]
- Kock, U.F.; Tome, C.N.; Wenk, H.R. Texture and Anisotropy: Preferred Orientation in Polycrystals and Their Effect on Materials Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 2005; pp. 36–58. [Google Scholar]
- Liang, Z.; Xu, J.; Wang, F. Three Dimensional Orientation Analysis on Textured Materials—ODF Analysis; Northeastern University of Technology Press: Shenyang, China, 1986; pp. 80–116. [Google Scholar]
- Roe, R.J.; Krigbaum, W.R. Description of crystallite orientation in polycrystal materials III. General solution to pole figure inversion. J. Appl. Phys 1965, 36, 2024–2031. [Google Scholar]
- Matthies, S. Reproducibility of the orientation distribution function of texture samples from pole figures (ghost phenomena). Phys. Status Solidi B 1979, 92, 135–138. [Google Scholar]
- Matthies, S.; Vinel, G.W. On the reproduction of the orientation distribution function of texturized samples from reduced pole figures using the conception of a conditional ghost correction. Phys. Status Solidi B 1982, 112, 111–114. [Google Scholar]
- Matthies, S.; Wenk, H.R. ODF reproduction with conditional ghost correction. In Preferred Orientation in Deformed Metals and Rocks: An Introduction to Modern Texture Analysis; Wenk, H.R., Ed.; Academic Press Inc: New York, NY, USA, 1985; pp. 139–147. [Google Scholar]
- Matthies, S.; Wenk, H.R.; Vinel, G.W. Some basic concepts of texture analysis and comparison of three methods to calculate orientation distributions from pole figures. J. Appl. Crystallogr 1988, 21, 285–304. [Google Scholar]
- Schaeben, H. Entropy optimization in quantitative texture analysis. J. Appl. Phys 1988, 64, 2236–2237. [Google Scholar]
- Wang, F.; Xu, J.; Liang, Z. Inverse pole figure determination according to the maximum entropy method. Proceedings of Textures of Materials ICOTOM-8: The Eighth International Conference on Textures of Materials, Santa Fe, NM, USA; 1987. [Google Scholar]Kallend, J.S.; Cottstein, G. (Eds.) The Metallurgical Society; Warrendale, PA, USA, 1988; pp. 111–114.
- Wang, F.; Xu, J.; Liang, Z. Determination of the ODF of hexagonal symmetry materials according to the maximum entropy method. Textures Microstruct 1989, 10, 217–226. [Google Scholar]
- Wang, F.; Xu, J.; Liang, Z. Application of maximum entropy method to the inverse pole figure determination of cubic materials. J. Appl. Cryst 1991, 24, 126–128. [Google Scholar]
- Wang, F.; Xu, J.; Liang, Z. Determination of the cubic system materials by the maximum-entropy method. Textures Microstruct 1992, 19, 55–58. [Google Scholar]
- McIntyre, N.S.; Pratt, A.R.; Piao, H.; Maybury, D.; Splinter, S.J. Resolution enhancement of X-ray photoelectron spectra by maximum entropy de-convolution. Appl. Surf. Sci 1999, 144, 156–160. [Google Scholar]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep 2006, 426, 1–45. [Google Scholar]
- Sankaran, S.; Zabaras, N. A maximum entropy approach for property prediction of random microstructures. Acta Mater 2006, 54, 2265–2276. [Google Scholar]
- Abramov, R.V. An improved algorithm for the multidimensional moment-constrained maximum entropy problem. J. Comput. Phys 2007, 226, 621–644. [Google Scholar]
- Li, H.S. Maximum entropy method for probabilistic bearing strength prediction of pin joints in composite laminates. Compos. Struct 2013, 106, 626–634. [Google Scholar]
- Wang, H.; Liu, F.; Ehlen, G.J.; Herlach, D.M. Application of the maximal entropy production principle to rapid solidification: A multi-phase-field model. Acta Mater 2013, 61, 2617–2627. [Google Scholar]
- Tseng, C.Y.; Tuszynski, J. Maximum entropy in drug discovery. Entropy 2014, 16, 3754–3768. [Google Scholar]
- Harte, J.; Newman, E.A. Maximum information entropy: A foundation for ecological theory. Trends Ecol. Evol 2014, 29, 384–389. [Google Scholar]
- Martyushev, L.M.; Seleznev, V.D. The restrictions of the maximum entropy production principle. Physica A 2014, 410, 17–21. [Google Scholar]
- Harremoës, P.; Topsøe, F. Maximum entropy fundamentals. Entropy 2001, 3, 191–226. [Google Scholar]
- Puig, B.; Akian, J.L. Non-Gaussian simulation using Hermite polynomials expansion and maximum entropy principle. Probab. Eng. Mech 2004, 19, 293–305. [Google Scholar]
- Zhao, Q.; Kurata, H. Use of maximum entropy principle with Lagrange multipliers extends the feasibility of elementary mode analysis. J. Biosci. Bioeng 2010, 110, 254–261. [Google Scholar]
- Guo, C.; Li, F. An improved algorithm for support vector clustering based on maximum entropy principle and kernel matrix. Expert Syst. Appl 2011, 38, 8138–8143. [Google Scholar]
- Fogel, D.B. Evolutionary Computation: Toward a New Philosophy of Machine Intelligence, 3rd ed.; IEEE Press: New York, NY, USA, 2006; pp. 34–65. [Google Scholar]
- Hrstka, O.; Kucerova, A. Improvements of real coded genetic algorithms based on differential operators preventing premature convergence. Adv. Eng. Softw 2004, 35, 237–246. [Google Scholar]
- Rainer, S.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim 1997, 11, 341–359. [Google Scholar]
- Price, K.; Storn, R.; Lampinen, J. Differential Evolution—A Practical Approach to Global Optimization; Springer-Verlag: Berlin, Germany, 2005; pp. 19–45. [Google Scholar]
- Ali, M.M.; Torn, A. Population-set based global optimization algorithms: Some modifications and numerical studies. Comput. Oper. Res 2004, 10, 1703–1725. [Google Scholar]
- Kaelo, P.; Ali, M.M. A numerical study of some modified differential evolution algorithms. Eur. J. Oper. Res 2006, 169, 1176–1184. [Google Scholar]
- Bergey, P.K.; Ragsdale, C. Modified differential evolution: A greedy random strategy for genetic recombination. Omega 2005, 33, 255–265. [Google Scholar]
- Back, T.; Schwefel, H.P. An overview of evolutionary algorithms for parameter optimization. Evol. Comput 1993, 1, 1–23. [Google Scholar]
- Yao, X.; Liu, Y.; Lin, G. Evolutionary programming made faster. IEEE Trans. Evol. Comput 1999, 3, 82–102. [Google Scholar]
- Storn, R. System design by constraint adaptation and differential evolution. IEEE Trans. Evol. Comput 1999, 3, 22–34. [Google Scholar]
- Liang, K.H.; Yao, X.; Newton, C.S. Adapting self-adaptive parameters in evolutionary algorithms. Appl. Intell 2001, 15, 171–180. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. Lett 1957, 106, 620–630. [Google Scholar]
- Böhlke, T. Application of the maximum entropy method in texture analysis. Comput. Mater. Sci 2005, 32, 276–283. [Google Scholar]
- Böhlke, T. Texture simulation based on tensorial Fourier coefficients. Comput. Struct 2006, 84, 1086–1094. [Google Scholar]
- Junk, M.; Budday, J.; Böhlke, T. On the solvability of maximum entropy moment problems in texture analysis. Math. Models Methods Appl. Sci 2012, 22. [Google Scholar] [CrossRef]
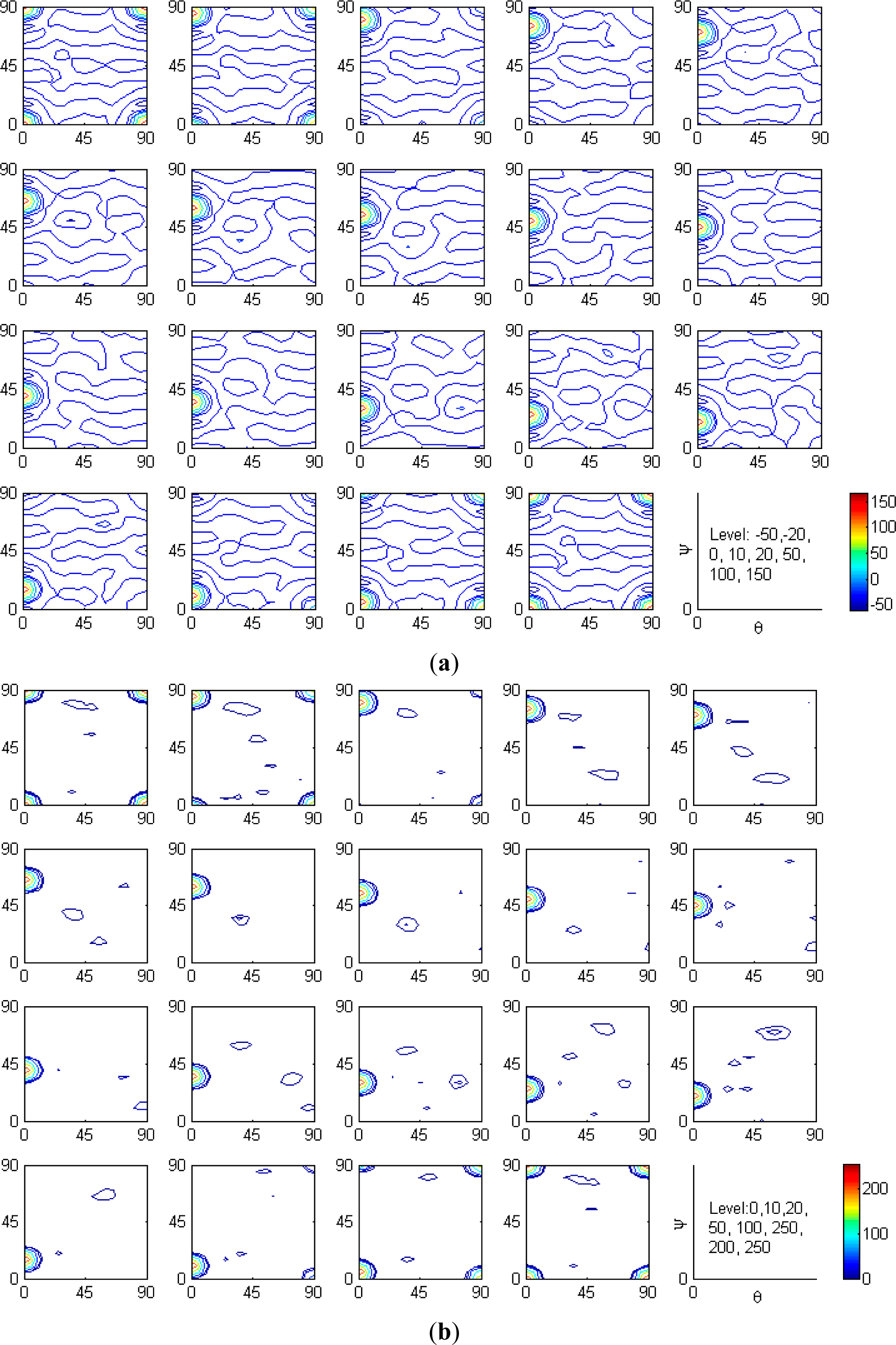
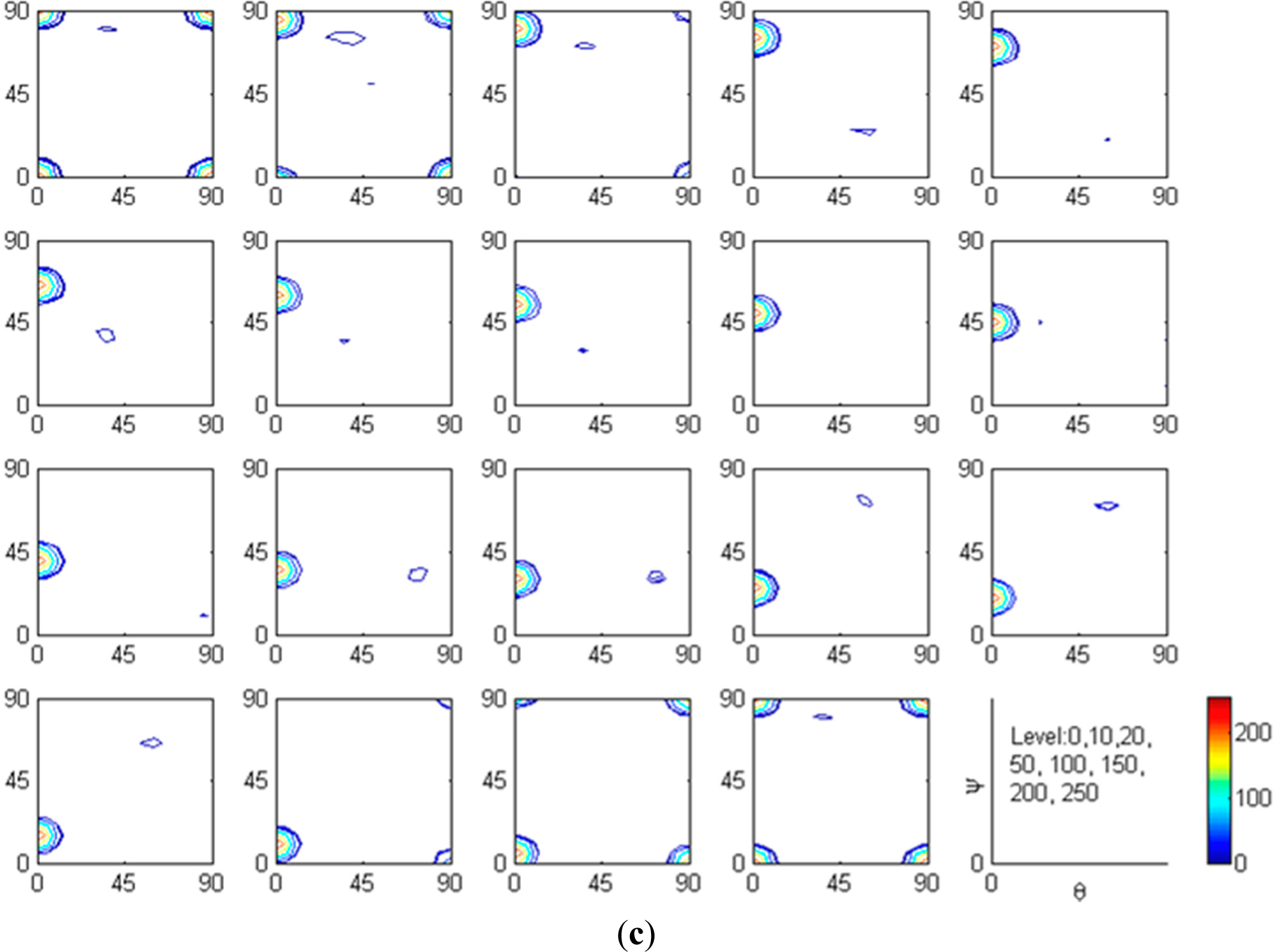

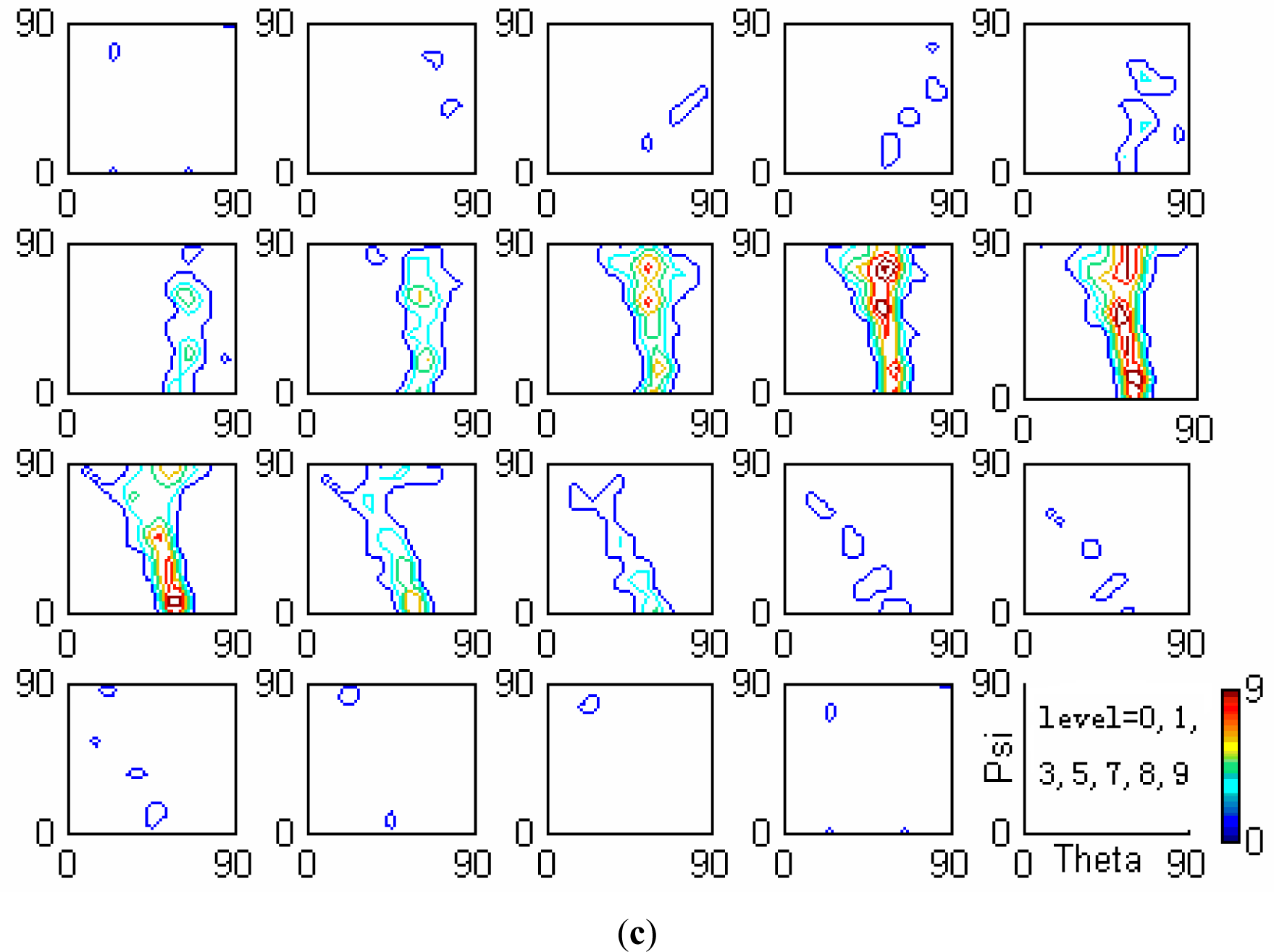
| Gmax | Maximum iteration number
| |||||
|---|---|---|---|---|---|---|
| 50 | 100 | 200 | 600 | 1000 | 4000 | |
| Objective values, Smin | 5.19 × 10−2 | 2.09 × 10−2 | 1.76 × 10−3 | 4.91 × 10−4 | 1.05 × 10−4 | 7.62 × 10−5 |
| CPU time, t (s) | 3.205 | 6.795 | 12.895 | 29.940 | 63.245 | 234.125 |
| ωmax | 283.07 | 281.95 | 263.50 | 265.97 | 264.96 | 265.95 |
| Gmax | Maximum iteration number
| |||||
|---|---|---|---|---|---|---|
| 50 | 100 | 200 | 500 | 1000 | 5000 | |
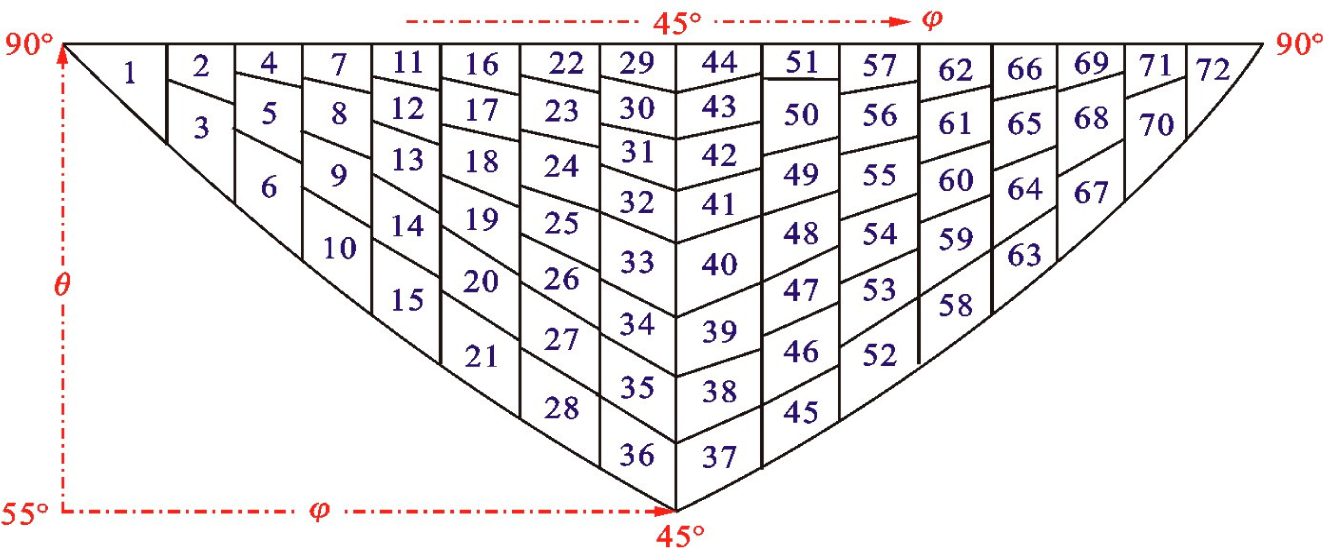
| φ = 45° section in details | 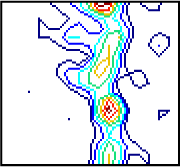 |  |  | 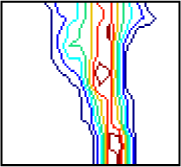 | 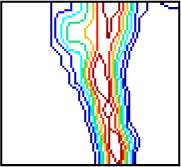 |  |
| Objective values, Smin | 5.19 × 10−2 | 2.09 × 10−2 | 3.76 × 10−3 | 4.97 × 10−4 | 1.35 × 10−4 | 3.94 × 10−5 |
| CPU time(s) | 3.205 | 6.795 | 12.895 | 29.940 | 83.765 | 312.350 |
| ωmax | 11.36 | 11.04 | 10.42 | 9.75 | 9.81 | 10.03 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Wang, D.; Wu, B.; Wang, F.; Liang, Z. An Evolutionary Algorithm for the Texture Analysis of Cubic System Materials Derived by the Maximum Entropy Principle. Entropy 2014, 16, 6477-6496. https://doi.org/10.3390/e16126477
Wang D, Wang D, Wu B, Wang F, Liang Z. An Evolutionary Algorithm for the Texture Analysis of Cubic System Materials Derived by the Maximum Entropy Principle. Entropy. 2014; 16(12):6477-6496. https://doi.org/10.3390/e16126477
Chicago/Turabian StyleWang, Dapeng, Dazhi Wang, Baolin Wu, Fu Wang, and Zhide Liang. 2014. "An Evolutionary Algorithm for the Texture Analysis of Cubic System Materials Derived by the Maximum Entropy Principle" Entropy 16, no. 12: 6477-6496. https://doi.org/10.3390/e16126477




