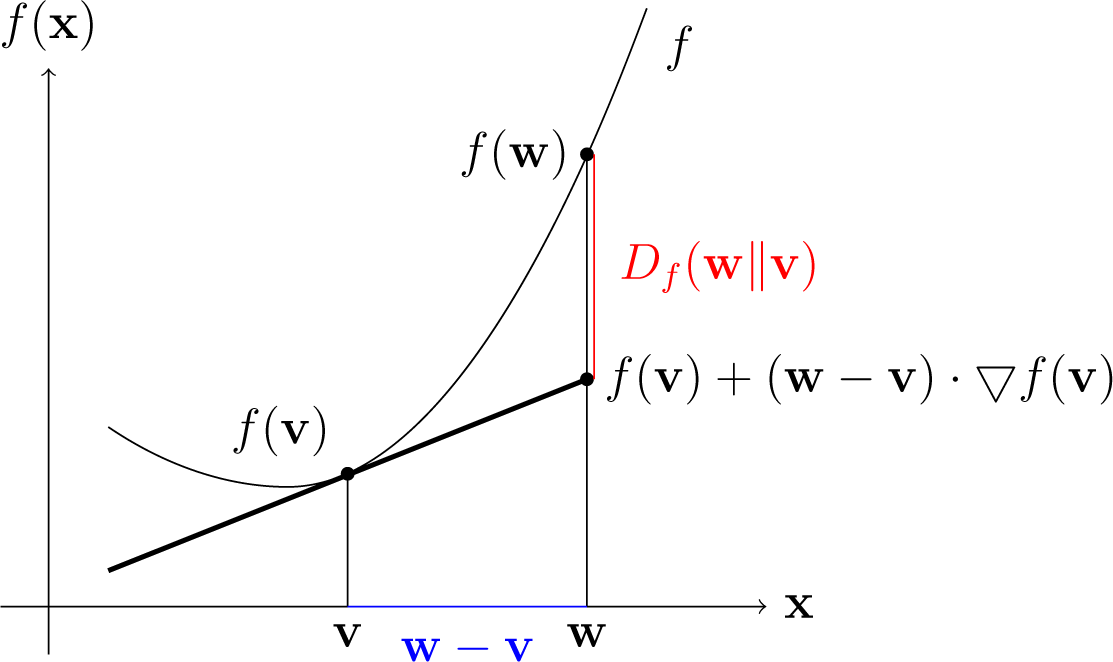2.2. Obdurate Operators
In this section, we approach averaging projective procedures using the framework of probabilistic knowledge merging as defined in [
5]. A probabilistic merging operator:
is a mapping that maps a finite collection of closed convex nonempty subsets of ⅅ
J, say
W1,…,
Wn, to a single closed convex nonempty subset of ⅅ
J. In the area of multi-expert reasoning, we can perhaps interpret ∆(
W1,…,
Wn) as a representation of
W1,…,
Wn, which themselves individually represent knowledge bases of
n experts.
A merging operator O is obdurate if, for every n ≥ 1 and any W1,…, Wn ⊆ ⅅJ, we have that
, where v is some fixed argument and F is an averaging projective procedure. Note that this operator always produces a singleton. Obdurate processes thus first represent sets as single probability functions, and then, they pool them by a pooling operator.
Although this may sound like a fairly restrictive setting, many existing natural probabilistic merging operators are of this form. The prominent example is the merging operator of Kern-Isberner and Rödder (
KIRP) [
23]. In this particular case,
v is the uniform probability function,
dv(·) is KL(·‖v) and Pool is given by:
Recall that
H(
w(i)) is the Shannon entropy of
w(i), which is, in fact, the most entropic point in
Wi.
In [
23], Kern-Isberner and Rödder argue that
W1,…,
Wn ⊆ ⅅ
J can by considered as marginal probabilities in a subset
U ⊆ ⅅ
J+n, such that every probability function
v ∈
U marginalizes to a ⅅ
J -probability function belonging to one and only one set
Wi. Since then, the point which
KIRP produces is, in fact, the ⅅ
J-marginal of the most entropic point in
U, following the justification of the Shannon entropy, they conclude that such a point is a natural interpretation of
W1,…,
Wn by a single probability function.
KIRP thus maps the uniform probability function to the ⅅ
J-marginal of the most entropic point in
U. To date,
KIRP has received much attention in the area of probabilistic knowledge merging.
However, any obdurate merging operator seems to be challenged by its violation of the following principle.
(CP) Consistency Principle. Let ∆ be a probabilistic merging operator. Then, we say that ∆ satisfies the consistency principle if, for every
n ≥ 1 and all
W1,…,
Wn ⊆ ⅅ
J:
(CP) can be interpreted as saying that if the knowledge bases of a set of experts are collectively consistent, then the merged knowledge base should not consist of anything else than what the experts agree on.
This principle often falls under the following philosophical criticism. One might imagine a situation where several experts consider a large set of probability functions as admissible, while one believes in a single probability function. Although this one is consistent with the beliefs of the rest of the group, one might argue that it is not justified to merge the knowledge of the whole group into that single probability function.
More rigorously, Williamson [
24] introduces a particular interpretation of the epistemological status of an expert’s knowledge base, which he calls “granting”. He rejects (CP), as several experts may grant the same piece of knowledge for inconsistent reasons.
On the other hand, Adamčík and Wilmers in [
5] assume that the way in which the knowledge was obtained is considered irrelevant, and each expert has incorporated all of his relevant knowledge into what he is declaring, contrary to Williamson’s granting. This is sometimes referred to as the principle of total evidence [
25] or the Watts assumption [
26]. They argue that, although overall knowledge of any human expert can never be fully formalized, as a formalization is always an abstraction from reality, the principle of total evidence needs to be imposed in order to avoid confusion in any discussion related to methods of representing the collective knowledge of experts. Otherwise, there would be an inexhaustible supply of invalid arguments produced by a philosophical opponent challenging one’s reasoning using implicit background information, which is not included in the formal representation of a knowledge base.
However, in this paper, we do not wish to probe further into this philosophical argument, and instead, we present the following rather surprising theorem, which appeared for the first time in [
10].
Theorem 5. There is no obdurate merging operator O that satisfies the consistency principle (CP).
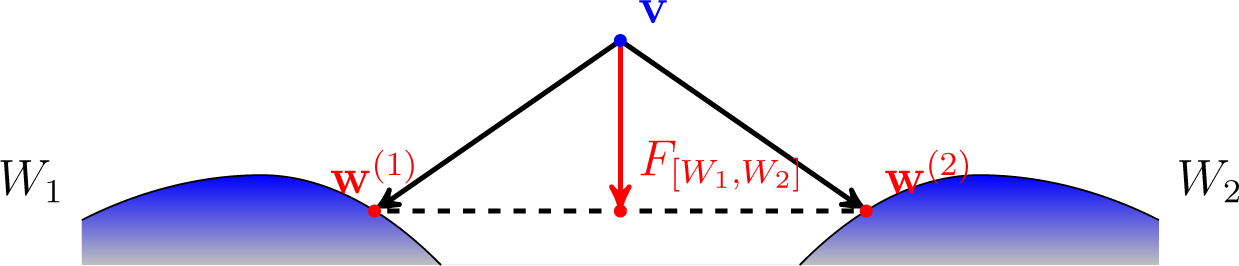
Proof. Suppose that J ≥ 3. Let d be the function to minimize from the definition of O, where, for simplicity, we suppress the constant superscript. Let v ∈ ⅅJ be the unique minimizer of d over some sufficiently large closed convex subset W of ⅅJ. Let w, u ∈ W be such that d(v) < d(w) < d(u) and w = λv + (1 − λ)u for some 0 < λ < 1 (in particular, w is a linear combination of v and u).
Let s ∈ W be such that d(v) < d(s) < d(w) and s is not a linear combination of v and u. Then, there is s′, such that s′ = λs + (1 − λ)w for some 0 < λ ≤ 1, and d is strictly increasing along the line from s′ to w. This is because d is strictly convex and d(s) < d(w). Note that if J = 2, then s would be always a linear combination of v and u. Moreover, for sufficiently large W ⊆ ⅅ3, we can always choose w, u, s and s′ in W as above.
Now, we show that
d is also strictly increasing along the line from
s′ to
u. Assume this is not the case. Then, by the same argument as before, there is
s″, such that
d(
s″) <
d(
s′). Due to the construction, the line from
v to
s″ intersects the line from
s′ to
w; let us denote the point of intersection as
r. Since
d is strictly increasing along the line from
s′ to
w, we have that
d(
r) >
d(
s′) >
d(
s″) >
d(
v). This, however, contradicts the convexity of
d. The situation is depicted in
Figure 5.
Now, assume that
W1 = {
λv + (1 −
λ)
w :
λ ∈ [0, 1]},
W2 = {
λs′ + (1 −
λ)
w :
λ ∈ [0, 1]},
V1 = {
λv + (1 −
λ)
u :
λ ∈ [0, 1]} and
V2 = {
λs′ + (1 −
λ)
u :
λ ∈ [0, 1]}. Since
v minimizes
d and along the lines from
s′ to
w and from
s′ to
u, the function
d is strictly increasing, we have that:
where
Pool is a pooling operator used in the second stage of
O. Suppose that
O satisfies (CP). Then,
O(
W1,
W2) = {
w} and
O(
V1,
V2) = {
u}, which contradicts
Equation (2).
The theorem above in some philosophical contexts can be used as an argument against the consistency principle, while from another perspective, it casts a shadow on the notion of an obdurate merging operator. This unfortunately includes the natural merging operator
OSEP, or obdurate social entropy process, defined as follows. For every
n ≥ 1 and all
W1,…,
Wn ⊆ ⅅ
J:
Recall that ME(
Wi) denotes the most entropic point in
Wi or equivalently the KL-projection of the uniform probability function into
Wi, and
is the family of weighting vectors
, one for every
n ≥ 1. It is easy to observe that OSEP is really an obdurate merging operator.
In [
10], it is proven that OSEP is (thus far, the only known) probabilistic merging operator satisfying a particular version of the independence principle, a principle that is an attempt to resurrect the notion of the independence preservation of pooling operators [
20] in the context of probabilistic merging operators.
One may say that the reason behind an obdurate merging operator not satisfying (CP) is its “forgetting” nature. In the first stage, it transforms sets W1,…, Wn into w(1),…, w(n) individually without taking into account other sets, thus “forgetting” any existing connections, such as the consistency. However, instead of changing the definition of an averaging projective procedure so as to make it not “forgetting”, we will take a different viewpoint on the procedure itself in the following subsection.
2.3. Fixed Points
Our second approach to an averaging projective procedure
F consists of considering the set of the fixed points of
F. That is, for given
n ≥ 1 and given closed convex nonempty sets
W1,…,
Wn ⊆ ⅅ
J, we are interested in whether there are any points
v ∈ ⅅ
J, such that:
Following the convincing justification for combining Bregman projections with the
-pooling operator (see Section 1.3), for every convex Bregman divergence
Df and a family of weighting vectors
, we consider here the averaging projective procedure
defined for every
n ≥ 1 and all closed convex nonempty sets
W1,…,
Wn ⊆ ⅅ
J by the following.
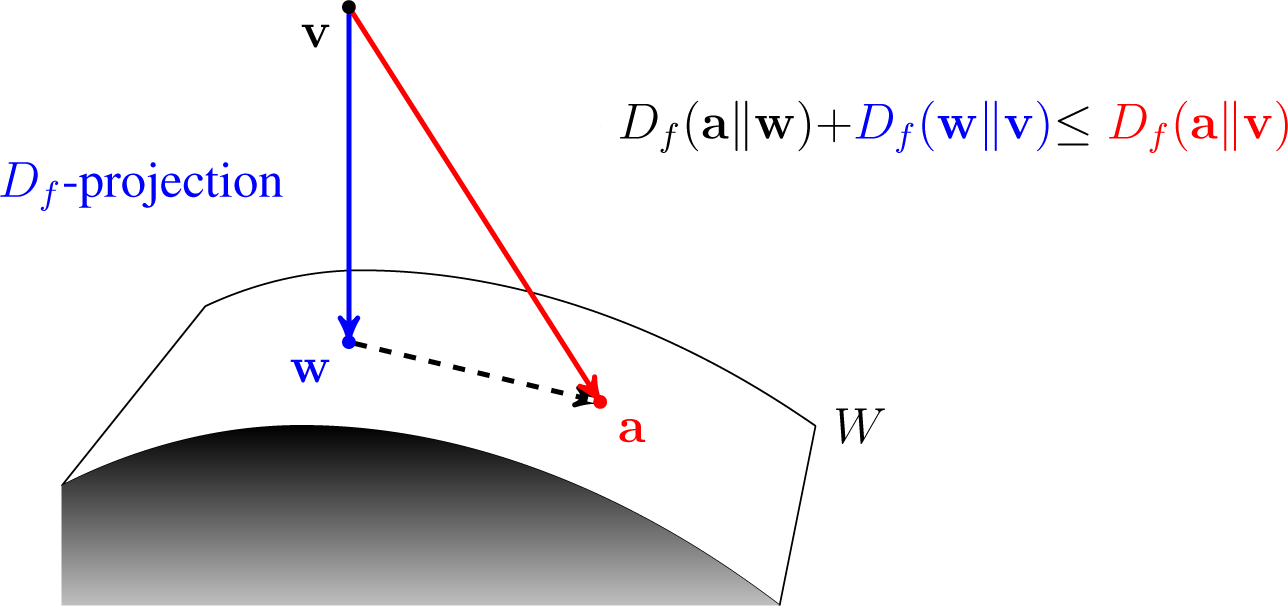
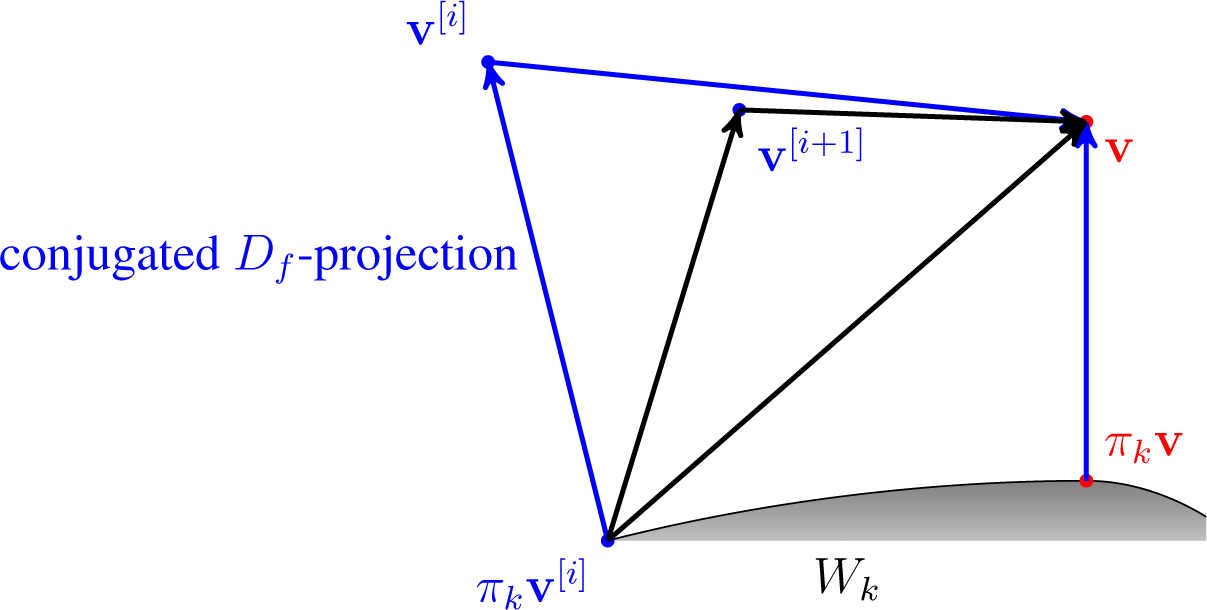
For an argument v ∈ ⅅJ, take w(i) the Df-projection of v into Wi for all 1 ≤ i ≤ n.
Set
, where a ∈
.
The restriction to convex Bregman divergences is needed for some later theorems and is adopted ad hoc. Therefore, unfortunately, we cannot provide any elaborate justification for it.
Given closed convex nonempty sets W1,…, Wn ⊆ ⅅJ, we will denote the set of all fixed points of
defined above by
, where a ∈
.
On the other hand, the conjugated parallelogram theorem (Theorem 4), suggesting the combination of the conjugated KL-projection with the LogOp-pooling operator, leads us to the consideration of those convex Bregman divergences, which are strictly convex also in the second argument. The squared Euclidean distance and the Kullback–Leibler divergence are instances of such divergences. A fairly general example is a Bregman divergence Df, such that
, where g is a strictly convex function (0, 1) → ℝ, which is three times differentiable, and g″(vj) − (wj − vj)g‴(vj) > 0 for all 1 ≤ j ≤ J and all w, v ∈ ⅅJ (this is easy to check by the Hessian matrix). Apart from the two divergences mentioned above, this condition is satisfied in particular if g(v) = vr, 2 ≥ r > 1. Note that the Bregman divergence generated by such a function g is also convex in both arguments.
Assuming strict convexity in the second argument of
Df, we can define the conjugated
Df-projection of
v ∈ ⅅ
J into a closed convex nonempty set
W ⊆ ⅅ
J as that unique
w ∈
W that minimizes ⅅ
f(
v‖w) subject only to
w ∈
W. Moreover, since a sum of strictly convex functions is a strictly convex function, for any
w(1),…,
w(n) ∈ ⅅ
J, there exists a unique minimizer of:
which we denote
. Thus, for a family of weighting vectors
, we can define the
-pooling operator. Note that
and that we do not need strict convexity in the second argument in these cases.
Theorem 6 (Conjugated Parallelogram Theorem).
Let Df be Bregman divergence,
ⅅ
J and a ∈ ⅅ
n. Then: Proof. Let
. We need to prove that:
or equivalently:
Since
, differentiation using the Lagrange multiplier method (since a differentiable convex function
f is necessarily continuously differentiable (see [
9]), the partial derivatives used above are all continuous and the Lagrange multiplier method is permissible) applied to the condition
produces
, where λ is a constant independent of
j. Therefore,
Equation (3) is equal to
, and the theorem follows.
The idea of defining a spectrum of pooling operators where the pooling operators LinOp and LogOp are special cases was developed previously in a similar manner, but in a slightly different framework of alpha-divergences;
cf. [
27].
Here, following [
1,
12], we will point out a geometrical relationship between pooling operators LinOp and Pool
Df, which will be helpful in illustrating some results of this paper.
Recall that the generator of a Bregman divergence Df is a strictly convex function f : (0, 1)J → ℝ, which is differentiable over ⅅJ. Let w ∈ ⅅJ. We define w∗ = ∇f(w). Since f is a strictly convex function, the mapping w → ∇ f (w) is injective; thus, the coordinates of w∗ form a coordinate system. There are two kinds of affine structures in ⅅJ. Df(w‖v) is convex in w with respect to the first structure and is convex in v∗ with respect to the second structure.
Therefore, the proof above, in fact, gives
, where
is a normalizing vector induced by
.
The only other type of averaging projective procedure
that we consider here will be generated by a convex differentiable Bregman divergence
Df, which is strictly convex in its second argument, and a family of weight
A and is defined for every
n ≥ 1 and all closed convex nonempty sets
W1,…,
Wn ⊆ ⅅ
J by the following.
For an argument v ∈ ⅅJ, take w(i) the conjugated Df-projection of v into Wi for all 1 ≤ i ≤ n.
Set
, where a ∈
.
Given closed convex nonempty sets W1,…, Wn ⊆ ⅅJ, we will denote the set of all fixed points of F^Df, A defined above by
, where a ∈
.
Note that we always require an additional assumption of Df being differentiable for this type of averaging projective procedure. This assumption is essential to the proofs of some results concerning this procedure. We note that both divergences KL and E2 are differentiable.
Given a family of weighting vectors
, our aim is to investigate
and
as operators acting on
. In particular, we ask the following questions. Given any closed convex nonempty sets
W1,…,
Wn ⊆ ⅅ
J and
a ∈
:
Are
and
always nonempty?
Are these sets always closed and convex?
If both answers are positive, then we can consider
and
as probabilistic merging operators. In such a case, the following question makes sense.
The fact that the answer to all three questions is “yes” is perhaps surprising, given that the much simpler obdurate merging operators do not satisfy (CP). We prove the above results in the following sequence of theorems, which conclude Section 2.
The following well-known lemma is a simple, but useful observation.
Lemma 1. Let Df be a Bregman divergence and a,
v,
w ∈ ⅅ
J. Then: Theorem 7. Let Df be a convex Bregman divergence, W1,…,
Wn ⊆ ⅅ
J be closed convex nonempty sets and a ∈ ⅅ
n. Let v,
w ∈ ⅅ
J,
u(1) ∈
W1,…,
u(n) ∈
Wn and w(1) ∈
W1,…,
w(n) ∈
Wn be such that v =
LinOpa (
u(1),…,
u(n)),
w =
LinOpa(
w(1),…,
w(n))
and u(i) are the Df-projection of v into Wi, 1 ≤
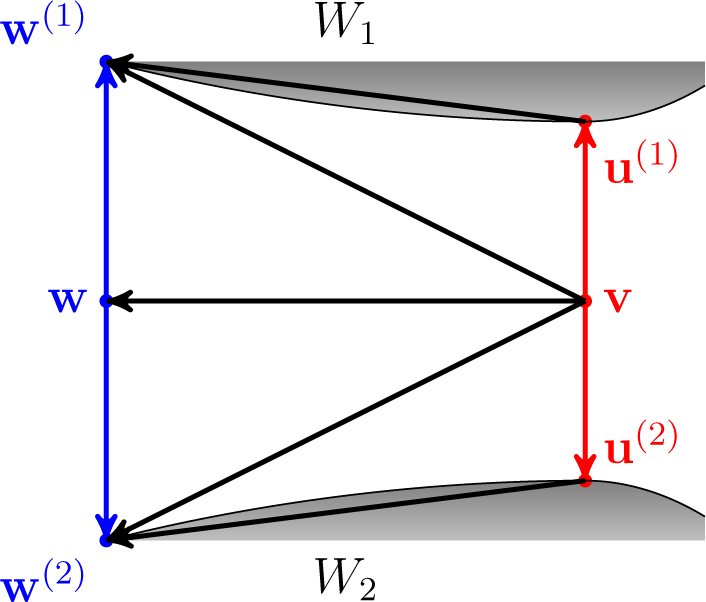
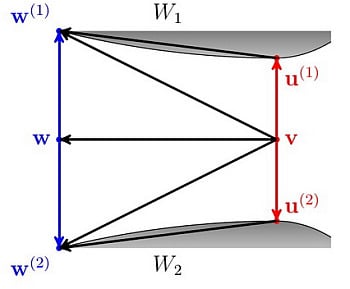
i ≤ n. Then: Proof. First of all, by the extended Pythagorean property, we have that:
By the parallelogram theorem:
Hence:
Since we assume that
Df(·‖·) is a convex function in both arguments by the Jensen inequality:
The Inequalities
(4) and
(5) give:
as required. □
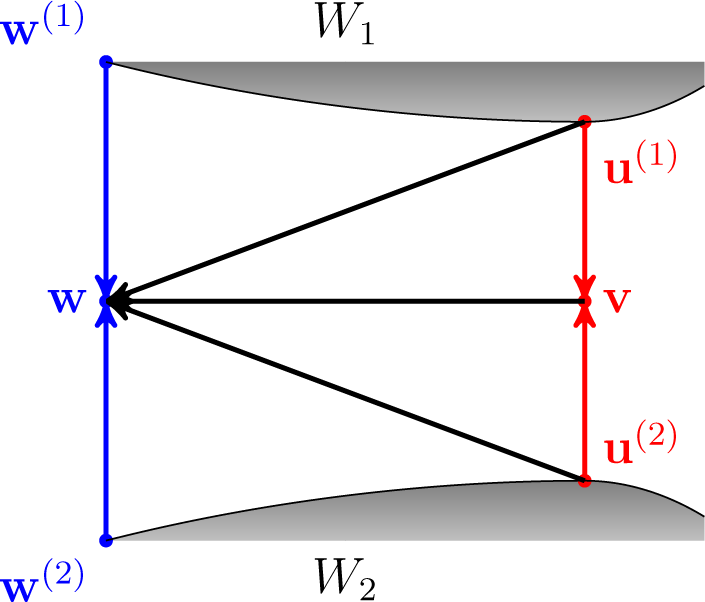
Figure 6 depicts the situation in the proof above for
n = 2. Arrows indicate corresponding divergences.
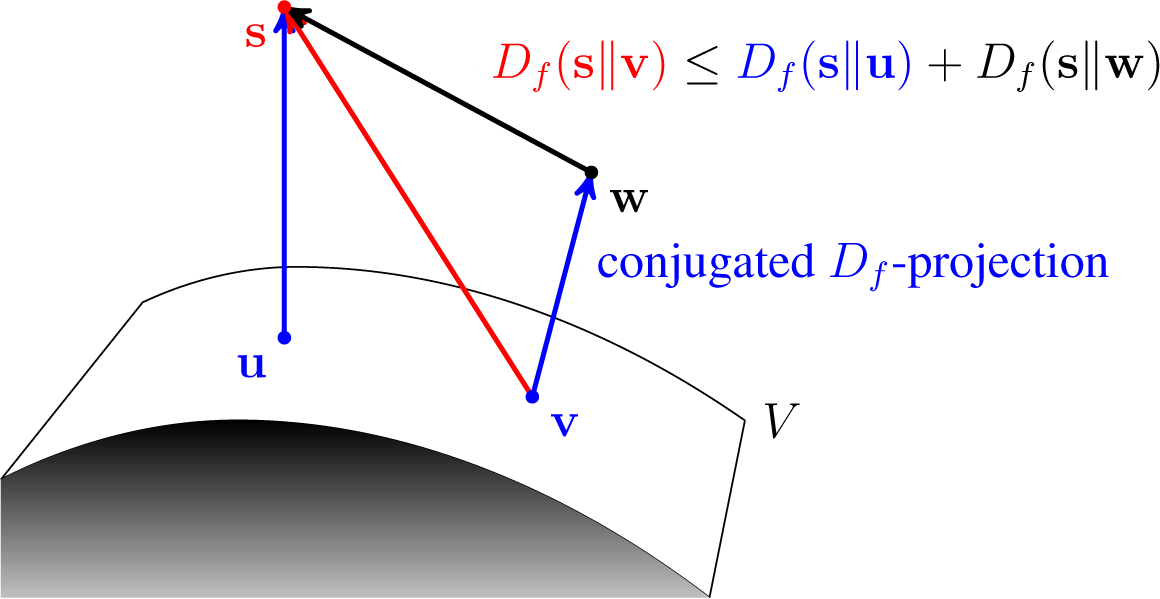
An interesting question related to conjugated Bregman projections arises as to whether a similar property to the Pythagorean property holds. It turns out that the corresponding property is the so-called four-point property, from to Csiszár and Tusnády. The following theorem in the case of the KL-divergence is a specific instance of a result in [
28], Lemma 3, but the formulation using the term “conjugated KL-projection” first appeared in [
21]. An illustration is depicted in
Figure 7.
Theorem 8 (Four-Point Property).
Let Df be a convex differentiable Bregman divergence, which is strictly convex in its second argument. Let V be a convex closed nonempty subset of ⅅ
J, and let v,
u,
w,
s ∈ ⅅ
J be such that v is the conjugated Df-projection of w into V and u ∈
V is arbitrary. Then: Proof. By Lemma 1, we have that:
We can rewrite the above as:
Since
Df(·‖·) is a convex differentiable function, by applying the first convexity condition twice, we have that:
Expressions
(6) and
(7) give that:
However, since
v is the conjugated
Df-projection of
w into
V, the gradient of
Df(
w‖·) at (
w,
v) in the direction to (
w,
u) must be greater than or equal to zero:
and the theorem follows. □
The following result appeared for the first time in [
10], but without considering the weighting.
Theorem 9 (Characterization Theorem for
).
Let Df be a convex Bregman divergence,
a ∈ ⅅ
n and W1,…,
Wn ⊆ ⅅ
J be closed convex nonempty sets. Then:where the right hand-side denotes the set of all possible minimizers. That is the set of all probability functions v ∈ ⅅ
J, which globally minimize,
subject only to w(1) ∈
W1,…,w
(n) ∈
Wn. Proof. It is easy to see that, given closed convex nonempty sets
W1,…,
Wn ⊆ ⅅ
J, we have that those
w(1) ∈
W1,…,
w(n) ∈
Wn, which together with
v ∈ ⅅ
J, globally minimize:
are also the
Df-projections of
v into
W1,…,
Wn respectively. This, together with
Equation (1) (the equation preceding Theorem 2), gives:
Now, assume that
and
Let us denote the
Df-projections of
v into
W1,…,
Wn by
w(1) …,
w(n), respectively. Accordingly, let us denote the
Df-projections of
u into
W1,…,
Wn by r
(1) …, r
(n), respectively. Suppose that
,
i.e.,
This contradicts Theorem 7, and therefore:
□
Let us now deviate for a while from the goals of this subsection and stress the importance of the restriction to the positive discrete probability functions, which was detailed in Section 1.1. The problem with the KL-divergence is that the function
is not differentiable if some
xj = 0. Without the adopted restriction, the KL-divergence is therefore usually defined by:
If
vj = 0 implies
wj = 0 for all 1 ≤
j ≤ J, we say that
v dominates
w and write
.
The first problem we would face with this definition is whether the notion of the KL-projection makes sense. For given v ∈ ⅅJ and closed convex nonempty set W ⊆ ⅅJ, the KL-projection of v into W makes sense only if there is at least one w ∈ W, such that
.
However, even if adding this condition to all of the discussion concerning the KL-projection above (this is perfectly possible, as seen in [
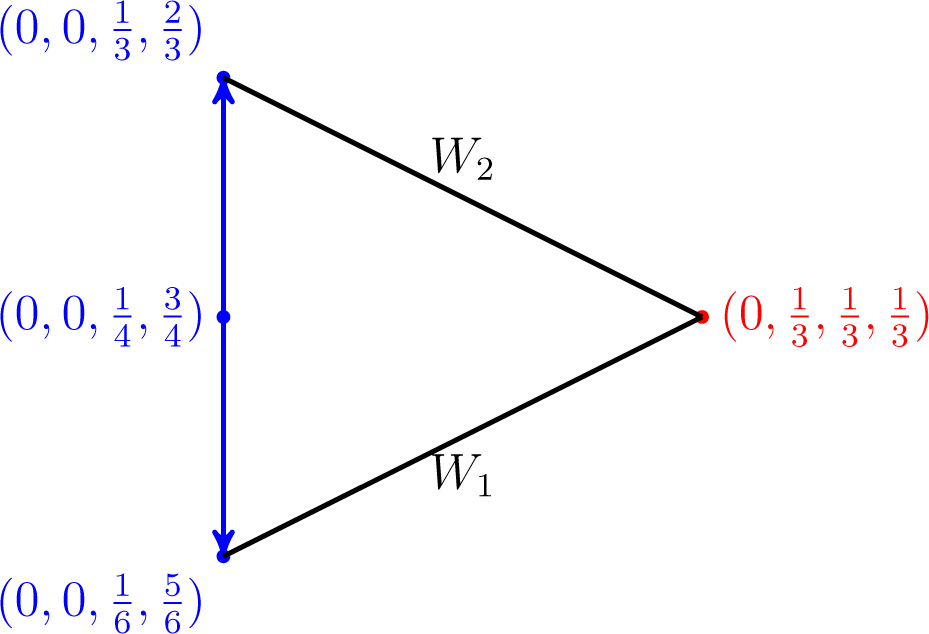
10]), Theorem 9 still could not hold, as the following example demonstrates.
Example 4. Let and.
Assume that It is easy to check that and are both fixed points, but the former does not belong to the set of global minimizers v of subject to w(1) ∈
W1 and w(2) ∈
W2.
An illustration is depicted in Figure 8.
Moreover, some variant of the above example would show that the set
is not convex, which would wreck our aims; more details are given in [
10].
On the other hand, neither of those Bregman divergences, which generate functions, are differentiable over the whole space of discrete probability functions (e.g., the squared Euclidean distance) and would encounter the difficulties of the KL-divergence. In particular, Theorem 9 formulated over the whole space of discrete probability functions (as opposed to only the positive ones) would still hold for such Bregman divergences.
Now, we shall go back and prove a theorem similar to Theorem 9 for the
-operator. In order to do that, we will need the following analogue of Theorem 7.
Theorem 10. Let Df be a convex differentiable Bregman divergence, which is strictly convex in its second argument, and let W1,…,
Wn ⊆ ⅅ
J be closed convex nonempty sets and a ∈ ⅅ
n. Let v,
w ∈ ⅅ
J and u(1) ∈
W1,…,
u(n) ∈
Wn and w(1) ∈
W1,…,
w n) ∈
Wn be such that,
and u(i) are the conjugated Df-projection of v into Wi, 1 ≤
i ≤ n. Then: Proof. By Theorem 6, we have that:
which by the four-point property (notice that we need the differentiability of
Df to employ the four-point property) (Theorem 8) becomes:
and hence:
as required, see
Figure 9. □
The theorem above is fairly similar to Theorem 7. Let us use the dual affine structure in ⅅJ defined after the proof of Theorem 6 to analyze this more closely. For W ⊂ ⅅJ, define W ∗ = {w∗; w ∈ W} and define the dual divergence
to the divergence Df by
. Since, by Theorem 6, we have that
, where
is a normalizing vector induced by
, the theorem above can be rewritten as follows.
Let
Df be a convex differentiable Bregman divergence, which is strictly convex in its second argument, and let
W1,…,
Wn⊆ ⅅ
J be closed convex nonempty sets and
a ∈ ⅅ
n. Let
v,
w ∈ ⅅ
J,
u(1)∈
W1,…, u
n) ∈
Wn and
w(1) ∈
W1.,…,
w(n)∈ Wn be such that v
∗ = LinOp ([u
(1)]
∗,…, [u
(n)]*) + c
v, w
∗ =
LinOpa([w
(1)]
∗ …, [w
(n)]
∗) + c
w and [u
(i)]
∗ are the
-projection of v
∗ into
, 1 ≤
i ≤
n. Then:
This illustrates that if Df is a convex differentiable Bregman divergence that is strictly convex in its second argument, then Theorems 7 and 10 are dual with respect to ∗.
Theorem 11 (Characterization Theorem for
.
Let Df be a convex differentiable Bregman divergence, which is strictly convex in its second argument, and let W1,…,
Wn ⊆ ⅅ
J be closed convex nonempty sets and a ∈ ⅅ
n. Then:where the right hand-side denotes the set of all possible minimizers. Proof. The proof is similar to the proof of Theorem 9. First, given closed convex nonempty sets
W1,…,
W ⊆ ⅅ
J, we have that those
w(1) ∈
W1,…,
w(n) ∈
Wn, which together with
v ∈ ⅅ
J, globally minimize:
that are also the conjugated
Df-projections of
v into
W1,…,
Wn, respectively. This together with the definition of
gives:
Second, assume that
and:
Let us denote the conjugated
Df-projections of
v into
W1,…,
Wn by
w(1),
…,
w(n), respectively. Accordingly, let us denote the conjugated
Df-projections of
u into
W1,…,
Wn by r
(1),
…, r
(n), respectively. Suppose that:
i.e.,
. This contradicts Theorem 10, and therefore:
□
The following simple observation originally from [
10] based on
Equation (1) (alternatively on the parallelogram theorem) will be used in the proof of the forthcoming theorem.
Lemma 2. Let Df be a convex Bregman divergence and a ∈ ⅅ
n. Then, the following are equivalent:The probability functions v,
w(1),…,
w(n) ∈ ⅅ
J minimize the quantity:subject to w(1) ∈
W1,…,
w(n) ∈
Wn. The probability functions w(1),…,
w(n) ∈ ⅅ
J minimize the quantity:subject to w(1) ∈
W1,…,
w(n) ∈
Wn and v =
LinOpa(
w(1),…,
w(n)).
Theorem 12. Let Df be a convex Bregman divergence. Then, for all nonempty closed convex sets W1,…, Wn ⊆ ⅅJ and a ∈ ⅅn, the set is a nonempty closed convex region of ⅅJ.
Proof. This proof is from [
10]. Let
v,
s ∈
, as the set is clearly nonempty. For convexity, we need to show that
λv + (1 −
λ)s ∈
for any λ ∈ [0, 1].
Assume that
w(1) ∈
W1,…,
w(n) ∈
Wn are such that
v =
LinOpa(
w(1),…,
w(n)) and
u(1) ∈
W1,…,
u(n) ∈
Wn are such that
s =
LinOpa(
u(1),…,
u(n)). It is easy to observe that the convexity of
Df(·
k·) implies convexity of:
Df( ‖ ) implies convexity of:
over the convex region specified by constraints x
(i) ∈
Wi, 1 ≤
i ≤
n. Moreover, the function
g attains its minimum over this convex region at points (
w(1),…,
w(n)) and (
u(1),…,
u(n)). We need to show that
g also attains its minimum at the point:
for any
λ ∈ [0, 1]. Since
g is convex by the Jensen inequality, we have that:
Since
g(
w(1),…,
w(n)) =
g(
u(1),…,
u(n)), the inequality above can only hold with equality, and therefore, by Lemma 2,
for any
λ ∈ [0, 1].
Moreover, since convexity implies continuity, the minimization of a convex function over a closed convex region produces a closed convex set. Therefore, the fact that W1,…, Wn are all closed and convex implies that the set of n-tuples (w(1),…, w(n)), which are global minimizers of g over the region specified by w(i) ∈ Wi, 1 ≤ i ≤ n, is closed. Additionally, since closed regions are preserved by projections in the Euclidean space, the set given by LinOpa(w(1),…, w(n)) is closed, as well.
The following observation immediately follows by the definition of
.
Lemma 3. Let Df be a convex Bregman divergence and a ∈ ⅅ
n. Then, the following are equivalent:The probability functions v,
w(1),…,
w(n) ∈ ⅅ
J minimize the quantity:subject to w(1) ∈
W1,…,
w(n) ∈
Wn.
The probability functions w(1),…,
w(n) ∈ ⅅ
J minimize the quantity:subject to w(1) ∈
W1,…,
w(n) ∈
Wn.and
Theorem 13. Let Df be a convex Bregman divergence. Then, for all nonempty closed convex sets W1,…, Wn ⊆ ⅅJ and a ∈ ⅅn, the set a nonempty closed convex region of ⅅJ.
Proof. Let v, s ∈
, as the set is clearly nonempty. For convexity, we need to show that λv + (1 − λ)s ∈
for any λ ∈ [0, 1].
Assume that
w(1) ∈
W1,…,
w(n) ∈
Wn are such that
and
u(1) ∈
W1,…,
u(n) ∈ Wn are such that
. Now, for any
λ ∈ [0, 1],
where the first inequality follows by convexity of
Df(·‖·) and the second by the definition of
as the unique minimizer. However, the inequality above can only hold with equality and, by Lemma 3,
for any
λ ∈ [0, 1].
Moreover, since convexity implies continuity, the minimization of a convex function over a closed convex region produces a closed convex set. Therefore, the fact that W1,…, Wn are all closed and convex implies that the set of n-tuples (w(1),…, w(n)), which are global minimizers of
over the region specified by w(i ∈ Wi, 1 ≤ i ≤ n, is closed. Additionally, since closed regions are preserved by projections in the Euclidean space, the set given by
is closed, as well. □
Finally, we can establish our initial claims:
Theorem 14. Let be a family of weighting vectors. The operator, where Df is a convex Bregman divergence, and the operator, where Df is a convex differentiable Bregman divergence, which is strictly convex in its second argument, are well defined probabilistic merging operators that satisfy (CP).
Proof. First, the fact that
is well defined as a probabilistic merging operator follows Theorems 9 and 12. Accordingly,
is a well-defined probabilistic merging operator by Theorems 11 and 13.
Second, let a ∈
(in particular a ∈ ⅅn) and W1,…, Wn ⊆ ⅅJ be closed, convex, nonempty and have a nonempty intersection. Clearly, every point in that intersection minimizes
and
subject to w(1) ∈ W1,…, w(n) ∈ Wn with both expressionsPattaining the zero value. Since Df(w‖v) = 0 only if w = v, those points in the intersection are the only points minimizing the above quantities. □
It turns out that, given closed convex nonempty sets
W1,…,
Wn ⊆ ⅅ
J and weighting a, the sets of fixed points
and
posses attractive properties, which make the operators
and
suitable for probabilistic merging. The following example taken from [
10] illustrates a possible philosophical justification for considering the set of all fixed points of a mapping consisting of a convex Bregman projection and a pooling operator.
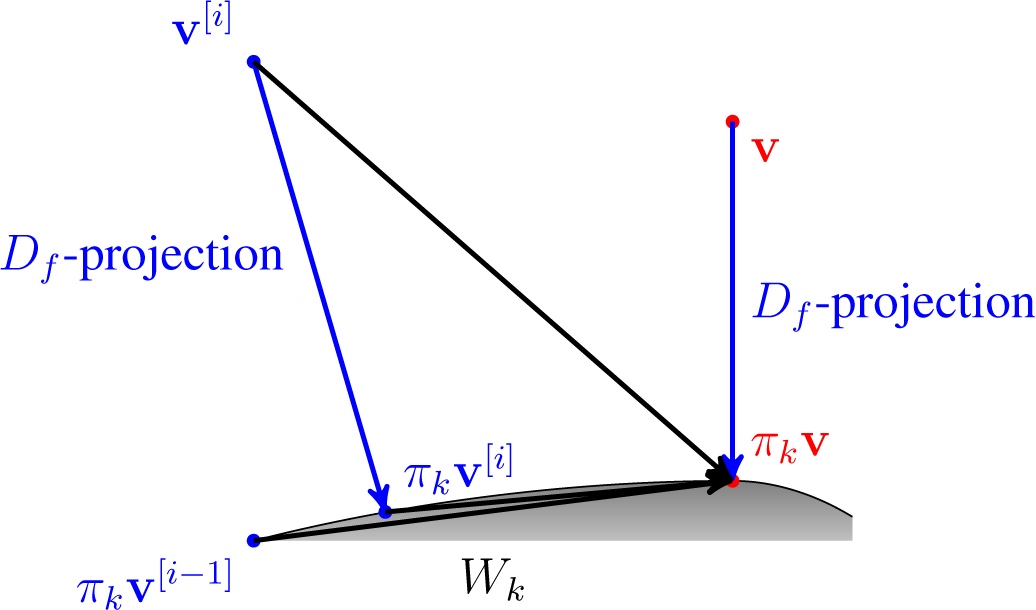
Example 5. Assume that there are n experts, each with his own knowledge represented by closed convex nonempty sets W1,…, Wn ⊆ ⅅJ, respectively. Say that an independent chairman of the college has announced a probability function v to represent the agreement of the college of experts. Each expert then naturally updates his own knowledge by what seems to be the right probability function. In other words, the expert “i” projects v to Wi, obtaining the probability function w(i). Each expert subsequently accepts w(i) as his working hypothesis, but he does not discard his knowledge base Wi; he only takes into account other people’s opinions. Then, it is easy for the chairman to identify the average of the actual beliefs w(1),…, w(n) of the experts. If he found that this average v′ did not coincide with the originally announced probability function v, then he would naturally feel unhappy about such a choice, so he would be tempted to iterate the process in the hope that, eventually, he will find a fixed point.
It seems that, in a broad philosophical setting, such as in the example above, we ought to study any possible combination of Bregman projections with pooling operators. The question as to which other combination produces a well-defined probabilistic merging operator satisfying the consistency principle (CP) is open to investigation.